압축 감지
Compressed sensing압축 감지(compressive sensing, 압축 샘플링 또는 희소 샘플링이라고도 함)는 덜 결정된 선형 시스템에 대한 솔루션을 찾아 신호를 효율적으로 획득하고 재구성하기 위한 신호 처리 기법이다.이는 최적화를 통해 신호의 첨단을 이용하여 나이키스트-샤논 샘플링 정리가 요구하는 것보다 훨씬 적은 샘플에서 신호를 복구할 수 있다는 원리에 근거한다.회복이 가능한 조건은 두 가지다.[1]첫 번째는 첨사성(sparsity)으로, 어떤 영역에서는 신호가 희박해야 한다.두 번째 것은 등축 성질을 통해 적용되는 불순성이다. 이는 희박한 신호에 충분하다.[2][3]null
개요
신호 처리 공학 분야의 공통 목표는 일련의 샘플링 측정에서 신호를 재구성하는 것이다.일반적으로 신호가 측정되지 않는 시간대에 신호를 재구성할 방법이 없기 때문에 이 작업은 불가능하다.그럼에도 불구하고 신호에 대한 사전 지식이나 가정을 통해 일련의 측정에서 신호를 완벽하게 재구성할 수 있는 것으로 밝혀진다(이 일련의 측정을 획득하는 것을 샘플링이라고 한다).시간이 지나면서 엔지니어들은 어떤 가정이 실용적이고 어떻게 일반화될 수 있는지에 대한 이해도를 향상시켰다.null
신호 처리의 초기 돌파구는 나이키스트-샤논 샘플링 정리였다.실제 신호의 최고 주파수가 샘플링 속도의 절반 이하일 경우 sinc 보간법을 통해 신호를 완벽하게 재구성할 수 있다는 것이다.주요 아이디어는 신호 주파수 제약에 대한 사전 지식으로 신호를 재구성하는 데 필요한 샘플 수가 적다는 것이다.null
2004년경, 에마뉘엘 칸데스, 저스틴 롬버그, 테렌스 타오, 데이비드 도노호 등은 신호의 첨사성에 대한 지식을 볼 때, 샘플링 정리가 요구하는 것보다 훨씬 적은 샘플로 신호를 재구성할 수 있다는 것을 증명했다.[4][5]이 생각은 압축감지의 기본이다.null
역사
압축감지는 L 기법에 의존하는데, 역사적으로 여러 다른 과학 분야가 이를 사용해 왔다.[6]통계에서 최소 제곱법은 라플레이스가 도입한 1 {\ L-norm로 보완되었다.선형 프로그래밍과 단치히의 심플렉스 알고리즘의 도입에 따라 1 -norm이 계산 통계에 사용되었다.통계학 이론에서 1 Lnorm은 조지 W. 브라운과 이후 작가들이 중위수 편중 추정기에 사용하였다.이것은 피터 J. 휴버와 다른 사람들이 사용했으며, 강력한 통계를 작성했다.L norm은 신호 처리에도 사용되었는데, 예를 들어 1970년대에 지진학자들이 나이키스트-샤논 기준을 만족하지 않는 것 같은 데이터에 기초하여 지구 내 반사층 이미지를 구축하였다.[7]1993년 매칭추격, 1996년[8] 로버트 티비시라니(Robert Tibshirani)의 LASSO 추정기, 1998년 베이시스추격에 사용되었다.[9]이러한 알고리즘이 희박한 솔루션을 복구한 시기를 설명하는 이론적 결과가 있었지만, 필요한 유형과 측정 횟수는 차선이었고, 그 후 압축 감지를 통해 크게 개선되었다.[citation needed]null
압축된 감지는 가장 높은 주파수가 아니라 해당 신호의 첨도에 따라 다르기 때문에 얼핏 보면, 압축된 감지가 샘플링 정리를 위반하는 것처럼 보일 수 있다.이것은 잘못된 생각이다, 왜냐하면 샘플링 정리는 필요한 조건이 아닌 충분한 조건을 주어 완벽한 재구성을 보장하기 때문이다.기존의 고정금리 샘플링과 근본적으로 다른 샘플링 방법은 샘플링 정리를 "위반"할 수 없다.고주파 성분을 가진 희소 신호는 기존의 고정 속도 샘플링에 비해 압축 감지를 사용해 고도로 과소 샘플링이 가능하다.[10]null
방법
결정되지 않은 선형 시스템
결정되지 않은 선형 방정식 시스템은 방정식보다 더 많은 미지수를 가지며 일반적으로 무한한 수의 해답을 가지고 있다.아래 그림은 에 대한 솔루션을 찾고자 하는 그러한 방정식 시스템을
그러한 시스템에 대한 해결책을 선택하기 위해서는 적절한 추가 제약이나 조건(평활도 등)을 부과해야 한다.압축 센싱에서는 극소수의 0이 아닌 계수를 갖는 용액만 허용하면서 첨탑성의 제약을 추가한다.결정되지 않은 모든 선형 방정식 시스템이 희박한 용액을 가지고 있는 것은 아니다.그러나 결정되지 않은 시스템에 고유한 희소성 솔루션이 있는 경우 압축 감지 프레임워크는 해당 솔루션을 복구할 수 있다.null
용액/재구성 방법

압축 감지 기능은 많은 흥미로운 신호에서 중복성을 활용한다. 즉, 순수한 노이즈가 아니다.특히 많은 신호는 희박하다. 즉, 일부 영역으로 표현했을 때 0에 가깝거나 같은 계수를 많이 포함하고 있다.[11]이것은 많은 형태의 손실 압축에 사용되는 것과 동일한 통찰력이다.null
압축 감지 기능은 일반적으로 신호가 희박하다고 알려진 기준과 다른 기준으로 압축 측정이라고도 하는 샘플의 가중 선형 조합을 취하는 것으로 시작한다.에마뉘엘 칸데스, 저스틴 롬버그, 테렌스 타오, 데이비드 도노호 등이 발견한 결과는 이러한 압축 측정치의 수가 적을 수 있고 여전히 거의 모든 유용한 정보를 포함하고 있다는 것을 보여주었다.따라서 이미지를 의도된 영역으로 다시 변환하는 작업은 전체 영상의 압축 측정 횟수가 픽셀 수보다 적기 때문에 결정되지 않은 매트릭스 방정식을 해결하는 것을 포함한다.그러나 초기 신호가 희박하다는 제약조건을 추가하면 이 미결정된 선형 방정식 시스템을 해결할 수 있다.null
이러한 문제에 대한 최소한의 해결책은 L 표준, 즉 시스템의 에너지 양을 최소화하는 것이다.이것은 보통 수학적으로 간단하다(표본 추출한 기초의 의사-반복에 의한 행렬 곱셈만 포함).그러나 이는 많은 실제 적용에서 좋지 않은 결과를 초래하며, 알 수 없는 계수가 0이 아닌 에너지를 갖는다.null
결정되지 않은 선형 방정식 시스템에 대해 해결할 때 첨경도 제약을 적용하기 위해 용액의 0이 아닌 성분 수를 최소화할 수 있다.벡터의 0이 아닌 성분의 수를 계산하는 함수를 데이비드 도노호(David Donohohoho)에 L 0{\L^{ "norm"이라고 불렀다.[note 1]null
Candes 외 연구진은 많은 문제에서 L 표준이 L 표준과 동일할 가능성이 있다고 입증했다.이 동등성 결과를 L } 문제를 해결할 수 있는데, 이는 L L 문제보다 쉽다.가장 L 1 규격을 가진 후보를 찾는 것은 효율적인 솔루션 방법이 이미 존재하는 선형 프로그램으로 비교적 쉽게 표현할 수 있다.[13]측정치에 제한된 양의 노이즈를 포함할 수 있는 경우, 소음 면에서의 가시성을 보존하고 정확한 선형 프로그램보다 빠르게 해결할 수 있기 때문에 선형 프로그래밍보다 기본 추적 디노잉이 선호된다.null
총 변동 기반 CS 재구성
동기 부여 및 적용
TV 정규화의 역할
총변동치는 실제값 함수의 공간(한 변수의 함수의 경우)이나 통합 가능한 함수의 공간(여러 변수의 함수의 경우)에 정의된 비음수 실질값 함수로 볼 수 있다.특히 신호의 경우, 총 변동은 신호의 절대 경사도의 적분을 가리킨다.신호와 영상 재구성의 경우, 과도한 디테일을 가진 신호의 총변동이 높고 이러한 디테일을 제거하면서 에지 등 중요한 정보를 유지하면 신호의 총변동을 줄이고 신호 대상을 보다 가깝게 만드는 것이 기본 원칙인 총변동 정규화로 적용된다.o 문제의 원래 신호null
신호 및 영상 재구성을 위해 1 최소화 모델을 사용한다.다른 접근법도 이 기사에서 이전에 논의한 것과 같은 최소 제곱을 포함한다.이 방법들은 극도로 느리고 그다지 완벽하지 않은 신호 재구성을 되돌려준다.현재의 CS 정규화 모델은 원본 이미지의 첨사성 이전(sparsity prior)을 통합하여 이 문제를 해결하려고 시도하는데, 그 중 하나가 총변동(TV)이다.종래의 TV 접근법은 조각처럼 일정한 해결책을 제공하도록 설계되었다.이들 중 일부는 (앞서 논의한 바와 같이) 반복적인 계획을 사용하는 제한된 l1-minimization을 포함한다.이 방법은 빠르기는 하지만 결과적으로 가장자리가 지나치게 스무팅되어 이미지 가장자리가 흐려지게 된다.[14]영상에서 큰 구배 값 크기의 영향을 줄이기 위해 반복적인 재가중 방식을 구현했다.이는 에지 보존 총 변동으로 알려진 방법으로 컴퓨터 단층 촬영(CT) 재구성에 사용되어 왔다.단, 데이터 충실도와 정규화 조건 사이의 상대적 페널티 가중치 추정에 구배 크기가 사용되므로 이 방법은 소음과 아티팩트에 강하지 않고 CS 영상/신호 재구성에 충분히 정확하지 않아 보다 작은 구조물을 보존하지 못한다.null
이 문제에 대한 최근의 진전은 CS 재건을 위해 반복적으로 방향성을 갖는 TV의 정교함을 사용하는 것을 포함한다.[15]이 방법에는 두 가지 단계가 있다. 첫 번째 단계는 주어진 이미지의 초기 방향 필드를 추정하고 다듬는 것이다. 즉, 가장자리 탐지를 통해 시끄러운 점별 초기 추정치로 정의된다.2단계에서는 방향성 TV 레귤레이터를 활용해 CS 재구성 모델을 제시한다.이러한 TV 기반 접근법 - 반복적으로 재가중된 l1 최소화, 방향 방향 분야와 TV를 사용한 가장자리 보존 TV 및 반복 모델 -에 대한 자세한 내용은 다음과 같다.null
기존 접근 방식
으로 l } 최소화
제한된 } 최소화를 사용하는 CS 재구성 모델에서는 l } 표준에서 더 큰 계수가 크게 불이익을 받는다.[16]0이 아닌 계수를 더욱 민주적으로 처벌할 수 있도록 된 l 1{\1} 최소화의 가중 공식화를 제안하였다.반복 알고리즘은 적절한 가중치를 구성하는데 사용된다.[17]각 반복마다 }의 정규와 더 가까운 오목한 벌칙 함수의 국소 최소값을 찾아내어 하나의 l 1 최소화 문제를 해결해야 한다.일반적으로 패널티 함수 곡선의 급격한 전환을 방지하기 위해 추가 모수를 반복 방정식에 도입하여 안정성을 보장하고 한 반복에서 0 추정치가 반드시 다음 반복에서 0 추정치로 이어지는 것은 아니다.그 방법은 다음 반복에서 사용될 가중치를 계산하기 위해 기본적으로 현재의 솔루션을 사용하는 것을 포함한다.null
장단점
초기에 반복하면 부정확한 표본 추정치를 발견할 수 있지만, 이 방법은 더 작은 0이 아닌 신호 추정치에 더 많은 가중치를 부여하기 위해 나중에 표본 추정을 하향 표본화할 것이다.단점 중 하나는 함수의 결함으로 인해 매번 글로벌 최소값을 얻지 못할 수 있으므로 유효한 출발점을 정의할 필요가 있다는 것이다.또 다른 단점은 이 방법이 기본 영상 구조와 관계없이 영상 구배를 균일하게 불이익을 주는 경향이 있다는 것이다.이는 특히 저대조 영역의 가장자리의 과도한 스무팅을 야기하여 결과적으로 저대조도 정보의 상실을 초래한다.이 방법의 장점은 희박한 신호에 대한 샘플링 속도 감소, 노이즈 및 기타 아티팩트의 제거에 강건한 상태에서 영상 재구성, 극소수의 반복 사용 등이다.이것은 또한 그라데이션이 희박한 영상을 복구하는 데도 도움이 될 수 있다.null
아래 그림에서 P1은 데이터 충실도 용어에 의해 제약되는 팬빔 기하학의 투영 매트릭스 P의 반복재건 프로세스의 첫 번째 단계를 가리킨다.여기에는 정규화가 수행되지 않으므로 노이즈 및 아티팩트가 포함될 수 있다.P1 최소화는 공차 구배 최소 제곱법을 통해 해결된다.P2는 가장자리 보존 총변동 정규화 용어를 사용하여 노이즈 및 아티팩트를 제거함으로써 재구성된 영상/신호의 품질을 개선하는 반복 재구성 프로세스의 두 번째 단계를 말한다.P2의 최소화는 간단한 구배 강하법을 통해 이루어진다.수렴이란 반복될 때 잔상 긍정에 테스트를 통해서 f − 1=0{\displaystyle f^{k-1}=0 k 때 fk− 1<>} 같은 경우는;0{\displaystyle f^{k-1}<를 확인하여;0}( 다른 x-ray선형 감쇠 계수에 우편의 다른 voxels에서 f{\displaystyle f}참조합니다 결정된다atient 이미지).null
에지 보존형 총 가변성(TV) 기반 압축 감지
이것은 저선량 CT에서 얻은 고도로 과소 샘플링된 데이터에서 낮은 전류 수준(밀리암페어)을 통해 CT 영상을 재구성하기 위해 가장자리 보존 TV 정규화가 적용된 반복 CT 재구성 알고리즘이다.영상 선량을 줄이기 위해 사용되는 접근법 중 하나는 스캐너 검출기가 획득한 X선 투영 횟수를 줄이는 것이다.그러나 CT 영상을 재구성하는 데 사용되는 투영 데이터가 불충분할 경우 줄무늬가 있는 아티팩트가 발생할 수 있다.더욱이 표준 TV 알고리즘에서 이러한 불충분한 예측을 사용하는 것은 결국 문제를 충분히 결정하지 못하고, 따라서 무한히 많은 가능한 해결책으로 이끈다.이 방법에서는 원래의 TV 규범에 추가적인 패널티 가중 기능이 할당된다.이를 통해 영상의 강도에 있는 날카로운 불연속부를 보다 쉽게 감지할 수 있으며, 따라서 신호/이미지 재구성 과정에서 중량을 조정하여 복구된 에지 정보를 저장할 수 있다.매개 변수 은 가장자리에 있는 픽셀에 적용되는 평활화 양을 제어하여 에지가 아닌 픽셀과 구별한다. 의 값은 그라데이션 규모 히스토그램 값을 기반으로 적응적으로 변경되어 픽셀의 특정 비율이 보다 크도록 한다 따라서 에지 보존 총 변동 기간은 더욱 가파르게 되어 구현 속도가 빨라진다.전방-후방 분할 알고리즘으로 알려진 2단계 반복 프로세스가 사용된다.[18]최적화 문제는 두 개의 하위 문제로 나뉘는데, 이 두 문제는 각각 결합 구배 최소 제곱법과[19] 단순 구배 강하법으로 해결된다.원하는 수렴을 달성했거나 최대 반복 횟수에 도달하면 메소드가 중지된다.[14]null
장단점
이 방법의 단점으로는 재구성된 영상에 작은 구조물이 없고 영상 분해능의 저하 등이 있다.그러나 TV 알고리즘을 보존하는 이 에지는 기존 TV 알고리즘보다 반복 횟수가 적다.[14]재구성된 영상의 수평 및 수직 강도 프로파일을 분석하면, 가장자리 지점에서는 날카로운 점프가, 가장자리 지점에서는 무시할 수 있는 사소한 변동이 있음을 알 수 있다.따라서 이 방법은 TV 방식에 비해 상대적 오류가 낮고 상관관계가 높은 것으로 이어진다.또한 줄무늬와 같은 영상 노이즈와 영상 아티팩트를 효과적으로 억제하고 제거한다.null
방향 방향장 및 방향 총변동을 이용한 반복모델
가장자리와 텍스처 디테일의 과도한 스무팅을 방지하고 노이즈와 아티팩트에 정확하고 견고한 재구성된 CS 영상을 얻기 위해 이 방법을 사용한다.먼저 이미지 의 점별 방향 필드의 초기 추정치를 구한다.이 노이즈 방향 필드는 방향 필드 추정에 대한 노이즈 영향을 줄이기 위해 나중에 조정할 수 있도록 정의된다.한 거친 오리엔테이션 현장 평가 이후로 공식화 해지는 구조 텐서에 의거한[20]J((나는 σ ∇))Gρ ∗(∇ 나는 σ ∇ 나는 ⊗ σ))(J11J12J12J22){\displaystyle J_{\rho}(\nabla I_{\sigma})=G_ᆯ*(\nabla I_{\sigma}\otimes\nabla I_{\sigma})={\begin{pma 소개됩니다.트라이J_{12}&.표준 편차를 가지고 있는 ρ{\displaystyle \rho}. G{G\displaystyle}은 가우스 커널{\displaystyle(0,\rho ^{2})}표준 편차(0,ρ 2)을 말한다 J_{22}\end{pmatrix}}}. 여기, J({\displaystyle J_{\rho}}은 구조 텐서 이미지 픽셀 점과 관련된(i,j) 말한다. . 은(는) 이미지 에 대해 수동으로 정의된 매개 변수를 말하며, 이 매개 변수는 에지 감지가 노이즈에 무감각한 경우 입니다. refers to the gradient of the image and refers to the tensor product obtained by using this gradient.[15]null
얻어진 구조 텐서는 방향 추정치의 를 개선하기위해 커널 G {\G}과(와) 융합되며, }은(는 알 수 없는 소음 수준을 감안하여 높은 값으로 설정된다.영상의 모든 픽셀(i,j)에 대해 구조 텐서 J는 대칭적이고 양의 반확정 행렬이다. 로 영상의 모든 픽셀을 조합하면 J {\ 매트릭스의 직교 고유 벡터 Ω 및 υ이 제공된다.대비가 가장 큰 지배적 방향의 Ω 포인트와 대비가 가장 작은 구조물 방향의 υ 포인트. 필드 거친 초기 추정 d {\d는) = 으로 정의된다.이 추정치는 가장자리가 강할 때 정확하다.그러나 약한 가장자리나 노이즈가 있는 지역에서는 신뢰성이 떨어진다.null
이러한 단점을 극복하기 위해 데이터 항이 노이즈의 영향을 줄이고 정확도를 향상시키는 정제된 방향 모델을 정의하고, L2-규격을 가진 두 번째 벌칙 항은 초기 거친 추정의 정확성을 보장하는 충실도 항이다.null
This orientation field is introduced into the directional total variation optimization model for CS reconstruction through the equation: 은(는) 복구해야 할 목표 신호다.Y는 해당 측정 벡터, d는 반복 정제 방향 필드, 은(는) CS 측정 매트릭스다.이 방법은 궁극적으로 몇 번의 반복을 거쳐 수렴을 유도한다. 는 이전 반복에서 재구성된 - 1 X의 대략적인 방향 필드 추정(융합 및 후속 광학적 성능을 확인하기 위해 previ).ous 반복을 사용한다.X 및 d 로 표시된 두 벡터 필드의 경우 { 은 X 및 d}의 각 수평 수직 벡터 원소의 곱셈을 의미한다.부차적인 덧셈이러한 방정식은 일련의 볼록 최소화 문제로 축소되며, 이후 가변 분할과 증강 라그랑지안(폐쇄형 폼 솔루션이 있는 FFT 기반 고속 해결사) 방법의 조합으로 해결된다.[15]It (증강된 라그랑지안)은 이 방법의 정합성을 보장하는 분할 Bregman 반복과 동등한 것으로 간주된다.방향 필드, d는( h, v ){\과(와) 같은 것으로 정의된다. 서 h, v 의 수평 및 수직 추정치를
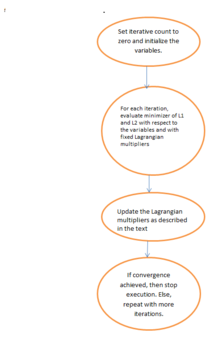
The Augmented Lagrangian method for the orientation field, , involves initializing 을(를) 선택한 다음 이러한 변수에 대한 }의 대략적인 최소값을 찾는다.그런 다음 라그랑비아 승수를 업데이트하고 수렴이 달성되면 반복 과정을 중단한다.반복적 방향 총변화 미세화 모델의 경우, 증강 래그랑지안 방법은 , , , , {, Q를 초기화하는 것을 포함한다[21]
Here, are newly introduced variables where = , = , = , and = . are the Lagrangian multipliers for . For each iteration, the approximate minimizer of with respect to변수(, , Q 를 계산한다.그리고 현장 미세화 모델에서와 같이 라그랑고 승수가 업데이트되고 정합화가 달성되면 반복 프로세스가 중단된다.null
오리엔테이션 필드 정제 모델의 경우 다음과 같이 반복 프로세스에서 라그랑지안 승수가 업데이트된다.
반복 방향 총변동 미세화 모델의 경우 다음과 같이 라그랑주 승수가 업데이트된다.
여기서 H, V , , Q 는 양의 상수다.null
장단점
피크 신호 대 잡음 비(PSNR)와 구조 유사도 지수(SSIM) 지표와 시험 성능을 위한 알려진 지상 진실 영상에 기초하여, 반복 방향 총 변동은 가장자리 및 질감 영역을 보존하는 비 반복 방법보다 재구성 성능이 우수하다는 결론을 내렸다.오리엔테이션 필드 미세화 모델은 가장자리가 있는 영역의 오리엔테이션 필드 일관성을 향상시키면서 평탄한 영역의 방향 없는 픽셀 수를 증가시키기 때문에 이러한 성능 향상에 큰 역할을 한다.null
적용들
압축 감지 분야는 신호 처리 및 계산 수학의 몇 가지 주제(예: 덜 결정된 선형 시스템, 그룹 테스트, 강타자, 희소 코딩, 멀티플렉싱, 희소 샘플링, 유한 혁신률)와 관련이 있다.그것의 넓은 범위와 일반성은 신호 처리와 압축, 역문제의 해결, 복사 시스템 설계, 레이더와 벽면 투과 영상화, 안테나 특성화에서 CS 강화 접근법을 몇 가지 혁신적으로 가능하게 했다.[22]압축감지와 강한 친화력을 갖는 영상 기법에는 코드화된 개구부와 컴퓨터 사진 촬영이 포함된다.null
기존 CS 재구성은 제한된 } 최소화를 통한 재구성에 희박한 신호(일반적으로 나이키스트 샘플링 속도보다 낮은 속도로 샘플링)를 사용한다.그러한 접근법의 초기 적용 중 하나는 표면 아래층 사이의 변화를 추적하기 위해 대역 제한 데이터의 희박한 반사 신호를 사용한 반사 지진학이었다.[23]1990년대에 희소성 모델의 선택을 위한 통계적 방법으로 LASSO 모델이 부각되었을 때,[24] 이 방법은 과완성 사전에서 희소성 신호 표현을 위한 계산 고조파 분석에서 더 많이 사용되었다.다른 응용 프로그램 중 일부는 레이더 펄스의 일관성 없는 샘플링을 포함한다.보이드 외 연구원의 작품.[16]희소성 모델 선택을 위해 아날로그-디지털 변환기(현재 변환기는 정량화된 섀넌 표현과 함께 나이키스트 속도보다 높은 샘플링 속도를 사용함)를 위해 LASSO 모델을 적용했다.여기에는 아날로그 신호의 극성이 높은 속도로 변화한 후 변환된 디지털 신호를 얻기 위해 각 시간 간격의 끝에 적분을 디지털화하는 병렬 아키텍처가 포함될 수 있다.null
사진
휴대전화 카메라 센서에는 압축 센싱이 사용된다.이 접근방식은 복잡한 감압 알고리즘의 비용으로 이미지당 이미지 획득 에너지를 15배만큼 감소시킬 수 있다. 계산에는 오프 디바이스 구현이 필요할 수 있다.[25]null
압축 센싱은 라이스 대학교의 싱글 픽셀 카메라에 사용된다.[26]벨랩스는 이 기술을 렌즈 없는 싱글픽셀 카메라에 적용했는데, 이 카메라는 그리드에서 임의로 선택한 구멍의 반복된 스냅샷을 사용하여 스틸을 촬영했다.이미지 품질은 스냅샷의 수에 따라 향상되며, 일반적으로 렌즈/초점 관련 이상을 제거하면서 기존 이미징의 데이터의 작은 부분을 필요로 한다.[27][28]null
홀로그래피
압축 센싱은 단일 홀로그램에서 유추할 수 있는 복셀 수를 늘려 홀로그래피에서 영상 재구성을 개선하는 데 활용할 수 있다.[29][30][31]광학[32][33] 및 밀리미터파[34] 홀로그래피에서 과소 샘플링된 측정에서 영상 검색에도 사용된다.null
안면인식
얼굴 인식 애플리케이션에는 압축 감지가 사용되어 왔다.[35]null
자기공명영상
압축 감지 기능은 기존 하드웨어에서 자기 공명 영상 스캔 세션을 단축하는 데 사용되어[36][37] 왔다.[38][39][40]재구성 방법에는 다음이 포함된다.
압축 감지 기능은 더 적은 푸리에 계수를 측정하여 더 빠른 획득을 가능하게 함으로써 높은 스캔 시간 문제를 해결한다.이는 상대적으로 스캔 시간이 짧은 고화질 이미지를 연출한다.또 다른 애플리케이션(앞에서도 논의)은 X선 투영 횟수가 적은 CT 재구성을 위한 것이다.이 경우 압축 감지는 높은 공간 구배 부분(주로 영상 노이즈 및 아티팩트)을 제거한다.이는 낮은 전류-mA 설정을 통해 낮은 방사선량에서 고해상도 CT 영상을 얻을 수 있기 때문에 엄청난 잠재력을 가지고 있다.[44]null
네트워크 단층 촬영
압축 감지는 네트워크 관리에 네트워크 단층촬영을 적용하는 데 탁월한 성과를 보였다.네트워크 지연 추정과 네트워크 정체 감지는 모두 계수 행렬이 네트워크 라우팅 매트릭스인 선형 방정식의 과소 결정된 시스템으로 모델링할 수 있다.더욱이, 인터넷에서는, 네트워크 라우팅 매트릭스는 보통 압축 센싱의 사용 기준을 만족시킨다.[45]null
단파 적외선 카메라
2013년에 한 회사는 압축 감지를 활용한 단파 적외선 카메라를 발표했다.[46]이 카메라는 0.9 µm에서 1.7 µm의 빛 민감도로 사람의 눈에는 보이지 않는 파장을 가지고 있다.null
애퍼처 합성 천문학
전파천문학과 광학천문 간섭계에서는 푸리에 평면의 완전한 커버리지가 일반적으로 없고 대부분의 하드웨어 구성에서 위상 정보를 얻지 못한다.조리개 합성 영상을 얻기 위해 다양한 압축 감지 알고리즘이 사용된다.[47]ö돔 CLEAN 알고리즘은 1974년부터 라디오 인터페로미터에서 얻은 영상의 재구성을 위해 사용되어 왔으며, 이는 위에서 언급한 일치추구 알고리즘과 유사하다.null
전송전자현미경
이동 간극과 결합된 압축 감지는 전송 전자 현미경에서 이미지의 획득률을 높이기 위해 사용되어 왔다.[48]스캐닝 모드에서는 전자빔의 무작위 스캐닝과 결합된 압축 감지가 전자빔에 민감한 물질의 이미징을 가능하게 하는 획득과 전자선량 감소 모두를 가능하게 했다.[49]null
참고 항목
메모들
참조
- ^ CS: 압축 유전자형, DNA Sudoku – 멀티플렉스 시료 분석을 위한 높은 처리량 시퀀싱 활용.
- ^ Donoho, David L. (2006). "For most large underdetermined systems of linear equations the minimal 1-norm solution is also the sparsest solution". Communications on Pure and Applied Mathematics. 59 (6): 797–829. doi:10.1002/cpa.20132. S2CID 8510060.
- ^ M. Davenport, 2013년 4월 12일 "압축 센싱의 기초" SigView.
- ^ Candès, Emmanuel J.; Romberg, Justin K.; Tao, Terence (2006). "Stable signal recovery from incomplete and inaccurate measurements" (PDF). Communications on Pure and Applied Mathematics. 59 (8): 1207–1223. arXiv:math/0503066. Bibcode:2005math......3066C. doi:10.1002/cpa.20124. S2CID 119159284. Archived from the original (PDF) on 2012-03-11. Retrieved 2011-02-10.
- ^ Donoho, D.L. (2006). "Compressed sensing". IEEE Transactions on Information Theory. 52 (4): 1289–1306. doi:10.1109/TIT.2006.871582. S2CID 206737254.
- ^ Vivek Goyal, Alyson Fletcher, Sundeep Rangan, The Feginal Bayesian의 L1 정규화 아이디어 목록: 압축감지의 복제본 방법 분석
- ^ Hayes, Brian (2009). "The Best Bits". American Scientist. 97 (4): 276. doi:10.1511/2009.79.276. S2CID 349102.
- ^ Tibshirani, Robert. "Regression shrinkage and selection via the lasso". Journal of the Royal Statistical Society, Series B. 58 (1): 267–288.
- ^ "기초적 추구에 의한 원자 분해" 스콧 샤오빙 첸, 데이비드 L.도노호, 마이클, A. 선더스.SIAM 과학 컴퓨팅 저널
- ^ Candès, Emmanuel J.; Romberg, Justin K.; Tao, Terence (2006). "Robust Uncertainty Principles: Exact Signal Reconstruction from Highly Incomplete Fourier Information" (PDF). IEEE Trans. Inf. Theory. 52 (8): 489–509. arXiv:math/0409186. CiteSeerX 10.1.1.122.4429. doi:10.1109/tit.2005.862083. S2CID 7033413.
- ^ Candes, E.J, & Wakin, M.B, 압축 샘플링 소개, IEEE 신호 처리 매거진, V.21, 2008년 3월 [1]
- ^ 스테판 롤위츠메트릭 선형 공간.
- ^ L1-Magic은 MATLAB 루틴의 모음입니다.
- ^ a b c Tian, Z.; Jia, X.; Yuan, K.; Pan, T.; Jiang, S. B. (2011). "Low-dose CT reconstruction via edge preserving total variation regularization". Phys Med Biol. 56 (18): 5949–5967. arXiv:1009.2288. Bibcode:2011PMB....56.5949T. doi:10.1088/0031-9155/56/18/011. PMC 4026331. PMID 21860076.
- ^ a b c Xuan Fei; Zhihui Wei; Liang Xiao (2013). "Iterative Directional Total Variation Refinement for Compressive Sensing Image Reconstruction". IEEE Signal Processing Letters. 20 (11): 1070–1073. Bibcode:2013ISPL...20.1070F. doi:10.1109/LSP.2013.2280571. S2CID 8156085.
- ^ a b Candes, E. J.; Wakin, M. B.; Boyd, S. P. (2008). "Enhancing sparsity by reweighted l1 minimization". J. Fourier Anal. Applicat. 14 (5–6): 877–905. arXiv:0711.1612. doi:10.1007/s00041-008-9045-x. S2CID 5879257.
- ^ 랜지, K.:최적화, 통계에서의 스프링거 텍스트.스프링거, 뉴욕(2004)
- ^ Combettes, P; Wajs, V (2005). "Signal recovery by proximal forward-backward splitting". Multiscale Model Simul. 4 (4): 1168–200. doi:10.1137/050626090. S2CID 15064954.
- ^ Hestenes, M; Stiefel, E (1952). "Methods of conjugate gradients for solving linear systems". Journal of Research of the National Bureau of Standards. 49 (6): 409–36. doi:10.6028/jres.049.044.
- ^ Brox, T.; Weickert, J.; Burgeth, B.; Mrázek, P. (2006). "Nonlinear structure tensors". Image Vis. Comput. 24 (1): 41–55. CiteSeerX 10.1.1.170.6085. doi:10.1016/j.imavis.2005.09.010.
- ^ Goldluecke, B.; Strekalovskiy, E.; Cremers, D.; Siims, P.-T. A. I. (2012). "The natural vectorial total variation which arises from geometric measure theory". SIAM J. Imaging Sci. 5 (2): 537–563. CiteSeerX 10.1.1.364.3997. doi:10.1137/110823766.
- ^ Andrea Massa; Paolo Rocca; Giacomo Oliveri (2015). "Compressive Sensing in Electromagnetics – A Review". IEEE Antennas and Propagation Magazine. 57 (1): 224–238. Bibcode:2015IAPM...57..224M. doi:10.1109/MAP.2015.2397092. S2CID 30196057.
- ^ Taylor, H.L.; Banks, S.C.; McCoy, J.F. (1979). "Deconvolution with the 1 norm". Geophysics. 44 (1): 39–52. doi:10.1190/1.1440921.
- ^ Tibshirani, R (1996). "Regression shrinkage and selection via the lasso" (PDF). J. R. Stat. Soc. B. 58 (1): 267–288. doi:10.1111/j.2517-6161.1996.tb02080.x.
- ^ David Schneider (March 2013). "New Camera Chip Captures Only What It Needs". IEEE Spectrum. Retrieved 2013-03-20.
- ^ "Compressive Imaging: A New Single-Pixel Camera". Rice DSP. Archived from the original on 2010-06-05. Retrieved 2013-06-04.
- ^ "Bell Labs Invents Lensless Camera". MIT Technology Review. 2013-05-25. Retrieved 2013-06-04.
- ^ Gang Huang; Hong Jiang; Kim Matthews; Paul Wilford (2013). Lensless Imaging by Compressive Sensing. 2013 IEEE International Conference on Image Processing. Vol. 2393. pp. 2101–2105. arXiv:1305.7181. Bibcode:2013arXiv1305.7181H. doi:10.1109/ICIP.2013.6738433. ISBN 978-1-4799-2341-0.
- ^ Brady, David; Choi, Kerkil; Marks, Daniel; Horisaki, Ryoichi; Lim, Sehoon (2009). "Compressive holography". Optics Express. 17 (15): 13040–13049. Bibcode:2009OExpr..1713040B. doi:10.1364/oe.17.013040. PMID 19654708.
- ^ Rivenson, Y.; Stern, A.; Javidi, B. (2010). "Compressive fresnel holography". Display Technology, Journal of. 6 (10): 506–509. Bibcode:2010JDisT...6..506R. CiteSeerX 10.1.1.391.2020. doi:10.1109/jdt.2010.2042276. S2CID 7460759.
- ^ Denis, Loic; Lorenz, Dirk; Thibaut, Eric; Fournier, Corinne; Trede, Dennis (2009). "Inline hologram reconstruction with sparsity constraints" (PDF). Opt. Lett. 34 (22): 3475–3477. Bibcode:2009OptL...34.3475D. doi:10.1364/ol.34.003475. PMID 19927182.
- ^ Marim, M.; Angelini, E.; Olivo-Marin, J. C.; Atlan, M. (2011). "Off-axis compressed holographic microscopy in low-light conditions". Optics Letters. 36 (1): 79–81. arXiv:1101.1735. Bibcode:2011OptL...36...79M. doi:10.1364/ol.36.000079. PMID 21209693. S2CID 24074045.
- ^ Marim, M. M.; Atlan, M.; Angelini, E.; Olivo-Marin, J. C. (2010). "Compressed sensing with off-axis frequency-shifting holography". Optics Letters. 35 (6): 871–873. arXiv:1004.5305. Bibcode:2010OptL...35..871M. doi:10.1364/ol.35.000871. PMID 20237627. S2CID 9738556.
- ^ Fernandez Cull, Christy; Wikner, David A.; Mait, Joseph N.; Mattheiss, Michael; Brady, David J. (2010). "Millimeter-wave compressive holography". Appl. Opt. 49 (19): E67–E82. Bibcode:2010ApOpt..49E..67C. CiteSeerX 10.1.1.1018.5231. doi:10.1364/ao.49.000e67. PMID 20648123.
- ^ 고도로 정확한 얼굴 인식을 테스트하는 엔지니어
- ^ Lustig, Michael (2007). "Sparse MRI: The application of compressed sensing for rapid MR imaging". Magnetic Resonance in Medicine. 58 (6): 1182–1195. doi:10.1002/mrm.21391. PMID 17969013. S2CID 15370510.
- ^ Lustig, M.; Donoho, D.L.; Santos, J.M.; Pauly, J.M. (2008). "Compressed Sensing MRI;". IEEE Signal Processing Magazine. 25 (2): 72–82. Bibcode:2008ISPM...25...72L. doi:10.1109/MSP.2007.914728. S2CID 945906.
- ^ Jordan EllenbergEmail Author (2010-03-04). "Fill in the Blanks: Using Math to Turn Lo-Res Datasets Into Hi-Res Samples Wired Magazine". Wired. Vol. 18, no. 3. Retrieved 2013-06-04.
{{cite magazine}}:author=일반 이름 포함(도움말) - ^ 압축 감지가 CSI "향상" 기술이 아닌 이유...아직!
- ^ 틀림없이 당신은 시나리오 작가에게 농담을 하고 있을 것이다.
- ^ Zhang, Y.; Peterson, B. (2014). "Energy Preserved Sampling for Compressed Sensing MRI". Computational and Mathematical Methods in Medicine. 2014: 546814. arXiv:1501.03915. Bibcode:2015CMMM.201514104T. doi:10.1155/2014/546814. PMC 4058219. PMID 24971155.
- ^ Zhang, Y. (2015). "Exponential Wavelet Iterative Shrinkage Thresholding Algorithm for Compressed Sensing Magnetic Resonance Imaging". Information Sciences. 322: 115–132. doi:10.1016/j.ins.2015.06.017.
- ^ Zhang, Y.; Wang, S. (2015). "Exponential Wavelet Iterative Shrinkage Thresholding Algorithm with Random Shift for Compressed Sensing Magnetic Resonance Imaging". IEEJ Transactions on Electrical and Electronic Engineering. 10 (1): 116–117. doi:10.1002/tee.22059.
- ^ Figueiredo, M.; Bioucas-Dias, J.M.; Nowak, R.D. (2007). "Majorization–minimization algorithms for wavelet-based image restoration". IEEE Trans. Image Process. 16 (12): 2980–2991. Bibcode:2007ITIP...16.2980F. doi:10.1109/tip.2007.909318. PMID 18092597. S2CID 8160052.
- ^ [압축된 감지를 통한 네트워크 단층 촬영 http://www.ee.washington.edu/research/funlab/Publications/2010/CS-Tomo.pdf]
- ^ "InView web site". inviewcorp.com. Archived from the original on 2013-03-31.
- ^ 무선 간섭계를 위한 압축 감지 영상 기술
- ^ Stevens, Andrew; Kovarik, Libor; Abellan, Patricia; Yuan, Xin; Carin, Lawrence; Browning, Nigel D. (13 August 2015). "Applying compressive sensing to TEM video: a substantial frame rate increase on any camera". Advanced Structural and Chemical Imaging. 1 (1). doi:10.1186/s40679-015-0009-3.
- ^ Kovarik, L.; Stevens, A.; Liyu, A.; Browning, N. D. (17 October 2016). "Implementing an accurate and rapid sparse sampling approach for low-dose atomic resolution STEM imaging". Applied Physics Letters. 109 (16): 164102. Bibcode:2016ApPhL.109p4102K. doi:10.1063/1.4965720.
추가 읽기
- "압축 감지의 기초" 파트 1, 파트 2 및 파트 3: IEEE 신호 처리 협회 자습서 라이브러리 시그뷰에서 조지아 공대 마크 데이븐포트의 비디오 자습서
- Math를 사용하여 Lo-Res 데이터 집합을 고-Res 샘플 유선 매거진 문서로 변환
- 라이스 대학의 압축 센싱 자원.
- 모든 픽셀을 세는 압축 센싱 – AMS의 수학적 과학 시리즈 기사
- 희박한 재건 위키



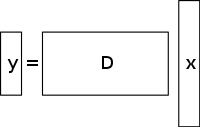
















 (는) 복구해야 할 목표 신호다.Y는 해당 측정 벡터, d는 반복 정제 방향 필드,
(는) 복구해야 할 목표 신호다.Y는 해당 측정 벡터, d는 반복 정제 방향 필드,  (는) CS 측정 매트릭스다.이 방법은 궁극적으로 몇 번의 반복을 거쳐 수렴을 유도한다.
(는) CS 측정 매트릭스다.이 방법은 궁극적으로 몇 번의 반복을 거쳐 수렴을 유도한다. 



 .
.



















 양의 상수다.null
양의 상수다.null


