푸리에 변환

푸리에 변환
푸리에 변환 푸리에 급수 이산 시간 푸리에 변환 이산 푸리에 변환 환 위의 이산 푸리에 변환 유한군에 대한 푸리에 변환 푸리에 분석 관련 변환

물리학과 수학에서 푸리에 변환(FT)은 함수를 원래 함수에 존재하는 주파수를 설명하는 형태로 변환하는 변환입니다.변환의 출력은 주파수의 복소 값 함수입니다.푸리에 변환이라는 용어는 이 복소수 함수와 수학적 연산을 모두 나타냅니다.구별이 필요할 때 푸리에 변환은 때때로 원래 함수의 주파수 영역 표현이라고 불립니다.푸리에 변환은 음악 코드의 소리를 구성 음정의 강도로 분해하는 것과 유사합니다.

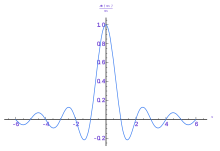
시간 영역에서 국소화된 함수는 주파수 영역에 걸쳐 퍼져 있는 푸리에 변환을 가지며, 그 반대의 경우는 불확정성 원리로 알려진 현상입니다.이 원리의 중요한 경우는 가우스 함수이며, 확률 이론과 통계뿐만 아니라 정규 분포(예: 확산)를 나타내는 물리 현상 연구에서도 상당히 중요합니다.가우시안 함수의 푸리에 변환은 또 다른 가우시안 함수입니다.조셉 푸리에는 열 전달에 대한 연구에서 가우스 함수가 열 방정식의 해로 나타나는 변형을 소개했습니다.

푸리에 변환은 부적절한 리만 적분으로 공식적으로 정의될 수 있으며, 이 정의는 더 정교한 적분 이론을 필요로 하는 많은 응용에 적합하지 않습니다.^{[note 1]}예를 들어, 비교적 간단한 많은 응용 프로그램들은 디랙 델타 함수를 사용하는데, 디랙 델타 함수는 함수인 것처럼 형식적으로 취급될 수 있지만, 그 정당성을 위해서는 수학적으로 더 정교한 관점이 필요합니다.^{[note 2]}

푸리에 변환은 또한 유클리드 공간에 있는 여러 변수의 함수로 일반화될 수 있으며, 3차원 '위치 공간'의 함수를 3차원 운동량의 함수(또는 공간과 시간의 함수를 4차원 운동량의 함수)로 보낼 수 있습니다.이 아이디어는 파동의 연구에서 공간 푸리에 변환을 매우 자연스럽게 만들 뿐만 아니라 파동 해를 위치 또는 운동량의 함수로 나타낼 수 있는 것이 중요하고 때로는 둘 다의 함수로 나타낼 수 있는 양자 역학에서도 매우 자연스럽게 만듭니다.일반적으로 푸리에 방법을 적용할 수 있는 함수는 복소 값이며 벡터 값일 수도 있습니다.^{[note 3]}R 또는 R의 원래 푸리에 변환 외에도 이산 시간 푸리에 변환(DTFT, 그룹 = Z), 이산 푸리에 변환(DFT, 그룹 = Z mod N) 및 푸리에 시리즈 또는 원형 푸리에 변환(그룹 = S, 단위 원 ≈ 닫힌 유한 int)을 포함하는 그룹에 대한 기능에 추가적인 일반화가 가능합니다.endpoints가 식별된 erval).후자는 주기적인 기능을 처리하기 위해 일상적으로 사용됩니다.고속 푸리에 변환(FFT)은 DFT를 계산하기 위한 알고리즘입니다.

정의들

R에 대한 푸리에 변환

푸리에 변환은 가장 일반적인 형태로 복잡한 지수 함수의 사용을 도입한 푸리에 급수의 확장입니다.예를 들어, f($x{\displaystyle )}$ ${\displaystyle f(x))$의 경우 주파수 $n$ P, ${\displaystyle \frac{n}{}}$∈ ${\displaystyle Z}$ ${\displaystyle {\frac$ {n$}{P}},$ n$\in \mathbb$ {$Z}}$에서 주파수$$구성 요소의 진폭 및 위상은 다음과 같은 복소수로 지정됩니다$.$

${\displaystyle c_{n}={\tfrac {1}{P}}\int_{P}f(x)\,e^{-i2\pi {\frac {n}{P}}\,dx.}$

(푸리에 급수를 리만 합으로 만들고 결국 리만 적분으로 푸리에 변환하는$$주기성 $P$ → ∞ ${\displaystyle P\to \infty })$ 확장은 무한 적분 영역을 사용하여 성분의 주파수 연속체($$ξ ∈ ${\displaystyle R),}$ ${\displaystyle \left(\xi \in \mathbb {R} \right)$를 제공합니다.

여기서, 빈도 ξ ${\displaystyle \xi}$에서 함수 $f$ ${\displaystyle (x)}$ ${\displaystyle f(x))}$의 변환은 복소수 $f{\displaystyle \stackrel{}{^}}$ ${\displaystyle (}$ξ${\displaystyle )}$ ${\displaystyle {\hat {f}}(\xi )}$로 표시되며$,$ 이는 몇 가지 일반적인 규약 중 하나일 뿐입니다.ξ ${\displaystyle$ \xi$}의$모든 값에 대해 Equ.1을 계산하면 주파수 도메인 함수가 생성됩니다.독립 변수($x {\displaystyle$ x$\})$가 시간(종종 $t$ ${\displaystyle t}$로 표시됨)을 나타내는 경우 변환 변수(ξ ${\displaystyle \xi$는 빈도($종종$ f ${\displaystyle f}$로 표시됨)를 나타냅니다.예를 들어, 시간이 초 단위로 측정되는 경우 주파수는 헤르츠 단위입니다.

각 주파수에 대해 복소값의 크기(절대값)는 해당 주파수가 도메인에 통합된 구성 복소동체의 진폭을 나타내고 복소값의 인수는 해당 복소동체의 위상 오프셋을 나타냅니다.주파수가 없는 경우 변환은 해당 주파수에 대해 0의 값을 가집니다.푸리에 변환은 시간의 함수에 국한되지 않지만 원래 함수의 도메인은 일반적으로 시간 도메인이라고 합니다.푸리에 반전 정리는 주파수 영역 표현으로부터 원래의 함수를 재창조하는 합성 과정을 제공합니다.

식 1을 해석하기 위한 중요한 $점$은${\displaystyle f}$( x$$) {\$displaystyle f(x$))에${\displaystyle {}^{}}$e - ${\displaystyle i^{}}$ 2 π ξ$$x {\$displaystyle e^{-i2\pi$ \$xi$x}를 곱하면 함수 $f$ (${\displaystyle }$x${\displaystyle }$)의 모든 빈도수 성분에서 ${\displaystyle \xi$ }$$ξ를 뺀다는 것입니다$.$ {\$displaystyle f(x)).$$}$(음의 주파수도 참조) 따라서 $ξ$ ${\displaystyle \xi}$에 있던 구성 요소는 결국 0 헤르츠가 되고, 적분은 진폭을 만들어냅니다. 왜냐하면 다른 구성 요소들은 모두 진동적이고 무한한 간격으로 0으로 적분되기 때문입니다.

함수 $f{\displaystyle }$ ${\displaystyle f}$와 $f{\displaystyle \stackrel{}{}}$ ${\displaystyle \stackrel{}{^}}$ ${\$을(를) 푸리에 변환 쌍이라고 합니다$$.^[2]변환 쌍을 지정하는 일반적인 표기는 다음과 같습니다.^[3]

${\displaystyle f(x)\{\stackrel {\mathcal {F}}{\long left right arrow}}}\{\hat {f}(\xi)\quad {\text{따라서}\quad \operatorname {rect}(x)\{\stackrel {\mathcal {F}{\long left right arrow}}}\ \operatorname {sinc}(\xi )}$

함수는 적합한 조건에서 푸리에 영상 시리즈에서 복구할 수 있습니다.이것이 가능한 경우, 푸리에 급수는 반전 공식을 제공합니다.

${\displaystyle f(x)=\sum _{n=-\infty}^{\infty}c_{n}\,e^{i2\pi {\tfrac {n}{P}}x}}$

마찬가지로, $f{\displaystyle }$ ${\displaystyle f}$의 적절한 조건 하에서, $R{\displaystyle \mathbb{}}$$$${\displaystyle$ \$mathbb$ {R$}}$의 푸리에 반전 공식은 다음과$$ 같습니다.

복소수인 $f{\displaystyle \stackrel{}{^}}$ (${\displaystyle }$ξ${\displaystyle }$) ${\displaystyle {\hat {f}}(\xi )}$는$$주파수 ξ ${\displaystyle \xi$}의 진폭과 위상을 모두 전달합니다$.$ 따라서 식 2는 $복소수$ 지수 함수의 가중 합으로 f ${\displaystyle (x)}$ ${\displaystyle f(x))}$를 나타냅니다.이것은 푸리에 반전 정리로 알려져 있으며, 현대 표준에 의한 증명은 훨씬 나중까지 주어지지 않았지만 ^[4][5]푸리에의 열 분석 이론에서 처음 소개되었습니다.^[6][7]

기타 표기 규칙

일반 주파수 ξ 대신 각 주파수 ω를 사용하는 것을 포함한 기타 일반적인 규약 및 표기에 대해서는 아래의 기타 규약 및 기타 표기를 참조하십시오.유클리드 공간의 푸리에 변환은 별도로 취급되는데, 변수 x는 종종 위치와 ξ 운동량을 나타냅니다.이 글에서 선택한 규칙은 조화 분석의 규칙이며, 르베그 측정을 재규격화하지 않고 푸리에 변환이 L에서² 단일하고 L에서¹ L로^∞ 대수 동형화하는 독특한 규칙으로 특징지어집니다.^[8]

푸리에 변환의 다른 많은 특성들이 존재합니다.예를 들어, 스톤-본 노이만 정리를 사용합니다. 푸리에 변환은 하이젠베르크 그룹의 심플렉틱 및 유클리드 슈뢰딩거 표현에 대한 고유한 유니터리 인터트위너입니다.

비주기 함수의 푸리에 급수로서의 푸리에 변환

FT(Fourier Transform)는 FS(Fourier Series)의 극한으로 푸리에 급수에서 확장할 함수는 주기성 P → ∞, 즉 함수는 비주기적입니다.즉, 비주기적 함수의 FS는 그것의 FT입니다.^[1]

1차원 공간(x축)에 대하여, 우리는 이산 주파수를 ξ = n / P로 나타내고, 여기서 n은 정수이고, 인접한 주파수들 사이의 차이는 ∆ξ = 1 / P입니다. 그리고 우리는 다음과 같이 정의합니다.

${\displaystyle \stackrel{}{f}}$ ${\displaystyle \stackrel{}{^}}$( $ξ$x${\displaystyle \stackrel{}{}}$n )${\displaystyle \stackrel{}{=}\int }$ - ∞ ∞ ${\displaystyle {}_{}^{}}$ ${\displaystyle x}$f (${\displaystyle x\stackrel{}{}}$) ${\displaystyle \exp }$ $⁡$ (${\displaystyle \stackrel{}{-}i}$ ${\displaystyle 2}$ ${\displaystyle {}_{}}$ ξ x ${\displaystyle {}_{}}$x )$${\$displaystyle${\$hat {f}$ {\$xi}_{$xn$}$)=\$int$ _${-\infty}^{\in$ dxf$\left$ (-$i2\pi {\xi}_{xn}x\right)}}.$

우리는 FS를 다음과 같이 씁니다.

$=$$x'\right)\exp \left$

극한 P → ∞에서는 (리만 합)이 됩니다.

$ξ$$\delta {{\xi}}\to \int _{-\infty}^{\infty}{d{\x}}{{x}}{\hat {f}}\left({\xi}_{x}\right)\exp \left$$i2\pi {{\xi}_{x}x\right)}}.$

함수 $f{\displaystyle }$( ${\displaystyle x)}$ ${\displaystyle f(x)}$ 및 $f{\displaystyle \stackrel{}{^}}$ (${\displaystyle }$ξ x${\displaystyle {}_{}}$ ${\displaystyle {\hat {f}}(\xi_{x})}$은(는) FT 쌍을 구성합니다.

${\displaystyle \stackrel{f}{}^}$ $ξ$x )${\displaystyle \stackrel{}{=}\int }$ - ∞ ∞ ${\displaystyle d}$ ${\displaystyle x}$ f${\displaystyle }$(${\displaystyle x\stackrel{}{}}$) ${\displaystyle \exp }$ $⁡$(${\displaystyle \stackrel{}{-}\mathrm{i}}$ 2 ${\displaystyle {}_{}}$ ξ${\displaystyle {}_{}}$ ) ${\displaystyle {\hat {f}$ {\$xi}_{x}$ (-$i2\pi {\xi}$x\$right)},$

${\displaystyle f}$ (${\displaystyle x}$ $=$ ${\displaystyle \mathrm{\int \; -}{}_{}^{}}$∞ ${\displaystyle \infty }$ ${\displaystyle {}_{}^{}}$ ${\displaystyle \xi }$ x ${\displaystyle {}_{}}$ ${\displaystyle ^}$ (${\displaystyle \xi }$ x${\displaystyle {}_{}}$) ${\displaystyle e\mathrm{xp}}$ ⁡ (${\displaystyle \mathrm{i\; 2}}$ π ξ ${\displaystyle {}_{}}$) ${\displaystyle f\left(x\ri$)=\$int _{-\infty}^{\infty }{d$ ({ {\$xi}_{x}\right)}\exp \left$}_${x}x\right)}}.$

비주기적 함수의 FS와 FT는 여기와 같이 동일합니다.그러나 주기 함수의 FS와 FT는 반드시 동일하지는 않습니다("주기 함수의 푸리에 변환" 장 참조).

배경

역사

1822년, 푸리에는 연속적이든 불연속적이든 어떤 함수도 일련의 사인으로 확장될 수 있다고 주장했습니다.^[9]그 중요한 작업은 그 이후 사용된 다양한 형태의 푸리에 변환의 기초를 제공하기 위해 다른 사람들에 의해 수정되고 확장되었습니다.

복소 정현파

일반적으로 계수 $f{\displaystyle \stackrel{}{^}}$ (${\displaystyle }$ξ${\displaystyle }$) ${\displaystyle {\hat {f}}(\xi )}$는 복소수이며, 두 개의 동치 형태를 갖습니다 (오일러 공식 참조).

${\displaystyle {\hat {f}}(\xi )=\underbrace {Ae^{i\theta}} _{\text{극좌표형}} =\underbrace {A\cos(\theta )+iA\sin(\theta )} _{\text{rectang좌표형}}$

${\displaystyle {ei}^{}}$ ${\displaystyle 2^{}}$ π ξ x ${\displaystyle e^{i2\pi \xi x}}($Eq.2)의 제품 형태는 다음과 같습니다.

${\displaystyle {\hat {f}(\xi )\cdot e^{i2\pi \xi x}=Ae^{i\theta}=\cdot e^{i2\pi \xi x}}_{\text{극좌표형}}_{\text{극좌표형}}=\cos(2\pi \xi x+\theta )+iA\sin(2\pi \xi x+\theta )}_{\text{ rectang좌표형}}}$

극형을 이용해 얼마나 쉽게 곱을 단순화했는지, 오일러 공식을 적용해 직사각형 형태를 얼마나 쉽게 추론했는지 주목할 만합니다.

음빈도

종종 혼동되는 푸리에 변환의 한 측면은 음의 주파수를 사용하는 것입니다.어떤 일이 얼마나 자주 일어나는지 또는 물리학에서 T의 일정 기간 동안 1/T로 간주되는 빈도.그러한 빈도 개념은 본질적으로 긍정적입니다.그러나 Equ.1의$$ξ {\$displaystyle$ \$xi}$의 값은 임의의 실수를 취할 수 있습니다.

실제 값 함수의 경우 양과 음의 ξ ${\displaystyle$ \$xi }$에 대한 푸리에 변환 값 사이에 간단한 관계가 있습니다(아래 공액 참조).이를 통해 사인 및 코사인 변환을 사용하여 음의 주파수 주제를 피할 수 있습니다.그러나 대부분의 저자들은 두 가지 변환을 사용하기 보다는 Equ.1을 사용하는 것을 선호합니다.이에 대한 한 가지 이유는 많은 응용 프로그램이 편미분 방정식, 레이더, 비선형 광학, 양자 역학 등과 같은 복잡한 값의 함수의 푸리에 변환을 수행해야 하기 때문입니다.이러한 경우 음의 주파수에서 푸리에 변환 값은 실제 주파수에서 값과 구별되며 중요합니다.이러한 상황에서 주파수가 무엇인지에 대한 개념은 속도나 주기에 호소하기보다는 푸리에 변환에 의해 정의됩니다.

주기함수에 대한 푸리에 변환

주기 함수의 푸리에 변환은 적분 공식을 직접 사용하여 정의할 수 없습니다.식 1에서 적분을 정의하려면 함수가 절대적으로 적분 가능해야 합니다.대신 푸리에 영상 시리즈를 사용하는 것이 일반적입니다.강화 분포로 간주하여 주기 함수를 포함하도록 정의를 확장할 수 있습니다.

이를 통해 수렴 푸리에 급수를 갖는 주기 함수에 대한 푸리에 급수와 푸리에 변환 사이의 연결을 확인할 수 있습니다.$만약{\displaystyle }$ f (${\displaystyle x)}$ ${\displaystyle f(x))}$가 주기$$ $P{\displaystyle }$ ${\displaystyle P$이고 수렴 푸리에 급수를 갖는 주기 함수라면, 다음과 같습니다.

${\displaystyle {\hat {f}}(\xi )=\sum _{n=-\infty}^{\infty}c_{n}\cdot \delta \left(\xi - {\tfrac {n}{P}\right),}$

여기서 ${\displaystyle n_{}}$ ${\displaystyle$ c_{$n}}$은 ${\displaystyle$ f$}$의 푸리에 급수 계수이고,$$δ ${\displaystyle \delta}$는 디랙 델타 함수입니다.다시 말해, 푸리에 변환은 톱니에 푸리에 급수 계수를 곱한 디랙 빗 함수입니다.

푸리에 변환 샘플링

적분 가능한 함수 $f{\displaystyle }$ ${\displaystyle f}$의 푸리에 변환은${\displaystyle \frac{\mathrm{1P}}{}}$의 $일정$한 간격으로 $샘플링$될 수 있습니다. {\displaystyle {\tfrac {$1}{P}}.$$}$이러한$$ 표본은 포아송 합 공식에 의해 해당 표본에 비례하는 푸리에 급수 계수를 갖는 주기$$ 함수 $f{\displaystyle {}_{}}$ ${\displaystyle P_{}}$ ${\$의 한 주기에서 추론할 수 있습니다.

${\displaystyle f_{P}(x)\triangleq \sum _{n=-\infty}^{\infty}f(x+nP)={\frac {1}{P}}\sum _{k=-\infty}^{\infty}{\hat {f}}\left ({\tfrac {k}{P}\right)e^{i2\pi {\frac {k}{P}},\quad \모든 k\in \mathbb {Z}}}$

${\displaystyle f}$의 통합성을 사용하면 주기적인 합이$$ 수렴됩니다.따라서$$ 샘플 $f{\displaystyle \hat{}}$(${\displaystyle \frac{\mathrm{kP}}{})}$ ${\$

${\displaystyle {\hat {f}}\left ({\tfrac {k}{P}\right)=\int_{P}f_{P}(x)\cdote^{-i2\pi {\frac {k}{P}}\,dx.}$

$f{\displaystyle (x)}$ ${\displaystyle f(x)}$에 콤팩트 지원이 있는$$ 경우 ${\displaystyle {fP}_{}x)}$ ${\displaystyle f_{P}(x)}$에는 통합 간격 내에 한정된 수의 항이 있습니다$$.$f{\displaystyle }$ (${\displaystyle x)}$ ${\displaystyle f($${\displaystyle x}$$)}$에 콤팩트 지원이 없는$$ 경우 $f{\displaystyle {}_{}}$ P (${\displaystyle {}_{}{x}_{})}$ ${\displaystyle f_{P}(x)}$에 대한 수치 평가를 수행하려면 $f{\displaystyle }$ (${\displaystyle x)}$ ${\displaystyle f(x)}$ 축소 또는$$ 항 수 자르기와 같은 근사치가 필요합니다$$.

예

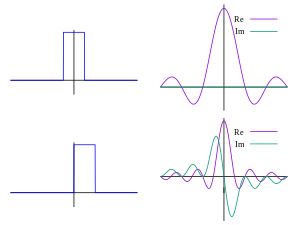
다음 그림은 푸리에 변환이 특정 함수에 주파수가 존재하는지 여부를 측정하는 방법을 시각적으로 보여줍니다.표시된 함수 f(t) = cos(6 πt) e는 3Hz(t가 초를 측정하는 경우)로 진동하고 빠르게 0으로 늘어납니다. (이 식의 두 번째 요인은 연속적인 동축을 짧은 펄스로 만드는 엔벨로프 함수입니다.일반적인 형태는 가우스 함수)입니다.이 함수는 쉽게 플롯할 수 있는 실제 푸리에 변환을 갖도록 특별히 선택되었습니다.첫 번째 이미지는 해당 그래프를 포함합니다.$f{\displaystyle \hat{}}$(${\displaystyle 3)}$ ${\displaystyle {\hat {f}}(3)}$을(를) 계산하려면 ef^−i2π(3t)(t)를 적분해야 합니다.두 번째 이미지는 이 함수의 실제 부분과 가상 부분의 플롯을 보여줍니다.f(t)가 음수일 때 e의^−i2π(3t) 실수 부분도 음수이기 때문에 적분기의 실수 부분은 거의 항상 양수입니다.f(t)가 양수일 때는 같은 속도로 진동하기 때문에 e의^−i2π(3t) 실제 부분도 마찬가지입니다.결과적으로 적분의 실제 부분을 적분하면 상대적으로 많은 수를 얻을 수 있습니다(이 경우).1/2). 한편, $f{\displaystyle \stackrel{}{}}$ ${\displaystyle \stackrel{}{^}}$ ${\displaystyle (5)}$ ${\displaystyle {\hat {f}}(5)}$을(를) 볼 때와 같이 존재하지 않는 빈도를 측정하려고 하면$$세 번째 이미지에 표시된 것처럼 함수의 실수 성분과 허수 성분이 양과 음의 값 사이에서 급격하게 변화하는 것을 알 수 있습니다.따라서 이 경우 적분기는 충분히 빠르게 진동하므로 적분기가 매우 작고 해당 주파수에 대한 푸리에 변환 값은 거의 0에 가깝습니다.

일반적인 상황은 이것보다 조금 더 복잡할 수 있지만, 실제로는 이것이 함수 f(t)에 개별 주파수가 얼마나 존재하는지를 푸리에 변환이 측정하는 방법입니다.

• 

  3Hz 진동을 보여주는 원래 기능.

• 

  3 Hz에서 푸리에 변환을 위한 적분기의 실수부와 허수부

• 

  5 Hz의 푸리에 변환을 위한 적분기의 실수부와 허수부

• 

  3 Hz 및 5 Hz 레이블이 지정된 푸리에 변환의 크기

푸리에 변환의 성질

여기서 f(x), g(x) 및 h(x)가 적분 가능한 함수라고 가정합니다. 르베그 실선에서 측정 가능:

우리는 이러한 함수의 푸리에 변환을 각각 f ̂(ξ), ĝ(ξ) 및 ĥ(ξ)로 나타냅니다.

기본속성

푸리에 변환은 다음과 같은 기본 속성을 갖습니다.^[10]

선형성

임의의 복소수 a 및 b에 대하여, h(x) = a f(x) + b g(x)이면, ĥ(ξ) = a f ̂(ξ) + b ĝ(ξ).

번역/시간 이동

임의의 실수 x에 대하여, 만약 h(x) = f(x - x)이면, ĥ(ξ) = f ξ(̂).

변조/주파수 이동

임의의 실수 ξ에 대해 h(x) = f(x)이면 ĥ(ξ) = f ̂(ξ - ξ).

타임스케일링

0이 아닌 실수 a의 경우, 만약 h(x) = f(ax)라면,

$${\displaystyle {\hat {h}}(\xi )={\frac {1}{a}}}{\hat {f}}\left ({\frac {\xi}{a}\right).}$$

a = -1인 경우는 시간-reversal 속성으로 이어지는데, h(x) = f (-x)인 경우 ĥ(ξ) = f ̂(- ξ)입니다.

대칭성

복소함수의 실수부와 허수부를 짝수부와 홀수부로 분해하면, 아래에 첨자 RE, RO, IE, IO로 표시되는 4개의 성분이 있습니다.그리고 복잡한 시간 함수의 네 요소와 복잡한 주파수 변환의 네 요소 사이에는 일대일 매핑이 있습니다.$begin$$RE}}\quad &+\quad &f_{{$$RO}}\quad &+\quadi\&f_{{$$IE}}\quad &+\quad &\underbrace {i\f_{{$$IO}}\\&{\Bigg \Updownarrow}{\mathcal {F}}&{\Bigg \Updownarrow}{\mathcal {F}}&\{\mathcal {F}&\ \\Bigg \Updownarrow}{\mathcal {F}&\{\mathcal \F}&\{\mathsf {F}&\{\mathsf {주파수\domain}\quad &{\hat {f}}\quad &{\hat {f}\quad &+\overbrace {i\hat {f}_{\hat {f}}\quad &+\hat {f}_{{i\hat {\hat {f}_{{}_{{}_{{{{}}_{{{{hat {f}}_{{{{}}_{{{{{{}})\"$$IO}}\quad &+\quadi\{\hat {f}_{$$IE}\quad &+\quad &{\hat {f}_{$$RO}\end{aligned}}$

이를 통해 다양한 관계를 알 수 있습니다. 예를 들어 다음과 같습니다.

• 실수 값 함수 (f+ f)의 변환은 ̂인 경우 짝수 대칭 함수 f ̂+입니다.반대로, 짝수대칭 변환은 실제 값의 시간 영역을 의미합니다.
• 허수 값 함수의 변환(if+ if)은 ̂이면 홀수 대칭 함수 f ̂+이고, 그 반대는 참입니다.
• 짝수대칭 함수의 변환(f+ if)은 실수값 함수 f ̂+ f ̂이고, 그 반대는 참입니다.
• 홀수 대칭 함수의 변환(f+ if)은 ̂이면 ̂+이고, 반대면 참이면 허수 값 함수입니다.

컨쥬게이션

만약 h(x) = f(x)이면,

$${\displaystyle {\hat {h}}(\xi )={\overline {{\hat {f}}(-\xi )}}}}$$

특히 f 가 진짜라면 현실 조건을 가지고 있습니다.

$${\displaystyle {\hat {f}}(-\xi )={\overline {{\hat {f}}(\xi )}},}$$

즉, f ̂는 에르미트 함수입니다.그리고 f가 순전히 허수라면,

$${\displaystyle {\hat {f}}(-\xi)=-{\hat {f}(\xi)}.$$

실제 및 가상의 시간 부분

• $h$ (${\displaystyle x}$ )${\displaystyle }$= ℜ (${\displaystyle f}$( ${\displaystyle x}$)${\displaystyle h$( x ) =\$Re {(f (x))}}$인 경우 $h$$^$${\displaystyle \stackrel{}{}(}$ξ )${\displaystyle }$= 12${\displaystyle }$( ${\displaystyle \frac{\mathrm{f}}{}}$ ${\displaystyle \stackrel{}{^}}$ (${\displaystyle }$ξ${\displaystyle }$)${\displaystyle }$+ ${\displaystyle f\stackrel{}{\stackrel{}{^}}}$( -${\displaystyle \stackrel{}{}}$ξ${\displaystyle \stackrel{}{}}$) ¯${\displaystyle }$) ${\displaystyle {\hat {$h} $(\xi$ ) = {\$frac {1}{2}}\left$ ({\$hat {$f} $(\xi$ ) + ${\overline {{\hat {f$ $(-\xi )}\right )}.$
• if $h{\displaystyle }$( ${\displaystyle x}$ )${\displaystyle }$= ℑ${\displaystyle }$( ${\displaystyle f}$( ${\displaystyle x}$)${\displaystyle h(x$)=$\backslash$$Im {(f(x))}},$$h{\displaystyle ^(}$$ξ$${\displaystyle )}$ $=$ ${\displaystyle \frac{\mathrm{12i}}{}}$ ${\displaystyle \frac{}{}f^(}$$ξ$${\displaystyle )}$- f${\displaystyle \stackrel{}{^(}}$ -${\displaystyle \stackrel{}{}}$$ξ$${\displaystyle \stackrel{}{)}}$$¯$$) {\displaystyle {\hat {h}(\xi$) $=$ {\$frac {1}{2i}}\left$ $({$\$hat {f}(\xi)-{\overline {{\hat$ {f$}(-\xi )}\right)}.$

영주파수 성분

정의에 ξ = 0을 대입하면 다음을 얻을 수 있습니다.

$${\displaystyle {\hat {f}}(0)=\int _{-\infty}^{\infty}f(x)\, dx.}$$

이는 f 의 모든 도메인에 대한 적분과 동일하며 함수의 평균값 또는 DC 바이어스라고도 합니다.

가역성과 주기성

함수 $f$ ${\displaystyle f}$의 적합한 조건 하에서$$푸리에 변환 $f$ ${\displaystyle \stackrel{}{^}}$ ${\displaystyle {\hat {f}}$로부터 복구할 수 있습니다$.$ 실제로 $F$ ${\displaystyle {\mathcal {F}}$로 푸리에 변환 연산자를 나타내므로$$${\displaystyle F}$ ${\displaystyle :}$= ${\displaystyle f}$ ${\displaystyle \stackrel{}{^}}$ ${\mathcal${$F}f:$$={\hat {f}},$그 다음 적절한 함수에 대해 푸리에 변환을 두 번 적용하면 간단히 함수가 뒤집힙니다:$$( ${\displaystyle {F2}^{}}$ ${\displaystyle {}^{}}$)${\displaystyle }$( x${\displaystyle }$) $=$ ${\displaystyle f}$(${\displaystyle }$- ${\displaystyle x}$) ${\displaystyle \left$$({$$\mathcal {F}^{2}f\right)(x)$$=$$f(-x$역방향 시간은 2 periodic이므로 이를 두 번 ${\displaystyle {적용}^{}}$하면 F 4${\displaystyle {}^{}}$(${\displaystyle f}$ )${\displaystyle }$= ${\mathcal {F}^{4}(f$) =$f$가 되므로 푸리에 변환 연산자는 4 periodic이며 마찬가지로 푸리에 변환을 세 번 적용하면 역 푸리에 변환을 얻을 수 있습니다.${\displaystyle {}^{}F}$ ${\displaystyle 3^{}}$ (${\displaystyle {\mathcal{}}^{}f}$ ${\displaystyle \stackrel{}{^}}$ )$=$ f ${\displaystyle {\mathcal {F}}^{3}\left({\hat {f})$)=$f$ 특히 푸리에 변환은 (적절한 조건에서) 가역적입니다.

보다 정확하게, 패리티 $연산자$ P ${\displaystyle {\mathcal {P}}$를 $({\displaystyle Pf}$ )${\displaystyle }$( ${\displaystyle x}$) = ${\displaystyle f}$( -${\displaystyle }$x )${\displaystyle ({\mathcal {P}}) (x$) = f$(-x)}$ 로 정의하면 다음과 같습니다$.$

${\displaystyle {\begin{aligned}{\mathcal {F}}^{0}&=\mathrm {id},\{\mathcal {F}&={\mathcal {F}},\{\mathcal {F}}^{2}&={\mathcal {P}},\{\mathcal {F}^{3}&={\mathcal {F}={\mathcal {P}},\circ {\mathcal {F}={\mathcal {F},\circ {\mathcal {F}^{4}&=\mathcal {id}\end{aligned}}},\circ {\mathcal {F}},\circ {\mathcal {F}^{F}& {\mathcal {id},\circ {\mathcal {-1}},\circ {\mathcal {F},\circ {\mathcal {F}},\circ {\mathcal {F},\mathcal {F},\mathcal {F},\circ {\mathcal {F},\mathcal {F},\circ {\mathcal {F},\mathcal {F},\col {$

연산자의 이러한 균등성은 함수의 균등성을 정의하면서 문제가 되는 함수의 공간에 대한 신중한 정의를 요구합니다(모든 지점에서의 균등성?).거의 모든 곳에서 동등함?)과 연산자의 동등함을 정의합니다. 즉, 문제의 함수 공간과 연산자 공간에 대한 토폴로지를 정의하는 것입니다.이것들은 모든 함수에 대해 성립하는 것은 아니지만, 푸리에 반전 정리의 다양한 형태의 내용인 다양한 조건에서 성립합니다.

푸리에 변환의 이 4배 주기성은 평면을 90° 회전하는 것과 유사하며, 특히 2배 반복이 역전을 산출하기 때문에 실제로 이 비유는 정확하게 이루어질 수 있습니다.푸리에 변환은 단순히 시간 영역과 주파수 영역을 바꾸는 것으로 해석될 수 있지만, 역 푸리에 변환이 그것들을 다시 바꾸는 것으로 더 기하학적으로 그것은 시간-주파수 영역에서 90°만큼 회전하는 것으로 해석될 수 있습니다(시간을 x축으로 그리고 주파수를 y축으로 생각함), 그리고 푸리에 변환은 다음과 같습니다.다른 각도에 의한 회전을 수반하는 분수 푸리에 변환으로 일반화됩니다.이것은 아래의 불확도 원리에 해당하는 보존된 심플렉틱 형태로 시간-주파수 평면에 대한 특별한 선형₂ 그룹 SL(R)의 작용으로 시각화될 수 있는 선형 표준 변환으로 더 일반화될 수 있습니다.이 접근법은 특히 시간-주파수 분석 하에서 신호 처리에서 연구됩니다.

단위와 이중성

빈도 변수는 원래 함수 도메인의 단위(일반적으로 t 또는 x로 명명됨)와 반대의 단위를 가져야 합니다.예를 들어, t가 초 단위로 측정되는 경우 ξ는 초 단위 또는 헤르츠 단위의 사이클이어야 합니다.시간 척도가 2 π 초 단위인 경우 일반적으로 다른 그리스 문자 ω가 대신 사용되어 각 주파수(여기서 ω = 2 πξ)를 초당 라디안 단위로 나타냅니다.길이 단위에 x를 사용하는 경우 ξ는 파수와 같은 역길이여야 합니다.즉, 실제 선에는 두 가지 버전이 있습니다. 하나는 t의 범위이고 t의 단위로 측정된 것이고, 다른 하나는 ξ의 범위이며 t의 단위와 역 단위로 측정된 것입니다.실제 선의 이 두 가지 다른 버전은 서로 동일시될 수 없습니다.따라서 푸리에 변환은 한 공간의 함수에서 다른 공간의 함수, 즉 정의 영역이 다른 함수로 변환됩니다.

일반적으로 ξ은 항상 정의역의 공간상에서 직선형을 취하여야 하며, 즉 두 번째 실수선은 첫 번째 실수선의 이중 공간이라는 것입니다.더 공식적인 설명과 더 자세한 내용은 선형대수학 기사를 참조하세요.이 관점은 푸리에 급수의 경우를 포함하여 일반 대칭군으로의 푸리에 변환의 일반화에서 필수적인 것이 됩니다.

푸리에 변환에 관련된 두 버전의 실제 선을 비교할 수 있는 바람직한 방법이 하나도 없기 때문에(한 선에 단위를 고정하는 것이 다른 선에 단위의 크기를 강제하지 않기 때문에) 푸리에 변환의 정의에 대한 경쟁 규칙이 너무 많아지는 이유가 됩니다.다양한 단위 선택의 결과로 나타나는 다양한 정의는 다양한 상수에 따라 다릅니다.

$f{\displaystyle {\stackrel{}{}}_{}}$^ ${\displaystyle 1_{}}$ (${\displaystyle }$ξ$$) {\$displaystyle {\hat {f}}_{$1}(\$xi )}$을 일반 주파수 ξ에서 푸리에 변환의 형태라고 하자.

ξ =$$ω ${\displaystyle 2}$ π ${\displaystyle \xi$ = {\$tfrac {\omega$}{2$\pi$ $\}\}\}$이므로 대체 형식 f^${\displaystyle {\stackrel{}{}}_{}}3$ (ω)${\displaystyle {\hat$ {f$}_{3}(\omega )}($푸리에 변환 § 다른 규칙에서는 각도 주파수에서 비일원 형식을 부름)는 정의에 요인이 없습니다.

${\displaystyle {\hat {f}}_{3}(\omega )\mathrel {\mathrm {def}{=}\int_{-\infty}^{\infty}f(x)\,e^{-i\omega x}\, dx={\hat {f}_{1}\left ({\frac {\omega }{2\pi}\right)}$

그러나 해당 반전 공식에서 $12$ π ${\displaystyle {\tfrac {1}{2\pi}}$의 인자를 갖습니다.

${\displaystyle f(x)={\frac {1}{2\pi}}\int _{-\infty}^{\infty}{\hat {f}_{3}(\omega )\,e^{i\omega \,x}\,d\omega.}$

대체 형식 $f{\displaystyle {\stackrel{}{^}}_{}}$ ${\displaystyle 2_{}}$ ${\displaystyle {}_{}}$ω${\displaystyle )}$ ${\displaystyle {\hat {f}}_{2}(\omega )}($푸리에 변환 § 기타 규칙에서 각도 주파수의 유니터리 형식이라고 함)는 정의에서 π ${\displaystyle {\tfrac {1}{\sqrt {2\pi}}$의 인자를 갖습니다.

${\displaystyle {\hat {f}}_{2}(\omega)\mathrel {\mathrm {def}{=}}{\frac {1}{\sqrt {2\pi}}\int _{-\infty}^{\infty}f(x)\,e^{-i\omega \,x}\, dx}$

또한 해당 반전 공식에서 12 π ${\displaystyle {\tfrac$ {1$}{\$sqrt {2$\pi$}}}의 동일한 인자를 가지며 대칭 관계를 생성합니다.

${\displaystyle f(x)={\frac {1}{\sqrt {2\pi}}\int_{-\infty}^{\infty}{\hat {f}_{2}(\omega )\,e^{i\omega \,x}\,d\omega.}$

다른 규칙에서, 푸리에 변환은 -i 대신 지수에 i를 가지며, 반전 공식의 경우에도 그 반대입니다.이 규칙은 현대 물리학에서^[11] 일반적이며 볼프람 알파의 기본값이며, 복잡한 파동의 진동수에 대한 표준 정의가 없기 때문에 진동수가 음수가 된 것을 의미하지는 않습니다.단순히, 전자파 ${\displaystyle {\mathrm{e}}^{}}$ ${\displaystyle i}$ 2$$ξ$$x {\$displaystyle$ e$^{i2\pi$ \$xi$}}(\${\displaystyle {\mathrm{xi}}^{}}$ $)}$가 아닌 $f$${\displaystyle {^}^{}}$ (${\displaystyle }$π ξ ) ${\displaystyle e^{-i2\pi$\$xi x$$}($전자는 전자파 방정식의 정현 평면파 해에 대한 시간 의존성에서 종종 보입니다.또는 양자파동 함수에 대한 시간 의존성).푸리에 변환과 관련된 많은 항들은 명시적으로 관련된 모든 항들이 -i로 대체된다면, 그러한 항들에서 여전히 유효합니다.전기공학에서 문자 j는 일반적으로 전류에 사용되기 때문에 i 대신 가상 단위에 사용됩니다.

무차원 단위를 사용하는 경우 변환 정의에 상수 인자가 기록되지 않을 수도 있습니다.예를 들어, 확률이론에서 연속형 임의변수 X의 확률밀도함수 f의 특성함수 φ는 지수에 음의 부호 없이 정의되며, x의 단위는 무시되므로 2개의 π도 존재하지 않습니다.

${\displaystyle \phi (\lambda)=\int _{-\infty}^{\infty}f(x)e^{i\lambda x}\, dx.}$

(확률론과 수학 통계학에서는 푸리에-슈틸트제스 변환을 사용하는 것이 선호되는데, 이는 매우 많은 확률 변수들이 연속형이 아니며 밀도 함수를 갖지 않기 때문이며, 함수가 아닌 분포, 즉 "원자"를 갖는 측도를 처리해야 하기 때문입니다.)

훨씬 더 추상적인 그룹 문자의 높은 관점에서 볼 때, 국소적으로 콤팩트한 아벨 군에 대한 함수의 푸리에 변환의 개념을 다루는 이 글의 뒷부분에서 설명되듯이, 이러한 임의의 선택은 모두 사라집니다.

균일 연속성과 리만-레베그 보조정리

푸리에 변환은 일부 경우에 비적분 함수에 대해 정의될 수 있지만, 적분 가능 함수의 푸리에 변환은 몇 가지 강력한 특성을 갖습니다.

임의의 적분 가능한 함수 f 의 푸리에 변환 f ̂는 균일하게 연속적이고

${\displaystyle \left\{\hat {f}}\right\_{\infty}\leq \left\f\right\_{1}$

리만-레베그 보조정리에 의하여,^[13]

${\displaystyle {\hat {f}}(\xi )\to 0{\text{as}}\xi \to \infty.}$

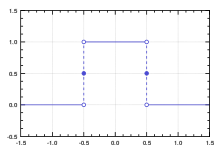
그러나 $f{\displaystyle \hat{}}$ ${\$은(는) 통합할 필요가$$ 없습니다.예를 들어, 적분이 가능한 직사각형 함수의 푸리에 변환은 절대 수렴하지 않고 합으로 수렴하는 데 있어 르베그의 부적절한 적분이 교호 조화 급수와 유사하게 작용하기 때문에 적분이 불가능한 싱 함수입니다.

역변환을 르베그 적분으로 쓰는 것은 일반적으로 불가능합니다.그러나 f 와 $f{\displaystyle \stackrel{}{}}$^ ${\$ 가 모두 적분 가능한$$ 경우, 역으로 동일함

${\displaystyle f(x)=\int _{-\infty}^{\infty}{\hat {f}}(\xi)^{i2\pix\xi}\,d\xi }$

거의 모든 곳에서 개최됩니다.즉, 푸리에¹ 변환은 L(R)에 대하여 주사적입니다. (그러나 f가 연속이면 모든 x에 대하여 등식이 성립합니다.)

플랑셰럴 정리와 파르스발 정리

f(x)와 g(x)를 적분 가능하고 f ̂(ξ)와 ĝ(ξ)를 푸리에 변환이라고 합니다.f(x)와 g(x)도 제곱적분이 가능한 경우 파싱발 공식은 다음과 같습니다.^[14]

${\displaystyle \langle f,g\rangle _{L^{2}}=\int _{-\infty}^{\infty}f(x){\overline {g(x))}\, dx=\int _{-\infty}^{\infty}^{\hat {f}(\xi){\overline {\hat {g}(\xi )}\,d\xi,}$

여기서 막대는 복소 켤레를 나타냅니다.

위로부터 이어지는 플랑셰렐 정리는 다음과^[15] 같이 말합니다.

${\displaystyle \ f\ _{L^{2}}^{2}=\int _{-\infty}^{\infty}\left f(x)\right ^{2}\, dx=\int _{-\infty}^{\infty}}\left {\hat {f}(\xi )\right ^{2}\,d\xi.}$

플랑셰렐의 정리는 연속성 인수에 의해 L(R)의 단일² 연산자로 푸리에 변환을 확장하는 것을 가능하게 합니다.L(R) ∩ L(R)에서 이 확장은 L(R)에 정의된 원래 푸리에 변환과 일치하므로 푸리에 변환의 도메인을 L(R) + L(R)로 확장합니다(따라서 1 ≤ p ≤ 2인 경우 L(R).플랑셰렐의 정리는 과학에서 푸리에 변환이 원래 양의 에너지를 보존한다는 해석을 가지고 있습니다.이 공식들의 용어는 표준화되어 있지 않습니다.파르스발의 정리는 푸리에 급수에 대해서만 증명되었고, 랴푸노프에 의해 처음 증명되었습니다.그러나 파르스발의 공식은 푸리에 변환에도 일리가 있으며, 따라서 비록 푸리에 변환의 맥락에서 그것이 플랑셰렐에 의해 증명되었지만, 그것은 여전히 종종 파르스발의 공식, 또는 파르스발의 관계, 또는 심지어 파르스발의 정리로 언급됩니다.

국부적으로 콤팩트한 아벨 군의 맥락에서 이 개념의 일반적인 공식에 대해서는 폰트랴긴 이중성을 참조.

포아송 합산 공식

포아송 합 공식(PSF)은 함수의 주기적 합의 푸리에 급수 계수를 함수의 연속 푸리에 변환 값과 연관시키는 방정식입니다.포아송 합 공식은 충분히 규칙적인 함수 f에 대해,

${\displaystyle \sum _{n}{\hat {f}}(n)=\sum _{n}f(n)}$

푸리에 변환의 스케일링 및 시변 특성을 적용하여 기본적인 형태로부터 도출되는 다양한 유용한 형태를 가지고 있습니다.이 공식은 공학, 물리학, 수론에 응용됩니다.표준 포아송 합 공식의 주파수 영역 이중은 이산 시간 푸리에 변환이라고도 합니다.

포아송 합은 일반적으로 원 위의 열전도와 같은 주기적인 매체의 물리학과 관련이 있습니다.원 위의 열 방정식의 근본적인 해는 세타 함수라고 불립니다.수론에서 모듈형 형태의 일종으로 밝혀진 세타 함수의 변환 특성을 증명하는 데 사용되며, 셀버그 추적 공식의 한 면에 나타나는 오토모픽 형태 이론과 더 일반적으로 연결됩니다.

차별화

f(x)가 절대 연속 미분 가능 함수이고 f와 그 도함수 f'가 모두 적분 가능하다고 가정합니다.그렇다면 도함수의 푸리에 변환은 다음과 같이 주어집니다.

${\displaystyle {\widehat {f'\,}(\xi )={\mathcal {F}}\left\{\frac {d}{dx}f(x)\right\}=i2\pi \xi {\hat {f}(\xi )}$

더 일반적으로, n번째 도함수 f의⁽ⁿ⁾ 푸리에 변환은 다음과 같이 주어집니다.

${\displaystyle {\widehat {f^{(n)}}(\xi )={\mathcal {F}}\left\{\frac {d^{n}}{f(x)\right\}=(i2\pi \xi )^{n}{\hat {f}(\xi)}$

유사하게 $F$ {${\displaystyle dn}$ ${\displaystyle \frac{d^{}}{}}$ ξ ${\displaystyle \frac{n^{}}{}}$ ${\displaystyle \frac{{}^{}}{}}$ ${\displaystyle \stackrel{}{^}}$ (${\displaystyle }$ξ${\displaystyle }$) ${\displaystyle \}}$ =${\displaystyle }$( ${\displaystyle i}$ ${\displaystyle 2}$ π ${\displaystyle x{}^{}}$) ${\displaystyle {}^{}}$ f${\displaystyle }$( x${\displaystyle }$) ${\displaystyle {\mathcal {F}\left\{\frac {d^{n}}{\hat {f}(\xi)\right$\}=($i2\pix)^{n}}{(x)},$즉${\displaystyle }F$ { ${\displaystyle x^{}}$ ${\displaystyle {}^{}}$ f${\displaystyle }$(${\displaystyle x}$ )${\displaystyle }$= ${\displaystyle {\frac{i2}{}}^{}}$ π )${\displaystyle {\frac{}{}}^{}}$n ${\displaystyle \frac{{}^{}}{}}$ ${\displaystyle {}^{}}$ ξ ${\displaystyle \frac{{}^{}}{}}$ f ${\displaystyle \stackrel{}{^}}$(ξ ) .${\mathcal {F}}\left\{x^{n}f(x)\right$\}=\$left({\frac {i}{2\pi$}}\$right)$$^{n}{\frac {d^{n}}{d\xi^{n}}{\hat {f}}(\xi).}$

푸리에 변환을 적용하고 이 공식들을 사용함으로써, 일부 일반적인 미분 방정식들은 훨씬 풀기 쉬운 대수 방정식으로 변환될 수 있습니다.이 공식들은 또한 경험칙 "f(x)는 f ̂(ξ)가 ξ → ∞에 대해 0으로 빨리 떨어지는 경우에만 매끄럽다." 역 푸리에 변환에 대한 유사한 규칙을 사용함으로써 "f(x)는 x → ∞에 대해 0으로 빨리 떨어진다. f ̂(ξ)가 매끄러울 경우에만"라고 말할 수 있습니다.

컨볼루션 정리

푸리에 변환은 함수의 컨볼루션과 곱셈 사이를 변환합니다.f(x)와 g(x)가 각각 푸리에 변환 f ξ(ξ)와 ĝ(ξ)와 적분 가능한 함수인 경우, 컨볼루션의 푸리에 변환은 푸리에 변환 f ̂(ξ)과 ĝ(̂)의 곱으로 주어집니다(푸리에 변환의 정의에 대한 다른 규약에서는 상수 인자가 나타날 수 있음).

이는 다음을 의미합니다.

${\displaystyle h(x)=(f*g)(x)=\int_{-\infty}^{\infty}f(y)g(x-y)\,dy,}$

여기서 ∗는 컨벌루션 연산을 의미하며, 다음과 같습니다.

${\displaystyle {\hat {h}}(\xi )={\hat {f}(\xi )\,{\hat {g}}(\xi )}$

선형 시간 불변(LTI) 시스템 이론에서, 단위 임펄스를 f(x)로 대체하면 h(x) = g(x)를 얻을 수 있기 때문에, g(x)를 입력 f(x)와 출력 h(x)를 갖는 LTI 시스템의 임펄스 응답으로 해석하는 것이 일반적입니다.이 경우 ĝ(ξ)는 시스템의 주파수 응답을 나타냅니다.

반대로, f(x)가 두 개의 제곱 적분 가능 함수 p(x)와 q(x)의 곱으로 분해될 수 있다면, f(x)의 푸리에 변환은 각각의 푸리에 변환 p(ξ)와 q ̂(ξ)의 컨볼루션에 의해 주어집니다.

교차 상관 정리

유사한 방법으로, h(x)가 f(x)와 g(x)의 교차 상관관계라면 다음과 같이 나타낼 수 있습니다.

${\displaystyle h(x)=(f\star g)(x)=\int _{-\infty}^{\infty}{\overline {f(y)}}g(x+y)\,dy}$

그렇다면 h(x)의 푸리에 변환은 다음과 같습니다.

${\displaystyle {\hat {h}}(\xi )={\overline {{\hat {f}}(\xi )}\,{\hat {g}(\xi )}.$

특수한 경우 함수 f(x)의 자기 상관은 다음과 같습니다.

${\displaystyle h(x)=(f\star f)(x)=\int_{-\infty}^{\infty}{\overline {f(y)}}f(x+y)\,dy}$

어떤 이유로

${\displaystyle {\hat {h}}(\xi )={\overline {{\hat {f}}(\xi )}}{\hat {f}(\xi )=\left {\hat {f}(\xi )\right ^{2}}.$

고유함수

푸리에 변환은 $F$[λ ∈]${\displaystyle }$=$$λ ψ${\displaystyle ,}$ ${\displaystyle {\mathcal {F}}[\psi$ ]=\displaystyle \psi$,}$를 따르는 고유 함수를 갖는 선형 변환입니다${\displaystyle .}$ ${\displaystyle \$lambda$\in$ \mathbb {$C} .}$

고유 함수들의 집합은 동차 미분 방정식에 주목함으로써 발견됩니다.

${\displaystyle \left[U\left({\frac {1}{2\pi}}}{\frac {d}{dx}}\right)+U(x)\right]\psi(x)=0}$

푸리에 변환 하에서 방정식의 형태가 불변인 한 푸리에 $변환$ F ${\displaystyle {\mathcal {F}}$의 고유 함수${\displaystyle }$ψ (${\displaystyle x)}$ ${\displaystyle \psi(x))}$로 이어집니다.즉, 모든 해 ψ${\displaystyle (x)}$ ${\displaystyle \psi(x))}$과 그 푸리에 변환 ψ ${\displaystyle \stackrel{}{^(}}$ξ${\displaystyle )}$ ${\displaystyle {\hat {\psi}}(\xi )}$은(는) 동일한 방정식을 따릅니다.해의 유일성을 가정할 때, 모든 해 ψ ${\displaystyle (x)}$ ${\displaystyle \psi(x)}$는 따라서 푸리에 변환의 고유 함수여야 합니다.${\displaystyle \mathrm{모든}}$ 항에 대해${\displaystyle }$± ${\displaystyle 1,}$± ${\displaystyle i}$ ${\displaystyle$ \$pm$1 중 하나의 동일한 인자를 갖는$멱급수$에서 U (x) {\displaystyle $U(x)}$를 확장할 수 있다면$$ 푸리에 변환 하에서 방정식의 형태는 변하지 않습니다$.$$\pm i}$는 동차 미분 방정식을 푸리에 변환할 때 미분 규칙에 의해 도입된$$ ${\$의 인자들로부터 발생하는데$$, 그 이유는 이 인자가 취소될 수 있기 때문입니다.가장 간단한 허용 $U{\displaystyle (x)}$ = ${\displaystyle x}$ ${\displaystyle U(x$) = $x}$는 표준 정규 분포로 이어집니다.

더 일반적으로, 고유 함수들의 집합은 또한 미분 규칙들이 통상적인 미분 방정식을 암시한다는 것에 주목함으로써 발견됩니다.

${\displaystyle \left[W\left({\frac {i}{2\pi}}}{\frac {d}{dx}}\right)+W(x)\right]\psi(x)=C\psi(x)}$

$C{\displaystyle }$ ${\displaystyle C}$ 상수이고$$ ${\displaystyle W}$ (${\displaystyle }$x${\displaystyle }$) ${\displaystyle W(x)}$ 가 일정하지 않은 짝수 함수인$$ 경우, F$${\$displaystyle {\$mathcal {$F}}$ 를 식의 양변에$$ 적용할 때 형태는 불변입니다.가장 간단한 예는 양자 고조파 발진기에 대한 슈뢰딩거 방정식을 고려하는 것과 같은 $W{\displaystyle (x)}$=$x$ ${\displaystyle 2^{}}$ ${\displaystyle W(x$) = x$^{2}$로 제공됩니다.해당 해는² L(R)에 대한 정규 표준 기저의 중요한 선택을 제공하며 "물리학자의" 헤르마이트 함수에 의해 제공됩니다.이와 동등하게 사용할 수 있습니다.

${\displaystyle \psi _{n}(x)={\frac {\sqrt[{4}]{2}}{\sqrt {n!}}}e^{-\pi x^{2}}\mathrm {He} _{n}\left(2x{\sqrt {\pi}}\right),}$

여기서 He_n(x)는 다음과 같이 정의되는 "확률론자"의 헤르마이트 다항식입니다.

${\displaystyle \mathrm {He} _{n}(x)= (-1)^{n}e^{{\frac {1}{2}}\left ({\frac {d}{dx}\right)^{n}e^{-{\frac {1}{2}}x^{2}}}}$

푸리에 변환에 대한 이 관례에 따라, 우리는 다음을 갖습니다.

${\displaystyle {\hat {\psi }}_{n}(\xi )= (-i)^{n}\psi _{n}(\xi )}$

다시 말해, 헤르마이트 함수는² L(R)의 푸리에 변환에 대한 완전한 정규 함수 체계를 형성합니다.^[10][18]그러나 이러한 고유 함수 선택은 고유한 것이 아닙니다.${\displaystyle {F4}^{}}$ = ${\displaystyle \mathrm{id}}$ ${\displaystyle {\mathcal {F}}^{4$}=\$mathrm {id}}$ 때문에 푸리에 변환의 서로 다른 고유값은 4개(단일성 ±1 및 ±i의 네 번째 뿌리)뿐이며 동일한 고유값을 갖는 고유함수의 선형 조합은 또 다른 고유함수를 제공합니다.그 결과, L(R²)을^k 단순히 i의 곱으로 푸리에 변환이 He에_k 작용하는 4개의 공간 H₀, H₁, H₂, H의₃ 직접합으로 분해할 수 있습니다.

에르미트 함수들의 완전한 집합 ψ는 동일성의 해상도를 제공하므로, 그들은 푸리에 연산자를 대각화합니다. 즉, 푸리에 변환은 위의 고유값으로 가중된 항들의 합으로 표현될 수 있고, 이 합은 명시적으로 합산될 수 있습니다:

${\displaystyle {\mathcal {F}}[f](\xi )=\int dxf(x)\sum _{n\geq 0}(-i)^{n}\psi _{n}(x)\psi _{n}(\xi )~.}$

푸리에 변환을 정의하는 이 접근법은 노버트 위너에 의해 처음 제안되었습니다.^[20]다른 특성 중 헤르마이트 함수는 주파수 영역과 시간 영역 모두에서 기하급수적으로 빠르게 감소하므로 푸리에 변환의 일반화, 즉 시간-주파수 분석에 사용되는 분수 푸리에 변환을 정의하는 데 사용됩니다.^[21]물리학에서 이 변형은 에드워드 콘돈에 의해 도입되었습니다.^[22]이 기저 함수의 변화는 푸리에 변환이 올바른 규약을 사용할 때 단일 변환이기 때문에 가능합니다.따라서 적절한 조건에서 다음을 통해 자체$$^[23] 인접 제너레이터 $N{\displaystyle }$ ${\displaystyle$ N$}$에서 발생할 수 있습니다.

${\displaystyle {\mathcal {F}}[\psi ]=e^{-itN}\psi.}$

연산자 $N{\displaystyle }$ ${\displaystyle N}$은 다음과 같이 쓰여진 양자^[24][25] 고조파 발진기의 숫자 연산자입니다.

${\displaystyle N\equiv {\frac {1}{2}}\left(x-{\frac {\partial }{\partial x}}\left)\left(x+{\frac {\partial}{\(- x}}\right)={\frac {1}{2}}\left partial {\frac {\partial x^{2}}+x^{2}-1\right).}$

그것은 임의의 t 값에 대한 분수 푸리에 변환의 생성기로 해석할 수 있으며, 해당 능동 변환을 구현하는 멜러 커널이 있는 특정 값 $t$ = π${\displaystyle }$/ ${\displaystyle 2,}$ ${\displaystyle$t =\$pi$/ 2$,}$에 대한 기존의 연속 푸리에 $변환$ ${\mathcal {F}$의 생성기로 해석할 수 있습니다.$N$ ${\displaystyle N}$의 고유 함수는 Hermite 함수 ψ ${\displaystyle n_{}}$ (${\displaystyle {}_{}x)}$ ${\displaystyle \psi _{n}(x))$이며, 따라서 $F$.${\displaystyle {\mathcal {F}}$의 고유 함수이기도 합니다.

푸리에 변환을 분포로 확장할 때 디랙 빗은 푸리에 변환의 고유 함수이기도 합니다.

하이젠베르크 그룹과의 연관성

하이젠베르크 군은 실선 상의 제곱 적분 가능 복소수 함수 f의 힐베르트 공간 L(R) 위의 특정 유니터리 연산자 그룹으로, (Tf)(x) = f (x + y)와 e, (Mf)(x) = e f (x)의 곱셈에 의해 생성됩니다.이러한 연산자는 (그룹) 정류자가 다음과 같이 통근하지 않습니다.

${\displaystyle \left(M_{\xi}^{-1}T_{y}^{-1}M_{\xi}T_{y}f\right)(x)=e^{i2\pi \xiy}f(x)}$

이 값은 상수(x와는 무관) e ∈ U(1)(단위 계수 복소수의 원군)를 곱한 값입니다.추상군으로서, 하이젠베르크 군은 군 법칙을 갖는 3차원 삼중항 (x, ∈, z) ξ R × U(1)의 리 군입니다.

${\displaystyle \left(x_{1},\xi _{1}, t_{1}\right)\cdot \left(x_{2},\xi _{2}, t_{2}\right)=\left(x_{1}+x_{2},\xi _{1}+\xi _{2}, t_{1}t_{2}e^{i2\pi \left(x_{1})\xi _{1}+x_{2}}\xi _{2} +x_{1}\xi_{2}\right)}\right).$

하이젠베르크 군을 H로₁ 표시합니다.위의 절차는 그룹 구조뿐만 아니라 힐베르트 공간에서 H의 표준 단위 표현도 설명하는데, 우리는 이를 ρ: H → B(L(R))로 나타냅니다.다음으로² R의 선형 자기 변형을 정의합니다.

${\displaystyle J{\begin{pmatrix}x\xi \end{pmatrix}}={\begin{pmatrix}-\x\end{pmatrix}}$

J = -I가 되도록 합니다.이 J는 H의₁ 고유한 자기 변형으로 확장될 수 있습니다.

${\displaystyle j\left(x,\xi,t\right)=\left (-\xi,x,te^{-i2\pi \xi x}\right).}$

스톤-본 노이만 정리에 따르면, 유니터리 표현 ρ와 ρ ∘ j는 단위적으로 동치이므로, 다음과 같은 쌍성자 W ∈ U(L(R))가 있습니다.

${\displaystyle \rho \circ j=W\rho W^{*}}$

이 연산자 W는 푸리에 변환입니다.

푸리에 변환의 많은 표준 특성은 이 보다 일반적인 프레임워크의 즉각적인 결과입니다.^[26]예를 들어, 푸리에 변환의 제곱인 W는 J = -I와 연관된 쌍성자이므로 (Wf)(x) = f(-x)는 원래 함수 f의 반사입니다.

복소영역

푸리에 변환을 위한 적분

${\displaystyle {\hat {f}}(\xi )=\int _{-\infty}^{\infty}e^{-i2\pi \xiit}f(t)\,dt}$

인수 ξ의 복잡한 값에 대해 연구할 수 있습니다.f 의 속성에 따라 이 값은 실제 축에서 전혀 수렴되지 않거나 ξ = σ + i τ의 모든 값에 대한 복잡한 분석 함수로 수렴될 수 있습니다.

페일리-위너 정리는 f가 매끄럽고(즉, 모든 양의 정수 n에 대해 n배 미분 가능), f ̂ (σ + i τ)가 상수 a > 0이 존재하는 정칙 함수일 경우에만 압축적으로 지지된다고 말합니다.

${\displaystyle \left\vert \xi ^{n}{\hat {f}}(\xi )\right\vert \leq Ce^{a\vert \tau \vert}}$

어떤 일정한 C에 대하여. (이 경우 f는 [-a, a]에서 지원됩니다.)이는 f ̂가 σ에서 급격하게 감소하고(고정 τ의 경우), τ에서 기하급수적으로 증가하는(균일하게 σ의 경우) 전체 함수라고 말함으로써 표현될 수 있습니다.

(f가 매끄럽지 않고 L만인 경우, 문장은 n = 0인 경우에도 유지됩니다.)복소수 변수의 그러한 함수들의 공간을 Paley-Wiener 공간이라고 합니다.이 정리는 반단순 리 군으로 일반화되었습니다.^[30]

f가 반선 t ≥ 0에서 지원되는 경우 물리적으로 실현 가능한 필터의 충격 반응 함수가 원인보다 앞서는 효과가 없으므로 이 속성을 가져야 하므로 f는 "원인"이라고 합니다.페일리와 위너는 f ̂가 τ이 무한대로 갈수록 0으로 변하는 복잡한 하부 반평면 τ < 0에서 동형 함수로 확장됨을 보여주었습니다.역은 거짓이며 인과 함수의 푸리에 변환을 특성화하는 방법은 알려져 있지 않습니다.^[32]

라플라스 변환

푸리에 변환 f ̂(ξ)은 라플라스 변환 F(s)와 관련이 있으며, 미분 방정식 해와 필터 분석에도 사용됩니다.

푸리에 적분이 실제 축에 전혀 수렴하지 않는 함수 f는 그럼에도 불구하고 복소 평면의 일부 영역에서 정의된 복소 푸리에 변환을 가질 수 있습니다.

예를 들어, f(t)가 지수 성장이면, 즉,

${\displaystyle \vert f(t)\vert <Ce^{a\vert t\vert}}$

일부 상수 C, ≥ 0의 경우

${\displaystyle {\hat {f}}(i\tau)=\int_{-\infty}^{\infty}e^{2\pi \tau t}f(t)\,dt,}$

모든 2개의 πτ에 대하여 수렴 < -a, 는 양면 라플라스 변환 off입니다.

라플라스 변환의 더 일반적인 버전("편측")은

${\displaystyle F(s)=\int _{0}^{\infty}f(t)e^{-st}\,dt.}$

f 가 인과적이고 분석적인 경우${\displaystyle \stackrel{}{:}}$ $f{\displaystyle ^}$ (${\displaystyle i}$τ )${\displaystyle }$=${\displaystyle \mathrm{F}}$ ( -${\displaystyle }$π τ )$$. {\$displaystyle${\$hat$ {$f}$ (i$\$tau ) = F ($-2\pi$\tau )$$}$$ 따라서 복소 도메인으로 푸리에 변환을 확장한다는 것은 라플라스 변환을 인과 함수의 경우 특별한 경우로 포함시키지만 변수 s = i2 πξ의 변화로 포함한다는 것을 의미합니다.

다른, 아마도 더 고전적인 관점에서, 그것의 형태에 의한 라플라스 변환은 푸리에 변환이 정의된 가상의 선 밖에서 수렴할 수 있는 추가 지수 조절 항을 포함합니다.이와 같이, 그것은 기껏해야 지수 함수적으로 발산하는 급수와 적분에 대해 수렴할 수 있는 반면, 원래의 푸리에 분해는 수렴할 수 없고, 발산 또는 임계 요소가 있는 시스템의 분석을 가능하게 합니다.선형 신호 처리의 두 가지 특별한 예는 임계 콤브에서 모든 통과 필터 네트워크의 구성과 단위 원의 정확한 극-제로 제거를 통한 완화 필터입니다.이러한 설계는 반사에서와 같이 고도의 비선형 위상 응답이 요구되는 오디오 처리에서 일반적입니다.

또한, 신호 처리 작업을 위해 임펄스 응답과 같은 확장된 펄스를 추구할 때, 그것을 생성하는 가장 쉬운 방법은 발산 시간 응답을 생성하는 하나의 회로를 가진 후 지연된 반대 응답 및 보상 응답을 통해 발산을 취소하는 것입니다.거기서, 그 사이의 지연 회로만이 고전적인 푸리에 설명을 허용하는데, 이것은 매우 중요합니다.측면으로 가는 두 회로 모두 불안정하며, 수렴 푸리에 분해를 인정하지 않습니다.그러나, 그들은 복잡한 평면(또는 이산형의 경우, Z-평면)에서 수렴의 동일한 반평면을 갖는 라플라스 도메인 설명을 인정하고, 그 효과는 취소됩니다.

현대 수학에서 라플라스 변환은 일반적으로 이지스 푸리에 방법에 포함됩니다.두 가지 모두 훨씬 더 일반적이고 추상적인 조화 분석 개념에 포섭되어 있습니다.

반전

만약 f ̂가 a ≤ ≤ b에 대하여 복소해석적이면,

${\displaystyle \int _{-\infty}^{\infty}{\hat {f}}(\sigma +ia)e^{i2\pi \xit}\,d\sigma =\int _{-\infty}^{\infty}{\hat {f}}(\sigma +ib)e^{i2\pi \xit}\,d\sigma }$

코시의 적분 정리로따라서 푸리에 반전 공식은 실제 축과 평행한 서로 다른 선을 따라 적분을 사용할 수 있습니다.^[34]

정리:일부 상수 C에 대해 f(t) = 0 for t < 0, f(t) < Ce일 경우 a > 0,

${\displaystyle f(t)=\int _{-\infty}^{\infty}{\hat {f}}(\sigma +i\tau)^{i2\pi \xit}\,d\sigma,}$

모든 τ < -a/2 π에 대해.

이 정리는 라플라스 변환에 대한 멜린 반전 공식을 의미하며,^[33]

${\displaystyle f(t)={\frac {1}{i2\pi}}\int_{b-i\infty}^{b+i\infty}F(s)e^{st}\,ds}$

임의의 b > a에 대하여, 여기서 F(s)는 f(t)의 라플라스 변환입니다.

f가 t(cf)의 닫힌 이웃에서 경계 변동일 경우 칼레슨과 헌트의 결과와 같이 f(t) e가^−at L이¹ 되는 가설이 약화될 수 있습니다.디리클레-디니 정리), 지방의 값은 왼쪽과 오른쪽 한계의 산술 평균으로 간주되며, 적분이 코시 주값의 의미로 취해진다고 가정합니다.^[35]

이러한² 반전 공식의 L 버전도 사용할 수 있습니다.^[36]

유클리드 공간에서의 푸리에 변환

푸리에 변환은 임의의 수의 차원 n으로 정의될 수 있습니다.1차원의 경우와 마찬가지로 많은 관습이 있습니다.적분 가능한 함수 f(x)의 경우, 이 문서는 다음의 정의를 취합니다.

${\displaystyle {\hat {f}}({\bold 기호 {\xi}})={\mathcal {F}(f)({\bold 기호 {\xi}})=\int_{\mathbb {R}^{n}f(\mathbf {x})e^{-i2\pi {\bold 기호 {\xi}}\cdot \mathbf {x}}$

여기서 x와 ξ는 n차원 벡터이고, x· ξ는 벡터의 점곱입니다.대안적으로${\displaystyle {,}^{}}$ ξ는 이중 $벡터$ 공간 ${\displaystyle {}^{}}$⋆ {\$displaystyle$ \$mathbb {R}^{$n\$star}}$에 속한다고 볼 수 있으며$,$ 이 경우 점 곱은 x와 ξ의 축약이 되며, 보통 ⟨x, ξ⟩로 표기됩니다.

위에 나열된 모든 기본적인 성질들은 플랑셰렐의 정리와 파르스발의 정리와 마찬가지로 n차원 푸리에 변환을 유지합니다.함수가 적분 가능할 때, 푸리에 변환은 여전히 균일하게 연속적이고 리만-르베그 보조정리가 성립합니다.^[13]

불확정성원칙

일반적으로 말하면, f(x)가 더 집중될수록, 그 푸리에 변환 f ξ(̂)가 더 많이 퍼져야 합니다.특히, 푸리에 변환의 스케일링 특성은 다음과 같이 보일 수 있습니다: x에서 함수를 압축하면 푸리에 변환이 ξ으로 확장됩니다.함수와 푸리에 변환을 모두 임의로 집중시킬 수는 없습니다.

함수의 압축과 푸리에 변환 사이의 균형은 함수와 푸리에 변환을 시간-주파수 영역의 심플렉틱 형태에 대한 공액 변수로 봄으로써 불확정성 원리의 형태로 공식화될 수 있습니다: 선형 표준 변환의 관점에서, 푸리에 transform은 시간-주파수 영역에서 90°씩 회전하는 것이며, 심플렉틱 형태를 보존합니다.

f(x)가 적분 가능하고 제곱 가능한 함수라고 가정합니다.일반성을 잃지 않고 f(x)가 정규화되었다고 가정합니다.

${\displaystyle \int _{-\infty}^{\infty} f(x)^{2}\, dx=1.}$

f ̂(ξ)도 정규화된다는 것은 플랑셰럴 정리에서 따온 것입니다.

x = 0 주위의 퍼짐은 다음과 같이 정의된 0에 대한 분산에 의해 측정될 수 있습니다.

${\displaystyle D_{0}(f)=\int _{-\infty}^{\infty}x^{2} f(x)^{2}\, dx.}$

확률적으로 말하면, 이는 0에 대한 f(x)의 두 번째 순간입니다.

불확정성 원리는 만약 f(x)가 절대적으로 연속이고 함수 x·f(x)와 f'(x)가 제곱 적분 가능하다면^[10],

${\displaystyle D_{0}(f)$$D_{0}({\hat {f}})\geq {\frac {1}{16\pi ^{2$

경우에만 평등을 달성할 수 있습니다.

${\displaystyle {\begin{aligned}f(x)&=C_{1}\,e^{-\pi {\frac {x^{2}}{\sigma ^{2}}}\\\\therefore {\hat {f}(\xi)&=\sigma C_{1}\,e^{-\pi \sigma ^{2}\xi^{2}\end{aligned}}$

여기서 σ > 0은 임의이고 f가 L 정규화되도록 C = √2/√σ입니다.즉, f는 분산 σ/2 π를 갖는 (정규화된) 가우시안 함수이며, 중심은 0이고, 그 푸리에 변환은 분산 σ/2 π를 갖는 가우시안 함수입니다.

사실 이 부등식은 다음을 의미합니다.

${\displaystyle \left(\int _{-\infty }^{\infty }(x-x_{0})^{2}^{2}\left(\int _{-\infty }^{\infty }^{2})(\xi -\xi _{0})^{2}\left {\hat {f}(\xi )\right ^{2}\,d\xi \right)\geq {\frac {1}{16\pi ^{2}}}$

임의의 x에 대하여, ξ ∈ R.

양자역학에서 운동량과 위치 파동 함수는 플랑크 상수의 1배 이내로 푸리에 변환 쌍입니다.이 상수를 적절히 고려하면 위의 부등식은 하이젠베르크 불확정성 원리의 진술이 됩니다.^[39]

더 강력한 불확정성 원칙은 다음과 같이 표현되는 허쉬만 불확정성 원칙입니다.

${\displaystyle H\left(\left f\right ^{2}\right)+H\left(\left {\hat {f}}\right ^{2}\right)\geq \log \left({\frac {e}{2}}\right)}$

여기서 H(p)는 확률밀도함수 p(x)의 미분 엔트로피입니다.

${\displaystyle H(p)=-\int _{-\infty}^{\infty}p(x)\log {\bigl (}p(x){\bigr )}\, dx}$

로그가 일치하는 모든 베이스에 있을 수 있습니다.앞의 경우와 마찬가지로 가우시안에 대해서도 동일성을 가집니다.

사인 및 코사인 변환

푸리에의 원래 변환 공식은 복소수가 아니라 사인과 코사인을 사용했습니다.통계학자 등은 여전히 이 양식을 사용합니다.푸리에 반전이 유지되는 절대적 적분 가능 함수 f는 (때로는 물리적으로 해석하기 어려운 것으로 간주되는 음의 주파수를 피함) λ에 따라 확장될 수 있습니다.

${\displaystyle f(t)=\int _{0}^{\infty}{\bigl (}a(\lambda)\cos(2\pi \lambda t)+b(\lambda)\sin(2\pi \lambda t){\bigr )}\,d\lambda.}$

이를 삼각 적분 또는 푸리에 적분 확장이라고 합니다.계수 함수 a와 b는 푸리에 코사인 변환과 푸리에 사인 변환의 변형을 사용하여 찾을 수 있습니다(정규화는 다시 표준화되지 않았습니다).

${\displaystyle a(\lambda)=2\int _{-\infty}^{\infty}f(t)\cos(2\pi \lambda t)\,dt}$

그리고.

${\displaystyle b(\lambda)=2\int _{-\infty}^{\infty}f(t)\sin(2\pi \lambda t)\,dt.}$

오래된 문헌은 두 변환 함수인 푸리에 코사인 변환 a와 푸리에 사인 변환 b를 언급합니다.

함수 f 는 를 사용하여 사인 및 코사인 변환으로부터 복원할 수 있습니다.

${\displaystyle f(t)=2\int _{0}^{\infty }\int _{-\infty }^{\infty }f(\tau)\cos {\bigl(}2\pi \lambda(\tau -t){\bigr)}\,d\lambda \,d\tau.}$

삼각형 정체성과 함께.이를 푸리에 적분 공식이라고 합니다.^{[33][41][42][43]}

구면 조화

R에ⁿ 대한 차수 k의 동차 조화 다항식 집합을 A로_k 표시합니다.집합 A는_k k도의 고체 구형 고조파로 구성됩니다.입체 구면 조화는 1차원의 헤르마이트 다항식과 고차원에서 유사한 역할을 합니다.구체적으로, A의 일부 P(x)에 대해 f(x) = eP(x)이면 f ̂(ξ) = if(ξ)입니다.집합 H를_k P(x)가 A에_k 있는 f(x)P(x) 형태의 함수들의 선형 조합들의² L(Rⁿ)에서의 폐쇄라고 합니다.공간 L²(Rⁿ)은 공간 H의_k 직접 합이고 푸리에 변환은 각 공간 H를 자신에게_k 매핑하며 각 공간 H에_k 대한 푸리에 변환의 작용을 특성화할 수 있습니다.^[13]

f(x) = f(x)P(x)를 (A에 P(x))로 하면,

${\displaystyle {\hat {f}}(\xi )=F_{0}(\xi)P(\xi)}$

어디에

${\displaystyle F_{0}(r)=2\pi i^{-k}r^{-{\frac {n+2k-2}{2}}}\int_{0}^{\infty}f_{0}(s)J_{\frac {n+2k-2}{2}}(2\pir)s^{\frac {n+2k}{2}}\,ds.}$

여기서 J는_{(n + 2k − 2)/2} n + 2k - 2/2 순서의 첫 번째 종류의 베셀 함수를 나타냅니다.k = 0이면 방사 함수의 푸리에 변환에 유용한 공식을 제공합니다.이것은 본질적으로 행켈 변형입니다.또한, 1차원 함수로부터 방사 함수의 3차원 푸리에 변환과 같은 계산을 허용하는 경우 n + 2와 n과^[45] 관련된 간단한 재귀가 있습니다.

제한문제

더 높은 차원에서 푸리에 변환에 대한 제한 문제를 연구하는 것은 흥미로워집니다.적분 가능한 함수의 푸리에 변환은 연속적이며 이 함수의 모든 집합에 대한 제한이 정의됩니다.그러나 제곱 적분 가능 함수의 경우 푸리에 변환은 제곱 적분 가능 함수의 일반적인 클래스가 될 수 있습니다.이와² 같이, Lⁿ(R) 함수의 푸리에 변환의 제한은 측정값 0의 집합에서 정의될 수 없습니다.1 < p < 2에 대한 L의^p 제한 문제를 이해하는 것은 여전히 활발한 연구 영역입니다.놀랍게도, S가 0이 아닌 곡률을 가진다면 푸리에 변환의 제한을 집합 S로 정의하는 것이 가능합니다.S가 R에서ⁿ 단위 구인 경우가 특히 관심사입니다.이 경우 토마스-슈타인 제한 정리는 R의ⁿ 단위 구에 대한 푸리에 변환의 제한이 1 ≤ p ≤ 2n + 2/n + 3인 L에^p 대한 유계 연산자임을 나타냅니다.

1차원 대 고차원의 푸리에 변환 사이의 한 가지 주목할 만한 차이점은 부분합 연산자에 관한 것입니다.원점에 중심을 둔 반지름 R의 공 또는 변 2R의 정육면체와 같이 R ∈ (0, ∞)에 의해 색인화된 측정 가능한 집합 E의 증가하는 집합을 고려합니다.주어진 적분 가능한 함수 f에 대해 다음과 같이 정의된 함수 f를_R 고려합니다.

${\displaystyle f_{R}(x)=\int _{E_{R}}{\hat {f}}(\xi)e^{i2\pix x\cdot \xi}\, d\xi,\quad x\in \mathbb {R}^{n}}$

추가로 f가 L(R)을 ∈한다고 가정합니다.n = 1 및 1 < p < ∞, E = (-R, R)을 취하면, 힐베르트 변환의 경계성에 의해, R이 무한대가 됨에 따라 f는 L에서 f로 수렴합니다.순진하게도 n > 1에 대해서도 마찬가지이기를 바랄 수 있습니다.E가_R 변의 길이가 R인 정육면체가 될 경우 수렴은 여전히 유지됩니다.또 다른 자연 후보는 유클리드 공 E = {ξ : ξ < R}입니다.이 부분합 연산자가 수렴하기 위해서는 단위 공에 대한 승수가 L^p(Rⁿ)로 경계지어져야 합니다.n ≥ 2의 경우 단위 공의 승수는 p = 2가 아니면 경계가 없다는 것이 찰스 페퍼먼의 유명한 정리입니다.사실, p ≠ 2일 때, 이것은 f가 L에서 f로 수렴하는 것에 실패할 수 있을 뿐만 아니라, 일부 함수 f ∈ L(R)에 대하여, f는 심지어 L의 원소가 아니라는 것을 보여줍니다.

함수 공간에 대한 푸리에 변환

L공간에^p

온엘¹

적분 공식에 의한 푸리에 변환의 정의

${\displaystyle {\hat {f}}(\xi )=\int_{\mathbb {R}^{n}}f(x)e^{-i2\pi \xi \cdot x}\,dx}$

는 르베그 적분 가능 함수 f, 즉 f ∈ L(R)에 유효합니다.

푸리에 변환 F : L(R) → L(R)은 유계 연산자입니다.이것은 다음과 같은 관찰을 통해서.

${\displaystyle \left\vert {\hat {f}}(\xi )\right\vert \leq \int _{\mathbb {R} ^{n}}\vert f(x)\vert \,dx,}$

이는 연산자 노름이 1로 경계지어짐을 보여줍니다.실제로 1과 같으며, 이는 예를 들어 직함수의 변환을 통해 알 수 있습니다.L의¹ 상은 무한대에서 0이 되는 경향이 있는 연속 함수의 공간₀ C(Rⁿ)의 부분 집합입니다.실제로 이미지의 단순한 특징은 없습니다.

온엘²

콤팩트하게 지원되는 매끄러운 함수는² L(Rⁿ)에서 적분 가능하고 밀도가 높기 때문에, 플랑셰럴 정리는 연속성 인수에 의해 푸리에ⁿ 변환의 정의를 L²(R)의 일반 함수로 확장할 수 있습니다.L²(Rⁿ)의 푸리에 변환은 더 이상 일반적인 르베그 적분에 의해 주어지지 않지만, 부적절한 적분에 의해 계산될 수 있음에도 불구하고, 여기서 L 함수² f에 대해,

${\displaystyle {\hat {f}}(\xi )=\lim _{R\to \infty}\int _{ x \leq R}e^{-i2\pi \xi \cdot x}\, dx}$

L의² 의미에서 극한을 취합니다. (보다 일반적으로 L과¹ L의² 교집합에 있고 L-norm에서² f로 수렴하는 함수의 순서를 취하여 f의 푸리에 변환을 이들 함수의 푸리에 변환의 L-한계로² 정의할 수 있습니다.)^[46]

L에서¹ 푸리에 변환의 많은 속성들은 적절한 제한 인수에 의해 L로² 전달됩니다.

또한 F : L(R) → L(R)은 유니터리 연산자입니다.연산자가 단일할 때는 그것이 비사적이고 내부 곱을 보존한다는 것을 보여주면 충분하므로 이 경우 이들은 임의의 f, g ∈ L(R)에 대해 다음을 갖는다는 사실과 결합된 푸리에 반전 정리로부터 따릅니다.

${\displaystyle \int _{\mathbb {R} ^{n}}f(x){\mathcal {F}g(x)\,dx=\int _{\mathbb {R} ^{n}}{\mathcal {F}f(x)g(x)\,dx.}$

특히 L²(Rⁿ)의 이미지는 그 자체로 푸리에 변환 하에 있습니다.

기타 L에^p

푸리에 변환의 정의는 L의 뚱뚱한 꼬리² 부분과 L의¹ 뚱뚱한 몸통 부분으로 분해함으로써 1≤p≤2에 대한 L^p(Rⁿ)의 함수로 확장될 수 있습니다.각 공간에서 L(R)의 함수의 푸리에 변환은 L(R)에 있으며, 여기서 q = p/p - 1은 (하우스도르프에 의해) p의 ö더 켤레입니다.젊은 불평등).그러나 p = 2를 제외하고는 이미지의 특징이 쉽게 나타나지 않습니다.추가적인 확장은 더욱 기술적인 것이 됩니다.범위 2 < p < ∞에 대한 L의 함수의 푸리에 변환은 분포 연구를 필요로 합니다.실제로, 푸리에 변환이 함수로 정의되지 않도록 p > 2인 L에^p 함수가 있음을 알 수 있습니다.^[13]

강화분포

일반화된 함수 또는 분포를 고려하여 L¹ + L에서² 푸리에 변환의 도메인을 확장하는 것을 고려할 수 있습니다.R에ⁿ 대한 분포는 적합한 토폴로지를 갖춘 콤팩트하게 지원되는 평활 함수의 공간 C_c(Rⁿ)에 대한 연속 선형 함수입니다.그 다음 전략은 C_c(Rⁿ)에 대한 푸리에 변환의 작용을 고려하고 이중성에 의해 분포로 전달하는 것입니다.이렇게 하는 데 방해가 되는 것은 푸리에 변환이 C(Rⁿ)를_c C_c(Rⁿ)에 매핑하지 않는다는 것입니다.사실 C_c(Rⁿ)에서 원소의 푸리에 변환은 열린 집합에서 사라질 수 없습니다. 불확정성 원리에 대한 위의 논의를 참조하십시오.여기서 오른쪽 공간은 슈워츠 함수의 약간 더 큰 공간입니다.푸리에 변환은 위상 벡터 공간인 슈워츠 공간에서의 오토모피즘이며, 따라서 이중성인 강화 분포 공간에서 오토모피즘을 유도합니다.^[13]강화된 분포는 위에서 언급한 모든 통합 가능한 함수뿐만 아니라 다항식 성장 및 소형 지지 분포의 양호한 함수를 포함합니다.

강화 분포의 푸리에 변환의 정의를 위해, f와 g를 적분 가능한 함수라고 하고, f ̂와 ĝ를 각각 푸리에 변환이라고 합니다.그러면 푸리에 변환은 다음과 같은 곱셈 공식을 따릅니다.^[13]

${\displaystyle \int _{\mathbb {R} ^{n}}{\hat {f}(x)\, dx=\int _{\mathbb {R} ^{n}}f(x){\hat {g}(x)\, dx.}$

모든 적분 가능한 함수 f는 관계에 의해 분포 T를_f 정의(유도)합니다.

${\displaystyle T_{f}(\varphi )=\int_{\mathbb {R}^{n}}f(x)\varphi(x)\,dx}$

모든 Schwartz 함수에 대해 φ.따라서 T의 푸리에 변환 T ̂을 다음과 같이 정의하는 것이 타당합니다.

${\displaystyle {\hat {T}}_{f}(\varphi )=T_{f}\left({\hat {\varphi}}\right)}$

모든 Schwartz 함수에 대해 φ.이를 모든 강화 분포 T로 확장하면 푸리에 변환의 일반적인 정의를 얻을 수 있습니다.

분포를 미분할 수 있으며, 미분과 컨볼루션을 가진 푸리에 변환의 위에서 언급된 호환성은 강화된 분포에서 그대로 유지됩니다.

일반화

푸리에-슈틸트제스 변환

R에ⁿ 대한 유한 보렐 측정 μ의 푸리에 변환은 다음과 같이 주어집니다.^[48]

${\displaystyle {\hat {\mu}}(\xi )=\int_{\mathbb {R}^{n}e^{-i2\pix\cdot \xi}\,d\mu.}$

이 변환은 적분 가능한 함수의 푸리에 변환의 많은 특성을 계속해서 즐깁니다.한 가지 주목할 만한 차이점은 리만-레베그 보조정리가 측도에 실패한다는 것입니다.^[12]dμ = f(x) dx인 경우 위의 공식은 f 의 푸리에 변환에 대한 일반적인 정의로 줄어듭니다.μ가 임의 변수 X와 관련된 확률 분포인 경우, 푸리에-슈틸트제스 변환은 특성 함수와 밀접한 관련이 있지만 확률 이론의 일반적인 규칙은 e 대신^−i2πξx e를^iξx 사용합니다.^[10]분포에 확률 밀도 함수가 있는 경우, 이 정의는 확률 밀도 함수에 적용되는 푸리에 변환으로 감소하며, 상수의 선택이 다릅니다.

푸리에 변환은 측도의 특성화를 위해 사용될 수 있습니다.보흐너의 정리는 원에 대한 양의 측도의 푸리에-슈틸트제스 변환으로 어떤 함수가 발생할 수 있는지를 특징짓습니다.^[12]

또한 디랙 델타 함수는 함수는 아니지만 유한 보렐 측도입니다.푸리에 변환은 상수 함수입니다(특정 값은 사용되는 푸리에 변환의 형태에 따라 달라집니다).

국소 콤팩트 아벨 군

푸리에 변환은 임의의 국소 콤팩트 아벨 군으로 일반화될 수 있습니다.국소 콤팩트 아벨리아 군은 아벨리아 군이며, 동시에 국소 콤팩트 하우스도르프 위상 공간이므로 군 연산이 연속적입니다.만약 G가 국소적으로 콤팩트한 아벨 군이라면, 그것은 Haar measure라고 불리는 병진 불변 측정 μ를 갖습니다.국소적으로 콤팩트한 아벨 군 G의 경우 축소할 수 없는, 즉 1차원, 단일 표현의 집합을 문자라고 합니다.자연스러운 그룹 구조와 콤팩트 집합에 대한 균일한 수렴의 위상($즉$, G ${\displaystyle G}$에서 원 그룹으로 이어지는 모든 연속 함수의 공간에서 콤팩트 오픈 위상에 의해 유도되는 위상)을 가진 문자 집합 ĝ는 그 자체로 G의 폰트랴긴 이중이라고 불리는 국소적인 콤팩트 아벨 군입니다.L¹(G)의 함수 f에 대하여, 그 푸리에 변환은 다음과^[12] 같이 정의됩니다.

${\displaystyle {\hat {f}}(\xi )=\int _{G}\xi(x)f(x)\,d\mu \quad {\text{any}}}\xi \in {\hat {G}}}$

이 경우에는 리만-레베그 보조정리가 성립합니다. f ̂(ξ)는 ĝ에서 무한대로 사라지는 함수입니다.

T = R/Z에 대한 푸리에 변환이 한 예입니다. 여기서 T는 국부적으로 콤팩트한 아벨 군이며 T의 Haar 측정 μ는 [0,1]에 대한 르베그 측정으로 생각할 수 있습니다.1차원 복소 벡터 공간인 복소 평면 C에서의 T의 표현을 생각해보세요.표현 그룹(C가 1차원이므로 축소할 수 없음)$${ ${\displaystyle {ek}_{}}$ :${\displaystyle {}_{}T}$ → ${\displaystyle {}_{}}$ ${\displaystyle 1_{}}$ (${\displaystyle {}_{}C}$ )${\displaystyle }$= ${\displaystyle {}^{}}$ ∗ ∣${\displaystyle k}$ ∈ ${\displaystyle Z}$ ${\displaystyle \}}$ ${\displaystyle \{e_{k$}}가 있습니다$.$$T$$\$오른쪽 $화살표 GL_{1}(C)=C^{*}\mid k\in$ Z$\},$ 여기서 x$$$∈$ ${\displaystyle T}$ ${\displaystyle x\in T}$에 대해${\displaystyle {}_{}{\mathrm{ek}}^{}}$ ($x)$$=$ ei 2 $π$ k x {\displaystyle $e_{k}(x$)$=$ e$^{i2\pikx}}.$

각 $x$ ∈ ${\displaystyle T}$ ${\displaystyle x\in T}$ 및 ${\displaystyle k}$ ∈ Z ${\displaystyle k\in Z}$에 대한 ${\displaystyle e_{}x)}$ ${\displaystyle k\$in Z$}$의 추적인 이러한 표현의 문자는$$${\displaystyle {ei}^{}}$ ${\displaystyle 2^{}}$ π k ${\displaystyle x^{}}$ ${\displaystyle e^{i2\pikx}$ 그 자체입니다.유한 그룹 표현의 경우, 그룹 G의 문자 표는 각 행이 G의 축소할 수 없는 하나의 표현의 문자인 벡터의 행이고, 이 벡터는 슈어의 보조자에 의해 G에서 C로 매핑되는 클래스 함수의 공간의 정규 표준 기저를 형성합니다.이제 그룹 T는 더 이상 유한하지 않고 여전히 압축적이며 문자 테이블의 직교성을 보존합니다.테이블의 각 행은 $x$ ∈ ${\displaystyle T,}$ ${\displaystyle x\in T,}$의 함수 ${\displaystyle {ek}_{}}$(${\displaystyle x)}$ ${\displaystyle e_{k}(x))$이며 두 ${\displaystyle \mathrm{클래스}}$ 함수(T가 아벨리안이므로 모든 함수가 클래스 함수임) $f$,${\displaystyle }$g ∈ ${\displaystyle {}^{}}$ 2 (${\displaystyle T^{},}$ ${\displaystyle d}$ μ${\displaystyle )}$ ${\displaystyle f,g\in$ L$^{2}(T,d\mu )}$이(가) ⟨ $f$,$g$ ⟩ = 1 $\frac{T}{}$ ∫ ${[0,}_{}$ $1_{}$ )${}_{}f$( y$$) $g$ ¯ ($$y$$) $d$ $\mu$( y$$)$${$\$${\displaystyle textstyle}$$$f$,$g$\$$rangle$ $=$ {\$frac$ {$1}{$T$}}\int _{[0,1]}f(y){\overline {g}}(y)d\mu(y)}$와 정규화 인자 T$$$=$$1입니다.$수열$${${\displaystyle {ek}_{}}$ ∣ ${\displaystyle k}$ ∈ ${\displaystyle Z\}}$ ${\displaystyle \{e_{k}\mid k\in$ Z$\}$는 클래스 함수 $L2$ ${\displaystyle d}$ ${\displaystyle \mu )}$ ${\displaystyle$ L$^{2}(T,d\mu )}$의 정규 공간 기반입니다$.$

유한 그룹 G의 임의의 표현 V에 대하여, χ v ${\displaystyle \chi _{v}}$는 스판$$∑ $\underset{}{i}$ ⟨ χ $v_{}$ χ vi ⟩ χ ${{vi}_{}}_{}${\$textstyle \sum _{i}\left\$lang $\chi _{v},\chi _{v_{i}}\right\rangle \chi _{v_{i}}($${\displaystyle {Vi}_{}}$ ${\displaystyle V_{i})$는 ⟨ χ v,${}_{}$χ ${{vi}_{}}_{}$ = 1 $\frac{G}{}$ ∑ $\underset{}{G}$ χ $v_{}$ ${}_{}g)$ χ ¯ ${{vi}_{}}_{}$ ${{}_{}}_{}g)${\$textstyle \left\l$$각도 \chi _$$\{$$v},\chi _{v_{i}}\right\rangle$ $=$ ${\frac {1}{G }}\sum _{g\in$ G$}\chi _{v}(g){\overline {\chi }}_{v_{i}}(g$ ${\displaystyle \mathrm{마찬가지}}$로 G $=$$$T {\$displaystyle$ G$=$$T$} $및{\displaystyle }$f $∈$ ${\displaystyle {}^{}}$ ${\displaystyle 2^{}}$(${\displaystyle T,}$ d $)$ {\$displaystyle f\in L^{$2}($T$$, d$\mu$$$)\},$ $f$( x ) $=$ $∈$ $\underset{}{k}$ $∑$ $\underset{}{Z}$ $\underset{}{}^(k_{}$ ) e$$k {\$textstyle$ f$(x$)$=$ $_sum$ {$k\in$ Z$}{\hat {f}e_{k}}.$Pontriagin $이중{\displaystyle \stackrel{}{}}$T$^$ {\$displaystyle {\hat {T}}$는 $\{$ ${\displaystyle e_{}}$ k${\displaystyle }$∈ ${\displaystyle Z\}}${\$displaystyle$\{$e_{k}\}(k\in$ Z$)}$이고, $f$ ∈ ${\displaystyle {L2}^{}T,}$ ${\displaystyle d}$ μ${\displaystyle )}${\$displaystyle$ f$\in$ L$^{2}(T,d\mu )},$$f$ $\stackrel{}{^}$ $(k)$= $1$ $\frac{T}{}$ ∫ [${0,}_{}$ $1_{}$) ${}_{}$($y$ ) ${}^{}$- $i^{}$ $2^{}$ π k ${}^{}$y {\textstyle {\hat ${f}(k$) = {\$frac {1}{T}}\int _{[0,1]}f(y)e^{-i2\pi$ ky$}dy}$는 e k ∈ ${\displaystyle T\stackrel{}{^}}$ ${\$$text}$에 대한 푸리에 변환입니다.$aystyle$ e_{$k$$in {\hat$ {$T}}.$

겔판 변환

푸리에 변환은 겔판 변환의 특별한 경우이기도 합니다.이러한 특수한 맥락에서, 그것은 위에서 정의된 Pontryagin 이중성 지도와 밀접한 관련이 있습니다.

하르 측도를 사용하여 정의된 공간 L¹(G)을 고려하기 전과 같이 아벨리안 국소 콤팩트 하우스도르프 위상 그룹 G가 주어집니다.L¹(G)는 아벨리안 바나흐 대수입니다.또한 *에 의해 주어진 involution을 가지고 있습니다.

${\displaystyle f^{*}(g)={\overline {f\left(g^{-1}\right)}}}$

가장 큰 C*-노름에 대한 완성을 취하면 G의 C*-대수 C*(G) 그룹이라고 불리는 C*-대수를 포함합니다. (L¹(G)의 모든 C*-노름은 L¹ 노름에 의해 경계지어지므로 그들의 우월성이 존재합니다.)

임의의 아벨리안 C*대수 A가 주어졌을 때, 겔판드 변환은 A와₀ C(A^) 사이에 동형을 제공하며, 여기서 A^는 약한-* 위상을 가진 A에 대한 곱셈 선형 함수, 즉 1차원 표현입니다.지도는 간단히 다음과 같이 제공됩니다.

${\displaystyle a\maps to {\bigl(}\varphi \maps to \varphi(a){\bigr )}}$

C*(G)의 곱셈 선형 함수는 적절한 식별 후에 정확히 G의 문자이며, 겔판 변환은 밀도가 높은 부분 집합 L¹(G)로 제한될 때 푸리에-퐁트랴긴 변환임이 밝혀졌습니다.

컴팩트한 비벨리안 그룹

푸리에 변환은 그룹이 콤팩트한 경우 비 아벨리안 그룹의 함수에 대해서도 정의할 수 있습니다.기본 그룹이 아벨리안이라는 가정을 제거하면 축소 불가능한 단일 표현이 항상 1차원일 필요는 없습니다.이것은 비 아벨리안 그룹의 푸리에 변환이 힐베르트 공간 연산자로 값을 취한다는 것을 의미합니다.^[49]콤팩트 그룹의 푸리에 변환은 표현 이론과^[50] 비가환 조화 분석의 주요 도구입니다.

G를 콤팩트 하우스도르프 위상군이라 하자.σ가 각 σ σ ∈ 에 대해 유한 차원 d의 힐베르트 공간 H에 대한 표현 U의 확실한 선택과 함께 유한 차원 축소 불가능한 단일 표현의 모든 동형 사상 클래스의 집합을 나타내도록 하자. μ가 G에 대한 유한 보렐 측도라면, μ의 푸리에-슈틸트제스 변환은 다음과 같이 정의된 H에 대한 연산자입니다.

${\displaystyle \left\langle {\hat {\mu}},\eta \right\rangle _{H_{\sigma}}=\int _{G}\left\rangle {\overline {U}}_{g}^{(\sigma )}\xi,\eta \right\rangle \,d\mu(g))}$

여기서 U는 H에 작용하는 U의 복소-공액 표현입니다. 만약 μ가 G에 대한 좌불변 확률 측도 λ에 대하여 절대적으로 연속이면 다음과 같이 표현됩니다.

${\displaystyle d\mu =f\,d\lambda }$

일부 f ∈ L(λ)에 대하여, f 의 푸리에 변환을 μ의 푸리에-슈틸트제 변환으로 식별합니다.

지도를

${\displaystyle \mu \maps to {\hat {\mu}}}$

유한 보렐 측도의 바나흐 공간 M(G)과 바나흐 공간 C(σ)의 닫힌 부분 공간 사이의 동형을 정의하며, 이는 (bounded) 선형 연산자 E: H → H의 σ에 의해 지수화된 모든 수열 E = (E)로 구성됩니다.

${\displaystyle \E\ =\sup _{\sigma \in \Sigma}\left\E_{\sigma}\right\}$

유한합니다."해면 정리"는 더 나아가 바나흐 공간의 이 동형이 사실 C*-대수를 C_∞(C)의 부분 공간으로 하는 동형이라는 것을 주장합니다.M(G)에 대한 곱셈은 측도의 컨볼루션과 다음에 의해 정의된 적분 *에 의해 주어집니다.

${\displaystyle f^{*}(g)={\overline {f\left(g^{-1}\right)}},}$

그리고 C(σ)는 힐베르트 공간 연산자로서 자연적인 C*대수 구조를 가지고 있습니다.

피터-웨일 정리는 성립하며, 푸리에 반전 공식의 버전(플랑쉐럴 정리)은 다음과 같습니다: 만약 ∈ L(G)이면,

${\displaystyle f(g)=\sum _{\sigma \in \Sigma }d_{\sigma }\연산자 이름 {tr} \left ({\hat {f}(\sigma )U_{g}^{(\sigma)}\right)}$

여기서 합은 L 의미에서² 수렴하는 것으로 이해됩니다.

비호환적 상황으로의 푸리에 변환의 일반화는 또한 비호환적 기하학의 발전에 부분적으로 기여했습니다.^{[citation needed]}이러한 맥락에서, 푸리에 변환을 비상호적 그룹으로 범주적으로 일반화하는 것은 타나카-크레인 이중성이며, 이는 문자 그룹을 표현 범주로 대체합니다.그러나 이 경우 고조파 함수와의 연결이 끊어집니다.

대안

신호 처리 용어에서, (시간의) 함수는 시간 분해능은 완벽하지만 주파수 정보는 없는 신호의 표현인 반면, 푸리에 변환은 주파수 분해능은 완벽하지만 시간 정보는 없습니다: 한 점에서의 푸리에 변환의 크기는 주파수 내용의 양이지만 위치는 오직 ph에 의해서만 주어집니다.ase(한 점에서 푸리에 변환의 주장), 그리고 정상파는 시간적으로 국부화되지 않습니다. 사인파는 붕괴되지 않고 무한대로 계속됩니다.이는 시간적으로 국부화된 신호, 특히 과도 신호 또는 유한한 범위의 신호를 분석하는 푸리에 변환의 유용성을 제한합니다.

시간-주파수 분석에서 시간-주파수 변환 또는 시간-주파수 분포를 사용하여 시간 정보와 주파수 정보가 있는 형태로 신호를 표현합니다. 불확정성 원리에 의해 이들 사이에 균형이 있습니다.이것들은 짧은 시간 푸리에 변환 또는 분수 푸리에 변환과 같은 푸리에 변환의 일반화이거나 (연속) 푸리에 변환의 웨이블릿 아날로그가 연속 웨이블릿 변환인 경우와 같이 신호를 나타내는 다른 함수일 수 있습니다.^[21]

적용들

한 도메인(시간 또는 빈도)에서 수행되는 선형 작업은 다른 도메인에서 해당 작업을 수행하기가 더 쉬운 경우도 있습니다.시간 영역에서의 미분 연산은 빈도에 의한 곱셈에 해당하므로,^{[note 6]} 일부 미분 방정식은 빈도 영역에서 분석하기가 더 쉽습니다.또한 시간 영역에서의 컨볼루션은 주파수 영역에서의 보통의 곱셈에 해당합니다(Convolution 정리 참조).원하는 작업을 수행한 후 결과를 시간 영역으로 변환할 수 있습니다.하모닉 분석은 주파수 영역과 시간 영역 사이의 관계를 체계적으로 연구하는 것으로, 하나 또는 다른 영역에서 "단순"한 함수 또는 연산의 종류를 포함하며 현대 수학의 많은 영역과 깊은 연관성을 가지고 있습니다.

미분방정식의 해석

아마도 푸리에 변환의 가장 중요한 용도는 편미분 방정식을 푸는 것일 것입니다.19세기의 수학 물리학의 많은 방정식들은 이런 식으로 취급될 수 있습니다.푸리에는 1차원과 무차원 단위에서 열 방정식을 연구했습니다.

${\displaystyle {\frac {\partial ^{2}y(x,t)}{\partial ^{2}x}}={\frac {\partial y(x,t)}{\partial t}}}}$

조금 더 어려운 예는 1차원의 파동 방정식입니다.

${\displaystyle {\frac {\partial ^{2}y(x,t)}{\partial ^{2}x}}={\frac {\partial ^{2}y(x,t)}{\partial ^{2}t}}}}$

평소처럼 문제는 해결책을 찾는 것이 아닙니다. 무한히 많습니다.문제는 이른바 "경계 문제"의 문제입니다. "경계 조건"을 만족시키는 해결책을 찾는 것입니다.

${\displaystyle y(x,0)=f(x),\qquad {\frac {\partial y(x,0)}{\partial t}}=g(x)}$

여기서 f와 g는 주어진 함수입니다.열 방정식의 경우 경계 조건은 하나(일반적으로 첫 번째)만 필요합니다.하지만 파동 방정식의 경우, 첫 번째 경계 조건을 만족시키는 해 y는 여전히 무한히 많습니다.그러나 두 조건을 모두 부과할 때 가능한 해결책은 하나뿐입니다.

해를 직접 찾는 것보다 해의 푸리에 변환 ŷ을 찾는 것이 더 쉽습니다.이는 푸리에 변환이 푸리에-이중 변수에 의한 곱셈으로 미분을 취하고, 따라서 원래 함수에 적용된 편미분 방정식이 변환된 함수에 적용된 이중 변수의 다항식 함수에 의한 곱셈으로 변환되기 때문입니다.ŷ이 결정된 후 역 푸리에 변환을 적용하여 y를 찾을 수 있습니다.

푸리에의 방법은 다음과 같습니다.첫째, 양식의 어떤 기능이든

${\displaystyle \cos {\bigl(}2\pi \xi(x\pm t){\bigr )}{\mbox{ or }}\sin {\bigl(}2\pi \xi(x\pm t){\bigr )}$

파동 방정식을 만족합니다.이것들은 기본적인 해결책이라고 불립니다.

둘째, 따라서 어떤 적분도

는 임의의 a₊, a₋, b, b에₊₋ 대한 파동방정식을 만족합니다.이 적분은 선형 방정식에 대한 해의 연속적인 선형 조합으로 해석될 수 있습니다.

이제 이것은 함수의 푸리에 합성 공식과 비슷합니다.사실 이것은 변수 x에서 a와_± b의_± 실제 역푸리에 변환입니다.

세 번째 단계는 경계 조건을 만족시키는 y로 이어질 특정 미지의 계수 함수 a와_± b를_± 찾는 방법을 조사하는 것입니다.우리는 t = 0에서 이 해들의 값에 관심이 있습니다. 그래서 우리는 t = 0을 설정할 것입니다. 푸리에 반전에 필요한 조건이 만족된다고 가정하면, 우리는 양변의 푸리에 사인과 코사인 변환 (변수 x에서)을 구하고 다음을 얻을 수 있습니다.

${\displaystyle 2\int _{-\infty}^{\infty}y(x,0)\cos(2\pi \xxx)\, dx=a_{+}+a_{-}$

그리고.

${\displaystyle 2\int _{-\infty}^{\infty}y(x,0)\sin(2\pi \xxx)\, dx=b_{+}+b_{-}}$

마찬가지로, t에 대하여 y의 도함수를 취한 후 푸리에 사인 및 코사인 변환을 적용하면 산출됩니다.

${\displaystyle 2\int _{-\infty}^{\infty}{\frac {\partial y(u,0)}{\partial t}\sin(2\pi \xi)\, dx=(2\pi \xi )\left (-a_{+}+a_{-}\right)}$

그리고.

${\displaystyle 2\int _{-\infty}^{\infty}{\frac {\partial y(u,0)}{\partial t}}\cos(2\pi \xi)\, dx=(2\pi \xi )\left(b_{+}-b_{-}\right)}$

이것들은 경계 조건의 푸리에 사인 및 코사인 변환의 관점에서, 이들 변환이 발견될 수 있다면 쉽게 해결되는 4개의 미지 a_± 및 b에_± 대한 4개의 선형 방정식입니다.

요약하면, 우리는 ξ에 의해 매개변수화된 일련의 기본 솔루션을 선택했는데, 그 중 일반 솔루션은 매개변수 ξ에 대한 적분 형태의 (연속) 선형 조합입니다.하지만 이 적분은 푸리에 적분의 형태였습니다.다음 단계는 경계 조건을 이러한 적분으로 표현하고 주어진 함수 f와 g와 같게 설정하는 것이었습니다.그러나 이 표현들은 또한 도함수의 푸리에 변환의 특성 때문에 푸리에 적분의 형태를 취했습니다.마지막 단계는 양변에 푸리에 변환을 적용하여 푸리에 반전을 이용하여 주어진 경계 조건 f와 g의 관점에서 계수 함수_± a와 b에_± 대한 식을 구했습니다.

더 높은 관점에서, 푸리에의 절차는 더 개념적으로 재구성될 수 있습니다.두 개의 변수가 있기 때문에 공간 변수에서만 변환을 수행한 푸리에처럼 연산하기보다는 x와 t 모두에서 푸리에 변환을 사용할 것입니다.y(x, t)는 L이 되지 않기 때문에 ŷ은 분포의 의미에서 고려되어야 합니다: 파동으로서, 시간에 걸쳐 지속되므로 일시적인 현상이 아닙니다.그러나 그것은 경계가 있을 것이고 따라서 그것의 푸리에 변환은 분포로 정의될 수 있습니다.이 방정식과 관련된 푸리에 변환의 연산 특성은 x에서 i2 πξ에 의한 곱셈에 대한 미분과 i2 πf에 의한 곱셈에 대한 미분이 필요하다는 것입니다. 여기서 f는 주파수입니다.그러면 파동 방정식은 ŷ에서 대수적 방정식이 됩니다.

${\displaystyle \xi ^{2}{\hat {y}}(\xi,f)=f^{2}{\hat {y}}(\xi,f).}$

이는 ξ = ±f가 아닌 한 ŷ(ξ, f) = 0을 필요로 하는 것과 같습니다.이것은 우리가 이전에 만든 기본 솔루션을 선택한 이유를 설명해 줍니다. f ̂ = δ(ξ ± f)가 솔루션이 될 것입니다.이러한 델타 함수에 푸리에 반전을 적용하면 앞서 선택한 기본 해를 얻을 수 있습니다.그러나 높은 관점에서 보면 기본 해를 선택하는 것이 아니라 (퇴행) 원뿔 ξ - f = 0에서 지원되는 모든 분포의 공간을 고려합니다.

우리는 다음과 같이 선 ξ = f 위의 한 변수에 대한 분포와 선 ξ = -f 위의 분포에 의해 제공되는 원뿔에 지원되는 분포를 고려할 수도 있습니다. 만약 φ가 어떤 검정 함수라면,

${\displaystyle \iint {\hat {y}}\phi(\xi,f)\,d\xi \,df=\ints_{+}\phi(\xi,\xi )\,d\xi +\ints_{-}\phi(\xi,-\xi )\,d\xi,}$

여기서 s와₊ s는₋ 하나의 변수의 분포입니다.

그리고 푸리에 반전은 경계 조건에 대해 우리가 더 구체적으로 위에 가졌던 것과 매우 유사한 것을 제공합니다(임의 다항식 성장에 대해 분명히 φ(ξ, f) = e).

${\displaystyle y(x,0)=\int {\bigl \{}s_{+}(\xi)+s_{-}(\xi){\bigr \}e^{i2\pi \xi x+0}\,d\xi }$

그리고.

${\displaystyle {\frac {\partial y(x,0)}{\partial t}=\int {\bigl \{}s_{+}(\xi)-s_{-}(\xi){\bigr \}i2\pi \xi e^{i2\pi \xi x+0}\,d\xi.}$

이제 이전과 마찬가지로 변수 x의 1변수 푸리에 변환을 x의 이러한 함수에 적용하면 두 미지의 분포 s에서_± 두 개의 방정식이 생성됩니다(경계 조건이 L¹ 또는 L인² 경우 일반 함수로 간주될 수 있음).

계산적 관점에서 보면, 경계조건의 푸리에 변환을 먼저 계산하고, 이로부터 해를 조립한 후 역 푸리에 변환을 계산해야 하는 단점이 있습니다.닫힌 형태 공식은 활용할 수 있는 기하학적 대칭이 있을 때를 제외하고는 드물고, 적분의 진동 특성 때문에 수치 계산이 어렵습니다. 이는 수렴이 느리고 추정하기 어렵습니다.실제 계산의 경우 다른 방법을 사용하는 경우가 많습니다.

20세기에는 이러한 방법이 다항식 계수를 가진 모든 선형 편미분 방정식으로 확장되었고, 푸리에 변환의 개념을 푸리에 적분 연산자를 포함하도록 확장함으로써 일부 비선형 방정식도 볼 수 있었습니다.

푸리에 변환 분광법

푸리에 변환은 핵자기공명(NMR)과 적외선(FTIR)과 같은 다른 종류의 분광학에서도 사용됩니다.NMR에서 지수형 자유 유도 붕괴(FID) 신호는 시간 영역에서 획득되고 주파수 영역에서 로렌츠 선 모양으로 푸리에 변환됩니다.푸리에 변환은 자기공명영상(MRI) 및 질량분석에도 사용됩니다.

양자역학

푸리에 변환은 양자역학에서 적어도 두 가지 다른 방법으로 유용합니다.우선, 양자역학의 기본 개념 구조는 하이젠베르크 불확정성 원리에 의해 연결된 상보 변수 쌍의 존재를 가정합니다.예를 들어, 1차원에서 입자의 공간 변수 q는 입자의 운동량 p에 대한 정보를 잃는 비용으로 양자역학적 "위치 연산자"에 의해서만 측정될 수 있습니다.따라서 입자의 물리적 상태는 q의 "파동 함수"라고 불리는 함수 또는 p의 함수로 설명될 수 있지만 두 변수의 함수로 설명될 수는 없습니다.변수 p를 q에 대한 켤레 변수라고 합니다.고전 역학에서, 입자의 물리적 상태(1차원에 존재하며, 표현의 단순성을 위해)는 p와 q 모두에 동시에 정칙값을 할당함으로써 주어질 것입니다.따라서, 모든 가능한 물리적 상태의 집합은 위상 공간이라고 불리는 p축과 q축을 갖는 2차원 실제 벡터 공간입니다.

이와는 대조적으로, 양자역학은 q축과 같이 1/2 차원의 부분 공간을 선택하고, 점만 고려하는 대신 이 축의 모든 복소수 "파동 함수" 집합을 선택한다는 점에서 이 공간의 편광을 선택합니다.그럼에도 불구하고, p축을 선택하는 것은 똑같이 유효한 편광이며, 입자의 가능한 물리적 상태의 집합에 대한 다른 표현을 산출합니다.파동함수의 두 표현은 다음과 같은 푸리에 변환에 의해 연관됩니다.

${\displaystyle \phi(p)=\int dq\,\psi(q)e^{-ipq/h}}$

아니면, 그와 동등하게

${\displaystyle \psi(q)=\int dp\,\phi(p)e^{ipq/h}}$

물리적으로 실현 가능한 상태는 L이고², 따라서 플랑셰럴 정리에 의해, 그들의 푸리에 변환 또한² L입니다. (Q는 거리 단위이고 p는 운동량 단위이므로, 지수에 플랑크 상수가 있는 것은 지수 차원을 무차원으로 만듭니다.)

따라서 푸리에 변환은 입자의 상태를 나타내는 한 가지 방법에서 위치의 파동 함수에 의해 입자의 상태를 나타내는 다른 방법인 운동량의 파동 함수에 의해 전달되는 데 사용될 수 있습니다.무한히 많은 다양한 분극이 가능하며, 모두 동일하게 유효합니다.푸리에 변환에 의해 한 표현에서 다른 표현으로 상태를 변환할 수 있는 것은 편리할 뿐만 아니라 하이젠베르크 불확정성 원리의 근본적인 이유이기도 합니다.

양자역학과 양자장 이론에서 푸리에 변환의 다른 용도는 적용 가능한 파동 방정식을 푸는 것입니다.비상대론적 양자역학에서 슈뢰딩거의 방정식은 외력이 아닌 1차원에서의 시간가변 파동함수에 대한 다음과 같습니다.

${\displaystyle -{\frac {\partial ^{2}}{\partial x^{2}}\psi(x,t)=i{\frac {h}{2\pi}}{\frac {\partial t}}\psi(x,t)}$

이는 허수 단위 i가 존재하는 것을 제외하고는 열 방정식과 같습니다.푸리에 방법은 이 방정식을 푸는 데 사용될 수 있습니다.

퍼텐셜 에너지 함수 V(x)에 의해 주어진 퍼텐셜이 존재하는 경우, 방정식은

${\displaystyle -{\frac {\partial ^{2}}{\partial x^{2}}\psi(x,t)+V(x)\psi(x,t)=i{\frac {h}{2\pi}}{\frac {\partial t}}\partial(x,t)}$

우리가 위에서 언급한 바와 같이 "element해"는 입자의 소위 "정지 상태"이며, 위에서 설명한 바와 같이 푸리에의 알고리즘은 t = 0에 대한 값을 고려할 때 ψ의 미래 진화의 경계 값 문제를 해결하는 데 여전히 사용될 수 있습니다.양자역학에서는 이 두 가지 접근법 모두 실용적이지 않습니다.경계 값 문제와 파동 함수의 시간 진화는 실용적인 관심사가 아닙니다. 가장 중요한 것은 정지 상태입니다.

상대론적 양자역학에서 슈뢰딩거 방정식은 복소수 파동이 고려되는 것을 제외하고는 고전 물리학에서 일반적으로 그랬던 것처럼 파동 방정식이 됩니다.다른 입자나 장들과의 상호작용이 없는 간단한 예는 자유 1차원 클라인-고든-슈뢰딩거-폭 방정식이며, 이번에는 무차원 단위로,

${\displaystyle \left ({\frac {\partial ^{2}}{\partial x^{2}}+1\right)\psi(x,t)={\frac {\partial ^{2}}{\partial t^{2}}}\psi(x,t)}$

이는 수학적 관점에서 보면 위에서 풀린 고전물리학의 파동 방정식과 같습니다(그러나 방법에 차이가 없는 복잡한 값의 파동으로).이것은 양자장 이론에서 매우 유용합니다. 파동의 각 개별 푸리에 성분은 별개의 고조파 진동자로 취급된 후 "두 번째 양자화"라고 알려진 절차로 양자화될 수 있습니다.푸리에 방법은 사소한 상호 작용도 다루기 위해 적용되었습니다.

마지막으로, 양자 조화 진동자의 수 연산자는 예를 들어 멜러 커널을 통해 푸리에 변환 $F{\displaystyle \mathcal{}}$ ${\$의 생성자로 해석될 수 있습니다$.$^[24]

신호처리

푸리에 변환은 시계열의 스펙트럼 분석에 사용됩니다.그러나 통계적 신호 처리의 주제는 일반적으로 신호 자체에 푸리에 변환을 적용하지 않습니다.실제 신호가 실제로 일시적인 경우에도, 신호의 특성 특성이 전체 시간에 걸쳐 일정하다는 점에서 정지된 함수(또는 확률적 프로세스)에 의해 신호를 모델링하는 것이 실제로 권장되는 것으로 밝혀졌습니다.그러한 함수의 푸리에 변환은 일반적인 의미에서 존재하지 않으며 대신 자기 상관 함수의 푸리에 변환을 취하는 것이 신호 분석에 더 유용한 것으로 밝혀졌습니다.

함수 f 의 자기 상관 함수 R 은 다음과 같이 정의됩니다.

${\displaystyle R_{f}(\tau )=\lim _{T\rightarrow \infty}{\frac {1}{2T}}\int _{-T}^{T}f(t)f(t+\tau )\,dt.}$

이 함수는 상관 관계에 있는 f 값 사이의 시차 τ의 함수입니다.

실제로 발생하는 대부분의 함수 f의 경우, R은 시차 τ의 유계 이븐 함수이며, 전형적인 잡음 신호의 경우 τ = 0에서 최대치로 균일하게 연속인 것으로 나타났습니다.

적절한 방법으로 정규화되지 않는 한 자기 상관 함수라고 하는 자기 상관 함수는 시차로 구분된 f 값 사이의 상관 관계의 강도를 측정합니다.이것은 자신의 과거와의 상관관계를 탐색하는 방법입니다.신호 분석 이외의 다른 통계 작업에도 유용합니다.예를 들어 f(t)가 시간 t에서의 온도를 나타내는 경우 24시간 시차에서 온도와 강한 상관 관계가 있을 것으로 예상됩니다.

푸리에 변환을 가지고 있고,

${\displaystyle P_{f}(\xi )=\int _{-\infty}^{\infty}R_{f}(\tau )e^{-i2\pi \xi \xi tau }\,d\tau.}$

이 푸리에 변환을 f의 거듭제곱 스펙트럼 밀도함수라고 합니다. (모든 주기성분을 f에서 먼저 걸러내지 않는 한, 이 적분은 발산할 것이지만, 그러한 주기성을 걸러내는 것은 쉽습니다.)

이 밀도 함수 P로 표시된 전력 스펙트럼은 주파수 ξ에 의해 데이터에 기여하는 분산의 양을 측정합니다.전기 신호에서 분산은 평균 전력(단위 시간당 에너지)에 비례하므로 전력 스펙트럼은 서로 다른 주파수가 신호의 평균 전력에 얼마나 기여하는지를 설명합니다.이 프로세스를 시계열의 스펙트럼 분석이라고 하며 시계열(ANOVA)이 아닌 일반적인 데이터 분산 분석과 유사합니다.

이러한 의미에서 어떤 주파수가 "중요"한지에 대한 지식은 필터의 적절한 설계와 측정 장치의 적절한 평가를 위해 매우 중요합니다.또한 데이터 생성에 책임이 있는 현상을 과학적으로 분석하는 데 유용할 수 있습니다.

신호의 전력 스펙트럼은 협대역 외부의 모든 주파수가 필터링된 후 신호에 남아 있는 평균 전력을 측정하여 직접 측정할 수도 있습니다.

스펙트럼 분석은 시각적 신호에 대해서도 수행됩니다.전력 스펙트럼은 모든 위상 관계를 무시하며, 이는 여러 용도로 충분하지만, 비디오 신호의 경우 다른 유형의 스펙트럼 분석도 사용해야 하며, 여전히 푸리에 변환을 도구로 사용합니다.

기타 표기법

f ̂(ξ)의 다른 일반적인 표기는 다음과 같습니다.

${\displaystyle {\tilde {f}}(\xi),\F(\xi),\{\mathcal {F}(\xi),\left({\mathcal {F}\right)(\xi),\{\mathcal {F}(f),\{\mathcal {F}},\{\mathcal {F\},\{mathcal {F},{\bigr},\{\mathcal {F}},{\bigl \f(t)},{\mathcal {F},{bigr \}}.$

변환되는 함수의 문자(예: f(x)) 및 F(ξ)에 대응하는 대문자로 푸리에 변환을 나타내는 것은 특히 과학 및 공학에서 일반적입니다.전자공학에서는 각진동수로 해석되어 ω 대신 오메가(ω)를 사용하는 경우가 많은데, 라플라스 변환과의 관계를 나타내기 위해 F(j π)로 표기하기도 하고, 보통의 진동수를 사용하기 위해 비공식적으로 F(2 ξf)로 표기하기도 합니다.입자 물리학과 같은 일부 맥락에서, 같은 기호 $f{\displaystyle }$ ${\displaystyle f}$는 함수뿐만 아니라 푸리에 변환에도 사용될 수 있으며$$, 둘은 오직 그들의 인수에 의해서만 구별됩니다${\displaystyle :}$ $f{\displaystyle }$ (${\displaystyle {}_{}{k\mathrm{}}_{}}$ ${\displaystyle {}_{}}$ +${\displaystyle {}_{}{k\mathrm{}}_{}}$ 2$$) {\$displaystyle$ f$(k_{$1} +$k_{2$})}는 운동량 인수 때문에 푸리에 변환을 언급할 것이고$$,$f$ (${\displaystyle {}_{}}$ ${\displaystyle 0_{}}$ +${\displaystyle {}_{}}$π ${\displaystyle r}$ →${\displaystyle }$) ${\displaystyle f(x_{0}+\pi {\vec {r}})}$이(가) 위치 인수 때문에 원래 함수를 참조합니다.$f{\displaystyle \stackrel{}{}}$~ ${\displaystyle {\tilde {f}}$처럼 틸드를 사용하여 푸리에 변환을 나타낼 수 있지만 d $k$ ~${\displaystyle \stackrel{}{}}$= d ${\displaystyle k}$ (${\displaystyle \frac{2}{}}$π${\displaystyle \frac{{}^{}}{}}$ 32 ω ${\displaystyle {\tilde {dk$}}={\$frac {dk}{(2\pi)^{3}2\omega}}}$와 같이 더 로렌츠 불변의 형태를 가진 수량의 수정을 나타낼 때도 틸드를 사용할 수 있으므로 주의해야 합니다$.$마찬가지로 $f{\displaystyle \hat{}}$ ${\$는 종종$$$${\$displaystyle$f}의 힐베르트 변환을 나타냅니다$.$

복소 함수 f ̂(ξ)의 해석은 극좌표 형태로 표현함으로써 도움이 될 수 있습니다.

${\displaystyle {\hat {f}}(\xi)=A(\xi)e^{i\varphi(\xi )}$

두 개의 실제 함수 A(ξ) 및 φ(ξ)에 관하여, 여기서:

${\displaystyle A(\xi )=\left {\hat {f}}(\xi )\right,}$

진폭과

${\displaystyle \varphi (\xi )=\arg \left ({\hat {f}(\xi )\right),}$

는 위상입니다(arg 함수 참조).

그러면 역변환은 다음과 같이 쓸 수 있습니다.

${\displaystyle f(x)=\int _{-\infty}^{\infty}A(\xi )\e^{i{\bigl (}2\pi \xi x+\varphi (\xi ){\bigr )}\,d\xi,}$

f(x)의 모든 주파수 성분의 재조합입니다.각 성분은 진폭이 A(ξ)이고 초기 위상각(x = 0)이 φ(ξ)인 형태의 복잡한 동축입니다.

푸리에 변환은 함수 공간에 대한 매핑으로 간주될 수 있습니다.이 매핑은 여기서 F로 표시되며 F(f)는 함수 f의 푸리에 변환을 나타내는 데 사용됩니다.이 매핑은 선형이며, 이는 F가 함수 공간에 대한 선형 변환으로도 볼 수 있으며 벡터(여기서 함수 f)에 선형 변환을 적용하는 선형 대수학의 표준 표기법을 사용하여 F(f) 대신 F f를 쓸 수 있음을 의미합니다.푸리에 변환을 적용한 결과는 다시 함수이므로 변수에 대한 값 ξ에서 평가된 이 함수의 값에 관심을 가질 수 있으며, 이는 Ff(ξ) 또는 (Ff)(ξ)로 표시됩니다.전자의 경우, F가 f에 먼저 적용된 후 결과 함수가 반대가 아니라 ξ에서 평가된다는 것을 암시적으로 이해할 수 있습니다.

수학 및 다양한 응용 과학에서 함수 f와 f 값을 구별하는 것은 종종 필요합니다.이것은 F(f(x))와 같은 표기법이 공식적으로 f 의 값들의 푸리에 변환으로 해석될 수 있다는 것을 의미합니다. 이 결함에도 불구하고 이전 표기법은 종종 특정 함수 또는 특정 변수의 함수가 변환되어야 할 때 나타납니다.예를들면,

${\displaystyle {\mathcal {F}}{\bigl(}\operatorname {rect}(x){\bigr )}=\operatorname {sinc}(\xi )}$

직사각형 함수의 푸리에 변환이 sinc 함수라는 것을 표현하기 위해 때때로 사용됩니다.

${\displaystyle {\mathcal {F}}{\bigr}={\mathcal {F}{\bigr}}{\bigl(}f(x){\bigr}}\,e^{i2\pix_{0}\xi}}$

푸리에 변환의 이동 속성을 표현하는 데 사용됩니다.

마지막 예제는 변환된 함수가 x의₀ 함수가 아니라 x의 함수라는 가정 하에서만 정확합니다.

기타 규약

푸리에 변환은 또한 각 주파수로 표기할 수 있습니다.

${\displaystyle \omega = 2\pi \xi,}$

초당 라디안 단위입니다.

위 수식에 ξ = ω/2 π를 대입하면 다음과 같은 규칙이 생성됩니다.

${\displaystyle {\hat {f_{3}}(\omega )=\int _{-\infty}^{\infty}f(x)\cdote^{-i\omega \,x}\, dx={\hat {f}\left ({\tfrac {\omega}{2\pi}}\right).}$

이 규칙에서 역변환은 다음과 같습니다.

${\displaystyle f(x)={\frac {1}{2\pi}}\int _{-\infty}^{\infty}{\hat {f_{3}}(\omega )\cdote^{i\omega \,x}\,d\omega.}$

이 글에서 따르는 관례와 달리 푸리에 변환을 이렇게 정의하면 L(R²)에서 더 이상 유니터리 변환이 아닙니다.또한 푸리에 변환 공식과 그 역 공식 사이의 대칭이 적습니다.

또 다른 규칙은 2 π의 인자를 푸리에 변환과 그 역수 사이에 균등하게 분할하는 것이며, 이는 정의로 이어집니다.

${\displaystyle {\begin{aligned}{\hat {f_{2}}(\omega)&={\frac {1}{\sqrt {2\pi}}\int _{-\infty}^{\infty}f(x)\cdot e^{-i\omega x}\, dx={\frac {1}{\sqrt {2\pi}}\cdot {\hat {f}}\left ({\tfrac {2\pi}}\right),\f(x)&={\frac {1}{\sqrt {2\pi}}}\int _{-\infty}^{\hat {f_{2}}(\omega )\cdot e^{i\omega x}\,d\omega.\end{aligned}}$

이 규칙에 따라, 푸리에 변환은 다시² L(R)에 대한 유니터리 변환입니다.또한 푸리에 변환과 그 역 사이의 대칭을 복원합니다.

순방향 변환과 역방향 변환 모두의 복소 지수 커널을 결합하여 세 가지 규칙의 변형을 만들 수 있습니다.표지판이 반대여야 합니다.그 외에 선택은 관례의 문제입니다.

푸리에 변환의 인기 형태 요약, 1차원

통상주파수 ξ(Hz)	단일의	${\displaystyle {\begin{aligned}{\hat {f}}_{1}(\xi)\&{\stackrel {\mathrm {def}}{=}}\int _{-\infty}^{\infty}f(x)\,e^{-i2\pi \xi}\, dx={\sqrt {2\pi }\,{\hat {f}_{2}(2\pi \xi )={\hat {f}_{3}(2\pi \xi )\f(xi )=\int _{-\infty}^{\hat {f}_{1}(\xi )\,e^{i2\pi x\xi }\,d\xi \end{aligned}}$
각 주파수 ω(rad/s)	단일의	${\displaystyle {\begin{aligned}{\hat {f}}_{2}(\omega )\{\stackrel {\mathrm {def}}{=}}\{\frac {1}{\sqrt {2\pi}}\int _{-\infty}^{\infty}f(x)\,e^{-i\omega x}\, dx={\frac {1}{\sqrt {2\pi}},{\hat {f}_{1}\!\left ({\frac {\omega }{2\pi}}\right)={\frac {1}{\sqrt {2\pi}}\,{\hat {f}_{3}(\omega )\f(x)&={\frac {1}{\sqrt {2\pi}}\int_{-\infty }^{\infty }{\hat {f}_{2}(\omega )\,e^{i\omega x}\,d\omega \end{align}}$
	비일원의	${\displaystyle {\begin{aligned}{\hat {f}}_{3}(\omega )\{\stackrel {\mathrm {def}}{=}}\int_{-\infty}^{\infty}f(x)\,e^{-i\omega x}\,dx={\hat {f}_{1}\left ({\frac {\omega }{2\pi }\right)={\sqrt {2\pi}},{\hat {f}_{2}(\omega )&={\frac {1}{2\pi }}\int_{-\infty}^{\hat {f}_3}(\omega )\,e^{i\omega x}\,d\omega \end{aligned}}}$

n차원 함수에 대한 일반화

통상주파수 ξ(Hz)	단일의	${\displaystyle {\begin{aligned}{\hat {f}}_{1}(\xi)\&{\stackrel {\mathrm {def}}{=}}\\int _{\mathbb {R}^{n}}f(x)e^{-i2\pi \xi \cdot x}\, dx=(2\pi )^{\frac {n}{2}{\hat {f}_{2}(2\pi \xi )={\hat {f}_{3}(2\pi \xi )\f(xi )&=\int _{\mathbb {R}^{n}}{\hat {f}_{1}(\xi )e^{i2\pi \cdot x}\,d\xi \end{align}}$
각 주파수 ω(rad/s)	단일의	${\displaystyle {\begin{aligned}{\hat {f}}_{2}(\omega )\{\stackrel {\mathrm {def}}{=}}\{\frac {1}^{\frac {n}{2}}}\int _{\mathbb {R}^{n}^{f(x)e^{-i\omega \cdot x}\, dx={\frac {1}{(2\pi )}^{\frac {n}}}{\hat {f}_1}\!\left ({\frac {\fromega }{2\pi}}\right)={\frac {1}{(2\pi )^{\frac {n}{2}}}}{\hat {f}_{3}(\omega )\f(x)&={\frac {1}{(2\pi )^{\frac {n}}}\int_{\mathbb {R}^{n}}{\hat {f}_{2}(\omega )e^{i\omega \cdot x}\,d\omega \end{align}}}}\n}$
	비일원의	${\displaystyle {\begin{aligned}{\hat {f}}_{3}(\omega )\{\stackrel {\mathrm {def}}{=}}\int_{\mathbb {R}^{n}f(x)e^{-i\omega \cdot x}\, dx={\hat {f}_{1}\left ({\frac {\omega }{2\pi}}\right)=(2\pi )^{\frac {n}{2}}{\hat {f}_{2}(\omega )\f(x)&={\frac {1}{(2\pi )^{n}}\int_{\mathbb {R}^{n}}{\hat {f}_{3}(\omega )e^{i\omega \cdot x}\,d\omega \end{aligned}}$

위에서 논의한 바와 같이, 랜덤 변수의 특성 함수는 분포 측도의 푸리에-슈틸제스 변환과 동일하지만, 이러한 맥락에서 상수에 대해 다른 규약을 취하는 것이 일반적입니다.일반적으로 특성 함수가 정의됩니다.

${\displaystyle E\left(e^{it\cdot X}\right)=\inte^{it\cdot x}\,d\mu _{X}(x)}$

위의 "비균일 각진동수" 협약의 경우와 마찬가지로 정규화 상수와 지수 모두에서 2π의 인자가 나타나지 않습니다.위에 나타나는 임의의 규약과 달리, 이 규약은 지수에서 반대 부호를 사용합니다.

계산법

적절한 계산 방법은 크게 원래의 수학적 함수를 어떻게 표현하고 출력 함수를 원하는 형태로 표현하느냐에 달려 있습니다.

푸리에 변환의 기본적인 정의는 적분이기 때문에, 닫힌 형태의 표현으로 표현될 수 있는 함수는 결과로서 푸리에 변환 공액 변수에서 닫힌 형태의 표현을 산출하기 위해 적분을 해석적으로 작업하여 일반적으로 계산됩니다.이 방법은 아래 표(Fourier transform#중요한 푸리에 변환의 표)를 포함하여 ^[51]푸리에 변환의 표를 생성하는 데 사용되는 방법입니다.

Matlab과 Mathematica와 같은 기호적 통합이 가능한 많은 컴퓨터 대수 시스템은 푸리에 변환을 해석적으로 계산할 수 있습니다.예를 들어, cos(6 πt)의 푸리에 변환을 계산하기 위해 명령을 입력할 수 있습니다.integrate cos(6*pi*t) exp(−pi*t^2) exp(-i*2*pi*f*t) from -inf to inf볼프람 알파로.^{[note 7]}

밀폐형 함수의 수치적 적분

입력 함수가 닫힌 형태이고 원하는 출력 함수가 지정된 도메인에 대한 일련의 순서 쌍(예를 들어 그래프가 생성될 수 있는 값의 표)인 경우, 푸리에 변환은 푸리에 공액 변수의 각 값(주파수,예를 들어, 출력 변수의 값이 필요한 경우.^[52]이 방법은 푸리에 변환 값이 필요한 주파수 값 각각에 대해 별도의 수치 적분을 계산해야 합니다.^[53][54]수치 적분 접근법은 닫힌 형태의 푸리에 변환 적분이 없는 함수에 대해 결과를 산출하기 때문에 분석 접근법보다 훨씬 더 넓은 종류의 함수에서 작동합니다.

일련의 순서쌍들의 수치적 적분

입력 함수가 일련의 순서 쌍(예를 들어, 출력 변수를 시간 간격에 걸쳐 반복적으로 측정하여 얻은 시계열)이면 출력 함수도 일련의 순서 쌍(예를 들어, 특정 주파수 영역에서 복소수 대 주파수)이어야 합니다.출력 함수가 폐쇄형 식에 의해 근사화될 수 있도록 특정 가정과 근사치가 만들어지지 않는 한.순서 쌍의 사용 가능한 입력 시리즈가 간격(예를 들어, 진폭 대 시간)에 걸친 연속 함수를 나타내는 샘플로 가정되는 일반적인 경우, 원하는 출력 함수를 나타내는 순서 쌍의 시리즈는 각 값에서 사용 가능한 간격에 대한 입력 데이터의 수치 적분에 의해 얻어질 수 있습니다.푸리에 변환 값이 필요한 푸리에 공액 변수(예: 빈도)^[55]의 e.

순서 쌍에 대한 명시적 수치 적분은 공액 푸리에 변환 변수(예를 들어, 주파수)의 임의의 원하는 값에 대한 푸리에 변환 출력 값을 산출할 수 있으므로 스펙트럼은 진폭, 주파수의 정확한 결정을 위해 임의의 원하는 스텝 크기 및 임의의 원하는 변수 범위에 걸쳐 생성될 수 있습니다.그리고 고립된 피크에 해당하는 위상.DFT 및 FFT 방법의 제한과 달리 명시적 수치 적분은 원하는 스텝 크기를 가질 수 있으며 공액 푸리에 변환 변수(예: 주파수)의 원하는 범위에 걸쳐 푸리에 변환을 계산할 수 있습니다.

이산 푸리에 변환 및 빠른 푸리에 변환

원래 입력 함수를 나타내는 순서 쌍이 입력 변수에서 동일한 간격으로 존재하는 경우(예를 들어, 동일한 시간 단계), 푸리에 변환은 이산 푸리에 변환(DFT)으로 알려져 있으며, 이는 명시적인 수치 적분, DFT 정의의 명시적 평가에 의해 계산될 수 있습니다.또는 고속 푸리에 변환(FFT) 방법을 사용합니다.입력 데이터의 명시적인 통합과는 대조적으로, DFT 및 FFT 방법을 사용하면 원래 샘플링 간격의 역수와 동일한 스텝 크기의 순서 쌍으로 설명되는 푸리에 변환이 생성됩니다.예를 들어 입력 데이터가 10초마다 샘플링되는 경우 DFT 및 FFT 방법의 출력은 0.1Hz 주파수 간격을 갖게 됩니다.

중요한 푸리에 변환의 표

다음 표에서는 몇 가지 닫힌 형태의 푸리에 변환을 기록합니다.함수 f(x)와 g(x)는 f ̂와 ĝ에 의한 푸리에 변환을 나타냅니다.가장 일반적인 세 가지 규칙만 포함됩니다.엔트리 105가 함수의 푸리에 변환과 원래 함수 사이의 관계를 제공한다는 것을 알아차리는 것이 유용할 수 있으며, 이는 푸리에 변환과 그 역을 연관시키는 것으로 볼 수 있습니다.

기능적 관계, 일차원

이 표의 푸리에 변환은 Erdelyi(1954) 또는 Kamler(2000, 부록)에서 찾을 수 있습니다.

	기능.	푸리에 변환 단일, 통상 주파수	푸리에 변환 단일, 각진동수	푸리에 변환 비단일, 각진동수	언급
	${\displaystyle f(x)\,}$	${\displaystyle {\begin{aligned}&{\hat {f}}(\xi )\triangleq {\hat {f}_{1}(\xi )\&=\int _{-\infty}^{\infty }e^{-i2\pi \xi}\, dx\end{aligned}}$	${\displaystyle {\begin{aligned}&{\hat {f}}(\omega )\triangleq {\hat {f}_{2}(\omega )\&={\frac {1}{\sqrt {2\pi}}\int _{-\infty}^{\infty}f(x)e^{-i\omega x}\, dx\end{aligned}}$	${\displaystyle {\begin{aligned}&{\hat {f}}(\omega )\triangleq {\hat {f}_{3}(\omega )\&=\int _{-\infty}^{\infty }f(x)e^{-i\omega x}\, dx\end{aligned}}$	정의들
101	${\displaystyle a\,f(x)+b\,g(x)\,}$	${\displaystyle a\,{\hat {f}}(\xi )+b\,{\hat {g}(\xi )\,}$	${\displaystyle a\,{\hat {f}}(\omega )+b\,{\hat {g}(\omega )\,}$	${\displaystyle a\,{\hat {f}}(\omega )+b\,{\hat {g}(\omega )\,}$	선형성
102	${\displaystyle f(x-a)\,}$	${\displaystyle e^{-i2\pi \xia}{\hat {f}(\xi )\,}$	${\displaystyle e^{-ia\omega}{\hat {f}}(\omega )\,}$	${\displaystyle e^{-ia\omega}{\hat {f}}(\omega )\,}$	시간영역이동
103	${\displaystyle f(x)e^{iax}\,}$	${\displaystyle {\hat {f}}\left(\xi -{\frac {a}{2\pi}}\right)\,}$	${\displaystyle {\hat {f}}(\omega -a)\,}$	${\displaystyle {\hat {f}}(\omega -a)\,}$	주파수 영역 이동, 102의 이중
104	${\displaystyle f(ax)\,}$	${\displaystyle {\frac {1}{a}}}{\hat {f}}\left ({\frac {\xi}{a}\right)\,}$	${\displaystyle {\frac {1}{a}}{\hat {f}}\left ({\frac {\omega}{a}\right)\,}$	${\displaystyle {\frac {1}{a}}{\hat {f}}\left ({\frac {\omega}{a}\right)\,}$	시간 도메인의 스케일링.a가 크면 f(ax)는 0 주위에 집중되고 ${\displaystyle {\frac {1}{a}}{\hat {f}}\left ({\frac {\omega}{a}\right)\,}$ 펴지고 납작해집니다.
105	${\displaystyle {\hat {f_{n}}(x)\,}$	${\displaystyle {\hat {f}}_{1}(x)\{\stackrel {\mathcal {F}_{1}}{\long left right arrow}}}\f(-\xi )\,}$	${\displaystyle {\hat {f}}_{2}(x)\{\stackrel {\mathcal {F}_{2}}{\long left right arrow}}}\f(-\omega )\,}$	${\displaystyle {\hat {f}}_{3}(x)\{\stackrel {{\mathcal {F}_{3}}{\long left right arrow}}\2\pif(-\omega )\,}$	동일한 변환이 두 번 적용되지만, 첫 번째 변환 후에 x가 빈도 변수(ξ 또는 ω)를 대체합니다.
106	${\displaystyle {\frac {d^{n}f(x)}{dx^{n}}\,}$	${\displaystyle (i2\pi \xi )^{n}{\hat {f}}(\xi )\,}$	${\displaystyle (i\omega )^{n}{\hat {f}}(\omega )\,}$	${\displaystyle (i\omega )^{n}{\hat {f}}(\omega )\,}$	n차th 도함수 f 가 슈워츠 함수인 것처럼
	${\displaystyle \int_{-\infty}^{x}f(\tau)d\tau }$	${\displaystyle {\frac {\hat {f}}(\xi )}{i2\pi \xi}}+C\,\delta(\xi )}$			통합.[56]참고:$$delta {\$displaystyle$ \δ}은(는) 디랙 델타 함수이고 $C$ ${\displaystyle C}$는 $f$ (${\displaystyle x)}$ ${\displaystyle f(x)}$의 평균(DC) 값이므로 ∫ -${\displaystyle {}_{}^{}}$∞ ∞ ${\displaystyle f{}_{}^{}}$(${\displaystyle x}$) -${\displaystyle C}$) ${\displaystyle d}$ = ${\displaystyle 0}$ ${\displaystyle \int$ _${-\infty }^{\infty$}($f(x)$ - $C)\,dx$=$0}$
107	${\displaystyle x^{n}f(x)\,}$	${\displaystyle \left ({\frac {i}{2\pi}}\right)^{n}{\frac {d^{n}{\hat {f}}(\xi )}{d\xi ^{n}}\,}$	${\displaystyle i^{n}{\frac {d^{n}{\hat {f}}(\omega )}{d\omega ^{n}}}}$	${\displaystyle i^{n}{\frac {d^{n}{\hat {f}}(\omega )}{d\omega ^{n}}}}$	이것은 106의 듀얼입니다.
108	${\displaystyle (f*g)(x)\,}$	${\displaystyle {\hat {f}}(\xi ){\hat {g}(\xi )\,}$	${\displaystyle {\sqrt {2\pi}}{\hat {f}}(\omega ){\hat {g}(\omega )\,}$	${\displaystyle {\hat {f}}(\omega ){\hat {g}(\omega )\,}$	∗ g 표기는 f 와 g 의 컨볼루션을 나타냅니다. 이 규칙은 컨볼루션 정리입니다.
109	${\displaystyle f(x)g(x)\,}$	${\displaystyle \left ({\hat {f}}*{\hat {g}\right)(\xi )\,}$	${\displaystyle {\frac {1}{\sqrt {2\pi}}\left ({\hat {f}}*{\hat {g}\right)(\omega )\,}$	${\displaystyle {\frac {1}{2\pi}}\left ({\hat {f}*{\hat {g}}\right)(\omega )\,}$	이것은 108의 듀얼입니다.
110	f(x)의 경우에는 순수하게 진짜입니다.	${\displaystyle {\hat {f}}(-\xi )={\overline {{\hat {f}}(\xi )}\,}$	${\displaystyle {\hat {f}}(-\omega )={\overline {{\hat {f}}(\omega )}\,}$	${\displaystyle {\hat {f}}(-\omega )={\overline {{\hat {f}}(\omega )}\,}$	에르미트 대칭. z는 복소수 켤레를 나타냅니다.
113	f(x)의 경우 순수 허수	${\displaystyle {\hat {f}}(-\xi )=-{\overline {{\hat {f}}(\xi )}\,}$	${\displaystyle {\hat {f}}(-\omega )=-{\overline {{\hat {f}}(\omega )}\,}$	${\displaystyle {\hat {f}}(-\omega )=-{\overline {{\hat {f}}(\omega )}\,}$	z는 복소 켤레를 나타냅니다.
114	${\displaystyle {\overline {f(x))}}$	${\displaystyle {\overline {{\hat {f}}(-\xi )}}$	${\displaystyle {\overline {{\hat {f}}(-\omega )}}$	${\displaystyle {\overline {{\hat {f}}(-\omega )}}$	복소접합, 110과 113의 일반화
115	${\displaystyle f(x)\cos(ax)}$	${\displaystyle {\frac {\hat {f}}\left(\xi -{\frac {a}{2\pi}}\right)+{\hat {f}\left(\xi +{\frac {a}{2\pi}}\right)}{2}}}$	${\displaystyle {\frac {{\hat {f}}(\omega -a)+{\hat {f}(\omega +a)}{2}\,}$	${\displaystyle {\frac {{\hat {f}}(\omega -a)+{\hat {f}(\omega +a)}{2}}}$	다음은 오일러 공식을 사용하는 규칙 101과 103에서 따온 것입니다. ${\displaystyle \cos(ax)={\frac {e^{iax}+e^{-iax}}{2}}}$
116	${\displaystyle f(x)\sin(ax)}$	${\displaystyle {\frac {\hat {f}}\left(\xi -{\frac {a}{2\pi}}\right)-{\hat {f}\left(\xi +{\frac {a}{2\pi}}\right)}{2i}}}$	${\displaystyle {\frac {\hat {f}}(\omega -a)-{\hat {f}(\omega +a)}{2i}}$	${\displaystyle {\frac {\hat {f}}(\omega -a)-{\hat {f}(\omega +a)}{2i}}$	다음은 오일러 공식을 사용한 101과 103에서 따온 것입니다. ${\displaystyle \sin(ax)={\frac {e^{iax}-e^{-iax}}{2i}}}.$

사각형 일체형 함수, 1차원

이 표의 푸리에 변환은 Campbell & Foster(1948), Erdelyi(1954) 또는 Kamler(2000, 부록)에서 찾을 수 있습니다.

	기능.	푸리에 변환 단일, 통상 주파수	푸리에 변환 단일, 각진동수	푸리에 변환 비단일, 각진동수	언급
	${\displaystyle f(x)\,}$	${\displaystyle {\begin{aligned}&{\hat {f}}(\xi )\triangleq {\hat {f}_{1}(\xi )\&=\int _{-\infty}^{\infty }e^{-i2\pi \xi}\, dx\end{aligned}}$	${\displaystyle {\begin{aligned}&{\hat {f}}(\omega )\triangleq {\hat {f}_{2}(\omega )\&={\frac {1}{\sqrt {2\pi}}\int _{-\infty}^{\infty}f(x)e^{-i\omega x}\, dx\end{aligned}}$	${\displaystyle {\begin{aligned}&{\hat {f}}(\omega )\triangleq {\hat {f}_{3}(\omega )\&=\int _{-\infty}^{\infty }f(x)e^{-i\omega x}\, dx\end{aligned}}$	정의들
201	${\displaystyle \operatorname {rect}(ax)\,}$	${\displaystyle {\frac {1}{a}}\,\operator name {sinc}\left ({\frac {\xi}{a}\right)}$	${\displaystyle {\frac {1}{\sqrt {2\pi a^{2}}}\,\operator name {sinc}\left ({\frac {\omega}{2\pi a}\right)}$	${\displaystyle {\frac {1}{a}}\,\operator name {sinc}\left ({\frac {\omega}{2\pia}}\right)}$	직사각형 펄스 및 정규화된 sinc 함수, 여기서 sinc(x) = sin( πx)/ πx로 정의됩니다.
202	${\displaystyle \operatorname {sinc}(축)\,}$	${\displaystyle {\frac {1}{a}}\,\operator name {rect}\left ({\frac {\xi}{a}\right)\,}$	${\displaystyle {\frac {1}{\sqrt {2\pi a^{2}}}\,\operator name {rect}\left ({\frac {\omega}{2\pi a}\right)}$	${\displaystyle {\frac {1}{a}}\,\operator name {rect}\left ({\frac {\omega}{2\pia}}\right)}$	규칙 201의 이중성.직사각형 함수는 이상적인 저역 통과 필터이고, sinc 함수는 그러한 필터의 비원인 임펄스 응답입니다.sinc 함수는 여기서 sinc(x) = sin( πx)/ πx로 정의됩니다.
203	${\displaystyle \operatorname {sinc}^{2}(ax)}$	${\displaystyle {\frac {1}{a}}\,\operator name {tri}\left ({\frac {\xi}{a}\right)}$	${\displaystyle {\frac {1}{\sqrt {2\pi a^{2}}}\,\operatorname {tri}\left ({\frac {\omega}{2\pi a}\right)}$	${\displaystyle {\frac {1}{a}}\,\operator name {tri}\left ({\frac {\omega}{2\pia}}\right)}$	함수 tri(x)는 삼각 함수입니다.
204	${\displaystyle \operatorname {tri}(ax)}$	${\displaystyle {\frac {1}{a}}\,\operator name {sinc}^{2}\left ({\frac {\xi}{a}\right)\,}$	${\displaystyle {\frac {1}{\sqrt {2\pi a^{2}}}\,\operatorname {sinc}^{2}\left ({\frac {\omega}{2\pi a}\right)}$	${\displaystyle {\frac {1}{a}}\,\operatorname {sinc}^{2}\left ({\frac {\omega}{2\pia}}\right)}$	규칙 203의 이중화.
205	${\displaystyle e^{-ax}u(x)\,}$	${\displaystyle {\frac {1}{a+i2\pi \xi}}$	${\displaystyle {\frac {1}{\sqrt {2\pi}}}(a+i\omega)}}$	${\displaystyle {\frac {1}{a+i\omega}}}$	함수 u(x)는 헤비사이드 단위 스텝 함수이고 a > 0입니다.
206	${\displaystyle e^{-\alpha x^{2}}\,}$	${\displaystyle {\sqrt {\frac {\pi}}{\alpha}}\,e^{-{\frac {(\pi \xi)^{2}}{\alpha}}}}$	${\displaystyle {\frac {1}{\sqrt {2\alpha}}\,e^{-{\frac {\omega^{2}}{4\alpha}}}}$	${\displaystyle {\sqrt {\frac {\pi}}{\alpha}}\,e^{-{\frac {\omega^{2}}{4\alpha}}}}$	이것은 단일 푸리에 변환의 경우 가우스 함수 e가−αx2 α의 일부 선택에 대한 자체 푸리에 변환임을 보여줍니다.이것이 적분 가능하려면 Re(α) > 0이어야 합니다.
208	${\displaystyle e^{-a x }\,}$	${\displaystyle {\frac {2a}{a^{2}+4\pi^{2}\xi^{2}}}}$	${\displaystyle {\sqrt {\frac {2}{\pi}}}\,{\frac {a}{a^{2}+\omega^{2}}}}$	${\displaystyle {\frac {2a}{a^{2}+\omega^{2}}}}$	Re(a) > 0에 대하여. 즉, 양면 붕괴 지수 함수의 푸리에 변환은 로렌츠 함수입니다.
209	${\displaystyle \operatorname {sech}(축)\,}$	${\displaystyle {\frac {\pi}{a}}\operator name {sech}\left ({\frac {\pi ^{2}}{a}}\xi \right)}$	${\displaystyle {\frac {1}{a}}{\sqrt {\frac {\pi}{2}}\operatorname {sech}\left ({\frac {\pi}{2a}\omega \right)}$	${\displaystyle {\frac {\pi}{a}}\operator name {sech}\left ({\frac {\pi}{2a}\omega \right)}$	쌍곡 시언트는 그 자체의 푸리에 변환입니다.
210	${\displaystyle e^{-{\frac {a^{2}x^{2}}{2}}}H_{n}(ax)\,}$	${\displaystyle {\frac {\sqrt {2\pi}}(-i)^{a}}e^{-{\frac {2\pi ^{2}\xi ^{2}}{a^{2}}}H_{n}\left({\frac {2\pi \xi}{a}}\right)}$	${\displaystyle {\frac {(-i)^{n}}{a}}e^{-{\frac {\omega ^{2}}{2a^{2}}}}H_{n}\left({\frac {\omega}}{a}}\right)}$	${\displaystyle {\frac {(-i)^{n}{\sqrt {2\pi}}{a}}{a}^{-{\frac {\omega ^{2}}{2a^{2}}}}H_{n}\left({\frac {\omega}}{a}}\right)}$	그는n n차 헤르마이트 다항식입니다.a = 1이면 가우스-에르마이트 함수는 푸리에 변환 연산자의 고유 함수입니다.도함수에 대해서는 헤르마이트 다항식을 참조하십시오.공식은 n = 0의 경우 206으로 줄어듭니다.

분포, 일차원

이 표의 푸리에 변환은 Erdelyi(1954) 또는 Kamler(2000, 부록)에서 찾을 수 있습니다.

	기능.	푸리에 변환 단일, 통상 주파수	푸리에 변환 단일, 각진동수	푸리에 변환 비단일, 각진동수	언급
	${\displaystyle f(x)\,}$	${\displaystyle {\begin{aligned}&{\hat {f}}(\xi )\triangleq {\hat {f}_{1}(\xi )\&=\int _{-\infty}^{\infty }e^{-i2\pi \xi}\, dx\end{aligned}}$	${\displaystyle {\begin{aligned}&{\hat {f}}(\omega )\triangleq {\hat {f}_{2}(\omega )\&={\frac {1}{\sqrt {2\pi}}\int _{-\infty}^{\infty}f(x)e^{-i\omega x}\, dx\end{aligned}}$	${\displaystyle {\begin{aligned}&{\hat {f}}(\omega )\triangleq {\hat {f}_{3}(\omega )\&=\int _{-\infty}^{\infty }f(x)e^{-i\omega x}\, dx\end{aligned}}$	정의들
301	${\displaystyle 1}$	${\displaystyle \delta(\xi )}$	${\displaystyle {\sqrt {2\pi}},\delta(\omega )}$	${\displaystyle 2\pi \delta(\omega )}$	분포 δ( ξ)는 Dirac delta 함수를 나타냅니다.
302	${\displaystyle \delta(x)\,}$	${\displaystyle 1}$	${\displaystyle {\frac {1}{\sqrt {2\pi}}\,}$	${\displaystyle 1}$	규칙 301의 이중성.
303	${\displaystyle e^{iax}}$	${\displaystyle \delta \left(\xi -{\frac {a}{2\pi}}}\right)}$	${\displaystyle {\sqrt {2\pi}},\delta(\omega -a)}$	${\displaystyle 2\pi \delta(\omega -a)}$	이것은 103과 301부터 이어집니다.
304	${\displaystyle \cos(ax)}$	${\displaystyle {\frac {\delta \left(\xi - {\frac {a}{2\pi}}\right)+\delta \left(\xi + {\frac {a}{2\pi}}\right)}{2}}}{2}}}$	${\displaystyle {\sqrt {2\pi}}\,{\frac {\delta(\omega -a)+\delta(\omega +a)}{2}}}$	${\displaystyle \pi \left(\delta(\omega -a)+\delta(\omega +a)\right)}$	오일러 공식을 사용하는 규칙 101과 303은 다음과 같습니다. ${\displaystyle \cos(ax)={\frac {e^{iax}+e^{-iax}}{2}}}$
305	${\displaystyle \sin(ax)}$	${\displaystyle {\frac {\delta \left(\xi - {\frac {a}{2\pi}}\right)-\delta \left(\xi + {\frac {a}{2\pi}}\right)}{2i}}}$	${\displaystyle {\sqrt {2\pi}}\,{\frac {\delta(\omega -a)-\delta(\omega +a)}{2i}}$	${\displaystyle -i\pi {\bigl(})\delta(\omega -a)-\delta(\omega +a){\bigr )}$	이는 101과 303을 사용하여 다음과 같습니다. ${\displaystyle \sin(ax)={\frac {e^{iax}-e^{-iax}}{2i}}}.$
306	${\displaystyle \cos \left(ax^{2}\right)}$	${\displaystyle {\sqrt {\pi }{a}}\cos \left ({\frac {\pi ^{2}\xi ^{2}}{a}}-{\frac {\pi }{4}\right)}$	${\displaystyle {\frac {1}{\sqrt {2a}}\cos \left ({\frac {\omega^{2}}{4a}}-{\frac {\pi}{4}\right)}$	${\displaystyle {\sqrt {\pi}{a}}\cos \left ({\frac {\omega ^{2}}{4a}}-{\frac {\pi}{4}\right)}$	이는 101과 207을 사용하여 다음과 같습니다. ${\displaystyle \cos(ax^{2})={\frac {e^{iax^{2}}+e^{-iax^{2}}}{2}}}}.$
307	${\displaystyle \sin \left(ax^{2}\right)}$	${\displaystyle -{\sqrt {\pi }{a}}\sin \left ({\frac {\pi ^{2}\xi ^{2}}{a}}-{\frac {\pi }{4}\right)}$	${\displaystyle {\frac {-1}{\sqrt {2a}}\sin \left ({\frac {\omega^{2}}{4a}}-{\frac {\pi}{4}\right)}$	${\displaystyle -{\sqrt {\pi}{a}}\sin \left ({\frac {\omega^{2}}{4a}}-{\frac {\pi}{4}\right)}$	이는 101과 207을 사용하여 다음과 같습니다. ${\displaystyle \sin(ax^{2})={\frac {e^{iax^{2}}-e^{-iax^{2}}}{2i}}}}.$
308	${\displaystyle e^{-\piii\alpha x^{2}}\,}$	${\displaystyle {\frac {1}{\sqrt {\alpha}}\,e^{-i{\frac {\pi}{4}}e^{i{\frac {\pi \xi ^2}}{\alpha}}}$	${\displaystyle {\frac {1}{\sqrt {2\pi \alpha}}\,e^{-i{\frac {\pi}{4}}e^{i{\frac {\omega ^{2}}{4\pi \alpha}}}$	${\displaystyle {\frac {1}{\sqrt {\alpha}}\,e^{-i{\frac {\pi}{4}}e^{i{\frac {\omega ^2}}{4\pi \alpha}}}$	$여기$서는 α ${\displaystyle \alpha}$가 실수라고 가정합니다.알파가 복잡할 경우 위의 표 항목 206을 참조하십시오.
309	${\displaystyle x^{n}\,}$	${\displaystyle \left ({\frac {i}{2\pi}}\right)^{n}\delta ^{(n)}(\xi )}$	${\displaystyle i^{n}{\sqrt {2\pi}}\ delta ^{(n)}(\omega )}$	${\displaystyle 2\pi i^{n}\delta ^{(n)}(\omega )}$	여기서 n은 자연수이고 δ(ξ)는 디랙 델타 함수의 n차 분포 도함수입니다.이 규칙은 규칙 107과 301을 따릅니다.이 규칙을 101과 결합하면 모든 다항식을 변환할 수 있습니다.
310	${\displaystyle \delta ^{(n)}(x)}$	${\displaystyle (i2\pi \xi )^{n}$	${\displaystyle {\frac {(i\omega)^{n}}{\sqrt {2\pi}}}$	${\displaystyle (i\omega)^{n}$	규칙 309의 이중성. δ(ξ)는 디랙 델타 함수의 n차 분포 도함수.이 규칙은 106과 302의 규칙을 따릅니다.
311	${\displaystyle {\frac {1}{x}}$	${\displaystyle -i\pi \operatorname {sgn}(\xi )}$	${\displaystyle -i{\sqrt {\frac {\pi}{2}}\operatorname {sgn}(\omega )}$	${\displaystyle -i\pi \operatorname {sgn}(\omega )}$	여기서 sgn( ξ)은 부호 함수입니다.1/x는 분포가 아닙니다.Schwartz 함수에 대해 테스트할 때는 Cauchy principal 값을 사용해야 합니다.이 규칙은 힐베르트 변환을 연구하는 데 유용합니다.
312	${\displaystyle {\begin{aligned}&{\frac {1}{x^{n}}\&:={\frac {(-1)^{n-1}}{(n-1)!}}{\frac {d^{n}}{dx^{n}}\log x \end{aligned}}$	${\displaystyle -i\pi {\frac {(-i2\pi \xi)^{n-1}}{(n-1)!}}}\operator name {sgn}(\xi )}$	${\displaystyle -i{\sqrt {\pi}{2}}\,{\frac {(-i\omega)^{n-1}}{(n-1)!}}}\operator name {sgn}(\omega )}$	${\displaystyle -i\pi {\frac {(-i\omega)^{n-1}}{(n-1)!}}}\operator name {sgn}(\omega )}$	1/x는n 분포 도함수에 의해 정의된 균질 분포입니다. ${\displaystyle {\frac {(-1)^{n-1}}{(n-1)!}}{\frac {d^{n}}{dx^{n}}\log x }$
313	${\displaystyle x ^{\alpha}}$	${\displaystyle - {\frac {2\sin \left ({\frac {\pi \alpha}{2}}\right)\Gamma(\alpha +1)}{2\pi \xi^{\alpha +1}}}}$	${\displaystyle {\frac {-2}{\sqrt {2\pi}}\,{\frac {\sin \left ({\frac {\pi \alpha}{2}\right)\Gamma (\alpha +1)}{ \omega ^{\alpha +1}}}}$	${\displaystyle - {\frac {2\sin \left ({\frac {\pi \alpha}{2}}\right)\Gamma (\alpha +1)}{ \omega ^{\alpha +1}}}}$	이 공식은 0 > α > -1에 유효합니다.α > 0의 경우 318을 미분함으로써 찾을 수 있는 몇 가지 특이항들이 원점에서 발생합니다.Re α > -1이면 x는 국소적으로 적분 가능한 함수이므로 강화 분포입니다.함수 α ↦ x는 오른쪽 반평면에서 강화 분포의 공간으로 가는 동형 함수입니다.강화 분포에 대한 고유한 동형 확장을 인정하며, α ≠ -1, -3, ...에 대해서도 x를 나타냅니다(동형 분포 참조).
	${\displaystyle {\frac {1}{\sqrt {x}}}}$	${\displaystyle {\frac {1}{\sqrt {\xi}}}}$	${\displaystyle {\frac {1}{\sqrt { \omega}}}}}$	${\displaystyle {\frac {\sqrt {2\pi}}}{\sqrt { \omega}}}}$	특수사건 313호.
314	${\displaystyle \operatorname {sgn}(x)}$	${\displaystyle {\frac {1}{i\pi \xi}}}$	${\displaystyle {\sqrt {\frac {2}{\pi}}}{\frac {1}{i\omega}}}}$	${\displaystyle {\frac {2}{i\omega}}}$	규칙 311의 이중성.이번에는 푸리에 변환을 코시 주값으로 간주해야 합니다.
315	${\displaystyle u(x)}$	${\displaystyle {\frac {1}{2}}\left ({\frac {1}{i\pi \xi}}+\delta(\xi )\right)}$	${\displaystyle {\sqrt {\pi}{2}}\left ({\frac {1}{i\pi \omega}}+\delta(\omega )\right)}$	${\displaystyle \pi \left ({\frac {1}{i\pi \omega}}+\delta(\omega )\right)}$	함수 u(x)는 헤비사이드 단위 스텝 함수이며, 이는 규칙 101, 301 및 314에 따릅니다.
316	${\displaystyle \sum _{n=-\infty}^{\infty}\delta(x-nT)}$	${\displaystyle {\frac {1}{T}}\sum _{k=-\infty}^{\infty}\delta \left(\xi -{\frac {k}}{T}}\right)}$	${\displaystyle {\frac {\sqrt {2\pi}}{T}}\sum _{k=-\infty}^{\infty}\delta \left(\omega -{\frac {2\pik}}}T}}\right)}$	${\displaystyle {\frac {2\pi}{T}}\sum _{k=-\infty}^{\infty}\delta \left(\omega -{\frac {2\pik}{T}}\right)}$	이 함수를 디랙 빗 함수라고 합니다.이 결과는 302와 102에서 도출될 수 있습니다. ${\displaystyle {\begin{aligned}&\sum _{n=-\infty}^{\infty}e^{inx}\={}&2\pi \sum _{k=-\infty}^{\infty}\delta(x+2\pi)\end{aligned}}$ 분배로
317	${\displaystyle J_{0}(x)}$	${\displaystyle {\frac {2\,\operatorname {rect}(\pi \xi )}{\sqrt {1-4\pi^{2}\xi^{2}}}}$	${\displaystyle {\sqrt {\frac {2}{\pi}}\,{\frac {\operatorname {rect}\left ({\frac {\omega}{2}\right)}{\sqrt {1-\omega^{2}}}}}$	${\displaystyle {\frac {2\,\operatorname {rect} \left ({\frac {\omega}{2}}\right)}{\sqrt {1-\omega^{2}}}}$	함수 J0(x)는 1종의 0차 베셀 함수입니다.
318	${\displaystyle J_{n}(x)}$	${\displaystyle {\frac {2 (-i)^{n}T_{n}(2\pi \xi )\operator name {rect}(\pi \xi )}{\sqrt {1-4\pi^{2}\xi^{2}}}}$	${\displaystyle {\sqrt {\frac {2}{\pi}}}{\frac {(-i)^{n}T_{n}(\omega )\operatorname {rect} \left({\frac {\omega}{2}}\right)}{\sqrt {1-\omega^{2}}}}}$	${\displaystyle {\frac {2 (-i)^{n}T_{n}(\omega )\operatorname {rect} \left({\frac {\omega}{2}}\right)}{\sqrt {1-\omega^{2}}}}}$	이것은 317의 일반화입니다.함수 Jn(x)는 제1종의 n차 베셀 함수입니다.함수 Tn(x)는 첫 번째 종류의 체비셰프 다항식입니다.
319	${\displaystyle \log \left x\right}$	${\displaystyle -{\frac {1}{2}}{\frac {1}{\left \xi \right}}-\gamma \left(\xi \right)}$	${\displaystyle -{\frac {\frac {\pi}{2}}{\left \omega \right }}-{\sqrt {2\pi}}\gamma \left(\omega \right)}$	${\displaystyle -{\frac {\pi}{\left \omega \right}}-2\pi \gamma \delta \left(\omega \right)}$	γ은 오일러-마스케로니 상수입니다.Schwartz 함수에 대해 1/ ω 또는 1/ ξ를 테스트할 때는 유한 부품 적분을 사용해야 합니다.이에 대한 세부 정보는 델타 함수의 계수를 변경시킬 수 있습니다.
320	${\displaystyle \left(\mpix\right)^{-\alpha}}$	${\displaystyle {\frac {\left(2\pi \right)^{\alpha}}{\Gamma \left(\alpha \right)}}u\left(\pm \xi \right)\left(\pm \xi \right)^{\alpha -1}}$	${\displaystyle {\frac {\sqrt {2\pi}}{\Gamma \left(\alpha \right)}u\left(\pm \omega \right)\left(\pm \omega \right)^{\alpha -1}}$	${\displaystyle {\frac {2\pi}{\Gamma \left(\alpha \right)}u\left(\pm \omega \right)\left(\pm \omega \right)^{\alpha -1}}$	이 공식은 1 > α > 0에 유효합니다.미분을 사용하여 상위 지수에 대한 공식을 유도합니다.u는 헤비사이드 함수입니다.

2차원 함수

	기능.	푸리에 변환 단일, 통상 주파수	푸리에 변환 단일, 각진동수	푸리에 변환 비단일, 각진동수	언급
400	${\displaystyle f(x,y)}$	${\displaystyle {\begin{aligned}&{\hat {f}}(\xi_{x},\xi_{y})\triangleq \&\iint f(x,y)e^{-i2\pi(\xi_{x}x+\xi_{y}y}}\, dx\,dy\end{aligned}}$	${\displaystyle {\begin{aligned}&{\hat {f}}(\omega_{x},\omega_{y})\triangleq \&{\frac {1}{2\pi}}\iint f(x,y)e^{-i(\omega_{x}x+\omega_{y}y}}\, dx\,dy\end{aligned}}$	${\displaystyle {\begin{aligned}&{\hat {f}}(\omega_{x},\omega_{y})\triangleq \&\iint f(x,y)e^{-i(\omega_{x}x+\omega_{y}y}}\, dx\,dy\end{aligned}}$	변수 ξ, ξ, ω, ω은 실수입니다.통합체는 비행기 전체를 장악합니다.
401	${\displaystyle e^{-\pi \left(a^{2}x^{2}+b^{2}y^{2}\right)}}$	${\displaystyle {\frac {1}{ab }}e^{-\pi \left ({\frac {\xi _{x}^{2}}{a^{2}}}+{\frac {\xi _{y}^{2}}{b^{2}}\right)}}$	${\displaystyle {\frac {1}{2\pi \, ab }}e^{-{\frac {1}{4\pi }}\left ({\frac {\omega _{x}^{2}}{a^{2}}}+{\frac {\omega _{y}^{2}}{b^{2}}\right)}}$	${\displaystyle {\frac {1}{ab}}}e^{-{\frac {1}{4\pi}}\left ({\frac {\omega_{x}^{2}}{a^{2}}+{\frac {\omega_{y}^{2}}{b^{2}}\right)}}$	두 함수 모두 가우스 함수이므로 단위 볼륨이 없을 수 있습니다.
402	${\displaystyle \operatorname {circ} \left ({\sqrt {x^{2}+y^{2}}}}\right)}$	${\displaystyle {\frac {J_{1}\left(2\pi {\sqrt {\xi_{x}^{2}}+\xi_{y}^{2}}\right)}{{\sqrt {\xi_{x}^{2}+\xi_{y}^{2}}}}$	${\displaystyle {\frac {J_{1}\left({\sqrt {\omega_{x}^{2}}+\omega_{y}^{2}}\right)}{{\sqrt {\omega_{x}^{2}+\omega_{y}^{2}}}}}$	${\displaystyle {\frac {2\pi J_{1}\left({\sqrt {\omega_{x}^{2}}+\omega_{y}^{2}}\right)}{{\sqrt {\omega_{x}^{2}+\omega_{y}^{2}}}}$	함수는 0 ≤ r ≤ 1일 경우 circ(r) = 1로 정의되며, 그렇지 않으면 0입니다.결과는 Airy 디스크의 진폭 분포이며, J1(첫 번째 종류의 order-1 Bessel 함수)를 사용하여 표현됩니다.[57]
403	${\displaystyle {\frac {1}{\sqrt {x^{2}+y^{2}}}}}$	${\displaystyle {\frac {1}{\sqrt {\xi_{x}^{2}}+\xi_{y}^{2}}}}$	${\displaystyle {\frac {1}{\sqrt {\omega_{x}^{2}}+\omega_{y}^{2}}}}$	${\displaystyle {\frac {2\pi}}{\sqrt {\omega_{x}^{2}}+\omega_{y}^{2}}}}$	이것은 2-D 푸리에 "자기 변환"인 r의−1 행켈 변환입니다.[58]
404	${\displaystyle {\frac {i}{x+iy}}$	${\displaystyle {\frac {1}{\xi_{x}+i\xi_{y}}}}$	${\displaystyle {\frac {1}{\omega_{x}+i\omega_{y}}}}$	${\displaystyle {\frac {2\pi}{\omega_{x}+i\omega_{y}}}}$

일반 n차원 함수 공식

	기능.	푸리에 변환 단일, 통상 주파수	푸리에 변환 단일, 각진동수	푸리에 변환 비단일, 각진동수	언급
500	${\displaystyle f(\mathbf {x})\,}$	${\displaystyle {\begin{aligned}&{\hat {f_{1}}({\bold 기호 {\xi}})\triangleq \&\int _{\mathbb {R}^{n}}f(\mathbf {x})e^{-i2\pi {\bold 기호 {\xi}}\cdot \mathbf {x}\,d\mathbf {x} \end{aligned}}$	${\displaystyle {\begin{aligned}&{\hat {f_{2}}({\bold 기호 {\omega}})\triangleq \&{\frac {1}{(2\pi)}^{\frac {n}{2}}}}\int _{\mathbf {R}^{n}}f(\mathbf {x})e^{-i{\bold 기호 {\omega}}\cdot \mathbf {x}}\,d\mathbf {x} \end{aligned}}$	${\displaystyle {\begin{aligned}&{hat {f_{3}}({\bold 기호 {\omega}})\triangleq \&\int _{\mathbb {R}^{n}f(\mathbf {x})e^{-i{\bold 기호 {\omega}}\cdot \mathbf {x}\,d\mathbf {x} \end{aligned}}$
501	${\displaystyle \chi _{[0,1]}( \mathbf {x})\left(1- \mathbf {x}^{2}\right)^{\delta }}$	${\displaystyle {\frac {\Gamma(\delta +1)}{\pi ^{\delta }\, {\bold 기호 {\xi}}^{\frac {n}{2}}+\delta }}}J_{\frac {n}{2}}+\delta }(2\pi {\bold 기호 {\xi}})$	${\displaystyle 2^{\delta }\,{\frac {\Gamma(\delta +1)}{\left {\bold 기호 {\omega }}\right ^{\frac {n}{2}}+\delta }}}J_{\frac {n}{2}}+\delta }({\bold 기호 {\omega }})$	${\displaystyle {\frac {\Gamma(\delta +1)}{\pi ^{\delta }}\left {\frac {\bold 기호 {\omega }}{2}}\right ^{-{\frac {n}{2}}-\delta }J_{\frac {n}{2}}+\delta }(\! {\bold 기호 {\omega }} \!)$	함수 χ는 [0, 1] 구간의 지시 함수입니다.γ(x) 함수는 감마 함수입니다.함수 J는 n/2 + δ 순서의 첫 번째 종류의 베셀 함수입니다.n = 2이고 δ = 0을 취하면 402가 생성됩니다.
502	${\displaystyle \mathbf {x} ^{-\alpha}},\quad0<\operatorname {Re} \alpha <n.}$	${\displaystyle {\frac {(2\pi )^{\alpha }}{c_{n,\alpha }}{\bold 기호 {\xi }}^{-(n-\alpha )}$	${\displaystyle {\frac {(2\pi))^{\frac {n}{2}}{c_{n,\alpha}}{\bold 기호 {\omega}}^{-(n-\alpha )}}$	${\displaystyle {\frac {(2\pi )^{n}}{c_{n,\alpha}}{\bold 기호 {\omega}}^{-(n-\alpha )}}$	상수가 주어진 Riesz 퍼텐셜 참조 ${\displaystyle c_{n,\alpha}=\pi ^{\frac {n}{2}}{\alpha }{\frac {\Gamma \left ({\frac {\alpha}{2}}\right)}{\Gamma \left ({\frac {n-\alpha}{2}\right)}}}.$ 이 공식은 또한 분석적 연속에 의해 모든 α ≠ n, n + 2, ...에 대해 성립하지만, 함수와 그 푸리에 변환은 적절하게 규칙화된 강화 분포로 이해될 필요가 있습니다.균질 분포 참조.[note 8]
503	${\displaystyle {\frac {1}{\left {\bold 기호 {\sigma}}}\right \left(2\pi \right)^{\frac {n}{2}}}^{-{\frac {1}{2}}\mathbf {x}^{\mathrm {T}{\bold 기호 {\sigma}}^{-\mathrm {T}^{\bold 기호 {\sigma}}^{\bold 기호 {\sigma}}^{-1}\mathbf {x}}}$	${\displaystyle e^{-2\pi ^{2}{\bold 기호 {\xi }}^{\mathrm {T}}{\bold 기호 {\sigma }}{\mathrm {T}}^{\bold 기호 {\xi }}}}$	${\displaystyle(2\pi)^{-{\frac {n}{2}}}e^{-{\frac {1}{2}}}{\bold 기호 {\omega}}}^{\bold 기호 {\sigma}}}{\bold 기호 {\sigma}}^{\mathrm {T}}{\bold 기호 {\omega}}}}^{\bold 기호 {\omega}}}$	${\displaystyle e^{-{\frac {1}{2}}{\bold 기호 {\omega}}}}{\mathrm {T}}{\bold 기호 {\sigma}}}{\mathrm {T}}{\bold 기호 {\omega}}}}}$	이 공식은 평균이 0인 1로 정규화된 다변량 정규 분포에 대한 공식입니다. 굵은 변수는 벡터 또는 행렬입니다.위 페이지의 표기에 따라 σ = σ σ, σ =
504	${\displaystyle e^{-2\pi \alpha \mathbf {x}}}$	${\displaystyle {\frac {c_{n}\alpha}{\left(\alpha ^{2}+ {\boldsymbol {\xi}}}^{{2}\right)^{\frac {n+1}{2}}}}$	${\displaystyle {\frac {c_{n}(2\pi)^{\frac {n+2}{2}}\alpha }{\left(4\pi ^{2}\alpha ^{2}+{\boldsymbol {\omega}}^{\frac {n+1}{2}}}}}$	${\displaystyle {\frac {c_{n}(2\pi)^{n+1}\alpha }{\left(4\pi ^{2}\alpha ^{2}+ {\boldsymbol {\omega}}^{2}\right)^{\frac {n+1}{2}}}}$	여기에[60] ${\displaystyle c_{n}={\frac {\Gamma \left ({\frac {n+1}{2}}\right)}{\pi ^{\frac {n+1}{2}}},}$Re(α) > 0

참고 항목

메모들

인용문

참고문헌

외부 링크

• 위키미디어 커먼즈(Wikimedia Commons)의 푸리에 변환 관련 매체
• 수학 백과사전
• Weisstein, Eric W. "Fourier Transform". MathWorld.