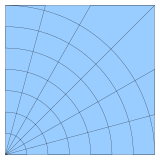
일반 그리드

일반 그리드의 예

규칙 그리드는 합동 평행동위원소(예: 벽돌)^[1]에 의한 n차원 유클리드 공간의 테셀레이션이다.이러한 유형의 그리드는 그래프 용지에 나타나며, 유한 요소 분석, 유한 체적 방법, 유한 차분 방법 및 일반적으로 파라미터 공간의 이산화에 사용될 수 있다.필드 변수의 도함수는 유한 ^[2]차분으로 편리하게 표현될 수 있기 때문에 구조화된 그리드는 주로 유한 차분 방법으로 나타난다.비정형 그리드는 정형 그리드보다 더 많은 유연성을 제공하므로 유한 요소 및 유한 볼륨 방법에 매우 유용합니다.

그리드 내의 각 셀은 2차원의 인덱스(i, j, k) 또는 3차원의 (i, j, $(i\cdot dx,j\cdot dy,k\cdot dz)$ )로 주소 지정할 수 있으며, 각 정점은 $(i\cdot dx,j\cdot dy)$ 좌표( $i$ d $(i\cdot dx,j\cdot dy)$ x , $(i\cdot dx,j\cdot dy)$ d $(i\cdot dx,j\cdot dy)$ y $)($ $i\cdot$ dx , $j\cdot$ dy $(i\cdot dx,j\cdot dy)$ ) 또는 $(i\cdot dx,j\cdot dy)$ $(i\cdot dx,j\cdot dy,k\cdot dz)$ ( $i$ $(i\cdot dx,j\cdot dy,k\cdot dz)$ , $(i\cdot dx,j\cdot dy,k\cdot dz)$ j \ $cdot$ )를 가진다.그리드 간격을 다시 설정합니다.

「」를 참조해 주세요.

레퍼런스

^ Uznanski, Dan. "Grid". From MathWorld--A Wolfram Web Resource, created by Eric W. Weisstein. Retrieved 25 March 2012.
^ J.F. Thompson, B. K . Soni & N.P. Weatherill (1998). Handbook of Grid Generation. CRC-Press. ISBN 978-0-8493-2687-5.

이 기초 기하학 관련 기사는 스텁입니다.위키피디아를 확장함으로써 위키피디아를 도울 수 있습니다.

[1] Uznanski, Dan. "Grid". From MathWorld--A Wolfram Web Resource, created by Eric W. Weisstein. Retrieved 25 March 2012.

[Preface,_P-1.1-2] J.F. Thompson, B. K . Soni & N.P. Weatherill (1998). Handbook of Grid Generation. CRC-Press. ISBN 978-0-8493-2687-5.

[1]

[2]

Search

일반 그리드

네임스페이스

더

관련 그리드

「」를 참조해 주세요.

레퍼런스

Search

일반 그리드

관련 그리드

「 」를 참조해 주세요.

레퍼런스

「」를 참조해 주세요.