전기와크 상호작용

입자물리학 표준모형
표준모델의 기초입자
배경 입자물리학 표준 모델 양자장 이론 게이지 이론 자연대칭파단 힉스 메커니즘
구성 요소 전기와크 상호작용 양자 색역학 CKM 행렬 표준모형수학
제한 사항 강력한 CP 문제 계층 문제 중성미자 진동 표준 모델을 벗어난 물리학
과학자들 러더퍼드 · 톰슨 · 채드윅 · 보스 · 수다르산 · 데이비스 주니어 · 앤더슨 · 페르미 · 디락 · 파인만 · 루비아 · 겔만 · 켄달 · 테일러 · 프리드먼 · 파월 · P. W. 앤더슨 · 글래쇼 · 일리오풀로스 · 레더만 · 마이아니 · 미어 · 코완 · 남부 · 체임벌린 · 카비보 · 슈워츠 · 펄 · 메이저나나 · 와인버그 · 리 · 병동 · 살람 · 코바야시 · 마스카와 · 반 데르 미어 · 밀스 · 양 · 유카와 · 't 후프트' · 벨트만 · 징그럽다 · 파이스 · 파울리 · 폴리티저 · 라인스 · 슈윙거 · 윌체크 · 크로닌 · 피치 · 블렉 · 힉스 · 잉글러트 · 브라우트 · 하겐 · 구랄니크 · 키블 · 산티아고 안투네즈 데 마욜로 · 세자르 라테스 · 즈베이그
v t

입자물리학에서 전기와악 상호작용 또는 전기와악력은 자연의 네 가지 알려진 기본 상호작용 중 두 가지인 전자와 약한 상호작용에 대한 통일된 설명이다.비록 이 두 힘이 매일 낮은 에너지에서는 매우 다르게 나타나지만, 이론은 그것들을 같은 힘의 두 가지 다른 측면으로 모델링한다.통일 에너지 위에서는 246 GeV의 명령에 따라 그들은 단일 세력으로 합쳐질 것이다.^[a]따라서 우주가 충분히 뜨겁다면(약 10K¹⁵, 빅뱅 직후부터 초과되었다고 믿어지지 않는 온도), 전자기력과 약한 힘이 결합된 전기약력으로 합쳐진다.쿼크 시대에는 전기약력이 전자기기로 갈라지고 힘이 약해진다.

셸던 글래쇼,^[1] 압두스 살람,^[2] 스티븐 와인버그는^[3] 와인버그-살람 이론으로 알려진 기초 입자 간의 약자와 전자기 상호작용을 통일하는 데 기여한 공로로 1979년 노벨 물리학상을 받았다.^[4][5]전기와크 상호작용의 존재는 두 단계로 실험적으로 확립되었는데, 첫째는 1973년 가가멜레 협업에 의해 중성미자가 산란된 상태에서 중성미자가 전류를 발견한 것이고, 둘째는 1983년 UA1과 UA2 협업에 의해 양성자-항트로톤 콜리에서의 W와 Z 게이지 보손의 발견과 관련된 것이다.변환된 Super Proton Synchrotron의 사이온.1999년, 제라르두스 후프트와 마르티누스 벨트만은 전기 약품 이론이 리노말릴 수 있다는 것을 보여줌으로써 노벨상을 받았다.

역사

Wu 실험이 약한 상호작용에서 패리티 위반을 발견한 후, 약한 상호작용과 전자기적 상호작용을 연관시키는 방법에 대한 검색이 시작되었다.셸던 글래쇼는 박사학위 자문위원 줄리안 슈윙거의 연구를 확장하면서 먼저 치랄과 아질랄 두 개의 서로 다른 대칭을 도입하는 실험을 했고, 이들의 전체적인 대칭이 깨지지 않도록 결합시켰다.이것은 신장할 수 있는 이론을 만들어내지 못했고, 그 게이지의 대칭은 자발적인 메커니즘이 알려져 있지 않았기 때문에 손으로 부숴져야 했지만, 새로운 입자인 Z 보손(Z boson)을 예측했다.이것은 거의 주목을 받지 못했는데, 그것은 실험적인 발견과 일치하지 않았기 때문이다.

1964년 살람과 워드는^[6] 같은 생각을 가지고 있었지만, 수동으로 대칭이 깨진 질량 없는 광자와 3개의 거대한 게이지 보슨을 예측했다.이후 1967년경, 자발적 대칭 파괴를 조사하던 중 웨인버그는 질량이 없고 중립적인 게이지 보손(boson)을 예측하는 일련의 대칭들을 발견했다.처음에는 그런 입자가 쓸모없다고 거부하다가 나중에 자신의 대칭이 전기약력을 발생시킨다는 것을 깨닫고 W와 Z 보손의 거친 질량을 예측해 나갔다.유의하게, 그는 이 새로운 이론이 새로워질 수 있다고 제안했다.^[3]1971년 Gerard't Hooft는 자연적으로 파손된 게이지 대칭이 거대한 게이지 보손으로도 알 수 있다는 것을 증명했다.

공식화

수학적으로 전자기학은 시스템의 역학을 변경하지 않고 전기취약계장에 적용할 수 있는 형식적인 연산을 기술한 SU(2)×U(1) 게이지 그룹과 함께 양-밀스 분야로서 약한 상호작용과 통일된다.이들 분야는 이소핀이 약한₁ 분야 W₂, W, W₃ 분야와 약한 과충전 분야 B 분야다.이 불협화음은 전기약 대칭이라고 알려져 있다.

SU(2)와 U(1)의 발전기에는 각각 약한 이소핀(T)과 약한 초충전(Y)이라는 이름이 붙는다.그런 다음 전기 약 상호작용을 중재하는 게이지 보손(약 이소핀(W₁, W₂, W₃)과 약한 과전하 B보손(약 초고속)을 각각 발생시키며, 모두 "초기" 무질량이다.이것들은 자발적 대칭이 깨지고 관련 힉스 메커니즘이 생기기 전, 아직 물리적 장이 아니다.

그 표준 모델, W±과 Z0 보손, 그리고 광자에서 전약 대칭 SU(2)×U(1)Y의 Uᆬem,[b]에 자발 대칭은 힉스 매커니즘의 영향으로 발생을 통해 생성된 정교한 양자 분야 이론적 현상이"자발적으로"은 좌우 대칭과 rearranges의 실현을 바꾸(또한 히그스 입자를 보).도자유의^{[8][9][10][11]}

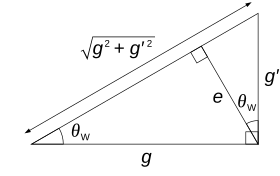
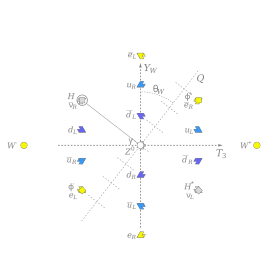
The electric charge arises as the particular linear combination (nontrivial) of Y_W (weak hypercharge) and the T₃ component of weak isospin ${\displaystyle ~\left(\,Q=T_{3}+{\tfrac {1}{2}}\,Y_{\mathrm {W} }\,\right)~}$ that does not couple to the Higgs boson.즉, 다음과 같다.힉스와 전자기장은 근본적인 힘 수준("나무 수준")에서는 서로 영향을 미치지 않는 반면, 과충전 및 약한 이소핀의 다른 조합은 힉스와 상호 작용해야 한다.이것은 힉스와 상호작용하는 약한 힘과 그렇지 않은 전자석 사이에 명백한 분리를 야기한다.수학적으로 전하가 그림에서 설명한 과전하와 T의₃ 특정한 조합이다.

U(1) _em(전자석의 대칭 그룹만 해당)는 이 특별한 선형 결합에 의해 생성된 그룹으로 정의되며,_em U(1) 그룹이 설명한 대칭은 힉스와 직접 상호작용하지 않기 때문에 파손되지 않는다.^[c]

위의 자발적 대칭 파괴는 W₃ 보손과 B 보손들을 서로 다른 질량을 가진 두 개의 다른 물리적 보손, 즉 Z보손과⁰
광자(
광자
),

${\displaystyle {\begin{pmatrix}\gamma \\\z^{0}\end{pmatrix}={\begin{pmatrix}}={pmatrix}}={\coses \theta _{\text}W}&\sin \theta _{\text{W}\\-\sin \theta _{\text{W}&\cos \theta _{\text{W}}\end{pmatrix}{\begin{pmatrix}B\\W_{3}\end{pmatrix},}$

여기서 θ은_W 약한 혼합각이다.입자를 나타내는 축은 θ_W 각도에 의해 (W₃, B) 평면에서 근본적으로 방금 회전되었다.이는 또한 Z의⁰
질량과 W^±
입자의 질량(각각 m과_Z m으로_W 표시됨) 사이에 불일치를 야기한다.

${\displaystyle m_{\text{Z}={\frac {m_{\text{\text}={\frac{\text}W}}{{}\,\cos \theta _{\text{W}\,}},}}$

W₁ 보손과 W₂ 보손은 차례로 결합하여 충전된 대형 보손 W^±
:

${\displaystyle W^{\pm }={\frac {1}{\sqrt {2\,}}\{\bigl (}\,W_{1}\mp iW_{2}\bigr )}.}$

라그랑기안

전기로 인한 대칭이 깨지기 전

전기약 상호작용에 대한 라그랑지안은 전기약 대칭 파괴가 나타나기 전에 네 부분으로 나뉘어져 있다.

${\displaystyle {\mathcal{L}_{\text{EW}}={\mathcal{L}_{g}+{\mathcal{L}_{f}+{\mathcal {{L}}+{{H}+{\mathcal{L}_{Y}}}.}$

$L{\displaystyle {\mathcal{}}_{}}$ ${\displaystyle g_{}}$ ${\$ 항은$$ 세 개의 W 벡터 보손과 B 벡터 보손 사이의 상호작용을 설명한다.

${\displaystyle {\mathcal {L}}_{g}=-{\tfrac {1}{4}}W_{a}^{\mu \nu }W_{\mu \nu }^{a}-{\tfrac {1}{4}}B^{\mu \nu }B_{\mu \nu }}$,

여기서 $W{\displaystyle {}^{}}$ ${\displaystyle {\mu }^{}}$ μ${\$ W$^{a\mu \nu }}($${\displaystyle }$= ${\displaystyle 1}$,${\displaystyle 2}$,${\displaystyle }$3 ${\displaystyle a=1,2,3$ 및 $B{\displaystyle {}^{}}$ ${\displaystyle {\mu }^{}}$ ${\displaystyle {\mu }^{}}$ $\$ {\$displaystyle B^{\mu \nu }}}}$는 약한 이소핀 및 약한 과충전 게이지장에 대한 자기장 강도 텐서이다.

${\displaystyle {\mathcal{L}}_{}}$ ${\displaystyle f_{}}$ ${\$는 표준 모형 페르미온의 운동 용어다.게이지 보손과 페르미온의 상호작용은 게이지 공변량 파생물을 통해 이루어진다.

${\$$\!\\;Q_{j}+{\overline{u}_{j}iD\!\!$$\!\/\;u_{j}+{\overline{d}_{j}iD\!\!$$\!\/\;d_{j}+{\overline{L}_{j}iD\!\!$$\!\\;L_{j}+{\overline{e}_{j}iD\!\!$$\!\/\;e_{j$

여기서 첨자 j는 페르미온의 3세대를 합한 것이다; Q, u, d는 왼손잡이 더블트, 오른손잡이 싱어 업, 오른손잡이 싱어크 쿼크 필드, 그리고 L과 e는 왼손잡이 더블트, 오른손잡이 싱어릿 전자장이다.파인만 $슬래시{\displaystyle }$ D${\displaystyle }$/ ${\$ D$\!\!$$\!/}$은(는) 디락 행렬로 4학년의 수축을 의미하며$$, 다음과 같이 정의된다.

$D\!\!\/\equiv \gamma ^{\\mu ^{}D_{\mu }}}}}$

공변량 파생상품(강력한 상호작용에 대한 글루온 게이지 필드 제외)은 다음과 같이 정의된다.

${\displaystyle D_{\mu }}\equiv \partial _{\mu }-i-{\frac {g'}{2}}Y\,B_{\mu }-i{\frac {g}{2}}:T_{j}\,W_{\mu}^{j}}}}}}}$

여기서 $Y{\displaystyle }$ ${\displaystyle Y}$은(는) 약한 과충전이고 T ${\displaystyle j_{}}$ ${\$는 약한$$ 이소핀의 성분이다.

$L$ ${\displaystyle h_{}}$ ${\$ 용어는 힉스 $필드{\displaystyle }$ h {\$displaystyle h}$과(와) 힉스 필드 h ${\$displaysty h} 및 그 자체 및 게이지 보손과의 상호작용을 설명한다.

${\displaystyle {\mathcal{L}}_{}}$ ${\displaystyle h_{}}$= ${\displaystyle D{}_{}}$ ${\displaystyle {\mu }_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {}^{\mathrm{}}}$ -${\displaystyle {}^{}\lambda {}^{}}$( ${\displaystyle h^{}}$ ${\displaystyle {{}^{\mathrm{}}}^{}}$- ${\displaystyle {\frac{{v\mathrm{}}^{}}{}}^{}}$ ${\displaystyle {\frac{{}^{}}{\mathrm{}}}^{}}$) ${\displaystyle {\mathrm{}}^{}}$ ${\$, ,

$여기$서 v ${\displaystyle v}$은(는) 진공 기대 값이다.

$L{\displaystyle {\mathcal{}}_{}}$ ${\displaystyle y_{}}$ ${\$ 용어는$$ 페르미온과의 유카와 교호작용을 설명한다.

${\displaystyle {\mathcal {L}}_{y}=-y_{u\,ij}\epsilon ^{ab}\,h_{b}^{\dagger }\,{\overline {Q}}_{ia}u_{j}^{c}-y_{d\,ij}\,h\,{\overline {Q}}_{i}d_{j}^{c}-y_{e\,ij}\,h\,{\overline {L}}_{i}e_{j}^{c}+h.c.~,}$

힉스 필드가 0이 아닌 진공 기대값을 획득할 때 나타나는 질량을 생성하고 다음에 논의한다.$y{\displaystyle {}_u^{}}$ , ${\displaystyle d_{}^{}}$, ${\displaystyle {}_{}^{}}$ ${\displaystyle j_{}^{}}$ ${\$는 유카와 커플링의 행렬이다$$.

전자위크 후 대칭 깨짐

라그랑지안은 힉스 보슨이 이전 섹션의 잠재력에 의해 지시된 비반사 진공 기대값을 획득함에 따라 스스로를 재편성한다.이 재작성 결과, 대칭 깨짐이 뚜렷해진다.우주의 역사에서 이는 뜨거운 빅뱅 직후 우주가 159.5±1.5GeV^[12](입자물리학의 표준모델로 가정)에 있을 때 일어난 것으로 여겨진다.

복잡성 때문에 이 라그랑지안은 다음과 같이 여러 부분으로 나누어 가장 잘 묘사된다.

${\displaystyle {\mathcal{L}_{\text{EW}}={\mathcal{L}_{\text{K}+{\mathcal{L}_{\text}{\text{\text}}N}+{\mathcal{L}_{\text{C}}+{\mathcal{L}_{\text{H}}+{\mathcal{L}_{\text{HV}+{\mathcal{L}_{\text{WWV}+{\mathcal{L}_{\text{WWVV}+{\mathcal{L}_{\text{Y}}.}$

운동 용어 $L{\displaystyle {\mathcal{}}_{}}$ ${\displaystyle K_{}}$ ${\$는 동적 용어(부분 파생 모델)와 질량 용어(대칭이 깨지기 전에 라그랑지아에서 대체로 없음)를 포함하는 라그랑지아의 모든 2차 항을 포함한다$$.

${\displaystyle {\begin{aligned}{\mathcal {L}}_{\text{K}}=\sum _{f}{\overline {f}}(i\partial \!\!\!/\!\;-m_{f})f-{\frac {1}{4}}A_{\mu \nu }A^{\mu \nu }-{\frac {1}{2}}W_{\mu \nu }^{}+}W^{-\mu \nu }+m_{W}^{2}W_{\mu }^{+}W^{-\mu }\\\qquad -{\frac {1}{4}}Z_{\mu \nu }Z^{\mu \nu }+{\frac {1}{2}}m_{Z}^{2}Z_{\mu }Z^{\mu }+{\frac {1}{2}}(\partial ^{\mu }H)(\partial _{\mu }H)-{\frac {1}{2}}m_{H}^{2}H^{2}^{2}~,\end{정렬}}}$

where the sum runs over all the fermions of the theory (quarks and leptons), and the fields ${\displaystyle A_{\mu \nu }}$, ${\displaystyle Z_{\mu \nu }}$, ${\displaystyle W_{\mu \nu }^{-}}$, and ${\displaystyle W_{\mu \nu }^{+}\equiv (W_{\mu \nu }^{-})$$^{\message }}$은(는) 다음과 같이 주어진다$$

${\displaystyle X_{\mu \nu }^{a}=\partial _{\mu }-{\mu }-{\mu }-{\nu }-{\nu }-{\nu }-}-{\nu }+gf^{abc^{b}X_{c},},},}},}}}}}}}}}$

'${\displaystyle }$ ${\displaystyle X$과(와) 관련 필드($A{\displaystyle }$ ${\displaystyle$ $A$$\},$ $Z{\displaystyle {}^{}}$ ${\displaystyle$ Z$\},$ W${\displaystyle {}^{}}$± ${\$로, f를 해당^abc 게이지 그룹의 구조 상수로 교체한다.

그 중립 현재 나는 N{\displaystyle{{나는\mathcal}}_{\text{.N}}}과}현재 나는 C{\displaystyle{{나는\mathcal}을 입건했다_{\text{.C}}}은 Lagrangian의 구성 요소는 fermions 및 사용 게이지 bosons, 사이의 상호 작용을 포함하고 있다.

${\displaystyle {\mathcal{L}_{\text{N}}=e\,J_{\mu}^{\text{12포인트 전각.}}\,A^{\mu}+{\frac{g}{\,\cos \theta_{W}\,}}\,(\,J_{\mu}^{3}-\sin ^{2}\theta_{W}\,J_{\mu}^{\text{12포인트 전각.}}),)\,Z^{\mu}~,}.$

어디서 e)g죄 ⁡ θ W)g′. 왜냐하면 ⁡ θ W.{\displaystyle ~e=g\,\sin \theta_{\text{.W}}=g'\,\cos \theta_{\text{W}}일.}그 전자기 현재 Jμ 12포인트 전각.{\displaystyle\;.J_{\mu}^{\text{12포인트 전각.}}\;}은

${\displaystyle J_{\mu}^{\text{12포인트 전각.}}=\sum _{f}\,q_{f}\,{\overline{f}}\,\gamma _{\mu}\,f~,}.$

어디 qf{\displaystyle q_{f}^{}}은 fermions의 전기 요금.그 중립적인 약전류 J3{\displaystyle\와 같이 μ.J_{\mu}^{3}\.}은

${\displaystyle J_{\mu}^{3}=\sum _{f}\,I_{f}^{3}\,{\overline{f}}\,\gamma _{\mu}\,{\frac{\,1-\gamma ^{5}\,}{2}}\,f~,}.$

$여기$서 I ${\displaystyle f_{}^{}}$ ${\displaystyle {\mathrm{}}_{}^{}}$ ${\$}}{3$}}$는 페르미온의 약한 이소스핀이다.^[d]

라그랑지아의 충전 전류 부분은 다음과 같이 주어진다.

${\displaystyle {\mathcal{L}_{\text{{\c}=-{\frac {g}{\\\sqrt {2\,}\,}\},\lift[,\overline {u}_{i}\ma}\\\\frcH00},{5},}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}M_{ij}^{{ij}^{\text{CKM}}\,d_{j}}+{\coverline{\\\nu }}}\\no_{i}\no }\,\gamma ^{5}\,},{2}}\;e_{i}\,\,\, 오른쪽]\,W_{\mu }^{+}+{\text{h.c.}}~,}$

여기서 ${\displaystyle \nu }$ ${\$은(는) 오른손잡이 싱클레트 중성미자 필드로$$, CKM 매트릭스 ${\displaystyle {\mathrm{Mi}}_{}^{}}$ j ${\displaystyle {\text{CKM}}_{}^{}}$ $displaystyle \,M_{ij}^{\text{CKM}\}\}}}}}}$은 쿼크의 질량과 약한 고유질 사이의 혼합을 결정한다$$.^[d]

${\$$H}}$에는 힉스 3점 및 4점 자가 상호작용 용어가 들어 있으며,

${\displaystyle {\mathcal{L}_{\text{H}}=-{\frac {\,g\,m_{\text{H}}^{2}\,}{\,4\,m_{\text{W}}\,}}\;H^{3}-{\frac {\,g^{2}\,m_{\text{H}}^{2}\,}{32\,m_{\text{W}^{2}}:}\;H^{4}~.}$

${\$$HV}}$에는 게이지 벡터 보손과의 힉스 교호작용이 포함되어$$ 있으며,

${\displaystyle {\mathcal{L}_{\text{HV}=\왼쪽(\,g\,m_{\text{HV}+{\frac {\,g^{2}\,}{4}\;H^{2}\,\오른쪽)\왼쪽(\,W_{\mu }^{}+}\,W^{-\mu }+{1}\\frac {1}{\\2\,\cos ^{2}\theta _{\text}W}}\,}}\;Z_{\mu }\,Z^{\mu }\,\오른쪽)~}$

${\$$WWV}}$에는 게이지 3점 자가 교호작용이 포함되어$$ 있으며,

${\displaystyle {\mathcal{L}_{\text{WWV}}=-i\,g\,\left[\;\left(\,W_{\mu \nu }^{+}\,W^{-\mu }-W^{+\mu }\,W_{\mu \nu }^{-}\,\right)\left(\,A^{\nu }\,\sin \theta _{\text{W}}-Z^{\nu }\,\cos \theta _{\text{W}}\,\오른쪽)+W_{\nu }^{-}\,W_{\mu }^{+}\,\왼쪽(\,A^{\mu \nu }\,\sin \theta _{\text{W}}-Z^{\mu \nu }\,\cos \theta _{\text{W}\,\오른쪽)\;\오른쪽].}$

$displaystyle \,{\mathcal{L}_{\text{$$WWV}\,}$은(는) 게이지 4-포인트 자체 상호작용을 포함하며$$,

${\displaystyle {\begin{aigned}{\mathcal {L}_{\text}{WWV}}=-{\\frac{2}\,}{4}\,{\Biggl \{}\,&\Bigl [}\\\,2\,W_}^{\mu }^{+}\,W^{}^{-\a_\mu }\,\cext.W}}-Z_{\mu }\,\cos \theta _{\text{W}}\,)^{2}\,{\Bigr ]}^{2}\\&-{\Bigl [}\,W_{\mu }^{+}\,W_{\nu }^{-}+W_{\nu }^{+}\,W_{\mu }^{-}+\left(\,A_{\mu }\,\sin \theta _{\text{W}}-Z_{\mu }\,\cos \theta _{\text{W}\,\오른쪽)\왼쪽(\,A_{\nu }\,\sin \theta _{\text{W}-Z_{\nu }\,\cos \theta _{\text{W}\,\오른쪽)\,{\Bigr ]}^{2}\,{\Biggr \}}~~\end{정렬}}}$

$displaystyle \,{\mathcal {L}_{\text{$$Y}}\,}$은(는) 페르미온과 힉스 필드 사이의 유카와 교호작용을 포함한다$$.

${\displaystyle {\mathcal{L}_{\text{Y}}=-\sum _{f}\,{\frac {\,g\,m_{f}\,}{2\,m_{\text}{W}}}\;{\overline{f}\,f\,H~}$

참고 항목

• 양-밀스 이론
• 근본력
• 양자장 이론의 역사
• 표준 모형(수학적 공식)
• 단위성 게이지
• 와인버그 각

메모들

참조

추가 읽기

일반 독자

• B. A. Schumm (2004). Deep Down Things: The Breathtaking Beauty of Particle Physics. Johns Hopkins University Press. ISBN 0-8018-7971-X. 정규 수학 없이 표준 모델의 많은 부분을 전달한다.약한 상호작용에 대해 아주 철저하다.

텍스트

• D. J. Griffiths (1987). Introduction to Elementary Particles. John Wiley & Sons. ISBN 0-471-60386-4.
• W. Greiner; B. Müller (2000). Gauge Theory of Weak Interactions. Springer. ISBN 3-540-67672-4.
• G. L. Kane (1987). Modern Elementary Particle Physics. Perseus Books. ISBN 0-201-11749-5.

기사들

• E. S. Abers; B. W. Lee (1973). "Gauge theories". Physics Reports. 9 (1): 1–141. Bibcode:1973PhR.....9....1A. doi:10.1016/0370-1573(73)90027-6.
• Y. Hayato; et al. (1999). "Search for Proton Decay through p → νK⁺ in a Large Water Cherenkov Detector". Physical Review Letters. 83 (8): 1529–1533. arXiv:hep-ex/9904020. Bibcode:1999PhRvL..83.1529H. doi:10.1103/PhysRevLett.83.1529. S2CID 118326409.
• J. Hucks (1991). "Global structure of the standard model, anomalies, and charge quantization". Physical Review D. 43 (8): 2709–2717. Bibcode:1991PhRvD..43.2709H. doi:10.1103/PhysRevD.43.2709. PMID 10013661.
• S. F. Novaes (2000). "Standard Model: An Introduction". arXiv:hep-ph/0001283.
• D. P. Roy (1999). "Basic Constituents of Matter and their Interactions – A Progress Report". arXiv:hep-ph/9912523.