슈뢰더-베른슈타인 정리

집합론에서, 슈뢰더-번스타인 정리는 만약 $집합$ $A$ 와 B 사이에 $사함수 f$ : $A$ → $B$ 와 g : B → A가 존재한다면, $사함수$ h : $A$ → $B$ 가 존재한다는 것을 말합니다.

두 집합의 카디널리티의 관점에서, 이것은 고전적으로 A ≤ $B$ 및 $B$ ≤ $A이면$ $A$ = $B$ ; 즉, $A$ 와 B가 등분성임을 암시합니다.이 기능은 기수 순서를 정렬할 때 유용한 기능입니다.

이 정리는 펠릭스 베른슈타인과 에른스트 슈뢰더의 이름을 따서 지어졌습니다.이 정리는 칸토어-베른슈타인 정리 또는 칸토어-슈뢰더-베른슈타인 정리로도 알려져 있는데, 이 정리는 게오르크 칸토어의 이름을 따서 처음으로 발표된 것입니다.

증명

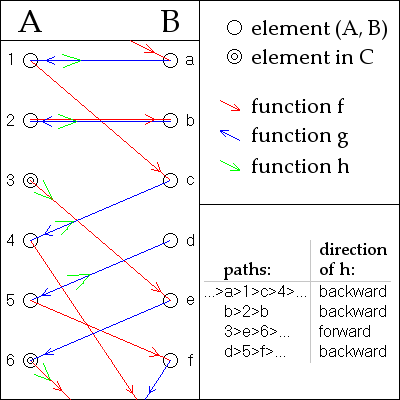
주어진 예제 주입 f:A → B 및 g:B → A의 *쌍사출* h:A → B에 대한 König의 정의. A와 B의 원소는 각각 숫자와 문자로 표시됩니다.수열 3 → e → 6 → ...는 정의 h(3) = f(3) = e, h(6) = f(6), ...로 이어지는 A-stopper입니다.수열 d → 5 → f = ...는 h(5) = g(5) → d, ...로 *이어지는* B-stopper입니다.순서가...→ a → 1 → c → 4 → ...는 h(1) = g(1) = a, h(4) = g(4) = c, ...로 *이어지는* 이중 무한대입니다.수열 b → 2 → b는 h(2) = g(2) = b로 *이어지는* 순환형입니다.

다음의 증거는 줄리어스 쾨닉의 ^[1]것입니다.

일반성을 잃지 않고 A와 B가 서로소인 것으로 가정합니다.B의 A 또는 B에 있는 임의의 $a$ 에 대해 f ${\$ $g^{-1}$ f $}$ 와 g - 1 {\ $displaystyle$ g^{- $1}$ 를 $g^{-1}$ A에서 B로, $g$ {\ $displaystyle$ g $}$ 와 $g$ $f^{-1}$ f - $f^{-1}$ {\ $displaystyle$ f $^{-1}$ 를 $f^{-1}$ B에서 A로(정의된 경우, 역 f $f^{-1}$ - $f^{-1}$ {\ $displaystyle$ f $^{-1}$ 와 $f^{-1}$ $g^{-1}$ g - $g^{-1}$ {\displaystyle f^{-1})로 반복 $f$ 으로써 A와 B가 교대로 있는 독특한 요소의 양면 시퀀스를 형성할 수 있습니다. $\displaystyle$ g $^{-1}}$ 는 $g^{-1}$ 부분 함수로 이해됩니다.)

$\cdots \right arrow f^{-1}(a))\right arrow g^{-1}(a)\right arrow f(a)\right arrow g(f(a))\right arrow \cdots$

특정 a의 $f^{-1}$ f - 1 {\ $displaystyle$ f $}$ 또는 g - 1 {\ $displaystyle g^{-1$ }}이( $f^{-1}$ ) 정의되지 않은 지점에서 이 시퀀스가 왼쪽으로 종료되거나 종료되지 않을 수 있습니다.

f ${\displaystyle$ f $}$ $g$ g ${\displaystyle$ g $}$ 이 $g$ ( $가$ ) 주입 함수이기 때문에, A의 각 a와 B의 각 a는 동일성 내에 있는 그러한 수열에 있습니다. 만약 어떤 요소가 두 수열에서 발생한다면, 그 수열의 정의에 의해 왼쪽과 오른쪽의 모든 요소는 양쪽에서 동일해야 합니다.따라서 수열은 A와 B의 (이음) 결합의 분할을 형성합니다.따라서 다음과 같이 각각의 수열에서 A와 B의 원소 사이에 비접사를 생성하는 것으로 충분합니다.

시퀀스가 A의 요소에서 멈추면 A-stopper라고 부르고, B의 요소에서 멈추면 B-stopper라고 부릅니다.그렇지 않으면 모든 원소가 서로 다르거나 반복되는 경우에는 이를 이중 무한이라 합니다.예를 보려면 그림을 참조하십시오.

A 스톱퍼의 경우 $함수$ f ${\displaystyle$ f $}$ 은 $f$ (는) A의 요소와 B의 요소 사이의 빗변입니다.
B-스토퍼의 경우 $함수$ g{\ $displaystyle$ g $}$ 은 $g$ (는) B의 원소와 A의 원소 사이의 빗접사입니다.
이중 무한 시퀀스 또는 순환 시퀀스의 경우 f{\ $displaystyle$ f $}$ $g$ g{\ $displaystyle$ g $}$ 중 $g$ $f$ 만 사용하면 됩니다( $사진$ 에서 g{\ $displaystyle$ g $}$ 이 $g$ (가) 사용됩니다).

또다른 증거

$f:A\to B$ A → $f:A\to B$ ${\displaystyle$ f $:$ $A\toB}$ $g:B\to A$ : B $→$ $g:B\to A$ {\ $displaystyle$ g : $B\toA}$ 는 $g:B\to A$ 두 개의 주사 함수입니다.

그런 다음 집합을 정의합니다. $C_{0}=A\setminus g(B)\quad$ $k\in \{0,1,2,3,...\}$ $C_{0}=A\setminus g(B)\quad$ $\quad C_{k+1}=g(f(C_{k}))$ $k\in \{0,1,2,3,...\}$ $displaystyle C$ $=$ $A\setminus$ g $B)\quad}$ $\quad C_{k+1}=g(f(C_{k}))$ $\quad C_{k+1}=g(f(C_{k}))$ $C_{0}=A\setminus g(B)\quad$ $\quad C_{k+1}=g(f(C_{k}))$ $\quad C_{k+1}=g(f(C_{k}))$ = $\quad C_{k+1}=g(f(C_{k}))$ {\ $displaystyle \displaystyle C_{$ $C_{0}=A\setminus g(B)\quad$ $+1$ } = $g(f(C_{k}))$ { $k\in \{0,1,2,3,...\}$ $k\in \{0,1,2,3,...\}$ $k\in \{0,1,2,3,...\}$ $k\in \{0,1,2,3,...\}$ $k\in \{0,1,2,3,...\}$ ${\displaystyle$ k $\in \{0,$ 1, $2, 3,$ 3,... $\}}$ 그리고 $\quad C=\bigcup _{k=0}^{\infty }C_{k}$ 으로 C $=$ $⋃$ $\quad C=\bigcup _{k=0}^{\infty }C_{k}$ $=$ $\quad C=\bigcup _{k=0}^{\infty }C_{k}$ $∞$ $\quad C=\bigcup _{k=0}^{\infty }C_{k}$ ${\displaystyle \displaystyle$ \ $displaycup _{k$ $=$ $0}^{\infty }C_{k}}$

$\;h(x):={\begin{cases}f(x),&\mathrm {for} \ x\in C\\g^{-1}(x),&\mathrm {for} \ x\in A\setminus C\end{cases}}\quad$ ( $\;h(x):={\begin{cases}f(x),&\mathrm {for} \ x\in C\\g^{-1}(x),&\mathrm {for} \ x\in A\setminus C\end{cases}}\quad$ ) : $\;h(x):={\begin{cases}f(x),&\mathrm {for} \ x\in C\\g^{-1}(x),&\mathrm {for} \ x\in A\setminus C\end{cases}}\quad$ = { $\;h(x):={\begin{cases}f(x),&\mathrm {for} \ x\in C\\g^{-1}(x),&\mathrm {for} \ x\in A\setminus C\end{cases}}\quad$ ( $\;h(x):={\begin{cases}f(x),&\mathrm {for} \ x\in C\\g^{-1}(x),&\mathrm {for} \ x\in A\setminus C\end{cases}}\quad$ $\;h(x):={\begin{cases}f(x),&\mathrm {for} \ x\in C\\g^{-1}(x),&\mathrm {for} \ x\in A\setminus C\end{cases}}\quad$ $\;h(x):={\begin{cases}f(x),&\mathrm {for} \ x\in C\\g^{-1}(x),&\mathrm {for} \ x\in A\setminus C\end{cases}}\quad$ ∈ $\;h(x):={\begin{cases}f(x),&\mathrm {for} \ x\in C\\g^{-1}(x),&\mathrm {for} \ x\in A\setminus C\end{cases}}\quad$ - $\;h(x):={\begin{cases}f(x),&\mathrm {for} \ x\in C\\g^{-1}(x),&\mathrm {for} \ x\in A\setminus C\end{cases}}\quad$ ( $\;h(x):={\begin{cases}f(x),&\mathrm {for} \ x\in C\\g^{-1}(x),&\mathrm {for} \ x\in A\setminus C\end{cases}}\quad$ $\;h(x):={\begin{cases}f(x),&\mathrm {for} \ x\in C\\g^{-1}(x),&\mathrm {for} \ x\in A\setminus C\end{cases}}\quad$ $\;h(x):={\begin{cases}f(x),&\mathrm {for} \ x\in C\\g^{-1}(x),&\mathrm {for} \ x\in A\setminus C\end{cases}}\quad$ ∈ $\;h(x):={\begin{cases}f(x),&\mathrm {for} \ x\in C\\g^{-1}(x),&\mathrm {for} \ x\in A\setminus C\end{cases}}\quad$ ∖ $\;h(x):={\begin{cases}f(x),&\mathrm {for} \ x\in C\\g^{-1}(x),&\mathrm {for} \ x\in A\setminus C\end{cases}}\quad$ $displaystyle$ \; $h(x):$ $={\mathrm{case$ }f $(x),&\mathrm$ {for} \ $x\in$ C $\\g^{-1}(x),&\mathrm {for} \$ x $\in$ A $\setminus C\end{$ case}}\ $quad$ }은(는) 사함수 $\quad h:A\to B\quad$ 를 $\quad h:A\to B\quad$ 합니다. A $→$ B ${\displaystyle$ \ $displayh:$ $A\toB\quad$

증명을 $g(f(C))=g(f(\bigcup _{k=0}^{\infty }C_{k}))=\bigcup _{k=0}^{\infty }g(f(C_{k}))=\bigcup _{k=0}^{\infty }C_{k+1}=\bigcup _{k=1}^{\infty }C_{k}$ 먼저 g $g(f(C))=g(f(\bigcup _{k=0}^{\infty }C_{k}))=\bigcup _{k=0}^{\infty }g(f(C_{k}))=\bigcup _{k=0}^{\infty }C_{k+1}=\bigcup _{k=1}^{\infty }C_{k}$ ( $g(f(C))=g(f(\bigcup _{k=0}^{\infty }C_{k}))=\bigcup _{k=0}^{\infty }g(f(C_{k}))=\bigcup _{k=0}^{\infty }C_{k+1}=\bigcup _{k=1}^{\infty }C_{k}$ ( $g(f(C))=g(f(\bigcup _{k=0}^{\infty }C_{k}))=\bigcup _{k=0}^{\infty }g(f(C_{k}))=\bigcup _{k=0}^{\infty }C_{k+1}=\bigcup _{k=1}^{\infty }C_{k}$ ) = $g(f(C))=g(f(\bigcup _{k=0}^{\infty }C_{k}))=\bigcup _{k=0}^{\infty }g(f(C_{k}))=\bigcup _{k=0}^{\infty }C_{k+1}=\bigcup _{k=1}^{\infty }C_{k}$ ( $g(f(C))=g(f(\bigcup _{k=0}^{\infty }C_{k}))=\bigcup _{k=0}^{\infty }g(f(C_{k}))=\bigcup _{k=0}^{\infty }C_{k+1}=\bigcup _{k=1}^{\infty }C_{k}$ ( ⋃ $g(f(C))=g(f(\bigcup _{k=0}^{\infty }C_{k}))=\bigcup _{k=0}^{\infty }g(f(C_{k}))=\bigcup _{k=0}^{\infty }C_{k+1}=\bigcup _{k=1}^{\infty }C_{k}$ = $g(f(C))=g(f(\bigcup _{k=0}^{\infty }C_{k}))=\bigcup _{k=0}^{\infty }g(f(C_{k}))=\bigcup _{k=0}^{\infty }C_{k+1}=\bigcup _{k=1}^{\infty }C_{k}$ ∞ $g(f(C))=g(f(\bigcup _{k=0}^{\infty }C_{k}))=\bigcup _{k=0}^{\infty }g(f(C_{k}))=\bigcup _{k=0}^{\infty }C_{k+1}=\bigcup _{k=1}^{\infty }C_{k}$ ) ) = ⋃ $g(f(C))=g(f(\bigcup _{k=0}^{\infty }C_{k}))=\bigcup _{k=0}^{\infty }g(f(C_{k}))=\bigcup _{k=0}^{\infty }C_{k+1}=\bigcup _{k=1}^{\infty }C_{k}$ = $g(f(C))=g(f(\bigcup _{k=0}^{\infty }C_{k}))=\bigcup _{k=0}^{\infty }g(f(C_{k}))=\bigcup _{k=0}^{\infty }C_{k+1}=\bigcup _{k=1}^{\infty }C_{k}$ ∞ $g(f(C))=g(f(\bigcup _{k=0}^{\infty }C_{k}))=\bigcup _{k=0}^{\infty }g(f(C_{k}))=\bigcup _{k=0}^{\infty }C_{k+1}=\bigcup _{k=1}^{\infty }C_{k}$ ( $g(f(C))=g(f(\bigcup _{k=0}^{\infty }C_{k}))=\bigcup _{k=0}^{\infty }g(f(C_{k}))=\bigcup _{k=0}^{\infty }C_{k+1}=\bigcup _{k=1}^{\infty }C_{k}$ ( $g(f(C))=g(f(\bigcup _{k=0}^{\infty }C_{k}))=\bigcup _{k=0}^{\infty }g(f(C_{k}))=\bigcup _{k=0}^{\infty }C_{k+1}=\bigcup _{k=1}^{\infty }C_{k}$ k $g(f(C))=g(f(\bigcup _{k=0}^{\infty }C_{k}))=\bigcup _{k=0}^{\infty }g(f(C_{k}))=\bigcup _{k=0}^{\infty }C_{k+1}=\bigcup _{k=1}^{\infty }C_{k}$ = ⋃ $g(f(C))=g(f(\bigcup _{k=0}^{\infty }C_{k}))=\bigcup _{k=0}^{\infty }g(f(C_{k}))=\bigcup _{k=0}^{\infty }C_{k+1}=\bigcup _{k=1}^{\infty }C_{k}$ = $g(f(C))=g(f(\bigcup _{k=0}^{\infty }C_{k}))=\bigcup _{k=0}^{\infty }g(f(C_{k}))=\bigcup _{k=0}^{\infty }C_{k+1}=\bigcup _{k=1}^{\infty }C_{k}$ ∞ $g(f(C))=g(f(\bigcup _{k=0}^{\infty }C_{k}))=\bigcup _{k=0}^{\infty }g(f(C_{k}))=\bigcup _{k=0}^{\infty }C_{k+1}=\bigcup _{k=1}^{\infty }C_{k}$ k + $g(f(C))=g(f(\bigcup _{k=0}^{\infty }C_{k}))=\bigcup _{k=0}^{\infty }g(f(C_{k}))=\bigcup _{k=0}^{\infty }C_{k+1}=\bigcup _{k=1}^{\infty }C_{k}$ = ⋃ $g(f(C))=g(f(\bigcup _{k=0}^{\infty }C_{k}))=\bigcup _{k=0}^{\infty }g(f(C_{k}))=\bigcup _{k=0}^{\infty }C_{k+1}=\bigcup _{k=1}^{\infty }C_{k}$ = $g(f(C))=g(f(\bigcup _{k=0}^{\infty }C_{k}))=\bigcup _{k=0}^{\infty }g(f(C_{k}))=\bigcup _{k=0}^{\infty }C_{k+1}=\bigcup _{k=1}^{\infty }C_{k}$ ∞ $g(f(C))=g(f(\bigcup _{k=0}^{\infty }C_{k}))=\bigcup _{k=0}^{\infty }g(f(C_{k}))=\bigcup _{k=0}^{\infty }C_{k+1}=\bigcup _{k=1}^{\infty }C_{k}$ k $g(f(C))=g(f(\bigcup _{k=0}^{\infty }C_{k}))=\bigcup _{k=0}^{\infty }g(f(C_{k}))=\bigcup _{k=0}^{\infty }C_{k+1}=\bigcup _{k=1}^{\infty }C_{k}$ {\ $displaystyle$ g $(f(C$ )) = $g(f(\bigcup$ _ ${k$ = $0}^{\infty }C_{k$ }) =\ $bigcup _{k$ =0}^{\ $infty }g(f(C_{$ k}) =\ $bigcup _{k$ = $0}^{\infty }C_{k+1$ }=\ $bigcup$ _{k=1 $}^{\infty }C_{k$ }}

$h$ ${\displaystyle$ h $}$ 은 $h$ (는) 실제로 다음과 같은 함수입니다. $x\in C\subset A\quad$ $x\in C\subset A\quad$ ∈ $x\in C\subset A\quad$ ⊂ $x\in C\subset A\quad$ A {\ $displaystyle x\in$ C\ $subset A$ \quad $x\in C\subset A\quad$ }이면 $h(x)=f(x)\in B\quad$ h (x $h(x)=f(x)\in B\quad$ = $h(x)=f(x)\in B\quad$ ( $h(x)=f(x)\in B\quad$ ∈ $h(x)=f(x)\in B\quad$ ${\displaystyle$ h $(x$ ) = $f(x)\$ $in$ B $\quad }$ 이고, $\quad x\in A\setminus C\subset A\setminus C_{0}=g(B)\quad$ x ∈ $\quad x\in A\setminus C\subset A\setminus C_{0}=g(B)\quad$ ∖ $\quad x\in A\setminus C\subset A\setminus C_{0}=g(B)\quad$ ⊂ A ∖ C $\quad x\in A\setminus C\subset A\setminus C_{0}=g(B)\quad$ quad $\quad x\in A\setminus C\subset A\setminus C_{0}=g(B)\quad$ 0 = $\quad x\in A\setminus C\subset A\setminus C_{0}=g(B)\quad$ ( ${\displaystyle$ \displaystyle x\in A $\setminus C_{0$ }= g( $B)\quad }$ 이면 h ( $\quad h(x)=g^{-1}(x)$ = $\quad h(x)=g^{-1}(x)$ - $\quad h(x)=g^{-1}(x)$ ( $\quad h(x)=g^{-1}(x)$ {\ $displaystyle \displaystyle$ h $(x$ ) = $g^{-1}(x$ )}가 존재하고 $B$ B {\ $displaystyle$ B에서 하나의 요소입니다 $.$ $}$ $g:B\to A$ g : $g:B\to A$ $→$ $g:B\to A$ ${\displaystyle$ g : $B\toA}$ 은 $g:B\to A$ (는) 주사형입니다.

$h$ ${\displaystyle$ h $}$ 은(는) 주입형입니다. $h(x_{1})=h(x_{2})$ $x$ $h(x_{1})=h(x_{2})$ $=$ ( $h(x_{1})=h(x_{2})$ {\ $displaystyle$ h $(x_{$ $1$ }) = $h(x_{2})}$
- $x_{1},x_{2}\in C$ 1 $x_{1},x_{2}\in C$ $x_{1},x_{2}\in C$ 2 ∈ $x_{1},x_{2}\in C$ {\ $displaystyle x_{1}, x_{2}\in$ C $}$ 이면 h $h(x_{1})=f(x_{1})=f(x_{2})=h(x_{2})$ 1 $h(x_{1})=f(x_{1})=f(x_{2})=h(x_{2})$ = $h(x_{1})=f(x_{1})=f(x_{2})=h(x_{2})$ ( $h(x_{1})=f(x_{1})=f(x_{2})=h(x_{2})$ 2 $h(x_{1})=f(x_{1})=f(x_{2})=h(x_{2})$ = $h(x_{1})=f(x_{1})=f(x_{2})=h(x_{2})$ ( $h(x_{1})=f(x_{1})=f(x_{2})=h(x_{2})$ 2 $h(x_{1})=f(x_{1})=f(x_{2})=h(x_{2})$ {\ $displaystyle$ h $(x_{1$ }) = $f(x_{2$ }) = $h(x_{1})=f(x_{1})=f(x_{2})=h(x_{2})$ h( $x_{2}}$ 이므로 f{\ $displaystyle$ $x_{$ 1} $x_{1}=x_{2}$ = $x_{2$ }}는 f {\ $displaystyle$ x_{ $2}}$ 입니다.
- 그리고 $x_{1},x_{2}\in A\setminus C$ x 1 $x_{1},x_{2}\in A\setminus C$ $x_{1},x_{2}\in A\setminus C$ 2 ∈ $x_{1},x_{2}\in A\setminus C$ ∖ $x_{1},x_{2}\in A\setminus C$ ${\displaystyle x_{1}, x_{2}\in$ A $\setminus$ C $}$ 이면 $g^{-1}(x_{1})=g^{-1}(x_{2})$ $g(g^{-1}(x_{1}))=x_{1}=x_{2}=g(g^{-1}(x_{2}))$ g - $g^{-1}(x_{1})=g^{-1}(x_{2})$ ( $g(g^{-1}(x_{1}))=x_{1}=x_{2}=g(g^{-1}(x_{2}))$ $g^{-1}(x_{1})=g^{-1}(x_{2})$ 1 ) = $g^{-1}(x_{1})=g^{-1}(x_{2})$ - $g^{-1}(x_{1})=g^{-1}(x_{2})$ $g(g^{-1}(x_{1}))=x_{1}=x_{2}=g(g^{-1}(x_{2}))$ ( $g(g^{-1}(x_{1}))=x_{1}=x_{2}=g(g^{-1}(x_{2}))$ $g^{-1}(x_{1})=g^{-1}(x_{2})$ 2 ) $g^{-1}(x_{1})=g^{-1}(x_{2})$ $g(g^{-1}(x_{1}))=x_{1}=x_{2}=g(g^{-1}(x_{2}))$ $displaystyle$ g $^{-1}($ $g(g^{-1}(x_{1}))=x_{1}=x_{2}=g(g^{-1}(x_{2}))$ ${1$ $g(g^{-1}(x_{1}))=x_{1}=x_{2}=g(g^{-1}(x_{2}))$ = $g(g^{-1}(x_{1}))=x_{1}=x_{2}=g(g^{-1}(x_{2}))$ $^{-1}(x_{2})}$ $displaystyle g(g^{-1$ }( $x_$ {1 $g(g^{-1}(x_{1}))=x_{1}=x_{2}=g(g^{-1}(x_{2}))$ = $x_$ {1 $g(g^{-1}(x_{1}))=x_{1}=x_{2}=g(g^{-1}(x_{2}))$ = $x_{2$ = $g$ }
- $x_{1}\in C,x_{2}\in A\setminus C$ $f(x_{1})=g^{-1}(x_{2})$ $x_{1}\in C,x_{2}\in A\setminus C$ 1 $h(x_{1})=h(x_{2})$ $f(x_{1})=g^{-1}(x_{2})$ $h(x_{1})=h(x_{2})$ $x_{1}\in C,x_{2}\in A\setminus C$ ( $x_{1}\in C,x_{2}\in A\setminus C$ 2) $x_{2}=g(g^{-1}(x_{2}))=g(f(x_{1}))\in g(f(C))=\bigcup _{k=1}^{\infty }C_{k}\subset C$ h( $h(x_{1})=h(x_{2})$ 2 $h(x_{1})=h(x_{2})$ ${\displaystyle x_{1}\in$ C, $x_{2}\in$ A $\setminus$ C에서는 $f(x_{1})=g^{-1}(x_{2})$ 할 수 $f(x_{1})=g^{-1}(x_{2})$ h( $x_{1}\in C,x_{2}\in A\setminus C$ 1) = h $($ $f(x_{1})=g^{-1}(x_{2})$ 2 $f(x_{1})=g^{-1}(x_{2})$ {\ $displaystyle$ h $(x_$ $x_{1}\in C,x_{2}\in A\setminus C$ $1$ }) $x_{2}=g(g^{-1}(x_{2}))=g(f(x_{1}))\in g(f(C))=\bigcup _{k=1}^{\infty }C_{k}\subset C$ $f(x_{1})=g^{-1}(x_{2})$ $($ $f(x_{1})=g^{-1}(x_{2})$ {2})} ${\displaystyle$ f $(x_$ $x_{1}\in C,x_{2}\in A\setminus C$ $1$ }) $x_{2}=g(g^{-1}(x_{2}))=g(f(x_{1}))\in g(f(C))=\bigcup _{k=1}^{\infty }C_{k}\subset C$ $g^{-1}(x_{2})}.$ $x_{2}=g(g^{-1}(x_{2}))=g(f(x_{1}))\in g(f(C))=\bigcup _{k=1}^{\infty }C_{k}\subset C$ $x_{1}\in C,x_{2}\in A\setminus C$ $x_{2}=g(g^{-1}(x_{2}))=g(f(x_{1}))\in g(f(C))=\bigcup _{k=1}^{\infty }C_{k}\subset C$ 2 $x_{2}=g(g^{-1}(x_{2}))=g(f(x_{1}))\in g(f(C))=\bigcup _{k=1}^{\infty }C_{k}\subset C$ g ( $x_{2}=g(g^{-1}(x_{2}))=g(f(x_{1}))\in g(f(C))=\bigcup _{k=1}^{\infty }C_{k}\subset C$ - $x_{2}=g(g^{-1}(x_{2}))=g(f(x_{1}))\in g(f(C))=\bigcup _{k=1}^{\infty }C_{k}\subset C$ ( $x_{2}=g(g^{-1}(x_{2}))=g(f(x_{1}))\in g(f(C))=\bigcup _{k=1}^{\infty }C_{k}\subset C$ $x_{1}\in C,x_{2}\in A\setminus C$ 2 $x_{2}=g(g^{-1}(x_{2}))=g(f(x_{1}))\in g(f(C))=\bigcup _{k=1}^{\infty }C_{k}\subset C$ ) = $x_{2}=g(g^{-1}(x_{2}))=g(f(x_{1}))\in g(f(C))=\bigcup _{k=1}^{\infty }C_{k}\subset C$ ( x $x_{1}\in C,x_{2}\in A\setminus C$ $x_{2}=g(g^{-1}(x_{2}))=g(f(x_{1}))\in g(f(C))=\bigcup _{k=1}^{\infty }C_{k}\subset C$ ) $x_{2}=g(g^{-1}(x_{2}))=g(f(x_{1}))\in g(f(C))=\bigcup _{k=1}^{\infty }C_{k}\subset C$ ( $x_{1}\in C,x_{2}\in A\setminus C$ $x_{2}=g(g^{-1}(x_{2}))=g(f(x_{1}))\in g(f(C))=\bigcup _{k=1}^{\infty }C_{k}\subset C$ $x_{1}\in C,x_{2}\in A\setminus C$ ) = $x_{1}\in C,x_{2}\in A\setminus C$ $x_{2}=g(g^{-1}(x_{2}))=g(f(x_{1}))\in g(f(C))=\bigcup _{k=1}^{\infty }C_{k}\subset C$ $x_{2}=g(g^{-1}(x_{2}))=g(f(x_{1}))\in g(f(C))=\bigcup _{k=1}^{\infty }C_{k}\subset C$ $x_{2}=g(g^{-1}(x_{2}))=g(f(x_{1}))\in g(f(C))=\bigcup _{k=1}^{\infty }C_{k}\subset C$ $x_{2}=g(g^{-1}(x_{2}))=g(f(x_{1}))\in g(f(C))=\bigcup _{k=1}^{\infty }C_{k}\subset C$ {\ $displaystyle$ $x_{1}\in C,x_{2}\in A\setminus C$ $_{2$ }= g $(g^{-1})(x_{2})$ 를 $f(x_{1})=g^{-1}(x_{2})$ 하므로 $x_{1}\in C,x_{2}\in A\setminus C$ x $h(x_{1})=h(x_{2})$ = g ( $x_{2}=g(g^{-1}(x_{2}))=g(f(x_{1}))\in g(f(C))=\bigcup _{k=1}^{\infty }C_{k}\subset C$ $x_{2}=g(g^{-1}(x_{2}))=g(f(x_{1}))\in g(f(C))=\bigcup _{k=1}^{\infty }C_{k}\subset C$ $x_{1}\in C,x_{2}\in A\setminus C$ 1 ) ∞ $x_{2}=g(g^{-1}(x_{2}))=g(f(x_{1}))\in g(f(C))=\bigcup _{k=1}^{\infty }C_{k}\subset C$ ( g - $x_{1}\in C,x_{2}\in A\setminus C$ 1 ) ∈ g ( $x_{2}=g(g^{-1}(x_{2}))=g(f(x_{1}))\in g(f(C))=\bigcup _{k=1}^{\infty }C_{k}\subset C$ $x_{1}\in C,x_{2}\in A\setminus C$ 2}) ∖) $=g(f(x_{1})\ing(f(C$ )) $=$ \ $bigcup$ _ ${k=1}^{\infty }C_{k}\subset$ C}(!) 그리고 x $x_{2}\in C,x_{1}\in A\setminus C$ $∈$ $, x_{1}\in$ C\ $setminus$ C에 $x_{2}\in C,x_{1}\in A\setminus C$ 모순이 발생합니다 $.$

$h$ ${\displaystyle$ h $}$ 이(가) 주관적임: $y\in B$ $e$ $y\in B$ $y\in B$ $y\in B$ ${\displaystyle$ y $\in$ B $}$
- y ∈ $y\in f(C)$ ( $y\in f(C)$ ) $y\in f(C)$ {\ $displaystyle$ y $\in$ f $(C))}$ 이면 h $h(x)=f(x)=y$ ( $h(x)=f(x)=y$ = $h(x)=f(x)=y$ ( $h(x)=f(x)=y$ ) = $h(x)=f(x)=y$ {\ $displaystyle$ h $(x$ ) = $f($ x) = $y$ }인 $x\in C$ ∈ $x\in C$ {\ $displaystyle$ x $\in$ C $}$ 가 있습니다.
- $y\in B\setminus f(C)$ y $y\in B\setminus f(C)$ ∈ $y\in B\setminus f(C)$ ∖ f $y\in B\setminus f(C)$ ( $y\in B\setminus f(C)$ ) {\ $displaystyle y\in$ B\ $setminus$ f ( $C)}$ 이면 g{\ $displaystyle$ g $}$ 는 주입형이므로 $g(y)\notin g(f(C))$ g ( $g(y)\notin g(f(C))$ ∉ $g(y)\notin g(f(C))$ ( $g(y)\notin g(f(C))$ ( $g(y)\notin g(f(C))$ ) $g(y)\notin g(f(C))$ {\ $displaystyle$ g $(y)\noting(f(C))}$ 입니다. $g(y)\notin g(f(C))=\bigcup _{k=1}^{\infty }C_{k}$ g $g(y)\notin g(f(C))=\bigcup _{k=1}^{\infty }C_{k}$ ( $g(y)\notin g(f(C))=\bigcup _{k=1}^{\infty }C_{k}$ ∉ $g(y)\notin g(f(C))=\bigcup _{k=1}^{\infty }C_{k}$ ( $g(y)\notin g(f(C))=\bigcup _{k=1}^{\infty }C_{k}$ ( $g(y)\notin g(f(C))=\bigcup _{k=1}^{\infty }C_{k}$ ) = ⋃ $g(y)\notin g(f(C))=\bigcup _{k=1}^{\infty }C_{k}$ = $g(y)\notin g(f(C))=\bigcup _{k=1}^{\infty }C_{k}$ ∞ $g(y)\notin g(f(C))=\bigcup _{k=1}^{\infty }C_{k}$ ${\displaystyle$ g $(y)\noting(f(C$ )) =\ $bigcup$ _{ $k$ = $1$ }^{\ $infty }C_{$ k $}}$ $g(y)\in g(B)$ ( $g(y)\in g(B)$ y) ∈ g ( $)$ {\ $displaystyle g(y$ )\ $noting($ B)}, $g(y)\notin C_{0}=A\setminus g(B)$ g ( $g(y)\notin C_{0}=A\setminus g(B)$ ∉ $g(y)\notin C_{0}=A\setminus g(B)$ 0 = $g(y)\notin C_{0}=A\setminus g(B)$ ∖ $g(y)\notin C_{0}=A\setminus g(B)$ ( $)$ {\ $displaystyle$ g( $y)\notin$ C_ ${0$ } = $A\setminus$ g( $B$ 따라서 $g(y)\notin C$ g ( $g(y)\notin C$ ) ∉ $g(y)\notin C$ ${\displaystyle$ g $(y)\notin$ C $}$ 이므로 $h(g(y))=g^{-1}(g(y))=y\quad$ ( $h(g(y))=g^{-1}(g(y))=y\quad$ ( $h(g(y))=g^{-1}(g(y))=y\quad$ ) = $h(g(y))=g^{-1}(g(y))=y\quad$ - $h(g(y))=g^{-1}(g(y))=y\quad$ ( $h(g(y))=g^{-1}(g(y))=y\quad$ ( $h(g(y))=g^{-1}(g(y))=y\quad$ ) $h(g(y))=g^{-1}(g(y))=y\quad$ = $h(g(y))=g^{-1}(g(y))=y\quad$ {\ $displaystyle$ h( $g(y$ )) = $g$ $x=g(y)$ $1}(g(y$ )) = $h(g(y))=g^{-1}(g(y))=y\quad$ $displaystyle$ x = g $(y$ )} $h(x)=y$ 은 $h(x)=y$ h $h(x)=y$ ( $h(x)=y$ ) = y {\ $displaystyle$ h(x) = $y$ 입니다.

Q.E.D.^[2]^[3]

예

[ $[0,1]\to [0,1)$ $[0,1]\to [0,1)$ → [ $[0,1]\to [0,1)$ $[0,1]\to [0,1)$ $[0,1]\to [0,1]$ 의 사영 함수: 참고 $[0,1)$ [ $[0,1)$ ) $[0,1]$ 은 $[0,1)$ (는) 경계 0을 포함하고 경계 1을 제외한 0에서 1까지의 반열림 집합입니다.; $f(x)=x/2;\;$ $f:[0,1]\to [0,1)\;$ : $f:[0,1]\to [0,1)\;$ [ $f:[0,1]\to [0,1)\;$ ] → [ $f:[0,1]\to [0,1)\;$ ] $f(x)=x/2;\;$ f ( x $f(x)=x/2;\;$ = $f(x)=x/2;\;$ / $f(x)=x/2;\;$ ${\displaystyle$ f : [ $0,1]\to$ $[0,1]\;},$ ${\displaystyle$ f ( $x$ → $f(x)=x/2;\;$ $g(x)=x;\;$ $2;\;}$ $g:[0,1)\to [0,1]\;$ g $g:[0,1)\to [0,1]\;$ : [ $g:[0,1)\to [0,1]\;$ $g:[0,1)\to [0,1]\;$ $g(x)=x;\;$ ${\$ $displaystyle$ g : [ $0,1]\to [$ 0,1 $]\$ to [0,1]\ $to$ [0 $,$ $1]\;}$ 이전 증명 절차와 같이 두 개의 주입 함수를 사용합니다 $.$; $C_{0}=\{1\},\;C_{k}=\{2^{-k}\},\;C=\bigcup _{k=0}^{\infty }C_{k}=\{1,{\tfrac {1}{2}},{\tfrac {1}{4}},{\tfrac {1}{8}},...\}$ $C_{0}=\{1\},\;C_{k}=\{2^{-k}\},\;C=\bigcup _{k=0}^{\infty }C_{k}=\{1,{\tfrac {1}{2}},{\tfrac {1}{4}},{\tfrac {1}{8}},...\}$ 0 = { $C_{0}=\{1\},\;C_{k}=\{2^{-k}\},\;C=\bigcup _{k=0}^{\infty }C_{k}=\{1,{\tfrac {1}{2}},{\tfrac {1}{4}},{\tfrac {1}{8}},...\}$ $C_{0}=\{1\},\;C_{k}=\{2^{-k}\},\;C=\bigcup _{k=0}^{\infty }C_{k}=\{1,{\tfrac {1}{2}},{\tfrac {1}{4}},{\tfrac {1}{8}},...\}$ k = { $C_{0}=\{1\},\;C_{k}=\{2^{-k}\},\;C=\bigcup _{k=0}^{\infty }C_{k}=\{1,{\tfrac {1}{2}},{\tfrac {1}{4}},{\tfrac {1}{8}},...\}$ $C_{0}=\{1\},\;C_{k}=\{2^{-k}\},\;C=\bigcup _{k=0}^{\infty }C_{k}=\{1,{\tfrac {1}{2}},{\tfrac {1}{4}},{\tfrac {1}{8}},...\}$ k $C_{0}=\{1\},\;C_{k}=\{2^{-k}\},\;C=\bigcup _{k=0}^{\infty }C_{k}=\{1,{\tfrac {1}{2}},{\tfrac {1}{4}},{\tfrac {1}{8}},...\}$ $C_{0}=\{1\},\;C_{k}=\{2^{-k}\},\;C=\bigcup _{k=0}^{\infty }C_{k}=\{1,{\tfrac {1}{2}},{\tfrac {1}{4}},{\tfrac {1}{8}},...\}$ = ⋃ $C_{0}=\{1\},\;C_{k}=\{2^{-k}\},\;C=\bigcup _{k=0}^{\infty }C_{k}=\{1,{\tfrac {1}{2}},{\tfrac {1}{4}},{\tfrac {1}{8}},...\}$ = $C_{0}=\{1\},\;C_{k}=\{2^{-k}\},\;C=\bigcup _{k=0}^{\infty }C_{k}=\{1,{\tfrac {1}{2}},{\tfrac {1}{4}},{\tfrac {1}{8}},...\}$ ∞ $C_{0}=\{1\},\;C_{k}=\{2^{-k}\},\;C=\bigcup _{k=0}^{\infty }C_{k}=\{1,{\tfrac {1}{2}},{\tfrac {1}{4}},{\tfrac {1}{8}},...\}$ $C_{0}=\{1\},\;C_{k}=\{2^{-k}\},\;C=\bigcup _{k=0}^{\infty }C_{k}=\{1,{\tfrac {1}{2}},{\tfrac {1}{4}},{\tfrac {1}{8}},...\}$ = { $C_{0}=\{1\},\;C_{k}=\{2^{-k}\},\;C=\bigcup _{k=0}^{\infty }C_{k}=\{1,{\tfrac {1}{2}},{\tfrac {1}{4}},{\tfrac {1}{8}},...\}$ $C_{0}=\{1\},\;C_{k}=\{2^{-k}\},\;C=\bigcup _{k=0}^{\infty }C_{k}=\{1,{\tfrac {1}{2}},{\tfrac {1}{4}},{\tfrac {1}{8}},...\}$ 2 $C_{0}=\{1\},\;C_{k}=\{2^{-k}\},\;C=\bigcup _{k=0}^{\infty }C_{k}=\{1,{\tfrac {1}{2}},{\tfrac {1}{4}},{\tfrac {1}{8}},...\}$ $C_{0}=\{1\},\;C_{k}=\{2^{-k}\},\;C=\bigcup _{k=0}^{\infty }C_{k}=\{1,{\tfrac {1}{2}},{\tfrac {1}{4}},{\tfrac {1}{8}},...\}$ 4 $C_{0}=\{1\},\;C_{k}=\{2^{-k}\},\;C=\bigcup _{k=0}^{\infty }C_{k}=\{1,{\tfrac {1}{2}},{\tfrac {1}{4}},{\tfrac {1}{8}},...\}$ $C_{0}=\{1\},\;C_{k}=\{2^{-k}\},\;C=\bigcup _{k=0}^{\infty }C_{k}=\{1,{\tfrac {1}{2}},{\tfrac {1}{4}},{\tfrac {1}{8}},...\}$ $C_{0}=\{1\},\;C_{k}=\{2^{-k}\},\;C=\bigcup _{k=0}^{\infty }C_{k}=\{1,{\tfrac {1}{2}},{\tfrac {1}{4}},{\tfrac {1}{8}},...\}$ {\ $displaystyle$ C_ ${0$ }=\{ $1\},\;C_{k$ }=\{ $2^{-k}\},\;C$ =\ $bigcup$ _ ${k$ = $0}^{\infty}C_{k$ }=\{ $1,{\tfrac {1}{2}},{\tfrac$ {1}{ $4},{\tfrac {1}},...\}$; $\;h(x)={\begin{cases}{\frac {x}{2}},&\mathrm {for} \ x\in C\\x,&\mathrm {for} \ x\in [0,1]\setminus C\end{cases}}\;$ h ( $\;h(x)={\begin{cases}{\frac {x}{2}},&\mathrm {for} \ x\in C\\x,&\mathrm {for} \ x\in [0,1]\setminus C\end{cases}}\;$ ) = { $\;h(x)={\begin{cases}{\frac {x}{2}},&\mathrm {for} \ x\in C\\x,&\mathrm {for} \ x\in [0,1]\setminus C\end{cases}}\;$ $\;h(x)={\begin{cases}{\frac {x}{2}},&\mathrm {for} \ x\in C\\x,&\mathrm {for} \ x\in [0,1]\setminus C\end{cases}}\;$ $\;h(x)={\begin{cases}{\frac {x}{2}},&\mathrm {for} \ x\in C\\x,&\mathrm {for} \ x\in [0,1]\setminus C\end{cases}}\;$ ≥ $\;h(x)={\begin{cases}{\frac {x}{2}},&\mathrm {for} \ x\in C\\x,&\mathrm {for} \ x\in [0,1]\setminus C\end{cases}}\;$ $\;h(x)={\begin{cases}{\frac {x}{2}},&\mathrm {for} \ x\in C\\x,&\mathrm {for} \ x\in [0,1]\setminus C\end{cases}}\;$ $\;h(x)={\begin{cases}{\frac {x}{2}},&\mathrm {for} \ x\in C\\x,&\mathrm {for} \ x\in [0,1]\setminus C\end{cases}}\;$ $\;h(x)={\begin{cases}{\frac {x}{2}},&\mathrm {for} \ x\in C\\x,&\mathrm {for} \ x\in [0,1]\setminus C\end{cases}}\;$ [ $\;h(x)={\begin{cases}{\frac {x}{2}},&\mathrm {for} \ x\in C\\x,&\mathrm {for} \ x\in [0,1]\setminus C\end{cases}}\;$ $\;h(x)={\begin{cases}{\frac {x}{2}},&\mathrm {for} \ x\in C\\x,&\mathrm {for} \ x\in [0,1]\setminus C\end{cases}}\;$ ] ∈ $\;h(x)={\begin{cases}{\frac {x}{2}},&\mathrm {for} \ x\in C\\x,&\mathrm {for} \ x\in [0,1]\setminus C\end{cases}}\;$ $displaystyle$ \;h $(x$ )={\ $display{case}{\$ frac { $x}{2}},&\mathrm {for}$ \ $x\in$ C $\x,&\mathrm {for}$ \ $x\in$ [ $0,1]\setminus$ C\ $end{case}\;}$ 는 [0 $[0,1]\to [0,1)$ $[0,1]\to [0,1)$ → [0 $,$ ] $displaystyle$ [0 $,1]\$ to [ $0,1]}$ 의 $[0,1]\to [0,1)$ 사영 함수입니다.

[ $[0,2)\to [0,1)^{2}$ $[0,2)\to [0,1)^{2}$ → [ $[0,2)\to [0,1)^{2}$ $[0,2)\to [0,1)^{2}$ $[0,2)\to [0,1)^{2}$ {\ $displaystyle [0, 2]\to [0, 1]^{2}}$ 의 사함수: $f:[0,2)\to [0,1)^{2}\;$ 를 f 로 하면 : $f:[0,2)\to [0,1)^{2}\;$ [ $f:[0,2)\to [0,1)^{2}\;$ ] → [ $f(x)=(x/2;0);\;$ $f:[0,2)\to [0,1)^{2}\;$ $f:[0,2)\to [0,1)^{2}\;$ ) $f:[0,2)\to [0,1)^{2}\;$ $displaystyle$ f $:[0,2]\to$ $[0,1]^{2}\;},$ $f(x)=(x/2;0);\;$ f $f(x)=(x/2;0);\;$ ( $f(x)=(x/2;0);\;$ / $f(x)=(x/2;0);\;$ 2 ; $);$ {\ $displaystyle$ f $(x$ )= (x / $2;0);\;}$; $\;a_{k},b_{k}\in \{0,1,...,9\}\;$ 다음 $\;a_{k},b_{k}\in \{0,1,...,9\}\;$ ( $(x;y)\in [0,1)^{2}\;$ $(x;y)\in [0,1)^{2}\;$ ∈ [ 0 $(x;y)\in [0,1)^{2}\;$ ) $(x;y)\in [0,1)^{2}\;$ {\ $displaystyle (x;y)\in [0,1]^{2}\;}$ $\;x=\sum _{k=1}^{\infty }a_{k}\cdot 10^{-k}\;$ x $\;x=\sum _{k=1}^{\infty }a_{k}\cdot 10^{-k}\;$ = ∑ $\;x=\sum _{k=1}^{\infty }a_{k}\cdot 10^{-k}\;$ = $\;x=\sum _{k=1}^{\infty }a_{k}\cdot 10^{-k}\;$ ∞ $\;x=\sum _{k=1}^{\infty }a_{k}\cdot 10^{-k}\;$ $\;x=\sum _{k=1}^{\infty }a_{k}\cdot 10^{-k}\;$ ⋅ $\;x=\sum _{k=1}^{\infty }a_{k}\cdot 10^{-k}\;$ - k $\;x=\sum _{k=1}^{\infty }a_{k}\cdot 10^{-k}\;$ {\ $displaystyle$ \;x=\ $sum$ _ ${k$ = $1}^{\infty }a_{k}\cdot$ 10 $^{-k}\;}$ $\;y=\sum _{k=1}^{\infty }b_{k}\cdot 10^{-k}\;$ y = ∑ $\;y=\sum _{k=1}^{\infty }b_{k}\cdot 10^{-k}\;$ = $\;y=\sum _{k=1}^{\infty }b_{k}\cdot 10^{-k}\;$ ∞ $\;y=\sum _{k=1}^{\infty }b_{k}\cdot 10^{-k}\;$ k ⋅ $\;y=\sum _{k=1}^{\infty }b_{k}\cdot 10^{-k}\;$ $\;y=\sum _{k=1}^{\infty }b_{k}\cdot 10^{-k}\;$ k $\;y=\sum _{k=1}^{\infty }b_{k}\cdot 10^{-k}\;$ {\ $displaystyle$ \;y=\ $sum$ _{k= $1}^{\infty }\cdot$ 10 $^{-k}\;}$ {\ $displaystyle$ \; $a_{k},$ ..., $\;a_{k},b_{k}\in \{0,1,...,9\}\;$ displaystyle $\;$ a_{k}, $b_{k}\in$ $\{0,1,...,9\}\;}$; 이제 g $g(x;y)=\sum _{k=1}^{\infty }(10\cdot a_{k}+b_{k})\cdot 10^{-2k}$ ( $g(x;y)=\sum _{k=1}^{\infty }(10\cdot a_{k}+b_{k})\cdot 10^{-2k}$ ) = ∑ $g(x;y)=\sum _{k=1}^{\infty }(10\cdot a_{k}+b_{k})\cdot 10^{-2k}$ = $g(x;y)=\sum _{k=1}^{\infty }(10\cdot a_{k}+b_{k})\cdot 10^{-2k}$ ∞ ( $g(x;y)=\sum _{k=1}^{\infty }(10\cdot a_{k}+b_{k})\cdot 10^{-2k}$ ⋅ $g(x;y)=\sum _{k=1}^{\infty }(10\cdot a_{k}+b_{k})\cdot 10^{-2k}$ + $g(x;y)=\sum _{k=1}^{\infty }(10\cdot a_{k}+b_{k})\cdot 10^{-2k}$ k ) ⋅ $g(x;y)=\sum _{k=1}^{\infty }(10\cdot a_{k}+b_{k})\cdot 10^{-2k}$ $g(x;y)=\sum _{k=1}^{\infty }(10\cdot a_{k}+b_{k})\cdot 10^{-2k}$ $g(x;y)=\sum _{k=1}^{\infty }(10\cdot a_{k}+b_{k})\cdot 10^{-2k}$ $g(x;y)=\sum _{k=1}^{\infty }(10\cdot a_{k}+b_{k})\cdot 10^{-2k}$ {\ $displaystyle$ g $(x;y$ ) =\ $sum$ _ ${k$ = $1}^{\infty}(10\cdot a_{k}+b_{k})\cdot$ 10 $^{-2k}$ 를 $g(x;y)=\sum _{k=1}^{\infty }(10\cdot a_{k}+b_{k})\cdot 10^{-2k}$ 할 수 있으며, 이는 [0 $[0,1)^{2}\to [0,2)\;$ $[0,1)^{2}\to [0,2)\;$ → [ $[0,1)^{2}\to [0,2)\;$ $[0,1)^{2}\to [0,2)\;$ ${\displaystyle [0, 1]^{2}\to [0, 2$ . (예: $g({\tfrac {1}{3}};{\tfrac {2}{3}})=0.363636...={\tfrac {12}{33}}$ ( $g({\tfrac {1}{3}};{\tfrac {2}{3}})=0.363636...={\tfrac {12}{33}}$ 3 $g({\tfrac {1}{3}};{\tfrac {2}{3}})=0.363636...={\tfrac {12}{33}}$ ; $g({\tfrac {1}{3}};{\tfrac {2}{3}})=0.363636...={\tfrac {12}{33}}$ ) = $g({\tfrac {1}{3}};{\tfrac {2}{3}})=0.363636...={\tfrac {12}{33}}$ $g({\tfrac {1}{3}};{\tfrac {2}{3}})=0.363636...={\tfrac {12}{33}}$ $={\tfrac {12}{33$; 따라서 $f(x)$ ( $f(x)$ ${\displaystyle$ f $(x)}$ 및 $f(x)$ $g^{-1}(x)$ - $g^{-1}(x)$ $g^{-1}(x)$ x $)$ {\ $displaystyle g^{-1}($ x $g^{-1}(x)$ 을 $f(x)$ 하여 투영 $함수$ h{\ $displaystyle$ h $}$ 를 $h$ 구성할 수 있습니다.; 이 $C_{0}=[1,2)$ $C_{0}=[1,2)$ 0 = [ $C_{0}=[1,2)$ ] ${\displaystyle$ C_ ${0$ }= [ $1, 2]}$ 은(는) 여전히 쉽지만 $C_{1}=g(f(C_{0}))=g(\{(x;0)|x\in [{\tfrac {1}{2}},1)\,\})\;$ $C_{1}=g(f(C_{0}))=g(\{(x;0)|x\in [{\tfrac {1}{2}},1)\,\})\;$ 1 = $C_{1}=g(f(C_{0}))=g(\{(x;0)|x\in [{\tfrac {1}{2}},1)\,\})\;$ ( $C_{1}=g(f(C_{0}))=g(\{(x;0)|x\in [{\tfrac {1}{2}},1)\,\})\;$ ( $C_{1}=g(f(C_{0}))=g(\{(x;0)|x\in [{\tfrac {1}{2}},1)\,\})\;$ ) = $C_{1}=g(f(C_{0}))=g(\{(x;0)|x\in [{\tfrac {1}{2}},1)\,\})\;$ ( $C_{1}=g(f(C_{0}))=g(\{(x;0)|x\in [{\tfrac {1}{2}},1)\,\})\;$ { ( $C_{1}=g(f(C_{0}))=g(\{(x;0)|x\in [{\tfrac {1}{2}},1)\,\})\;$ ) $C_{1}=g(f(C_{0}))=g(\{(x;0)|x\in [{\tfrac {1}{2}},1)\,\})\;$ ∈ [ $C_{1}=g(f(C_{0}))=g(\{(x;0)|x\in [{\tfrac {1}{2}},1)\,\})\;$ 2 $C_{1}=g(f(C_{0}))=g(\{(x;0)|x\in [{\tfrac {1}{2}},1)\,\})\;$ ) $C_{1}=g(f(C_{0}))=g(\{(x;0)|x\in [{\tfrac {1}{2}},1)\,\})\;$ ${\displaystyle$ C_ ${1$ } = $g(f(C_$ {0}) = $g(\{(x;0) x\in [{\tfrac {1}}, 1)\,\}\;}$ 이(가) 상당히 복잡해집니다.; 참고: 물론 (역사적) 함수 $g_{2}(x;y)=2\cdot \sum _{k=1}^{\infty }(10\cdot a_{k}+b_{k})\cdot 10^{-2k}$ $g_{2}(x;y)=2\cdot \sum _{k=1}^{\infty }(10\cdot a_{k}+b_{k})\cdot 10^{-2k}$ 2 $g_{2}(x;y)=2\cdot \sum _{k=1}^{\infty }(10\cdot a_{k}+b_{k})\cdot 10^{-2k}$ ( $g_{2}(x;y)=2\cdot \sum _{k=1}^{\infty }(10\cdot a_{k}+b_{k})\cdot 10^{-2k}$ ) = $g_{2}(x;y)=2\cdot \sum _{k=1}^{\infty }(10\cdot a_{k}+b_{k})\cdot 10^{-2k}$ ⋅ $g_{2}(x;y)=2\cdot \sum _{k=1}^{\infty }(10\cdot a_{k}+b_{k})\cdot 10^{-2k}$ = $g_{2}(x;y)=2\cdot \sum _{k=1}^{\infty }(10\cdot a_{k}+b_{k})\cdot 10^{-2k}$ ∞ ( $g_{2}(x;y)=2\cdot \sum _{k=1}^{\infty }(10\cdot a_{k}+b_{k})\cdot 10^{-2k}$ ⋅ $g_{2}(x;y)=2\cdot \sum _{k=1}^{\infty }(10\cdot a_{k}+b_{k})\cdot 10^{-2k}$ k + $g_{2}(x;y)=2\cdot \sum _{k=1}^{\infty }(10\cdot a_{k}+b_{k})\cdot 10^{-2k}$ ) ⋅ $g_{2}(x;y)=2\cdot \sum _{k=1}^{\infty }(10\cdot a_{k}+b_{k})\cdot 10^{-2k}$ - $g_{2}(x;y)=2\cdot \sum _{k=1}^{\infty }(10\cdot a_{k}+b_{k})\cdot 10^{-2k}$ k $g_{2}(x;y)=2\cdot \sum _{k=1}^{\infty }(10\cdot a_{k}+b_{k})\cdot 10^{-2k}$ {\ $displaystyle g_{2}(x;y$ ) = $2\cdot \sum$ _ ${k$ = $1}^{\infty }(10\cdot$ a_ ${k}$ + $b_{k})\cdot$ 10 $^{-2k$ 를 사용하는 더 간단한 방법이 있습니다. $C$ C ${\displaystyle$ C $}$ 가 빈 집합이 $h(x)=g_{2}^{-1}(x)$ 모든 x에 대해 h ( $h(x)=g_{2}^{-1}(x)$ ) $h(x)=g_{2}^{-1}(x)$ = $h(x)=g_{2}^{-1}(x)$ 2 - $h(x)=g_{2}^{-1}(x)$ ( $h(x)=g_{2}^{-1}(x)$ ) $h(x)=g_{2}^{-1}(x)$ {\ $displaystyle$ h $(x$ ) = $g_{2}^{-1}(x$ )}이 $($ 가) 됩니다.

역사

슈뢰더-번스타인(Schröder-Bernstein)이라는 전통적인 이름은 1898년에 독립적으로 출판된 두 개의 증명에 기반을 두고 있습니다.칸토어는 1887년에 처음으로 정리를 언급했기 때문에 자주 추가되고, 슈뢰더의 이름은 종종 생략되는데, 그의 증명이 결함이 있는 것으로 밝혀졌기 때문에 처음으로 증명한 리처드 데데킨트의 이름은 정리와 연결되지 않습니다.번스타인에 따르면, 칸토어는 동등성 정리(äquivalenzsatz)^[4]라는 이름을 제시했습니다.

칸토어의 정리의 첫 번째 진술(1887)^[5]

1887년 칸토어는 증명 ^[5]^[4]없이 정리를 발표했습니다.
1887년 7월 11일, 데데킨트는 (선택 ^[6]공리에 의존하지 않는) 그 정리를 증명하지만, 그의 증명을 발표하지도 않고, 칸토어에게 그것에 대해 말하지도 않습니다.에른스트 체르멜로는 데데킨트의 증명을 발견하고 1908년에^[7] 데데킨트의 논문 Wasindunds sollen die Zahlen?^[4]^[8]에서 연쇄이론을 바탕으로 자신의 증명을 발표합니다.
1895 칸토어는 집합론과 초정수에 관한 그의 첫번째 논문에서 그 정리를 언급합니다.그는 그것을 기수의 ^[9]^[10]^[11]선형 순서의 쉬운 결과로 얻습니다.그러나, 그는 1915년에 프리드리히 ^[4]^[12]모리츠 하르토크스에 의해 선택의 공리와 동등하다는 것을 보여주는 후자의 정리를 증명할 수 없었습니다.
1896년 슈뢰더는 증명을 발표합니다.^[13]
1897년 칸토어 세미나의 19세 학생 번스타인이 자신의 ^[14]^[15]증명을 제시합니다.
1897 거의 동시에, 그러나 독립적으로, ^[14]^[15]슈뢰더는 증거를 발견합니다.
1897년 번스타인이 방문한 후, 데데킨트는 독립적으로 두 번째로 그 정리를 증명했습니다.
1898년 베른슈타인의 증명(선택 공리에 의존하지 않음)은 에밀 보렐에 의해 ^[16]함수에 관한 그의 책에서 출판되었습니다. (1897년 취리히에서 열린 국제 수학자 대회에서 칸토어에 의해 전달됨.같은 해, 번스타인의 ^[17]^[4]논문에도 그 증거가 등장합니다.
1898년 슈뢰더는 1902년 알윈 ^[4]^[20]라인홀드 ^[19]코르셀트(Alwin Reinhold Korselt)에 의해 결함이 있음을 보여주는^[18] 그의 증거를 발표하지만, 코르셀트의 논문은 1911년에야 발표됩니다.

데데킨트의 두 증거는 그의 유명한 1888년 회고록 Was sindund was len die Zahlen?에 근거하고 있으며, A ⊆ B ⊆ C 및 A = C는 A = B = C를 암시한다고 하는 칸토어의 논문의 문장 C와 동등한 명제의 결과로 도출됩니다.칸토어는 일찍이 1882/83년에 집합론과 초한수를 연구하는 동안 이 성질을 관찰했고, 따라서 암묵적으로 선택의 공리에 의존했습니다.

전제조건

1895년 칸토어에 의한 증명은 결과를 잘 정렬된 ^[10]^[11]정리의 결과로 추론함으로써 사실상 선택 공리에 의존했습니다.그러나 위에서 제시한 쾨니히의 증명은 선택 공리를 사용하지 않고도 결과를 증명할 수 있음을 보여줍니다.

반면 쾨닉의 증명은 사례분석을 통해 결론을 도출하기 위해 배제중의 원리를 사용하고 있습니다.이와 같이 위 증명은 건설적인 증명이 아닙니다.실제로 직관주의 ${\mathsf {IZF}}$ ${\mathsf {IZF}}$ ${\$ {\ $mathsf {IZF$ 와 같은 구성 집합론에서는 슈뢰더-베른슈타인 정리가 ^[21]후자를 내포한다고 가정하면 분리의 완전한 공리를 채택하지만 배제된 중의 원리를 분사합니다.결국, 이 이론이나 더 약한 이론에서는 쾨닉의 결론에 대한 증거가 없습니다.따라서 직관주의자들은 슈뢰더-번스타인 ^[22]정리의 진술을 받아들이지 않습니다.

타르스키의 고정점 ^[23]정리를 이용한 증명도 있습니다.

참고 항목

마이힐 동형 정리
서로 다른 차원의 공간 사이에서 슈뢰더-베른슈타인 정리에 의해 구성된 사영은 연속적일 수 없는 네토 정리
측정 가능 공간에 대한 슈뢰더-베른슈타인 정리
연산자 대수에 대한 슈뢰더-베른슈타인 정리
슈뢰더-베른슈타인 재산

메모들

^ J. König (1906). "Sur la théorie des ensembles". Comptes Rendus Hebdomadaires des Séances de l'Académie des Sciences. 143: 110–112.
^ 독일어와 프랑스어 위키백과 자매 기사 덕분에, 예를 들어 fr:칸토어번스타인 극장 #프리미어 시연
^ "CSM25 - The Cantor-Schröder-Bernstein Theorem" (PDF). www.cs.swan.ac.uk. Retrieved 4 December 2022. (실제로 증명은 3페이지부터 시작합니다.)
^ ^a ^b ^c ^d ^e ^f – Felix Hausdorff (2002), Egbert Brieskorn; Srishti D. Chatterji; et al. (eds.), Grundzüge der Mengenlehre (1. ed.), Berlin/Heidelberg: Springer, p. 587, ISBN 978-3-540-42224-2 오리지널판 (1914)
^ ^a ^b Georg Cantor (1887), "Mitteilungen zur Lehre vom Transfiniten", Zeitschrift für Philosophie und philosophische Kritik, 91: 81–125
재인쇄: 여기: p.413 bottom
^ Richard Dedekind (1932), Robert Fricke; Emmy Noether; Øystein Ore (eds.), Gesammelte mathematische Werke, vol. 3, Braunschweig: Friedr. Vieweg & Sohn, pp. 447–449 (Ch.62)
^ Ernst Zermelo (1908), Felix Klein; Walther von Dyck; David Hilbert; Otto Blumenthal (eds.), "Untersuchungen über die Grundlagen der Mengenlehre I", Mathematische Annalen, 65 (2): 261–281, here: p.271–272, doi:10.1007/bf01449999, ISSN 0025-5831, S2CID 120085563
^ Richard Dedekind (1888), Was sind und was sollen die Zahlen? (2., unchanged (1893) ed.), Braunschweig: Friedr. Vieweg & Sohn
^ ^a ^b Georg Cantor (1932), Adolf Fraenkel (Lebenslauf); Ernst Zermelo (eds.), Gesammelte Abhandlungen mathematischen und philosophischen Inhalts, Berlin: Springer, pp. 285 ("Satz B")
^ ^a ^b Georg Cantor (1895). "Beiträge zur Begründung der transfiniten Mengenlehre (1)". Mathematische Annalen. 46 (4): 481–512 (Theorem see "Satz B", p.484). doi:10.1007/bf02124929. S2CID 177801164.
^ ^a ^b (Georg Cantor (1897). "Beiträge zur Begründung der transfiniten Mengenlehre (2)". Mathematische Annalen. 49 (2): 207–246. doi:10.1007/bf01444205. S2CID 121665994.)
^ Friedrich M. Hartogs (1915), Felix Klein; Walther von Dyck; David Hilbert; Otto Blumenthal (eds.), "Über das Problem der Wohlordnung", Mathematische Annalen, 76 (4): 438–443, doi:10.1007/bf01458215, ISSN 0025-5831, S2CID 121598654
^ Ernst Schröder (1896). "Über G. Cantorsche Sätze". Jahresbericht der Deutschen Mathematiker-Vereinigung. 5: 81–82.
^ ^a ^b Oliver Deiser (2010), Einführung in die Mengenlehre – Die Mengenlehre Georg Cantors und ihre Axiomatisierung durch Ernst Zermelo, Springer-Lehrbuch (3rd, corrected ed.), Berlin/Heidelberg: Springer, pp. 71, 501, doi:10.1007/978-3-642-01445-1, ISBN 978-3-642-01444-4
^ ^a ^b Patrick Suppes (1972), Axiomatic Set Theory (1. ed.), New York: Dover Publications, pp. 95 f, ISBN 978-0-486-61630-8
^ Émile Borel (1898), Leçons sur la théorie des fonctions, Paris: Gauthier-Villars et fils, pp. 103 ff
^ Felix Bernstein (1901), Untersuchungen aus der Mengenlehre, Halle a. S.: Buchdruckerei des Waisenhauses
재인쇄:
^ Ernst Schröder (1898), Kaiserliche Leopoldino-Carolinische Deutsche Akademie der Naturforscher (ed.), "Ueber zwei Definitionen der Endlichkeit und G. Cantor'sche Sätze", Nova Acta, 71 (6): 303–376 (proof: p.336–344)
^ Alwin R. Korselt (1911), Felix Klein; Walther von Dyck; David Hilbert; Otto Blumenthal (eds.), "Über einen Beweis des Äquivalenzsatzes", Mathematische Annalen, 70 (2): 294–296, doi:10.1007/bf01461161, ISSN 0025-5831, S2CID 119757900
^ Korselt (1911), p.295
^ Pradic, Pierre; Brown, Chad E. (2019). "Cantor-Bernstein implies Excluded Middle". arXiv:1904.09193 [math.LO].
^ Ettore Carruccio (2006). Mathematics and Logic in History and in Contemporary Thought. Transaction Publishers. p. 354. ISBN 978-0-202-30850-0.
^ R. 울, "타르스키의 고정점 정리"는 에릭 W가 만든 수학 세계 – 울프램 웹 리소스에서 나온 것입니다.Weisstein. (예 3)

참고문헌

Martin Aigner & Gunter M. Ziegler (1998) The BOOK의 증명, § 3 분석:세트와 기능 스프링어북 MR1723092 , 5판 2014 MR3288091 , 6판 2018 MR3823190
Hinkis, Arie (2013), Proofs of the Cantor-Bernstein theorem. A mathematical excursion, Science Networks. Historical Studies, vol. 45, Heidelberg: Birkhäuser/Springer, doi:10.1007/978-3-0348-0224-6, ISBN 978-3-0348-0223-9, MR 3026479
Searcóid, Míchaél Ó (2013). "On the history and mathematics of the equivalence theorem". Mathematical Proceedings of the Royal Irish Academy. 113A (2): 151–68. doi:10.1353/mpr.2013.0006. JSTOR 42912521. S2CID 245841055.

외부 링크

Weisstein, Eric W. "Schröder-Bernstein Theorem". MathWorld.
nLab에서의 칸토어-슈뢰더-번스타인 정리
마르셀 크랩베의 반링에서의 칸토어-번스타인의 정리.
이 기사는 Creative Commons Attribution-ShareAlike 3.0 Unportported License에 따라 라이센스가 부여되지만 GFDL에는 포함되지 않는 Citizendium 기사 "Schröder-Bernstein_theorem"의 자료를 통합합니다.

[1] J. König (1906). "Sur la théorie des ensembles". Comptes Rendus Hebdomadaires des Séances de l'Académie des Sciences. 143: 110–112.

[2] 독일어와 프랑스어 위키백과 자매 기사 덕분에, 예를 들어 fr:칸토어번스타인 극장 #프리미어 시연

[3] "CSM25 - The Cantor-Schröder-Bernstein Theorem" (PDF). www.cs.swan.ac.uk. Retrieved 4 December 2022. (실제로 증명은 3페이지부터 시작합니다.)

[Brieskorn.Chatterji.2002-4] ^ ^a ^b ^c ^d ^e ^f – Felix Hausdorff (2002), Egbert Brieskorn; Srishti D. Chatterji; et al. (eds.), Grundzüge der Mengenlehre (1. ed.), Berlin/Heidelberg: Springer, p. 587, ISBN 978-3-540-42224-2 오리지널판 (1914)

[Cantor.1932-5] Georg Cantor (1887), "Mitteilungen zur Lehre vom Transfiniten", Zeitschrift für Philosophie und philosophische Kritik, 91: 81–125
재인쇄: 여기: p.413 bottom

[6] Richard Dedekind (1932), Robert Fricke; Emmy Noether; Øystein Ore (eds.), Gesammelte mathematische Werke, vol. 3, Braunschweig: Friedr. Vieweg & Sohn, pp. 447–449 (Ch.62)

[7] Ernst Zermelo (1908), Felix Klein; Walther von Dyck; David Hilbert; Otto Blumenthal (eds.), "Untersuchungen über die Grundlagen der Mengenlehre I", Mathematische Annalen, 65 (2): 261–281, here: p.271–272, doi:10.1007/bf01449999, ISSN 0025-5831, S2CID 120085563

[8] Richard Dedekind (1888), Was sind und was sollen die Zahlen? (2., unchanged (1893) ed.), Braunschweig: Friedr. Vieweg & Sohn

[Cantor.1895-9] Georg Cantor (1932), Adolf Fraenkel (Lebenslauf); Ernst Zermelo (eds.), Gesammelte Abhandlungen mathematischen und philosophischen Inhalts, Berlin: Springer, pp. 285 ("Satz B")

[Cantor.1895b-10] Georg Cantor (1895). "Beiträge zur Begründung der transfiniten Mengenlehre (1)". Mathematische Annalen. 46 (4): 481–512 (Theorem see "Satz B", p.484). doi:10.1007/bf02124929. S2CID 177801164.

[Cantor.1897-11] (Georg Cantor (1897). "Beiträge zur Begründung der transfiniten Mengenlehre (2)". Mathematische Annalen. 49 (2): 207–246. doi:10.1007/bf01444205. S2CID 121665994.)

[12] Friedrich M. Hartogs (1915), Felix Klein; Walther von Dyck; David Hilbert; Otto Blumenthal (eds.), "Über das Problem der Wohlordnung", Mathematische Annalen, 76 (4): 438–443, doi:10.1007/bf01458215, ISSN 0025-5831, S2CID 121598654

[13] Ernst Schröder (1896). "Über G. Cantorsche Sätze". Jahresbericht der Deutschen Mathematiker-Vereinigung. 5: 81–82.

[Deiser.2010-14] Oliver Deiser (2010), Einführung in die Mengenlehre – Die Mengenlehre Georg Cantors und ihre Axiomatisierung durch Ernst Zermelo, Springer-Lehrbuch (3rd, corrected ed.), Berlin/Heidelberg: Springer, pp. 71, 501, doi:10.1007/978-3-642-01445-1, ISBN 978-3-642-01444-4

[Suppes.1972-15] Patrick Suppes (1972), Axiomatic Set Theory (1. ed.), New York: Dover Publications, pp. 95 f, ISBN 978-0-486-61630-8

[16] Émile Borel (1898), Leçons sur la théorie des fonctions, Paris: Gauthier-Villars et fils, pp. 103 ff

[17] Felix Bernstein (1901), Untersuchungen aus der Mengenlehre, Halle a. S.: Buchdruckerei des Waisenhauses
재인쇄:

[18] Ernst Schröder (1898), Kaiserliche Leopoldino-Carolinische Deutsche Akademie der Naturforscher (ed.), "Ueber zwei Definitionen der Endlichkeit und G. Cantor'sche Sätze", Nova Acta, 71 (6): 303–376 (proof: p.336–344)

[19] Alwin R. Korselt (1911), Felix Klein; Walther von Dyck; David Hilbert; Otto Blumenthal (eds.), "Über einen Beweis des Äquivalenzsatzes", Mathematische Annalen, 70 (2): 294–296, doi:10.1007/bf01461161, ISSN 0025-5831, S2CID 119757900

[20] Korselt (1911), p.295

[21] Pradic, Pierre; Brown, Chad E. (2019). "Cantor-Bernstein implies Excluded Middle". arXiv:1904.09193 [math.LO].

[22] Ettore Carruccio (2006). Mathematics and Logic in History and in Contemporary Thought. Transaction Publishers. p. 354. ISBN 978-0-202-30850-0.

[23] R. 울, "타르스키의 고정점 정리"는 에릭 W가 만든 수학 세계 – 울프램 웹 리소스에서 나온 것입니다.Weisstein. (예 3)

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[20]

[19]

[18]

[21]

[22]

[23]

v t 집합론
개요	세트(수학)
공리	부조 선택. 헤아릴 수 있는 의존하는 세계적인 시공성(V=L) 결정성 확장성 Infinity 크기제한 페어링 멱집합 규칙성 유니언 마틴의 공리 공리 스키마 대체품 사양
작전	데카르트 곱 상보(즉, 설정 차이) 드 모르간의 법칙 분열결합 아이덴티티 교차로 멱집합 대칭차 유니언
컨셉트 방법들	거의. 카디널리티 기수(대) 학급 구성 가능한 우주 연속체 가설 대각선 논법 요소 순서쌍 튜플로 장식한 가족 강요 일대일 대응 순서수 세트빌더 표기법 트랜스피니트 유도 벤 다이어그램
종류설정	무정형 세어볼 수 빈 유한(유전적) 필터 기초 서브베이스 극세필터 퍼지 무한 (Dedekind-infinite) 재귀적 싱글턴 부분 집합 · 초집합 트랜지티브 셀 수 없음 유니버설
이론들	대안 공리적 순진한 칸토어 정리 저멜로 일반적 수학 원리 새 재단 제르멜로프랑켈 폰 노이만-베르네이스-괴델 모스켈리 크립케-플라텍 타르스키그로텐디크
역설 문제	러셀의 역설 설린의 문제 부랄리-포르티 역설
이론가를 설정	폴 버네이스 게오르크 칸토어 폴 코언 리처드 데데킨트 아브라함 프랑켈 쿠르트 괴델 토마스 제흐 요한 폰 노이만 윌러드 퀸 버트런드 러셀 토랄프 스콜렘 에른스트 체르멜로

Search