끈장론
String field theory| 끈 이론 |
|---|
 |
| 기본 객체 |
| 섭동설 |
| 동요하지 않는 결과 |
| 현상학 |
| 수학 |
스트링 필드 이론(SFT)은 상대론적 스트링의 역학이 양자 필드 이론의 언어로 재구성되는 스트링 이론의 형식주의입니다.이것은 끈 산란 진폭에 대한 파인만 다이어그램과 같은 확장을 제공하는 끈 전파자뿐만 아니라 끈을 결합하고 분할하기 위한 정점 모음을 찾아 섭동 이론 수준에서 달성됩니다.대부분의 문자열 필드 이론에서 이 확장은 자유 문자열을 두 번째 양자화하고 상호 작용 항을 추가하여 발견된 고전적인 동작에 의해 인코딩됩니다.2차 양자화에서 일반적으로 그렇듯이, 2차 양자화 이론의 고전적인 필드 구성은 원래 이론의 파동 함수에 의해 제공됩니다.문자열 필드 이론의 경우, 이것은 일반적으로 문자열 필드라고 불리는 고전적인 구성이 자유 문자열 포크 공간의 요소에 의해 제공된다는 것을 의미합니다.
형식주의의 주요 장점은 오프셸 진폭의 계산을 허용하고 고전적인 동작이 가능할 때 끈 산란의 표준 속 확장에서 직접 볼 수 없는 비섭동 정보를 제공한다는 것입니다.특히, 아쇼크 [1]센의 연구에 이어, 불안정한 D-브레인의 타키온 응축 연구에 유용했습니다.위상 문자열 이론,[2] 비가환 [3]기하학 및 [4]저차원 문자열에도 적용되었습니다.
문자열 필드 이론은 두 번째 양자화되는 문자열 유형에 따라 다양합니다.열린 문자열 필드 이론은 열린 문자열의 산란을 설명하고, 닫힌 문자열 필드 이론은 닫힌 문자열을 설명하는 반면, 열린 문자열 필드 이론은 열린 문자열과 닫힌 문자열을 모두 포함합니다.
게다가, 원래의 자유 끈 이론에서 세계 시트 미분 동형과 등각 변환을 고정하는 데 사용되는 방법에 따라, 결과적인 끈 필드 이론은 매우 다를 수 있습니다.라이트 콘 게이지를 사용하여 라이트 콘 스트링 필드 이론을 산출하는 반면, BRST 양자화를 사용하여 공변 스트링 필드 이론을 찾습니다.또한 빛-콘 및 BRST 게이지 고정 문자열 필드 [5]이론의 요소를 모두 사용하는 공변광-콘 문자열 필드 이론으로 알려진 하이브리드 문자열 필드 이론도 마찬가지입니다.
배경 독립 오픈 스트링 필드 이론으로 알려진 스트링 필드 이론의 마지막 형태는 매우 다른 형태를 취합니다; 세계 시트 스트링 이론을 두 번째 양자화하는 대신, 2차원 양자 필드 [6]이론의 공간을 두 번째 양자화합니다.
광원뿔현장론
라이트 콘 끈 장 이론은 스탠리 만델스탐에[7][8] 의해 도입되었고 만델스탐, 마이클 그린, 존 슈바르츠, 라스 [9][10][11][12][13]브링크에 의해 개발되었습니다.광콘 끈의 두 번째 양자화에 대한 명시적인 설명은 미치오 카쿠와 [14][15]키카와 케이지에 의해 제공되었습니다.
라이트콘 스트링 필드 이론은 최초로 구성된 스트링 필드 이론이며 라이트콘 게이지에서 스트링 산란의 단순성을 기반으로 합니다.예를 들어, 보손 닫힌 끈의 경우, 세계 시트 산란 다이어그램은 자연스럽게 파인만 다이어그램과 같은 형태를 취하며, 두 가지 요소, 즉 전파자,
세 개의 전파기를 접착하는 데 사용할 수 있는 두 개의 꼭짓점과 끈을 나누고 결합하는 데 사용할 수 있는 두 개의 꼭짓점,
이러한 정점과 전파기는n{ n점 닫힌 문자열 산란 의 모듈리 공간의 단일 커버를 생성하므로 고차 정점이 [16]필요하지 않습니다.열린 문자열에 대해 유사한 정점이 있습니다.
라이트 콘 양자화된 슈퍼 스트링을 고려할 때 라이트 콘 정점이 충돌할 때 [17]차이가 발생할 수 있기 때문에 논의가 더 미묘합니다.일관된 이론을 생성하려면, 발산을 취소하기 위해 접촉 항이라고 불리는 고차 정점을 도입해야 합니다.
라이트콘 스트링 필드 이론은 매니페스트 로렌츠 불변성을 깨는 단점이 있습니다.그러나 빛과 같은 킬링 벡터가 있는 배경에서는 문자열 동작의 양자화를 상당히 단순화할 수 있습니다.게다가 베르코비츠 문자열이[18] 등장하기 전까지는 라몬드-라몬드 필드가 있는 상태에서 문자열을 양자화하는 유일한 방법이었습니다.최근 연구에서 라이트콘 스트링 필드 이론은 pp-wave [19]배경의 스트링을 이해하는 데 중요한 역할을 했습니다.
자유 공변 문자열 장 이론
공변 문자열 장 이론(명백한 로렌츠 불변성 보존)의 구성에서 중요한 단계는 공변 운동 항의 구성이었습니다.이 운동 용어는 그 자체로 끈장 이론, 즉 자유 끈의 끈장 이론으로 간주될 수 있습니다.Warren [20]Siegel의 연구 이후, 자유 끈 이론을 먼저 BRST 양자화한 다음, 끈 필드 이론의 고전적인 분야가 물질 필드뿐만 아니라 유령을 포함하도록 두 번째 양자화하는 것이 표준화되었습니다.예를 들어, 26차원 평평한 시공간에서 보손 열린 끈 이론의 경우, BRST 양자화 끈의 포크 공간의 일반적인 요소는 (상반 평면의 방사형 양자화에서) 다음과 같은 형태를 취합니다.
서 0µ{{ 0은 자유 문자열 진공이며 점은 더 무거운 필드를 나타냅니다.월드시트 문자열 이론에서 T {\ T ( {\및( {\는 다양한 기본 상태에서 발견되는 문자열의 진폭을 나타냅니다.두 번째 양자화 후, 그들은 대신 TT 게이지 A{\ 및 고스트 필드{\를 나타내는 고전적인 필드로 해석됩니다.
월드시트 스트링 이론에서, Fock 공간의 비물리적 요소는 Q_ \ \= 및 동등 관계 δ ~+ QB \da \ \\\da 을 부과하여 제거합니다.두 번째 양자화 후 동등성 관계는 게이지 불변성으로 해석되는 반면, 이 물리적인 조건은 운동 방정식으로 해석됩니다.물리적 필드는 고스트 넘버원에서 살기 때문에 문자열 필드 \이(가) 포크 공간의 고스트 넘버원 요소라고 가정하기도 합니다.
개방 보손 끈의 경우, 적절한 대칭과 운동 방정식을 가진 게이지 미고정 동작은 원래 안드레 네베우, 헤르만 니콜라이, 피터 C에 의해 얻어졌습니다. 서부.[21] 그것은 에 의해 주어집니다.
여기서\Psi는 [22]의 BPZ 이중입니다.
보손 닫힌 문자열의 경우, BRST 불변 운동 용어를 구성하려면 추가로( ~ ) {\ \ \ \rangle \langle \langle \langle \rangle rang 0 \langle \langle \l 운동학적 용어는 다음과 같습니다.
슈퍼스트링이 슈퍼고스트 제로 모드를 처리하려면 추가적인 고려 사항이 필요합니다.
위튼의 입방체 오픈 스트링 필드 이론
가장 잘 연구되고 단순한 공변 상호 작용 문자열 장 이론은 에드워드 [23]위튼에 의해 구성되었습니다.그것은 보손 열린 끈의 역학을 설명하고 자유 열린 끈 동작에 입방 꼭짓점을 추가함으로써 주어집니다.
- ( ) B + ⟩ ψ ψ lang ψ ψ{\ \ )=Psi \ \ \ \Psi
여기서, 자유 사례에서와 같이, \Psi는 BRST 양자화된 자유 보손 개방 끈 포크 공간의 유령 번호 1 요소입니다.
입방정점,
총 고스트 번호 3의 문자열 필드 3개를 사용하여 숫자를 산출하는 삼선 맵입니다.비가환 기하학의 아이디어에 의해 동기 부여된 Witten에 이어, 다음을 통해 암묵적으로 정의된*}-제품을 도입하는 것이 일반적입니다.
- 곱과 입방 꼭짓점은 다음과 같은 여러 가지 중요한 특성을 만족시킵니다({i
- 순환성:
- BRST 불변성:
∗{\ - 제품의 경우, 는 QB 가 등급 파생으로 작용함을 합니다.
- 연상
입방 꼭짓점의 관점에서,
이 방정식에서 ) {\gn은의 고스트 번호를 .
게이지 불변성
입방 꼭짓점의 이러한 특성은 S \ S가 양-밀스와 같은 게이지 변환 하에서 을 보여주기에 충분합니다.
여기서 는 무한소 게이지 파라미터입니다.유한 게이지 변환은 다음과 같은 형태를 취합니다.
지수는 다음과 같이 정의됩니다.
운동 방정식
운동 방정식은 다음 방정식에 의해 제공됩니다.
문자열 필드 는 일반적인 고전적 필드의 무한 집합이기 때문에, 이러한 방정식은 비선형 결합 미분 방정식의 무한 집합을 나타냅니다.솔루션을 찾는 방법에는 두 가지가 있습니다.먼저 수치적으로 문자열 필드를 잘라내어 "레벨 잘라내기"[24]라고 하는 절차인 고정 경계 미만의 질량을 가진 필드만 포함할 수 있습니다.이것은 운동 방정식을 유한한 수의 결합 미분 방정식으로 줄이고 많은 [25][26]해결책을 발견하게 했습니다.둘째, 마틴 슈나블론의 연구를 따라 별의 곱셈과 BRST 연산자의 작용 하에서 간단한 행동을 하는 안사츠를 신중하게 선택하여 분석적 해결책을 찾을 수 있습니다.이것은 한계 변형, 타키온 진공 솔루션[28] 및 시간 독립적인 D-브레인 [29]시스템을 나타내는 솔루션으로 이어졌습니다.
양자화
S를 일관되게 하려면 게이지를 고정해야 합니다전통적인 선택은 파인만-시겔 게이지였습니다.
게이지 변환 자체가 중복되기 때문에(게이지 변환의 게이지 변환이 있음), 게이지 고정 절차는 BV 형식주의를 [30]통해 무한한 수의 유령을 도입해야 합니다.전체 게이지 고정 동작은 다음과 같습니다.
여기서 필드 \Psi는 임의의 고스트 번호일 수 있습니다.이 게이지에서 파인만 다이어그램은 단일 전파기와 정점으로 구성됩니다.전파자는 너비({ 및 T({T})의 월드 시트 스트립 형태를 취합니다.
선을 따라 bb}-고스트의 적분이 삽입됩니다.계수 T})는 0에서 \infty까지 통합되어 있습니다.
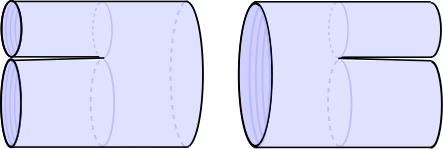
세 개의 꼭짓점은 다음 그림과 같이 세 개의 전파기를 접착하는 방법으로 설명할 수 있습니다.
3차원에 내장된 정점을 나타내기 위해 전파자는 중간점을 따라 반으로 접혀 있습니다.결과 기하학은 세 전파자의 중간점이 만나는 단일 곡률 특이점을 제외하고는 완전히 평평합니다.
이러한 파인만 다이어그램은 열린 끈 산란 다이어그램의 모듈리 공간에 대한 완전한 커버를 생성합니다.따라서 온셸 진폭의 경우, 위튼의 열린 문자열 필드 이론을 사용하여 계산된 n점 열린 문자열 진폭은 표준 월드시트 [31][32]방법을 사용하여 계산된 것과 동일합니다.
초대칭 공변 오픈 스트링 장 이론
위튼의 입방 오픈 스트링 필드 이론의 초대칭 확장에는 두 가지 주요 구성이 있습니다.첫 번째는 보손 사촌과 형태가 매우 유사하며 수정된 입방 초끈 이론으로 알려져 있습니다.두 번째는 Nathan Berkovits로 인해 매우 다르며 WZW 유형의 동작을 기반으로 합니다.
수정된 입방 초끈장 이론
비텐의 보손 개방 끈 이론의 RNS 끈에 대한 최초의 일관된 확장은 크리스찬 프리츠초프, 찰스 손, 스콧 요스트에 의해 구성되었고 독립적으로 이리나 아레페바, P. B. 메드베데프,[33][34] A. P. 주바레프에 의해 구성되었습니다.NS 문자열 필드는 작은 힐버트 공간(,⟩ 0 0 { \ \ \rangle 0)에서 고스트 넘버원 그림 0 문자열 필드로 간주됩니다.그 작용은 보손 작용과 매우 유사한 형태를 취합니다.
어디에,
는 역방향 그림 변경 연산자입니다.제안된 그림 번호 확장은 이 이론을 라몬드 섹터로 확장하는 것이 문제가 될 수 있습니다.
이 작용은 나무 수준의 진폭을 재현하는 것으로 나타났으며 올바른 [35]에너지를 가진 타키온 진공 용액을 가지고 있습니다.동작의 한 가지 미묘한 점은 중앙점에 그림 변화 연산자를 삽입하는 것이며, 이는 선형화된 운동 방정식이 형태를 취한다는 것을 의미합니다.
(Y {\ Y Y[36]가 사소하지 않은 커널을 가지고 있기 에의 코호몰로지에 없는 추가 솔루션이 수 있습니다. 그러나 이러한 솔루션은 중간점 근처에 연산자 삽입이 있고 잠재적으로 단일입니다.그리고 이 문제의 중요성은 여전히 불분명합니다.
베르코비츠 초현장 이론
열린 끈에 대한 매우 다른 초대칭 작용은 Nathan Berkovits에 의해 구성되었습니다.형태를[37] 취합니다.
여기서 모든 제품은 반연산자 를 포함한 {{ 제품을 사용하여 수행됩니다.그리고 ( \ hat \ 는 ( ( Δ \ \ 와 같은 문자열 필드입니다. 문자열 필드 \ displaystyle \ 는 Hilbert의 큰 공간에 사용됩니다.0 모드의{\ \를 포함합니다. 일부 예비 아이디어가 [38]존재하지만 R 섹터를 통합하는 방법은 알려져 있지 않습니다.
운동 방정식은 형태를 취합니다.
게이지 변환에서 작용은 불변합니다.
이 작업의 주요 이점은 그림을 변경하는 연산자를 삽입할 필요가 없다는 것입니다.트리 레벨[39] 진폭을 올바르게 재현하는 것으로 나타났으며 수치적으로 적절한 [40][41]에너지를 가진 타키온 진공이 있는 것으로 확인되었습니다.고전적인 운동 방정식에 대한 알려진 분석 솔루션에는 타키온[42] 진공 및 주변 변형이 포함됩니다.
공변 개방 초끈 이론의 다른 공식화
비최소 순수 스피너 변수를 사용한 초끈장 이론의 공식은 [43]버코비츠에 의해 도입되었습니다.작업은 입방체이며 커널이 사소한 중간점 삽입을 포함합니다.순수 스피너 공식 내에서 항상 그렇듯이, 라몬드 섹터는 쉽게 처리될 수 있습니다.그러나 GSO- 부문을 형식주의에 어떻게 통합하는지는 알려지지 않았습니다.
수정된 입방체 이론의 문제가 된 중간점 삽입을 해결하기 위해, 베르코비츠와 시겔은 커널 없이 중간점 삽입을 사용하는 RNS [44]문자열의 비최소 확장에 기초한 초끈 필드 이론을 제안했습니다.이러한 삽입이 사소한 커널이 아닌 중간점 삽입보다 더 나은지는 확실하지 않습니다.
공변 닫힌 문자열 장 이론
공변 폐쇄 끈 장 이론은 개방 끈 사촌보다 상당히 복잡합니다.닫힌 문자열 사이의 트리 수준 상호 작용만 재현하는 문자열 필드 이론을 구성하고 싶어도, 고전적인 동작은 문자열 [46][47]다면체로 구성된 무한한 수의 정점을 포함해야 합니다.
문자열 커플링의 모든 순서에 대해 온셸 산란 다이어그램을 재현할 것을 요구하는 경우, 더 높은 속(따라서 {\ \hbar의 더 높은 순서)에서 발생하는 추가 정점도 포함해야 합니다.일반적으로, 명백하게 BV 불변의 양자화 가능한 작용은 다음과[48] 같은 형태를 취합니다.
여기서{({\g})는 g} 표면에서 하는 n})정점을 나타내며 ({displaystyle 는 닫힌 문자열 결합입니다.꼭짓점의 구조는 원칙적으로 최소 면적 [49]처방에 의해 결정되지만, 다면체 꼭짓점에 대해서도 명시적인 계산이 5차 [50][51]순서로만 수행되었습니다.
공변 이질 문자열 장 이론
베르코비츠, 오카와, [52]즈위바흐가 이질적인 끈의 NS 섹터 공식을 제공했습니다.이 공식은 보손 폐쇄 끈 필드 이론과 베르코비츠의 초끈 필드 이론을 결합합니다.
참고 항목
레퍼런스
- ^ Sen, Ashoke (1999-12-29). "Universality of the tachyon potential". Journal of High Energy Physics. 1999 (12): 027. arXiv:hep-th/9911116. Bibcode:1999JHEP...12..027S. doi:10.1088/1126-6708/1999/12/027. ISSN 1029-8479. S2CID 1506387.
- ^ E. Witten, "끈 이론으로서의 Chern-Simons 게이지 이론", Prog.수학. 133637, (1995)
- ^ E. Witten, "비가환 타키온과 끈장 이론", hep-th/0006071
- ^ Gaiotto, Davide; Rastelli, Leonardo (2005-07-25). "A paradigm of open/closed duality Liouville D-branes and the Kontsevich model". Journal of High Energy Physics. 2005 (7): 053. arXiv:hep-th/0312196. Bibcode:2005JHEP...07..053G. doi:10.1088/1126-6708/2005/07/053. ISSN 1029-8479. S2CID 15225459.
- ^ Hata, Hiroyuki; Itoh, Katsumi; Kugo, Taichiro; Kunitomo, Hiroshi; Ogawa, Kaku (1986). "Manifestly covariant field theory of interacting string I". Physics Letters B. Elsevier BV. 172 (2): 186–194. Bibcode:1986PhLB..172..186H. doi:10.1016/0370-2693(86)90834-8. ISSN 0370-2693.
- ^ Witten, Edward (1992-12-15). "On background-independent open-string field theory". Physical Review D. 46 (12): 5467–5473. arXiv:hep-th/9208027. Bibcode:1992PhRvD..46.5467W. doi:10.1103/physrevd.46.5467. ISSN 0556-2821. PMID 10014938. S2CID 1135319.
- ^ Mandelstam, S. (1973). "Interacting-string picture of dual-resonance models". Nuclear Physics B. Elsevier BV. 64: 205–235. Bibcode:1973NuPhB..64..205M. doi:10.1016/0550-3213(73)90622-6. ISSN 0550-3213.
- ^ Mandelstam, S. (1974). "Interacting-string picture of the Neveu-Schwarz-Ramond model". Nuclear Physics B. Elsevier BV. 69 (1): 77–106. Bibcode:1974NuPhB..69...77M. doi:10.1016/0550-3213(74)90127-8. ISSN 0550-3213. S2CID 120638932.
- ^ Green, Michael B.; Schwarz, John H. (1982). "Supersymmetric dual string theory: (II). Vertices and trees". Nuclear Physics B. Elsevier BV. 198 (2): 252–268. Bibcode:1982NuPhB.198..252G. doi:10.1016/0550-3213(82)90556-9. ISSN 0550-3213.
- ^ Green, Michael B.; Schwarz, John H. (1983). "Superstring interactions". Nuclear Physics B. Elsevier BV. 218 (1): 43–88. Bibcode:1983NuPhB.218...43G. doi:10.1016/0550-3213(83)90475-3. ISSN 0550-3213.
- ^ Green, Michael B.; Schwarz, John H.; Brink, Lars (1983). "Superfield theory of type (II) superstrings". Nuclear Physics B. Elsevier BV. 219 (2): 437–478. Bibcode:1983NuPhB.219..437G. doi:10.1016/0550-3213(83)90651-x. ISSN 0550-3213.
- ^ Green, Michael B.; Schwarz, John H. (1984). "Superstring field theory". Nuclear Physics B. Elsevier BV. 243 (3): 475–536. Bibcode:1984NuPhB.243..475G. doi:10.1016/0550-3213(84)90488-7. ISSN 0550-3213.
- ^ Mandelstam, Stanley (1986). "Interacting-String Picture of the Fermionic String". Progress of Theoretical Physics Supplement. Oxford University Press (OUP). 86: 163–170. Bibcode:1986PThPS..86..163M. doi:10.1143/ptps.86.163. ISSN 0375-9687.
- ^ Kaku, Michio; Kikkawa, K. (1974-08-15). "Field theory of relativistic strings. I. Trees". Physical Review D. American Physical Society (APS). 10 (4): 1110–1133. Bibcode:1974PhRvD..10.1110K. doi:10.1103/physrevd.10.1110. ISSN 0556-2821.
- ^ Kaku, Michio; Kikkawa, K. (1974-09-15). "Field theory of relativistic strings. II. Loops and Pomerons". Physical Review D. American Physical Society (APS). 10 (6): 1823–1843. Bibcode:1974PhRvD..10.1823K. doi:10.1103/physrevd.10.1823. ISSN 0556-2821.
- ^ D'Hoker, Eric; Giddings, Steven B. (1987). "Unitarity of the closed bosonic Polyakov string". Nuclear Physics B. Elsevier BV. 291: 90–112. Bibcode:1987NuPhB.291...90D. doi:10.1016/0550-3213(87)90466-4. ISSN 0550-3213.
- ^ Greensite, J.; Klinkhamer, F.R. (1987). "New interactions for superstrings". Nuclear Physics B. Elsevier BV. 281 (1–2): 269–288. Bibcode:1987NuPhB.281..269G. doi:10.1016/0550-3213(87)90256-2. ISSN 0550-3213.
- ^ Berkovits, Nathan (2000-04-15). "Super-Poincare covariant quantization of the superstring". Journal of High Energy Physics. 2000 (4): 018. arXiv:hep-th/0001035. Bibcode:2000JHEP...04..018B. doi:10.1088/1126-6708/2000/04/018. ISSN 1029-8479.
- ^ M. 스프래들린과 A.Volovich, "평면파에서의 라이트 콘 스트링 필드 이론", 이탈리아 트리에스테의 ICTP 스프링 스쿨에서 슈퍼 스트링 이론 및 관련 주제에 대한 강의, 2003년 3월 31일 - 4월 8일) hep-th/0310033.
- ^ W. Siegel, "BRST를 통한 스트링 필드 이론", Santa Barbara 1985, Proceedings, Unified String Theory, 593;
W. Siegel, "끈장 이론 입문", Adv. Ser.수학. 물리. 8. hep-th/0107094로 재인쇄됨 - ^ Neveu, A.; Nicolai, H.; West, P. (1986). "New symmetries and ghost structure of covariant string theories". Physics Letters B. Elsevier BV. 167 (3): 307–314. Bibcode:1986PhLB..167..307N. doi:10.1016/0370-2693(86)90351-5. ISSN 0370-2693.
- ^ Belavin, A.A.; Polyakov, A.M.; Zamolodchikov, A.B. (1984). "Infinite conformal symmetry in two-dimensional quantum field theory". Nuclear Physics B. Elsevier BV. 241 (2): 333–380. Bibcode:1984NuPhB.241..333B. doi:10.1016/0550-3213(84)90052-x. ISSN 0550-3213.
- ^ Witten, Edward (1986). "Non-commutative geometry and string field theory". Nuclear Physics B. Elsevier BV. 268 (2): 253–294. Bibcode:1986NuPhB.268..253W. doi:10.1016/0550-3213(86)90155-0. ISSN 0550-3213.
- ^ Kostelecký, V. Alan; Samuel, Stuart (1989-01-15). "Spontaneous breaking of Lorentz symmetry in string theory". Physical Review D. American Physical Society (APS). 39 (2): 683–685. Bibcode:1989PhRvD..39..683K. doi:10.1103/physrevd.39.683. hdl:2022/18649. ISSN 0556-2821. PMID 9959689.
- ^ Zwiebach, Barton (2001). "Is the String Field Big Enough?". Fortschritte der Physik. Wiley. 49 (4–6): 387. Bibcode:2001ForPh..49..387Z. doi:10.1002/1521-3978(200105)49:4/6<387::aid-prop387>3.0.co;2-z. ISSN 0015-8208.
- ^ Taylor, Washington; Zwiebach, Barton (2004). "D-Branes, Tachyons, and String Field Theory". Strings, Branes and Extra Dimensions. World Scientific. pp. 641–670. arXiv:hep-th/0311017. doi:10.1142/9789812702821_0012. ISBN 978-981-238-788-2.
- ^ Schnabl, Martin (2006). "Analytic solution for tachyon condensation in open string field theory". Advances in Theoretical and Mathematical Physics. 10 (4): 433–501. arXiv:hep-th/0511286. doi:10.4310/atmp.2006.v10.n4.a1. ISSN 1095-0761.
- ^ Fuchs, Ehud; Kroyter, Michael (2011). "Analytical solutions of open string field theory". Physics Reports. 502 (4–5): 89–149. arXiv:0807.4722. Bibcode:2011PhR...502...89F. doi:10.1016/j.physrep.2011.01.003. ISSN 0370-1573. S2CID 119203368.
- ^ Erler, Theodore; Maccaferri, Carlo (2014). "String field theory solution for any open string background". Journal of High Energy Physics. Springer Nature. 2014 (10): 029. arXiv:1406.3021. Bibcode:2014JHEP...10..029E. doi:10.1007/jhep10(2014)029. ISSN 1029-8479.
- ^ Thorn, Charles B. (1989). "String field theory". Physics Reports. Elsevier BV. 175 (1–2): 1–101. Bibcode:1989PhR...175....1T. doi:10.1016/0370-1573(89)90015-x. ISSN 0370-1573.
- ^ Giddings, Steven B.; Martinec, Emil; Witten, Edward (1986). "Modular invariance in string field theory". Physics Letters B. Elsevier BV. 176 (3–4): 362–368. Bibcode:1986PhLB..176..362G. doi:10.1016/0370-2693(86)90179-6. ISSN 0370-2693.
- ^ Zwiebach, Barton (1991). "A proof that Witten's open string theory gives a single cover of moduli space". Communications in Mathematical Physics. Springer Science and Business Media LLC. 142 (1): 193–216. Bibcode:1991CMaPh.142..193Z. doi:10.1007/bf02099176. ISSN 0010-3616. S2CID 121798009.
- ^ Preitschopf, Christian R.; Thorn, Charles B.; Yost, Scott (1990). "Superstring field theory". Nuclear Physics B. Elsevier BV. 337 (2): 363–433. Bibcode:1990NuPhB.337..363P. doi:10.1016/0550-3213(90)90276-j. ISSN 0550-3213. OSTI 7241635.
- ^ Aref'eva, I.Ya.; Medvedev, P.B.; Zubarev, A.P. (1990). "New representation for string field solves the consistency problem for open superstring field theory". Nuclear Physics B. Elsevier BV. 341 (2): 464–498. Bibcode:1990NuPhB.341..464A. doi:10.1016/0550-3213(90)90189-k. ISSN 0550-3213.
- ^ Erler, Theodore (2008-01-07). "Tachyon vacuum in cubic superstring field theory". Journal of High Energy Physics. 2008 (1): 013. arXiv:0707.4591. Bibcode:2008JHEP...01..013E. doi:10.1088/1126-6708/2008/01/013. ISSN 1029-8479.
- ^ N. Berkovits, "개방형 초끈장 이론의 검토", hep-th/0105230
- ^ Berkovits, Nathan (1995). "Super-Poincaré invariant superstring field theory". Nuclear Physics B. Elsevier BV. 450 (1–2): 90–102. arXiv:hep-th/9503099. Bibcode:1995NuPhB.450...90B. doi:10.1016/0550-3213(95)00259-u. ISSN 0550-3213. S2CID 14495743.
- ^ Michishita, Yoji (2005-01-07). "A Covariant Action with a Constraint and Feynman Rules for Fermions in Open Superstring Field Theory". Journal of High Energy Physics. 2005 (1): 012. arXiv:hep-th/0412215. Bibcode:2005JHEP...01..012M. doi:10.1088/1126-6708/2005/01/012. ISSN 1029-8479.
- ^ Berkovits, Nathan; Echevarria, Carlos Tello (2000). "Four-point amplitude from open superstring field theory". Physics Letters B. Elsevier BV. 478 (1–3): 343–350. arXiv:hep-th/9912120. Bibcode:2000PhLB..478..343B. doi:10.1016/s0370-2693(00)00246-x. ISSN 0370-2693. S2CID 17003177.
- ^ Berkovits, Nathan (2000-04-19). "The tachyon potential in open Neveu-Schwarz string field theory". Journal of High Energy Physics. 2000 (4): 022. arXiv:hep-th/0001084. Bibcode:2000JHEP...04..022B. doi:10.1088/1126-6708/2000/04/022. ISSN 1029-8479.
- ^ Berkovits, Nathan; Sen, Ashoke; Zwiebach, Barton (2000). "Tachyon condensation in superstring field theory". Nuclear Physics B. 587 (1–3): 147–178. arXiv:hep-th/0002211. Bibcode:2000NuPhB.587..147B. doi:10.1016/s0550-3213(00)00501-0. ISSN 0550-3213. S2CID 11853254.
- ^ Erler, Theodore (2013). "Analytic solution for tachyon condensation in Berkovits' open superstring field theory". Journal of High Energy Physics. 2013 (11): 7. arXiv:1308.4400. Bibcode:2013JHEP...11..007E. doi:10.1007/jhep11(2013)007. ISSN 1029-8479. S2CID 119114830.
- ^ Berkovits, Nathan (2005-10-27). "Pure spinor formalism as an N= 2 topological string". Journal of High Energy Physics. 2005 (10): 089. arXiv:hep-th/0509120. Bibcode:2005JHEP...10..089B. doi:10.1088/1126-6708/2005/10/089. ISSN 1029-8479.
- ^ Berkovits, Nathan; Siegel, Warren (2009-11-05). "Regularizing cubic open Neveu-Schwarz string field theory". Journal of High Energy Physics. 2009 (11): 021. arXiv:0901.3386. Bibcode:2009JHEP...11..021B. doi:10.1088/1126-6708/2009/11/021. ISSN 1029-8479. S2CID 16824165.
- ^ Sonoda, Hidenori; Zwiebach, Barton (1990). "Covariant closed string theory cannot be cubic". Nuclear Physics B. Elsevier BV. 336 (2): 185–221. Bibcode:1990NuPhB.336..185S. doi:10.1016/0550-3213(90)90108-p. ISSN 0550-3213.
- ^ Saadi, Maha; Zwiebach, Barton (1989). "Closed string field theory from polyhedra". Annals of Physics. Elsevier BV. 192 (1): 213–227. Bibcode:1989AnPhy.192..213S. doi:10.1016/0003-4916(89)90126-7. ISSN 0003-4916.
- ^ Kugo, Taichiro; Suehiro, Kazuhiro (1990). "Nonpolynomial closed string field theory: Action and its gauge invariance". Nuclear Physics B. Elsevier BV. 337 (2): 434–466. Bibcode:1990NuPhB.337..434K. doi:10.1016/0550-3213(90)90277-k. ISSN 0550-3213.
- ^ Zwiebach, Barton (1993). "Closed string field theory: Quantum action and the Batalin-Vilkovisky master equation". Nuclear Physics B. 390 (1): 33–152. arXiv:hep-th/9206084. Bibcode:1993NuPhB.390...33Z. doi:10.1016/0550-3213(93)90388-6. ISSN 0550-3213. S2CID 119509701.
- ^ Zwiebach, Barton (1990-12-30). "Quantum Closed Strings from Minimal Area". Modern Physics Letters A. World Scientific Pub Co Pte Lt. 05 (32): 2753–2762. Bibcode:1990MPLA....5.2753Z. doi:10.1142/s0217732390003218. ISSN 0217-7323.
- ^ Moeller, Nicolas (2007-03-12). "Closed bosonic string field theory at quintic order: five-tachyon contact term and dilaton theorem". Journal of High Energy Physics. 2007 (3): 043. arXiv:hep-th/0609209. Bibcode:2007JHEP...03..043M. doi:10.1088/1126-6708/2007/03/043. ISSN 1029-8479. S2CID 11634790.
- ^ Moeller, Nicolas (2007-09-26). "Closed bosonic string field theory at quintic order II: marginal deformations and effective potential". Journal of High Energy Physics. 2007 (9): 118. arXiv:0705.2102. Bibcode:2007JHEP...09..118M. doi:10.1088/1126-6708/2007/09/118. ISSN 1029-8479. S2CID 16383969.
- ^ Berkovits, Nathan; Okawa, Yuji; Zwiebach, Barton (2004-11-16). "WZW-like Action for Heterotic String Field Theory". Journal of High Energy Physics. 2004 (11): 038. arXiv:hep-th/0409018. Bibcode:2004JHEP...11..038B. doi:10.1088/1126-6708/2004/11/038. ISSN 1029-8479. S2CID 16151394.



 자유 문자열 진공이며 점은 더 무거운 필드를 나타냅니다.월드시트 문자열 이론에서 T
자유 문자열 진공이며 점은 더 무거운 필드를 나타냅니다.월드시트 문자열 이론에서 T

 다양한 기본 상태에서 발견되는 문자열의 진폭을 나타냅니다.두 번째 양자화 후, 그들은 대신
다양한 기본 상태에서 발견되는 문자열의 진폭을 나타냅니다.두 번째 양자화 후, 그들은 대신 




 물리적인 조건은 운동
물리적인 조건은 운동 





 BRST 양자화된 자유 보손 개방 끈 포크 공간의 유령 번호 1 요소입니다.
BRST 양자화된 자유 보손 개방 끈 포크 공간의 유령 번호 1 요소입니다. 





 등급 파생으로 작용함을
등급 파생으로 작용함을 





 무한소 게이지 파라미터입니다.유한 게이지 변환은 다음과 같은 형태를 취합니다.
무한소 게이지 파라미터입니다.유한 게이지 변환은 다음과 같은 형태를 취합니다.














 사소하지 않은 커널을 가지고 있기
사소하지 않은 커널을 가지고 있기 




 Hilbert의 큰 공간에 사용됩니다.0 모드의
Hilbert의 큰 공간에 사용됩니다.0 모드의






 닫힌 문자열 결합입니다.꼭짓점의 구조는 원칙적으로 최소 면적
닫힌 문자열 결합입니다.꼭짓점의 구조는 원칙적으로 최소 면적 


