자기홀극
Magnetic monopole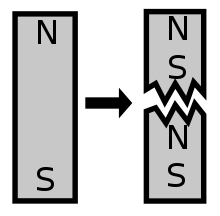
입자물리학에서 자기홀극(自氣 monop極, )은 자기극이 하나만 있는 고립된 자석(남극이 없는 북극 또는 그 반대)인 가상의 기본 입자입니다.자기 모노폴은 북쪽 또는 남쪽의 "자기 전하"를 가지고 있습니다.그 개념에 대한 현대의 관심은 입자 이론, 특히 그들의 존재를 예측하는 거대한 통일 이론과 초끈 이론에서 비롯됩니다.[3][4][full citation needed]전하를 가진 알려진 기본 입자는 전기 모노폴입니다.
막대 자석과 전자석에서의 자성은 자기 모노폴에 의해 발생하지 않으며, 실제로 자기 모노폴이 존재한다는 알려진 실험적 또는 관측적 증거는 없습니다.
일부 응축된 물질계는 효과적인(비분리된) 자기 모노폴 준입자를 포함하거나 [5]자기 모노폴과 수학적으로 유사한 현상을 포함합니다.[6]
역사적 배경
초기과학과 고전물리학
많은 초기 과학자들은 로드스톤의 자성이 서로 다른 두 개의 "자기 유체" (effluvia) 때문이라고 생각합니다. 한 쪽 끝에는 북극 유체가, 다른 쪽에는 남극 유체가, 양전하와 음전하에 비유하여 서로를 끌어당기고 밀어내는 것입니다.[7][8]그러나 19세기 전자기력에 대한 개선된 이해는 로드스톤의 자성이 자기 모노폴 유체에 의해서가 아니라 전류, 전자 자기 모멘트 및 다른 입자의 자기 모멘트의 조합에 의해 적절히 설명된다는 것을 보여주었습니다.맥스웰 방정식 중 하나인 가우스의 자기 법칙은 자기홀극이 존재하지 않는다는 수학적 진술입니다.그럼에도 불구하고, 피에르 퀴리는 1894년에[9] 지금까지 본 적이 없음에도 불구하고 자기홀극이 존재할 수 있다고 지적했습니다.
양자역학
자기 전하의 양자 이론은 1931년 물리학자 폴 디랙의 논문으로 시작되었습니다.[10]이 논문에서 디랙은 우주에 자기홀극이 존재한다면, 우주의 모든 전하가 양자화되어야 한다는 것을 보여주었습니다(디랙 양자화 조건).[11]전하는 사실상 양자화되어 있으며, 이는 모노폴의 존재와 일치하지만 증명되지는 않습니다.[11]
디랙의 논문 이후로 몇 가지 체계적인 모노폴 탐색이 수행되었습니다.1975년과[12] 1982년의[13] 실험들은 처음에는 모노폴로 해석되었으나 현재는 결론이 나지 않는 것으로 간주되는 후보 사건들을 만들어냈습니다.[14]따라서 모노폴이 존재하는지 여부는 여전히 미해결 문제로 남아 있습니다.이론적 입자 물리학의 추가적인 발전, 특히 대통합 이론과 양자 중력의 발전은 모노폴이 존재한다는 더 강력한 주장(아래 세부 사항)을 이끌어냈습니다.끈이론학자인 조셉 폴친스키(Joseph Polchinski)는 모노폴의 존재를 "물리학에 대해 아직 보지 못한 가장 안전한 내기 중 하나"라고 설명했습니다.[15]이 이론들은 실험적 증거와 반드시 일치하지는 않습니다.일부 이론적 모델에서 자기홀극은 입자 가속기에서 생성하기에는 너무 무겁고(아래 § 자기홀극 검색 참조), 우주에서는 입자 검출기에 진입하기에는 너무 드물기 때문에 관측될 가능성이 높지 않습니다.
일부 응축된 물질 시스템은 플럭스 튜브라고 알려진 자기 모노폴과 표면적으로 유사한 구조를 제안합니다.플럭스 튜브의 끝단은 자기 쌍극자를 형성하지만, 독립적으로 움직이기 때문에, 그것들은 독립적인 자기 단극 준입자로서 다양한 목적으로 취급될 수 있습니다.2009년 이후, 대중 매체의[16][17] 수많은 뉴스 보도들은 이 시스템들을 오랫동안 기다려온 자기홀극의 발견으로 잘못 묘사하고 있지만, 이 두 현상들은 표면적으로만 서로 관련되어 있을 뿐입니다.[18][19]이러한 축합계는 여전히 활발한 연구 분야로 남아 있습니다. (아래 축합계의 § "단극" 참조)
보통 물질의 극과 자성
주기율표의 모든 원자와 표준모형의 모든 입자를 포함하여 현재까지 분리된 모든 물질은 자기홀극 전하가 0입니다.그러므로 자기와 자석의 일반적인 현상은 자기홀극에서 유래하지 않습니다.
대신에, 일반적인 물질에서의 자성은 두 가지 원천에 기인합니다.첫째, 전류는 앙페르의 법칙에 따라 자기장을 형성합니다.둘째로, 많은 기본 입자들은 고유 자기 모멘트를 가지고 있는데, 그 중 가장 중요한 것은 양자-기계 스핀과 관련된 전자 자기 쌍극자 모멘트입니다.
수학적으로, 물체의 자기장은 종종 다극 확장으로 설명됩니다.이것은 특정 수학 형태를 갖는 성분 필드의 합으로 필드를 표현한 것입니다.팽창의 첫 번째 항은 모노폴 항, 두 번째 항은 다이폴, 그 다음에 4중극, 그 다음에 8중극 등으로 불립니다.예를 들어, 전기장의 다극 확장에는 이러한 용어가 있을 수 있습니다.그러나 자기장의 다극 확장에서 "단극" 항은 항상 정확히 0입니다.자기 단극자가 존재한다면, 단극자 항이 0이 아닌 자기장을 생성하는 정의적인 특성을 가질 것입니다.
자기 쌍극자는 자기장이 다극자 팽창의 자기 쌍극자 항에 의해 주로 또는 정확히 묘사되는 것입니다.쌍극자라는 용어는 두 개의 극을 의미하며, 쌍극자 자석이 일반적으로 한 면에 북극과 다른 면에 남극을 포함한다는 사실에 해당합니다.이것은 한 쪽에 양전하가 있고 다른 쪽에 음전하가 있는 전기 쌍극자와 유사합니다.그러나 전기 쌍극자와 자기 쌍극자는 근본적으로 상당히 다릅니다.일반적인 물질로 만들어진 전기 쌍극자에서 양전하는 양성자로, 음전하는 전자로 만들어지지만 자기 쌍극자는 북극과 남극을 만드는 다른 물질을 가지고 있지 않습니다.대신, 두 자극은 자석 전체에 걸쳐 모든 전류와 고유 모멘트의 집합 효과에서 동시에 발생합니다.이 때문에, 자기 쌍극자의 두 극은 항상 동등하고 반대의 강도를 가져야 하고, 두 극은 서로 분리될 수 없습니다.
맥스웰 방정식
맥스웰의 전자기 방정식은 전기장과 자기장을 서로 연관시키고 전하와 전류의 분포를 연관시킵니다.표준 방정식은 전하를 제공하지만 자기 전하와 전류가 0임을 나타냅니다.이 제약 조건을 제외하고 방정식은 전기장과 자기장의 교환 하에서 대칭됩니다.맥스웰 방정식은 진공에서와 같이 전하와 전류 밀도가 모든 곳에서 0일 때 대칭됩니다.
만약 전하와 유사한 "자기 전하"를 허용한다면 맥스웰 방정식은 완전히 대칭적인 형태로 쓰여질 수도 있습니다.[20]자기 전하의 밀도에 대한 변수, 예를 들어 ρ를 포함하면 방정식에 "자기 전류 밀도" 변수, j도 있습니다.
만약 자기 전하가 존재하지 않거나 존재하지만 공간에 존재하지 않는다면 맥스웰 방정식의 새로운 항들은 모두 0이고, 확장된 방정식은 ∇ ⋅ B = 0과 같은 기존의 전자기 방정식으로 줄어듭니다(여기서 ∇⋅는 발산 연산자, B는 자속 밀도).
가우스 cgs 단위로 표시
확장된 맥스웰 방정식은 CGS-가우스 단위로 다음과 같습니다.[23]
| 이름. | 자기홀극 미포함 | 마그네틱 모노폴 포함 |
|---|---|---|
| 가우스의 법칙 | ||
| 암페르의 법칙 (막스웰의 확장과 함께) | ||
| 가우스의 자기 법칙 | ||
| 패러데이 유도 법칙 | ||
| 로렌츠 힘 법칙[23][24] | ||
이 식들에서 ρ는 자기 전하 밀도, j는 자기 전류 밀도, q는 시험 입자의 자기 전하로, 모두 전하와 전류의 관련 양과 유사하게 정의됩니다. v는 입자의 속도, c는 빛의 속도입니다.다른 모든 정의와 자세한 내용은 맥스웰 방정식을 참조하십시오.비차원 형태의 방정식의 경우 c의 인자를 제거합니다.
SI 단위로
SI와 함께 사용되는 국제 수량 체계에서는 자기 전하 q를 정의하기 위한 두 가지 규약이 있으며, 각각 다른 단위인 웨버(Wb)와 암페어계(A ⋅m)가 있습니다.단위가 1Wb = 1H ⋅A = (1H ⋅m) (1A ⋅m)이므로 이들 사이의 변환은 q = μq입니다. 여기서 H는 인덕턴스의 SI 단위인 헨리입니다.
맥스웰 방정식은 다음과 같은 형태를 취합니다.[notes 1]
| 이름. | 마그네틱 미포함 단극의 | 마그네틱 모노폴 포함 | |
|---|---|---|---|
| 베버협약 | 암페어 미터 규약 | ||
| 가우스의 법칙 | |||
| 암페르의 법칙 (막스웰의 확장과 함께) | |||
| 가우스의 자기 법칙 | |||
| 패러데이 유도 법칙 | |||
| 로렌츠 힘 방정식 | |||
포텐셜 제형
맥스웰 방정식은 다음과 같이 퍼텐셜로 표현할 수 있습니다.
| 이름. | 가우스 단위 | SI 단위(Wb) | SI단위(A ⋅m) |
|---|---|---|---|
| 맥스웰 방정식 (Lorenz 게이지 가정) | |||
| 로렌츠 게이지 조건 | |||
| 필드와의 관계 | |||
어디에
텐서 공식화
텐서의 언어로 된 맥스웰 방정식은 로렌츠 공분산을 명확하게 합니다.이 글에서는 전자기 텐서와 예비 4벡터를 다음과 같이 소개합니다.
| 이름. | 표기법 | 가우스 단위 | SI 단위(Wb 또는 A ⋅m) |
|---|---|---|---|
| 전자기 텐서 | |||
| 이중 전자기 텐서 | |||
| 사류 | |||
| 포퍼텐셜 | |||
| 포포스 | |||
여기서:
| 맥스웰 방정식 | 가우스 단위 | SI 단위(Wb) | SI단위(A ⋅m) |
|---|---|---|---|
| 앙페르-가우스 법칙 | |||
| 패러데이-가우스 법칙 | |||
| 로렌츠 힘 법칙 | |||
| 이름. | 가우스 단위 | SI 단위(Wb) | SI단위(A ⋅m) |
|---|---|---|---|
| 맥스웰 방정식 | |||
| 로렌츠 게이지 조건 | |||
| 필드와의 관계 (캐비보–페라리-샨무가드하산 관계) |
|
| |
여기서 ε은 레비-시비타 기호입니다.
이중 변환
일반화된 맥스웰 방정식은 이중성 변환이라 불리는 일정한 대칭성을 가지고 있습니다.임의의 실제 각도 ξ를 선택할 수 있으며, 동시에 다음과 같이 우주의 모든 곳에서 필드와 전하를 변경할 수 있습니다(가우시안 단위).
| 전하 및 전류 | 필드 |
|---|---|
여기서 프라이밍된 양은 변환 전 전하와 필드이고, 프라이밍되지 않은 양은 변환 후입니다.이 변환 후의 장들과 전하들은 여전히 같은 맥스웰 방정식을 따릅니다.행렬은 2차원 회전 행렬입니다.
이중성 변환 때문에, 입자의 거동을 관찰하고 맥스웰 방정식과 비교하는 것만으로는 입자가 전하를 갖는지, 자기 전하를 갖는지, 또는 둘 다를 갖는지를 유일하게 결정할 수 없습니다.예를 들어, 전자는 전하를 가지지만 자기 전하는 가지 않는다는 것은 맥스웰 방정식의 요구 사항이 아니라 단지 관례에 불과합니다. ξ = π/2 변환 후에는 그 반대가 됩니다.중요한 경험적 사실은 지금까지 관측된 모든 입자들이 전하에 대한 자기 전하의 비율이 같다는 것입니다.[29]이중성 변환은 임의의 숫자 값으로 비율을 변경할 수 있지만 모든 입자가 동일한 비율을 갖는다는 것을 변경할 수는 없습니다.이 경우에는 이 비율을 0으로 설정하여 모든 입자가 자기 전하를 갖지 않도록 하는 이중 변환을 할 수 있습니다.이러한 선택은 전기와 자기에 대한 "통상적인" 정의의 기초가 됩니다.[29]
디랙의 양자화
양자 이론의 결정적인 진보 중 하나는 상대론적 양자 전자기학을 개발한 폴 디랙의 연구였습니다.그의 공식화 전에 전하의 존재는 양자역학 (QM)의 방정식에 단순히 "삽입"되었지만 1931년 디랙은 QM에서 분리된 전하가 자연스럽게 "빠짐"을 보여주었습니다.[30]즉, 우리는 맥스웰 방정식의 형태를 유지하면서도 자기 전하를 가질 수 있습니다.
하나의 정지 전기 모노폴(전자, 예를 들어)과 하나의 정지 자기 모노폴로 구성된 계를 생각해 보면, 서로에게 어떤 힘도 작용하지 않습니다.고전적으로 이들을 둘러싼 전자기장은 포인팅 벡터에 의해 주어진 운동량 밀도를 가지며, 또한 곱 qq에em 비례하는 총 각운동량을 가지며, 이들 사이의 거리에 무관합니다.
그러나, 양자역학은 각운동량이 ħ의 배수로 양자화되므로, 생성물 qq도 양자화되어야 한다고 지시합니다.이는 우주에 단 하나의 자기홀극이라도 존재하고 맥스웰 방정식의 형태가 유효하다면 모든 전하가 양자화된다는 것을 의미합니다.
위의 예제에서 전체 각운동량을 찾기 위해 모든 공간에 걸쳐 단순히 적분하는 것이 가능하지만, 디랙은 다른 접근법을 취했습니다.이것은 그를 새로운 아이디어로 이끌었습니다.그는 자기장이 qm/r처럼 2 행동하고 원점에 위치한 반경 방향으로 향하는 점과 같은 자기 전하를 고려했습니다.B의 발산은 r = 0에서 자기 모노폴의 위치를 제외한 모든 곳에서 0이기 때문에 벡터 퍼텐셜 A의 컬이 자기장 B와 같도록 벡터 퍼텐셜을 국소적으로 정의할 수 있습니다.
그러나 자기장의 발산은 원점에서 디랙 델타 함수에 비례하기 때문에 벡터 퍼텐셜은 전역적으로 정확하게 정의될 수 없습니다.우리는 "북반구"(입자 위의 반공간 z > 0)의 벡터 퍼텐셜에 대한 함수 집합과 "남반구"에 대한 다른 함수 집합을 정의해야 합니다.이 두 벡터 퍼텐셜은 "equator"(입자를 통한 평면 z = 0)에서 일치하며, 게이지 변환에 의해 다릅니다."방정식" 주위를 도는 대전된 입자("프로브 전하")의 파동함수는 일반적으로 아하로노프-봄 효과와 같이 위상에 의해 변화합니다.이 단계는 프로브의 전하 q와e 소스의 자기 전하 q에m 비례합니다.디랙은 원래 파동함수가 디랙 방정식으로 설명되는 전자를 고려하고 있었습니다.
전자가 적도 주위를 완전히 돌고 나면 같은 지점으로 되돌아오기 때문에 파동함수 e의 위상 φ는 변하지 않아야 하며, 이는 파동함수에 추가되는 위상 φ가 2π의 배수여야 한다는 것을 의미합니다.이를 Dirac 양자화 조건이라고 합니다.이 상태는 다양한 단위로 다음과 같이 표현할 수 있습니다.
유닛 조건. SI 단위(웹 협약)[31] SI 단위(암페어 미터 규약) 가우스-cgs 단위
여기서 ε는 진공 유전율, ħ = h/2 π는 감소된 플랑크 상수, c는 광속, ℤ는 정수의 집합입니다.
자기홀극이 존재한다는 가설은 전하가 특정 단위로 양자화되어야 한다는 것을 의미하며, 또한 전하의 존재는 가설 자기홀극의 자기 전하가 존재한다면 기본 전하에 반비례하는 단위로 양자화되어야 한다는 것을 의미합니다.
그 당시에는 그런 것이 존재하는지 심지어 존재해야 하는지 명확하지 않았습니다.결국, 모노폴 없이 전하 양자화를 설명할 수 있는 또 다른 이론이 나올 수 있습니다.그 컨셉은 여전히 호기심으로 남아있었습니다.그러나 이 획기적인 연구가 출판된 이후로 전하 양자화에 대한 다른 널리 받아들여진 설명은 나타나지 않았습니다.(국소 게이지 불변성의 개념(게이지 이론 참조)은 자기 모노폴의 필요성을 유발하지 않고 전하 양자화에 대한 자연스러운 설명을 제공합니다. 그러나 U(1) 게이지 그룹이 콤팩트한 경우에만, 어쨌든 우리는 자기 모노폴을 가지고 있습니다.)
남반구에 대한 벡터 퍼텐셜의 정의를 최대로 확장하면 원점에서 북극 방향으로 뻗어 있는 반무한 선을 제외한 모든 곳에서 정의됩니다.이 반무한 선을 디랙 끈이라고 하며 파동함수에 대한 효과는 아하로노프-봄 효과에서 솔레노이드의 효과와 유사합니다.양자화 조건은 Dirac 문자열 주변의 위상이 사소한 것이라는 요구 사항에서 비롯되며, 이는 Dirac 문자열이 물리적이지 않아야 한다는 것을 의미합니다.Dirac 문자열은 사용된 좌표 차트의 아티팩트일 뿐이므로 심각하게 간주해서는 안 됩니다.
디랙 모노폴은 맥스웰 방정식의 유일한 해(공간에서 세계선을 제거해야 하기 때문에)이며, 좀 더 정교한 이론에서는 't Hooft-Polyakov 모노폴'과 같은 매끄러운 해로 대체됩니다.
위상해석
디랙 문자열
전자기와 같은 게이지 이론은 시공간의 각 경로에 그룹 요소를 연결하는 게이지 필드에 의해 정의됩니다.무한소 경로의 경우 그룹 요소는 아이덴티티에 가깝고 긴 경로의 경우 그룹 요소는 무한소 그룹 요소의 연속적인 산물입니다.
전기역학에서 군은 U(1), 곱셈 하에 단위 복소수입니다.무한소 경로의 경우 그룹 요소는 1 + iAdx이며μμ, 이는 s로 매개 변수화된 유한 경로의 경우 그룹 요소는 다음과 같습니다.
경로에서 그룹 원소로의 지도는 윌슨 루프 또는 홀로노미라고 불리며, U(1) 게이지 그룹의 경우 하전 입자의 파동 함수가 경로를 가로지를 때 획득하는 위상 계수입니다.루프의 경우:
그래서 하전 입자가 고리를 통과할 때 얻는 위상은 고리를 통과하는 자속입니다.작은 솔레노이드에 자속이 있을 경우 충전된 입자의 간섭 무늬가 솔레노이드 주변이나 솔레노이드의 여러 측면을 따라다니며 존재를 드러냅니다.
그러나 모든 입자 전하가 e의 정수배일 경우, 어떤 하전 입자에 대한 위상계수가 exp(2 πi) = 1이기 때문에 플럭스가 2 π/e인 솔레노이드는 간섭무늬가 없습니다. 이러한 솔레노이드는 충분히 얇으면 양자역학적으로 보이지 않습니다.이러한 솔레노이드가 2 π/e의 플럭스를 운반하는 경우, 플럭스가 한쪽 끝에서 누출될 때 모노폴과 구별할 수 없습니다.
디랙의 모노폴 해는 사실 한 점에서 끝나는 무한소 선 솔레노이드를 설명하며, 솔레노이드의 위치는 해의 특이한 부분인 디랙 스트링입니다.디랙 끈은 자기 전하가 반대인 모노폴과 안티모노폴을 연결하지만, 디랙 버전에서는 끈이 무한대로 끊어집니다.문자열을 관찰할 수 없기 때문에 아무 곳에나 놓을 수 있으며, 두 개의 좌표 패치를 사용하여 문자열을 볼 수 없는 곳으로 밀어 각 패치의 필드를 비정형으로 만들 수 있습니다.
대통합론
양자화된 전하를 가진 U(1) 게이지 그룹에서 그룹은 반지름 2 π/e의 원입니다.이러한 U(1) 게이지 그룹을 콤팩트라고 합니다.대통합 이론(GUT)에서 나오는 모든 U(1)는 콤팩트합니다. 콤팩트한 고게이지 그룹만이 의미가 있기 때문입니다.게이지 그룹의 크기는 역결합 상수의 측정값이므로, 큰 부피 게이지 그룹의 한계에서 고정된 표현의 상호작용은 0이 됩니다.
U(1) 게이지 그룹의 경우는 특수한 경우인데, 그 이유는 모든 축소 불가능한 표현이 동일한 크기이기 때문입니다. 전하량은 정수만큼 크지만 필드는 여전히 단지 복소수이기 때문입니다. 그래서 U(1) 게이지 필드 이론에서는 모순 없이 분해되지 않은 극한을 취할 수 있습니다.전하의 양자는 작아지지만, 각각의 하전 입자는 엄청난 수의 전하 양자를 가지고 있기 때문에 전하는 유한하게 유지됩니다.비콤팩트 U(1) 게이지 군 이론에서 입자의 전하는 일반적으로 단일 단위의 정수배가 아닙니다.전하 양자화는 실험적으로 확실하기 때문에, 전자기력의 U(1) 게이지 그룹이 콤팩트하다는 것은 분명합니다.
GUT는 콤팩트한 U(1) 게이지 그룹으로 이어지므로 전하 양자화를 자기 모노폴로부터 논리적으로 독립적으로 보이는 방식으로 설명합니다.그러나 장거리에서 U(1) 게이지 그룹으로 분해되는 GUT에는 자기 모노폴이 있기 때문에 본질적으로 설명은 동일합니다.
그 논쟁은 위상학적인 것입니다.
- 게이지 필드 맵의 홀로노미(holonomy)는 게이지 그룹의 요소에 루프를 연결합니다.무한소 루프는 아이덴티티에 무한소로 가까운 그룹 요소에 매핑됩니다.
- 만약 당신이 우주에서 큰 구체를 상상한다면, 당신은 북극에서 시작하고 끝나는 무한소 고리를 다음과 같이 변형시킬 수 있습니다. 고리가 거대한 원이 될 때까지 서반구 위에 뻗은 다음 (북극에서 시작하고 끝나는) 동반구 위에 있는 동안 고리가 작은 고리로 다시 줄어들게 합니다.이것은 구를 라소잉(lassoing the sphere)이라고 불립니다.
- 라소잉은 루프의 연속이므로 홀로노미는 그것을 게이지 그룹의 연속 경로인 그룹 요소의 연속에 매핑합니다.Lassoing 시작 부분의 루프가 끝 부분의 루프와 동일하기 때문에 그룹의 경로는 닫힙니다.
- 라소잉 절차와 관련된 그룹 경로가 U(1) 주위를 감으면 구에는 자기 전하가 포함됩니다.라소잉을 하는 동안 홀로노미는 구를 통과하는 자속의 양에 따라 변합니다.
- 처음과 끝의 홀로노미가 동일성이기 때문에 총자속은 양자화됩니다.자기 전하는 권선 수 N에 비례하며, 구체를 통과하는 자기 플럭스는 2 πN/e와 같습니다.이 조건은 Dirac 양자화 조건이며, 장거리 U(1) 게이지 필드 구성이 일치해야 하는 위상 조건입니다.
- U(1) 게이지 그룹이 콤팩트한 Li 그룹을 깨뜨리는 것에서 나올 때, U(1) 그룹을 충분히 감는 경로는 큰 그룹에서 위상적으로 사소한 것입니다.비 U(1) 콤팩트 리 군에서 커버링 공간은 동일한 리 대수를 가지지만 모든 닫힌 고리가 수축 가능한 리 군입니다.거짓말 그룹은 균질하므로 그룹의 어떤 사이클도 동일성에서 시작하여 커버링 그룹으로의 리프트는 동일성의 리프트인 P에서 종료됩니다.루프를 두 바퀴 돌면 P2, 세3 바퀴 돌면 정체가 드러납니다.하지만 리프트가 쌓일 수 없기 때문에 정체성에 대한 리프트는 한정적으로 많을 뿐입니다.예를 들어 GUT 그룹이 SO(3)이고 커버링 그룹이 SU(2)이고, 임의의 루프를 두 바퀴 도는 것은 수축 가능하도록 루프를 횡단해야 하는 이 횟수가 적습니다.
- 이는 GUT 그룹에 연속적인 게이지 필드 구성이 있다는 것을 의미하며, U(1) 모노폴 구성이 U(1)에 머무르지 않는 비용으로 짧은 거리에서 스스로를 풀 수 있습니다.이것을 가능한 한 적은 에너지로 하려면, 당신은 모노폴의 중심이라고 불리는 한 점의 근처에 U(1) 게이지 그룹만 남겨두어야 합니다.중심핵의 바깥쪽에 있는 모노폴은 자기장 에너지만 가지고 있습니다.
따라서 디랙 모노폴은 콤팩트 U(1) 게이지 이론의 위상 결함입니다.GUT가 없을 때 결함은 특이점으로, 코어가 일 지점까지 수축됩니다.그러나 시공간에 어떤 종류의 단거리 조절자가 있을 때, 모노폴은 유한한 질량을 갖습니다.모노폴은 격자 U(1)에서 발생하며, 중심부 크기는 격자 크기입니다.일반적으로 단거리 조정기가 있을 때마다 발생할 것으로 예상됩니다.
끈이론
우주에서 양자중력은 조절자를 제공합니다.중력이 포함된 경우 모노폴 특이점은 블랙홀이 될 수 있으며, 큰 자기 전하와 질량의 경우 블랙홀 질량이 블랙홀 전하와 같아 자기 블랙홀의 질량이 무한하지 않습니다.만약 블랙홀이 호킹 복사에 의해 완전히 붕괴될 수 있다면, 가장 가벼운 하전 입자는 너무 무거울 수 없습니다.[32]가장 가벼운 모노폴은 자연 단위의 전하량보다 작거나 비슷한 질량을 가져야 합니다.
그래서 끈 이론이 유일하게 알려진 유일한 예인 일관된 홀로그래픽 이론에서는 항상 유한 질량의 단극이 존재합니다.일반적인 전자기학의 경우, 상단 질량 한계는 플랑크 질량과 거의 같은 크기이기 때문에 그다지 유용하지 않습니다.
수학 공식화
수학에서, (고전적) 게이지 필드는 시공간에 걸친 주 G-번들에 대한 연결로 정의됩니다.G는 게이지 그룹이며, 번들의 각 섬유에 개별적으로 작용합니다.
G-묶음의 연결부는 M의 근처 지점에서 섬유를 접착하는 방법을 알려줍니다.섬유 F에 작용하는 연속대칭 그룹 G에서 시작하여 그룹 요소를 각 극소 경로와 연관시킵니다.임의 경로에 따른 그룹 곱셈은 경로에 연결된 G 요소가 파이버 F에 작용하도록 함으로써 번들의 한 지점에서 다른 지점으로 이동하는 방법을 알려줍니다.
수학에서 묶음의 정의는 위상수학을 강조하기 위해 고안된 것이므로 연결의 개념은 뒤늦은 생각으로 추가됩니다.물리학에서 연결은 기본적인 물리적 대상입니다.대수적 위상학의 특성 클래스 이론에서 기본적인 관찰 중 하나는 자명하지 않은 주 번들의 많은 동형 구조가 그것에 대한 어떤 연결에 대한 어떤 다항식의 적분으로 표현될 수 있다는 것입니다.사소한 번들을 통한 연결은 결코 중요하지 않은 주 번들을 제공할 수 없습니다.
시공간이 ℝ이면 G-bundle의 가능한 모든 연결의 공간이 연결됩니다.그러나 시공간에서 시간과 같은 세계선을 제거할 때 어떤 일이 일어나는지 생각해 보세요.결과 시공간은 위상 구 S와2 동치입니다.
S2 위의 주요 G 묶음은 S를2 열린 2개의 공과 동형인 두 개의 차트로 덮음으로써 정의되며, 그들의 교집합은 스트립 S1×I와 동형입니다. 2개의 공은 동형 사소하고 스트립은 원 S와1 동형입니다.따라서 가능한 연결에 대한 위상 분류는 전이 함수를 분류하는 것으로 줄어듭니다.전이 함수는 스트립을 G로 매핑하고 스트립을 G로 매핑하는 다양한 방법은 G의 첫 번째 호모토피 그룹에 의해 제공됩니다.
따라서 G-묶음 공식에서 게이지 이론은 G가 단순히 연결되어 있지 않다면 디랙 모노폴을 인정합니다. 상수 경로(이미지가 하나의 점으로 구성된 경로)로 변형될 수 없는 그룹 주위를 도는 경로가 있을 때마다.양자화된 전하를 가진 U(1)는 단순히 연결되어 있지 않고 디랙 모노폴을 가질 수 있는 반면, 보편적 커버링 그룹인 ℝ은 단순히 연결되어 있고 양자화된 전하를 가지고 있지 않으며 디랙 모노폴을 인정하지 않습니다.수학적 정의는 물리학적 정의와 같으며, 디랙 이후에는 패치 단위로만 정의되는 게이지 필드가 허용되고, 게이지 변환 후에는 다른 패치의 게이지 필드가 접착됩니다.
총 자속은 다름아닌 주 묶음의 첫 번째 체른 수이며, 주 묶음의 선택에만 의존하며, 주 묶음에 대한 특정 연결에 의존하지 않습니다.다른 말로 하면 위상 불변입니다.
단극에 대한 이 논쟁은 순수한 U(1) 이론에 대한 라소 논쟁의 재진술입니다.몇 가지 방법으로 d ≥ 2로 d + 1차원으로 일반화합니다.한 가지 방법은 U(1)개의 단극이 d - 3의 시트가 되도록 모든 것을 여분의 차원으로 확장하는 것입니다.또 다른 방법은 호모토피 그룹 π(G)가 있는 한 점에서 위상 특이점의 유형을 조사하는 것입니다.
대통합론
최근 몇 년간, 새로운 종류의 이론들이 자기홀극의 존재를 암시하기도 했습니다.
1970년대 초, 전기약 이론과 강한 핵력의 수학의 발전에서 양자장 이론과 게이지 이론의 성공은 많은 이론가들이 대통합 이론(GUT)으로 알려진 하나의 이론으로 그것들을 결합하려고 시도하게 만들었습니다.몇 가지 GUT가 제안되었는데, 대부분 실제 자기 모노폴 입자의 존재를 암시했습니다.더 정확하게, GUTs는 다이온으로 알려진 입자의 범위를 예측했고, 그 중 가장 기본적인 상태는 모노폴이었습니다.GUTs에 의해 예측된 자기 모노폴의 전하는 이론에 따라 1 또는 2 gD입니다.
양자장 이론에서 나타나는 대부분의 입자는 불안정하며, 다양한 보존 법칙을 만족시켜야 하는 다양한 반응에서 다른 입자로 붕괴됩니다.안정한 입자는 붕괴하면서도 보존 법칙을 만족시키는 가벼운 입자가 없기 때문에 안정적입니다.예를 들어, 전자는 경입자 수가 1이고 전하 수가 1이고, 이러한 값을 보존하는 더 가벼운 입자는 없습니다.반면, 본질적으로 무거운 전자인 뮤온은 전자에 에너지 2양자를 더한 형태로 붕괴될 수 있기 때문에 안정적이지 않습니다.
이러한 GUT의 다이온은 또한 안정적이지만, 전혀 다른 이유에서입니다.다이온은 초기 우주의 조건들의 "동결" 또는 대칭 깨짐의 부작용으로 존재할 것으로 기대됩니다.이 시나리오에서 다이온은 원래의 디랙 이론에 따라 우주의 특정 영역의 진공 구성으로 인해 발생합니다.그들은 보존 상태 때문이 아니라 붕괴할 수 있는 더 단순한 위상 상태가 없기 때문에 안정적으로 유지됩니다.
이 특수 진공 구성이 존재하는 길이 척도를 시스템의 상관 길이라고 합니다.상관 길이는 인과율이 허용하는 것보다 클 수 없으므로 자기홀극을 만들기 위한 상관 길이는 적어도 팽창하는 우주의 메트릭에 의해 결정되는 지평선 크기만큼 커야 합니다.그 논리에 따르면, 대칭 파괴가 일어났을 때처럼 수평 부피당 적어도 하나의 자기 모노폴이 있어야 합니다.
빅뱅 이후의 사건들에 대한 우주론적 모델들은 지평선 부피가 무엇이었는지에 대한 예측을 하고, 이는 현재의 모노폴 밀도에 대한 예측으로 이어집니다.초기 모델들은 실험적 증거와 명백하게 모순되는 거대한 모노폴 밀도를 예측했습니다.[33][34]이것은 "단극 문제"라고 불렸습니다.그것의 널리 받아들여지는 해상도는 모노폴의 입자 물리학 예측의 변화가 아니라 현재 밀도를 추론하는 데 사용되는 우주론 모델의 변화였습니다.구체적으로, 최근의 우주 팽창 이론들은 예측된 자기홀극의 수를 인간이 한 번도 본 적이 없다는 것을 놀랄 만큼 충분히 작은 밀도로 대폭 줄였습니다.[35]"단극 문제"의 이 해결은 우주 팽창 이론의 성공으로 간주되었습니다. (그러나 물론 입자-물리학적 단극 예측이 정확하다면 주목할 만한 성공일 뿐입니다.)[36]이러한 이유로 1970년대와 80년대에 모노폴은 양성자 붕괴와 같은 GUT에 대한 다른 "접근 가능한" 예측과 함께 주요 관심사가 되었습니다.
이러한 GUT에 의해 예측된 다른 많은 입자들은 현재의 실험이 감지할 수 있는 능력을 넘어서는 것이었습니다.예를 들어, X와 Y 보손으로 알려진 광범위한 종류의 입자들은 전기약력과 강한 힘의 결합을 매개할 것으로 예측되지만, 이 입자들은 매우 무겁고 어떤 합리적인 입자 가속기가 만들어낼 수 있는 능력 이상입니다.
자기홀극 탐색
자기 모노폴에 대한 실험적 검색은 기존의 자기 모노폴을 감지하려는 것과 새로운 자기 모노폴을 생성하고 감지하려는 것, 두 가지 범주 중 하나로 분류될 수 있습니다.
자기 모노폴을 도선의 코일에 통과시키면 코일에 알짜 전류가 유도됩니다.순 유도 전류가 0인 자기 쌍극자 이상의 자극에는 해당되지 않으므로 자기 단극의 존재에 대한 명확한 검정으로 효과를 사용할 수 있습니다.유한한 저항을 갖는 와이어에서는 유도 전류가 에너지를 열로 빠르게 소멸시키지만 초전도 루프에서는 유도 전류가 수명이 길어집니다.매우 민감한 "초전도 양자 간섭 장치"(SQUID)를 사용하면 원칙적으로 단일 자기 모노폴도 감지할 수 있습니다.
표준 인플레이션 우주론에 따르면 인플레이션 이전에 생성된 자기홀극은 오늘날 극도로 낮은 밀도로 희석되었을 것입니다.자기 모노폴은 팽창 후 재가열 과정에서 열적으로 생성되었을 수도 있습니다.그러나 재가열 온도에 대한 전류 한계는 18배에 달하며 결과적으로 오늘날 자기 모노폴의 밀도는 이론에 의해 잘 제한되지 않습니다.
기존의 자기홀극에 대한 많은 연구가 있었습니다.1982년 2월 14일 밤에 블라스 카브레라 나바로가 기록한 감질나는 사건이 있지만([13]따라서 "발렌타인 데이 모노폴"이라고도 함),[37] 자기 모노폴의 존재에 대한 재현 가능한 증거는 없었습니다.이러한 사건의 부재는 핵자 10개당29 약 1개의 모노폴의 수에 상한을 둡니다.
1975년의 또 다른 실험은 P가 이끄는 연구팀에 의해 우주선 속에서 움직이는 자기홀극의 발견을 발표하는 결과를 낳았습니다. 뷰포드 프라이스.[12]프라이스는 나중에 그의 주장을 철회했고, 알바레즈는 대안적인 설명을 제시했습니다.[38]그의 논문에서 자기 모노폴에 의해 주장된 우주선 사건의 경로는 백금 핵이 먼저 오스뮴으로 붕괴되고, 이어서 탄탈륨으로 붕괴되는 경로로 재현될 수 있음을 증명했습니다.
고에너지 입자 충돌기는 자기 모노폴을 만들기 위해 사용되어 왔습니다.자기 전하의 보존 때문에, 자기 모노폴은 북쪽과 남쪽으로 한 쌍으로 만들어져야 합니다.에너지 보존 때문에 질량이 충돌하는 입자의 질량 중심 에너지의 절반 이하인 자기홀극만 생성할 수 있습니다.이 외에도, 이론적으로 고에너지 입자 충돌에서 자기 모노폴의 생성에 대해서는 거의 알려져 있지 않습니다.이것은 그들의 큰 자기 전하 때문이며, 이것은 모든 일반적인 계산 기법을 무효화합니다.결과적으로 충돌기 기반의 자기 모노폴 탐색은 아직 자기 모노폴의 질량에 대한 하한을 제공할 수 없습니다.그러나 이들은 에너지의 함수로서 쌍 생성의 확률(또는 횡단면)에 대한 상한을 제공할 수 있습니다.
대형 강입자 충돌기의 ATLAS 실험은 현재 드렐-얀 쌍 생산을 통해 생성된 1 디랙 전하와 2 디랙 전하의 자기 모노폴에 대한 가장 엄격한 단면 제한을 가지고 있습니다.웬디 테일러(Wendy Taylor)가 이끄는 팀은 이러한 입자들을 고도로 이온화(물질과의 상호작용이 대부분 이온화)할 뿐만 아니라 오래 산 것으로 정의하는 이론을 바탕으로 찾고 있습니다.2019년 ATLAS 검출기의 자기 모노폴 검색은 질량 중심 에너지가 13 TeV인 LHC Run 2 충돌에서 수집된 데이터에서 첫 번째 결과를 보고했는데, 이는 34.4 fb로−1 지금까지 분석된 데이터 세트 중 가장 큽니다.[39]
대형 강입자 충돌기(Large Hadron Collider)에 설치된 MoEDAL 실험은 현재 핵궤도 탐지기와 LHCb의 VELO 탐지기 주변의 알루미늄 막대를 이용하여 자기홀극과 대형 초대칭 입자를 탐색하고 있습니다.그것이 찾는 입자는 다양한 식별 기능과 함께 핵궤도 탐지기를 구성하는 플라스틱 시트에 손상을 입힙니다.게다가 알루미늄 막대는 충분히 천천히 움직이는 자기 모노폴을 잡을 수 있습니다.그런 다음 막대를 SQUID에 통과시켜 분석할 수 있습니다.
천체물리학자 이고르 노비코프는 거시 블랙홀의 장들이 잠재적인 자기홀극이며, 이는 아인슈타인-로젠 다리의 입구를 나타낸다고 주장합니다.[40]
축합물질계의 "단극"
2003년경부터, 다양한 응축 물질 물리학 그룹들은 서로 다른, 대부분 관련이 없는 현상을 설명하기 위해 "자기홀극"이라는 용어를 사용해 왔습니다.[18][19]
진정한 자기홀극은 새로운 기본입자가 될 것이고, 자기 ∇⋅B = 0에 대한 가우스의 법칙을 위반할 것입니다. 1931년 폴 디랙이 공식화한 전하양자화 법칙을 설명하는 데 도움이 되는 이런 종류의 단극은 실험에서 관찰된 적이 없습니다.
응축된 물질 그룹에 의해 연구된 모노폴은 이러한 특성을 가지고 있지 않습니다.그것들은 새로운 기본 입자가 아니라 일상적인 입자(양성자, 중성자, 전자, 광자)의 시스템에서 나타나는 현상입니다. 즉, 그것들은 준입자입니다.이들은 B장의 근원이 아니며(즉, ∇⋅B = 0), H장, "B*장"(초유체 소용돌이와 관련된) 또는 다양한 다른 양자장의 근원입니다.그것들은 대통합 이론이나 입자 물리학의 다른 측면과 직접적으로 관련이 없으며, 유사한 상황에 대한 연구가 관련된 수학적 분석이 타당하다는 것을 확인하는 데 도움이 되는 한 전하 양자화를 설명하는 데 도움이 되지 않습니다.[46]
응축된 물질 물리학에는 집단 행동이 스핀 얼음 물질을 [17][47][48][49]포함하여 특정한 측면에서 자기홀극과 유사한 신흥 현상으로 이어지는 많은 예가 있습니다.[5][50]진공에 존재하는 가상의 기본 모노폴과 혼동해서는 안 되지만, 그럼에도 불구하고 유사한 특성을 가지고 있으며 유사한 기술을 사용하여 조사할 수 있습니다.
일부 연구자들은 스핀 아이스에서 자기 모노폴 준입자의 조작을 "전기"라는 단어에 비유하여 자기력이라는 용어를 사용합니다.[51][52][50][53]
자기 모노폴 준입자에 대한 연구의 한 예는 2009년 9월 사이언스 저널에 발표된 논문으로, 연구자들은 자기 모노폴과 유사한 준입자의 관찰에 대해 설명했습니다.얼음 물질인 티타네이트 디스프로슘의 단결정은 0.6 켈빈에서 2.0 켈빈 사이의 온도로 냉각되었습니다.중성자 산란 관측을 사용하여 자기 모멘트는 디랙 끈과 유사한 튜브형 다발로 정렬되는 것으로 나타났습니다.각 튜브의 끝에 의해 형성된 결함에서 자기장은 모노폴처럼 보입니다.계의 대칭을 깨기 위해 가해진 자기장을 사용하여, 연구원들은 이 끈들의 밀도와 방향을 조절할 수 있었습니다.또한 이러한 준입자의 유효 가스로 인한 시스템의 열용량에 대한 기여도 설명되었습니다.[16][54]이 연구는 응축된 물질 물리학으로 2012년 유럽 물리학상을 수상했습니다.
또 다른 예로, Nature Physics 2011년 2월 11일호에 실린 논문은 스핀 얼음에서 긴 수명의 자기 모노폴 준입자 전류의 생성과 측정에 대해 설명하고 있습니다.저자들은 0.36K의 티탄산 디스프로슘 결정에 자기장 펄스를 인가함으로써 수 분 동안 지속되는 완화된 자기 전류를 만들었습니다.그들은 민감한 증폭기에 연결된 솔레노이드에 유도된 기전력을 이용하여 전류를 측정하고, Onsager에 따르는 점상 전하의 화학적 운동 모델을 이용하여 전류를 정량적으로 묘사했습니다.캐리어 해리와 재결합의 빈 메커니즘.따라서 그들은 스핀 아이스에서 모노폴 운동의 미시적 매개 변수를 도출하고 자유 전하와 속박된 자기 전하의 뚜렷한 역할을 확인했습니다.[53]
초유체에는 초유체 소용돌이성과 관련된 B*장이 있는데, 이는 수학적으로 자기 B-장과 유사합니다.유사성 때문에, B*장은 "합성 자기장"이라고 불립니다.2014년 1월, 스피너 보스-아인슈타인 응축수에서 B*장을 위한 모노폴 준입자가[55] 생성되어 연구되었다고 보고되었습니다.[6]이것은 양자장 이론에 의해 지배되는 시스템 내에서 관찰되는 준자기 모노폴의 첫 번째 예를 구성합니다.[46]
참고 항목
메모들
- ^ 자기 전하가 웨버를 단위로 하는 규약에 대해서는 Jackson 1999를 참조하십시오.특히 맥스웰 방정식의 경우 섹션 6.11, 방정식 (6.150), 273페이지를 참조하고 로렌츠 힘 법칙의 경우 290페이지, 연습 6.17(a)를 참조합니다.자기 전하가 암페어 미터 단위를 갖는 규약에 대해서는 arXiv:physics/0508099v1, eqn(4)을 참조하십시오.
참고문헌
- ^ Hooper, Dan (October 6, 2009). Dark Cosmos: In Search of Our Universe's Missing Mass and Energy. Harper Collins. ISBN 9780061976865 – via Google Books.
- ^ "Particle Data Group summary of magnetic monopole search" (PDF). lbl.gov.
- ^ Wen, Xiao-Gang; Witten, Edward, "초끈 모형의 전기 및 자기 전하", 핵물리학 B, 261권, pp. 651-677
- ^ S. 콜먼, 대칭의 측면에서 재인쇄된 "50년 후의 자기 모노폴"
- ^ a b c Castelnovo, C.; Moessner, R.; Sondhi, S. L. (January 3, 2008). "Magnetic monopoles in spin ice". Nature. 451 (7174): 42–45. arXiv:0710.5515. Bibcode:2008Natur.451...42C. doi:10.1038/nature06433. PMID 18172493. S2CID 2399316.
- ^ a b c Ray, M. W.; Ruokokoski, E.; Kandel, S.; Möttönen, M.; Hall, D. S. (2014). "Observation of Dirac monopoles in a synthetic magnetic field". Nature. 505 (7485): 657–660. arXiv:1408.3133. Bibcode:2014Natur.505..657R. doi:10.1038/nature12954. ISSN 0028-0836. PMID 24476889. S2CID 918213.
- ^ Chisholm, Hugh (June 26, 2018). "The Encyclopaedia Britannica: A Dictionary of Arts, Sciences, Literature and General Information". [Cambridge] University Press – via Google Books.
- ^ Magie, William Francis (June 26, 2018). "Principles of Physics: Designed for Use as a Textbook of General Physics". Century Company – via Google Books.
- ^ Pierre Curie (1894). "Sur la possibilité d'existence de la conductibilité magnétique et du magnétisme libre" [On the possible existence of magnetic conductivity and free magnetism]. Séances de la Société Française de Physique (in French). Paris: 76–77.
- ^ Dirac, Paul (1931). "Quantised Singularities in the Electromagnetic Field". Proceedings of the Royal Society A. London. 133 (821): 60. Bibcode:1931RSPSA.133...60D. doi:10.1098/rspa.1931.0130.
- ^ a b 캘리포니아 대학교 버클리 캠퍼스의 Robert Littlejohn의 강의노트, 2007-08
- ^ a b Price, P. B.; Shirk, E. K.; Osborne, W. Z.; Pinsky, L. S. (August 25, 1975). "Evidence for Detection of a Moving Magnetic Monopole". Physical Review Letters. 35 (8): 487–490. Bibcode:1975PhRvL..35..487P. doi:10.1103/PhysRevLett.35.487.
- ^ a b Cabrera, Blas (May 17, 1982). "First Results from a Superconductive Detector for Moving Magnetic Monopoles". Physical Review Letters. 48 (20): 1378–1381. Bibcode:1982PhRvL..48.1378C. doi:10.1103/PhysRevLett.48.1378.
- ^ 밀턴 p. 60
- ^ a b Polchinski, Joseph (February 1, 2004). "Monopoles, Duality, and String Theory". International Journal of Modern Physics A. 19 (supp01): 145–154. arXiv:hep-th/0304042. Bibcode:2004IJMPA..19S.145P. doi:10.1142/S0217751X0401866X. S2CID 831833.
- ^ a b "Magnetic Monopoles Detected in a Real Magnet for the First Time". Science Daily. September 4, 2009. Retrieved September 4, 2009.
- ^ a b 실험실에서 자기 모노폴과 다른 외피를 만들기, Symmetry Breaking, 2009년 1월 29일.2009년 1월 31일 회수.
- ^ a b 2009년 9월 3일, 물리학 세계, "가시 속에서 발견된 자기홀극""[이 분야의 연구자인] 존스 홉킨스 대학의 올레크 체르니쇼프는 이 이론과 실험이 스핀 아이스에 특화되어 있으며 디랙이 예측한 것처럼 자기홀극을 밝힐 가능성은 낮다고 경고합니다."
- ^ a b Gibney, Elizabeth (January 29, 2014). "Quantum cloud simulates magnetic monopole". Nature. doi:10.1038/nature.2014.14612. S2CID 124109501.
This is not the first time that physicists have created monopole analogues. In 2009, physicists observed magnetic monopoles in a crystalline material called spin ice, which, when cooled to near-absolute zero, seems to fill with atom-sized, classical monopoles. These are magnetic in a true sense, but cannot be studied individually. Similar analogues have also been seen in other materials, such as in superfluid helium. ... Steven Bramwell, a physicist at University College London who pioneered work on monopoles in spin ices, says that the [2014 experiment led by David Hall] is impressive, but that what it observed is not a Dirac monopole in the way many people might understand it. 'There's a mathematical analogy here, a neat and beautiful one. But they're not magnetic monopoles.'
- ^ Griffiths, David J. (2013). Introduction to electrodynamics (Fourth ed.). Boston: Pearson. p. 339. ISBN 978-0-321-85656-2.
- ^ Parker, C. B. (1994). McGraw-Hill Encyclopaedia of Physics (2nd ed.). McGraw-Hill. ISBN 978-0-07-051400-3.
- ^ Mansfield, M.; O'Sullivan, C. (2011). Understanding Physics (4th ed.). John Wiley & Sons. ISBN 978-0-47-0746370.
- ^ a b Moulin, F. (2001). "Magnetic monopoles and Lorentz force". Nuovo Cimento B. 116 (8): 869–877. arXiv:math-ph/0203043. Bibcode:2001NCimB.116..869M.
- ^ Rindler, Wolfgang (November 1989). "Relativity and electromagnetism: The force on a magnetic monopole". American Journal of Physics. 57 (11): 993–994. Bibcode:1989AmJPh..57..993R. doi:10.1119/1.15782.
- ^ Heras, J. A.; Baez, G. (2009). "The covariant formulation of Maxwell's equations expressed in a form independent of specific units". European Journal of Physics. 30 (1): 23–33. arXiv:0901.0194. Bibcode:2009EJPh...30...23H. doi:10.1088/0143-0807/30/1/003. S2CID 14707446.
- ^ Moulin, F. (2002). "Magnetic monopoles and Lorentz force". Nuovo Cimento B. 116 (8): 869–877. arXiv:math-ph/0203043. Bibcode:2001NCimB.116..869M.
- ^ Shanmugadhasan, S (1952). "The Dynamical Theory of Magnetic Monopoles". Canadian Journal of Physics. 30 (3): 218–225. Bibcode:1952CaJPh..30..218S. doi:10.1139/p52-021.
- ^ Fryberger, David (February 1989). "On Generalized Electromagnetism and Dirac Algebra" (PDF). Foundations of Physics. 19 (2): 125–159. Bibcode:1989FoPh...19..125F. CiteSeerX 10.1.1.382.3733. doi:10.1007/bf00734522. S2CID 13909166.
- ^ a b c 잭슨 1999, 섹션 6.11.
- ^ Farmelo, Graham (2009). The Strangest Man: The Hidden Life of Paul Dirac, Quantum Genius. London: Faber and Faber. pp. 185–9. ISBN 978-0-571-22278-0. [미국에서 가장 이상한 남자로 출간: 폴 디랙의 숨겨진 삶, 미스틱 오브 더 아톰.ISBN 978-0-465-01827-7]
- ^ Jackson 1999, 섹션 6.11, 등식 (6.153), 페이지 275
- ^ Arkani-Hamed, Nima; Motl, Luboš; Nicolis, Alberto; Vafa, Cumrun (2007). "The string landscape, black holes and gravity as the weakest force". Journal of High Energy Physics. 2007 (6): 060. arXiv:hep-th/0601001. Bibcode:2007JHEP...06..060A. doi:10.1088/1126-6708/2007/06/060. S2CID 16415027.
- ^ Zel'dovich, Ya. B.; Khlopov, M. Yu. (1978). "On the concentration of relic monopoles in the universe". Phys. Lett. B79 (3): 239–41. Bibcode:1978PhLB...79..239Z. doi:10.1016/0370-2693(78)90232-0.
- ^ Preskill, John (1979). "Cosmological production of superheavy magnetic monopoles" (PDF). Phys. Rev. Lett. 43 (19): 1365–1368. Bibcode:1979PhRvL..43.1365P. doi:10.1103/PhysRevLett.43.1365.
- ^ Preskill, John (1984). "Magnetic Monopoles". Annu. Rev. Nucl. Part. Sci. 34 (1): 461–530. Bibcode:1984ARNPS..34..461P. doi:10.1146/annurev.ns.34.120184.002333.
- ^ 리스, 마틴.(1998).Before the Beginning (뉴욕: Basic Books) p. 185 ISBN 0-201-15142-1
- ^ Brumfiel, Geoff (May 6, 2004). "Physics: The waiting game". Nature. 429 (6987): 10–11. Bibcode:2004Natur.429...10B. doi:10.1038/429010a. PMID 15129249. S2CID 4425841.
- ^ Alvarez, Luis W. "Analysis of a Reported Magnetic Monopole". In Kirk, W. T. (ed.). Proceedings of the 1975 international symposium on lepton and photon interactions at high energies. International symposium on lepton and photon interactions at high energies, Aug 21, 1975. p. 967. Archived from the original on February 4, 2009. Retrieved May 25, 2008.
- ^ Aad, Georges el al (2020). "Search for magnetic monopoles and stable high-electric-charge objects in 13 TeV proton-proton collisions with the ATLAS detector". Phys. Rev. Lett. 124 (3): 031802. arXiv:1905.10130. Bibcode:2020PhRvL.124c1802A. doi:10.1103/PhysRevLett.124.031802. PMID 32031842.
- ^ "Could wormholes really exist?". All About Space. No. 24. April 2014.
If the structures of the magnetic fields appear to be magnetic monopoles, that are macroscopic in size, then this is a wormhole.
[저자 누락] - ^ "전자장의 양자화된 특이점들" 폴 디랙, 왕립학회 회보, 1931년 5월 29일.2014년 2월 1일 검색.
- ^ Magnetic Monopoles, Particle data group 보고서, D에 의해 2015년 8월 업데이트됨.밀스테드와 E.J. 와인버그."현재까지 자기 전하를 가지고 있는 이국적인 입자에 대한 확인된 관찰은 없습니다."
- ^ Arttu Rajantie (2016). "The search for magnetic monopoles". Physics Today. 69 (10): 40. Bibcode:2016PhT....69j..40R. doi:10.1063/PT.3.3328.
Magnetic monopoles have also inspired condensed-matter physicists to discover analogous states and excitations in systems such as spin ices and Bose–Einstein condensates. However, despite the importance of those developments in their own fields, they do not resolve the question of the existence of real magnetic monopoles. Therefore, the search continues.
- ^ T. Ollikainen; K. Tiurev; A. Blinova; W. Lee; D. S. Hall; M. Möttönen (2017). "Experimental Realization of a Dirac Monopole through the Decay of an Isolated Monopole". Phys. Rev. X. 7 (2): 021023. arXiv:1611.07766. Bibcode:2017PhRvX...7b1023O. doi:10.1103/PhysRevX.7.021023. S2CID 54028181.
- ^ Yakaboylu, E.; Deuchert, A.; Lemeshko, M. (December 6, 2017). "Emergence of Non-Abelian Magnetic Monopoles in a Quantum Impurity Problem". Physical Review Letters. 119 (23): 235301. arXiv:1705.05162. Bibcode:2017PhRvL.119w5301Y. doi:10.1103/PhysRevLett.119.235301. PMID 29286703. S2CID 206304158.
- ^ a b Elizabeth Gibney (January 29, 2014). "Quantum cloud simulates magnetic monopole". Nature. doi:10.1038/nature.2014.14612. S2CID 124109501.
- ^ Zhong, Fang; Nagosa, Naoto; Takahashi, Mei S.; Asamitsu, Atsushi; Mathieu, Roland; Ogasawara, Takeshi; Yamada, Hiroyuki; Kawasaki, Masashi; Tokura, Yoshinori; Terakura, Kiyoyuki (2003). "The Anomalous Hall Effect and Magnetic Monopoles in Momentum Space". Science. 302 (5642): 92–95. arXiv:cond-mat/0310232. Bibcode:2003Sci...302...92F. doi:10.1126/science.1089408. PMID 14526076. S2CID 41607978.
- ^ Qi, X.-L.; Li, R.; Zang, J.; Zhang, S.-C. (2009). "Inducing a Magnetic Monopole with Topological Surface States". Science. 323 (5918): 1184–1187. arXiv:0811.1303. Bibcode:2009Sci...323.1184Q. doi:10.1126/science.1167747. PMID 19179491. S2CID 206517194.
- ^ "Artificial magnetic monopoles discovered". sciencedaily.com.
- ^ a b Bramwell, S. T.; Giblin, S. R.; Calder, S.; Aldus, R.; Prabhakaran, D.; Fennell, T. (October 15, 2009). "Measurement of the charge and current of magnetic monopoles in spin ice". Nature. 461 (7266): 956–959. arXiv:0907.0956. Bibcode:2009Natur.461..956B. doi:10.1038/nature08500. PMID 19829376. S2CID 4399620.
- ^ "'Magnetricity' Observed And Measured For First Time". Science Daily. October 15, 2009. Retrieved June 10, 2010.
- ^ M.J.P. Gingras (2009). "Observing Monopoles in a Magnetic Analog of Ice". Science. 326 (5951): 375–376. arXiv:1005.3557. doi:10.1126/science.1181510. PMID 19833948. S2CID 31038263.
- ^ a b Giblin, S. R.; Bramwell, S. T.; Holdsworth, P. C. W.; Prabhakaran, D.; Terry, I. (February 13, 2011). "Creation and measurement of long-lived magnetic monopole currents in spin ice". Nature Physics. 7 (3): 252–258. Bibcode:2011NatPh...7..252G. doi:10.1038/nphys1896.
- ^ D.J.P. Morris; D.A. Tennant; S.A. Grigera; B. Klemke; C. Castelnovo; R. Moessner; C. Czter-nasty; M. Meissner; K.C. Rule; J.-U. Hoffmann; K. Kiefer; S. Gerischer; D. Slobinsky & R.S. Perry (September 3, 2009) [2009-07-09]. "Dirac Strings and Magnetic Monopoles in Spin Ice Dy2Ti2O7". Science. 326 (5951): 411–4. arXiv:1011.1174. Bibcode:2009Sci...326..411M. doi:10.1126/science.1178868. PMID 19729617. S2CID 206522398.
- ^ Pietilä, Ville; Möttönen, Mikko (2009). "Creation of Dirac Monopoles in Spinor Bose–Einstein Condensates". Phys. Rev. Lett. 103 (3): 030401. arXiv:0903.4732. Bibcode:2009PhRvL.103c0401P. doi:10.1103/physrevlett.103.030401. PMID 19659254.
서지학
- Atiyah, M. F.; Hitchin, N. (1988). The Geometry and Dynamics of Magnetic Monopoles. Princeton University Press. ISBN 0-691-08480-7.
- Brau, C. A. (2004). Modern Problems in Classical Electrodynamics. Oxford University Press. ISBN 978-0-19-514665-3.
- Hitchin, N. J.; Murray, M. K. (1988). "Spectral curves and the ADHM method". Comm. Math. Phys. 114 (3): 463–474. Bibcode:1988CMaPh.114..463H. doi:10.1007/BF01242139. S2CID 123573860.
- Jackson, J. D. (1999). Classical Electrodynamics (3rd ed.). Wiley. ISBN 978-0-471-30932-1.
- Lacava, F. (2022). Classical Electrodynamics: From Image Charges to the Photon Mass and Magnetic Monopoles (2nd ed.). Springer. ISBN 978-3-031-05098-5.
- Lechner, K. (2018). Classical Electrodynamics: A Modern Perspective. Springer. ISBN 978-3-319-91808-2.
- Lochak, G.; Stumpf, H. (2015). The Leptonic Magnetic Monopole: Theory and Experiments. Elsevier. ISBN 978-0-12-802463-8.
- Milton, K. A. (2006). "Theoretical and experimental status of magnetic monopoles". Reports on Progress in Physics. 69 (6): 1637–1711. arXiv:hep-ex/0602040. Bibcode:2006RPPh...69.1637M. doi:10.1088/0034-4885/69/6/R02. S2CID 119061150.
- Shnir, Y. M. (2005). Magnetic Monopoles. Springer. ISBN 978-3-540-25277-1.
- Sutcliffe, P. M. (1997). "BPS monopoles". Int. J. Mod. Phys. A. 12 (26): 4663–4706. arXiv:hep-th/9707009. Bibcode:1997IJMPA..12.4663S. doi:10.1142/S0217751X97002504. S2CID 16765577.
- Vonsovsky, S. V. (1975). Magnetism of Elementary Particles. Mir Publishers.
외부 링크
이 문서에는 Creative Commons Attribution/Share-Alike License 및 GNU Free Documentation License에 따라 라이센스가 부여된 의 자료가 통합되어 있습니다.




















































![{\displaystyle f_{\alpha }=\left[q_{\mathrm {e} }F_{\alpha \beta }+q_{\mathrm {m} }{{\tilde {F}}_{\alpha \beta }}\right]{\frac {v^{\beta }}{c}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/169d4547315ead04de4cebbd248c3efa737c2725)
![{\displaystyle f_{\alpha }=\left[q_{\mathrm {e} }F_{\alpha \beta }+{\frac {q_{\mathrm {m} }}{\mu _{0}c}}{{\tilde {F}}_{\alpha \beta }}\right]v^{\beta }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2cbbb0f18649c481e798363d1aa6a84ca1d9392e)
![{\displaystyle f_{\alpha }=\left[q_{\mathrm {e} }F_{\alpha \beta }+{\frac {q_{\mathrm {m} }}{c}}{{\tilde {F}}_{\alpha \beta }}\right]v^{\beta }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b9a14a873a8fba2d419f5bb2690bc792f88b14d5)





















