리만 가설
Riemann hypothesis
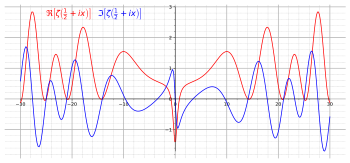

곡선은 ζ(1/2 - 30 i) = -0.12 + 0.58 i에서 t = -30 시작하여 ζ(1/2 + 30 i) = -0.12 - 0.58 i에서 시작점 아래 대칭적으로 끝납니다.
원점(0,0)이 통과할 때 궤도를 따라 6개의 ζ 0이 발견되며, 이는 허수부 Im(s) = ±14.135, ±21.022 및 ±25.011에 해당합니다.
| 밀레니엄 현상 문제 |
|---|
수학에서 리만 가설(Riemann hypothesis)은 리만 제타 함수가 음수인 짝수와 실수가 있는 복소수에서만 0을 갖는다는 가정입니다. 1/2. 많은 사람들이 순수수학에서 가장 중요한 미해결 문제라고 생각합니다.[2] 소수의 분포에 대한 결과를 내포하기 때문에 정수론에 큰 관심을 가지고 있습니다. 베른하르트 리만(Bernhard Riemann, 1859)에 의해 제안되었으며, 그 이름을 따서 명명되었습니다.
리만 가설과 그 일반화 중 일부는 골드바흐 추측과 쌍둥이 소수 추측과 함께 데이비드 힐버트의 23개 미해결 문제 목록에서 힐버트의 여덟 번째 문제를 구성합니다. 그것은 클레이 수학 연구소의 밀레니엄 상 문제 중 하나이기도 합니다. 그 중 하나를 해결하는 사람에게 백만 달러를 제공합니다. 이 이름은 유한장 위의 곡선에 대한 리만 가설과 같이 밀접하게 관련된 유사체에도 사용됩니다.
리만 제타 함수 ζ(s)는 인수가 1이 아닌 복소수일 수 있고 값도 복소수인 함수입니다. 음수 짝수 정수에서 0을 갖습니다. 즉, s가 -2, -4, -6, ... 중 하나일 때 ζ = 0입니다. 이것들은 사소한 0이라고 불립니다. 제타 함수는 s의 다른 값에 대해서도 0이며, 이 값을 non-trivial 0이라고 합니다. 리만 가설은 이들 자명하지 않은 0의 위치와 관련이 있으며, 다음과 같이 기술합니다.
리만 제타 함수의 모든 자명하지 않은 0의 실수 부분은 1/2입니다.
따라서 가설이 옳다면 모든 자명하지 않은 0은 복소수 1/2 + it로 구성된 임계선 위에 놓이게 되는데, 여기서 t는 실수이고 i는 허수 단위입니다.
리만 제타 함수
리만 제타 함수는 절대 수렴 무한급수에 의해 실수부가 1보다 큰 복소수에 대해 정의됩니다.
레온하르트 오일러는 이미 1730년대에 바젤 문제에 대한 그의 해결책과 함께 s의 실수 값에 대해 이 급수를 고려했습니다. 그는 또한 그것이 오일러 곱과 같다는 것을 증명했습니다.
여기서 무한 곱은 모든 소수 p에 걸쳐 확장됩니다.[3]
리만 가설은 이 급수와 오일러 곱의 수렴 영역을 벗어난 0을 논의합니다. 가설을 이해하기 위해서는 함수를 분석적으로 계속하여 모든 복합체에 대해 유효한 형태를 얻을 필요가 있습니다. 제타 함수는 동형이기 때문에 이 분석적 연속을 수행하는 방법에 대한 모든 선택 사항은 동일성 정리에 의해 동일한 결과로 이어질 것입니다. 이 연속의 첫 번째 단계는 제타 함수와 디리클레타 함수에 대한 급수가 관계를 만족하는 것을 관찰하는 것입니다.
두 급수의 수렴 영역 내에 있습니다. 그러나 오른쪽의 제타 함수 급수는 s의 실수 부분이 1보다 클 때뿐만 아니라 일반적으로 s가 양의 실수 부분을 가질 때 수렴합니다. 따라서 제타 함수는ηs) /( - /) 2s}}}로 재정의할 수 있으며, Re(s) > 1에서 더 큰 도메인으로 확장됩니다. 단, - / /2^{s}}가 0인 은 제외됩니다. = 1+ π in / log 2 {\displaystyle s= 1+2\pi in /\log 2}입니다. 여기서 n {\displaystyle n}은 0이 아닌 정수일 수 있습니다. 제한을 적용하여 제타 함수를 이러한 값으로도 확장할 수 있습니다(Dirichlet eta function § Landau의 ζ = η/0 문제 및 솔루션 참조). s = 1에서 단순 극을 제외하고 양의 실수부를 갖는 모든 s 값에 대해 유한한 값을 제공합니다.
스트립 0 < Re(s) < 1 에서 제타 함수의 이 확장은 함수 방정식을 만족합니다.
그런 다음 이 방정식을 스트립 외부에 적용하고 s가 양이 아닌 실수부(및 s ≠ 0)를 가질 때마다 ζ(s)가 방정식의 오른쪽과 같도록 하여 나머지 모든 0이 아닌 복소수(Re(s) ≤ 0 및 s ≠ 0)에 대한 ζ(s)를 정의할 수 있습니다.
s가 음의 짝수이면 ζ = 0이 되는데, 이는 sin(sin) 인자가 사라지기 때문입니다. 이들은 제타 함수의 사소한 0입니다. (s가 양의 짝수이면 이 인수는 적용되지 않습니다. 왜냐하면 사인 함수의 0은 음의 정수 인수를 사용하기 때문에 감마 함수의 극에 의해 취소되기 때문입니다.)
값 ζ(0) = -1/2는 함수 방정식에 의해 결정되는 것이 아니라 0에 가까워질 때 ζ의 한계 값입니다. 함수 방정식은 또한 제타 함수가 자명한 0 이외의 음의 실수 부분을 갖는 0이 없으므로 모든 자명하지 않은 0은 s가 0과 1 사이의 실수 부분을 갖는 임계 스트립에 놓여 있음을 의미합니다.
기원.
... Essisthr Wahrcheinlich, dass alle Wurzeln reellsind. 히어본 웨얼레르는 스트렝거 베베이스 주 hen첸의 알레르딩; 이흐하베 인디스 다이 오푸충 데셀벤 나흐티겐 플뤼히티겐 베르게블리첸 베르수첸 보를레이그베이 시테 젤라센, 데어 퓌르덴 뉘흐스텐 eck크 마이너 운터수충 엔트베를리히 쉬엔.
... 모든 뿌리가 진짜일 가능성이 매우 높습니다. 물론 사람들은 여기서 엄격한 증거를 원할 것입니다. 저는 잠깐의 헛수고 끝에 당분간 이에 대한 조사는 잠정적으로 보류했습니다. 제 조사의 즉각적인 목적을 위해 불필요한 것으로 보이기 때문입니다.— Riemann's statement of the Riemann hypothesis, from (Riemann 1859). (He was discussing a version of the zeta function, modified so that its roots (zeros) are real rather than on the critical line.)
리만이 사망했을 때, 그의 논문 중에서 "문제의 함수인 ζ의 이러한 성질들은 그것의 표현으로부터 추론되지만, 나는 그것을 출판할 만큼 충분히 단순화하는 데 성공하지 못했습니다."라는 메모가 발견되었습니다. 우리는 여전히 그 표현이 무엇인지 전혀 알지 못합니다. 그가 단순히 발음한 성질에 관해서는, 내가 그것들 중 하나를 제외한 모든 것을 증명할 수 있을 때까지 약 30년이 걸렸습니다 [리만 가설 자체].
— Jacques Hadamard, The Mathematician's Mind, VIII. Paradoxical Cases of Intuition
제타 함수와 그 0을 연구한 리만의 원래 동기는 주어진 수 x보다 작거나 같은 수의 소수 π(x)에 대한 그의 명시적 공식에서의 그들의 발생 때문이었습니다. 그의 공식은 관련 함수의 관점에서 주어졌습니다.
소수와 소수를 x까지 세고 소수를n pas로 세는 것. 1 ⁄n. 이 함수로부터 뫼비우스 반전 공식을 이용하여 소수를 구할 수 있습니다.
여기서 μ는 뫼비우스 함수입니다. 리만의 공식은 다음과 같습니다.
합이 제타 함수의 사소한 0 위에 있고 π는 불연속점에서의 값을 상한과 하한의 평균으로 대체하는 약간 수정된 버전의 π입니다.
리만 공식의 합은 절대 수렴적인 것이 아니라, 그들의 허수부의 절대값의 순서대로 0 ρ을 취함으로써 평가될 수 있습니다. 첫 번째 항에서 발생하는 함수 li는 발산적분의 코시 주값으로 주어진 (비상향) 로그 적분 함수입니다.
제타 함수의 0을 포함하는 용어 li(x)는 li가 0과 1에 분기점을 가지고 있으므로 정의에 약간의 주의가 필요하며 Re(ρ) > 0 영역의 복잡한 변수 ρ에서 분석적 연속에 의해 (x > 1의 경우) 정의됩니다. 즉, 이들은 Ei(ρ 로그 x)로 간주되어야 합니다. 다른 항들도 0에 해당합니다. 지배항 li(x)는 다중도 -1의 0으로 간주되는 s = 1의 극에서 나오고, 나머지 작은 항들은 사소한 0에서 나옵니다. 이 시리즈의 처음 몇 항의 합계에 대한 그래프는 Riesel & Göhl(1970) 또는 Jagier(1977)를 참조하십시오.
이 공식은 리만 제타 함수의 0이 "예상" 위치를 중심으로 한 소수의 진동을 제어한다는 것을 말합니다. 리만은 제타 함수의 trivial이 아닌 0이 s = 1/2 + 그것을 중심으로 대칭적으로 분포되어 있다는 것을 알고 있었고, 모든 trivial이 아닌 0은 0 ≤ Re(s) ≤ 1의 범위에 있어야 한다는 것을 알고 있었습니다. 그는 0 중 몇 개가 실수부 1/2의 임계선에 놓여 있다는 것을 확인하고 모두 그렇게 한다고 제안했는데, 이것이 리만 가설입니다.
수학에서 겉보기에는 관련이 없어 보이는 두 분야, 즉 이산을 연구하는 수론과 연속적인 과정을 다루는 복소해석학을 연결하는 것은 너무나 놀라운 일이기 때문에 대부분의 수학자들의 상상을 사로잡은 결과입니다(버튼 2006, 페이지 376).
결과들
리만 가설의 실제적인 용도에는 리만 가설 하에서 참이라고 알려진 많은 명제들과 리만 가설과 동등하다고 보여질 수 있는 명제들이 포함됩니다.
소수의 분포
주어진 수보다 작은 소수의 수에 대한 리만의 명시적 공식은 리만 제타 함수의 0에 대한 합의 관점에서, 그들의 예상 위치 주변의 소수의 진동의 크기는 제타 함수의 0의 실수 부분에 의해 제어된다는 것을 말합니다. 특히 소수 정리에서 오차항은 0의 위치와 밀접한 관련이 있습니다. 예를 들어, β가 0의 실수 부분의 상한일 경우,π ()- () =O(xβ log x). {\displaystyle \pi (x)-\operatorname {li} (x)=1/2 ≤ β ≤ 1인 것은 이미 알려져 있습니다.[5]
본 코흐(Von Koch, 1901)는 리만 가설이 소수 정리의 오류에 대한 "최상의 가능한" 경계를 내포한다는 것을 증명했습니다. 쇤펠트(Soenfeld, 1976)에 의한 Koch의 결과의 정확한 버전은 리만 가설이 다음을 의미한다고 말합니다.
여기서π(x) \pi(x)}는 소수 counting이고 li(x {\displaystyle\operatorname {li}(x)}는 로그 적분 함수이며, 로그 (x) {\displaystyle \log(x)}는 x의 자연 로그입니다.
쇤펠트(Soenfeld, 1976)는 또한 리만 가설이 다음을 암시한다는 것을 보여주었습니다.
여기서ψ(x) psi(x)}는 Chebyshev의 두 번째 함수입니다.
두데크(2014)는 리만 가설이 ≥ 2 {\x\geq 2}에 대하여 만족하는 p p}가 존재함을 의미함을 증명했습니다.
- - x로그 x < p ≤ x {}} { x < p\leq x}.
x를 충분히 크게 할 경우 상수 4/ π은 (1 + ε)으로 감소할 수 있습니다. 이것은 크라메르 정리의 명시적인 버전입니다.
산술 함수의 성장
리만 가설은 위의 소수 계산 함수 외에도 많은 다른 산술 함수의 성장에 대한 강한 경계를 암시합니다.
한 가지 예는 뫼비우스 함수 μ를 포함합니다. 그 방정식은 다음과 같다.
는 실수 부분이 1/2보다 큰 모든 것에 대해 유효하며, 우변의 합은 리만 가설과 동등합니다. 이로부터 우리는 또한 메르텐스 함수가 다음과 같이 정의될 경우
라는 주장.
모든 긍정적인 ε은 리만 가설과 동등하기 때문입니다(J. E. Littlewood, 1912; 예를 들어 Titchmarsh(1986)의 14.25항 참조). (이 기호들의 의미에 대해서는 Big O 표기법을 참조하십시오.) 차수 n Redheffer 행렬의 행렬식은 M(n)과 같으므로, 이러한 행렬식의 성장에 대한 조건으로서 리만 가설도 말할 수 있습니다. Littlewood의 결과는 Edmund Landau,[6] Edward Charles Titchmarsh,[7] Helmut Maier와 Hugh Montgomery,[8] Kannan Soundararajan에 의해 그 이후로 여러 차례 개선되었습니다.[9] Soundararajan의 결과는
Odlyzko & ter Riele(1985)가 약간 더 강한 Mertens 추측을 반증했기 때문에, 리만 가설은 M의 성장에 다소 엄격한 제약을 가합니다.
또 다른 밀접한 관련이 있는 결과는 Björner(2011)에 기인합니다. 리만 가설은 가분성 하에서 정수의 격자에 의해 결정되는 단순 복합체의 오일러 특성이 ϵ > 0\epsilon > 0에 o 1/ +ϵ) ^{1/ 2epsilon })}라는 문장과 동일하다는 것입니다(입사 대수 참조).
리만 가설은 μ(n)을 제외한 다른 산술 함수의 성장 속도에 대한 다른 많은 추측과 동등합니다. 대표적인 예는 σ(n)이 시그마 함수이면 다음과 같은 로빈의 정리입니다.
그리고나서
리만 가설이 참일 경우에만 모든 n > 5040에 대하여, 여기서 γ은 오일러-마스케로니 상수입니다.
2002년 제프리 라가리아스는 리만 가설이 다음 문장과 동일하다는 것을 증명했습니다.
모든 자연수 n > 1에 대하여 는 n번째 조화수입니다.[11]
리만 가설 또한 부등식일 경우에만 참입니다.
는 모든 n개의 ≥ p#에 대하여 참이며, 여기서 φ(n)은 오일러의 토텐티브 함수이고 p#은 첫 번째 120569개 소수들의 곱입니다.
또 다른 예는 제롬 프랑엘에 의해 발견되었고, 란다우에 의해 확장되었습니다(Franel & Landau (1924) 참조). 리만 가설은 파리 수열의 항들이 상당히 규칙적이라는 것을 보여주는 여러 문장들과 동등합니다. 이러한 동등성의 하나는 다음과 같습니다. 만약 F가 1/n부터 시작하여 1/1까지 순서 n의 Farey 수열이라면, 모든 ε > 0에 대한 주장
는 리만 가설과 동치입니다. 여기서
는 차수 n의 Farey 수열에 있는 항의 개수입니다.
군론의 예를 들어, g(n)이 n차n 대칭군 S의 원소들의 최대 차수에 의해 주어진 란다우 함수라면, Massias, Nicolas & Robin (1988)은 리만 가설이 경계와 동등하다는 것을 보여주었습니다.
충분히 큰 n에 대하여
Lindelöf 가설과 제타 함수의 성장
리만 가설은 또한 다양한 약한 결과를 가지고 있습니다; 하나는 임계선 상의 제타 함수의 성장 속도에 대한 린델뢰프 가설로, 임의의 ε > 0에 대하여,
→ ∞ toinfty}.
리만 가설은 또한 임계 스트립의 다른 영역에서 제타 함수의 성장률에 대한 매우 급격한 경계를 암시합니다. 예를 들어, 그것은 다음과 같은 것을 암시합니다.
따라서 ζ(1+it)의 증가율과 그 역수는 2배까지 알 수 있습니다.
큰 소수점차 추측
소수 정리는 평균적으로 소수 p와 그것의 계승자 사이의 간격이 log p임을 의미합니다. 그러나 소수 사이의 일부 간격은 평균보다 훨씬 클 수 있습니다. 크라머는 리만 가설을 가정할 때, 모든 갭은 O(√ 로그 p)라는 것을 증명했습니다. 이것은 리만 가설을 사용하여 증명할 수 있는 최선의 경계조차도 참으로 보이는 것보다 훨씬 약한 경우입니다. 크라메르의 추측은 모든 간격이 O((log p)2임을 암시하며, 이는 평균 간격보다 크지만 리만 가설이 암시하는 경계보다 훨씬 작습니다. 수치적 증거는 크라머의 추측을 뒷받침합니다.[14]
리만 가설과 동등한 해석 기준
리만 가설과 동등한 진술들이 많이 발견되었지만, 지금까지 그들 중 어느 것도 그것을 증명(또는 반증)하는 데 큰 진전을 가져오지 않았습니다. 몇 가지 대표적인 예는 다음과 같습니다. (다른 예들은 약수 함수 σ(n)을 포함합니다.)
리에즈 기준은 리에즈(Riesz, 1916)에 의해 다음과 같이 정의되었습니다.
리만 가설이 성립하는 경우에만 모든 ε > 0을 나타냅니다. 하디-리틀우드 기준도 참조하십시오.
Nyman(1950)은 리만 가설이 참이라는 것을 증명했습니다. 이는 다음과 같은 형태의 함수 공간이 존재하는 경우에만 가능합니다.
여기서 ρ(z)는 z의 분수 부분이고, 0 ≤ θ ≤ 1이며,
- }
는 단위 구간의 제곱 적분 가능 함수의 힐베르트 공간2 L(0,1)에 조밀합니다. Beurling(1955)은 이p 함수 공간이 L(0,1)에서 조밀할 경우에만 제타 함수가 1/p보다 큰 실수 부분을 갖는 0이 없음을 보여줌으로써 이를 확장했습니다. 이 Nyman-Beurling 기준은θ ν ∈{ / k k ≥ 1 \theta _{\n.
Salem(1953)은 적분방정식이 성립하는 경우에만 리만 가설이 참임을 보여주었습니다.
1< σ < 1 1/2 <\sigma < 1}에대한 비 trivial 경계 솔루션ϕ \}이(가) 없습니다.
Weil의 기준은 어떤 함수의 양수가 리만 가설과 동등하다는 진술입니다. 이와 관련된 것은 리의 기준으로, 특정 수열의 양수가 리만 가설과 동등하다는 진술입니다.
스피어(1934)는 리만 가설이 ζs) {\displaystyle \의 도함수인 ζ (s) zeta '(s)}가 띠에 0이 없다는 진술과 동일하다는 것을 증명했습니다.
ζ {\displaystyle \zeta(s)}가 임계선에 단순한 0만 있는 것은 임계선에 0이 없는 도함수와 같습니다.
파리 수열은 1924년 제롬 프랑엘과 에드먼드 란다우로 인해 두 가지 동등성을 제공합니다.
드 브루인-뉴먼 상수는 λ(Nicola)에 의해 표시되며 니콜라스 고베르 드 브루인(Nicolaas Govert de Bruijn)과 샤를 M(Charles M)의 이름을 따서 명명되었습니다. 뉴먼은 함수의 고유 실수로 정의됩니다.
- ,
실제 매개변수 λ에 의해 매개변수화되고, 복소 변수 z를 가지며, 초 expon적으로 붕괴하는 함수를 사용하여 정의됩니다.
- .
λ ≥ λ인 경우에만 실수 0을 갖습니다. 리만 가설은 H(0, z)의 모든 이 실수라는 주장과 동치이므로, 리만 가설은 λ ≤ 0 {\displaystyle \Lambda \leq 0}이라는 가정과 동치입니다. 브래드 로저스와 테렌스 타오는 이 상수의 하한임을 증명함으로써 동치가 실제로 λ = 0 displaystyle \= 0}임을 발견했습니다. 따라서 0을 증명하는 것은 리만 가설을 증명하는 것이기도 합니다. 2020년 4월 현재 상한은λ ≤ 0.2 0.2}입니다.
일반화된 리만 가설의 결과
몇몇 응용들은 리만 가설만이 아니라 숫자장들의 디리클레 L-시리즈 또는 제타 함수들에 대해 일반화된 리만 가설을 사용합니다. 리만 제타 함수의 많은 기본 성질들은 모든 디리클레 L-급수에 쉽게 일반화될 수 있으므로, 리만 제타 함수에 대한 리만 가설을 증명하는 방법은 디리클레 L-함수에 대한 일반화 리만 가설에도 적용될 가능성이 있습니다. 일반화된 리만 가설을 사용하여 처음에 증명된 몇 가지 결과는 나중에 사용하지 않고 무조건적인 증명을 제공받았지만, 이것들은 일반적으로 훨씬 더 어려웠습니다. 다음 목록의 많은 결과는 Conrad(2010)에서 가져온 것입니다.
- 1913년, 그론월은 일반화된 리만 가설이 가우스의 클래스 번호 1의 가상 이차장 목록이 완전하다는 것을 암시한다는 것을 보여주었지만, 베이커, 스타크, 헤그너는 나중에 일반화된 리만 가설을 사용하지 않고 이에 대한 무조건적인 증명을 내놓았습니다.
- 1917년 하디와 리틀우드는 일반화된 리만 가설이 체비셰프의 추측을 암시한다는 것을 보여주었습니다. 이것은 어떤 의미에서는 소수 3 mod 4가 소수 1 mod 4보다 더 일반적이라는 것을 의미합니다. (관련 결과는 소수 정리 § 소수 경주를 참조하십시오.)
- 1923년 하디와 리틀우드는 일반화된 리만 가설이 홀수에 대한 골드바흐 추측의 약한 형태를 암시한다는 것을 보여주었습니다: 충분히 큰 모든 홀수는 세 소수의 합이지만 1937년 비노그라도프는 무조건적인 증거를 제시했습니다. 1997년 데쇼일러, 에핑거, 테 릴레, 지노비예프는 일반화된 리만 가설이 5보다 큰 모든 홀수는 세 소수의 합이라는 것을 암시한다는 것을 보여주었습니다. 2013년에 하랄드 헬프고트는 데이비드 J. 플랫의 도움으로 완성된 광범위한 계산에 따라 GRH 의존성이 없는 3원 골드바흐 추측을 증명했습니다.
- 1934년, Chowla는 일반화된 리만 가설이 어떤 고정 상수 K에 대해 mod의 첫 번째 소수가 최대 Kmlog2(m)2임을 암시한다는 것을 보여주었습니다.
- 1967년 훌리는 일반화된 리만 가설이 원시적 근에 대한 아르틴의 추측을 암시한다는 것을 보여주었습니다.
- 1973년 와인버거는 일반화된 리만 가설이 오일러의 아이디얼 수 목록이 완전하다는 것을 암시한다는 것을 보여주었습니다.
- 와인버거(1973)는 모든 대수적 수 필드의 제타 함수에 대한 일반화된 리만 가설이 클래스 번호가 1인 모든 수 필드가 유클리드 또는 판별 -19, -43, -67 또는 -163의 가상 이차 수 필드임을 의미한다는 것을 보여주었습니다.
- 1976년, G. Miller는 일반화된 리만 가설이 어떤 숫자가 다항식 시간에 소수인지를 Miller 검정을 통해 검정할 수 있다는 것을 암시한다는 것을 보여주었습니다. 2002년 Manindra Agrawal, Neeraj Kayal, Nitin Saxena는 AKS primality test를 이용하여 이 결과를 무조건 증명했습니다.
- Odlyzko(1990)는 일반화된 리만 가설을 사용하여 수 필드의 판별자 및 클래스 번호에 대한 더 날카로운 추정치를 제공할 수 있는 방법에 대해 논의했습니다.
- Ono & Soundararajan (1997)은 일반화된 리만 가설이 Ramanujan의 적분2 이차 형식2 x + y + 10z가2 정확히 18개의 예외를 제외하고 로컬에서 나타내는 모든 정수를 나타낸다는 것을 암시한다는 것을 보여주었습니다.
- 2021년, 알렉산더 (알렉스) 던과 막심 래지는 GRH의 가정 하에 패터슨의 추측을 증명할 것입니다.[18]
제외중
RH의 일부 결과는 또한 부정의 결과이므로 정리입니다. 헤케, 듀링, 모델, 헤이브론 정리, 아일랜드 & 로젠(1990, 페이지 359)에 대한 그들의 논의에서 다음과 같이 말합니다.
여기 있는 증명 방법은 정말 놀랍습니다. 일반화된 리만 가설이 참이면 정리는 참입니다. 일반화된 리만 가설이 거짓이면 정리는 참입니다. 따라서, 그 정리는 참입니다!! (원본 punct화)
일반화된 리만 가설이 거짓이라고 말하는 것이 무엇을 의미하는지 이해하는 데 주의가 필요합니다. 어떤 클래스의 디리클레 급수가 반례를 갖는지 정확히 지정해야 합니다.
리틀우드 정리
이것은 소수 정리의 오류의 부호에 관한 것입니다. 모든 x ≤ 10에 대해 π(x) < li(x)로 계산되었으며(이 표 참조), 어떤 π(x) > li(x)에 대해서는 x의 값이 알려져 있지 않습니다.
1914년 리틀우드는 임의로 큰 x 값들이 존재한다는 것을 증명했습니다.
그리고 x의 값이 임의로 크다는 것도.
따라서 차이 π(x) - li(x)는 부호가 무한히 많이 바뀝니다. 스큐의 수는 첫 번째 부호 변화에 해당하는 x 값의 추정치입니다.
Littlewood의 증명은 두 가지 경우로 나누어집니다: RH는 거짓으로 추정됩니다(Ingham 1932, Chapt의 약 반 페이지). V)RH는 참인 것으로 간주됩니다(약 12페이지). Staniswaw Knapowski(1962)는 를따라δ {\\Delta()} 구간에서 δ {\displaystyle \Delta(n)} 변경 기호에 대한 논문을 작성했습니다.
가우스의 등급 번호 추측
이것은 주어진 클래스 번호를 가진 허수 이차장이 무한히 많다는 추측(가우스의 발견 산술 제303조에서 처음 언급됨)입니다. 이를 증명하는 한 가지 방법은 판별자 D → - ∞가 클래스 번호 h(D) → ∞임을 보여주는 것입니다.
리만 가설과 관련된 다음 일련의 정리들은 아일랜드 & 로젠 1990, 페이지 358–361에 설명되어 있습니다.
정리(Heck; 1918) - D < 0을 허수 이차수 필드 K의 판별식이라고 합니다. 모든 허수 이차 디리클레 문자의 L-함수에 대한 일반화된 리만 가설을 가정합니다. 그러면 절대 상수 C가 존재하므로,
정리(Deuring; 1933) — RH가 거짓이면 D가 충분히 크면 h(D) > 1입니다.
정리(Mordell; 1934) — RH가 거짓이면 h(D) → D → - ∞로 ∞합니다.
정리(Heilbronn; 1934) — 만약 일반화된 RH가 어떤 가상의 이차 디리클레 문자의 L-함수에 대해 거짓이면, h(D) → ∞는 D → - ∞입니다.
(헤케와 헤이브론의 연구에서 발생하는 유일한 L-함수는 허수 이차 문자에 첨부된 함수이며, 오직 해당 L-함수에 대해서만 GRH가 참이거나 GRH가 거짓인 것을 의도합니다. 3차 디리클레 문자의 L-함수에 대한 GRH의 실패는 엄밀히 말해서 GRH가 거짓임을 의미합니다. 그러나 하일브론은 그런 GRH의 실패를 염두에 두고 있지 않았으므로, 그의 가정은 단순히 GRH가 거짓이라는 것보다 더 제한되었습니다.
1935년 칼 시겔은 이후 RH나 GRH를 전혀 사용하지 않고 결과를 강화했습니다.[citation needed]
오일러 토텐티브의 성장
일반화 및 아날로그
Dirichlet L-시리즈 및 기타 숫자 필드
리만 가설은 리만 제타 함수를 형식적으로는 유사하지만 훨씬 더 일반적인 전역 L-함수로 대체함으로써 일반화될 수 있습니다. 이 광범위한 설정에서 전역 L-함수의 소수가 아닌 0은 실수 부분 1/2을 가질 것으로 예상합니다. 수학에서 리만 가설의 진정한 중요성을 설명하는 것은 단일 리만 제타 함수에 대한 고전적인 리만 가설이 아니라 이러한 추측입니다.
일반화된 리만 가설은 리만 가설을 모든 디리클레 L-함수로 확장합니다. 특히 시겔 0(1/2에서 1 사이의 L-함수의 0)은 존재하지 않는다는 추측을 암시합니다.
확장된 리만 가설은 리만 가설을 대수적 정수장의 모든 데데킨트 제타 함수로 확장합니다. 유리수의 아벨 확장에 대한 확장 리만 가설은 일반화된 리만 가설과 동등합니다. 리만 가설은 숫자장의 헤케 문자의 L-함수로도 확장될 수 있습니다.
그랜드 리만 가설은 이를 헤케 고유 형태의 멜린 변환과 같은 모든 자동형 제타 함수로 확장합니다.
유한장 이상의 다양한 종류의 함수장과 제타 함수
Artin(1924)은 (2차) 함수장의 전역 제타 함수를 도입하고 그에 대한 리만 가설의 유사체를 추측했는데, 이는 속 1 사례에서 Hasse에 의해 그리고 일반적으로 Weil(1948)에 의해 증명되었습니다. 예를 들어, 크기 q(q 홀수)의 유한 필드의 2차 문자인 가우스 합이 절대값 를 갖는다는 사실은 실제로 함수 필드 설정에서 리만 가설의 예입니다. 이로 인해 Weil(1949)은 모든 대수적 품종에 대해 유사한 문장을 추론하게 되었고, 그 결과 Weil 추측은 Pierre Deligne(1974, 1980)에 의해 증명되었습니다.
산술 체계의 산술 제타 함수와 그 L-팩터
산술 제타 함수는 리만 및 데데킨트 제타 함수뿐만 아니라 유한 필드에 걸친 다양한 제타 함수를 모든 산술 체계 또는 정수에 대한 유한 유형 체계로 일반화합니다. 크로네커 차원 n의 규칙적으로 연결된 등차원 산술 체계의 산술 제타 함수는 적절하게 정의된 L-인자와 보조 인자 장-피에르 세레(Jean-Pierre Serre, 1969–1970)의 곱으로 분해될 수 있습니다. 함수 방정식과 메로모픽 연속을 가정할 때, L-인자에 대한 일반화된 리만 가설은 임계 스트립 ℜ∈ ( (0, n)\Re(s)\in (0, n)} 의 0이 중심선에 있다는 것을 말합니다. 이에 대응하여, 정규 연결 등차원 산술 체계의 산술 제타 함수에 대한 일반화된 리만 가설은 임계 스트립 내부의 0이 수직선ℜ(s) = 1 32, …, n - 1/2 {\display \Re(s) = 1/2, 3/2,\dots,과 임계 스트립 내부의 극은 수직 선(s) 2, …, n - 1 {\displaystyle \Re(s) 1, 2,\,n-1}에 놓여 있습니다. 이것은 긍정적인 특성을 가진 스킴으로 알려져 있으며 Pierre Deligne(, 1980)의 것을 따르지만, 특성 0에서는 완전히 알려지지 않은 상태로 남아 있습니다.
셀베르크 제타 함수
Selberg(1956)는 리만 곡면의 Selberg zeta 함수를 도입했습니다. 이것들은 리만 제타 함수와 유사합니다: 함수 방정식과 오일러 곱과 유사하지만 소수가 아닌 닫힌 측지학을 인수한 무한 곱을 갖습니다. 셀버그 추적 공식은 소수 이론에서 명시적 공식의 이러한 함수에 대한 아날로그입니다. 셀버그는 셀버그 제타 함수가 리만 표면의 라플라시안 연산자의 고유값과 관련된 0의 허수 부분과 함께 리만 가설의 아날로그를 만족한다는 것을 증명했습니다.
이하라 제타 함수
유한 그래프의 이하라 제타 함수는 셀버그 제타 함수의 아날로그로, 이하라 야스타카에 의해 2x2 p-아딕 특수 선형 그룹의 이산 하위 그룹의 맥락에서 처음 도입되었습니다. 정규 유한 그래프는 효율적인 통신 네트워크의 수학적 모델인 라마누잔 그래프로, 이하라 제타 함수가 T가 지적한 리만 가설의 아날로그를 만족하는 경우에만 해당됩니다. 수나다.
몽고메리의 쌍 상관 추론
몽고메리(Montgomery, 1973)는 제타 함수의 (적절하게 정규화된) 0의 상관 함수가 무작위 에르미트 행렬의 고유값의 상관 함수와 동일해야 한다는 쌍 상관 추측을 제안했습니다. Odlyzko(1987)는 이러한 상관 함수의 대규모 수치 계산에 의해 이것이 뒷받침됨을 보여주었습니다.
몽고메리는 (리만 가설을 가정하면) 모든 0의 2/3은 단순하며, 관련 추측은 제타 함수의 모든 0은 단순하다는 것입니다(또는 일반적으로 그들의 허수 부분들 사이에 사소한 정수 선형 관계가 없습니다). 리만 제타 함수를 일반화하는 대수적 정수장의 데데킨트 제타 함수는 종종 복소 0을 여러 개 가지고 있습니다.[20] 데데킨트 제타 함수는 L-함수에서 아르틴의 거듭제곱의 곱으로 소인수분해되므로, L-함수에서 아르틴의 0은 때때로 데데킨트 제타 함수의 복수의 0을 발생시키기 때문입니다. 여러 개의 0이 있는 제타 함수의 다른 예로는 일부 타원 곡선의 L-함수가 있습니다. 이들은 임계선의 실제 지점에서 여러 개의 0을 가질 수 있습니다. 버치-스위너턴-다이어 추측은 이 0의 다중성이 타원 곡선의 순위라고 예측합니다.
기타 제타 함수
리만 가설의 유사체와 함께 제타 함수의 다른 많은 예가 있으며, 그 중 일부는 증명되었습니다. 함수장의 고제타 함수는 Sheats(1998)에 의해 증명된 리만 가설을 가지고 있습니다. 이와사와 이론의 주요 추측은 순환론적 장들에 대해 배리 마주르와 앤드루 와일스에 의해 증명되었고, 와일스는 완전한 실제 장들에 대해 p-아딕 L-함수의 0을 연산자의 고유값과 동일시하므로 힐베르트의 유사체로 생각될 수 있습니다.p-아딕 L-함수에 대한 폴랴 추측.[21]
증명 시도
몇몇 수학자들이 리만 가설을 제기했지만, 그들의 시도 중 어느 것도 아직 증명으로 받아들여지지 않았습니다. Watkins(2021)는 몇 가지 잘못된 해결책을 나열합니다.
연산자론
힐베르트와 폴랴는 리만 가설을 도출하는 한 가지 방법은 실제 고유값에 대한 기준을 적용할 때 ζ의 0의 실수 부분에 대한 진술이 뒤따를 수 있는 자기 인접 연산자를 찾는 것이라고 제안했습니다. 이 아이디어에 대한 일부 지원은 리만 제타 함수의 여러 유사체에서 비롯됩니다. 유한장에 대한 다양한 제타 함수의 0은 에탈 코호몰로지 군의 프로베니우스 원소의 고유값에 해당합니다. 셀베르크 제타 함수의 0은 리만 표면의 라플라시안 연산자의 고유값이며, p-아딕 제타 함수의 0은 이상적인 클래스 그룹에 대한 갈루아 작용의 고유 벡터에 해당합니다.
Odlyzko(1987)는 리만 제타 함수의 0의 분포가 가우스 유니터리 앙상블에서 도출된 랜덤 행렬의 고유값과 일부 통계적 속성을 공유한다는 것을 보여주었습니다. 이것은 힐베르트 가족에게 약간의 지지를 줍니다.폴랴 추측.
1999년, 마이클 베리와 조나단 키팅은 고전 해밀토니안 H = xp의 미지의 H {H가 존재한다고 추측하여 다음과 같이,
유한장에 대한 리만 가설과의 비유는 0에 해당하는 고유 벡터를 포함하는 힐베르트 공간이 정수의 스펙트럼 스펙(Z)의 일종의 첫 번째 코호몰로지 그룹일 수 있음을 시사합니다. Deninger(1998)는 이러한 코호몰로지 이론을 찾기 위한 시도들 중 일부를 설명했습니다.[23]
Jagier(1981)는 라플라시안 연산자 아래에서 리만 제타 함수의 0에 해당하는 고유값을 갖는 상반평면 위에 불변 함수들의 자연 공간을 구성하고, 이 공간 위에 적합한 양의 정 확정 내적이 존재한다는 것을 보여줄 수 있는 가능성이 없는 경우에는, 리만 가설이 뒤따를 것입니다. 카르티에(1982)는 이상한 버그로 인해 컴퓨터 프로그램이 리만 제타 함수의 0을 동일한 라플라시안 연산자의 고유값으로 나열한 관련 사례를 논의했습니다.
Schumayer & Hutchinson(2011)은 Riemann zeta 함수와 관련된 적합한 물리적 모델을 구성하려는 시도 중 일부를 조사했습니다.
리-양 정리
리-양 정리는 통계 역학에서 특정 분할 함수의 0은 모두 실수 부분이 0인 "임계선" 위에 놓여 있으며, 이는 리만 가설과의 관계에 대한 추측으로 이어졌습니다.[24]
투란의 결과
비상호기하학
Connes(1999, 2000)는 리만 가설과 비상호기하학 사이의 관계를 설명했으며, 아델 클래스 공간에 대한 idèle 클래스 그룹의 작용에 대한 셀버그 추적 공식의 적절한 유사체가 리만 가설을 암시한다는 것을 보여주었습니다. 이러한 아이디어 중 일부는 Lapidus(2008)에 자세히 설명되어 있습니다.
전체 함수의 힐베르트 공간
Louis de Branges(1992)는 리만 가설이 전체 함수의 특정 힐베르트 공간에 대한 양의 조건에서 따를 것임을 보여주었습니다. 그러나 Conrey & Li(2000)는 필요한 양의 조건이 충족되지 않음을 보여주었습니다. 이런 장애에도 불구하고 드브랑제는 같은 선을 따라 리만 가설의 증명을 시도하는 작업을 계속해 왔지만, 이는 다른 수학자들에게 널리 받아들여지지 않았습니다.[25]
준결정
리만 가설은 제타 함수의 0이 준결정을 형성한다는 것을 의미하며, 푸리에 변환도 이산 지원을 갖는 분포입니다. Dyson(2009)은 1차원 준결정을 분류하거나 적어도 연구함으로써 리만 가설을 증명하려고 노력할 것을 제안했습니다.
숫자장에 대한 타원곡선 모형의 산술 제타함수
기하학적 차원 1(예: 대수적 숫자장)에서 기하학적 차원 2(예: 숫자장에 대한 타원 곡선의 정규 모델)로 갈 때, 모델의 산술 제타 함수에 대한 일반화된 리만 가설의 2차원 부분은 제타 함수의 극을 다룹니다. 1차원에서 테이트의 논문에서 제타 적분에 대한 연구는 리만 가설에 대한 새로운 중요한 정보로 이어지지 않습니다. 이와는 반대로, 차원에서 테이트의 논문의 2차원 일반화에 대한 이반 페센코의 두 가지 연구는 제타 함수와 밀접하게 관련된 제타 적분의 적분 표현을 포함합니다. 1차원에서 가능하지 않은 이 새로운 상황에서, 제타 함수의 극은 제타 적분 및 관련 아델 그룹을 통해 연구될 수 있습니다. 제타 적분과 관련된 경계 함수의 네 번째 도함수의 긍정성에 대한 페센코(2010)의 관련 추측은 본질적으로 일반화된 리만 가설의 극 부분을 암시합니다. 스즈키(2011)는 일부 기술적 가정과 함께 후자가 페센코의 추측을 암시한다는 것을 증명했습니다.
다중 제타 함수
Deligne의 유한장에 대한 Riemann 가설의 증명은 원래 제타 함수의 실수 부분을 묶기 위해 0과 극이 원래 제타 함수의 0과 극의 합에 해당하는 제품 품종의 제타 함수를 사용했습니다. 유사하게, Kurokawa(1992)는 0과 극이 리만 제타 함수의 0과 극의 합에 해당하는 다중 제타 함수를 도입했습니다. 급수를 수렴시키기 위해 그는 모두 음이 아닌 허수 부분을 가진 0 또는 극의 합으로 제한했습니다. 지금까지 알려진 다중 제타 함수의 0과 극에 대한 경계는 리만 제타 함수의 0에 대한 유용한 추정치를 제공할 만큼 충분히 강하지 않습니다.
0의 위치
0의 수
논법 원리와 결합된 함수 방정식은 허수부가 0과 T 사이인 제타 함수의 0의 개수는 다음과 같이 주어짐을 의미합니다.
s=1/2+iT의 경우, ∞+iT에서 인수 0부터 시작하여 Im(s)=T와의 선을 따라 연속적으로 변경하여 인수를 정의합니다. 이것은 크지만 잘 알려진 용어의 합입니다.
그리고 작지만 다소 신비로운 용어.
따라서 T 근처의 허수부를 갖는 0의 밀도는 log(T)/2 π 정도이고, 함수 S는 이로부터 작은 편차를 설명합니다. 함수 S(t)는 제타 함수의 각 영점에서 1만큼 점프하며, t ≥ 8의 경우 -log에 가까운 도함수를 가진 0 사이에서 단조적으로 감소합니다.
Trudgian (2014)은 만약 > > e이면
Karatsuba(1996)는 ≥T + ε T {27}{82varepsilon }에 대한 모든 간격(T, T+H)이 적어도 포함되어 있음을 증명했습니다.
함수 S(t)가 부호를 변경하는 점.
Selberg (1946)는 S의 짝수 거듭제곱의 평균 모멘트는 다음과 같이 주어짐을 보여주었습니다.
이는 S(T)/(log log T)가 평균이 0이고 분산이 2 π인 가우스 랜덤 변수와 유사함을 시사합니다(Ghosh (1983)는 이 사실을 증명했습니다). 특히 S(T)는 일반적으로 (로그 로그 T) 주변에 있지만,1/2 때때로 훨씬 더 큽니다. S(T)의 정확한 성장 순서는 알려져 있지 않습니다. 리만 가설이 약간 더 작은 바운드 S(T)=O(log T)를 의미하지만, 리만의 원래 바운드 S(T)=O(log T/log T)에 대한 무조건적인 개선은 없었습니다. S(T)와 동일한 분포를 갖는 랜덤 함수는 로그(T)에 대해 차수가 증가하는 경향이 있기 때문에 실제 크기의 차수는 이보다 다소 적을 수 있습니다.1/2 반대로 너무 작을 수 없습니다. Selberg(1946)는 S(T)가 ≠ o((log T)/(log T)임을 보여주었고, 리만 가설을 가정한 몽고메리는 S(T)가 ≠ o(log T)/(log T)임을 보여주었습니다.
수치 계산을 통해 S는 매우 느리게 성장함을 확인할 수 있습니다: T < 280의 경우 S(T) < 1, T < 6800000의 경우 S(T) < 2, 그리고 지금까지 발견된 S(T)의 가장 큰 값은 3보다 크지 않습니다.[26]
Riemann의 추정치 S(T) = O(log T)는 0 사이의 간격이 경계를 이루고 있음을 의미하며, Littlewood는 이를 약간 개선하여 가상 부분 사이의 간격이 0인 경향이 있음을 보여줍니다.
하다마르와 드 라 발레 푸생의 정리
하다마드(1896)와 드 라 발레-푸신(1896)은 서로 독립적으로 어떤 0도 Re(s) = 1 선 위에 놓일 수 없다는 것을 증명했습니다. 함수 방정식과 실수부가 1보다 큰 0이 없다는 사실과 함께, 이것은 모든 trivial이 아닌 0은 임계 띠 0 < Re(s) < 1의 내부에 있어야 한다는 것을 보여주었습니다. 이것은 그들이 소수 정리를 처음으로 증명하는 데 중요한 단계였습니다.
제타 함수가 실수부 1과 0이 없다는 원래 증명은 모두 유사하며, ζ(1+it)가 사라지면 ζ(1+2it)가 단수이므로 불가능하다는 것을 보여주는 것에 달려 있습니다. 이를 수행하는 한 가지 방법은 불평등을 사용하는 것입니다.
σ > 1, 실수, 한계를 σ → 1로 봅니다. 이 부등식은 오일러 곱의 로그의 실수 부분을 취함으로써 다음을 알 수 있습니다.
합이n 모든 소수 p 위에 있으므로,
부등식으로 인해 합에 있는 모든 항이 양수이므로 최소 1입니다.
제로 프리 지역
리만 가설의 반례에 대한 플랫과 트루지안의 가장 광범위한 컴퓨터 검색은 3 ⋅ {\t \ 310^{12}에 대해 검증되었습니다. 그 외에도 제로 프리 영역은 0일 수 있는 σ + it에 관한 부등식으로 알려져 있습니다. 가장 오래된 버전은 어떤 양의 상수 C에 대해 1 - σ ≥ C/log(t)를 만족하는 0이 없는 영역이 있다는 것을 증명한 델라 발레 푸신(1899–1900)의 것입니다. 즉, 0은 선 σ = 1에 너무 가까이 있을 수 없습니다. 이 선에 가까운 곳에 0이 없는 영역이 있습니다. 이는 여러 저자들에 의해 비노그라도프의 평균값 정리와 같은 방법을 사용하여 확대되었습니다.
Mossinghoff, Trudgian 및 Yang의 가장 최근 논문은[27] 2022년 12월부터이며 2002년 케빈 포드, 2015년 Mossinghoff 및 Trudgian 자체, 2022년 10월 페이스 닐슨이 포드를 약간 개선한 4개의 제로 프리 지역을 제공합니다.
- σ ≥- . t igma \geq 1-{\frac {1}{5.558691\log t}} t가 2 {\displaystyle t \geq }를 ≥할 때마다,
- whenever (largest known region in the bound . 1027 {\displaystyle 3.0001753328\cdot 10^{12}\leq \exp(64.1)\ 6.89\cdot 10^{27}},
- whenever 14 {\t \ 1cdot10^{14}} (바운드 exp 에서 가장 큰 알려진 영역(64.1) ≤ t ≤ exp (1000) 1.97 10 434 {\displaystyle \exp(64.1)\leq \exp(1000)\ 1.97\cdot 10^{434}}) 및
- () \geq \exp(1000)} (자체 경계에서 가장 큰 알려진 영역)
이 논문은 t {\가 단지 논문의 증명 요건을 충족하기에 "충분히 큰" 것으로 가정되기 때문에 경계를 알 수 없는 두 번째 제로 프리 영역에 대한 개선을 가지고 있습니다. 이 지역은.
≥ - 148) 2 / 3 로그 로그 t) 1 / 3 {\displaystyigma \geq 1-{\frac {1}{48.1588(\log {t})^{2/3}(\log {\log {t})^{1/3}}}.
임계선의 0
하디(1914)와 하디 & 리틀우드(1921)는 제타 함수와 관련된 특정 함수의 모멘트를 고려하여 임계선에 무한히 많은 0이 존재한다는 것을 보여주었습니다. 셀버그(Selberg, 1942)는 적어도 (작은) 양의 비율의 0이 선 위에 있다는 것을 증명했습니다. 레빈슨(Levinson, 1974)은 제타 함수의 0을 도함수의 0과 연관시켜 0의 3분의 1로 개선했고, 콘레이(Conrey, 1989)는 이를 5분의 2로 더 개선했습니다. 2020년, 이 추정치는 제타 함수의 고차 도함수와 이와 관련된 클루스터만 합을 수용할 수 있는 확장된 연체동물을 고려하여 Pratt, Robles, Zaharescu 및 Zeindler에[28] 의해 5/12로 확장되었습니다.
대부분의 0은 임계선에 가까이 놓여 있습니다. 좀 더 정확하게 말하면, Bohr & Landau (1914)는 임의의 양의 ε에 대해 실수부가 1/2+ ε 이상이고 허수부가 T 사이에 있는 0의 수는 O(T) O(T)}임을 보여주었습니다. 임계 스트립의 영점이 임계선에 대해 대칭이라는 사실과 임계 스트립의 총 영점 수가θ로그 T) \Theta(T\log T)}라는 사실을 결합하면 거의 모든 사소한 영점은 임계선의 거리 ε 내에 있습니다. Ivić(1985)는 이 결과의 몇 가지 더 정확한 버전을 제공하는데, 이를 0 밀도 추정이라 하며, 최대 T의 허수 부분과 최소 1/2+의 실수 부분이 있는 영역의 0의 수를 묶었습니다.
하디-리틀우드 추측
1914년 고드프리 해럴드 하디는ζ(+ it) }}+itright)}가 무한히 많은 실수 0을 가지고 있음을 증명했습니다.
ζ의 실수 0 사이의 거리(+ 2}+right)}와 간격)의 ζ0 12 + 2}+it\right)}에 대한 하디와 존 에덴서 리틀우드의 다음 두 추측. for sufficiently large , and and with as small as possible value of , where is an arbitrarily small number, 리만 제타 함수의 조사에서 두 가지 새로운 방향을 엽니다.
- For any there exists a lower bound such that for and the interval + ] 에는 함수 + it) {\displaystyle \ {2}}+itbigr)}}의 홀수 순서가 포함되어 있습니다.
Let be the total number of real zeros, and be the total number of zeros of odd order of the function lying on the interval .
- 임의의ε > 0 \ > 0}에 대해 T =T0 (ε > 0 {\displaystyle{0} = T_{0} (\varepsilon) > 0}이 하며 일부 c = c (ε) > 0 {\displaystyle c = c(\varepsilon) > 0}, T ≥ T T\geq T_{0}} 및 H = T 12 + ε {\displaystyle H=T^{\tfrac {1}{2}}+\varepsilon } 부등식 N 0 (T + H ) - N 0 (T) ≥ C {\displaystyle N_{0} (T + H) - N_{0} (T)\geq cH} 가 참입니다.
셀베르크의 제타 함수 추측
Atle Selberg(1942)는 Hardy-Littlewood 2의 문제를 조사하여 임의의 ε > 에 T 0 = 0 (ε > 0 {\displaystyle 0} = T_{0}(\varepsilon) > 0} 및 c = c(ε) > 0, 즉 T≥ T 0 {\displaystyle T\geq T_{0}} 및 H = T 0.5 + ε {\displaystyle H = T^{0}이 존재함을 증명했습니다. 부등식 N+ H)- N c T N(T + H)-T)\geq cH\log T} 가 참입니다. Selberg는 이것이 = T 0.5 H = T.5}}로 강화될 수 있다고 추측했습니다. A. A. Karatsuba(1984a, 1984b, 1985)는 조건 0 < ε < 0.001을 만족하는 고정 ε에 대해 충분히 큰 T와 H = Ta + ε {\displaystyle H = T^{a+\varepsilon}}, = 82 = - {\ a = {\{278}} = {\tfrac {1}{3}-{\tfrac {1}{246}}, 간격(T, T+H)은 리만 제타함수 ζ(12 + it) {\displaystyle \zeta \lt ({\tfrac {1}{2}+it\right}의 최소 cH log(T) 실수 0을 포함하므로 셀버그 추측을 확인했습니다. 셀버그와 카라츠바의 추정치는 T → ∞로서 성장의 순서와 관련하여 개선될 수 없습니다.
카라츠바(1992)는 셀버그 추측의 유사체가 거의 모든 간격(T, T+H), H = ε {\=varepsilon에 대해 유지된다는 것을 증명했으며, 여기서 ε는 임의로 작은 고정 양수입니다. 카라츠바 방법을 사용하면 임계선의 "초단" 간격, 즉 간격(T, T+H)에서 리만 제타 함수의 0을 조사할 수 있으며, 길이 H는 임의로 작은 정도 T보다 느리게 증가합니다. 특히, 그는 주어진 ε에 대해ε 1 {\varepsilon_{1}}이 0< ε, ε 1 < 1 {\varepsilon,\varepsilon_{1}<1}을 거의 모든 간격(T, T+H] for contain at least zeros of the function . 이 추정치는 리만 가설에서 나온 추정치와 상당히 유사합니다.
수치계산
함수.
임계띠에서 제타 함수와 같은 0이 있고, 함수방정식 때문에 임계선상에서 실수하므로, 이 점들에서 함수가 반대 부호를 갖는다는 것을 수치로 확인함으로써 두 점 사이의 실수선상에서 정확히 0의 존재를 증명할 수 있습니다. 보통은 글을 씁니다.
여기서 하디의 Z 함수와 리만-시겔 세타 함수 θ는 θ(0)=0인 매끄러운 실수 함수라는 조건에 의해 고유하게 정의됩니다. 함수 Z가 부호를 바꾸는 많은 구간을 찾으면 임계선에 많은 0이 있음을 알 수 있습니다. 주어진 0의 허수부 T까지 리만 가설을 검증하려면 이 영역에 더 이상 선을 벗어난 0이 없는지도 확인해야 합니다. 이것은 튜링의 방법을 사용하여 영역의 전체 0의 수를 계산하고 선에서 발견된 0의 수와 동일한지 확인함으로써 수행할 수 있습니다. 이를 통해 원하는 T 값까지 계산적으로 리만 가설을 검증할 수 있습니다(이 영역에서 제타 함수의 모든 0이 단순하고 임계선에 있는 경우).
이러한 계산을 x displaystyle x의 유한 범위에대한π) \pi(x))을 추정할 수도 있습니다. 예를 들어 2020년의 최신 결과( 0 3 10^{12}})를 사용하면 다음과 같은 결과가 나타납니다.
일반적으로, 이 불평등은 다음과 같습니다.
- geq x x ≤ T,{\{9.{{\frac {x}}{\log {x}}}\leq T,}
여기서 T는 알려진 가장 큰 값이므로, 리만 가설은 \leftρ)∈ T)\rho }인 모든 0 ρ \rho }에 대해 참입니다.
제타 함수의 0에 대한 일부 계산은 아래에 나열되어 있으며, 여기서 0의 "높이"는 가상 부분의 크기이고 n번째 0의 높이는 γ으로 표시됩니다. 지금까지 확인된 모든 0은 임계선에 있고 단순합니다. (0이 여러 개이면 0 찾기 알고리즘에 문제가 생길 것이고, 0 사이의 부호 변화를 찾는 것에 달려 있습니다.) 0의 표는 Hasselgrove & Miller(1960) 또는 Odlyzko를 참조하십시오.
| 연도 | 0의 수 | 작가. |
|---|---|---|
| 1859? | 3 | B. Riemann은 Riemann-Siegel 공식을 사용했습니다(미발표, 1932년 Siegel에서 보고). |
| 1903 | 15 | J. P. 그램(1903)은 오일러-매클로린 공식을 사용하여 그램의 법칙을 발견했습니다. 그는 자신이 발견한 근들의 역수 10제곱의 합을 계산함으로써 허수부가 최대 50 범위인 10개의 0 모두가 실수부 1/2과의 임계선에 놓여 있다는 것을 보여주었습니다. |
| 1914 | 79(γ ≤200) | R. J. Backund (1914)는 제타 함수의 인수 S(T)를 연구함으로써 그 지점까지의 모든 0이 선에 있는지 확인하는 더 나은 방법을 소개했습니다. |
| 1925 | 138(γ ≤300) | J. I. 허친슨(J. I. Hutchinson, 1925)은 Gram 지점에서 Gram 법칙의 첫 번째126 실패를 발견했습니다. |
| 1935 | 195 | E. C. Titchmarsh(1935)는 최근 재발견된 리만-시겔 공식을 사용했는데, 이는 오일러-매클로린의 합보다 훨씬 빠릅니다. 허수 부분이 T보다 작은 0을 확인하는 데는 약 O(T3/2+ε) 단계가 소요되는 반면, 오일러-매클로린 방법은 약 O(T2+ε) 단계가 소요됩니다. |
| 1936 | 1041 | E. C. Titchmarsh (1936)와 L. J. Comrie는 마지막으로 손으로 0을 찾았습니다. |
| 1953 | 1104 | A. M. Turing (1953)은 Z가 연속된 여러 그램 지점에서 올바른 부호를 가지고 있는지 확인하고 S(T)가 평균값이 0이라는 사실을 사용함으로써 어떤 지점까지의 모든 0이 선 위의 0에 의해 설명되는지 확인하는 보다 효율적인 방법을 발견했습니다. 그램 점에서 Z의 부호는 0을 찾는 것으로부터 이미 알려져 있고 여전히 일반적으로 사용되는 방법이기 때문에 추가 작업이 거의 필요하지 않습니다. 이것은 0을 계산하기 위한 디지털 컴퓨터의 첫 번째 사용이었습니다. |
| 1956 | 15000 | D. H. 레머(D. H. Lehmer, 1956)는 제타 함수에 "정의로울 뿐"인 0이 있는 몇 가지 경우를 발견했습니다: 제타 함수의 두 개의 0은 너무 가까이 있어서 그들 사이의 부호 변화를 발견하는 것은 이례적으로 어렵습니다. 이것은 "레머 현상"이라고 불리며, 허수부 7005.063과 7005.101을 가진 0에서 처음 발생하는데, 이 점 근처의 다른 0들 사이의 평균 간격은 약 1이지만 단지 0.04만큼만 차이가 납니다. |
| 1956 | 25000 | D. H. Lehmer |
| 1958 | 35337 | N. A. 멜러 |
| 1966 | 250000 | R.S. 리먼 |
| 1968 | 3500000 | Rosser, Yohe & Schoenfeld (1969)는 Rosser의 법칙을 다음과 같이 기술했습니다. |
| 1977 | 40000000 | R. P. 브렌트 |
| 1979 | 81000001 | R. P. 브렌트 |
| 1982 | 200000001 | R. P. Brent, J. van de Lune, H. J. J. Teriele, D. T. 윈터 |
| 1983 | 300000001 | J. van de Lune, H. J. J. te Riele |
| 1986 | 1500000001 | van de Lune, ter Riele & Winter (1986)는 0에 대한 일부 통계 데이터를 제공하고 비정상적인 행동을 하는 장소에서 Z의 그래프를 여러 개 제공했습니다. |
| 1987 | 큰 키 몇개12(~10) | A. M. Odlyzko(1987)는 Montgomery의 쌍 상관 추측을 확인하기 위해 훨씬 더 큰 높이, 약 10개의12 더 작은 수의 0을 높은 정밀도로 계산했습니다. |
| 1992 | 큰 키 몇개20(~10) | A. M. Odlyzko (1992)는 약 1억20 7천 5백만 개의 높이를 10개 정도로 계산하고 2×1020 정도의 높이 몇 개를 더 계산하여 결과에 대한 광범위한 논의를 했습니다. |
| 1998 | 10000 대(~1021) 높이 | A. M. Odlyzko (1998)는 약 1021 정도의 높이의 0을 계산했습니다. |
| 2001 | 10000000000 | J. van de Lune (미공개) |
| 2004 | ~900000000000[30] | S. Wedeniwski (ZetaGrid 분산 컴퓨팅) |
| 2004 | 100000000000000000 및 몇 개의 큰 높이(최대 10개24) | X. Gourdon(2004)과 Patrick Demichel은 Odlyzko-Schönhage 알고리즘을 사용했습니다. 그들은13 또한14 10, 1024, 10, 10 높이 주변에서 20억 개의 0을 확인했습니다. |
| 2020 | 12363153437138 최고 높이 300017532800 | Platt & Trudgian (2021). 그들은 또한 Gourdon(2004)과 다른 사람들의 연구를 검증했습니다. |
그램 포인트
그램 포인트는 임계선 1/2 + 임계선 1/2 + 제타 함수가 실수이고 0이 아닌 점입니다. 임계선의 제타 함수에 대한 표현을 사용하여 ζ(1/2 + it) = Z(t)e, 여기서 하디의 함수인 Z는 실수이고, θ는 리만-시겔 세타 함수이며, sin(θ(t) = 0일 때 제타가 실수임을 알 수 있습니다. 이는 π(t)가 θ의 정수배임을 의미합니다. θ에 대한 공식을 뒤집어서 그램 포인트의 위치를 상당히 쉽게 계산할 수 있습니다. 일반적으로 n = 0, 1, ...에 대해 g로 번호가 매겨집니다. 여기서 g는 θ(t) = n π의 고유한 용액입니다.
그램은 임의의 두 그램 점 사이에 종종 정확히 하나의 제타 함수가 존재한다는 것을 관찰했습니다. 허친슨은 이 관찰을 그램의 법칙이라고 불렀습니다. 때때로 그램 법칙이라고도 불리는 밀접하게 관련된 문장이 몇 가지 있습니다. 예를 들어, (-1)nZ(gn)는 보통 양수이거나, Z(t)는 보통 연속적인 그램 지점에서 반대 부호를 갖습니다. 처음 몇 개의 0(파란색)과 처음 몇 개의 그램 포인트 g의 허수부 γ은 다음 표에 주어집니다.
| g−1 | γ1 | g0 | γ2 | g1 | γ3 | g2 | γ4 | g3 | γ5 | g4 | γ6 | g5 | ||
| 0 | 3.436 | 9.667 | 14.135 | 17.846 | 21.022 | 23.170 | 25.011 | 27.670 | 30.425 | 31.718 | 32.935 | 35.467 | 37.586 | 38.999 |
그람의 법칙의 첫 번째 실패는 "잘못된" 순서인 127번째 0과 그람 지점 g에서126 발생합니다.
| g124 | γ126 | g125 | g126 | γ127 | γ128 | g127 | γ129 | g128 |
|---|---|---|---|---|---|---|---|---|
| 279.148 | 279.229 | 280.802 | 282.455 | 282.465 | 283.211 | 284.104 | 284.836 | 285.752 |
제타 함수가 1/2 +에서 양수이면 그램 포인트 t가 좋다고 합니다. Z가 "잘못된" 부호를 갖는 "나쁜" 그램 지점의 지수는 126, 134, 195, 211, ... (OEIS의 시퀀스 A114856)입니다. 그램 블록은 두 개의 좋은 그램 점들이 경계를 이루어서 그들 사이의 모든 그램 점들이 나쁘다는 것을 의미합니다. Rosser, Yohe & Schoenfeld (1969)로 인해 Rosser의 법칙이라고 불리는 그램의 법칙을 개선한 결과, 블록의 개별 그램 간격 중 일부가 정확히 하나의 0을 가지고 있지 않을 수도 있지만, 그램 블록은 종종 예상되는 0의 수(그램 간격의 수와 동일)를 가지고 있다고 말합니다. 예를 들어, g와125 g로127 경계를 이루는 구간은 고유한 나쁜 그램 점 g를126 포함하는 그램 블록이며, 두 그램 구간 모두 고유한 0을 포함하지 않지만 예상되는 숫자 2의 0을 포함합니다. Roser et al. 전체 제타 함수에 대한 로서의 규칙에는 무한히 많은 예외가 있지만, 처음 300만 개의 0에서 로서의 규칙에는 예외가 없다는 것을 확인했습니다.
그램의 법칙과 로저의 법칙은 둘 다 어떤 의미에서는 0이 그들의 예상 위치에서 너무 멀리 벗어나지 않는다고 말합니다. 예상 위치에서 0의 거리는 위에서 정의한 함수 S에 의해 제어되며, 이 함수는 매우 느리게 증가합니다. 평균값은 (로그 로그 T) 정도이며,1/2 T의24 경우 10 정도만 2에 도달합니다. 이것은 두 규칙 모두 작은 T에 대해 대부분의 시간을 유지하지만 결국 자주 고장난다는 것을 의미합니다. 실제로 Trudgian(2011)은 Gram의 법칙과 Rosser의 법칙이 모두 실패하는 경우가 양의 비율임을 보여주었습니다. 구체적으로 말하면, 약 66%에서 하나의 0은 연속적인 두 개의 그램 포인트로 둘러싸여 있을 것으로 예상되지만, 17%에서는 0이 없고 17%에서는 두 개의 0이 장기적으로 항가(2020)에서 그러한 그램 간격에 있을 것입니다.
리만 가설에 대한 찬반 논쟁
리만 가설에 관한 수학 논문들은 그 진리에 대해 조심스럽게 논박하지 않는 경향이 있습니다. 의견을 표명하는 저자들 중 리만(1859)이나 봄비에리(2000)와 같은 대부분의 저자들은 그것이 사실이기를 기대(또는 최소한 희망)하고 있음을 암시합니다. 이에 대해 심각한 의심을 표하는 몇 안 되는 저자로는 회의론의 이유를 나열한 이비치(2008)와 거짓이라고 믿는다고 단호하게 말하는 리틀우드(1962)가 있습니다. 이에 대한 증거가 없고 그것이 사실일 것이라는 상상할 수 있는 이유가 없습니다. 조사 기사(Bombieri 2000, Conrey 2003 및 Sarnak 2005)의 일치된 의견은 증거가 강력하지만 압도적이지는 않다는 것이며, 따라서 사실이지만 합리적인 의심이 있을 수 있습니다.
Sarnak(2005), Conrey(2003), Ivić(2008)에 의해 리만 가설에 대한 찬성과 반대의 논거는 다음과 같습니다.
- 리만 가설의 여러 유사점은 이미 증명되었습니다. Deligne(1974)의 유한장 이상의 품종에 대한 리만 가설의 증명은 아마도 리만 가설을 지지하는 가장 강력한 이론적 이유일 것입니다. 이는 자동 형태와 관련된 모든 제타 함수가 특수한 경우로 고전적인 리만 가설을 포함하는 리만 가설을 만족한다는 보다 일반적인 추측에 대한 증거를 제공합니다. 마찬가지로 Selberg zeta 함수는 리만 가설의 아날로그를 만족하며, 어떤 면에서는 함수 방정식과 오일러 곱 팽창과 유사한 무한 곱 팽창을 갖는 리만 zeta 함수와 유사합니다. 그러나 또한 몇 가지 주요 차이점이 있습니다. 예를 들어, 이들은 디리클레 급수에 의해 주어지지 않습니다. Sheats(1998)는 Gosszeta 함수에 대한 Riemann 가설을 증명했습니다. 이러한 긍정적인 예와 달리 일부 엡스타인 제타 함수는 임계선에 무한히 많은 0을 가지고 있음에도 불구하고 리만 가설을 만족하지 않습니다.[13] 이 함수들은 리만 제타 함수와 상당히 유사하며, 디리클레 급수 전개와 함수 방정식을 갖지만, 리만 가설이 실패한 것으로 알려진 함수들은 오일러 곱이 없고, 오토모픽 표현과 직접적인 관련이 없습니다.
- 처음에는 많은 0이 선 위에 놓여 있다는 수치적 검증이 그것에 대한 강력한 증거로 보입니다. 그러나 분석적인 수론은 많은 추측들이 거짓으로 판명된 실질적인 수치적 증거에 의해 뒷받침되었습니다. 리만 가설과 관련된 그럴듯한 추측에 대한 첫 번째 예외가 약 10개316 정도 발생하는 악명 높은 예는 스큐스 숫자를 참조하십시오. 이 크기의 가상 부분이 있는 리만 가설의 반례는 현재 직접적인 접근법을 사용하여 계산할 수 있는 어떤 것도 훨씬 능가할 것입니다. 문제는 동작이 로그 T와 같이 매우 천천히 증가하는 함수에 의해 영향을 받는 경우가 많은데, 로그 T는 무한대인 경향이 있지만 계산으로 감지할 수 없을 정도로 느립니다. 이러한 함수는 제타 함수의 이론에서 발생하며, 예를 들어 위의 함수 S(T)는 (로그 로그 T)의 평균 크기를 갖습니다.1/2 S(T)가 리만 가설의 반례에서 적어도 2만큼 점프하므로, S(T)가 커졌을 때만 리만 가설의 반례가 나타나기 시작할 것으로 예상할 수 있습니다. 계산된 바로는 결코 3을 넘지 않지만 무한대로 알려져 있으며, 이는 계산이 아직 제타 함수의 일반적인 행동 영역에 도달하지 않았을 수 있음을 시사합니다.
- Denjoy의 리만 가설에 대한 확률론적 주장은 만약 μ(x)가 "1"s와 "-1"s의 임의의 수열이라면, 모든 ε > 0에 대하여 부분합은 (단순 랜덤 워크에서의 위치 값은) 경계를 만족합니다.확률 1로 리만 가설은 뫼비우스 함수 μ와 이로부터 같은 방식으로 도출된 메르텐스 함수 M에 대한 이 경계와 동등합니다. 즉, 리만 가설은 어떤 의미에서는 μ(x)가 동전 던지기의 무작위 순서처럼 행동한다고 말하는 것과 같습니다. μ(x)가 0이 아닐 때 부호는 x의 소인수의 패리티를 제공하므로 비공식적으로 리만 가설은 정수의 소인수의 패리티가 임의로 행동한다고 말합니다. 수론에서 이와 같은 확률론적 논쟁은 종종 정답을 제시하지만, 엄밀하게 말하기는 매우 어려운 경향이 있으며, 마이어 정리와 같은 일부 결과에 대해 때때로 틀린 답을 제시하기도 합니다.
- Odlyzko(1987)의 계산은 제타 함수의 0이 무작위 에르미트 행렬의 고유값과 매우 유사하게 행동한다는 것을 보여주며, 이는 리만 가설을 암시하는 일부 자기 인접 연산자의 고유값임을 시사합니다. 그러한 연산자를 찾기 위한 모든 시도가 실패했습니다.
- 충분히 큰 홀수에 대한 골드바흐의 약한 추측과 같은 몇 가지 정리가 있는데, 이 정리는 처음에는 일반화된 리만 가설을 사용하여 증명되었고, 나중에는 무조건 사실로 밝혀졌습니다. 이는 일반화된 리만 가설에 대한 몇 가지 "예측"이 사실이기 때문에 약한 증거로 간주될 수 있습니다.
- 두 개의 0이 때때로 매우 가까운 [32]레머의 현상은 리만 가설을 믿지 않는 이유로 제시되기도 합니다. 그러나 사람들은 리만 가설이 사실일지라도 우연히 이런 일이 종종 일어날 것으로 예상할 수 있으며, 오드리즈코의 계산은 몽고메리의 추측에 의해 예측된 만큼 가까운 0의 쌍이 자주 발생한다는 것을 암시합니다.
- 패터슨은 대부분의 수학자들에게 리만 가설의 가장 강력한 이유는 소수가 가능한 한 규칙적으로 분포되기를 바라는 희망 때문이라고 제안합니다.[33]
메모들
- ^ ζ에 대한 값은 예를 들어 제타(1/2 - 30 i)를 계산하면 알 수 있습니다."Wolframalpha computational intelligence". wolframalpha.com. Wolfram. Retrieved 2 October 2022.
- ^ 봄비에리(2000).
- ^ 오일러, 레온하르트 (1744). Variae 관측은 infinitas를 중심으로 한 시리즈를 관측합니다. Commentarii academices cesientiarum Petropolitanae 9, pp. 160–188, 정리 7 및 8. 정리 7에서 오일러는 특수한 = s=1}에서 공식을 증명하고, 정리 8에서는 보다 일반적으로 공식을 증명합니다. 그의 정리 7의 첫 번째 결과에서 그는ζ (1= 로그 ∞ {\displaystyle \ (1)=\log \infty}이며, 이 후자의 결과를 그의 정리 19에서 활용하여 소수의 역수의 합이 로그 ∞ 로그 {\displaystyle \log \infty}임을 보여줍니다.
- ^ 잉햄(1932), 정리 30, 페이지 83; 몽고메리 & 본(2007), 페이지 430.
- ^ Ingham (1932), p. 82.
- ^ Landau, Edmund (1924), "Über die Möbiussche Funktion", Rend. Circ. Mat. Palermo, 48 (2): 277–280, doi:10.1007/BF03014702, S2CID 123636883
- ^ Titchmarsh, Edward Charles (1927), "A consequence of the Riemann hypothesis", J. London Math. Soc., 2 (4): 247–254, doi:10.1112/jlms/s1-2.4.247
- ^ Maier, Helmut; Montgomery, Hugh (2009), "The sum of the Möbius function", Bull. London Math. Soc., 41 (2): 213–226, doi:10.1112/blms/bdn119, hdl:2027.42/135214, S2CID 121272525
- ^ Soundararajan, Kannan (2009), "Partial sums of the Möbius function", J. Reine Angew. Math., 2009 (631): 141–152, arXiv:0705.0723, doi:10.1515/CRELLE.2009.044, S2CID 16501321
- ^ 로빈(1984).
- ^ Lagarias, Jeffrey C. (2002), "An elementary problem equivalent to the Riemann hypothesis", The American Mathematical Monthly, 109 (6): 534–543, arXiv:math/0008177, doi:10.2307/2695443, ISSN 0002-9890, JSTOR 2695443, MR 1908008, S2CID 15884740
- ^ Broughan (2017), Corollary 5.35.
- ^ a b c Titchmarsh (1986).
- ^ 나이스(1999).
- ^ Baez-Duarte, Luis (2005). "A general strong Nyman-Beurling criterion for the Riemann hypothesis". Publications de l'Institut Mathématique. Nouvelle Série. 78 (92): 117–125. doi:10.2298/PIM0578117B. S2CID 17406178.
- ^ 로저스&타오 (2020).
- ^ a b Platt & Trudgian (2021).
- ^ "Caltech Mathematicians Solve 19th Century Number Riddle". California Institute of Technology. October 31, 2022.
- ^ 리벤보임 (1996), 320쪽.
- ^ Radziejewski (2007).
- ^ 와일스(2000).
- ^ Connes (1999).
- ^ Leichtnam (2005).
- ^ Knauf (1999).
- ^ Sarnak (2005).
- ^ Odlyzko (2002).
- ^ Mossinghoff, Michael J.; Trudgian, Timothy S.; Yang, Andrew (2022-12-13). "Explicit zero-free regions for the Riemann zeta-function". arXiv:2212.06867 [math.NT].
- ^ Pratt, Kyle; Robles, Nicolas; Zaharescu, Alexandru; Zeindler, Dirk (2020). "More than five-twelfths of the zeros of ζ are on the critical line". Res Math Sci. 7. arXiv:1802.10521. doi:10.1007/s40687-019-0199-8. S2CID 202542332.
- ^ Johnston, David R. (29 July 2022). "Improving bounds on prime counting functions by partial verification of the Riemann hypothesis". The Ramanujan Journal. 59 (4): 1307–1321. arXiv:2109.02249. doi:10.1007/s11139-022-00616-x. S2CID 237420836.
- ^ Weisstein, Eric W., "Riemann Zeta Function Zeros", MathWorldWeisstein, Eric W., "Riemann Zeta Function Zeros", MathWorld"제타 그리드(Zeta Grid)는 가능한 한 많은 0을 계산하려고 시도하는 분산 컴퓨팅 프로젝트입니다. 2005년 2월 18일 현재 1,0299억 개의 0에 도달했습니다."
- ^ 에드워즈(1974).
- ^ Lehmer (1956).
- ^ p. 75: "자연수가 생각할 수 있는 가장 완벽한 아이디어이고, 이것이 가장 일반적인 방식으로 유통되는 소수들과만 호환되기를 기대하는 '플라토닉' 이유를 이 목록에 추가해야 할 것입니다.."
참고문헌
- Artin, Emil (1924), "Quadratische Körper im Gebiete der höheren Kongruenzen. II. Analytischer Teil", Mathematische Zeitschrift, 19 (1): 207–246, doi:10.1007/BF01181075, S2CID 117936362
- Backlund, R. J. (1914), "Sur les Zéros de la Fonction ζ(s) de Riemann", C. R. Acad. Sci. Paris, 158: 1979–1981
- Beurling, Arne (1955), "A closure problem related to the Riemann zeta-function", Proceedings of the National Academy of Sciences of the United States of America, 41 (5): 312–314, Bibcode:1955PNAS...41..312B, doi:10.1073/pnas.41.5.312, MR 0070655, PMC 528084, PMID 16589670
- Björner, Anders (2011), "A cell complex in number theory", Advances in Applied Mathematics, 46 (1–4): 71–85, arXiv:1101.5704, doi:10.1016/j.aam.2010.09.007
- Bohr, H.; Landau, E. (1914), "Ein Satz über Dirichletsche Reihen mit Anwendung auf die ζ-Funktion und die L-Funktionen", Rendiconti del Circolo Matematico di Palermo, 37 (1): 269–272, doi:10.1007/BF03014823, S2CID 121145912
- Bombieri, Enrico (2000), The Riemann Hypothesis – official problem description (PDF), Clay Mathematics Institute, archived from the original (PDF) on 2015-12-22, retrieved 2008-10-25 에서 재인쇄(Borwein et al. 2008).
- Borwein, Peter; Choi, Stephen; Rooney, Brendan; Weirathmueller, Andrea, eds. (2008), The Riemann Hypothesis: A Resource for the Afficionado and Virtuoso Alike, CMS Books in Mathematics, New York: Springer, doi:10.1007/978-0-387-72126-2, ISBN 978-0-387-72125-5
- Borwein, Peter; Ferguson, Ron; Mossinghoff, Michael J. (2008), "Sign changes in sums of the Liouville function", Mathematics of Computation, 77 (263): 1681–1694, Bibcode:2008MaCom..77.1681B, doi:10.1090/S0025-5718-08-02036-X, MR 2398787
- de Branges, Louis (1992), "The convergence of Euler products", Journal of Functional Analysis, 107 (1): 122–210, doi:10.1016/0022-1236(92)90103-P, MR 1165869
- Broughan, Kevin (2017), Equivalents of the Riemann Hypothesis, Cambridge University Press, ISBN 978-1108290784
- Burton, David M. (2006), Elementary Number Theory, Tata McGraw-Hill Publishing Company Limited, ISBN 978-0-07-061607-3
- Cartier, P. (1982), "Comment l'hypothèse de Riemann ne fut pas prouvée", Seminar on Number Theory, Paris 1980–81 (Paris, 1980/1981), Progr. Math., vol. 22, Boston, MA: Birkhäuser Boston, pp. 35–48, MR 0693308
- Connes, Alain (1999), "Trace formula in noncommutative geometry and the zeros of the Riemann zeta function", Selecta Mathematica, New Series, 5 (1): 29–106, arXiv:math/9811068, doi:10.1007/s000290050042, MR 1694895, S2CID 55820659
- Connes, Alain (2000), "Noncommutative geometry and the Riemann zeta function", Mathematics: frontiers and perspectives, Providence, R.I.: American Mathematical Society, pp. 35–54, MR 1754766
- Connes, Alain (2016), "An Essay on the Riemann Hypothesis", in Nash, J. F.; Rassias, Michael (eds.), Open Problems in Mathematics, New York: Springer, pp. 225–257, arXiv:1509.05576, doi:10.1007/978-3-319-32162-2_5
- Conrey, J. B. (1989), "More than two fifths of the zeros of the Riemann zeta function are on the critical line", J. Reine Angew. Math., 1989 (399): 1–26, doi:10.1515/crll.1989.399.1, MR 1004130, S2CID 115910600
- Conrey, J. Brian (2003), "The Riemann Hypothesis" (PDF), Notices of the American Mathematical Society: 341–353 에서 재인쇄(Borwein et al. 2008).
- Conrey, J. B.; Li, Xian-Jin (2000), "A note on some positivity conditions related to zeta and L-functions", International Mathematics Research Notices, 2000 (18): 929–940, arXiv:math/9812166, doi:10.1155/S1073792800000489, MR 1792282, S2CID 14678312
- Deligne, Pierre (1974), "La conjecture de Weil. I", Publications Mathématiques de l'IHÉS, 43: 273–307, doi:10.1007/BF02684373, MR 0340258, S2CID 123139343
- Deligne, Pierre (1980), "La conjecture de Weil : II", Publications Mathématiques de l'IHÉS, 52: 137–252, doi:10.1007/BF02684780, S2CID 189769469
- Deninger, Christopher (1998), "Some analogies between number theory and dynamical systems on foliated spaces", Proceedings of the International Congress of Mathematicians, Vol. I (Berlin, 1998), Documenta Mathematica, pp. 163–186, MR 1648030
- Dudek, Adrian W. (2014-08-21), "On the Riemann hypothesis and the difference between primes", International Journal of Number Theory, 11 (3): 771–778, arXiv:1402.6417, Bibcode:2014arXiv1402.6417D, doi:10.1142/S1793042115500426, ISSN 1793-0421, S2CID 119321107
- Dyson, Freeman (2009), "Birds and frogs" (PDF), Notices of the American Mathematical Society, 56 (2): 212–223, MR 2483565
- Edwards, H. M. (1974), Riemann's Zeta Function, New York: Dover Publications, ISBN 978-0-486-41740-0, MR 0466039
- Fesenko, Ivan (2010), "Analysis on arithmetic schemes. II", Journal of K-theory, 5 (3): 437–557, doi:10.1017/is010004028jkt103
- Ford, Kevin (2002), "Vinogradov's integral and bounds for the Riemann zeta function", Proceedings of the London Mathematical Society, Third Series, 85 (3): 565–633, arXiv:1910.08209, doi:10.1112/S0024611502013655, MR 1936814, S2CID 121144007
- Franel, J.; Landau, E. (1924), "Les suites de Farey et le problème des nombres premiers" (Franel, 198–201); "Bemerkungen zu der vorstehenden Abhandlung von Herrn Franel (Landau, 202–206)", Göttinger Nachrichten: 198–206
- Ghosh, Amit (1983), "On the Riemann zeta function—mean value theorems and the distribution of S(T) ", J. Number Theory, 17: 93–102, doi:10.1016/0022-314X(83)90010-0
- Gourdon, Xavier (2004), The 1013 first zeros of the Riemann Zeta function, and zeros computation at very large height (PDF)
- Gram, J. P. (1903), "Note sur les zéros de la fonction ζ(s) de Riemann", Acta Mathematica, 27: 289–304, doi:10.1007/BF02421310, S2CID 115327214
- Hadamard, Jacques (1896), "Sur la distribution des zéros de la fonction ζ(s) et ses conséquences arithmétiques", Bulletin de la Société Mathématique de France, 14: 199–220, doi:10.24033/bsmf.545 에서 재인쇄(Borwein et al. 2008).
- Hanga, Catalin (2020), Random matrix models for Gram's law (phd), University of York
- Hardy, G. H. (1914), "Sur les Zéros de la Fonction ζ(s) de Riemann", C. R. Acad. Sci. Paris, 158: 1012–1014, JFM 45.0716.04 에서 재인쇄(Borwein et al. 2008).
- Hardy, G. H.; Littlewood, J. E. (1921), "The zeros of Riemann's zeta-function on the critical line", Math. Z., 10 (3–4): 283–317, doi:10.1007/BF01211614, S2CID 126338046
- Haselgrove, C. B. (1958), "A disproof of a conjecture of Pólya", Mathematika, 5 (2): 141–145, doi:10.1112/S0025579300001480, ISSN 0025-5793, MR 0104638, Zbl 0085.27102 에서 재인쇄(Borwein et al. 2008).
- Haselgrove, C. B.; Miller, J. C. P. (1960), Tables of the Riemann zeta function, Royal Society Mathematical Tables, Vol. 6, Cambridge University Press, ISBN 978-0-521-06152-0, MR 0117905 검토
- Hutchinson, J. I. (1925), "On the Roots of the Riemann Zeta-Function", Transactions of the American Mathematical Society, 27 (1): 49–60, doi:10.2307/1989163, JSTOR 1989163
- Ingham, A.E. (1932), The Distribution of Prime Numbers, Cambridge Tracts in Mathematics and Mathematical Physics, vol. 30, Cambridge University Press. Reprinted 1990, ISBN 978-0-521-39789-6, MR1074573
- Ireland, Kenneth; Rosen, Michael (1990), A Classical Introduction to Modern Number Theory (Second edition), New York: Springer, ISBN 0-387-97329-X
- Ivić, A. (1985), The Riemann Zeta Function, New York: John Wiley & Sons, ISBN 978-0-471-80634-9, MR 0792089 (2003년 도버 재인쇄)
- Ivić, Aleksandar (2008), "On some reasons for doubting the Riemann hypothesis", in Borwein, Peter; Choi, Stephen; Rooney, Brendan; Weirathmueller, Andrea (eds.), The Riemann Hypothesis: A Resource for the Afficionado and Virtuoso Alike, CMS Books in Mathematics, New York: Springer, pp. 131–160, arXiv:math.NT/0311162, ISBN 978-0-387-72125-5
- Karatsuba, A. A. (1984a), "Zeros of the function ζ(s) on short intervals of the critical line", Izv. Akad. Nauk SSSR, Ser. Mat. (in Russian), 48 (3): 569–584, MR 0747251
- Karatsuba, A. A. (1984b), "Distribution of zeros of the function ζ(1/2 + it)", Izv. Akad. Nauk SSSR, Ser. Mat. (in Russian), 48 (6): 1214–1224, MR 0772113
- Karatsuba, A. A. (1985), "Zeros of the Riemann zeta-function on the critical line", Trudy Mat. Inst. Steklov. (in Russian) (167): 167–178, MR 0804073
- Karatsuba, A. A. (1992), "On the number of zeros of the Riemann zeta-function lying in almost all short intervals of the critical line", Izv. Ross. Akad. Nauk, Ser. Mat. (in Russian), 56 (2): 372–397, Bibcode:1993IzMat..40..353K, doi:10.1070/IM1993v040n02ABEH002168, MR 1180378
- Karatsuba, A. A.; Voronin, S. M. (1992), The Riemann zeta-function, de Gruyter Expositions in Mathematics, vol. 5, Berlin: Walter de Gruyter & Co., doi:10.1515/9783110886146, ISBN 978-3-11-013170-3, MR 1183467
- Keating, Jonathan P.; Snaith, N. C. (2000), "Random matrix theory and ζ(1/2 + it)", Communications in Mathematical Physics, 214 (1): 57–89, Bibcode:2000CMaPh.214...57K, doi:10.1007/s002200000261, MR 1794265, S2CID 11095649
- Knapowski, S. (1962), "On sign-changes of the difference ", Acta Arithmetica, 7: 107–119, doi:10.4064/aa-7-2-107-119, MR 0133308
- Knauf, Andreas (1999), "Number theory, dynamical systems and statistical mechanics", Reviews in Mathematical Physics, 11 (8): 1027–1060, Bibcode:1999RvMaP..11.1027K, doi:10.1142/S0129055X99000325, MR 1714352
- von Koch, Niels Helge (1901), "Sur la distribution des nombres premiers", Acta Mathematica, 24: 159–182, doi:10.1007/BF02403071, S2CID 119914826
- Kurokawa, Nobushige (1992), "Multiple zeta functions: an example", Zeta functions in geometry (Tokyo, 1990), Adv. Stud. Pure Math., vol. 21, Tokyo: Kinokuniya, pp. 219–226, MR 1210791
- Lapidus, Michel L. (2008), In search of the Riemann zeros, Providence, R.I.: American Mathematical Society, doi:10.1090/mbk/051, ISBN 978-0-8218-4222-5, MR 2375028
- Lavrik, A. F. (2001) [1994], "Zeta-function", Encyclopedia of Mathematics, EMS Press
- Lehmer, D. H. (1956), "Extended computation of the Riemann zeta-function", Mathematika, 3 (2): 102–108, doi:10.1112/S0025579300001753, MR 0086083
- Leichtnam, Eric (2005), "An invitation to Deninger's work on arithmetic zeta functions", Geometry, spectral theory, groups, and dynamics, Contemp. Math., vol. 387, Providence, RI: Amer. Math. Soc., pp. 201–236, doi:10.1090/conm/387/07243, MR 2180209.
- Levinson, N. (1974), "More than one-third of the zeros of Riemann's zeta function are on σ = 1/2", Advances in Mathematics, 13 (4): 383–436, doi:10.1016/0001-8708(74)90074-7, MR 0564081
- Littlewood, J. E. (1962), "The Riemann hypothesis", The scientist speculates: an anthology of partly baked idea, New York: Basic books
- van de Lune, J.; te Riele, H. J. J.; Winter, D. T. (1986), "On the zeros of the Riemann zeta function in the critical strip. IV", Mathematics of Computation, 46 (174): 667–681, doi:10.2307/2008005, JSTOR 2008005, MR 0829637
- Massias, J.-P.; Nicolas, Jean-Louis; Robin, G. (1988), "Évaluation asymptotique de l'ordre maximum d'un élément du groupe symétrique", Acta Arithmetica, 50 (3): 221–242, doi:10.4064/aa-50-3-221-242, MR 0960551
- Mazur, Barry; Stein, William (2015), Prime Numbers and the Riemann Hypothesis
- Montgomery, Hugh L. (1973), "The pair correlation of zeros of the zeta function", Analytic number theory, Proc. Sympos. Pure Math., vol. XXIV, Providence, R.I.: American Mathematical Society, pp. 181–193, MR 0337821 에서 재인쇄(Borwein et al. 2008).
- Montgomery, Hugh L. (1983), "Zeros of approximations to the zeta function", in Erdős, Paul (ed.), Studies in pure mathematics. To the memory of Paul Turán, Basel, Boston, Berlin: Birkhäuser, pp. 497–506, ISBN 978-3-7643-1288-6, MR 0820245
- Montgomery, Hugh L.; Vaughan, Robert C. (2007), Multiplicative Number Theory I. Classical Theory, Cambridge studies in advanced mathematics, vol. 97, Cambridge University Press.ISBN 978-0-521-84903-6
- Nicely, Thomas R. (1999), "New maximal prime gaps and first occurrences", Mathematics of Computation, 68 (227): 1311–1315, Bibcode:1999MaCom..68.1311N, doi:10.1090/S0025-5718-99-01065-0, MR 1627813.
- Nyman, Bertil (1950), On the One-Dimensional Translation Group and Semi-Group in Certain Function Spaces, PhD Thesis, University of Uppsala: University of Uppsala, MR 0036444
- Odlyzko, A. M.; te Riele, H. J. J. (1985), "Disproof of the Mertens conjecture", Journal für die reine und angewandte Mathematik, 1985 (357): 138–160, doi:10.1515/crll.1985.357.138, MR 0783538, S2CID 13016831, archived from the original on 2012-07-11
- Odlyzko, A. M. (1987), "On the distribution of spacings between zeros of the zeta function", Mathematics of Computation, 48 (177): 273–308, doi:10.2307/2007890, JSTOR 2007890, MR 0866115
- Odlyzko, A. M. (1990), "Bounds for discriminants and related estimates for class numbers, regulators and zeros of zeta functions: a survey of recent results", Séminaire de Théorie des Nombres de Bordeaux, Série 2, 2 (1): 119–141, doi:10.5802/jtnb.22, MR 1061762
- Odlyzko, A. M. (1992), The 1020-th zero of the Riemann zeta function and 175 million of its neighbors (PDF) 이 미출간된 책은 알고리즘의 구현에 대해 설명하고 그 결과에 대해 자세히 논의합니다.
- Odlyzko, A. M. (1998), The 1021st zero of the Riemann zeta function (PDF)
- Ono, Ken; Soundararajan, K. (1997), "Ramanujan's ternary quadratic form", Inventiones Mathematicae, 130 (3): 415–454, Bibcode:1997InMat.130..415O, doi:10.1007/s002220050191, S2CID 122314044
- Patterson, S. J. (1988), An introduction to the theory of the Riemann zeta-function, Cambridge Studies in Advanced Mathematics, vol. 14, Cambridge University Press, doi:10.1017/CBO9780511623707, ISBN 978-0-521-33535-5, MR 0933558
- Platt, Dave; Trudgian, Tim (January 2021), "The Riemann hypothesis is true up to ", Bulletin of the London Mathematical Society, Wiley, 53 (3): 792–797, arXiv:2004.09765, doi:10.1112/blms.12460, S2CID 234355998
- Radziejewski, Maciej (2007), "Independence of Hecke zeta functions of finite order over normal fields", Transactions of the American Mathematical Society, 359 (5): 2383–2394, doi:10.1090/S0002-9947-06-04078-5, MR 2276625,
There are infinitely many nonisomorphic algebraic number fields whose Dedekind zeta functions have infinitely many nontrivial multiple zeros.
- Ribenboim, Paulo (1996), The New Book of Prime Number Records, New York: Springer, ISBN 0-387-94457-5
- Riemann, Bernhard (1859), "Ueber die Anzahl der Primzahlen unter einer gegebenen Grösse", Monatsberichte der Berliner Akademie라이프치히 테우브너, 게삼멜테 Riemann, Bernhard (1859), "Ueber die Anzahl der Primzahlen unter einer gegebenen Grösse", Monatsberichte der Berliner Akademie베르케에서 (1892), 뉴욕 도버에 의해 재인쇄 (1953). 원고 원본(영문 번역 포함). 에서 재인쇄(Borwein et al. 2008) 및 (Edwards 1974)
- Riesel, Hans; Göhl, Gunnar (1970), "Some calculations related to Riemann's prime number formula", Mathematics of Computation, 24 (112): 969–983, doi:10.2307/2004630, JSTOR 2004630, MR 0277489
- Riesz, M. (1916), "Sur l'hypothèse de Riemann", Acta Mathematica, 40: 185–190, doi:10.1007/BF02418544
- Robin, G. (1984), "Grandes valeurs de la fonction somme des diviseurs et hypothèse de Riemann", Journal de Mathématiques Pures et Appliquées, Neuvième Série, 63 (2): 187–213, MR 0774171
- Rodgers, Brad; Tao, Terence (2020), "The de Bruijn–Newman constant is non-negative", Forum of Mathematics, 8: e6, 62, doi:10.1017/fmp.2020.6, MR 40893932018년 1월 19일 타오 블로그 공지도 Rodgers, Brad; Tao, Terence (2020), "The de Bruijn–Newman constant is non-negative", Forum of Mathematics, 8: e6, 62, doi:10.1017/fmp.2020.6, MR 4089393참조
- Rosser, J. Barkley; Yohe, J. M.; Schoenfeld, Lowell (1969), "Rigorous computation and the zeros of the Riemann zeta-function. (With discussion)", Information Processing 68 (Proc. IFIP Congress, Edinburgh, 1968), Vol. 1: Mathematics, Software, Amsterdam: North-Holland, pp. 70–76, MR 0258245
- Rudin, Walter (1973), Functional Analysis, 1st edition (January 1973), New York: McGraw-Hill, ISBN 0-070-54225-2
- Salem, Raphaël (1953), "Sur une proposition équivalente à l'hypothèse de Riemann", Les Comptes rendus de l'Académie des sciences, 236: 1127–1128, MR 0053148
- Sarnak, Peter (2005), Problems of the Millennium: The Riemann Hypothesis (2004) (PDF), Clay Mathematics Institute, retrieved 2015-07-28 에서 재인쇄(Borwein et al. 2008).
- Schoenfeld, Lowell (1976), "Sharper bounds for the Chebyshev functions θ(x) and ψ(x). II", Mathematics of Computation, 30 (134): 337–360, doi:10.2307/2005976, JSTOR 2005976, MR 0457374
- Schumayer, Daniel; Hutchinson, David A. W. (2011), "Physics of the Riemann Hypothesis", Reviews of Modern Physics, 83 (2): 307–330, arXiv:1101.3116, Bibcode:2011RvMP...83..307S, doi:10.1103/RevModPhys.83.307, S2CID 119290777
- Selberg, Atle (1942), "On the zeros of Riemann's zeta-function", SKR. Norske Vid. Akad. Oslo I., 10: 59 pp, MR 0010712
- Selberg, Atle (1946), "Contributions to the theory of the Riemann zeta-function", Arch. Math. Naturvid., 48 (5): 89–155, MR 0020594
- Selberg, Atle (1956), "Harmonic analysis and discontinuous groups in weakly symmetric Riemannian spaces with applications to Dirichlet series", J. Indian Math. Soc., New Series, 20: 47–87, MR 0088511
- Serre, Jean-Pierre (1969–1970), "Facteurs locaux des fonctions zeta des varietés algébriques (définitions et conjectures)", Séminaire Delange-Pisot-Poitou, 19
- Sheats, Jeffrey T. (1998), "The Riemann hypothesis for the Goss zeta function for Fq[T]", Journal of Number Theory, 71 (1): 121–157, arXiv:math/9801158, doi:10.1006/jnth.1998.2232, MR 1630979, S2CID 119703557
- Siegel, C. L. (1932), "Über Riemanns Nachlaß zur analytischen Zahlentheorie", Quellen Studien zur Geschichte der Math. Astron. Und Phys. Abt. B: Studien 2: 45–80 게삼멜테 아반드룽겐에서 재인쇄, 1권. 베를린: 스프링어-베를라그, 1966.
- Speiser, Andreas (1934), "Geometrisches zur Riemannschen Zetafunktion", Mathematische Annalen, 110: 514–521, doi:10.1007/BF01448042, JFM 60.0272.04, S2CID 119413347, archived from the original on 2015-06-27
- Spira, Robert (1968), "Zeros of sections of the zeta function. II", Mathematics of Computation, 22 (101): 163–173, doi:10.2307/2004774, JSTOR 2004774, MR 0228456
- Stein, William; Mazur, Barry (2007), What is Riemann's Hypothesis? (PDF), archived from the original (PDF) on 2009-03-27
- Suzuki, Masatoshi (2011), "Positivity of certain functions associated with analysis on elliptic surfaces", Journal of Number Theory, 131 (10): 1770–1796, doi:10.1016/j.jnt.2011.03.007
- Titchmarsh, Edward Charles (1935), "The Zeros of the Riemann Zeta-Function", Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences, The Royal Society, 151 (873): 234–255, Bibcode:1935RSPSA.151..234T, doi:10.1098/rspa.1935.0146, JSTOR 96545
- Titchmarsh, Edward Charles (1936), "The Zeros of the Riemann Zeta-Function", Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences, The Royal Society, 157 (891): 261–263, arXiv:1004.4143, Bibcode:1936RSPSA.157..261T, doi:10.1098/rspa.1936.0192, JSTOR 96692
- Titchmarsh, Edward Charles (1986), The theory of the Riemann zeta-function (2nd ed.), The Clarendon Press Oxford University Press, ISBN 978-0-19-853369-6, MR 0882550
- Trudgian, Timothy S. (2014), "An improved upper bound for the argument of the Riemann zeta function on the critical line II", J. Number Theory, 134: 280–292, arXiv:1208.5846, doi:10.1016/j.jnt.2013.07.017
- Trudgian, Timothy (2011), "On the success and failure of Gram's Law and the Rosser Rule", Acta Arithmetica, 125 (3): 225–256, doi:10.4064/aa148-3-2
- Turán, Paul (1948), "On some approximative Dirichlet-polynomials in the theory of the zeta-function of Riemann", Danske Vid. Selsk. Mat.-Fys. Medd., 24 (17): 36, MR 0027305 에서 재인쇄(Borwein et al. 2008).
- Turing, Alan M. (1953), "Some calculations of the Riemann zeta-function", Proceedings of the London Mathematical Society, Third Series, 3: 99–117, doi:10.1112/plms/s3-3.1.99, MR 0055785
- de la Vallée-Poussin, Ch.J. (1896), "Recherches analytiques sur la théorie des nombres premiers", Ann. Soc. Sci. Bruxelles, 20: 183–256
- de la Vallée-Poussin, Ch.J. (1899–1900), "Sur la fonction ζ(s) de Riemann et la nombre des nombres premiers inférieurs à une limite donnée", Mem. Couronnes Acad. Sci. Belg., 59 (1) 에서 재인쇄(Borwein et al. 2008).
- Weil, André (1948), Sur les courbes algébriques et les variétés qui s'en déduisent, Actualités Sci. Ind., no. 1041 = Publ. Inst. Math. Univ. Strasbourg 7 (1945), Hermann et Cie., Paris, MR 0027151
- Weil, André (1949), "Numbers of solutions of equations in finite fields", Bulletin of the American Mathematical Society, 55 (5): 497–508, doi:10.1090/S0002-9904-1949-09219-4, MR 0029393 앙드레 바일 ISBN 0-387-90330-5에 의해 Oeuvres Scientificques/collected papers에 재인쇄.
- Weinberger, Peter J. (1973), "On Euclidean rings of algebraic integers", Analytic number theory ( St. Louis Univ., 1972), Proc. Sympos. Pure Math., vol. 24, Providence, R.I.: Amer. Math. Soc., pp. 321–332, MR 0337902
- Wiles, Andrew (2000), "Twenty years of number theory", Mathematics: frontiers and perspectives, Providence, R.I.: American Mathematical Society, pp. 329–342, ISBN 978-0-8218-2697-3, MR 1754786
- Zagier, Don (1977), "The first 50 million prime numbers" (PDF), Math. Intelligencer, Springer, 1: 7–19, doi:10.1007/BF03039306, MR 0643810, S2CID 189886510, archived from the original (PDF) on 2009-03-27
- Zagier, Don (1981), "Eisenstein series and the Riemann zeta function", Automorphic forms, representation theory and arithmetic (Bombay, 1979), Tata Inst. Fund. Res. Studies in Math., vol. 10, Tata Inst. Fundamental Res., Bombay, pp. 275–301, MR 0633666
인기 박람회
- Sabbagh, Karl (2003a), The greatest unsolved problem in mathematics, Farrar, Straus and Giroux, New York, ISBN 978-0-374-25007-2, MR 1979664
- Sabbagh, Karl (2003b), Dr. Riemann's zeros, Atlantic Books, London, ISBN 978-1-843-54101-1
- du Sautoy, Marcus (2003), The music of the primes, HarperCollins Publishers, ISBN 978-0-06-621070-4, MR 2060134
- Rockmore, Dan (2005), Stalking the Riemann hypothesis, Pantheon Books, ISBN 978-0-375-42136-5, MR 2269393
- Derbyshire, John (2003), Prime Obsession, Joseph Henry Press, Washington, DC, ISBN 978-0-309-08549-6, MR 1968857
- Watkins, Matthew (2015), Mystery of the Prime Numbers, Liberalis Books, ISBN 978-1782797814, MR 0000000
- Frenkel, Edward (2014), The Riemann Hypothesis Numberphile, 2014년 3월 11일 (영상)
Derbyshire 2003, Rockmore 2005, Sabbagh 2003, Sautoy 2003, Watkins 2015는 모두 비기술적입니다. Edwards 1974, Patterson 1988, Borwein/Choi/Rooney/Weirathmueller 2008, Majur/Stein 2015 및 Broughan 2017은 수학적 소개를 제공하며, Titchmarsh 1986, Ivich 1985 및 Karatsuba/Voron in 1992는 고급 모노그래프입니다.
외부 링크
- 미국 수학 연구소, 리만 가설
- Zeroes 데이터베이스, 103 800 788 359 0
- Apostol, Tom, Where are the zeros of zeta of s? 존 더비셔가 부른 리만 가설에 관한 시.
- Borwein, Peter, The Riemann Hypothesis (PDF), archived from the original (PDF) on 2009-03-27 (강의용 슬라이드)
- Conrad, K. (2010), Consequences of the Riemann hypothesis
- Conrey, J. Brian; Farmer, David W, Equivalences to the Riemann hypothesis, archived from the original on 2010-03-16
- Gourdon, Xavier; Sebah, Pascal (2004), Computation of zeros of the Zeta function (GUE 가설을 검토하고 광범위한 참고 문헌도 제공합니다.)
- Odlyzko, Andrew, Home page 제타 함수의 0에 관한 논문과 제타 함수의 0에 관한 표를 포함하여
- Odlyzko, Andrew (2002), Zeros of the Riemann zeta function: Conjectures and computations (PDF) 강연 슬라이드
- Pegg, Ed (2004), Ten Trillion Zeta Zeros, Math Games website, archived from the original on 2004-11-02, retrieved 2004-10-20Xavier Gourdon의 최초 10조개의 사소하지 않은 0에 대한 계산에 대한 Pegg, Ed (2004), Ten Trillion Zeta Zeros, Math Games website, archived from the original on 2004-11-02, retrieved 2004-10-20논의
- Rubinstein, Michael, algorithm for generating the zeros, archived from the original on 2007-04-27.
- du Sautoy, Marcus (2006), Prime Numbers Get Hitched, Seed Magazine, archived from the original on 2017-09-22, retrieved 2006-03-27
{{citation}}: CS1 maint: 잘못된 URL (링크) - Watkins, Matthew R. (2021-02-27), Proposed (dis)proofs of the Riemann Hypothesis, archived from the original on December 9, 2022
- Zetagrid(2002) 리만의 가설을 반증하고자 시도한 분산 컴퓨팅 프로젝트 2005년 11월 마감




















 .
.









































 단지 논문의 증명 요건을 충족하기에 "충분히 큰" 것으로 가정되기 때문에 경계를 알 수 없는 두 번째 제로 프리 영역에 대한 개선을 가지고 있습니다. 이 지역은.
단지 논문의 증명 요건을 충족하기에 "충분히 큰" 것으로 가정되기 때문에 경계를 알 수 없는 두 번째 제로 프리 영역에 대한 개선을 가지고 있습니다. 이 지역은. ![(T,T+H]](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a7f206ba185f5e71e82482b52823f9cab4a9d99)










![{\displaystyle (0,T]~}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32185e31a7ceddedfbd8767e0dd79a6afbb0582c)











