소수계산함수

수학에서 소수를 세는 함수는 어떤 실수 x보다 작거나 같은 소수의 개수를 세는 함수입니다.^[1][2] π(x)로 표시됩니다(숫자 π와 무관함).

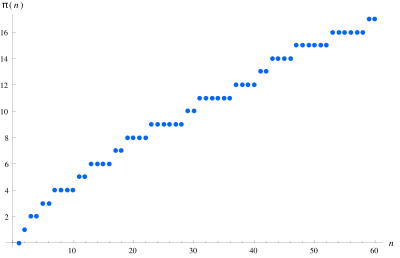
성장률

정수론에서 큰 관심을 끄는 것은 소수 계산 함수의 증가율입니다.^[3][4] 그것은 18세기 말에 가우스에 의해 추측되었고, 레전드레에 의해 대략적으로 추정되었습니다.

여기서 log는 자연로그이며, 다음과 같은 의미에서

이 문장이 소수 정리입니다. 이에 해당하는 문장은

여기서 li는 로그 적분 함수입니다. 소수 정리는 1896년 자크 하다마르와 샤를 드 라 푸신이 각각 독립적으로 1859년 리만에 의해 도입된 리만 제타 함수의 성질을 이용하여 처음으로 증명했습니다. 제타 함수나 복소해석을 사용하지 않는 소수 정리의 증명은 1948년경 아틀레 셀버그와 폴 에르트 ő스에 의해 발견되었습니다.

더 정확한 견적

1899년, 델라 발레 푸신은 다음과 같은 사실을 증명했습니다.

양의 상수 a에 대하여. 여기서 O(...)는 큰 O 표기법입니다.

${\displaystyle \mathrm{이제}}$π(x)${\displaystyle$\pi(x)\!}의 더 정확한 추정치가 알려졌습니다. 예를 들어, 2002년에 케빈 포드는 이것을^[7] 증명했습니다.

Mossinghoff와 Trudgian은$$π(x) ${\displaystyle$\pi(${\displaystyle x)\}}$와${\displaystyle \mathrm{li}}$⁡(x) {\$displaystyle$\$operatorname$ {li}(x)}의 차이에 대해 명시적인 상한을 증명했습니다.

$x$≥ 229 ${\displaystyle$ x$\backslash$geq 229}의 경우.

지나치게 크지 않은 $x$ ${\displaystyle x}$ 값의 경우, ${\displaystyle \mathrm{li}}$⁡($x)$ ${\displaystyle \operatorname {$li}(x)}이(x) π(x) {\displaystyle \pi(x)}보다 큽니다. 그러나 π(x) - li ⁡(x) {\displaystyle \pi(x)-\operatorname {li}(x)}(x)는 부호를 무한히 많이 변경하는 것으로 알려져 있습니다. 이에 대한 논의는 Skews의 번호를 참조하십시오.

정확한 양식

For ${\displaystyle x>1}$ let ${\displaystyle \pi _{0}(x)=\pi (x)-1/2}$ when ${\displaystyle x}$ is a prime number, and ${\displaystyle \pi _{0}(x)=\pi (x)}$ otherwise. 베른하르트 리만은 주어진 크기보다 작은 소수에 관한 그의 연구에서${\displaystyle }$π$$0 ${\displaystyle \pi_${0}(x)}가 다음과 같음을 증명했습니다.

어디에 μ(n)은 뫼비우스 함수, li(x)는 로그 적분 함수, ρ 지수는 리만 제타 함수의 0마다, li(x)는 분기 절단으로 평가되지 않고 Ei(ρ/n log x)로 간주되며, 여기서 Ei(x)는 지수 적분입니다. 자명한 0이 수집되고 합이 리만 제타 $함수$의 자명하지 않은 0 ρ 위에서만 취해지는 ${\displaystyle \mathrm{경우}}$,$$π 0 (x$) {\displaystyle$\pi_{0}(x)}은 다음과 같이 근사화될 수 있습니다.

리만 가설은 이러한 모든 비 trivial 0이 Re(s) = 1/2을 따라 놓여 있음을 시사합니다.

π(x), x / log x 및 li(x)의 표

표는 10의 거듭제곱에서 세 함수 π(x), x / log x 및 li(x)를 비교하는 방법을 보여줍니다. 참고,^[3][11] 그리고^[12]

x	π(x)	π(x) − x / log x	li(x) − π(x)	x / π(x)	x / log x % 오류
10	4	0	2	2.500	-8.57%
102	25	3	5	4.000	13.14%
103	168	23	10	5.952	13.83%
104	1,229	143	17	8.137	11.66%
105	9,592	906	38	10.425	9.45%
106	78,498	6,116	130	12.739	7.79%
107	664,579	44,158	339	15.047	6.64%
108	5,761,455	332,774	754	17.357	5.78%
109	50,847,534	2,592,592	1,701	19.667	5.10%
1010	455,052,511	20,758,029	3,104	21.975	4.56%
1011	4,118,054,813	169,923,159	11,588	24.283	4.13%
1012	37,607,912,018	1,416,705,193	38,263	26.590	3.77%
1013	346,065,536,839	11,992,858,452	108,971	28.896	3.47%
1014	3,204,941,750,802	102,838,308,636	314,890	31.202	3.21%
1015	29,844,570,422,669	891,604,962,452	1,052,619	33.507	2.99%
1016	279,238,341,033,925	7,804,289,844,393	3,214,632	35.812	2.79%
1017	2,623,557,157,654,233	68,883,734,693,928	7,956,589	38.116	2.63%
1018	24,739,954,287,740,860	612,483,070,893,536	21,949,555	40.420	2.48%
1019	234,057,667,276,344,607	5,481,624,169,369,961	99,877,775	42.725	2.34%
1020	2,220,819,602,560,918,840	49,347,193,044,659,702	222,744,644	45.028	2.22%
1021	21,127,269,486,018,731,928	446,579,871,578,168,707	597,394,254	47.332	2.11%
1022	201,467,286,689,315,906,290	4,060,704,006,019,620,994	1,932,355,208	49.636	2.02%
1023	1,925,320,391,606,803,968,923	37,083,513,766,578,631,309	7,250,186,216	51.939	1.93%
1024	18,435,599,767,349,200,867,866	339,996,354,713,708,049,069	17,146,907,278	54.243	1.84%
1025	176,846,309,399,143,769,411,680	3,128,516,637,843,038,351,228	55,160,980,939	56.546	1.77%
1026	1,699,246,750,872,437,141,327,603	28,883,358,936,853,188,823,261	155,891,678,121	58.850	1.70%
1027	16,352,460,426,841,680,446,427,399	267,479,615,610,131,274,163,365	508,666,658,006	61.153	1.64%
1028	157,589,269,275,973,410,412,739,598	2,484,097,167,669,186,251,622,127	1,427,745,660,374	63.456	1.58%
1029	1,520,698,109,714,272,166,094,258,063	23,130,930,737,541,725,917,951,446	4,551,193,622,464	65.759	1.52%

온라인 정수 시퀀스 백과사전에서 π(x) 열은 시퀀스 OEIS: A006880, π(x) - x/log x는 시퀀스 OEIS: A057835, li(x) - π(x)는 시퀀스 OEIS: A057752입니다.

π(10)의 값은 원래 J. Buete, J. Franke, A. Jost 및 T에 의해 계산되었습니다. 리만 가설을 가정한 클라인정.^[13] 나중에 D. J. Platt의 계산에서 무조건적으로 검증되었습니다.^[14] π(10)의 값은 J. Buete, J. Franke, A. Jost 및 T에 기인합니다. 클라인정.^[15] π(10)의 값은 DB 스테이플에 의해 계산되었습니다. 이 표의 다른 모든 이전 항목도 해당 작업의 일부로 확인되었습니다.

10에²⁷ 대한 가치는 2015년 데이비드 보와 킴 월리쉬에 의해 발표되었습니다.^[17]

10에²⁸ 대한 가치는 데이비드 보와 킴 월리쉬에 의해 2020년에 발표되었습니다.^[18]

10에²⁹ 대한 가치는 David Baugh와 Kim Walisch에 의해 2022년에 발표되었습니다.^[19]

π(x)를 평가하는 알고리즘

$x {\displaystyle$ x}가 너무 크지 않은 경우$$π (x) ${\displaystyle \$pi $($$x$)}를 찾는 간단한 방법은 에라토스테네스의 체를 사용하여 x${\displaystyle$ x} $이하$의$$소수를 생성한 다음 이를 세는 것입니다.

π$(x$)${\displaystyle }${\displaystyle \pi(x)}를 찾는 더 정교한 방법은 Legendre(포함-배제 원리를 사용하는) 덕분입니다. 만약 x {\displaystyle x}가 주어지면, p 1, p 2, …, p {\displaystyle p_{1}, p_{2},\ldots, p_{n}는 서로 다른 소수입니다. $그러면{\displaystyle {}_{}}$ x ${\displaystyle x}$보다 작거나$$ 같은 정수의 수를 ${\displaystyle {pi}_{}}$ ${\$가 아닌 경우$$

${\displaystyle \lfloor x\rfloor -\sum _{i}\left\lfloor {\frac {x}{p_{i}}}\right\rfloor +\sum _{i<j}\left\lfloor {\frac {x}{p_{i}p_{j}}}\right\rfloor -\sum _{i<j<k}\left\lfloor {\frac {x}{p_{i}p_{j}p_{k}}}\right\rfloor +\cdots }$

($여기서$⌊ x ⌋${\displaystyle \lfloor$ {x$}\$rfloor}는 바닥 함수를 나타냅니다.) 따라서 이 숫자는 다음과 같습니다.

${\displaystyle \pi(x)-\pi \left ({\sqrt {x}\right)+1}$

숫자 $p{\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$ ${\displaystyle {p\mathrm{}}_{}}$ ${\displaystyle {}_{}\dots ,}$ ${\displaystyle p_{}}$ ${\$가 $x{\displaystyle }$ ${\displaystyle$ x$}$의 제곱근 이하인 소수입니다$.$

미셀-레머 알고리즘

1870년과 1885년 사이에 출판된 일련의 기사에서 ${\displaystyle \mathrm{에른스트}}$ 메셀은${\displaystyle }$π을 평가하는 실용적인 조합 방법을 설명$($그리고 사용)했습니다. ${\displaystyle \pi$(${\displaystyle x}$)\ :}${\displaystyle {}_{}{p}_{}}$1${\displaystyle ,{}_{}}$ ${\displaystyle 2_{}}$, ${\displaystyle \dots ,}$ p${\displaystyle \p_{$1}, p_{$2},\$ldots,$p_{n}\ }$ be the first ${\displaystyle \ n\ }$ primes and denote by ${\displaystyle \Phi (m,n)}$ the number of natural numbers not greater than ${\displaystyle \ m\ }$ which are divisible by none of the ${\displaystyle \ p_{i}\ }$ for any ${\displaystyle \ i\leq n\ .$$}$그러면$$.

${\displaystyle \Phi (m,n)=\Phi (m,n-1)-\Phi \left({\frac {m}{p_{n}}},n-1\right).}$

자연수 ${\displaystyle m}$이 주어지면 ${\displaystyle$\ m$\,}$ ${\displaystyle 만약}$ n =$$π$$(m 3) {\displaystyle \$n$=\pi \$left$({\$sqrt$[{3$}]{$m}}\right)\} 그리고 μ = π (m) - n, {\displaystyle \mu =\pi \left ({\sqrt {m}}\right)-n\,} 그렇다면

${\displaystyle \pi (m)=\Phi (m,n)+n(\mu +1)+{\frac {\mu ^{2}-\mu }{2}}-1-\sum _{k=1}^{\mu }\pi \left({\frac {m}{p_{n+k}}}\right)\ .}$

이 접근 방식을 사용하여 x ${\displaystyle$\$$x\ }에 대해 5×10, 10, 10 및 10과 동일한 메셀 컴퓨터${\displaystyle }$π$($x ), ${\displaystyle \pi$ ($)\,}$을(를) 사용합니다.

1959년, 데릭 헨리 레머(Derrick Henry Lehmer)는 메셀(Misel)의 방법을 확장하고 단순화했습니다. Define, for real ${\displaystyle \ m\ }$ and for natural numbers ${\displaystyle \ n\ }$ and ${\displaystyle \ k\ ,}$ ${\displaystyle \ P_{k}(m,n)\ }$ as the number of numbers not greater than m with exactly k prime factors, all greater than ${\displaystyle p_n.}$${\displaystyle$\ $p_{n}\ .}$ 또한 ${\displaystyle P}$ ${\displaystyle 0_{}m,}$ $n$${\displaystyle )}$ = ${\$displaystyle \ P_{0}(m, $n$) = 1\ .} 그러면

${\displaystyle \ \Phi (m,n)=\sum _{k=0}^{+\infty }P_{k}(m,n)\ }$

합이 실제로 0이 아닌 항들을 아주 많이 가지는 경우. Let ${\displaystyle \ y\ }$ denote an integer such that ${\displaystyle \ {\sqrt[{3}]{m\ }}\leq y\leq {\sqrt {m\ }}\ ,}$ and set ${\displaystyle \ n=\pi (y)\ .}$ Then ${\displaystyle \ P_{1}(m,$$n)$k가 $≥$ 3일 때 $=\pi$ ($m$)-$n\$} 및 Pk$$(m, n) $=$ 0 {\displaystyle \ P_{k}(m, n) $=$ 0\}입니다. {\displaystyle \ k\geq 3\ .} 따라서,

${\displaystyle \ \pi (m)=\Phi (m,n)+n-1-P_{2}(m,n)\ }$

${\displaystyle {P2\mathrm{}}_{}}$(${\displaystyle m,}$ ${\displaystyle n)}$ ${\$\ $P_{2}(m,$ n$)\ }$의 계산은 다음과 같이 구할 수 있습니다$$.

${\displaystyle P_{2}(m,n)=\sum_{y<p\leq {\sqrt {m\}}\left(\pi \left ({\frac {m}}\right)-\pi(p)+1\right)\,}$

합이 소수를 넘는 경우.

한편,${\displaystyle }$φ${\displaystyle (}$m$,$ n) ${\displaystyle \$ $\Phi($m, n)\}의 계산은 다음 규칙을 사용하여 수행할 수 있습니다.

1. ${\displaystyle \ \ \Phi(m,0)=\lfloor m\rfloor \ }$
2. ${\displaystyle \ \Phi (m,b)=\Phi (m,b-1)-\Phi \left({\frac {m}{p_{b}}},b-1\right)\ }$

그의 방법과 IBM 701을 사용하여 Lehmer는${\displaystyle }$π${\displaystyle {}^{}}$109) ${\displaystyle \pi \left(10$^{9$}\$right)\}의 정확한 값을 계산할 수 있었고$$π(1010) ${\displaystyle \left($10^{10}\right)}의 정확한${\displaystyle }값$을 1만큼 놓쳤습니다.

이 방법에 대한 추가적인 개선은 Lagarias, Miller, Odlyzko, Deléglise 및 Rivat에 의해 이루어졌습니다.^[21]

기타 소인수 함수

다른 프라임 카운팅 기능들도 작업하기에 더 편리하기 때문에 사용됩니다.

리만의 소수 거듭제곱 계수 함수

Riemann's prime-power counting function is usually denoted as ${\displaystyle \ \Pi _{0}(x)\ }$ or ${\displaystyle \ J_{0}(x)\ .}$ It has jumps of ${\displaystyle \ {\tfrac {1}{\ n\ }}\ }$ at prime powers ${\displaystyle \ p^{n}\ ,$$}$그리고 이 값은 $π$(x)의 불연속에서 양변의 중간 값을 갖습니다. 이 추가된 세부 정보는 함수가 역 Mellin 변환에 의해 정의될 수 있기 때문에 사용됩니다.

형식적으로, 우리는${\displaystyle }$π$$0 (x) ${\displaystyle \Pi _{$0}(x)\}을 다음과 같이 정의할 수 있습니다.

${\displaystyle \ \Pi _{0}(x)={\frac {1}{2}}\left(\sum _{p^{n}<x}{\frac {1}{n}}~+~\sum _{p^{n}\leq x}{\frac {1}{n}}\right)\ }$

여기서 각 합의 변수 p는 지정된 한계 내의 모든 소수에 걸쳐 있습니다.

우리는 또한 쓸 수 있습니다.

${\displaystyle \ \Pi _{0}(x)=\sum _{n=2}^{x}{\frac {\Lambda (n)}{\log n}}-{\frac {\Lambda (x)}{2\log x}}=\sum _{n=1}^{\infty }{\frac {1}{n}}\pi _{0}{\bigl (}x^{1/n}{\bigr )}\ }$

여기서$$λ$($n) ${\displaystyle$ \ $\Lambda($n)\ }는 폰 망골트 함수이고,

${\displaystyle \pi _{0}(x)=\lim _{\varepsilon \to 0}{\frac {\pi (x-\varepsilon )+\pi (x+\varepsilon )\} {2}$

뫼비우스 반전 공식은 다음을 제공합니다.

${\displaystyle \pi _{0}(x)=\sum _{n=1}^{\infty }{\frac {\ \mu (n)\ }{n}}\ \Pi _{0}{\bigl (}x^{1/n}{\bigr )}\ ,}$

여기서 ${\displaystyle \mu (n)}$ ${\$는 뫼비우스 함수입니다.

리만 제타 함수의 로그와 폰 망골트 함수$$λ${\displaystyle$\Lambda$$ 사이의 관계를 알고 페론 공식을 사용하면

${\displaystyle \ \log \zeta (s)=s\int _{0}^{\infty }\Pi _{0}(x)x^{-s-1}\ \mathrm {d} x\ }$

체비셰프의 함수

Chebyhev 함수는 log(p)에 의한 소수 또는 소수 p의ⁿ 가중치를 부여합니다.

${\displaystyle \theta(x)=\sum _{p\leq x}\log p\}$

${\displaystyle \ \psi (x)\ =\ \sum _{p^{n}\leq x}\log p\ =\ \sum _{n=1}^{\infty }\theta {\bigl (}x^{1/n}{\bigr )}\ =\ \sum _{n\leq x}\Lambda (n)\ .}$

$x$≥ 2 ${\displaystyle$x$\backslash$geq 2}의 경우,

${\displaystyle \ \ \vartheta(x)=\pi(x)\ \log x\ -\int _{2}^{x}{\frac {\pi(t)\{t}}\ \mathrm {d} t\}$

그리고.

${\displaystyle \ \pi (x)={\frac {\vartheta (x)}{\ \log x\ }}+\int _{2}^{x}{\frac {\vartheta (t)}{\ t\ \log ^{2}(t)\ }}\ \mathrm {d} t\ .}$^[22]

소수 계산 함수에 대한 공식

소수 계산 함수에 대한 공식은 산술 공식과 분석 공식의 두 가지 종류가 있습니다. 소수 정리를 증명하기 위해 처음으로 사용된 것은 소수 계산에 대한 분석 공식이었습니다. 이들은 리만과 폰 망골트의 연구에서 비롯되었으며 일반적으로 명시적 공식으로 알려져 있습니다.^[23]

두 번째 체비셰프 함수 ψ에 대한 식을 다음과 같이 표현합니다.

${\displaystyle \psi _{0}(x)=x-\sum _{\rho }{\frac {x^{\rho }}{\rho }}-\log 2\pi -{\frac {1}{2}}\log \left(1-x^{-2}\right),}$

어디에

${\displaystyle \psi_{0}(x)=\lim_{\varepsilon \to 0}{\frac {\psi(x-\varepsilon )+\psi(x+\varepsilon )}{2}}$

여기서 ρ은 ρ의 실수 부분이 0과 1 사이인 임계 띠에서 리만 제타 함수의 0입니다. 이 공식은 관심 영역인 1보다 큰 x 값에 대해 유효합니다. 근 위의 합은 조건부 수렴이므로, 허수 부분의 절대값이 증가하는 순서로 취해야 합니다. 사소한 근에 대한 동일한 합은 공식의 마지막 하위 이해를 제공합니다.

π${\displaystyle }$0$(x$) {\displaystyle \Pi _{0}(x)}의 경우 더 복잡한 공식이 있습니다.

${\displaystyle \Pi_{0}(x)=\operatorname {li}(x)-\sum_{\rho}\operatorname {li}(x^{\rho})-\log 2+\int_{x}^{\infty}{\frac {dt}{t\left(t^{2}-1\right)\log t}}.$

다시 말하지만, 공식은 x > 1에 대해 유효하며, ρ는 절대값에 따라 순서가 매겨진 제타 함수의 자명하지 않은 0입니다. 적분값은 자명한 0에 대한 급수와 같습니다.

${\displaystyle \int _{x}^{\infty }{\frac {\mathrm {d} t}{t\left(t^{2}-1\right)\log t}}=\int _{x}^{\infty }{\frac {1}{t\log t}}\left(\sum _{m}t^{-2m}\right)\,\mathrm {d} t=\sum _{m}\int _{x}^{\infty }{\frac {t^{-2m}}{t\log t}}\,\mathrm {d} t\,\,{\overset {(u=t^{-2m})}{=}}-\sum _{m}\operatorname {li} (x^{-2m})}$

첫 번째 항 li(x)는 일반적인 로그 적분 함수입니다. 두 번째 항의 표현 li(x)는 Ei(ρ 로그 x)로 간주되어야 합니다. 여기서 Ei는 지수 적분 함수가 음의 실수에서 양의 실수를 따라 가지가 잘린 복소 평면으로의 분석적 연속입니다.

따라서 뫼비우스 반전 공식은 다음과^[10] 같습니다.

${\displaystyle \pi_{0}(x)=\operatorname {R}(x)-\sum_{\rho}\operatorname {R}(x^{\rho})-\sum_{m}\operatorname {R}(x^{-2m})}$

x > 1에 유효하며, 여기서

${\displaystyle \operatorname {R} (x)=\sum _{n=1}^{\infty }{\frac {\mu (n)}{n}}\operatorname {li} (x^{1/n})=1+\sum _{k=1}^{\infty }{\frac {(\log x)^{k}}{k!k\zeta (k+1)}}}$

는 리만의 R-함수이고^[24] μ(n)은 뫼비우스 함수입니다. 후자의 시리즈는 그램 시리즈로 알려져 있습니다.^[25][26] x > 0${\displaystyle$ x0에 대해 ⁡ ( ) < $x$ ${\displaystyle \log($x)<x}이기 때문에 이 시리즈는 x${\displaystyle$e^{x$}}$에 대한 시리즈와 비교하여 모든 양의 x에 대해 수렴합니다. 사소하지 않은 영점 기여에 대한 합계의 그램 시리즈의 $로그$는 로그$$⁡$x {\$${\displaystyle displaystyle}$ \rho \log x}로 평가되어야 하며 로그 ⁡ x ρ {\displaystyle \log x^{\rho }}로 평가해야 합니다.

포크마르 보르네만은 ^[27]리만 제타 함수의 모든 0이 단순하다는 가정을 할 때,^{[note 1]}

${\displaystyle \operatorname {R} (e^{-2\pi t})={\frac {1}{\pi }}\sum _{k=1}^{\infty }{\frac {(-1)^{k-1}t^{-2k-1}}{(2k+1)\zeta (2k+1)}}+{\frac {1}{2}}\sum _{\rho }{\frac {t^{-\rho }}{\rho \cos(\pi \rho /2)\zeta '(\rho )}}}$

여기서ρ ${\displaystyle$\rho}는 리만 제타의 사소하지 않은 0 위에서 $실행$되며t > 0 {\$displaystyle$ t>0}입니다.

π$(x$) {\$displaystyle \pi_{$0}(x)} 공식의 사소하지 않은 제타 0 위의 합은 π 0(x), {\displaystyle \pi_{0}(x)의 변동을 설명하고 나머지 항은 소수 계산 함수의 "평활한" 부분을 제공하므로 다음을 사용할 수 있습니다.

${\displaystyle \operatorname {R} (x)-\sum _{m=1}^{\infty}\operatorname {R} (x^{-2m})}$

x > 1에 대한$$π (x ) ${\displaystyle$\pi (x)}의 좋은 추정치입니다. 실제로 두 번째 항은 $x$ → ∞ {\$displaystyle$x\$to$infty}로서 0에 접근하는 반면, "noisy" 부분의 $진폭$은${\displaystyle }$x$$/ 로그$$⁡$x$ ${\displaystyle$ {\sqrt {x}}/\log x,$}$${\displaystyle R}$${\displaystyle }$$⁡$ (x) ${\displaystyle \$$pi$ ($x{\displaystyle )\}}$을 R $π$ (x${\displaystyle )}$ ${\displaystyle \$operatorname {R} (x)} 단독으로 추정하는 것도 마찬가지이며, 소수 분포의 변동을 함수로 명확하게 나타낼 수 있습니다.

${\displaystyle {\bigl(})\pi_{0}(x)-\operatorname {R}(x){\bigr)}{\frac {\log x}{\sqrt {x}}}$

부등식

다음은 π(x)에 대한 유용한 부등식입니다.

${\displaystyle {\frac {x}{\log x}}<\pi(x)<1.25506{\frac {x}{\log x}}}$

x ≥ 17의 경우.

왼쪽 부등식은 x ≥ 17을 나타내고 오른쪽 부등식은 x > 1을 나타냅니다. 상수 1.25506은 $\frac{30}{}$ $\frac{\mathrm{로그}}{}$ ⁡$113$${\textstyle {\frac$ {30\log 113}{113}}~소수점 5자리입니다. π (x) 로그 ⁡ x {\textstyle {\pi(x)\log x}{x}}의 최대값은 x = 113입니다.

Pierre Dusart는 2010년에 다음과 같이 증명했습니다.

$⁡$ 1< π ( x )${\displaystyle${\$frac {x}{\log$ $x-1{\displaystyle \}\}<\backslash \mathrm{pi}}$($))$ x ≥ $5393$displaystyle x\geq 5393}의 경우, 그리고

$x$${\displaystyle \mathrm{x}}$ $≥$ $60184 {\displaystyle x\$geq$$60184}의 경우 1$}}.$

여기 n번째 소수 p에_n 대한 몇 가지 부등식이 있습니다. 상한은 Rosser(1941),^[31] Dusart(1999)에 대한 하한은 Roser(1941)에 의한 것입니다.^[32]

(n $⁡$ ) - 1< <n$로그$⁡ (n$로그$⁡ n) ${\displaystyle n(\log(n\$log n))-1)<p_{n}<n\log(n\log n)} n ≥ 6에 대해.

왼쪽 부등식은 n ≥ 2를, 오른쪽 부등식은 n ≥ 6을 나타냅니다.

n번째 소수에 대한 근사치는

${\displaystyle p_{n}=n(\log(n\log n)-1)+{\frac {n(\log \log n-2)}{\log n}}+O\left({\frac {n(\log \log n)^{2}}{(\log n)^{2}}}\right).}$

라마누잔은^[33] 부등식이

${\displaystyle \pi(x)^{2}<{\frac {ex}{\log x}}\pi \left ({\frac {x}{e}}\right)}$

충분히 큰 $x{\displaystyle }$ ${\displaystyle$ x$}$ 값 모두에 대해 hold를 지정합니다$.$

Dusart는 ${\displaystyle \mathrm{n개}}$의$$≥ $688383 {\displaystyle n$geq 688383}에 대하여,

${\displaystyle p_{n}\leq n\left(\log n+\log \log n-1+{\frac {\log \log n-2}{\log n}\right),}$

$그리고$ ($명제$6.7)$n개$의 ≥ $3${\displaystyle n$\backslash$geq 3}에 대하여,

${\displaystyle p_{n}\geq n\left(\log n+\log \log n-1+{\frac {\log \log n-2.1}{\log n}\right)}$

더 최근에, 두사르트는^[34] (정리 5.1) > {\$display x$> 1$}$에 대하여

${\displaystyle }$(${\displaystyle \frac{x)}{}}$ ${\displaystyle \le }$ $로그$⁡ x (1 + 1${\displaystyle }$로그 ⁡ x + 2 로${\displaystyle 그}$ 2 ⁡ x + 7.59${\displaystyle }$로그 ⁡ x) {\displaystyle \pi (x)\leq {\frac {x}{\log x}}\left(1+{\frac {1}{\log x}}+{\frac {2}}{\log ^{2}x}+{\frac {7.59}{\log ^{3}x}\right)},

${\displaystyle \mathrm{그리고}}$ x ≥ $88789 {\displaystyle x\$geq$$88789}의 경우,

${\displaystyle \pi(x)>{\frac {x}{\log x}}\left(1+{\frac {1}{\log x}}+{\frac {2}{\log ^{2}x}}\right)}}$

리만 가설

리만 가설은$$π (x) ${\displaystyle$\pi $($x)}에 대한 추정의 오차에 대한 훨씬 더 엄격한 경계를 의미하며, 따라서 소수의 정규 분포를 의미합니다.

${\displaystyle \pi(x)=\operatorname {li}(x)+O({\sqrt {x}}\log {x}).}$

구체적으로.^[35]

${\displaystyle \pi(x)-\operatorname {li}(x) <{\frac {\sqrt {x}}{8\pi}}\,\log {x}}\qquad {\text{for all}x\geq 2657.}$

두데크(2015)는 리만 가설이 모든 $x$≥ 2 {\$displaystyle$x\geq 2}에 대하여 만족하는$소수$ p${\displaystyle$ p}가 존재함을 의미함을 증명했습니다.

-$π$ x로그 $⁡$ x < p ≤ x${\displaystyle x-{\frac$ {$4}{\pi$}} ${\sqrt$ {$x$ x < p\leq x}.

참고 항목

• 베르트랑의 공준
• 오퍼만 추측
• 라마누잔 소수

참고문헌

메모들

외부 링크

• 크리스 콜드웰, 프라임 페이지의 N번째 프라임 페이지.
• 토마스 올리베이라 에 실바, 소수를 세는 함수의 표.
• Dudek, Adrian W. (2015), "On the Riemann hypothesis and the difference between primes", International Journal of Number Theory, 11 (3): 771–778, arXiv:1402.6417, Bibcode:2014arXiv1402.6417D, doi:10.1142/S1793042115500426, ISSN 1793-0421, S2CID 119321107