파리스 수열

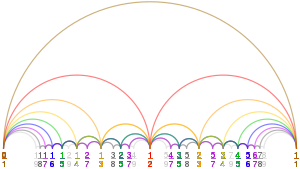
수학에서, 순서 n의 Farey 시퀀스는 0과 1 사이 또는 이 ^[a]제한 없이 완전히 감소된 분수의 시퀀스이며, 가장 낮은 용어에서 n보다 작거나 같은 분모를 갖는 경우 크기가 증가하는 순서대로 배열됩니다.

제한된 정의를 사용할 경우 각 Farey 시퀀스는 분수로 표시되는 값 0으로 시작합니다.0/1이며 분수 1/1로 표시되는 값 1로 끝납니다(일부 필자는 이러한 항을 생략합니다).

Farey 시퀀스를 Farey 시리즈라고 부르기도 하는데, 이는 항이 ^[2]합산되지 않기 때문에 정확하지 않습니다.

예

주문 1~8의 Farey 시퀀스는 다음과 같습니다.

F₁ = {0/1_, 1/1}

F₂ = {0/1_, 1/2_, 1/1}

F₃ = {0/1_, 1/3_, 1/2_, 2/3_, 1/1}

F₄ = {0/1_, 1/4_, 1/3_, 1/2_, 2/3_, 3/4_, 1/1 }

F₅ = {0/1_,, 1/5_, 1/4 1/3_, 2/5_,, 3/5_, 2/3_, 3/4_, 4/5_, 1/1 }

F₆ = {0/1_,, 1/6_, 1/5 1/4_, 1/3_, 2/5_, 1/2_, 3/3_,, 3/4_, 4/5_, 5/6_, 1/1 }

F₇ = {0/1_,, 1/7_, 1/6_, 1/5 1/4_, 2/7_,, 1/3_, 2/7_, 1/7_, 4/7_, 3/5_,, 3/7_,, 3/4 4/5_, 4/5_, 5/6_, 6/7 1/1 }

F₈ = {0/1_,, 1/8_, 1/7_, 1/6 1/6_, 1/4_, 2/7_, 1/3_, 3/8_,,, 2/8 1/2_, 4/7_, 3/5_, 2_,/8_, 2/3_, 3/4_, 4/4_, 4/5 5/6_, 6/7_, 7/8_, 1/1 }

F1 = {0/1, 1/1} F2 = {0/1, 1/2, 1/1} F3 = {0/1, 1/3, 1/2, 1/1} F4 = {0/1, 1/4, 1/3, 2/3, 2/3, 2/3, 2/3, 3, 3, 3, 3/4, 1/4, 1/1} F5, 1/4, 4, 4, 5, 4, 4, 5, 4, 5, 4/4, 4, 5, 4, 4/4, 5, 5, 4, 4, 4/1, 1/8, 1/7, 1/6, 1/5, 1/4, 2/7, 1/3, 3/8, 2/5, 3/7, 1/2, 4/7, 3/5, 5/8, 2/3, 5/7, 3/4, 4/5, 5/6, 6/7, 7/8, 1/1}

파어리 선버스트

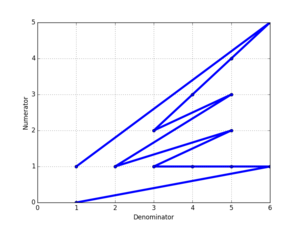
분자 대 Farey 시퀀스의 분모를 플롯하면 F에 표시된₆ 오른쪽의 분모와 같은 모양이 나타납니다.

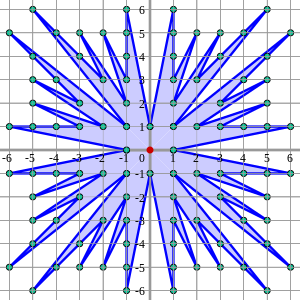
대각선과 주 축 주위에 이 모양을 반영하면 아래와 같이 Farey 선버스트가 생성됩니다.순서 n의 Farey Sunburst는 원점에서 중심이 되는 변 2n의 제곱에 있는 원점에서 가시적인 정수 그리드 점을 연결합니다.Pick의 정리를 사용하면 태양 폭발의 면적은 4(F-1)이며_n, 여기서_n F는 F의_n 분수입니다.

역사

'Farey series'의 역사는 매우 흥미롭습니다 - Hardy & Wright (1979)^[3]

다시 한번, 수학적 관계에 이름이 주어진 그 남자는 기록에 의하면 원래의 발견자가 아니었습니다.빌러 (1964)^[4]

Farey 시퀀스는 1816년 Philosophical Magazine에 이 시퀀스에 대한 편지가 출판된 영국 지질학자 John Farey, Sr.의 이름을 따서 명명되었습니다.Farey는 증거를 제시하지 않고 Farey 시퀀스 확장의 각 새로운 용어가 이웃의 중위수라고 추측했습니다.Farey의 편지는 Cauchy에 의해 읽혔고, 그는 그의 수학적 연습에서 증거를 제공했고, 이 결과를 Farey에게 돌렸습니다.사실, 또 다른 수학자인 찰스 하로스는 1802년에 비슷한 결과를 발표했는데, 이것은 파레이나 ^[4]코시에게도 알려지지 않았습니다.따라서 파레이의 이름과 이러한 시퀀스를 연결한 것은 역사적인 사고였습니다.이것은 스티글러의 가명 법칙의 한 예입니다.

특성.

분수의 시퀀스 길이 및 인덱스

순서 n의 Farey 시퀀스에는 하위 순서의 Farey 시퀀스의 모든 멤버가 포함됩니다.특히_n F는 F의 모든_n−1 구성원을 포함하고 n보다 작은 숫자와 coprime ton에 대한 추가 분수도 포함합니다.따라서₆ F는 1/6 및 5/6 분수와 함께 F로 구성됩니다₅.

Farey 수열_n F의 중간 항은 항상 1/2이고, n > 1입니다. 이로부터 오일러의 토텐던트_n $함수{\displaystyle \mathrm{\phi _<i>n</i>-1}}$(n$$) ${{displaystyle$ \$varphi$($n)):$

${\displaystyle F_{n} = F_{n-1} +\varphi (n)}$

F = 2라는 사실을₁ 이용하여 ^[5]F의_n 길이에 대한 식을 도출할 수 있습니다.

${\displaystyle F_{n} =1+\sum _{m=1}^{n}\varphi(m)=1+\Phi(n),}$

여기서 $\phi {\displaystyle \mathrm{}}$(${\displaystyle n}$) \ $displaystyle \Phi (n)$는 텐티너의 총합입니다.

또한 다음과 같은 기능도 제공합니다.

${\displaystyle F_{n} = floorfrac {1}{2}}\left(3+\sum_{d=1}^{n}\mu(d)\left\l floor {tfrac {n}}\right\rfloor ^{2}\right),}$

그리고 뫼비우스 반전 공식에 의해:

${\displaystyle F_{n} = displayfrac {1}{2}}(n+3)n-\sum _{d=2}^{n} F_{\lfloor n/d\rfloor },}$

여기서$$ µ(d)는 수론적 뫼비우스 함수이고, ${\displaystyle n\frac{}{}}$ $⌋{{\d}}\rfloor}는$바닥 함수입니다.

F의_n 점근적 거동은 다음과 같습니다.

${\displaystyle F_{n} \sim {{frac {3n^{2}}{\pi ^{2}}}.$

Farey 시퀀스 Fn = {ak, n : k = 0, 1, …, m } {\displaystyle F_{n} = k (a, n ) = k (a, n ) = k, 1, \ldots, n (k) }의 지수는 단순히 k \n \n \n \n \n \n \n \n \"의 위치를 차지한다.이것은 리만 가설의 대안적인 공식에 사용되기 때문에 특별한 관련성이 있습니다. 아래를 참조하십시오.다양한 유용한 속성은 다음과 같습니다.

${\displaystyle I_{n}(0/1)=0,}$

${\displaystyle I_{n}(1/n)=1,}$

${\displaystyle I_{n}(1/2)=( F_{n} -1)/2,}$

${\displaystyle I_{n}(1/1)= F_{n} -1,}$

${\displaystyle I_{n}(h/k)= F_{n} -1-I_{n}(k-h)/k)}$

여기서$$ /( 1) < $k$$$ / {$displaystyle$ n$/(i+1)$ <$k$ \ $leq$ n$/i}$ 및$n{\displaystyle }$ {{$displaystyle$n}은 첫 $번째{\displaystyle }$i \ $displaystyle$i 숫자$$ $중{\displaystyle }$ 가장 일반적인 배수 n$= l$(${\displaystyle 2,i}$)$${$displaystyle$n {$lcm}(2, i$는 ^[6]다음과 같이 구할 수 있습니다.

${\displaystyle I_{n}(1/k)=1+n\sum_{j=1}^{i}{\frac{\varphi(j)}{j}}-k\Phi(i)}.$

안녕 이웃들

Farey 시퀀스에서 인접한 용어인 분수를 Farey 쌍이라고 하며 다음과 같은 특성을 갖습니다.

a/b와 c/d가 a/b < c/d인 Farey 시퀀스의 인접 관계인 경우, 이들의 차이 c/d - a/b는 1/bd와 같습니다.부터

$display{style{\frac{c}{d}}-{\frac{a}{b}=tftfrac{bc-ad}{bd}}}$

이것은 이라고 말하는 것과 같습니다.

${\displaystyle \mathrm{bc}}$ ${\displaystyle -}$ ${\displaystyle d}$ $=$ ${displaystyle bc-ad=1$

따라서 1/3과 2/5는 F에서 인접₅ 관계이며, 차이는 1/15입니다.

그 반대도 사실입니다. 만약에.

${\displaystyle bc-ad=1} 표시$

< b 및 c < d를 갖는 양의 정수 a, b, c 및 d의 경우 a/b 및 c/d는 차수 max(b, d)의 Farey 시퀀스에서 인접 관계가 됩니다.

만약 p/q가 어떤 Farey 시퀀스에서 이웃 a/b와 c/d를 가지고 있다면,

$표시({style {\frac {a}{b}}<{\frac {p}{q}}<{\frac {c}{d}}})$

p/q는 a/b와 c/d의 중간값입니다. 즉,

$디스플레이 {{style {frac {p}{q}=sysfrac {a+c}{b+d}}$

bp – aq = qc – pd = 1이면 bp + pd = qc + aq, p(b + d) = q(a + c), p/q = a + c/b + d이기 때문에 이전 속성에서 쉽게 이 값을 따릅니다.

따라서 a/b와 c/d가 Farey 시퀀스의 인접 관계일 경우, Farey 시퀀스의 순서가 증가함에 따라 이들 사이에 나타나는 첫 번째 항은 다음과 같습니다.

$표시({style{frac{a+c}{b+d}$

이것은 farey 순서 b + d에 처음 나타납니다.

따라서 1/3에서 2/5 사이에 나타나는 첫 번째 항은 F에 나타나는₈ 3/8입니다.

F에서_n Farey 이웃 쌍의 총 수는_n 2 F - 3입니다.

Stern-Brocot 트리는 연속적인 중위수를 취함으로써 시퀀스가 0(= 0/1)과 1(= 1/1)에서 어떻게 구성되는지 보여주는 데이터 구조입니다.

등가 면적 해석

연속된 모든 Farey Rational 쌍의 면적은 ^[7]1입니다.x-y 평면에서 연속된 r = p/q₂ 및 r = p'/q'를₁ 벡터(p, q)로 해석하여 이를 확인합니다.A(p/q, p'/q')의 면적은 qp' - q'p로 주어집니다.이전의 두 개의 연속적인 Farey 시퀀스 분수 사이의 추가 분수는 중위수(σ)로 계산되므로 A(r₁, r₁₂₁) = A(r₁₁, r) + A(r₁, r₂₂) = 1(sr₁ = 1/0 및₂ r = 0/1이므로 면적은 1이어야 합니다.

이웃과의 이별과 연속 분수

Farey 시퀀스에서 인접 관계로 나타나는 분수는 연속 분수 확장과 밀접한 관련이 있습니다.모든 분수에는 두 개의 연속된 분수 확장이 있습니다. 하나는 최종 항이 1이고 다른 하나는 최종 항이 1만큼 큽니다.Farey 시퀀스_q F에서 처음 나타나는 p/q에 연속된 분수 확장이 있는 경우

[0; a₁, a₂, ..., a_{n − 1}, a_n, 1]

[0; a₁, a₂, ..., a_{n − 1}, a_n + 1]

그러면 F에서_q p/q의 가장 가까운 이웃(분모가 더 큰 이웃이 됨)은 연속적인 분수 확장을 갖습니다.

[0; a₁, a₂, ..., a_n]

그리고 그것의 다른 이웃은 지속적인 분수 확장을 가지고 있습니다.

[0; a₁, a₂, ..., a_{n − 1}]

예를 들어, 3/8은 두 개의 연속된 분수 확장 [0; 2, 1, 1]과 [0; 2, 1, 2]을 가지며 F의 인접₈ 관계는 [0; 2, 1, 1]로 확장할 수 있고 [0; 2, 1, 1]로 확장할 수 있는 2/5입니다.

운임 분수와 최소 공배수

lcm는 다음과 같이 Farey 분수의 곱으로 표현할 수 있습니다.

$표시({style{text{lcm}}[1,2,...,N]=e^{\psi(N)}=nbfrac{1}{2}}\left(\r\in F_{N},0<r\leq 1/2}2\sin(\pir)\right)^{2}}$

여기서${\displaystyle }\psi {\displaystyle }$ (${\displaystyle N}$) \\$displaystyle \psi (N)$는 두 번째 체비셰프 ^[8][9]함수입니다.

유리 분수와 최대 공약수

오일러의 토텐던트 함수는 gcd와 직접적으로 연결되어 있기 때문에_n F의 원소 수도 마찬가지입니다.

${\displaystyle F_{n} =1+\sum _{m=1}^{n}\varphi(m)=1+\sum \sum \sum _{m=1}^{m}\gcd(k,m)\cos {2\pifrac{k}{m}}}.$

3 Farey 분수 a/b, c/d 및 e/f의 경우 절대값에 있는 2x2 행렬 결정 요인의 gcd 사이의 다음 동일성이 유지됩니다.^[10]

$\"표시 스타일 \gcd \left({\begin{Vmatrix}a&c\b&d\end{Vmatrix}),{\begin{Vmatrix}a&e\b&f\end{Vmatrix}\right)=\gcd \left({\begin{Vmatrix}a&c&d\end{\begright})\cd\cd\right\traight\t}\cd\cd\trix\cd\cd$

^[6]

적용들

파리 시퀀스는 불합리한 숫자의 ^[11]합리적인 근사치를 찾는 데 매우 유용합니다.예를 들어, 3x+1 공정에서 사소한 주기의 길이에 대한 하한의 Eliahou에^[12] 의한 구성은 Farey 시퀀스를 사용하여 숫자₂ 로그(3)의 연속 분수 확장을 계산합니다.

공명 현상이 있는 물리적 시스템에서 Farey 시퀀스는 1D^{[13] [14]}및 2D로 공명 위치를 계산하는 매우 우아하고 효율적인 방법을 제공합니다.

Fairy 시퀀스는 예를 들어 계산 복잡성^[15] 또는 ^[16]최적성을 특성화하는 등 사각형 셀 그리드의 모든 각도 경로 계획 연구에서 두드러집니다.연결은 r 제약 경로, 즉 셀의 $최대{\displaystyle }$ r${displaystyle}$ 행과$$$$ $최대{\displaystyle }$ r${displaystyle}$ 열을 각각 통과하는 선 세그먼트로 구성된 경로로 고려할 수 있습니다.Q${displaystyle$ Q$}$를 벡터 집합$({\displaystyle q,p}$) {\$displaystyle(q, p$)}으로 하여 $1{\displaystyle \mathrm{}\le }$≤ r \$displaystyle 1\$$leq$\$leq$ $0{\displaystyle }$${\displaystyle \le }$ ${\displaystyle p}$ $≤$ ${\displaystyle q}$ {\$displaystyle$$$p$\backslash$$leq$ 및$p{\displaystyle }$ {\$displaystyleq},$q$$}를 동일한 값으로 $합니다{\displaystyle }$.Q ∗ {\displaystyle Q*}를 선 y = x {{\displaystyle y = x }에 반사시킨 결과라고 하자. S = { (± x, ± y ) : (x, y ) Q ∪ Q ∗ Q = \{(\pm x,\pm y): (x, y) \in Q\cup Q*}에서 Q-sty\displaysty\displaysty\type 벡터 사이의 경로는 제약 조건으로 설명될 수 있다\$displaystyle$ Q$}$ 및$$ ${\displaystyle \frac{\mathrm{pq}}{}}${{$tfrac${$p$에 $대한{\displaystyle \frac{}{}}$ ($,$ p ) {displaystyle$$$(q$, $p)}$ 매핑에${\displaystyle }$의해 주어진 $주문자{\displaystyle }${{$displaystyle$r}의$$ Farey 시퀀스$.$

포드계

Farey 시퀀스와 Ford 서클 사이에는 연관성이 있습니다.

모든 분수 p/q(가장 낮은 항에서)에 대해 (p/q, 1/2q)에서 중심이 (p/q²)인² Ford 원 C[p/q]가 있습니다.서로 다른 분수에 대한 두 개의 포드 원은 서로 분리되거나 서로 접합니다. 즉, 두 개의 포드 원은 서로 교차하지 않습니다.0 < p/q < 1이면 C[p/q]에 접하는 포드 원은 정확하게 Farey 시퀀스에서 p/q의 이웃인 분수에 대한 포드 원입니다.

따라서 C[2/5]는 C[1/2], C[1/3], C[3/7], C[3/8] 등과 접합니다.

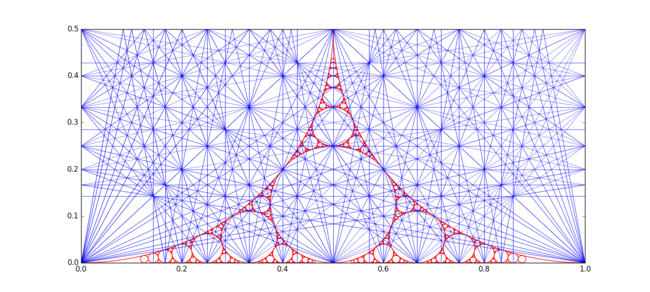
포드 원은 Apollonian 개스킷(0,0,1,1)에도 표시됩니다.아래 그림은 Farey 공진 라인과 ^[17]함께 이를 보여줍니다.

리만 가설

파리 수열은 리만 가설의 두 가지 동등한 공식에 사용됩니다.F{displaystyle F_{n}}의 항이 {ak, n : k = 0, 1, …, m n } {{a_{k,n} k = 0,1,\ldots,m_{n}\}이라고 가정합니다. d, n = a, n - k / m {displaystyle d_{k, n}, 즉 k와 k 사이의 항은 k의 차이입니다단위 구간에 균등하게 분포된 동일한 점 개수의 집합입니다.1924년에 제롬 프란넬은^[18] 그 진술이

${\displaystyle \sum _{k=1}^{m_{n}}d_{k,n}^{2}=O(n^{r})\quad \for all r>-1}$

리만 가설에 해당하며, 에드먼드 란다우는^[19] (프란넬의 논문 직후) 다음과 같이 언급했습니다.

${\displaystyle \sum _{k=1}^{m_{n}} d_{k,n} =O(n^{r})\quad \for all r>1/2}$

또한 리만 가설과 같습니다.

운임 분수를 포함한 기타 합계

순서 n의 모든 Farey 분수의 합은 요소 수의 절반입니다.

${\displaystyle \sum _{r\in F_{n}}r=nbfrac {1}{2}} F_{n}$

파레이 수열의 분모의 합은 분자의 합의 두 배이며 오일러의 토텐던트 함수와 관련이 있습니다.

${\displaystyle \sum _{a/b\in F_{n}}b=2\sum _{a/b\in F_{n}a=1+\sum _{i=1}^{n}i\varphi(i)}}$

해롤드 L에 의해 추측되었습니다.1962년에 아론이 시연했고 진 A에 의해 시연되었습니다.1966년의 블레이크.^[20]해롤드 L의 한 줄 증거.아론의 추측은 다음과 같습니다.분자의 $합$은 1${\displaystyle {\displaystyle }}$+${\displaystyle {\displaystyle \underset{}{}}}$≤ ${\displaystyle {\displaystyle \underset{}{2\mathrm{}}}}$≤ ${\displaystyle {\displaystyle \underset{}{b}}}$ ≤ ${\displaystyle {\displaystyle \underset{}{n}}}$ ${\displaystyle {\displaystyle \underset{}{\le }}}$ (${\displaystyle {\displaystyle \underset{}{a,b}}}$) $=$ ${\displaystyle {\displaystyle \underset{}{}}}$ a =${\displaystyle {\displaystyle 1}}$ + ${\displaystyle {\displaystyle \underset{}{}}}$ ${\displaystyle {\displaystyle \underset{}{2\mathrm{}}}}$≤ ${\displaystyle {\displaystyle \underset{}{b}}}$ ≤ ${\displaystyle {\displaystyle \underset{}{}}}$ ${\displaystyle {\displaystyle b\frac{}{}}}$ ${\displaystyle {\displaystyle \frac{\le }{}}}$ (${\displaystyle {\displaystyle \frac{b)}{}}}$ {{$displaystyle 1+\sum$_{$2\leq$b\$leq$ n$}\sum$ _${a,$b) $=1+\sum$ _${2\leq$ b}$frac{varphi (b$입니다.분모의 $합$은 2${\displaystyle {\displaystyle }}$+ ${\displaystyle {\displaystyle \underset{}{}\underset{}{}}}$ ${\displaystyle {\displaystyle \underset{}{2\mathrm{}\le }}}$ ${\displaystyle {\displaystyle \underset{}{b}}}$ ≤ ${\displaystyle {\displaystyle \underset{}{n}}}$ ${\displaystyle {\displaystyle \underset{}{}}}$ (${\displaystyle {\displaystyle \underset{}{a,b}}}$ )${\displaystyle {\displaystyle \underset{}{}=}}$ ${\displaystyle {\displaystyle \underset{}{}}}$ b = ${\displaystyle {\displaystyle 2}}$+ ∑ ${\displaystyle {\displaystyle \underset{}{2\mathrm{}}}}$≤ ${\displaystyle {\displaystyle \underset{}{b}}}$ ≤ n ${\displaystyle {\displaystyle \underset{}{}\phi }}$ ($)$ {{\$displaystyle$ 2$+\sum$ _${2\leq$b\$leq$ n$}\sum$ _${(a,$b) $=1}$b$=2+\sum$ _${2\leq b\varphi(b$입니다.두 번째 합에 의한 첫 번째 합의 몫은 ${$

b를 F의 순서_n 분모로 하고_j,^[21] 다음과 같이 합니다.

${\displaystyle \sum _{j=0}^{F_{n} -1}{\frac {b_{j}}{b_{j+1}}={3F_{n}-4}{2}}}$

그리고.

${\displaystyle \sum _{j=0}^{F_{n} -1}{\frac {1}{b_{j+1}b_{j}}=1}$

그렇다면 F의_n j번째 Farey 분수를 a/b로_j 하자_j,

$\displaystyle \sum _{j=1}^{F_{n} -1}(a_{j-1}b_{j+1}-a_{j+1}b_{j-1})=\sum_{j=1}^{F_{n}-1}{\b_{j+1}\b_{j+1}{j-1}{n}{n}{n}{n}}{n}{3}{n}}}{{{{{n}}}}}}}}{{{{{}}}}}}}}}$

에 ^[22]설명되어 있습니다.또한 이 참조에 따르면, 합 내부의 용어는 다양한 방법으로 표현될 수 있습니다.

${\displaystyle a_{j+1}b_a_{j+1}b_{j-1}={b_{j}}={a_{j-1}+a_{j+1}}={a_{j}}ac\leftfloorfloor{n+b_{j-1}}{j}\rflo}\rfloor.$

동일한 결과로 Farey 요소에 대해 이렇게 많은 다른 합계를 얻습니다.약 1/2의 대칭을 사용하면 이전 합은 다음과 같이 시퀀스의 절반으로 제한될 수 있습니다.

$표시 스타일 \sum _{j=1}^{\lfloor F_{n} /2\rfloor }(a_{j-1}b_{j+1}-a_{j+1}b_{j-1})=3(F_{n}-1)/2-n-\lceiln/2\rceil,}$

메르텐스 함수는 다음과 같이 Farey 분수에 대한 합으로 표현할 수 있습니다.

${\displaystyle M}$(${\displaystyle n)}$ $=$ -${\displaystyle 1}$ + ${\displaystyle \sum _{}}$ ${\displaystyle \underset{}{{\mathcal{}}_{}}}$ ${\displaystyle {Fine\mathrm{}}^{}}$ 2 ${\displaystyle {\pi }^{}}$ ${\displaystyle {\mathrm{ia}}^{}}$\$displaystyle$ M$(n$)=-$1+\sum$ _${a\in {\mathcal {F}_{n}e^{2\piia$$}$ ${\displaystyle {여기}_{}}$서$Fn$ {\$displaystyle${{$mathcal$ {$F}_{$n$$}은 n의 Frey 시퀀스입니다.

이 공식은 프랑켈-란다우 ^[23]정리의 증명에 사용됩니다.

다음 학기

F의 항을 전통적인 순서(상승) 또는 비전통적인 순서(하강_n)로 생성하는 놀랍도록 간단한 알고리즘이 존재합니다.알고리즘은 위에 주어진 중간 속성을 사용하여 이전 두 항목의 관점에서 연속된 각 항목을 계산합니다.a/b와 c/d가 주어진 두 항목이고 p/q가 알 수 없는 다음 항목이라면, c/d = a + p/b + q입니다. c/d가 가장 낮은 조건이므로 kc = a + p 및 kd = b + q와 같은 정수 k가 있어야 하며, p = kc - a 및 q = kd - b입니다.만약 우리가 p와 q를 k의 함수라고 생각한다면,

$표시{{style{frac{p(k)}{q(k)}}-{\frac{c}{d}}={frac{cb-da}{d(kd-b)}}}$

따라서 k가 클수록 p/q는 c/d에 가깝습니다.

시퀀스에서 다음 항을 지정하려면 kd - b ≤ n(분모가 n보다 크지 않은 숫자만 고려하고 있기 때문에)에 따라 k가 가능한 한 커야 합니다. sok은 최대 정수 n ≤ n + b/d입니다.k의 이 값을 p와 q에 대한 방정식에 다시 넣으면 다음과 같습니다.

$displaystyle p=\left\l floor {frac {n+b}{d}\right\rfloor c-a}$

${\displaystyle q=\left\l floor{frac{n+b}{d}}\right\rfloor-b}$

이는 Python에서 다음과 같이 구현됩니다.

디프 작별의 순서(n: 인트, 내림의: 쿨한 = 거짓의) -> 없음.:     """n't Farey 시퀀스를 인쇄합니다.오름차순 또는 내림차순을 허용합니다."""     (a, b, c, d) = (0, 1, 1, n)     한다면 내림의:         (a, c) = (1, n - 1)     인쇄물("{0}/{1}".서식을(a, b))     하는 동안에 (c <= n 그리고. 것은 아니다. 내림의) 또는 (a > 0 그리고. 내림의):         k = (n + b) // d         (a, b, c, d) = (c, d, k * c - a, k * d - b)         인쇄물("{0}/{1}".서식을(a, b)) 

이성에서 디오판틴 방정식에 대한 솔루션을 브루트 포스 검색은 종종 Farey 시리즈를 활용할 수 있습니다(감소된 형태만 검색).이 코드는 시퀀스의 처음 두 용어를 사용하여 a, b, c 및 d를 초기화하지만, 특정 ^[24]임계값보다 작거나 큰 용어를 제외하기 위해 인접한 용어 쌍을 대체할 수 있습니다.

참고 항목

• ABACABA 패턴
• 스턴브로콧나무
• 오일러의 토텐던트 함수

각주

레퍼런스

진일보한 내용

• Hatcher, Allen. "Topology of Numbers". Mathematics. Ithaca, NY: Cornell U.
• Graham, Ronald L.; Knuth, Donald E.; Patashnik, Oren (1989).구체적인 수학:컴퓨터 과학의 기초 (제2판).보스턴, 매사추세츠 주: 애디슨 웨슬리. 115–123 페이지, 133–139, 150, 462–463, 523–524.ISBN 0-201-55802-5입니다. — 특히, § 4.5 (페이지 115–123), 보너스 문제 4.61 (페이지 150, 523–524), § 4.9 (페이지 133–139), § 9.3, 문제 9.3.6 (페이지 462–463)을 참조하십시오.
• Vepstas, Linas. "The Minkowski Question Mark, GL(2,Z), and the Modular Group" (PDF). Stern-Brocot Tree의 동형화를 검토합니다.
• Vepstas, Linas. "Symmetries of Period-Doubling Maps" (PDF). Farey Fractals와 Fractals 사이의 연결을 검토합니다.
• Cobeli, Cristian; Zaharescu, Alexandru (2003). "The Haros–Farey sequence at two hundred years. A survey". Acta Univ. Apulensis Math. Inform. (5): 1–38. "pp. 1–20" (PDF). Acta Univ. Apulensis. "pp. 21–38" (PDF). Acta Univ. Apulensis.
• Matveev, Andrey O. (2017). Farey Sequences: Duality and Maps Between Subsequences. Berlin, DE: De Gruyter. ISBN 978-3-11-054662-0. 에라타 + 코드

외부 링크

• Bogomolny, Alexander. "Farey series". Cut-the-Knot.
• Bogomolny, Alexander. "Stern-Brocot Tree". Cut-the-Knot.
• Pennestri, Ettore. "A Brocot table of base 120".
• "Farey series", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Weisstein, Eric W. "Stern-Brocot Tree". MathWorld.
• OEIS 시퀀스 A005728(순서 n의 Farey 시리즈 분수 수)
• OEIS 시퀀스 A006842(순서 n의 Farey 시리즈 번호)
• OEIS 시퀀스 A006843(순서 n의 Farey 시리즈 분모)
• Ghostarchive 및 Wayback Machine에서 보관: