골드바흐 추측

골드바흐 추측

골드바흐가 1742년 6월 7일 오일러에게 보낸 편지(라틴어-독일어)[1]
들판	수론
에 의해 추측됩니다.	크리스티안 골드바흐
추측하다	1742
미해결문제	네.
결과들	골드바흐의 약한 추측

골드바흐의 추측은 정수론과 모든 수학에서 가장 오래되고 잘 알려진 미해결 문제 중 하나입니다. 2보다 큰 모든 짝수 자연수는 두 소수의 합이라고 말합니다.

이 추측은 4×10¹⁸ 미만의 모든 정수에 대해 성립하는 것으로 나타났지만 상당한 노력에도 불구하고 입증되지 않았습니다.

역사

오리진스

1742년 6월 7일, 프로이센의 수학자 크리스티안 골드바흐는 레온하르트 오일러에게 편지를 ^[2]써서 다음과 같은 추측을 제시했습니다.

골드바흐는 단위의 합이 소수의 합이 되도록 ^[3]1을 소수로 간주하는 지금은 폐기된 관례를 따르고 있었습니다. 그런 다음 그는 편지의 여백에 다음과 같은 두 번째 추측을 제안했습니다.^[4]

... 아인 제데 잘, 다이 그뢰세랄스 2, 아인 아그레타툼 삼뉴머로룸 프리모룸 세이.
2보다 큰 모든 정수는 세 개의 소수의 합으로 쓸 수 있습니다.

오일러는 1742년^[5] 6월 30일자 편지에 답장을 보내 골드바흐에게 그들이 나눈 이전의 대화를 상기시켰습니다("... 그래서 Ew vormals mit mir communitirt haben..."). 골드바흐는 이 두 가지 추측 중 첫 번째 추측이 이 진술로부터 뒤따를 것이라고 말했습니다.

이것은 사실 그의 두 번째 한계 추측에 해당합니다. 1742년 6월 30일자 편지에서 오일러는 다음과 같이 말했습니다.^[6][7]

이런... ein jeder numerus pareine summa duorum primorum sey, halteich fürainz gewisses theorema, ungeachtetich dasselbenicht demonstri kann.
그... 모든 짝수 정수는 두 소수의 합으로, 증명할 수는 없지만 완전히 확실한 정리로 간주합니다.

부분결과

강한 골드바흐 추측은 약한 골드바흐 추측보다 훨씬 어렵습니다. 비노그라도프의 방법을 사용하여 니콜라이 추다코프,^[8] 요하네스 판 데르 코르푸트,^[9] 테오도르 에스터만은^[10] 거의 모든 짝수를 두 소수의 합으로 쓸 수 있음을 보여주었습니다(N이 증가함에 따라 N까지 쓸 수 있는 짝수의 분수가 1을 향하는 경향이 있다는 의미에서). 1930년 레프 슈니렐만은 1보다 큰 자연수는 C 소수 이하의 합으로 쓸 수 있다는 것을 증명했습니다. 여기서 C는 효과적으로 계산 가능한 상수입니다. 슈니렐만 밀도를 참조하십시오.^[11][12] 슈니렐만 상수는 이 성질을 가진 가장 낮은 수 C입니다. 슈니렐만 자신은 C < 80만을 얻었습니다. 이 결과는 올리비에 라마레(Olivier Ramaré)와 같은 많은 저자에 의해 향상되었으며, 1995년에 모든 짝수 n ≥ 4는 사실 최대 6개의 소수의 합이라는 것을 보여주었습니다. 현재 가장 잘 알려진 결과는 하랄드 헬프고트의 약한 골드바흐 추측의 증명에서 비롯되며, 이는 모든 짝수 n ≥ 4가 최대 4개의 소수의 합임을 직접적으로 암시합니다.

1924년 하디와 리틀우드는 일반화된 리만 가설의 가정 하에 골드바흐 추측을 위반하는 X까지의 짝수의 수가 작은 c의 경우^{1⁄2 + c} X보다 훨씬 적다는 것을 보여주었습니다.^[16]

1948년 알프레데 레니(Alfréd Rényi)는 체 이론 방법을 사용하여 충분히 큰 모든 짝수를 기껏해야 K개의 인자를 갖는 소수와 거의 소수의 합으로 쓸 수 있음을 보여주었습니다.^[17] 1973년 천징룬(Chen Jingrun)은 체 이론을 사용하여 충분히 큰 짝수는 모두 두 소수의 합 또는 소수와 반 소수(두 소수의 곱)의 합으로 작성될 수 있음을 보여주었습니다.^[18] 자세한 내용은 Chen의 정리를 참조하십시오.

1975년 휴 로웰 몽고메리(Hugh Lowell Montgomery)와 밥 본(Bob Vaughan)은 "대부분의" 짝수가 두 소수의 합으로 표현 가능하다는 것을 보여주었습니다. 더 정확하게 말하면, 그들은 양의 상수 c와 C가 존재한다는 것을 보여주었고, 충분히 큰 모든 수 N에 대해 N보다 작은 모든 짝수는 기껏해야 CN^{1 − c} 예외를 제외하고 두 소수의 합입니다. 특히 두 소수의 합이 아닌 짝수 정수의 집합은 밀도가 0입니다.

1951년 유리 린닉(Yuri Linnik)은 충분히 큰 모든 짝수는 두 소수와 많아야 2의 K 거듭제곱의 합이 되도록 상수 K의 존재를 증명했습니다. 2020년 야노스 핀츠(János Pintz)와 임레 루자(Imre Ruzsa)는 K = 8이 작용한다는 것을 발견했습니다. 일반화된 리만 가설을 가정하면 2002년 Roger Heath-Brown과 Jan-Christoph Schlage-Puchta가 보여주듯이 K = 7도 작용합니다.

약한 추측에 대한 증거는 2013년 하랄트 헬프고트가 수학 연보 시리즈에 제출했습니다. 기사는 받아들여졌지만 헬프고트는 심판이 제시한 주요 수정 사항을 수행하기로 결정했습니다. 몇 번의 수정에도 불구하고 헬프고트의 증거는 동료 평가를 받은 출판물에 아직 나타나지 않았습니다.^[21][22][23] 약한 추측은 n - 3이 두 소수의 합이고, n이 세 소수의 합인 것처럼 강한 추측에 의해 암시됩니다. 그러나 헬프고트의 증명이 정확하다면 역의 의미와 따라서 강한 골드바흐 추측은 증명되지 않은 채로 남을 것입니다.

계산 결과

n의 작은 값의 경우 강한 골드바흐 추측(따라서 약한 골드바흐 추측)을 직접 검증할 수 있습니다. 예를 들어, 1938년 닐스 피핑은 n = 100000까지 열심히 추측을 검증했습니다. 컴퓨터의 등장으로 더 많은 n 값들이 확인되었습니다; T. Oliveirae Silva는 2013년 현재 n ≤ 4×10¹⁸ (그리고 최대 4×10¹⁷)에 대한 추측을 검증한 분산 컴퓨터 검색을 실행했습니다. 이 검색에서 얻은 한 가지 기록은 3325581707333960528이 하나가 9781보다 작은 두 소수의 합으로 쓸 수 없는 가장 작은 숫자라는 것입니다.^[25]

컬리-휴길과 두덱은 리만 가설에 대한 (부분 및 조건부) 결과를 증명합니다. 모든 x ≥ 2에 대해 구간 (x, x + 9696 log^2 x)에 두 홀수 소수의 합이 존재합니다.

대중문화에서

골드바흐 추측(Goldbach's Conpertures, 중국어: 哥德巴赫猜想)은 쉬치가 쓴 중국의 수학자이자 정수론자인 천징룬의 전기의 제목입니다.

이 추측은 1992년 그리스 작가인 아포스톨로스 독시아디스의 페트로스 삼촌과 골드바흐의 추측, 아이작 아시모프의 단편 소설 "6백만 조 조합"과 미셸 리치먼드의 2008년 추리 소설 "아무도 당신이 알지 못하는"의 줄거리에서 중심을 이룹니다.^[27]

골드바흐의 추측은 2007년 스페인 영화 페르마의 방의 줄거리의 일부입니다.

골드바흐의 추측은 2023년 프랑스-스위스 영화 마르그리트 정리에서 여배우 엘라 럼프의 캐릭터 마르그리트의 주요 연구 주제로 등장합니다.^[28]

정형명세서

세 가지 추측은 각각 1이 제외된 프라임의 현대적 정의 측면에서 자연스러운 유사성을 갖습니다. 첫 번째 추측의 현대판은 다음과 같습니다.

한계 추측의 현대적 버전은 다음과 같습니다.

그리고 오일러가 상기시킨 골드바흐의 오래된 추측의 현대판은 다음과 같습니다.

이러한 최신 버전은 해당하는 원래 문장과 완전히 동일하지 않을 수 있습니다. 예를 들어, 만약 pa 소수에 대해 4보다 큰 짝수 정수 N = p + 1이 있다면, 그것은 현대의 의미에서 두 소수의 합으로 표현될 수 없는 것이라면, 그것은 현대의 세 번째 추측의 반례가 될 것입니다. 따라서 현대 버전은 아마도 더 강할 것입니다(그러나 확인하려면 첫 번째 버전이 임의의 양의 짝수 정수 n에 자유롭게 적용되어 그러한 특정 반례 N의 존재를 배제할 수 없음을 증명해야 합니다). 어쨌든 현대의 진술은 이전의 진술과 동일한 관계를 가지고 있습니다. 즉, 두 번째와 세 번째 현대 진술은 동등하며, 첫 번째 현대 진술을 의미합니다.

세 번째 현대 문장(두 번째 문장에 해당)은 오늘날 추측이 일반적으로 표현되는 형태입니다. 이것은 "강한", "짝수" 또는 "이진" 골드바흐 추측으로도 알려져 있습니다. "골드바흐 약한 추측", "홀수 골드바흐 추측" 또는 "삼원 골드바흐 추측"으로 알려진 두 번째 현대 진술의 약한 형태는 다음과 같이 주장합니다.

휴리스틱 정당화

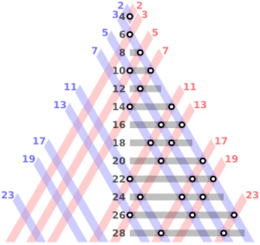
소수의 확률적 분포에 초점을 맞춘 통계적 고려 사항은 충분히 큰 정수에 대해 (약한 형태와 강한 형태 모두에서) 추측에 유리한 비공식적 증거를 제시합니다. 정수가 클수록 해당 숫자가 두 개 또는 세 개의 다른 숫자의 합으로 표현될 수 있는 방법이 더 많습니다. 그리고 "likely"이 많아질수록 이러한 표현 중 적어도 하나는 전적으로 소수로 구성됩니다.

(골드바흐 추측의 강력한 형태에 대한) 휴리스틱 확률론적 논증의 매우 조잡한 버전은 다음과 같습니다. 소수 정리는 임의로 선택된 정수 m이 소수일 확률이 약 1/lnm임을 주장합니다. 따라서 n이 큰 짝수 정수이고 m이 3에서 n/2 사이의 숫자라면 m과 n-m이 동시에 소수일 확률은 1/ln mln(n-m)이 될 것으로 예상할 수 있습니다. 이 휴리스틱을 추구한다면, 큰 짝수 정수 n을 홀수 두 소수의 합으로 쓰는 방법의 총 수는 대략적일 것으로 예상할 수 있습니다.

${\displaystyle \sum _{m=3}^{\frac {n}{2}}{\frac {1}{\ln m}}{\frac {1}{\ln(n-m)}}\approx {\frac {n}{2(\ln n)^{2}}}.}$

ln n ≪ √ n이기 때문에 이 양은 n이 증가함에 따라 무한대가 되며, 모든 큰 짝수 정수는 두 소수의 합으로서 하나의 표현만이 아니라 실제로 그러한 표현이 매우 많다고 예상할 수 있습니다.

이 휴리스틱 인수는 m과 n - m이 소수라는 사건이 통계적으로 서로 독립적이라고 가정하기 때문에 실제로 다소 부정확합니다. 예를 들어, m이 홀수이면 n - m도 홀수이고, m이 짝수이면 n - m은 짝수이며, 숫자 2 외에 홀수만 소수가 될 수 있기 때문에 사소하지 않은 관계입니다. 마찬가지로, 만약 n이 3으로 나누어지고 m이 이미 3이 아닌 소수였다면, n - m 또한 3과 동소수이므로 일반적인 수보다 약간 더 소수일 가능성이 높습니다. 1923년 G. H. Hardy와 John Edensor Littlewood는 (그들의 하디-리틀우드 소수 튜플 추측의 일부로서) 어떤 고정된 c ≥ 2의 경우, p ≤ ⋯ ≤ p인 c 소수 n = p + ⋯ + p의 합으로서 큰 정수 n의 표현 수는 점근적으로 다음과 같아야 한다고 추측했습니다.

${\displaystyle \left(\prod _{p}{\frac {p\gamma _{c,p}(n)}{(p-1)^{c}}}\right)\int _{2\leq x_{1}\leq \cdots \leq x_{c}:x_{1}+\cdots +x_{c}=n}{\frac {dx_{1}\cdots dx_{c-1}}{\ln x_{1}\cdots \ln x_{c}}},}$

여기서 곱은 모든 소수 p에 걸쳐 있고, γ(n)은 제약 조건 q, …, q ≠ 0 mod p에 따라 모듈러 산술에서 방정식 n = q + ⋯ + q mod p에 대한 해의 수이다. 이 공식은 이반 마트베비치 비노그라도프의 연구에서 c ≥ 3에 대해 점근적으로 유효하다는 것이 엄격하게 입증되었지만 여전히 c = 2일 때 추측에 불과합니다. 후자의 경우, 위의 공식은 n이 홀수일 때 0으로 단순화되고,

${\displaystyle 2\Pi _{2}\left(\prod _{p\mid n;p\geq 3}{\frac {p-1}{p-2}}\right)\int _{2}^{n}{\frac {dx}{(\ln x)^{2}}}\approx 2\Pi _{2}\left(\prod _{p\mid n;p\geq 3}{\frac {p-1}{p-2}}\right){\frac {n}{(\ln n)^{2}}}}$

n이 짝수일 때, 여기서 π는 하디-리틀우드의 쌍둥이 소수 상수입니다.

${\displaystyle \Pi _{2}:=\prod _{p\;{\rm {prime}}\geq 3}\left(1-{\frac {1}{(p-1)^{2}}\right)\approx 0.660 16\,1815 8\,4689\,57392\,78121\,10014\dots }$

이를 확장 골드바흐 추측이라고도 합니다. 강한 골드바흐 추측은 사실 쌍둥이 프라임 추측과 매우 유사하며, 두 추측은 대략 비슷한 난이도로 여겨집니다.

골드바흐 분할 함수는 두 소수의 합으로 분해할 수 있는 방법의 수를 각각의 짝수 정수와 연관시키는 함수입니다. 그것의 그래프는 혜성처럼 생겼고 따라서 골드바흐 혜성이라고 불립니다.^[29]

골드바흐의 혜성은 짝수의 표현 수에 대한 엄격한 상한과 하한을 두 소수의 합으로 제시하며, 또한 이러한 표현의 수는 숫자의 값 모듈로 3에 크게 의존한다는 것을 시사합니다.

관련 문제

골드바흐의 추측에 따르면 1보다 큰 모든 양의 정수는 많아야 세 개의 소수의 합으로 기록될 수 있지만, 각 단계에서 가능한 한 가장 큰 소수를 사용하는 탐욕스러운 알고리즘을 사용하여 그러한 합을 찾을 수 있는 것은 아닙니다. 필라이 수열은 탐욕스러운 표현에서 가장 많은 수의 소수를 필요로 하는 숫자를 추적합니다.^[30]

골드바흐 추측과 유사한 문제는 소수가 제곱과 같은 다른 특정한 수의 집합으로 대체되는 것입니다.

• 모든 양의 정수는 네 제곱의 합이라는 것이 라그랑주에 의해 증명되었습니다. 소수 거듭제곱의 합에 대한 와링의 문제와 관련된 와링-골드바흐 문제를 참조하십시오.
• 하디와 리틀우드는 그들의 추측 I: "모든 큰 홀수(n > 5)는 소수와 소수의 두 배의 합이다."^[31] 이 추측은 르모인의 추측으로 알려져 있으며 레비의 추측이라고도 합니다.
• 정수의 소수와 같은 수열인 실수에 대한 골드바흐 추측은 1984년 마르겐스테른에 의해 언급되었고,^[32] 1996년 멜피에 의해 증명되었습니다.^[33] 모든 짝수는 두 개의 실수의 합입니다.
• 하비 더브너(Harvey Dubner)는 4208보다 큰 모든 짝수 정수는 두 쌍의 소수의 합이라는 골드바흐 추측의 강화를 제안했습니다.^{[34][better source needed]} 4208보다 작은 34개의 짝수 정수만이 두 개의 쌍둥이 소수의 합이 아닙니다. 더브너는 이 목록이 ${\displaystyle 2^{}}$ ⋅$1010$까지 완전하다는 것을 계산적으로 확인했습니다. ${\displaystyle 2\cdot$10^{10}} 이 더 강한 추측의 증거는 골드바흐의 추측뿐만 아니라 쌍둥이 소수의 추측도 암시할 것입니다.

참고문헌

추가읽기

• Deshouillers, J.-M.; Effinger, G.; te Riele, H.; Zinoviev, D. (1997). "A complete Vinogradov 3-primes theorem under the Riemann hypothesis" (PDF). Electronic Research Announcements of the American Mathematical Society. 3 (15): 99–104. doi:10.1090/S1079-6762-97-00031-0.
• Montgomery, H. L.; Vaughan, R. C. (1975). "The exceptional set in Goldbach's problem" (PDF). Acta Arithmetica. 27: 353–370. doi:10.4064/aa-27-1-353-370.
• 테렌스 타오는 모든 홀수가 많아야 다섯 소수의 합이라는 것을 증명했습니다.
• 수학계의 골드바흐 추측.

외부 링크

• 위키미디어 커먼즈에서 골드바흐의 추측과 관련된 매체
• "Goldbach problem", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• 골드바흐가 오일러에게 보낸 원본 편지 — PDF 형식(독일어 및 라틴어)
• 골드바흐의 추측, 크리스 콜드웰의 프라임 페이지의 일부.
• 골드바흐 추측 검증, 토마스 올리베이라에 실바의 분산 컴퓨터 검색