양자 카오스

에 관한 일련의 기사의 일부
양자역학
${\displaystyle i\hbar {\frac t} \psi (t) \rangle = {H} \psi (t) \rangle }$ 슈뢰딩거 방정식
서론 용어집 역사
배경 고전 역학 구 양자론 브라켓 표기법 해밀턴식 방해다
기초 상보성 데코히렌스 얽힘 에너지 레벨 측정. 비국소성 양자수 주 중첩 대칭 터널링 불확실성 파동 함수 접다
실험 벨 부등식 데이비슨-게르머 더블 슬릿 엘리추르-바이드만 프랑크-헤르츠 레깃-가르그 부등식 마흐-젠더 포퍼 양자 지우개 선택 지연 슈뢰딩거의 고양이 스턴-게라크 휠러의 지연 선택
제제 개요 하이젠베르크 상호 작용 매트릭스 위상 공간 슈뢰딩거 Sum-over-History(경로 적분)
방정식 디락 클라인-고든 파울리 리드버그 슈뢰딩거
해석 개요 베이지안 일관성 있는 이력 코펜하겐 브로이쾅 앙상블 숨김 변수 현지의 다세계 객관적 붕괴 양자 논리 관계형 트랜잭션
상세 토픽 상대론적 양자역학 양자장론 양자정보과학 양자 컴퓨팅 양자 카오스 밀도 매트릭스 산란 이론 양자통계역학 양자 기계 학습
과학자 아하로노프 벨 베테 블래킷 블로치 쾅 보어 태어난 보스 드 브로글리 콤프턴 디락 데이비슨 데비 에렌페스트 아인슈타인 에버렛 폭 페르미 파인만 글라우버 거츠빌러 하이젠베르크 힐베르트 조던 크래머스 파울리 새끼 양 란다우 라우에 모즐리 밀리칸 온네스 플랑크 라비 라만 리드버그 슈뢰딩거 시몬스 솜메르펠트 폰 노이만 와일 빈 위그너 지만 자이링거
v t

양자 카오스는 물리학의 한 분야로, 어떻게 혼돈한 고전적 동적 시스템을 양자 이론의 관점에서 묘사할 수 있는지를 연구합니다.양자 혼돈이 답하고자 하는 주된 질문은 "양자 역학과 고전적 혼돈의 관계는 무엇인가?"이다.대응 원리는 고전 역학은 양자 역학의 고전적인 한계이며, 특히 계의 작용에 대한 플랑크 상수의 비율이 0인 경향이 있기 때문에 한계에서라고 말한다.만약 이것이 사실이라면, 고전적인 혼돈의 기초가 되는 양자 메커니즘이 있을 것이다.양자역학이 초기 조건에 대한 지수적 민감성을 보여주지 않는다면, 초기 조건에 대한 지수적 민감성은 양자역학의 ^[1][2]대응 원리 한계여야 하는 고전적 혼돈에서 어떻게 발생할 수 있을까요?

양자 혼돈의 기본적인 문제를 해결하기 위해 몇 가지 접근방식이 사용되었습니다.

1. 섭동이 이론상으로는 작다고 볼 수 없고 양자수가 큰 양자 문제를 해결하기 위한 방법의 개발.
2. 고유값(에너지 수준)에 대한 통계적 설명과 동일한 해밀턴(시스템)의 고전적 동작의 상관 관계.
3. 개별 고유 상태의 확률 분포에 대한 연구(흉터 및 양자 에르고디시티 참조).
4. 동적 시스템의 고전적 궤적을 양자 특성과 연결하는 주기적 궤도 이론과 같은 반고전적 방법.
5. 대응원칙의 직접적 적용.

역사

20세기 전반 동안, 역학의 혼란스러운 행동은 인식되었지만, 잘 이해되지 않았다.현대 양자역학의 토대는 그 시기에 마련되었고, 본질적으로 고전적 한계가 혼돈을 보이는 시스템의 양자 고전적 대응에 대한 문제는 제쳐두었다.

접근

대응 원리와 관련된 질문들은 핵에서 원자, 분자, 고체 물리학, 심지어 음향학, 전자파, 광학에 이르기까지 물리학의 많은 다른 분야에서 발생한다.그러나 카오스 이론에서 고전-양자 대응이 항상 가능한 것은 아니다.따라서, 고전적인 나비 효과의 일부 버전은 양자 ^[5]역학에서 다른 것을 가지고 있지 않다.

고전적으로 혼돈한 양자 시스템과 관련된 중요한 관찰은 스펙트럼 수준의 반발, 시간 진화의 동적 국재화(예를 들어 원자의 이온화 속도), 고전적 역학이 불안정한 궤적만 보이는 공간 영역(산란 등)에서 향상된 정지파 강도이다.양자 카오스의 반고전적 접근법에서 현상은 스펙트럼 라인의 통계적 분포를 분석하고 스펙트럼 주기성을 고전적 궤도와 연결함으로써 스펙트럼 분석에서 식별된다.다른 현상들은 양자 시스템의 시간 진화나 다양한 형태의 외부 힘에 대한 반응에서 나타난다.음향이나 마이크로파 등 일부 상황에서는 파형 패턴을 직접 관찰할 수 있으며 진폭 분포가 불규칙합니다.

양자 카오스는 일반적으로 수치 기법 또는 근사 체계를 사용하여 특성을 계산해야 하는 시스템을 다룬다(예: 참조).다이슨 시리즈).단순하고 정확한 해결책은 시스템 구성 요소가 서로 복잡한 방식으로 영향을 미치거나 일시적으로 변화하는 외부 힘에 의존한다는 사실에 의해 배제됩니다.

비교란적 체제에서의 양자역학

보수적 시스템의 경우, 비교동적 체제에서 양자 역학의 목표는 형태의 해밀턴의 고유값과 고유 벡터를 찾는 것이다.

${\displaystyle H=H_{s}+\varepsilon H_{ns},}$

${\displaystyle {여기}_{}}$서 H s$${\$displaystyle H_{s}$는 일부 좌표계에서 분리 가능하며 ${\displaystyle H_{}}$ ${\displaystyle n_{}}$ ${\displaystyle s_{}}${$displaystyle$ H_${ns}$는 H s {$displaystyle H_{s}}$가 분리되는 $좌표계$에서 분리되지 않으며 ${\$ {\$displaystyle \epsilon }$은 작다고 볼 수 없는 파라미터입니다.물리학자들은 역사적으로 분리할 수 없는 해밀턴이 가장 작은 좌표계를 찾고 분리할 수 없는 해밀턴을 섭동으로 처리함으로써 이러한 성격의 문제에 접근해 왔다.

이 분리가 수행될 수 있도록 운동 상수를 찾는 것은 어려운(때로는 불가능한) 분석 작업이 될 수 있습니다.고전적인 문제를 푸는 것은 양자 문제를 푸는 데 귀중한 통찰력을 줄 수 있다.만약 같은 해밀턴의 규칙적인 고전적 해법이 있다면, 운동의 대략적인 상수가 있고, 고전적인 문제를 해결함으로써 우리는 그것들을 찾는 방법을 단서들을 얻을 수 있다.

최근 몇 년 동안 다른 접근법이 개발되었습니다.하나는 해밀턴을 공간의 다른 영역에서 다른 좌표계로 표현하여 각 영역에서 해밀턴의 분리 불가능한 부분을 최소화하는 것입니다.이들 영역에서 파동함수를 구하고 경계조건을 일치시킴으로써 고유값을 구한다.

또 다른 접근법은 숫자 행렬 대각화이다.해밀턴 행렬이 완전히 계산될 경우 행렬의 대각화를 통해 고유값과 고유 벡터를 얻을 수 있습니다.그러나 모든 완전한 기본 집합은 무한하므로, 우리는 기본을 잘라내고 정확한 결과를 얻을 필요가 있습니다.이러한 기술은 정확한 파동 함수를 구성할 수 있는 잘린 기반을 선택하는 것으로 요약됩니다.행렬 스케일의 대각선화에 $필요$한 계산 시간은 ${\displaystyle {N\mathrm{}}^{}}$ 3$({$3$\})$입니다.$여기$서 N$({displaystyle$ N$})$은 행렬의 치수이므로 관련 파형 함수를 구성할 수 있는 최소 기준을 선택하는 것이 중요합니다.행렬 요소를 계산하는 것도 계산 부담이 될 수 있기 때문에 행렬이 희박하거나 행렬 요소가 단순한 대수식으로 주어지는 기초를 선택하는 것도 편리하다.

주어진 해밀턴의 운동 상수는 고전과 양자 역학 모두에서 동일합니다.양자 시스템은 이산 대칭(반사 대칭으로부터의 패리티 보존 등)에 대응하는 추가 양자 수를 가질 수도 있습니다.하지만, 만약 우리가 섭동 이론으로 접근할 수 없는 해밀턴의 양자 해법을 찾는다면, 우리는 양자 해법에 대해 많은 것을 배울 수 있지만, 양자 혼돈에 대해서는 거의 알지 못한다.그럼에도 불구하고, 그러한 양자 문제를 해결하는 방법을 배우는 것은 양자 혼돈에 대한 질문에 답하는 데 있어 중요한 부분이다.

양자역학의 통계적 설명과 고전적 행동의 상관관계

양자 카오스의 통계적 측정치는 복잡한 시스템의 스펙트럼 특성을 정량화하려는 욕망에서 탄생했다.랜덤 매트릭스 이론은 복잡한 핵의 스펙트럼을 특징짓기 위한 시도로 개발되었다.주목할 만한 결과는 해밀턴이 알려지지 않은 많은 시스템의 통계적 특성은 적절한 대칭 클래스의 랜덤 행렬을 사용하여 예측할 수 있다는 것이다.게다가, 랜덤 매트릭스 이론은 또한 알려진 해밀턴을 가진 많은 카오스 시스템의 고유값의 통계적 특성을 정확하게 예측한다.이는 계산을 위해 큰 수치적 노력이 필요한 스펙트럼 특성화를 위한 도구로 유용하다.

스펙트럼 특징을 간단한 방법으로 정량화하기 위해 많은 통계적 조치를 이용할 수 있다.고전적으로 혼돈된 시스템의 보편적인 통계적 동작이 있는지 여부는 매우 흥미롭다.그 통계적 시험 여기 언급했듯이, 자유의 몇도고 베리랑 Tabor[6] 프와송 분포에 대해 정기적인 운동의 경우, 그리고 호이슬러(알에 대한 치열한 논쟁이 앞으로 있는 시스템과 최소한 보편화 되어 있다.는 spe의 보편성을 주장하고 소위 Bohigas–Giannoni–Schmit는 억측의 준 고전적인 설명을 제시하[7].혼돈 동역학에서의 CTral 변동).에너지 수준의 가장 가까운 인접 분포(ND)는 상대적으로 해석하기 쉬우며 양자 카오스를 설명하는 데 널리 사용되어 왔다.

수준 격퇴의 정성적 관찰은 양자 시스템에서 고전 역학의 중요한 특징으로 여겨지는 NND를 사용하여 계량화되고 고전 역학과 관련될 수 있다.에너지 수준의 포아송 분포에 의해 규칙적인 고전 역학이 나타나는 것으로 생각된다.

$(\displaystyle P(s)=e^{-s}).\ }$

또한 카오스 고전 운동을 표시하는 시스템은 랜덤 행렬 고유값 앙상블의 통계로 특징지어질 것으로 예상된다.시간 반전 하에서 불변하는 시스템의 경우, 다수의 카오스 시스템의 에너지 수준 통계는 랜덤 행렬의 가우스 직교 앙상블(GOE) 예측과 잘 일치하는 것으로 나타났으며, 이 현상은 이 대칭을 가진 모든 카오스 시스템에 대해 일반적이라고 제안되었다.두 에너지 레벨 사이의 정규화 간격이 $s\backslash$$displaystyle$s인 경우 공간의 정규화 분포는 다음과 같이 근사됩니다.

${\displaystyle P(s)=secfrac {{pi }{2}}se^{-\pi s^{2}/4}.}$

고전적으로 적분할 수 있는(무혼란) 해밀턴의 많은 시스템은 포아송 분포를 따르는 가장 가까운 인접 분포를 산출하는 양자 솔루션을 가지고 있는 것으로 밝혀졌다.마찬가지로 고전적인 카오스를 나타내는 많은 시스템이 위그너-다이슨 분포를 갖는 양자 해와 함께 발견되어 위의 아이디어를 뒷받침하고 있다.한 가지 주목할 만한 예외는 반자성 리튬으로, 고전적인 혼돈을 나타내지만 짝수 패리티 에너지 레벨에 대한 위그너(혼돈) 통계와 홀수 패리티 에너지 레벨 ^[8]분포에 대한 거의 포아송(정규) 통계량을 보여준다.

반고전적 방법

주기 궤도 이론

주기적 궤도 이론은 시스템의 주기적 궤도로부터 스펙트럼을 계산하는 방법을 제공한다.아인슈타인-브릴루인-켈러 작용 양자화 방법과는 달리, 각 궤도로부터 개별 고유값을 계산하고, 각 주기 궤도가 정현파 변동을 발생시킨다고 주장한다.n 상태 밀도.

이 개발의 주요 결과는 반고전적 그린 함수의 트레이스이며 Gutzwiller 트레이스 공식에 의해 주어지는 상태의 밀도에 대한 표현이다.

${\displaystyle g_{c}(E)=\sum _{k}T_{k}\sum _{n=1}^{\infty}{\frac {2\sinh {\chi _{nk}/2)}}}}, e^{i(nS_{k}-\alpha _{pi / 2)}.}$

최근 스핀 또는 기타 내부 ^[9]자유도에서 비롯된 베리 위상 항을 포함하는 임의 매트릭스 해밀턴에 대한 이 공식의 일반화가 있었다.$(\displaystyle$ k$)$ 지수는$$ 초기 조건 집합의 최단 주기 궤도인 원시 주기 궤도를 구분한다.${\displaystyle T_{}}$k({$displaystyle T_{k$})는$$ 원시 주기 궤도의 주기이며, ${\displaystyle S_{}}$k({$displaystyle S_{k})$는 고전적인 작용이다.각 원시 궤도는 자체 궤도로 돌아가며, 작용 ${\displaystyle {}_{}}$ $S{\displaystyle }$ $(\$})와$$ 원시 기간의 정수 $배수{\displaystyle }$ n$(\displaystyle$ n$)$인 주기로 새로운 궤도로 이어진다.따라서 주기 궤도의 모든 반복은 또 다른 주기 궤도이다.이러한 반복은 $지수{\displaystyle }$ n$(\displaystyle$ n$)$에 대한 중간 합계에 의해 별도로 분류된다. ${\displaystyle {\alpha }_{}}$ n$(\display$ \$alpha$ _${nk})$는 궤도의 마슬로프 지수이다.$진폭{\displaystyle \mathrm{}}$ 계수${\displaystyle }$1/${\displaystyle \sinh }$δ ( ${\displaystyle {\delta }_{}}$ n${\displaystyle {}_{}{k}_{}}$ /${\displaystyle 2\mathrm{}}$)$${\$displaystyle$ 1$/\sinh${(\$chi _${nk$}/2$는 인접 궤도 밀도의 제곱근을 나타냅니다.불안정한 주기적 궤도의 인접 궤도는 주기적 궤도에서 시간에 따라 기하급수적으로 분산된다.${\displaystyle {\mathrm{\delta n}}_{}}$ k$(\displaystyle$ \$chi$ _${nk})$의 양은 궤도의 불안정성을 나타냅니다.안정된 궤도는 위상공간의 토러스 위에서 움직이고, 주변 궤도는 토러스 주위를 휘감는다.안정적인 궤도의 경우, ${\displaystyle \sinh }$ ${\displaystyle (}$ ( ${\displaystyle n_{}}$ n${\displaystyle {}_{}{k}_{}}$ /${\displaystyle 2\mathrm{}}$) { \ $displaystyle \sinh${ \ $chi$_ { $nk$} / $2$$$} { \ $displaystyle \sin${ \ $chi$_ { $nk$$$} / $2$}}} 은 sin${\displaystyle （}$ $display$ ${\displaystyle {\mathrm{nk}}_{}}$）가 ${\displaystyle \mathrm{됩니다}}$. 여기서 ${\displaystyle n_{}}$ ${\displaystyle n_{}}$k \ $displaystyle _$ { nk $}$는 주기 궤도의$$ 권수입니다.${\displaystyle {\chi }_{}}$ n k${\displaystyle {}_{}}$= ${\displaystyle 2}$ m {$displaystyle$ \$chi _$ { display } = $2 \pi$ m$$} 。 $여기서$m { $displaystyle$m$$ }은 인접 궤도가 한 주기에서 주기 궤도와 교차하는 횟수입니다.이것은 고전적인 분기에서는 sin${\displaystyle }$θ(${\displaystyle {\theta }_{}}$ ${\displaystyle n_{}}$k /${\displaystyle 2\mathrm{}}$) $=$ ${\displaystyle 0}${\$displaystyle \sin${(\$chi _{display}/2$)}=0$$$}$이므로 ${\displaystyle \mathrm{어려움}}$을 나타낸다.이것은 그 궤도의 에너지 밀도에 대한 기여도를 분산시키는 원인이 된다.이는 광흡수 스펙트럼의 맥락에서도 발생한다.

스펙트럼을 계산하기 위해 추적 공식을 사용하려면 시스템의 모든 주기적 궤도에 대한 합계가 필요하다.이것은 카오스 시스템에 몇 가지 어려움을 준다: 1) 작용의 함수로서 주기적 궤도의 수가 기하급수적으로 증가한다. 2) 주기적 궤도는 무한히 많고 주기적-궤도 이론의 수렴 특성은 알려져 있지 않다.이 어려움은 주기 궤도 이론을 정규 시스템에 적용할 때도 존재한다. 3) 장기 궤도는 대부분 불안정하고 반올림 오류와 수치 적분의 세부 사항에 민감하기 때문에 계산하기가 어렵다.

Gutzwiller는 추적 공식을 적용하여 반고전적으로 이방성 케플러 문제(이방성 질량 텐서를 가진 1/$\style$1/$r$의 단일 입자)에 접근했다.그는 쉽게 계산되는 주기적 궤도 중 작은 세트만을 사용하여 작은 이방성(n $= 6$까지$)$에 대한 낮은 거짓말($양자$ 계산)에 대한 양자 계산과 일치하지만, 큰 이방성에는 적합하지 않았다.

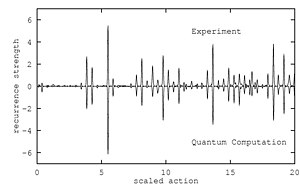
위의 그림은 주기적 궤도 이론을 테스트하기 위해 역접근법을 사용합니다.추적 공식은 각 주기 궤도가 스펙트럼에 정현파 항을 기여한다고 주장한다.상태의 밀도(에너지 수준)를 찾기 위해 장기 궤도에 둘러싼 계산상의 어려움을 다루는 대신에, 사람들은 표준 양자 역학적 섭동 이론을 사용하여 고유값(에너지 수준)을 계산하고 푸리에 변환을 사용하여 스펙트럼의 주기적인 변조를 찾을 수 있습니다.주기 궤도스펙트럼을 해석하는 것은 푸리에 변환의 피크에 해당하는 궤도를 찾는 것과 같습니다.

Gutzwiller 추적 공식에 도달하는 방법에 대한 대략적인 스케치

1. 먼저 시간에 의존하는 Green 함수(Van Vleck 전파기)의 반고전적 근사치부터 시작합니다.
2. 가성학에서는 설명이 분산되어 Maslov의 통찰력(약적으로 Fourier 변환되어 운동량 공간(h 작은 파라미터에 의한 정지 위상 근사)을 사용하여 이러한 점을 방지하고 나중에 다시 위치 공간으로 변환하면 그러한 차이를 해결할 수 있지만 위상 계수는 제공됨)을 사용합니다.
3. Greens 함수를 에너지 공간으로 변환하여 에너지 종속 Greens 함수를 얻습니다(다시 정적 위상 근사를 사용하여 대략적인 푸리에 변환).3단계와 동일한 방법으로 치료해야 하는 새로운 분기가 나타날 수 있습니다.
4. $d{\displaystyle }$ ${\displaystyle (E}$ ) ${\displaystyle =}$ - ${\displaystyle 1\frac{\mathrm{}}{}\pi \mathrm{}}$ （ ${\displaystyle \mathrm{Tr}}$ ${\displaystyle ）}$ （${\displaystyle G}$ ( ${\displaystyle {}^{}}$ , ${\displaystyle x{}^{}}$,${\displaystyle }$E )$${ $displaystyle$ d$(E$ ) = - { \ $frac {$1$}$ {\$pi }}}\Im$(\$operatorname {Tr}(G(x,x^{\$prime$})})$을 사용하여 대략적인 위치에서 다시 계산합니다.

참고: 궤적을 보면 닫힌 궤도만 기여한다는 것을 알 수 있으며, 정지 위상 근사치를 사용하면 매번 제한적인 조건을 얻을 수 있습니다.4단계에서는 초기 운동량과 최종 운동량이 동일한 궤도(즉, 주기 궤도)로 제한됩니다.많은 책들이 그렇듯이, 종종 이동 방향에 평행한 좌표계를 선택하는 것이 좋습니다.

닫힌 궤도 이론

닫힌 궤도 이론은 J.B.에 의해 개발되었다.델로스, M.L. Du, J. Gao, J.쇼. 그것은 닫힌 궤도 이론이 원자 및 분자 스펙트럼에만 적용 가능하며 특정한 초기 상태에서 발진기 강도 밀도(관측 가능한 광흡수 스펙트럼)를 산출하는 반면 주기 궤도 이론은 상태의 밀도를 산출한다는 점을 제외하면 주기 궤도 이론과 유사합니다.

닫힌 궤도 이론에서는 핵에서 시작해서 끝나는 궤도만이 중요하다.물리적으로 이것들은 단단히 묶인 전자가 높은 위치까지 들뜨면 발생하는 발신파와 관련되어 있습니다.Rydberg 원자와 분자의 경우, 핵에서 닫히는 모든 궤도는 닫힘 시간 또는 닫힘 시간의 두 배와 같은 주기의 주기적 궤도이다.

닫힌궤도 이론에 따르면 일정한 $(\displaystyle\epsilon)$에서의 평균 발진기 강도 밀도는 매끄러운 배경과 형태의 진동 합계를 더한 값입니다.

${\displaystyle f(w)=\sum _{k}\sum _{n=1}^{\infty}}D_{\it {pi nwtilde {S_{k}}-\phi _{\it {pi}}}.}$

${\displaystyle {}_{}}$§ $k (\displaystyle$ \$phi _{\it${nk$$}})는 마슬로프 지수 및 기타 궤도의 세부 사항에 따라 달라지는 단계이다.${\displaystyle {\mathit{Dn}}_{}^{}}$ $(\$는 소정의 초기 상태$(\displaystyle$ $)$에 대한 닫힌 궤도의 반복 진폭입니다.여기에는 궤도의 안정성, 초기 및 최종 방향, 초기 상태와 제로 에너지 쿨롱 파동 사이의 쌍극자 연산자의 매트릭스 요소에 대한 정보가 포함되어 있습니다.Rydberg 원자와 같은 강장 스케일링 시스템에서는$w$의 함수로서 고정된$(\$$displaystyle$\$epsilon$$)$에서 계산된 발진기 강도 스펙트럼의 푸리에 변환을 반복 스펙트럼이라고 한다.왜냐하면 폐쇄 궤도의 스케일링된 동작에 대응하는 피크를 제공하기 때문이다.$($ D_${\it {nk}}^{i$를 선택합니다.

닫힌 궤도 이론은 반자성 수소, 평행 전기장과 자기장의 수소, 반자성 리튬, 전장의 리튬, 교차 및 평행 전기장과 자기장의${\displaystyle {}^{}}$H -${-} 이온$, 전장의 바륨, 헬프를 포함한 많은 혼돈 시스템과 폭넓게 일치함을 발견했습니다.전기장에서의 암.

1차원 시스템과 가능성

경계 $조건{\displaystyle }$y (${\displaystyle 0)}$ $=$ ${\displaystyle 0}$ {\$displaystyle$y($0)=0$}인 1차원 시스템의 경우, Gutzwiller 공식에서 구한 상태의 밀도는 d${\displaystyle \frac{{1\mathrm{}}^{}}{}}$/${\displaystyle 2\frac{}{}}$ d ${\displaystyle \frac{{x\mathrm{}}^{}}{}}$1 / ${\displaystyle \frac{{2\mathrm{}}^{}}{}{}^{}}$V -${\displaystyle {}^{}1}$ (${\displaystyle }$x )$$ ${\displaystyle 2}$ = ${\displaystyle d\sqrt{}}$ ${\displaystyle \frac{N}{}}$(${\displaystyle \frac{}{}}$x ) ${\displaystyle \frac{}{}}$ $display$ style {\frac style {\$frac$$}$의 고전적 $시스템$의 전위 반전과 관련이 있다.${d^{1/2}}{dx^{1/2}}}V^{-1}(x)=2{\sqrt {pi}}{\frac {dN(x)}{dx}}$$여기$서 ${\displaystyle \frac{d}{}}$ N${\displaystyle \frac{(x)}{d}}$x$(\displaystyle$ {$frac {dN(x)}{dx}})$는 vX의 밀도이며, 고전적인 상태는 다음과 같습니다.

최근 지시 사항

하나의 미해결 질문은 표준 반고전적 한계가 적용되지 않는 유한 차원 국소 힐버트 공간을 가진 시스템에서 양자 혼돈을 이해하는 것이다.최근의 연구들은 그러한 양자 ^[10][11]다체계를 분석적으로 연구할 수 있었다.

양자 혼돈의 전통적인 주제는 스펙트럼 통계(범용 및 비범용 특징)와 다양한 혼돈 해밀턴의 고유 함수에 관한 연구이다.예를 들어, 흉터의 존재가 보고되기 전에, 이용 가능한 위상 공간을 랜덤 변동과 에너지 보존(양자 에르고디시티)까지 균등하게 채우기 위해 고전적으로 혼돈된 시스템의 고유 상태가 추측되었다.그러나 고전적으로 혼돈한 시스템의 양자 고유 상태는 흉터가 ^[12]될 수 있다. 즉, 고유 상태의 확률 밀도는 주기적 궤도 근방에서 궤도(scars)를 따라 통계적으로 기대되는 전형적인 밀도보다 높아진다.특히, 흉터는 일반적인 고전적 한계에서 벗어난 고전-양자 대응의 두드러진 시각적 예이자 혼돈의 양자 억제의 유용한 예이다.예를 들어, 이것은 섭동에 의해 유발되는 양자 ^{[13][14][15][16][17]}흉터에서 명백하다: 보다 구체적으로, 국소적인 잠재적 범프(불순물)에 의해 교란된 양자 점에서는, 일부 고유 상태가 교란되지 않은 고전적인 상대물의 주기적인 궤도를 따라 강하게 흉터된다.

추가 연구는 회피된 교차의 통계에서 반영되는 해밀턴의 파라메트릭($\displaystyle$ R$)$ 의존성 및 (파라메트릭) 국소 밀도 상태(LDOS)에서 반영되는 관련 혼합에 관한 것이다.변동, 반복, 양자 불가역성 문제 등을 포함한 웨이브패킷 역학에 관한 방대한 문헌이 있다.양자화된 지도의 역학을 연구하기 위한 특별한 장소: 표준 지도와 킥 회전 장치(kicked rotator)는 프로토타입 문제로 간주됩니다.

또한 작업은 해밀턴 ^[18]H${\displaystyle }$(${\displaystyle x}$ ,${\displaystyle p}$ ;${\displaystyle R}$ (${\displaystyle }$t$$) { $displaystyle$H ($x$ ,$p$ ;$R$ ($t$ )} ) } 에서는$$ 특히 단열 및 선형 응답 방식에 따라 시간에 의존합니다.또한 양자 혼돈 ^[19]산란에서 큰 노력뿐만 아니라 반고전적 정세에서 멀리 떨어진 다체 양자 시스템을 강하게 상호 작용시키기 위한 양자 혼돈의 개념을 형성하는 데 초점을 맞춘 상당한 노력이 있다.

베리-타보르 추측

1977년, 베리와 타보르는 여전히 개방적인 "일반적인" 수학적 추측을 했습니다. 대략적으로: 콤팩트한 리만 표면에서 측지학 흐름의 양자 역학의 경우, 양자 에너지 고유값은 기초 고전 역학이 완전히 존재한다면 일련의 독립적인 랜덤 변수처럼 행동합니다.지도할 ^[20][21][22]수 있습니다.

「 」를 참조해 주세요.

• 흉터(물리학)

레퍼런스

기타 자원

• Martin C. Gutzwiller (1971). "Periodic Orbits and Classical Quantization Conditions". Journal of Mathematical Physics. 12 (3): 343–358. Bibcode:1971JMP....12..343G. doi:10.1063/1.1665596.
• 마틴 C.Gutzwiller, Classical and Quantum Mechanics, (1990) Springer-Verlag, 뉴욕 ISBN 0-387-97173-4.
• Hans-Jürgen Stöckmann, Quantum Chaos: 개요, (1999) 케임브리지 대학 출판부 ISBN 0-521-59284-4.
• Eugene Paul Wigner; Dirac, P. A. M. (1951). "On the statistical distribution of the widths and spacings of nuclear resonance levels". Mathematical Proceedings of the Cambridge Philosophical Society. 47 (4): 790. Bibcode:1951PCPS...47..790W. doi:10.1017/S0305004100027237. S2CID 120852535.
• Fritz Haake, Quantum Signatures of Chaos, 2nd., (2001) 스프링거-벨라그, 뉴욕 ISBN 3-540-67723-2.
• Karl-Fredrik Berggren과 Sven Aberg, "Quantum Chaos Y2K 노벨 심포지엄 116" (2001) ISBN 978-981-02-4711-9
• L. E. Reichl, "혼돈으로의 이행: 보수적인 고전 시스템: 양자현상", 스프링어(2004), ISBN 978-0387987880

외부 링크

• Martin Gutzwiller의 양자 혼돈(1992년 및 2008년, Scientific American)
• Quantum Chaos Martin Gutzwiller Scholarpedia 2(12):3146.doi:10.4249/scholarpedia.3146
• 카테고리:양자 혼돈 스콜라피디아
• 뭐... Ze'ev Rudnick의 Quantum Chaos (2008년 1월, 미국 수학회 공지사항)
• 브라이언 헤이스, "리만의 스펙트럼"; 미국 과학자 권 91, 4호, 7월-2003년 8월 296~300쪽리만 제타 함수와의 관계를 설명합니다.
• Arnd Bécker에 의한 혼돈 양자 시스템의 고유 함수.
• ChaosBook.org