쿼크 모형
Quark model
입자 물리학에서 쿼크 모형은 강입자의 양자수를 발생시키는 쿼크와 반쿼크인 원자가 쿼크의 관점에서 강입자를 분류하는 체계이다.쿼크 모델은 1950년대부터 1960년대까지 발견되었던 다수의 가벼운 강입자를 정리한 성공적인 분류 체계인 "flavor SU(3)", 즉 "8중 방식"의 기초가 된다.1960년대 후반부터 실험 검증을 받았으며 현재까지 유효한 분류이다.이 모델은 물리학자인 머레이 겔-만([1]Murray Gell-Mann)이 간결한 논문에서 쿼크(quarks)라고 불렀고 조지 츠위그(George Zweig)[2][3]가 더 긴 원고를 통해 에이스(ace)를 제안했다.앙드레 페테르만은 1963년부터 1965년까지 양적 실증 [4][5]없이 중심 사상에 대해 언급했다.오늘날, 이 모델은 기본적으로 표준 모델이라고 불리는, 강력하고 약한 입자 상호작용의 확립된 양자장 이론의 구성 요소로서 흡수되었습니다.
강입자는 사실 "원소"가 아니며, 강입자의 양자수를 발생시키는 "원자 쿼크"와 반물질의 결합 상태로 간주될 수 있습니다.이들 양자수는 강입자를 식별하는 라벨로 두 가지 종류가 있습니다.한 세트는 Poincaré 대칭(JPC)에서 파생됩니다. 여기서 J, P 및 C는 각각 총 각운동량, P-대칭 및 C-대칭을 나타냅니다.
다른 한 세트는 이소스핀, 이상함, 매력 등 맛 양자수입니다.쿼크를 결합하는 강한 상호작용은 이러한 양자수에 민감하지 않기 때문에 쿼크의 변화는 같은 맛의 다중입자 내의 강입자 사이의 체계적인 질량과 결합 관계를 이끌어냅니다.
모든 쿼크에는 number의 바리온 번호가 할당됩니다.위 쿼크와 위 쿼크는 + µ의 전하를 가지며, 아래 쿼크는 - µ의 전하를 가집니다.고물들은 정반대의 양자수를 가지고 있다.쿼크는 스핀 입자이고, 따라서 페르미온이다.각 쿼크 또는 반쿼크는 개별적으로 겔-만-니시지마 공식에 따르기 때문에 이들 중 어떤 첨가물 집합체도 마찬가지입니다.
중간자는 원자가 쿼크-반쿼크 쌍(따라서 바리온 번호 0)으로 구성되고, 중입자는 3개의 쿼크(따라서 바리온 번호 1)로 구성됩니다.이 기사에서는 (대략적인 맛 SU(3) 대칭을 형성하는) 위, 아래 및 이상한 맛의 쿼크 모델에 대해 설명합니다.더 많은 맛에 대한 일반화가 있다.
역사
강입자의 분류 체계를 개발하는 것은 새로운 실험 기술이 너무 많은 강입자를 밝혀낸 후 시기 적절한 질문이 되었다.이러한 발견으로 볼프강 파울리는 "그것을 예견했다면 식물학을 공부했을 것이다."라고 외쳤고 엔리코 페르미는 그의 제자 레더맨에게 충고했다: "젊은이, 내가 이 입자들의 이름을 기억할 수 있었다면, 나는 식물학자가 되었을 것이다."이 새로운 계획들은 많은 개발의 선두에 선 루이스 알바레즈를 포함한 실험 입자 물리학자들에게 노벨상을 안겨주었다.하드론을 소수의 구성 요소로 묶인 상태로 구성하면 "주"를 구성할 수 있습니다.엔리코 페르미, 양첸닝(1949년), 사카타 모델(1956년) 등의 초기 제안도 중간자를 만족스럽게 커버했지만 중입자로는 실패했기 때문에 모든 데이터를 설명할 수 없었다.
Murray Gell-Man과 Kazuhiko Nishijima에 의해 개발된 Gell-Man-Nishima 공식은 1961년 Yuval Ne'eman의 중요한 독립적 공헌과 함께 Gell-Man에 의해 발명된 8중 경로 분류로 이어졌다.강입자는 강한 상호작용으로 인해 거의 동일한 질량의 SU(3) 표현 다중항, 옥텟 및 십중항으로 구성되었다. 그리고 강한 상호작용에 보이지 않는 맛 양자 숫자와 관련된 더 작은 질량 차이가 있었다.Gell-Mann-Okubo 질량 공식은 SU(3)의 명시적 대칭 파괴에 의해 제어되는 강입자 멀티플릿의 구성원들 사이의 이러한 작은 질량 차이의 정량화를 체계화했다.
회전하는 것... 3 22
−
b 바리온은 그 분류의 중요한 예측이었다.브룩헤이븐 국립연구소의 실험에서 발견된 후, 겔만은 1969년 팔중도에 대한 그의 연구로 노벨 물리학상을 받았다.
마침내 1964년, Gell-Mann과 George Zweig는 독립적으로 Eightfold Way 그림이 암호화하는 것을 식별했다.그들은 "업", "다운" 및 "이상한" 세 가지 기본 페르미온 성분인 "업", "다운" 및 "기묘한" 쿼크를 배치했는데, 이러한 구성 요소는 관찰되지 않으며, 자유 형태로 관찰할 수 없을 수도 있다.이 세 가지 성분과 그 반입자의 단순한 쌍방향 또는 삼중방향 조합은 경제적이고 촘촘한 구조에서 8중방향 분류의 기초가 되고 우아하게 부호화되므로 더욱 단순해집니다.하드론 질량 차이는 이제 구성 쿼크의 다른 질량과 관련이 있습니다.
이러한 쿼크의 예기치 않은 특성 및 물리적 현실을 보다 완벽하게 인식하려면 약 10년이 걸립니다(쿼크 참조).반직관적으로, 그것들은 결코 단독으로 관찰될 수 없으며(색 제한), 대신 항상 다른 쿼크와 결합하여 완전한 강입자를 형성하고, 그러면 갇힌 쿼크 자체에 대한 충분한 간접 정보를 제공합니다.반대로, 쿼크는 양자 색역학의 정의, 즉 강한 상호작용을 완전히 설명하는 기본 이론의 역할을 합니다; 그리고 8중 방법은 이제 그들 중 가장 가벼운 세 개의 맛 대칭 구조의 결과로 이해됩니다.
중간자
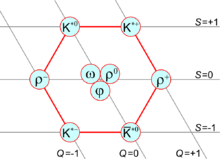
8배법 분류는 다음 사실에서 이름을 따왔다: 만약 우리가 세 가지 맛의 쿼크를 취한다면, 쿼크는 맛 SU(3)의 기본 표현인 3에 있다.고물들은 복합 켤레 표현 3에 있다.쌍으로 이루어진9 개의 스테이트(nonet)는, 1 개의 단순한 표현(싱글릿이라고 불립니다)과 8 개의 인접 표현(옥텟이라고 불립니다)으로 분해할 수 있습니다.이 분해의 표기법은 다음과 같습니다.
- 3 \ \3\ = \ 8 } \ \
그림 1은 중간자에 대한 이 분해의 적용을 나타내고 있습니다.맛의 대칭이 정확하다면(강력한 상호작용만 작동하고 전기약 상호작용은 개념적으로 꺼지는 한계에서와 같이), 9개의 중간자 모두 같은 질량을 가질 것이다.그러나 완전[clarification needed] 이론의 물리적 내용에는 쿼크 질량 차이에 의해 유발되는 대칭 파괴에 대한 고려와 다양한 다중항(예: 옥텟과 단일항) 간의 혼합 고려가 포함된다.
N.B. 그럼에도 불구하고, θ와
θ 사이의 질량 분할은 쿼크 모델이 수용할 수 있는 크기보다 크며,
이
"θ–
θ 퍼즐"은 인스턴트온 구성과 같은 강한 상호작용 진공의 위상 특성에 기원을 두고 있다.
중간자는 중입자 수가 0인 강입자입니다.쿼크-반쿼크 쌍이 궤도 각운동량 L 상태이고 스핀 S가 있다면,
- L - S j J l L + S, 여기서 S = 0 또는 1
- P = (-1),L + 1 여기서 지수에서 1은 쿼크-크래커 쌍의 고유 패리티에서 발생한다.
- 맛이 없는 중간자의 경우 C = (-1).L + S향미 중간자의 값은 C입니다.
- Isospin I = 1 및 0 상태의 경우, G = (-1)I + L + S이 되도록 G-parity라는 새로운 곱셈 양자수를 정의할 수 있다.
P = (-1)J이면 S = 1, 즉 PC = 1. 이러한 양자 수를 갖는 상태를 자연 패리티 상태라고 하며, 다른 모든 양자 수를 이국적 상태(예PC: J−− = 0)라고 한다.
바리온스
쿼크는 페르미온이기 때문에 스핀-통계정리는 두 쿼크의 교환 하에서는 바리온의 파동함수가 반대칭이어야 한다는 것을 의미한다.이 반대칭 파동 함수는 아래에서 설명한 바와 같이 완전히 반대칭 색상으로 만들고 맛, 스핀 및 공간을 모두 합친 대칭으로 함으로써 얻을 수 있습니다.세 가지 맛으로 맛의 분해는
쿼크의 기본 상태를 3가지 맛의 6가지 상태, 각 맛의 2회전 상태로 생각하는 것이 때때로 유용합니다.이 대략적인 대칭을 스핀 플레이버 SU(6)라고 합니다.이 점에서 분해는
향미 SU(3)에서 스핀과 향미의 대칭적 조합을 가진 56개 상태는 분해된다.
S = 1⁄2 옥텟 바리온은 두 개의 핵자(
p+
, n0
), 세 개의 시그마(
δ+
, δ0
−
), 두 개의 Xis(
δ0
, δ−
) 및 람다(
δ0
)이다.S = 3⁄2 데큐플렛 바리온은 4개의 델타(
δ++
, δ+
, δ0
, δ−
), 3개의 시그마(
δ∗+
, δ∗0
∗−
), 2개의 XIS(
δ∗0
, δ∗−
) 및 오메가(
δ−
)이다.
예를 들어, 양성자에 대한 구성 쿼크 모델 파동 함수는 다음과 같다.
![{\displaystyle |p_{\uparrow }\rangle ={\frac {1}{\sqrt {18}}}[2|u_{\uparrow }d_{\downarrow }u_{\uparrow }\rangle +2|u_{\uparrow }u_{\uparrow }d_{\downarrow }\rangle +2|d_{\downarrow }u_{\uparrow }u_{\uparrow }\rangle -|u_{\uparrow }u_{\downarrow }d_{\uparrow }\rangle -|u_{\uparrow }d_{\uparrow }u_{\downarrow }\rangle -|u_{\downarrow }d_{\uparrow }u_{\uparrow }\rangle -|d_{\uparrow }u_{\downarrow }u_{\uparrow }\rangle -|d_{\uparrow }u_{\uparrow }u_{\downarrow }\rangle -|u_{\downarrow }u_{\uparrow }d_{\uparrow }\rangle ].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9065e6a4a38b5ba8d274c20baad0a25ac6bc1457)
중입자 혼합, 다중점 내 및 다중점 사이의 질량 분할 및 자기 모멘트는 모델이 성공적으로 예측하는 다른 양입니다.
색채의 발견
색 양자수는 강한 힘의 특징적인 전하이며, 전기 약 상호작용에 전혀 관여하지 않습니다.이들은 쿼크 모델 분류의 결과로 발견되었는데, 이때 스핀 S = 3⁄2 바리온인 δ는++
평행 스핀과 소멸 궤도 각 운동량을 가진 3개의 업 쿼크를 필요로 했다.따라서 숨겨진 양자수가 없는 한 파울리 배제 원리에 의해 요구되는 반대칭 파동 함수를 가질 수 없었다.Oscar Greenberg는 1964년에 쿼크가 [6]패러페름이어야 한다고 제안하면서 이 문제를 지적했다.
대신, 6개월 후, 한무영과 난부 요이치로(南部 nam一郞)는 이 문제를 해결하기 위해 세 개의 쿼크의 존재를 제안했지만, 그 모델에는 맛과 색깔이 얽혀 있었다.그들은 [7]통근하지 않았다.
다른 모든 전하와 완전히 이동하며 강한 힘 전하를 제공하는 현대의 개념은 1973년 윌리엄 바딘, 하랄드 프리츠치 및 머레이 [8][9]겔만에 의해 명확히 표현되었습니다.
쿼크 모형 밖의 상태
쿼크 모델은 양자 색역학 이론에서 파생될 수 있지만, 하드론의 구조는 이 모델이 허용하는 것보다 더 복잡합니다.하드론의 완전한 양자역학적 파동 함수는 가상 글루온뿐만 아니라 가상 쿼크 쌍을 포함해야 하며 다양한 혼합을 허용합니다.쿼크 모델 외부에 있는 하드론이 있을 수 있습니다.이 중에는 글루볼(원자가 글루온만 포함), 하이브리드(원자가 쿼크뿐만 아니라 글루온도 포함) 및 엑소틱 하드론(예: 테트라쿼크 또는 펜타쿼크)이 있습니다.
「 」를 참조해 주세요.
메모들
- ^ Gell-Mann, M. (4 January 1964). "A Schematic Model of Baryons and Mesons". Physics Letters. 8 (3): 214–215. Bibcode:1964PhL.....8..214G. doi:10.1016/S0031-9163(64)92001-3.
- ^ Zweig, G. (17 January 1964). An SU(3) Model for Strong Interaction Symmetry and its Breaking (PDF) (Report). CERN Report No.8182/TH.401.
- ^ Zweig, G. (1964). An SU(3) Model for Strong Interaction Symmetry and its Breaking: II (PDF) (Report). CERN Report No.8419/TH.412.
- ^ Petermann, A. (1965). "Propriétés de l'étrangeté et une formule de masse pour les mésons vectoriels" [Strangeness properties and a mass formula for vector meson]. Nuclear Physics. 63 (2): 349–352. arXiv:1412.8681. Bibcode:1965NucPh..63..349P. doi:10.1016/0029-5582(65)90348-2.
- ^ Petrov, Vladimir A. (June 23–27, 2014). Half a Century with QUARKS. XXX-th International Workshop on High Energy Physics. Protvino, Moscow Oblast, Russia. arXiv:1412.8681.
- ^ Greenberg, O.W. (1964). "Spin and unitary-spin independence in a paraquark model of baryons and mesons". Physical Review Letters. 13 (20): 598–602. Bibcode:1964PhRvL..13..598G. doi:10.1103/PhysRevLett.13.598.
- ^ Han, M.Y.; Nambu, Y. (1965). "Three-triplet model with double SU(3) symmetry". Physical Review B. 139 (4B): 1006. Bibcode:1965PhRv..139.1006H. doi:10.1103/PhysRev.139.B1006.
- ^ Bardeen, W.; Fritzsch, H.; Gell-Mann, M. (1973). "Light cone current algebra, π0 decay, and e+ e− annihilation". In Gatto, R. (ed.). Scale and conformal symmetry in hadron physics. John Wiley & Sons. p. 139. arXiv:hep-ph/0211388. Bibcode:2002hep.ph...11388B. ISBN 0-471-29292-3.
- ^ Fritzsch, H.; Gell-Mann, M.; Leutwyler, H. (1973). "Advantages of the color octet gluon picture". Physics Letters B. 47 (4): 365. Bibcode:1973PhLB...47..365F. CiteSeerX 10.1.1.453.4712. doi:10.1016/0370-2693(73)90625-4.
레퍼런스
- S. Eidelman et al. Particle Data Group (2004). "Review of Particle Physics" (PDF). Physics Letters B. 592 (1–4): 1. arXiv:astro-ph/0406663. Bibcode:2004PhLB..592....1P. doi:10.1016/j.physletb.2004.06.001.
- Lichtenberg, D B (1970). Unitary Symmetry and Elementary Particles. Academic Press. ISBN 978-1483242729.
- Thomson, MA(2011), 강의 노트
- J.J.J. Kokkedee (1969). The quark model. W. A. Benjamin. ASIN B001RAVDIA.
