페르미의 상호작용
Fermi's interaction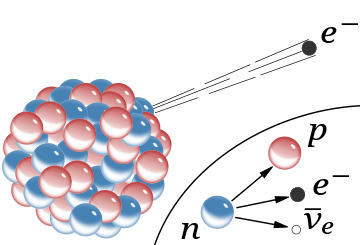
원자핵에서−
β 붕괴(반중성미립자는 생략). 삽입된 부분은 자유 중성자의 베타 붕괴를 보여줍니다. 두 과정 모두에서 가상 W−
보손의 중간 방출(전자와 반중성미자로 붕괴)은 표시되지 않습니다.
입자 물리학에서 페르미의 상호작용(베타 붕괴의 페르미 이론 또는 페르미 4-페르미온 상호작용)은 1933년 엔리코 페르미가 제안한 베타 붕괴에 대한 설명입니다.[1] 이 이론은 4개의 페르미온이 서로 직접적으로 상호작용한다고 가정합니다(관련된 파인만 도표의 한 꼭짓점에서). 이 상호작용은 중성자와 전자, 중성미자(후에 반중성미자로 결정됨) 및 양성자의 직접 결합에 의한 중성자의 베타 붕괴를 설명합니다.[2]
페르미는 1933년 베타 붕괴에 대한 그의 설명에서 이 커플링을 처음 소개했습니다.[3] 페르미 상호작용은 양성자-중성자와 전자-반중성자 사이의 상호작용이 가상 W− 보손에 의해 매개되는 약한 상호작용에 대한 이론의 전조였으며, 그 중 페르미 이론은 저에너지 유효장 이론입니다.
최초의 거부 및 이후의 출판 이력
페르미는 권위 있는 과학 저널 네이처에 베타 붕괴에 대한 그의 "잠정적인" 이론을 처음 제출했고, 네이처는 "그것이 독자들에게 관심을 갖기에는 현실과 너무 멀리 떨어져 있는 추측을 포함하고 있기 때문에" 그것을 거부했습니다.[4] 네이처는 나중에 그 거부가 역사상 위대한 편집상의 실수 중 하나라고 인정했습니다.[5] 그 후 페르미는 1933년과 1934년에 이 언어들을 받아들여 발표한 이탈리아어와 독일어 출판물에 논문의 수정본을 제출했습니다.[6][7][8][9] 이 논문은 당시 영어로 된 1차 간행물에 등장하지 않았습니다.[5] 이 학술지의 영문 번역본은 1968년 미국 물리학 저널에 실렸습니다.[9]
페르미는 논문의 초기 거부가 너무 괴로워서 이론 물리학을 잠시 쉬고 실험 물리학만 하기로 결정했습니다. 이것은 곧 느린 중성자로 핵을 활성화하는 그의 유명한 작업으로 이어질 것입니다.
"텐타티보"
정의들
이 이론은 직접적인 상호작용을 하는 것으로 추정되는 세 가지 유형의 입자를 다룹니다. 처음에는 "neutron 상태"에 있는 "중입자"(ρ = + 1 \ = + 1})를 처리한 다음 전자와 중성미자의 방출과 함께 "proton 상태"(ρ = - 1 {\displaystyle \rho = - 1})로 전환됩니다.
전자 상태
ψ{\\psi }는 단일 electron 파동 함수이고, ψ {\displaystyle \psi _{s}}는 정지 상태입니다.
는 Fock 에 작용하는 {\ s} 상태의 전자를 소멸시키는 연산자입니다.
∗ a_{s}^{*}이() 전자 상태 {\displaystyle s}의 생성 연산자이므로:
중성미자 상태
유사하게,
여기서ϕ phi }는 단일 neutrino 파동 함수이고 ϕ σ {\displaystyle \phi _{\sigma }}는 고정 상태입니다.
{\sigma}}는Fock 공간에작용하 상태 σ {\ \sigma}에서 중성미자를 소멸시키는 연산자입니다.
∗ {\displaystyleigma }^{*}는 중성미 상태 σ {\displaystigma }에 대한 생성 연산자입니다.
중입자 상태
\rho}는 무거운 입자 상태에 작용하는 하이젠베르크(나중에 아이소스핀으로 일반화됨)에 의해 도입된 연산자로, 입자가 중성자일 때 고유값이 +1이고 입자가 양성자일 때 -1입니다. 따라서, 중입자 상태는 2행 열 벡터로 표현될 것이고, 여기서
는 중성자를 나타내고,
양성자를 나타냅니다ρ \rho }이인 sigma zdisplaystyle \σ _{z} 스핀 매트릭스인 경우).
무거운 입자를 양성자에서 중성자로 바꾸는 연산자와 그 반대의 연산자는 각각 다음과 같이 표시됩니다.
그리고.
응답 는 상태의 중성자 응답 양성자에 대한 고유 함수입니다
해밀토니안
해밀토니안은 자유 중입자의 에너지를 나타내는 자유로운 빛 입자의 에너지를 나타내며 상호작용 .
여기서 과 P P는 각각 중성자와 양성자의 에너지 연산자이므로 ρ = 1displaystyle \ = 1이면 H. = N {\{h.p.}} - 1 displaystyle \rho 이면 H.p. P {\displaystyle H_text{h.p.}}
여기서 {\s}}는 의 쿨롱장에서 제{\ s 의 전자의 에너지입니다. 그리고 는 해당 상태의 전자 다; σ M_sigma}}는σ \sigma^{\text{th 의 중성미자 수이다, K σ {\displaystyle K_{\sigma} 에너지(자유 평면파 상태인 것으로 가정)입니다.
상호작용 부분에는 전자와 중성미자(현재는 반중성미자로 알려져 있음)의 방출과 함께 양성자가 중성자로 변환되는 것을 나타내는 용어가 포함되어야 합니다. 역과정에 대한 용어일 뿐만 아니라, 전자와 양성자 사이의 쿨롱 은 {\displaystyle \ - decay 과정과는 무관한 것으로 무시됩니다.
페르미는 }에 대해 두 가지 가능한 값을 제안합니다 첫째, 스핀을 무시하는 비론적 버전:
그 후 가벼운 입자는 4성분 디랙 스피너이지만 무거운 입자의 속도가 c에 비해 작으며 전자기 벡터 전위와 유사한 상호작용 항을 무시할 수 있다고 가정하는 버전이 있습니다.
서ψ \} 및 ϕ displaystyle \phi }는 이제4성분 ψ ~displaystyle {\tilde {\psi }는ψ {\displaystyle \psi 의 결합체를, δ {\displaystyle \delta }는 행렬입니다.
행렬요소
시스템의 상태는 튜플ρ,, 1, N 2, …, M 1, M 2, …, {\displaystyle \rho, n, N_{1}, N_{2},\ldots, M_{1}, M_{2},\ldots, ρ ± 1 {\displaystyle \rho =\pm 1}은 무거운 입자가 중성자인지 양성자인지 지정합니다. n은 중입자의 양자 상태이고, {\는{\ 상태의 전자 수이고 {\M_sigma}}는상태σ \sigma} 의 중성미자 수이다.
의. {\H_{\ 페르미는 가 {\ n}인 상태와 전자가 반응하지 않는 상태 사이의 행렬 요소를 제공합니다. 뉴트리노가 s 상태에 있습니다. displaystygma }, 양성자가 상태 m {\displaystyle m}이고 전자와 중성미자가 상태 {\displaystyle s 및 σ {\displaystygma }에 존재하는 상태는 다음과 같습니다.
여기서 적분은 무거운 입자의 전체 구성 공간을 차지합니다 \rho }ρ 제외). 은 총 광 입자 수가 홀수(-)인지 짝수(+)인지 여부에 따라 결정됩니다.
전이확률
일반적인 양자 섭동 이론에 따라 n 상태에서 중성자의 수명을 계산하려면 위의 행렬 요소를 모든 빈 전자 및 중성미자 상태에 대해 합산해야 합니다. 이는 전자와 중성미자 고유함수ψ {}}와ϕ σ displaystyle\phi_{\sigma}}가 핵 내에서 일정하다고 가정함으로써 단순화됩니다(즉, 콤프턴 파장이 핵의 크기보다 훨씬 작습니다). 이것은 다음으로 이어집니다.
여기서ψ psi_{s}} 및 ϕ σ {\displaystyle \phi _{\sigma }}은 이제 핵의 위치에서 평가됩니다.
페르미의 황금률에[further explanation needed] 따르면, 이 전이의 확률은
서 W W는 양성자와 중성자 상태의 에너지 차이입니다.
모든 양의 에너지 중성미자 스핀/운동량 방향에 대한 평균화(여기서ω - 1 ^{-1}는 중성미자 상태의 밀도이며, 결국 무한대로 이동함)를 구합니다.
여기서 는 중성미자의 나머지 질량이고 는 디랙 행렬입니다.
전이 확률은 - + s + Kσ = +H_{s}+sigma =0인 p σ에 대해 급격한 최대값을 갖는다는 점에 주목하면 다음과 같이 단순화됩니다.
서 pσ {\sigma 및 K σ {\displaystyle K_{\sigma}}는 W + Hs + K σ = 0 {\displaystyle -W+H_{s}+K_{\sigma} = 0}에 대한 값입니다.
페르미는 이 함수에 대해 다음과 같은 세 가지 의견을 제시합니다.
- 중성미자 상태는 자유 상태로 간주되므로 σ >μc 2 {\K_muc^{2}}, 연속\beta} - 의 상한은 ≤ W -μc 2 {\ -muc2입니다.
- 전자 > 의 경우 -decay가 발생하려면 양성자-중성자 에너지 가 ≥ + c 2 )c^{2}}이어야 합니다.
- 인자
- 전환 확률은 일반적으로 크기가 1이지만 특수한 경우에는 사라집니다. 이로 인해 beta } - decay에 대한 (대략적인) 선택 규칙이 발생합니다.
금지된 전환
위에서 언급한 바와 같이, 내부 제품 Q ∗ {\{와 v m {\ v_{m}} 사이의 중입자 {\ Q_{mn}^{*}가 사라지면 관련 전이가 "금지"됩니다(오히려 1에 더 가까운 경우보다 훨씬 가능성이 적습니다).
양성자와 중성자의 개별 양자 상태 측면에서 핵에 대한 설명이 좋다면, u u_{n}}와 v m {\v_{m}}이 각운동량이 동일하지 않는 한 ∗ {\ Q_{mn}^{*}가 사라집니다. 그렇지 않으면, 붕괴 전후의 핵 전체의 각운동량을 사용해야 합니다.
영향을 주다
페르미의 논문이 등장한 직후, 베르너 하이젠베르크는 볼프강[10] 파울리에게 보낸 편지에서 핵에서 중성미자와 전자의 방출과 흡수는 섭동 이론의 두 번째 순서로 양성자와 중성자 사이의 인력으로 이어져야 한다고 언급했습니다. 광자의 방출과 흡수가 전자기력으로 이어지는 것과 유사합니다. 그는 힘이 } 형태임을 발견했습니다 그러나 동시대의 실험 데이터는 100만 [11]배로 너무 작은 값으로 이어졌습니다.
이듬해 유카와 히데키는 이 아이디어를 떠올렸지만, [12]그의 이론에서 중성미자와 전자는 전자보다 약 200배 무거운 정지 질량을 가진 새로운 가상 입자로 대체되었습니다.[13]
후대의 발전
페르미의 4퍼미온 이론은 약한 상호작용을 놀라울 정도로 잘 설명합니다. 안타깝게도 계산된 단면 또는 상호 작용 확률은 에너지σ ≈ 2 E 2 {\ \rm E2}}의 제곱으로 증가합니다. 이 단면은 경계 없이 증가하기 때문에 이론은 약 100 GeV보다 훨씬 높은 에너지에서는 유효하지 않습니다. 여기서F G는 상호작용의 강도를 나타내는 페르미 상수입니다. 이것은 결국 4-퍼미온 접촉 상호작용을 전기약물 이론에서 설명된 바와 같이 W 또는 Z 보손의 교환인 보다 완전한 이론(UV complete)으로 대체했습니다.

상호작용은 뮤온, 전자-반중성미자, 뮤온-중성미자 및 전자의 결합을 통해 뮤온 붕괴를 설명할 수도 있습니다. 이 가설은 Gershtein과 Zeldovich가 제시한 것으로 벡터 전류 보존 가설로 알려져 있습니다.[14]
원래 이론에서 페르미는 상호작용의 형태가 두 벡터 전류의 접촉 결합이라고 가정했습니다. 그 후, 이씨와 양씨에 의해 축방향 패리티가 전류를 위반하는 현상이 나타나는 것을 방해하는 것은 아무것도 없다고 지적되었고, 이는 우친슝(吳親雄)이 수행한 실험에 의해 확인되었습니다.[15][16]
페르미의 상호작용에 패리티 위반이 포함된 것은 조지 가모프와 에드워드 텔러가 소위 가모프에서 한 것입니다.– 패리티 위반 "허용" 붕괴 및 패리티 보존 "초허용" 붕괴를 각각 반평행 및 평행 전자 및 중성미자 스핀 상태를 기준으로 페르미의 상호 작용을 설명하는 텔러 전이. 전기약력 이론과 표준 모델이 등장하기 전에, George Sudarshan과 Robert Marshak, 그리고 또한 독립적으로 Richard Feynman과 Murray Gell-Mann은 4-페르미온 상호작용의 정확한 텐서 구조(벡터에서 축 벡터, V - A)를 결정할 수 있었습니다.[17][18]
페르미 상수
페르미 상수의 가장 정확한 실험적 결정은 뮤온 수명의 측정에서 얻어지는데, 이는 G의F 제곱에 반비례합니다(W 보손의 질량에 대한 뮤온 질량을 무시할 때).[19] 현대 용어로 말하면, "감소된 페르미 상수", 즉 자연 단위에서의 상수는[3][20]
여기서 g는 약한 상호작용의 결합 상수이고, M은W 문제의 붕괴를 매개하는 W 보손의 질량입니다.
표준 모델에서 페르미 상수는 힉스 진공 기대값과 관련이 있습니다.
- =(G F 0 ) - 1 2 ≃ 246.22 GeV {\displaystyl v =\lt ({\sqrt {2}}\,G_{\rm {F}}^{0}\right)^{-1/2}\simeq 246.22\;{\textrm {GeV}}.
좀 더 직접적으로, 대략적으로 (표준 모델의 트리 수준),
이는 = θ Wtext{Z}}={\frac {M_{\text{\text{ 그래서
참고문헌
- ^ Yang, C. N. (2012). "Fermi's β-decay Theory". Asia Pacific Physics Newsletter. 1 (1): 27–30. doi:10.1142/s2251158x12000045.
- ^ Feynman, R.P. (1962). Theory of Fundamental Processes. W. A. Benjamin. Chapters 6 & 7.
- ^ a b Griffiths, D. (2009). Introduction to Elementary Particles (2nd ed.). pp. 314–315. ISBN 978-3-527-40601-2.
- ^ Pais, Abraham (1986). Inward Bound. Oxford: Oxford University Press. p. 418. ISBN 0-19-851997-4.
- ^ a b Close, Frank (February 23, 2012). Neutrino. Oxford University Press. Retrieved May 5, 2017.
- ^ Fermi, E. (1933). "Tentativo di una teoria dei raggi β". La Ricerca Scientifica (in Italian). 2 (12).
- ^ Fermi, E. (1934). "Tentativo di una teoria dei raggi β". Il Nuovo Cimento (in Italian). 11 (1): 1–19. Bibcode:1934NCim...11....1F. doi:10.1007/BF02959820. S2CID 123342095.
- ^ Fermi, E. (1934). "Versuch einer Theorie der beta-Strahlen. I". Zeitschrift für Physik (in German). 88 (3–4): 161. Bibcode:1934ZPhy...88..161F. doi:10.1007/BF01351864. S2CID 125763380.
- ^ a b Wilson, F. L. (1968). "Fermi's Theory of Beta Decay". American Journal of Physics. 36 (12): 1150–1160. Bibcode:1968AmJPh..36.1150W. doi:10.1119/1.1974382. 1934년 페르미의 논문을 독일어로 완벽하게 영어로 번역한 내용 포함
- ^ Pauli, Wolfgang (1985). Scientific Correspondence with Bohr, Einstein, Heisenberg a.o. Volume II:1930–1939. Springer-Verlag Berlin Heidelberg GmbH. p. 250, letter #341, Heisenberg to Pauli, January 18th 1934.
- ^ Brown, Laurie M (1996). The Origin of the Concept of Nuclear Forces. Institute of Physics Publishing. Section 3.3.
- ^ Yukawa, H. (1935). "On the interaction of elementary particles. I.". Proceedings of the Physico-Mathematical Society of Japan. 17: 1.
- ^ Mehra, Jagdish (2001). The Historical Development of Quantum Theory, Volume 6 Part 2 (1932–1941). Springer. p. 832.
- ^ Gerstein, S. S.; Zeldovich, Ya. B. (1955). "Meson corrections in the theory of beta decay". Zh. Eksp. Teor. Fiz.: 698–699.
- ^ Lee, T. D.; Yang, C. N. (1956). "Question of Parity Conservation in Weak Interactions". Physical Review. 104 (1): 254–258. Bibcode:1956PhRv..104..254L. doi:10.1103/PhysRev.104.254.
- ^ Wu, C. S.; Ambler, E; Hayward, R. W.; Hoppes, D. D.; Hudson, R. P. (1957). "Experimental Test of Parity Conservation in Beta Decay". Physical Review. 105 (4): 1413–1415. Bibcode:1957PhRv..105.1413W. doi:10.1103/PhysRev.105.1413.
- ^ Feynman, R. P.; Gell-Mann, M. (1958). "Theory of the Fermi interaction" (PDF). Physical Review. 109 (1): 193. Bibcode:1958PhRv..109..193F. doi:10.1103/physrev.109.193.
- ^ Sudarshan, E. C.; Marshak, R. E. (1958). "Chirality invariance and the universal Fermi interaction". Physical Review. 109 (5): 1860. Bibcode:1958PhRv..109.1860S. doi:10.1103/physrev.109.1860.2.
- ^ Chitwood, D. B.; MuLan Collaboration; et al. (2007). "Improved Measurement of the Positive-Muon Lifetime and Determination of the Fermi Constant". Physical Review Letters. 99 (3): 032001. arXiv:0704.1981. Bibcode:2007PhRvL..99c2001C. doi:10.1103/PhysRevLett.99.032001. PMID 17678280. S2CID 3255120.
- ^ "CODATA Value: Fermi coupling constant". The NIST Reference on Constants, Units, and Uncertainty. US National Institute of Standards and Technology. June 2015. Retrieved October 31, 2016.
- ^ Plehn, T.; Rauch, M. (2005). "Quartic Higgs coupling at hadron colliders". Physical Review D. 72 (5): 053008. arXiv:hep-ph/0507321. Bibcode:2005PhRvD..72e3008P. doi:10.1103/PhysRevD.72.053008. S2CID 10737764.















