양자 논리 게이트

양자 컴퓨팅, 구체적으로 계산의 양자 회로 모델에서 양자 논리 게이트(또는 간단히 양자 게이트)는 소수의 큐비트에서 작동하는 기본 양자 회로입니다.고전 논리 게이트가 기존의 디지털 회로를 위한 것처럼 양자 회로의 구성 요소입니다.

많은 고전 논리 게이트와 달리 양자 논리 게이트는 가역적입니다.가역 게이트만을 사용하여 고전적인 컴퓨팅을 수행할 수 있습니다.예를 들어, 가역적인 토폴리 게이트는 종종 보조 비트를 사용해야 하는 비용으로 모든 부울 함수를 구현할 수 있습니다.토폴리 게이트는 양자 회로가 고전 회로가 수행하는 모든 동작을 수행할 수 있음을 보여주는 직접 양자 등가를 가지고 있습니다.

양자 게이트는 단일 연산자이며, 일부 기초에 대해 단일 행렬로 설명됩니다.일반적으로 계산 기저가 사용되는데, 이는 d-수준 양자 시스템(큐비트, 양자 레지스터 또는 큐트릿 및 큐트릿 등)의 경우 직교 기저 벡터에 ${\displaystyle 0}$⟩${\displaystyle ,1}$ ⟩${\displaystyle ,}$ ${\displaystyle \dots ,}$d${\displaystyle }$- ${\displaystyle 1}$ ⟩ ${\displaystyle 0\rangle, 1\rangle,$ 1\$dots, d-1\rangle }$이라는 레이블이 붙거나$$이진 표기법을 사용합니다.

역사

양자 게이트의 현재 표기법은 아드리아노 바렌코, 찰스 베넷, 리처드 클레브, 데이비드 P 등 양자 정보 과학의 창시자들에 의해 개발되었습니다. 디 빈센조, 노먼 마골루스, 피터 쇼어, 타이코 슬레이터, 존 A. 1986년 리처드 파인만이 도입한 기보법에 기초한 스몰린과 하랄드 와인퍼터.^[2][3]

표현

양자 논리 게이트는 유니터리 행렬로 표시됩니다.$n개$의 ${\displaystyle n}$개의 큐비트에 작용하는 게이트는 ${\displaystyle {2n}^{}}$× ${\displaystyle {2n}^{}}$ ${\$ 2$^{n}$개의 유니터리$$ 행렬로 표현되며, 행렬 곱셈의^[a] 그룹 연산을 갖는 모든 그러한 게이트의 집합은 대칭 그룹 U(2ⁿ)입니다.^[2]게이트가 작용하는 양자 상태는 복잡한 유클리드 노름(2-노름)을 가진 ${\displaystyle {2n}^{}}$ ${\$ 복소$$ 차원의 단위 벡터입니다.^{[4]: 66 [5]: 56, 65} 기본 벡터(때로는 고유 상태라고도 함)는 측정할 경우 가능한 결과이며, 양자 상태는 이러한 결과의 선형 조합입니다.가장 일반적인 양자 게이트는 일반적인 고전 논리 게이트가 1~2비트로 작동하는 것처럼 1~2큐비트의 벡터 공간에서 작동합니다.

양자 논리 게이트는 연속 대칭 그룹에 속하지만 실제 하드웨어는 정확하지 않아 정밀도가 제한됩니다.게이트의 적용은 일반적으로 오류를 발생시키며, 양자 상태 충실도는 시간이 지남에 따라 감소합니다.오류 수정을 사용하면 사용 가능한 게이트가 유한 집합으로 추가로 제한됩니다.^{[4]: ch. 10 [1]: ch. 14} 이 글의 후반부에서는 이상적인 양자 게이트의 특성에 초점이 맞춰지기 때문에 이를 무시하기도 합니다.

양자 상태는 일반적으로 브라켓이라고 알려진 표기법에서 "켓"으로 표시됩니다.

단일 큐비트의 벡터 표현은

${\displaystyle a\rangle = v_{0} 0\rangle +v_{1} 1\rangle \rightarrow {\begin{bmatrix}v_{0}\v_{1}\end{bmatrix}}$

여기서 ${\displaystyle {v0\mathrm{}}_{}}$ ${\$와 ${\displaystyle {v1\mathrm{}}_{}}${\$displaystyle v_{1}$은 큐비트의 복잡한 확률 진폭입니다$$.이 값은 큐비트 상태를 측정할 때 0 또는 1을 측정할 확률을 결정합니다.자세한 내용은 아래 측정을 참조하십시오.

값 0은 ket ${\displaystyle 0}$ ⟩ =${\displaystyle }$[ ${\displaystyle \begin{array}{}10\\ \end{array}}$] ${\displaystyle 0\rangle$ = {\begin${bmatrix}1\0\end{bmatrix$로 표시되고 값 1은 ${\displaystyle ket}$ 1 ⟩ = [ ${\displaystyle \begin{array}{}0\\ \end{array}}$1 ]$${\$displaystyle 1\rangle$ = {\begin${bmatrix}0\1\end{bmatrix}}$로 표시됩니다$.$

텐서 곱(또는 크로네커 곱)은 양자 상태를 결합하는 데 사용됩니다.큐비트 레지스터의 결합 상태는 구성 큐비트의 텐서곱입니다.텐서 곱은 기호 ⊗ ${\displaystyle \otimes}$로 표시됩니다$.$

두 큐비트의 벡터 표현은 다음과 같습니다.^[6]

${\displaystyle ab\rangle = a\rangle \otimes b\rangle = v_{00} 00\rangle +v_{01} 01\rangle +v_{10} 10\rangle +v_{11} 11\rangle \rightarrow {\begin{bmatrix}v_{00}\v_{01}\v_{10}\v_{11}\end{bmatrix}}$

특정 양자 상태에 대한 게이트의 작용은 상태를 나타내는 벡터 ψ ${\displaystyle 1_{}}$ ⟩ ${\displaystyle \psi _{1}\rangle$에 게이트를 나타내는 행렬 $U$ ${\displaystyle U}$를 곱하여 알 수 있습니다.결과는 새 양자 상태 ψ ${\displaystyle 2_{}}$ ⟩ ${\displaystyle \psi_{2}\rangle }$입니다$.$

${\displaystyle U \psi _{1}\rangle = \psi _{2}\rangle.}$

주목할 만한 예

셀 수 없이 많은 게이트가 존재합니다.그들 중 일부는 다양한 작가들에 의해 이름이 지어졌고,^{[2][1][4][5][7][8][9]} 아래는 문헌에서 가장 자주 사용되는 것들 중 일부를 따릅니다.

아이덴티티 게이트

아이덴티티 게이트(identity gate)는 아이덴티티 행렬(identity matrix)로, 보통 I로 쓰이며, 단일 큐비트에 대해 다음과 같이 정의됩니다.

${\displaystyle I = {\bmatrix}1&0\0&1\end{bmatrix}}$

여기서 I는 기저 독립적이며 양자 상태를 수정하지 않습니다.아이덴티티 게이트는 다양한 게이트 연산의 결과를 수학적으로 설명하거나 멀티 큐비트 회로를 논의할 때 가장 유용합니다.

파울리게이츠(X,Y,Z)

파울리게이트$({\displaystyle X,Y,Z)}$ ${\displaystyle(X,Y,Z)}$은 3개의 파울리 행렬$($σ ${\displaystyle x_{}}$ σ ${\displaystyle y_{}}$ σ ${\displaystyle z_{}}$ ${\displaystyle(\sigma_{x},\sigma_{y},\sigma_{z})$이며 단일 큐비트에서 동작합니다.Pauli X, Y, Z는 각각 Bloch 구의 x, y, z 축을 중심으로 π ${\displaystyle \pi }$ 라디안으로 회전하는 것과 같습니다.

Pauli-X 게이트는 Bloch 구의 z 축을 구분하는$$표준 기저 ${\displaystyle 0}$ ⟩ ${\displaystyle 0\rangle$ ${\displaystyle 1}$ ⟩ ${\displaystyle 1\rangle}$에 대한 고전 컴퓨터의 NOT 게이트의 양자 등가물입니다.${\displaystyle 0}$ ⟩ ${\displaystyle 0\rangle$}을$($를) ${\displaystyle 1}$ ⟩$${\$displaystyle$ 1$\rangle}$에 매핑하고 1 ⟩$${\$displaystyle 1\rangle}$을$($를) 0 ⟩ ${\displaystyle 0\rangle}$에 매핑하므로 비트 플립이라고도 합니다. 마찬가지로$,$ Pauli-Y는 $0$ ⟩ ${\displaystyle 0\rangle$ $}$을 i 1 ⟩ ${\displaystyle$ i $1\rangle$ }에 매핑하고 ${\displaystyle 1}$ ⟩ ${\displaystyle 1\rangle }$을$$i ${\displaystyle 0}$ ⟩ ${\displaystyle -i 0\rangle$}에 매핑합니다.Pauli Z는 기본 상태 ${\displaystyle 0}$ ⟩ ${\displaystyle 0\rangle$}을(를$)$ 변경하지 않고 ${\displaystyle 1}$ ⟩ ${\displaystyle 1\rangle}$을(를) -${\displaystyle 1}$ ⟩ ${\displaystyle$ -$1\rangle}$에 매핑합니다$.$ 이러한 특성 때문에 Pauli Z는 위상 플립(phase-flip)이라고도 합니다.

이 행렬들은 보통 다음과 같이 표현됩니다.

${\displaystyle X=\sigma _{x}=\operatorname {NOT} = {\begin{bmatrix}0&1\1&0\end{bmatrix}}}$

${\displaystyle Y=\sigma _{y}={\begin{bmatrix}0&-i\i&0\end{bmatrix}},}$

${\displaystyle Z=\sigma _{z}={\begin{bmatrix}1&0\0&-1\end{bmatrix}}}$

파울리 행렬은 우연적인 것으로 파울리 행렬의 제곱이 항등 행렬임을 의미합니다.

${\displaystyle I^{2}=X^{2}=Y^{2}=Z^{2}=-iXYZ=I}$

파울리 행렬 또한 반 commute입니다. 예를 ${\displaystyle \mathrm{들어}}$ Z${\displaystyle X}$ = ${\displaystyle i}$ Y = - ${\displaystyle X}$ Z${\displaystyle .}$ ${\displaystyle ZX$=$iY$ = - $XZ.}$

파울리 행렬 σ j ${\displaystyle \sigma _{j}}$의 행렬 지수는 회전 연산자이며, $흔히$ e -${\displaystyle i^{}}$ σ j θ${\displaystyle {}^{}}$/ ${\displaystyle 2^{}}$로${\displaystyle {}^{}}$씁니다$.$ {\$displaystyle e^{-i\sigma _${j}\$theta$ /$2}}$

게이트제어

제어된 게이트는 2개 이상의 큐비트에서 작동하며, 여기서 하나 이상의 큐비트는 일부 작업에 대한 제어 역할을 합니다.^[2]예를 들어 제어되는 NOT 게이트(또는 CNOT 또는 CX)는 2 큐비트에 대해 작동하고 첫 번째 큐비트가 ${\displaystyle 1}$ ⟩ ${\displaystyle$1\rangle$}$인 경우에만 두 번째 큐비트에 대해 NOT 작업을 수행하며$,$ 그렇지 않은 경우에는 변경되지 않습니다.기본 ${\displaystyle 00}$ ⟩ ${\displaystyle 00\rangle$ ${\displaystyle 01}$ ⟩ ${\displaystyle 01\rangle$ ${\displaystyle 10}$ ⟩ ${\displaystyle 10\rangle$ ${\displaystyle 11}$ ⟩ ${\displaystyle 11\rangle}$에 대해 에르미트 단위 행렬로 표시됩니다$.$

${\displaystyle {\mbox{C없음}}={\begin{bmatrix}1&0&0\0&0\0&0\0&0\0&0\end{bmatrix}}$

CNOT(또는 제어되는 Pauli-X) 게이트는 ${\displaystyle \mathrm{기본}}$ ${\displaystyle \mathrm{상태}}$ ${\displaystyle a,}$ ${\displaystyle b}$ ⟩ ↦ a${\displaystyle ,}$ ⊕ ${\displaystyle b}$ ⟩ ${\displaystyle a,$ b$\rangle \mapsto a, a\oplus b\rangle }$을(를) 매핑하는 게이트로 설명할 수 있으며$,$ 여기서 ⊕ ${\displaystyle \oplus }$은 XOR입니다.

CNOT는 Pauli 기준으로 다음과 같이 표현할 수 있습니다.

${\displaystyle {\mbox{C없음}}=e^{i{\frac {\pi}{4}}(I-Z_{1})(I-X_{2})=e^{-i{\frac {\pi}{4}}(I-Z_{1})(I-X_{2}})}$

CNOT는 에르미트 단위 연산자로서 ${\displaystyle {ei}^{}}$ θ ${\displaystyle U^{}}$ =${\displaystyle }$(${\displaystyle \cos }$ ⁡ θ${\displaystyle )}$ ${\displaystyle I}$+${\displaystyle }$(${\displaystyle i}$ ${\displaystyle \mathrm{in}}$ ⁡ θ${\displaystyle )}$ U ${\displaystyle e^{i\theta$ U} = (\$cos \theta$) $I$+ ($i\sin \theta$) $U}$ 및 $U$ = ${\displaystyle {}^{}}$ ${\displaystyle i^{}}$ π 2${\displaystyle {}^{}}$(${\displaystyle I^{}}$- U${\displaystyle {}^{}}$)${\displaystyle {}^{}}$= ${\displaystyle {}^{}}$- i π 2 (${\displaystyle I^{}}$- ${\displaystyle U^{}}$ ) ${\$displaystyle U=e$^{i{\frac {\pi }{2}}(I$ - U) = $e^{i{\frac {\pi }{2}}(I$ - U$)}$이며$,$ 이는 관여적입니다.

일반적으로 U가 행렬 표현이 있는 단일 큐비트에서 작동하는 게이트인 경우

${\displaystyle U={\bmatrix}u_{00}&u_{01}\u_{10}&u_{11}\end{bmatrix}}}$

그러면 controlled-U 게이트는 첫 번째 큐비트가 제어 역할을 하는 방식으로 두 큐비트에서 작동하는 게이트입니다.다음과 같이 기본 상태를 매핑합니다.

${\displaystyle 00\rangle \maps to 00\rangle}$

${\displaystyle 01\rangle \maps to 01\rangle}$

${\displaystyle 10\rangle \maps to 1\rangle \otimes U 0\rangle = 1\rangle \otimes (u_{00} 0\rangle +u_{10} 1\rangle )}$

${\displaystyle 11\rangle \maps to 1\rangle \otimes U 1\rangle = 1\rangle \otimes (u_{01} 0\rangle +u_{11} 1\rangle )}$

제어된 U를 나타내는 행렬은

${\displaystyle {\mbox{C}}U={\begin{bmatrix}1&0&0\0&1&0\0&0&0\0&0&u_{00}&u_{01}\0&0&u_{10}&u_{11}\end{bmatrix}}$

U가 파울리 연산자 중 하나일 때, X,Y,Z 각각의 용어 "controlled-X", "controlled-Y" 또는 "controlled-Z"가 사용되기도 합니다.^{[4]: 177–185} 때때로 이것은 단지 CX, CY 및 CZ로 단축됩니다.

일반적으로, 임의의 단일 큐비트 유니트 $게이트$는 U${\displaystyle }$= ${\displaystyle {\mathrm{ei}}^{}}$ H$${\$displaystyle$ U = $e^{iH}}$와 같이 표현될 수 있으며$,$ 여기서 H는 에르미트 행렬이고, 그 다음 제어된 U는 ${\displaystyle \mathrm{CU}}$ = ${\displaystyle {ei}^{}}$ ${\displaystyle {\frac{12}{}}^{}}$ (${\displaystyle {}^{}}$I${\displaystyle {}^{}}$- ${\displaystyle Z^{}}$ ${\displaystyle {1_{}}^{}}$) ${\displaystyle {{}_{}}^{}}$ ${\displaystyle {2_{}}^{}}$.${\displaystyle CU$ = $e^{i{\frac {1}{2}}(I-Z_{1})$$H_{2}}:$

제어는 프로그래밍 언어에서 임의 수의 큐비트와^[2] 함수를 가진 게이트로 확장될 수 있습니다.^[10]중첩 상태에서 기능을 조절할 수 있습니다.^[11][12]

고전 제어

게이트는 또한 고전적인 논리에 의해 제어될 수 있습니다.양자 컴퓨터는 고전 컴퓨터에 의해 제어되며, 어떤 게이트를 어떤 큐비트로 실행할지에 대한 명령을 고전 컴퓨터로부터 받는 보조 프로세서처럼 행동합니다.^{[13]: 42–43 [14]}고전적인 제어는 단순히 양자 컴퓨터의 명령 순서에 게이트를 포함하거나 누락하는 것입니다.^{[4]: 26–28 [1]: 87–88}

위상 편이 게이트

위상 이동은 기본 상태 ${\displaystyle 0}$ ⟩ ↦ ${\displaystyle 0}$ ⟩ ${\displaystyle 0\rangle \maps$ to $0\rangle }$ ${\displaystyle 및}$ 1 ⟩ ↦ ${\displaystyle e}$ ${\displaystyle i^{}}$ φ 1 ⟩$${\$displaystyle$ 1$\rangle \mapsto e^{i\varphi} 1\rangle$}을(를) 매핑하는 단일 큐비트 게이트 계열입니다$.$ ${\displaystyle 0}$ ⟩$${\$displaystyle$ 0$\rangle$} ${\displaystyle 또는}$ 1 ⟩ {\$displaystyle$1\$rangle }$을(를) 측정할 확률은 이 게이트를 적용한 후 변경되지 않습니다.그러나 그것은 양자 상태의 위상을 수정합니다.$이$는 φ ${\displaystyle \varphi}$ 라디안으로 Bloch 구의 z축을 중심으로 한 회전 또는 수평 원을 추적하는 것과 같습니다.위상 이동 게이트는 다음 행렬로 표시됩니다.

${\displaystyle P(\varphi )={\begin{bmatrix}1&0\0&e^{i\varphi}\end{bmatrix}}$

여기서 φ ${\displaystyle \varphi}$은(는) 주기 2 π의 위상 이동입니다.몇 가지 일반적인 예로는 φ = π $\frac{4}{}$ ${\textstyle \varphi$ = {\$frac {\pi }{4}}($역사적으로 π ${\displaystyle /}$ ${\displaystyle 8}${\$displaystyle \pi /8}$ 게이트라고 함), 위상 게이트(S 게이트라고도 함), φ = π $\frac{2}{}$ ${\textstyle \varphi$ = {\$frac {\pi }{2}},$ φ = π ${\display$}인 Pauli-Z 게이트가 있습니다.$스타일 \varphi =$\$pi$

위상 편이 게이트는 다음과 같이 서로 관련이 있습니다.

${\displaystyle Z={\bmatrix}1&0\0&e^{i\pi}\end{bmatrix}}={\begin{bmatrix}1&0\0&-1\end{bmatrix}=P\left(\pi \right)}$

${\displaystyle S={\bmatrix}1&0\0&e^{i{\frac {\pi}{2}}\end{bmatrix}}={\begin{bmatrix}1&0\0&i\end{bmatrix}}=P\left({\frac {\pi}{2}}\right)={\sqrt {Z}}$

${\displaystyle T={\begin{bmatrix}1&0\0&e^{i{\frac {\pi}{4}}\end{bmatrix}}=P\left({\frac {\pi}{4}}\right)={\sqrt {S}}={\sqrt[{4}]{Z}}}$

위상 게이트 $P{\displaystyle (}$φ${\displaystyle )}$ ${\displaystyle P(\varphi )}$가 에르미트가 아닙니다(모든 φ ${\displaystyle }$= ${\displaystyle n}$ π${\displaystyle ,}$ ${\displaystyle n}$ ∈ ${\displaystyle Z}$ ${\displaystyle \varphi$ = $n\pi,n\in \mathbb {Z}).$이러한 게이트는 해당 에르미트 컨쥬게이트와 다릅니다$.$ $P{\displaystyle {}^{}}$†(${\displaystyle {}^{}}$φ${\displaystyle }$) = ${\displaystyle P(}$ -${\displaystyle }$φ${\displaystyle }$) ${\displaystyle P^{\dagger }(\varphi$ ) = P$(-\varphi )}.$두 개의 인접(또는 켤레 전치) 게이트 $S$ † ${\displaystyle$ S$^{\dagger}}$ 및 $T$ † ${\displaystyle$ T$^{\dagger}}$는 명령어 세트에 포함되기도 합니다.

하다마드 게이트

자크 하다마드(Jacques Hadamard)의 이름을 딴 하다마드(Hadamard) 또는 월시 하다마드(Walsh-Hadamard) 문. 프렌치:[아다마 ʁ])와 조셉 L. 월시는 단 하나의 큐비트로 행동합니다.기본 상태 $0$ ⟩ ↦ $\frac{0}{}$ ⟩$\frac{}{}$+ $\frac{1}{}$ ⟩ $\frac{}{}$ ${\textstyle 0\rangle \maps$ to ${\frac${ $0\rangle$+ $1\rangle }{\sqrt {2}},$ $1$ ⟩ ↦ $\frac{0}{}$ ⟩ -$\frac{1}{}$ ⟩ $\frac{}{}$ ${\textstyle 1\rangle \maps$ to ${\frac${ $0\rangle$ -$1\rangle }{\sqrt {2}}($계산 기저 상태가 주어지면 동일한 중첩 상태를 만듭니다.)두 상태${\displaystyle (}$⟩ +${\displaystyle }$⟩${\displaystyle )}$${\displaystyle }$/ ${\displaystyle 2}$ ${\displaystyle$ ($0\$${\displaystyle rangle}$ + 1$\rangle$ ) / ${\sqrt$ {$2}},$ (${\displaystyle 0}$$$⟩ -${\displaystyle }$⟩)${\displaystyle }$/${\displaystyle 2}$ ${\displaystyle (0\rangle$ -$1\rangle$ ) / ${\sqrt {2}}$는 각각 {\$displaystyle +\rangle$ } 및${\displaystyle }$-$$⟩ ${\displaystyle$ -\rangle $}$을(를)${\displaystyle }$쓰기도 합니다.하다마드 게이트는 Bloch 구에서 축$({\displaystyle x}$ ${\displaystyle \stackrel{}{^}}$+ ${\displaystyle z}$ ${\displaystyle \stackrel{}{^}}$) /${\displaystyle 2}$ ${\displaystyle({\hat$ {$x}}$ + {\$hat {z}}/{\sqrt {2}}$를 중심으로 π ${\displaystyle \pi}$을(를) 회전하므로, 이는 위법합니다.하다마드 행렬로 표시됩니다.

${\displaystyle H={\frac {1}{\sqrt {2}}{\begin{bmatrix}1&1\1&-1\end{bmatrix}}}$

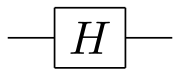
$H$ † =${\displaystyle {}^{}}$ - ${\displaystyle 1^{}}$ = ${\displaystyle H}${\$displaystyle$ H$^{\dagger$ } = H$^{-1$} = $H}$Hadamard 게이트를 사용하여 기저를 변경하면 $x{\displaystyle \stackrel{}{}}$^ ${\displaystyle {\hat {x}}$ 및 $z$ ${\displaystyle \stackrel{}{^}}$ ${\hat {z}}$이(가) 뒤집힙니다$.$ 예를 들어 H $Z$ ${\displaystyle H}$ = ${\displaystyle X}$ ${\displaystyle$ $HZH$= X$}$및 H ${\displaystyle X}$ ${\displaystyle H}$ = ${\displaystyle Z}$ = ${\displaystyle S}$.${\displaystyle$ H ${\sqrt {X}\;$$H={\sqrt {Z}}=S.}$

교환게이트

스왑 게이트는 두 큐비트를 스왑합니다.기본 ${\displaystyle 00}$ ⟩ ${\displaystyle 00\rangle$ ${\displaystyle 01}$ ⟩ ${\displaystyle 01\rangle$ ${\displaystyle 10}$ ⟩ ${\displaystyle 10\rangle$ ${\displaystyle 11}$ ⟩ ${\displaystyle 11\rangle}$에 대해 행렬로 표시됩니다$.$

${\displaystyle {\mbox{SWAP}}={\begin{bmatrix}1&0&0\0&0&0\0&0\0&1\end{bmatrix}}$

스왑 게이트는 합산 형태로 분해될 수 있습니다.

${\displaystyle {\mbox{SWAP}}={\frac {I\otimes I+X\otimes X+Y\otimes Y+Z\otimes Z}{2}}$

토폴리(CCNOT) 게이트

토폴리 게이트는 토마소 토폴리의 이름을 따서 CCNOT 게이트 또는 도이치 게이트 $D$(${\displaystyle }$π${\displaystyle }$/ ${\displaystyle 2)}$ ${\displaystyle D(\pi$/ $2)}$라고도 불리는$$3비트 게이트로 고전적이지만 양자 계산에는 보편적이지 않은 3비트 게이트입니다.양자 토폴리 게이트는 3 큐비트에 대해 정의된 동일한 게이트입니다.${\displaystyle 0}$ ⟩ ${\displaystyle 0\rangle}$ 및 ${\displaystyle 1}$ ⟩ ${\displaystyle 1\rangle}$인 입력 큐비트만 허용하면 처음 두 비트가 상태 ${\displaystyle 1}$ ⟩ ${\displaystyle 1\rangle}$인 경우 세 번째 비트에 Pauli-X(또는 NOT)를 적용합니다$.$CC-U(controlled-controlled Unitary) 게이트의 한 예입니다.고전적인 게이트의 양자 유사체이기 때문에, 그것은 진리표에 의해 완전히 지정됩니다.토폴리 게이트는 단일 큐비트 하다마드 게이트와 결합할 때 범용입니다.^[17]

진리표	매트릭스 형태
인풋 산출량 0 0 0 0 0 0 0 0 1 0 0 1 0 1 0 0 1 0 0 1 1 0 1 1 1 0 0 1 0 0 1 0 1 1 0 1 1 1 0 1 1 1 1 1 1 1 1 0	${\displaystyle {\begin{bmatrix}1\displaystyle {\display{bmatrix}1&0&0&0&0\displaystyle {\display{bmatrix}1\display}1&0&0&0&0&0&0&0&0&0&0&0&0&0&0\displaystyle {\display{bmatrix}}$

Toffoli 게이트는 ${\displaystyle 계산}$ 기반의 상태에서${\displaystyle a,}$ b, ${\displaystyle c}$ ⟩ ↦ ${\displaystyle a,}$ b, c$$⟩ ${\displaystyle b}$, c ⊕${\displaystyle }$(${\displaystyle a}$ ∧ ${\displaystyle b}$) ⊕ {\$displaystyle$ a, b, $c\mapsto$a, b, c$\opplus (a\land$ b$)\rangle$∧ {\$displaystyle a,$b, c\rangle \$mapsto a,$b, c\land b)\rangle ⟩}을(를) 매핑하는 작업을 수행할 때 고전적인 AND$($display {\displaystyle $\land$ \$land$ 작업과 관련이 있습니다.

토폴리 게이트는 파울리 행렬을 사용하여 다음과 같이 나타낼 수 있습니다.

${\displaystyle {\mbox{Toff}}=e^{i{\frac{\pi}{8}}(I-Z_{1})(I-Z_{2})(I-X_{3})=e^{-i{\frac{\pi}{8}}(I-Z_{1})(I-Z_{2})(I-X_{3}}).$

유니버셜 양자 게이트

범용 양자 게이트 집합은 양자 컴퓨터에서 가능한 모든 연산을 줄일 수 있는 게이트 집합입니다. 즉, 다른 단일 연산은 집합에서 유한한 게이트 시퀀스로 표현될 수 있습니다.기술적으로, 이것은 가능한 양자 게이트의 수는 셀 수 없는 반면 유한 집합에서 유한한 시퀀스의 수는 셀 수 있기 때문에 셀 수 없는 게이트 집합 이하에서는 불가능합니다.이 문제를 해결하기 위해서는 이 유한 집합의 게이트 시퀀스로 모든 양자 연산을 근사화할 수 있어야 합니다.또한 일정한 수의 큐비트의 단위체에 대해 솔로베이-키타예프 정리는 이것이 효율적으로 수행될 수 있음을 보장합니다.양자 게이트의 집합이 보편적인지 확인은 그룹 이론 방법^[18] 및/또는 (대략적인) 유니터리 t-설계와의^[19] 관계를 사용하여 수행할 수 있습니다.

범용 양자 게이트 집합에는 다음이 있습니다.

• 회전 연산자 R(θ), R(θ), R(θ), 위상 이동 게이트 P(φ) 및 CNOT는 범용 양자 게이트 세트를 구성하는 데 일반적으로 사용됩니다.
• 클리포드 집합 {CNOT, H, S} + T 게이트입니다.클리포드 집합은 고테스만-킬 정리에 따라 고전적으로 효율적으로 시뮬레이션될 수 있기 때문에 보편적인 양자 게이트 집합이 아닙니다.
• 토폴리 게이트 + 하다마드 게이트.^[17]토폴리 게이트는 단독으로 모든 고전적 계산을 포함하는 가역 부울 대수 논리 회로를 위한 범용 게이트 세트를 형성합니다.

도이치 게이트

보편적 양자 게이트의 단일 게이트 집합은 물리학자 데이비드 도이치의 이름을$$딴 매개 변수화된 3큐비트 도이치 게이트 $($θ) {\$displaystyle D(\theta )}$를 사용하여 공식화될 수도 있습니다.CC-U 또는 제어-제어-유니터리 게이트의 일반적인 경우이며 다음과 같이 정의됩니다.

${\displaystyle a,b,c\rangle \maps to {\begin{case}i\cos(\theta) a,b,c\rangle +\sin(\theta) a,b,1-c\rangle &{\mbox{for }}a=b=1\a,b,c\rangle &{\mbox{otherwise}.}}\end{case}}$

유감스럽게도, 작동중인 도이치 게이트는 프로토콜 부족으로 인해 연락이 닿지 않는 상태로 남아있습니다.중성 원자에서 쌍극자-쌍극자 상호작용을 갖는 도이치 게이트를 실현하기 위한 몇 가지 제안이 있습니다.^[22]

가역적 고전 컴퓨팅을 위한 범용 논리 게이트인 토폴리 게이트는 Deutsch 게이트, $D{\displaystyle (}$π ${\displaystyle \begin{array}{c}\frac{2}{})\end{array}}$ ${\displaystyle D({\begin{matrix}{\frac {\pi}{2}}\end{matrix})}$로 환원할 수 있으므로$$모든 가역적 고전 논리 연산이 범용 양자 컴퓨터에서 수행될 수 있음을 보여줍니다.

보편성을 위해 충분한 단일 2큐비트 게이트도 존재합니다.1996년 아드리아노 바렌코(Adriano Barenco)는 도이치 게이트가 단 하나의 2큐비트 게이트(Barenco gate)만을 사용하여 분해될 수 있음을 보여주었지만 실험적으로 실현하기는 어렵습니다.^{[1]: 93} 가역적이고 보편적인 고전적인 두 비트 게이트가 없기 때문에 이 기능은 양자 회로에만 국한됩니다.^{[1]: 93} 범용 2 큐비트 게이트는 고속 저전력 마이크로프로세서에서 고전적인 가역 회로를 개선하기 위해 구현될 수 있습니다.^{[1]: 93}

회로구성

직렬 연결 게이트

$n개$의 ${\displaystyle n}$개의$$ 큐비트에 작용하는 두 개의 게이트 A와 B가 있다고 가정합니다.직렬 회로에서 A 뒤에 B가 놓이면 두 게이트의 효과는 하나의 게이트 C로 설명할 수 있습니다.

${\displaystyle C=B\cdot A}$

여기서 ⋅ ${\displaystyle \cdot}$은(는) 행렬 곱셈입니다.결과 게이트 C는 A 및 B와 동일한 치수를 가질 것입니다.게이트가 회로도에 나타나는 순서는 게이트를 곱할 때 반대로 바뀝니다.^{[4]: 17–18,22–23,62–64 [5]: 147–169}

예를 들어, 둘 다 하나의 큐비트에 작용하는 파울리 Y 게이트 뒤에 파울리 X 게이트를 두는 것을 단일 결합 게이트 C라고 설명할 수 있습니다.

${\displaystyle C=X\cdot Y={\bmatrix}0&1\\1&0\end{bmatrix}}\cdot {\bmatrix}0&-i\i&0\end{bmatrix}={\begin{bmatrix}i&0\0&-i\end{bmatrix}=iZ}$

제품 기호( ⋅ ${\displaystyle \cdot$가 생략되는 경우가 많습니다.

양자문 지수

유니터리 행렬의 모든 실수 지수는 유니터리 행렬이고, 모든 양자 게이트는 유니터리 행렬입니다.

양의 정수 지수는 직렬로 연결된 게이트의 시퀀스($예$: X ${\displaystyle 3^{}}$ = ${\displaystyle X}$ ⋅ ${\displaystyle X}$ ⋅ ${\displaystyle X}$ ${\displaystyle X^{3$}= $X\cdot$ X$\cdot X$})와 같으며, 실제 지수는 직렬 회로의 일반화입니다.예를 들어 $X$ π ${\displaystyle X^{\pi}}$와 $X$ = ${\displaystyle {}^{}}$ $1$ ${\displaystyle {\sqrt {$X}=X$^{1/2}$는 모두 유효한 양자 게이트입니다.

${\displaystyle {}^{}}$$임의$의 유니터리 ${\displaystyle \mathrm{행렬}}$ U$${\$displaystyle U$$}$에 대한${\displaystyle {}^{}}$U ${\displaystyle 0^{}}$ ${\displaystyle {}^{}}$ I ${\displaystyle$ $^{0$}= $I}$입니다$.$ ID 행렬($$ ${\displaystyle I$은 NOP처럼 동작하며 양자 회로에서 베어 와이어로 표시되거나 표시되지 않을 수 있습니다.

$U$ † ${\displaystyle {}^{}}$ = ${\displaystyle {}^{}}$ † = ${\displaystyle I}$ ${\displaystyle$ U$^{\dagger$ }$U$=$UU^{\dagger$ } =$I}$ 및 $U$ † = U${\displaystyle {}^{}}$- ${\displaystyle 1^{}}$ ${\displaystyle$ U$^{\dagger$ } = $U^{-1},$ 여기서$$† ${\displaystyle \dagger$}는 켤레 전치입니다.이것은 게이트의 음의 지수가 양의 지수인 대응 지수의 단일 역수임을 의미합니다.${\displaystyle U^{}}$-${\displaystyle n^{}}$ $=$( ${\displaystyle U^{}{n}^{}}$ )${\displaystyle {}^{}}$${\displaystyle {†}^{}}$ ${\displaystyle$ U$^$} $=$ ($U^{n})^{\dagger}}.$예를 들어, 위상 편이 게이트의 일부 음의 $지수$는 T${\displaystyle {}^{}}$- ${\displaystyle 1^{}}$${\displaystyle {}^{}}$= ${\displaystyle {}^{}}$ ${\displaystyle {†}^{}}$ ${\displaystyle T^$${\displaystyle {\{}^{}}$$-1$} ${\displaystyle {}^{}}$ $T^{\dagger}}$이고, $T$${\displaystyle {}^{}}$- ${\displaystyle 2^{}}$ =${\displaystyle }$(${\displaystyle T^{}}$${\displaystyle 2^{}}$ ${\displaystyle {)}^{}}$${\displaystyle {}^{}}$† ${\displaystyle {}^{}}$= ${\displaystyle S}$ † ${\displaystyle T^$${\displaystyle {\{}^{}}$$-2$} = ($T^{2})^{\dagg$${\displaystyle e^{}}$$r$ } = S$^{\dagger }$입니다$.$

에르미트 행렬 $H$ † = ${\displaystyle H,}$ ${\displaystyle$ H$^{\dagger$ } = $H,}$이며, 단일성 때문에 H ${\displaystyle {}^{}}$ † = I${\displaystyle ,}$ ${\displaystyle$ $HH$$^{\dagger$ } = I$,}$이므로 모든 에르미트 게이트에 대해 ${\displaystyle H}$ ${\displaystyle 2^{}}$ = I ${\displaystyle$ H$^{2$} = I$}$입니다.그들은 고의적입니다.에르미트 문의 예로는 파울리 문, 하다마르 문, CNOT, SWAP, 토폴리 등이 있습니다.에르미트 단위 행렬 $H$ ${\displaystyle H}$에는 $속성$ ${\displaystyle \mathrm{ei}}$ θ ${\displaystyle H^{}}$ =${\displaystyle }$(${\displaystyle \cos }$ ⁡ θ${\displaystyle }$) I${\displaystyle }$+ ${\displaystyle (\mathrm{is}}$ in ⁡ θ${\displaystyle }$) ${\displaystyle H}$ ${\displaystyle e^{i\theta$H}= (\$cos \theta )I$+ ($i\sin \theta$)$H}$ 여기서 $H$ $=$ e ${\displaystyle {}^{}}$ $π$ 2${\displaystyle {}^{}}$( ${\displaystyle I^{}}$- ${\displaystyle H^{}}$) $=$ e -${\displaystyle i^{}}$ $π$ ${\displaystyle {\frac{2}{}}^{}}$( ${\displaystyle I^{}}$- H${\displaystyle {}^{}}$) .${\displaystyle$H$$$=$$e^{i{\frac {\pi }{2}}(I-H$)}$=$ $e^{-i{\frac {\pi }{2}}(I-H)}.$

평행게이트

두 양자 게이트의 텐서 곱(^{[4]: 71–75 [5]: 148} 또는 크로네커 곱)은 두 게이트와 평행한 게이트입니다.

그림과 같이 Pauli-Y 게이트와 Pauli-X 게이트를 병렬로 결합하면 다음과 같이 쓸 수 있습니다.

${\displaystyle C=Y\otimes X={\begin{bmatrix}0&-i\i&0\end{bmatrix}}\otimes{\begin{bmatrix}0&1\\1&0\end{bmatrix}}={\begin{bmatrix}0{\begin{bmatrix}0&1\\1&0\end{bmatrix}}&-i{\begin{bmatrix}0&1\1&0\end{bmatrix}}\i{\begin{bmatrix}0&1\1&0\end{bmatrix}}&0{\begin{bmatrix}0&1\1&0\end{bmatrix}}={\begin{bmatrix}0&0&0&0&0&i\0&0&0&0\end{bmatrix}}}$

파울리-X와 파울리-Y 게이트는 모두 하나의 큐비트에 작용합니다.결과 게이트 $C{\displaystyle }$ ${\displaystyle C}$는 두 큐비트에 작용합니다$$.

텐서 곱 기호가 생략되고 대신 연산자에 인덱스가 사용되는 경우도 있습니다.^[25]

하다마드 변환

게이트 $H$ ${\displaystyle 2_{}}$ = ${\displaystyle H}$ ⊗ H ${\displaystyle H_{2$}=$H\otimes$ H$}$는 2큐비트에 병렬로 적용된 하다마드 게이트($$ ${\displaystyle$ H$\})$입니다.다음과 같이 쓸 수 있습니다.

${\displaystyle H_{2}=H\otimes H={\frac {1}{\sqrt {2}}{\begin{bmatrix}1&1\1&1\end{bmatrix}}\otimes {\frac {1}{\sqrt {2}}{\frac {1}1&1\end{bmatrix}}={\frac {1}{2}{{{bmatrix}1&1&1\1&1\1&1\n1&1\end{bmatrix}}{{\frac {1&1}}}$

이 "2큐비트 병렬 하다마드 게이트"는 예를 들어, 2큐비트 영벡터(${\displaystyle 00}$ ⟩ ${\displaystyle 00\rangle })$에 적용될 때, ${\displaystyle 00}$ ⟩ ${\displaystyle 00\rangle$ ${\displaystyle 01}$ ⟩$${\$displaystyle 01\rangle$ ${\displaystyle 10}$ ⟩$${\$displaystyle 10\rangle$ 및 4개의 가능한 결과에서 관찰될 확률이 동일한 양자 상태를 생성합니다.${\displaystyle \mathrm{}11}$ ${\displaystyle ⟩}$ ${\displaystyle 11\rangle}.$ 다음과 같이 쓸 수 있습니다$.$

${\displaystyle H_{2} 00\rangle = {\frac {1}{2}}{{\begin{bmatrix}1&1&1\1&1\1&1&1\1&-1\1&1&-1\n1&1&1\n\n{bmatrix}}{\begin{bmatrix}1\0\0\0\0\0\0\0\0\n\end{bmatrix}}={\frac {1}{2}}={\frac {1}{2}}={\frac {2}},00\rangle +{\frac {1}{2}},01\frangle +{\frac {1}{2}},10\frangle +{\frac {1}{2}},11\frangle ={\frac {00\rangle +01\rangle +1}.0\rangle + 11\rangle }{2}}$

여기서 각각의 측정 가능한 상태에 대한 진폭은1 ⁄2. 어떤 상태를 관찰할 확률은 측정 가능한 상태 진폭의 절대값의 제곱이며, 위의 예에서 우리가 개별적인 네 경우 중 어느 하나를 관찰할 수 있다는 것을 의미합니다.자세한 내용은 측정 참조.

${\displaystyle {H2\mathrm{}}_{}}$ ${\$는 두 큐비트에 대해 하다마드 변환을 수행합니다$$.마찬가지로 게이트 $H$ ⊗ ${\displaystyle \underset{}{\underset{}{H}}}$ ⊗ ⋯ ⊗ H ⏟ ${\displaystyle \underset{}{\text{n번}}}$ = ⨂ 1 ${\displaystyle \underset{}{\overset{}{n}}}$ ${\displaystyle \underset{}{\overset{}{}}}$ = ${\displaystyle {}_{}}$ ⊗ ${\displaystyle n^{}}$ = ${\displaystyle H_{}}$ ${\displaystyle \underbrace {H\otimes H\otimes H} _{n{\text{times$}} =\$bigotimes _{1}^{n}H$=$H^{\otimes$n} =$H_{n}}:$ $n개$의 ${\displaystyle n}$개의$$ 큐비트 레지스터에 대해 하다마드 변환을 수행합니다$$.

${\displaystyle n개}$의 ${\$$displaystyle$ $n}$개 $큐비트$가 모두 0$$⟩ {\$displaystyle$ 0\rangle}(으)로 초기화된 레지스터에 적용되면$,$ 하다마드 변환은 양자 레지스터를 ${\displaystyle {2n개}^{}}$의 ${\displaystyle 2^{n}$개의 가능한 상태에서 측정될 확률이 동일한 중첩 상태에 놓이게 됩니다.

${\displaystyle \bigotimes _{0}^{n-1}(H 0\rangle )={\frac {1}{\sqrt {2^{n}}}}{\begin{bmatrix}}{\1\n\vdots \\1\end{bmatrix}}={\frac {1}{\sqrt {2^{n}}}{\big(} 0\rangle + 1\rangle + 2^{n}-1\rangle {\Big )}={\frac {1}{\sqrt {2^{n}}}\sum {i=0}^{2^{n}-1}i\rangle }$

이 상태는 균일한 중첩이며 진폭 증폭 및 위상 추정과 같은 일부 검색 알고리즘에서 첫 번째 단계로 생성됩니다.

이 상태를 측정하면 ${\displaystyle 0}$ ⟩ ${\displaystyle 0\rangle}$에서 ${\displaystyle 2^{}}$ n${\displaystyle {}^{}}$- ${\displaystyle 1}$ ⟩ ${\displaystyle 2^{n}-1\rangle}$ 사이의 난수가 됩니다$.$ 숫자가 얼마나 랜덤한지는 논리 게이트의 충실도에 따라 달라집니다.측정하지 않으면 가능한 각 상태에 대해$$ 확률 진폭 $1{\displaystyle \frac{\mathrm{}}{}}$ ${\displaystyle \frac{\sqrt{2^{}}}{}}$ n ${\$가 동일한 양자 상태입니다.

Hadamard 변환은 다음과 같이 $n개$의 {\$displaystyle$\psi$\rangle }$$$큐비트를 $가진$ 레지스터$$⨂ {\displaystyle \$rangle$ }에서 작동합니다(ψ ⟩ = i = 0 $\underset{}{\overset{}{\mathrm{n}}}$ - $1_{}$ psi i$\underset{}{\overset{}{}}$⟩ ${\textstyle \rangle$ =\$bigotimes _{i$=$0}^{n-1}$\psi $_{i}\rangle }).$

${\displaystyle \bigotimes _{0}^{n-1}H \psi \rangle =\bigotimes _{i=0}^{n-1}{\frac {0\rangle +(-1)^{\psi _{i}}{\sqrt {2}}={\frac {1}{\sqrt {2^{n}}}\bigotimes _{i=0}^{n-1}{\big (}) 0\rangle +(-1)^{\psi _{i}}1\rangle {\Big )}=H \psi _0}\rangle \otimes H \psi _{1}\rangle \cdots H \psi _{n-1}\rangle }$

엉킨 상태에 적용

둘 이상의 큐비트를 단일 양자 상태로 본다면, 이 결합 상태는 구성 큐비트의 텐서 곱과 같습니다.구성 하위 시스템에서 텐서 곱으로 작성할 수 있는 모든 상태를 분리 가능 상태라고 합니다.반면에, 얽힘 상태는 텐서-팩터화될 수 없는 상태, 즉 다른 말로 하면 다음과 같습니다.얽힌 상태는 구성 큐비트 상태의 텐서 곱으로 쓸 수 없습니다.엉킨 상태를 구성하는 구성 큐비트에 게이트를 적용할 때는 특히 주의해야 합니다.

만약 우리가 얽혀있는 N개의 큐비트 집합이 있고 그 집합의 M < N개의 큐비트에 양자 게이트를 적용하고자 한다면, 우리는 N개의 큐비트를 얻기 위해 게이트를 확장해야 할 것입니다.이 응용 프로그램은 게이트와 항등 행렬을 결합하여 텐서 생성물이 N개의 큐비트에 작용하는 게이트가 되도록 할 수 있습니다.아이덴티티 행렬(${\displaystyle }$ ${\displaystyle I$은 모든 상태를 자신에게 매핑하는 게이트의 표현입니다(즉, 아무것도 하지 않음).회로도에서 아이덴티티 게이트 또는 매트릭스는 종종 베어 와이어로 나타납니다.

예를 들어 하다마드 게이트($$ ${\displaystyle H$는 단일 큐비트에서 작동하지만, 얽힌 벨 상태 ${\displaystyle \frac{00}{}}$ ⟩${\displaystyle \frac{}{}}$+ ${\displaystyle \frac{11}{}}$ ⟩ ${\displaystyle \frac{}{}}$ ${\displaystyle {\frac {00\rangle$+ $11\rangle}}{\sqrt {2}}}}$개의 큐비트 중 첫 번째 큐비트를 입력하면 해당 작업을 쉽게 쓸 수 없습니다$.$ID 게이트 I ${\displaystyle I}$이($가{\displaystyle }$) 있는$하다마드{\displaystyle }$ 게이트 H {\$displaystyle H}$를 확장하여$$ 두 큐비트에 걸쳐 있는 양자 상태에 대해 작업할 수 있어야 합니다.

${\displaystyle K=H\otimes I={\frac {1}{\sqrt {2}}{\begin{bmatrix}1&1\1&-1\end{bmatrix}}\otimes {\begin{bmatrix}1&0\0\0&1\end{bmatrix}}={\frac {1}{\sqrt {2}}{\begin{bmatrix}1&0&0\0&1\0&0&1\end{bmatrix}}$

이제 게이트 $K{\displaystyle }$ ${\displaystyle K}$을(를) 얽히거나 다른 모든 2큐비트 상태에 적용할 수 있습니다$$.게이트 $K{\displaystyle }$ ${\displaystyle K}$은(는) 두 번째 큐비트를 그대로 두고 첫 번째 큐비트에 하다마드 변환을 적용합니다.예에서 Bell 상태에 적용할 경우 다음과 같이 쓸 수 있습니다.

${\displaystyle K{\frac {00\rangle + 11\rangle }{\sqrt {2}} = {\frac {1}{\sqrt {2}}}{\frac {1&0&0\0&0\0&1\0&0\1&0\0&0\0&0\0&1\end{bmatrix}{\frac {1}{\sqrt {2}}{{\begin{bmatrix}1\0\0\0\1\end{bmatrix}}={\frac {1}{2}}{\begin{bmatrix}1\1\1\-1\end{bmatrix}}={\frac {00\rangle + 01\rangle + 10\rangle - 11\rangle}{2}}}}{\frac {00\rangle + 01\rangle }}$

계산 복잡도 및 텐서 곱

두 $n{\displaystyle }$× ${\displaystyle n}$ ${\displaystyle n\times n}$ - 행렬에 곱하는 시간 복잡도는 최소 ω (${\displaystyle {}^{}}$2 ${\displaystyle \log }$ ⁡ ${\displaystyle n}$ )${\displaystyle \Omega$ ($n^{2}\log n)}$입니다$.$$q$ ${\displaystyle$$$$q}$큐비트에서 작동하는 게이트의 크기가 2 $q$ ×${\displaystyle 2^{}}$ $q {\displaystyle$ 2$^{q}\times$ 2$^{$q}이므로$$일반적으로 얽힌 상태에서 작동하는 양자 회로(게이트 곱하기)의 단계를 시뮬레이션하는 시간은 ω${\displaystyle (}$2${\displaystyle {q^{}}^{}}$ 2 ${\displaystyle \log }$ ⁡(2${\displaystyle q^{}}$ ${\displaystyle$ \$Omega({2^{q}}^{2}\log({2^{q$})}입니다$.$이러한 이유로 고전적인 컴퓨터를 사용하여 얽힌 큰 양자 시스템을 시뮬레이션하는 것은 다루기 어려운 것으로 여겨집니다.그러나 Clifford 게이트와 같은 게이트의 하위 집합 또는 고전적인 부울 함수만을 구현하는 회로의 사소한 경우(예: X, CNOT, Toffoli의 조합)는 고전적인 컴퓨터에서 효율적으로 시뮬레이션될 수 있습니다.

$n개$의 ${\displaystyle n}$개의$$ 큐비트가 있는 양자 레지스터의 상태 벡터는 ${\displaystyle {2n개}^{}}$의 ${\$개의$$ 복소 항목입니다.확률 진폭을 부동 소수점 값의 목록으로 저장하는 것은 $큰{\displaystyle }$ n ${\displaystyle n}$에서는 다루기 어렵습니다$.$

게이트의 유니터리 반전

모든 양자 논리 게이트는 가역적이기 때문에 여러 게이트의 구성도 가역적입니다.유니터리 행렬의 모든 곱과 텐서 곱(즉, 급수와 병렬 조합)도 유니터리 행렬입니다.이것은 게이트만 포함하는 한 모든 알고리즘과 함수의 역구성이 가능하다는 것을 의미합니다.

초기화, 측정, I/O 및 자발적 비간섭성은 양자 컴퓨터에서 부작용입니다.하지만 게이트는 순수하게 기능적이고 객관적입니다.

$U$ ${\displaystyle U}$이(가) 단일 행렬이면 $U$ † ${\displaystyle {}^{}}$ = ${\displaystyle U}$ † = ${\displaystyle I}$ ${\displaystyle U^{\dagger$$$} U$$=$$U$U^{\dagger$ } = $I}$ 및 $U$ † = ${\displaystyle U}$ -${\displaystyle 1^{}}$ ${\displaystyle U^{\dagger$ } = U$^{-1}$입니다.단검( † ${\displaystyle \dagger})$은$$켤레 전치를 나타냅니다.그것은 또한 에르미트 인접이라고도 불립니다.

함수 $F$ ${\displaystyle F}$$$가 $m$ ${\displaystyle$ m} $게이트$의 곱일 경우, $F$ = ${\displaystyle {}_{}}$ ${\displaystyle 1_{}}$ ⋅ A ${\displaystyle 2_{}}$ ⋅ ⋯ ⋅ ${\displaystyle {Am}_{}}$ ${\displaystyle$ F=$A_{1}\cdot A_{2}\cdot \$dots \$cdot A_{m$ 함수 $F$† {\$displaystyle$ F$^{\dagger }$의 단위 역수는 다음과 같이 구성할 수 있습니다.

왜냐하면$$(${\displaystyle \mathrm{UV}{}^{}}$ † = ${\displaystyle {}^{}}$ † U †$${\$displaystyle(UV)^{\dagger$ } = V$^{\dagger }U^{\dagger }$개를 반복적으로 적용한 결과,

${\displaystyle F^{\dagger }=\left(\prod_{i=1}^{m}A_{i}\right)^{\dagger}=\prod_{i=m}^{1}A_{i}^{\dagger }=A_{m}^{\dagger }\cdot \dots \cdot A_{2}^{\dagger }\cdot A_{1}^{\dagger }}$

마찬가지로 함수 $G$ ${\displaystyle G}$가 두 $개$의 게이트 $A$ ${\displaystyle$ A$}$와 B ${\displaystyle B}$로 병렬로 구성되어 있다면, $G$ = ${\displaystyle A}$ ⊗ B ${\$$displaystyle$ G=$A\otimes B}$와 $G$ † = ${\displaystyle (A}$ ⊗ ${\displaystyle B}$ )${\displaystyle {}^{}}$† = A † ⊗ $G^{\dagger$} = ($A\otimes$ B$)^{\dagger$ } = $A^{\dagger$ }\$otimes$ B$^{\dagger }}.$

그들 자신의 단일 역인 게이트는 에르미트 연산자 또는 자기 인접 연산자라고 불립니다.하다마드(H) 및 파울리 게이트(I, X, Y, Z)와 같은 일부 초등 게이트는 에르미트 연산자인 반면 위상 이동(S, T, P, CP) 게이트와 같은 다른 게이트는 일반적으로 그렇지 않습니다.

예를 들어, 덧셈 알고리즘은 "역으로 실행"되는 경우 뺄셈에 사용할 수 있습니다.역양자 푸리에 변환은 유니터리 역입니다.유니터리 반전은 계산 해제에도 사용할 수 있습니다.마이크로소프트의 Q#,^[10] 베른하르트 외메르의 QCL,^{[13]: 61} IBM의 Qiskit 등과 같은 양자 컴퓨터용 프로그래밍 언어는 함수 반전을 프로그래밍 개념으로 포함합니다.^[27]

측정.

측정은 관측된 양자 상태를 단일 값에 할당하기 때문에(때로는 관측이라고도 함) 비가역적이므로 양자 게이트가 아닙니다.측정은 양자 상태를 취하여 해당 기저 벡터를 따라 벡터 길이의 제곱(2-노름^{[4]: 66 [5]: 56, 65} )과 동일한 가능성을 갖는 기저 벡터 중 하나로 투영합니다.^{[1]: 15–17 [28][29][30]}이것은 Born 규칙으로 알려져 있으며 양자 상태를 측정된 상태를 나타내는 기본 벡터와 확률적으로 동일하게 설정하기 때문에 확률적으로 가역적이지 않은 연산으로 나타납니다^[e].측정 순간 상태는 측정된 확실한 단일 값으로 "붕괴"됩니다.측정 시 양자 상태가 붕괴되는 이유와 방법, 또는 양자 상태가 붕괴되는 경우에도^[31][32] 이를 측정 문제라고 합니다.

확률 $진폭$ ϕ가$${\$displaystyle \phi}$인 값을 측정할 확률은 $1$ ≥ ϕ ${\displaystyle {}^{}}$ ≥ ${\displaystyle 0}${\$displaystyle 1\geq \phi$^{$2}\geq 0}$이며$,$ 여기서 ⋅ $displaystyle \cdot}$은 모듈러스입니다.

양자 상태가 벡터 $a$ ${\displaystyle 0}$ ⟩${\displaystyle }$+ ${\displaystyle b}$ ${\displaystyle 1}$ ⟩ =${\displaystyle }$[ ${\displaystyle \begin{array}{}a\end{array}}$ b${\displaystyle \begin{array}{}\end{array}}$] ${\displaystyle$a$0\rangle$+ b $1\rangle$ = {\$displaystyle$$a$ ${bmatrix}$a\b\end$\{$bmatrix}}}인 ${\displaystyle {}^{}}$ 큐비트를 측정하면 $확률$이 2 {\$displaystyle$ 0\rangle $}$이고$$확률이 ${\displaystyle {}^{}}$ ${\displaystyle$b$^{2}$인 ⟩ ${\displaystyle 1\rangle }$이(가) ${\displaystyle 됩니다}$$.$

예를 들어, 양자 상태 ${\displaystyle \frac{0}{}}$ ⟩ -${\displaystyle \frac{}{}}$i ${\displaystyle \frac{1}{}}$ ⟩ ${\displaystyle \frac{}{}}$ = ${\displaystyle 1}$ ${\displaystyle \frac{\sqrt{2}}{}}$[ ${\displaystyle \begin{array}{c}1\end{array}}$ -${\displaystyle \begin{array}{}\end{array}}$i${\displaystyle \begin{array}{}\end{array}}$] ${\displaystyle$ {\$frac${0$\rangle -i 1\rangle}{\sqrt {$2}} = {\$frac {1}{\sqrt {2}}{\$begin${bmatrix}1\i\end{bmatrix}}$은(는) ${\displaystyle 0}$ ⟩ ${\displaystyle 0\rangle}$ 또는 ${\displaystyle 1}$ ⟩ ${\displaystyle 1\rangle}$의 확률이 동일합니다$.$

n개의 큐비트에 걸쳐 있는 양자 상태 ψ ⟩ ${\displaystyle \Psi \rangle }$을(를$)$ ${\displaystyle {2n}^{}}$ ${\displaystyle 2^{n}$ 복소 차원의 벡터로 쓸 수 있습니다: ψ ⟩ ∈ ${\displaystyle C}$ ${\displaystyle {{2n}^{}}^{}}$\$displaystyle \Psi \rangle \in \mathbb {C}^{2^{n}}.$n개의 큐비트의 텐서 곱이 ${\displaystyle {2n}^{}}$ ${\$차원의$$ 벡터이기 때문입니다.이러한 방식으로 n개의 큐비트 레지스터는 ${\displaystyle {n개}^{}}$의 클래식 비트 레지스터가 $2개$의 {\displaystyle $2$$^{n$$}$개의$$ 서로 다른 상태를 유지할 수 있는 것과 유사하게 $2n{\displaystyle {\mathrm{}}^{}}$ ${\$ $2$$^{n$}개의 서로$$ 다른 상태로 측정할 수 있습니다.양자 상태는 고전적인 컴퓨터의 비트와는 달리 동시에 측정 가능한 여러 값에서 0이 아닌 확률 진폭을 가질 수 있습니다.이것을 중첩이라고 합니다.

모든 결과에 대한 모든 확률의 합은 항상 1과 같아야 합니다.^[f]이것을 말하는 또 다른 방법은 $C$ ${\displaystyle {2^{}}^{}}$ n ${\displaystyle \mathbb {C} ^{2^{n}}$에 일반화된 피타고라스 정리가 n개의 큐비트를 갖는 모든 양자 상태 ψ ⟩ ${\displaystyle \Psi \rangle }$은 $1$ = ∑ $\underset{}{\overset{}{x}}$ = 0 $\underset{}{\overset{}{2}}$ $\underset{}{\overset{}{n^{}}}$ -$\underset{}{\overset{}{{}^{}}}$1 $a$ x ${}^{}$ ${\textstyle$1=\$sum _{x$=$0}^{2^{n}^{x}^{2}}$를 만족해야 하며, 여기서 ${\displaystyle x_{}}$ ${\displaystyle a_{x}$는 mea에 대한 확률 진폭입니다.surable state ${\displaystyle x}$ ⟩ ${\displaystyle$ x$\rangle$ 이에 대한 기하학적 해석은 n개의 큐비트를 갖는 양자 상태 ψ ⟩$${\$displaystyle \Psi \rangle$}의 가능한 값-공간이$$ {\$displaystyle \mathbb {C}^{2^{n}}$의 단위 구의 표면이며, 단위 변환(즉, 단위 변환)을 한다는 것입니다.양자 논리 게이트)에 적용되는 것은 구의 회전입니다.게이트가 수행하는 회전은 대칭 그룹 U(2)에ⁿ 있습니다.그러면 측정은 이 복잡한 구의 표면에 있는 점들을 공간에 걸쳐 있는 기본 벡터에 대한 확률적인 투영입니다(그리고 결과에 레이블을 붙입니다).

많은 경우 공간은 특정 ${\displaystyle {2n}^{}}$ ${\$ -차원$$ 복소 공간이 아닌$$ 힐베르트 공간 $H{\displaystyle \mathcal{}}$ ${\$로 표현됩니다.차원의 수(기본 벡터에 의해 정의되며, 따라서 측정에서 발생할 수 있는 결과)는 종종 피연산자에 의해 문제를 해결하는 데 필요한 상태 공간으로 암시됩니다.그로버의 알고리즘에서 로브는 이 일반 기저 벡터 집합을 "데이터베이스"라고 이름 지었습니다.

양자 상태를 측정하기 위한 기저 벡터의 선택은 측정 결과에 영향을 미칩니다.^{[1]: 30–35 [4]: 22, 84–85, 185–188 [33]}자세한 내용은 기초의 변화와 폰 노이만 엔트로피를 참조.이 기사에서는 항상 계산 기반을 사용합니다. 즉, n-큐비트 레지스터 ${\displaystyle 0}$⟩${\displaystyle ,}$ ${\displaystyle 1}$ ⟩${\displaystyle ,}$ ${\displaystyle 2}$ ⟩${\displaystyle ,}$⋯,${\displaystyle 2^{}}$ n -${\displaystyle {}^{}1}$ ⟩ ${\displaystyle 0\rangle, 1\rangle, 2\rangle,$ 2\$cdots, 2^{n}-1\rangle }$의 ${\displaystyle {2n}^{}}$ ${\displaystyle 2^{n}}$ 기본 벡터에 레이블을 지정하거나$$${\displaystyle 이진}$ 표현 0 ${\displaystyle {10}_{}}$ ⟩ = ${\displaystyle 0}$… ${\displaystyle {00}_{}}$ ${\displaystyle 2_{}}$ ⟩${\displaystyle }$= 0${\displaystyle }$… ${\displaystyle {01}_{}}$ ${\displaystyle 2_{}}$ ⟩${\displaystyle }$=${\displaystyle 0}$…${\displaystyle \mathrm{}{10}_{}2{}_{}⟩,\cdots ,}$ 2 ${\displaystyle n^{}\mathrm{-}{}^{}1}$ ${\displaystyle {}_{}}$ $=$ ${\displaystyle 111\mathrm{\dots }}$ ${\displaystyle {12}_{}}$ ⟩ ${\displaystyle 0_{10}\ra$dots $10_{2}\rangle,$ 2$^{n}-1\ra$=$\$dots $1_{2}\rangle입니다.$

양자역학에서 기저 벡터는 정규 기저를 구성합니다.

대체 측정 기준의 사용 예는 BB84 암호에 있습니다.

엉킨 상태에 대한 측정의 영향

두 개의 양자 상태(즉, 큐비트 또는 레지스터)가 얽혀 있는 경우(이들의 결합 상태를 텐서 곱으로 표현할 수 없음을 의미함), 한 레지스터의 측정은 다른 레지스터의 상태에도 영향을 미치거나 그 상태를 부분적으로 또는 전체적으로 붕괴시킴으로써 드러납니다.이 효과는 계산에 사용될 수 있으며 많은 알고리즘에 사용됩니다.

Hadamard-CNOT 조합은 다음과 같이 제로 상태에 작용합니다.

${\displaystyle \operatorname {CNOT} (H\otimes I) 00\rangle =\left ({\begin{bmatrix}1&0&0\0&0\0&1&0\0&0&0\0&0&0\0&0&0\end{bmatrix}\left ({\frac {1}{\sqrt {2}}{\begin{bmatrix}1&1\1&1\end{bmatrix}}\otimes {\begin{bmatrix}1&0\end{bmatrix}\right){\begin{bmatrix}1\0\0\0\0\end{bmatrix}}={\frac {1}{\sqrt {2}}{\begin{bmatrix}1\0\1\end.{bmatrix}}={\frac {00\rangle +11\rangle}{\sqrt {2}}}$

이 결과 상태는 Bell 상태 ${\displaystyle \frac{00}{}}$ ⟩${\displaystyle \frac{}{}}$+ ${\displaystyle \frac{11}{}}$ ⟩ ${\displaystyle \frac{}{}}$ = 1 ${\displaystyle \frac{\sqrt{2}}{}}$[ 1 ${\displaystyle \begin{array}{}0\end{array}}$ ${\displaystyle \begin{array}{}1\end{array}}$ ]${\displaystyle {\frac {00\rangle$+ $11\rangle}{\sqrt {$2}}={\$frac {1}{\sqrt {2}}{\$begin${bmatrix}1\0\0\1\end{bmatrix}}$입니다$.$이것은 두 큐비트의 텐서곱으로 설명할 수 없습니다.에 대한 해결책은 없습니다.

${\displaystyle {\begin{bmatrix}x\y\end{bmatrix}}\otimes {\begin{bmatrix}w\z\end{bmatrix}={\begin{bmatrix}xw\xz\yw\yz\end{bmatrix}}={\frac {1}{\sqrt {2}}{\begin{bmatrix}1\0\0\1\end{bmatrix}}}$

예를 들어 xw와 yw의 경우 w는 0이 아닌 것과 0이 되어야 하기 때문입니다.

양자 상태는 두 큐비트에 걸쳐 있습니다.이것을 얽힘이라고 합니다.이 Bell 상태를 구성하는 두 큐비트 중 하나를 측정하면 다른 큐비트는 논리적으로 동일한 값을 가져야 하며 둘 다 동일해야 합니다.상태 ${\displaystyle 00}$ ⟩ ${\displaystyle 00\rangle}$ 또는$$상태 ${\displaystyle 11}$ ⟩ ${\displaystyle 11\rangle}$에서 찾을 수 있습니다$.$ 큐비트 중 하나를 예를 들어 ${\displaystyle 1}$ ⟩$${\$displaystyle$ $1$$\rangle}$로 측정하는 경우 다른 큐비트도 ⟩ {\$displaystyle$ 1$\$$rangle}$이어야 합니다$.$ 이는 결합 ${\displaystyle 상태}$가 ⟩ {\$displaystyle 11$\rangle}이(가$)$ 되었기 때문입니다$.$ 측정값큐비트 중 하나의 nt는 두 큐비트에 걸쳐 있는 전체 양자 상태를 붕괴시킵니다.

GHZ 상태는 3개 이상의 큐비트에 걸쳐 있는 비슷한 얽힌 양자 상태입니다.

이러한 유형의 가치 할당은 모든 거리에서 순간적으로 발생하며 2018년 현재 최대 1200km의 거리에 대해 QUEESS에 의해 실험적으로 검증되었습니다.^[34][35][36]큐비트를 빛의 속도로 분리하는 거리를 통과하는 데 걸리는 시간이 아닌 순간적으로 현상이 나타나는 것을 EPR 역설이라고 하며, 이를 해결하는 방법은 물리학에서 열려 있는 문제입니다.원래는 지역적 리얼리즘의 가정을 포기하는 것으로 해결되었지만, 다른 해석들도 등장했습니다.자세한 내용은 Bell 검정 실험을 참조하십시오.비통신 정리는 이 현상이 고전 정보의 빛보다 빠른 통신에 사용될 수 없음을 증명합니다.

쌍으로 얽힌 큐비트가 있는 레지스터에서 측정

n개의 큐비트가 모두 ${\displaystyle 0}$ ⟩ ${\displaystyle 0\rangle}($으)로 초기화된 레지스터 A를 가져와$$평행한 하다마드 게이트 $H^{}$ ⊗ n ${\textstyle H^{\otimes n}($으)로 공급합니다$.$ 그러면 레지스터 $A$는 1 $\frac{\sqrt{2^{}}}{}$ $\frac{\sqrt{n}}{}$ ∑ $\underset{}{\overset{}{k}}$ = $\underset{}{\overset{}{0^{}}}$ $\underset{}{\overset{}{{}^{}}}$n - $1$ k ⟩ {\$textstyle {1}{\sqrt {2$^{n$}}}\sum _{k$=$0}^{2^{n}-1} k\rangle$} 상태로 들어갑니다.가능한 ${\displaystyle {2n}^{}}$ ${\displaystyle 2^{n}$개의 상태, ${\displaystyle 0}$ ⟩ ${\displaystyle 0\rangle}~$${\displaystyle {2n}^{}}$- ${\displaystyle 1}$ ⟩ ${\displaystyle 2^{n}-1\rangle}$개의 상태 중 하나입니다$.$ n개의 큐비트가 ${\displaystyle 0}$ ⟩ {\displaystyle $0\rangle}($으)로 초기화되고 각 p개의 큐비트에 대해 A ${\displaystyle P_{}}$ ${\displaystyle A_{p}$ 및 ${\displaystyle B_{}}$ P ${\$displaystyle A}의 큐비트와 쌍으로 CNOT합니다.$displaystyle$ ${\displaystyle {B\_}_{}}$${p}}:$ 상태 ${\displaystyle {}_{}}$ B p $⟩ =$ ${\displaystyle \frac{00}{}}$ $⟩$ ${\displaystyle \frac{+}{}}$ ${\displaystyle \frac{11}{}}$ $⟩$ ${\displaystyle \frac{}{}}$ ${\displaystyle A_{p}B_{p}\rangle$ $=$ {\$frac${ 00$\rangle$+$11\rangle}{\sqrt {2}}}.$

지금 레지스터 A의 큐비트를 측정하면 레지스터 B가 A와 같은 값을 포함하는 것으로 확인됩니다.대신 양자 논리 게이트 F를 A에 적용한 후 측정하면 ${\displaystyle A}$ ⟩ = F ${\displaystyle B}$ ⟩ ⟺ ${\displaystyle F}$ † ${\displaystyle A}$ ⟩ = ${\displaystyle B}$ ⟩ ${\displaystyle A\rangle$= F $B\rangle \iff$ F$^{\dagger$}$A\rangle$ = $B\rangle }$이며$,$ 여기서 $F$ † ${\displaystyle F^{\dagger }$는 F의 단위 역입니다.

게이트의 단위 역이 작용하기 때문에 $F$ † ${\displaystyle A}$ ⟩ = F${\displaystyle {}^{}}$- ${\displaystyle 1^{}}$(${\displaystyle A}$ ⟩ )${\displaystyle }$= ${\displaystyle B}$ ⟩ ${\displaystyle F^{\dagger$$$$} A\rangle$= F$^{-1}(A\rangle$ ) = $B\rangle }$입니다$.$ 예를 들어, $F{\displaystyle }$(${\displaystyle x}$ ) =${\displaystyle x}$ +${\displaystyle 3}$ (${\displaystyle mod}$ ${\displaystyle 2^{}}$n )$${\$displaystyle$ F$(x$) = x +$3 {\pmod {2^{n$ B ⟩ = ${\displaystyle A}$-${\displaystyle 3}$ (${\displaystyle mod}$ 2 ${\displaystyle n^{}}$)$${\$displaystyle B\rangle$ = $A-3{\pmod {2^{n}}\$rangle$}$라고 합니다.

F가 완료될 때까지 실행되었다고 가정하면 레지스터 A 또는 B에서 어느 순서로 측정을 수행하든 관계없이 등식이 유지됩니다.한 큐비트의 측정 할당은 다른 얽힌 큐비트로부터 가능한 값 공간을 제한하기 때문에 측정은 큐비트 단위로 무작위로 동시에 인터리빙될 수도 있습니다.

균등성이 유지되더라도 양자 검색 알고리즘의 의도처럼 F를 적용하면 가능한 결과를 측정할 확률이 달라질 수 있습니다.

얽힘을 통한 가치 공유의 이 효과는 쇼어의 알고리즘, 위상 추정 및 양자 계산에 사용됩니다.푸리에 변환을 사용하여 일부 문제에 대한 해 상태의 확률 진폭을 증폭하는 것은 "푸리에 낚시"로 알려진 일반적인 방법입니다.^[37]

논리함수합성

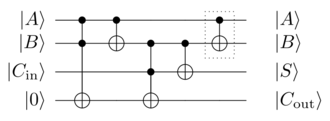
게이트만을 사용하는 함수와 루틴은 작은 게이트와 마찬가지로 행렬로 설명될 수 있습니다.$q$ ${\displaystyle q}$개의 큐비트에 작용하는 양자 함수를 나타내는 행렬의 크기는 2 ${\displaystyle q^{}}$ ×${\displaystyle {}^{}}$2 $q {\displaystyle$ 2$^{q}\times$ 2$^{$q}입니다$.$ 예를 들어, "큐바이트"(8개의 큐비트의 레지스터)에 작용하는 함수는 28 × ${\displaystyle {28}^{}}$=$$ × ${\displaystyle 256}$ ${\displaystyle$ 2$^{8}\times$ 2$^{8$}= 256$\times$ 256$}개$의 요소를 갖는 행렬로 표시됩니다.

양자 컴퓨터에서 기본적으로 사용할 수 있는 게이트 집합에 없는 단일 변환은 회로에서 사용 가능한 원시 게이트를 결합하여 합성하거나 근사화할 수 있습니다.이를 위한 한 가지 방법은 유니터리 변환을 사용 가능한 프리미티브 게이트의 텐서 곱(즉, 직렬 및 병렬 회로)으로 인코딩하는 행렬을 인수하는 것입니다.그룹 U(2^q)는 $q{\displaystyle }$ ${\displaystyle q}$개의$$ 큐비트에 작용하는 게이트에 대한 대칭 그룹입니다.^[2]인수분해는 원시 게이트의 생성 집합으로부터 U(2)의^q 경로를 찾는 문제입니다.솔로베이-키타예프 정리는 충분한 원시 게이트 집합이 주어지면 모든 게이트에 대해 효율적인 근사치가 존재함을 보여줍니다.큐비트 수가 많은 일반적인 경우에 이러한 회로 합성에 대한 직접적인 접근 방식은 다루기 어렵습니다.^[38][39]

게이트들은 단일 성질이기 때문에, 모든 함수들은 가역적이어야 하고, 항상 입력과 출력의 사영 매핑이어야 합니다.$F{\displaystyle {}^{}}$- ${\displaystyle 1^{}}$($F$(ψ ⟩))${\displaystyle }$=$$ψ ⟩ ${\displaystyle F^{-$$1$}($F( \$psi$\rangle$ })) = \psi $\rangle }$에 해당하는 함수 $F{\displaystyle {}^{}}$- 1 ${\displaystyle$ F^{-1$}$가 항상 존재해야 합니다$.$ 반전 불가능한 함수는 앤실라 큐비트를 입력 또는 출력 또는 둘 다에 추가하여 반전 가능하게 만들 수 있습니다.함수가 완료되면 앤실라 큐비트는 계산되지 않거나 그대로 둘 수 있습니다.계산되지 않은 앙실라 큐비트의 양자 상태를 측정하거나 붕괴시키면(예: 그 값을 다시 초기화하거나 자발적인 비간섭에 의해) 오류가 발생할 수 있습니다.^[40][41] 그 상태가 여전히 계산에 사용되고 있는 큐비트와 얽힐 수 있기 때문입니다.

논리적으로 되돌릴 수 없는 연산, 예를 들어 두 $n$의$${\$displaystyle n}$ - 큐비트 레지스터 a 및 b, $F{\displaystyle (a,}$ ${\displaystyle b)}$=${\displaystyle a}$ + b${\displaystyle (\mathrm{mod}}$ 2 ${\displaystyle n^{}}$)$${\$displaystyle$ F$(a,$b) = a + $b{\pmod${$2^{n$의 추가 모듈 ${\displaystyle 2^{}}$ n$${\$displaystyle$ F(a,b) = a + b{\pmod {2^{n}}를 출력에 추가하여 논리적으로 되돌릴 수 있도록 할 수 있습니다.${\displaystyle {\mathrm{함수}}^{}}$ $F{\displaystyle {}^{}}$- 1 ${\$ F$^{-1$}})$$이 있습니다.이 예제에서는 $입력$ 레지스터 중 하나를 출력으로 전달하여 수행할 수 있습니다. F ( ⟩ ⊗ ${\displaystyle b}$ ⟩ )${\displaystyle }$= ${\displaystyle a}$+ b${\displaystyle }$(${\displaystyle mod}$ 2 ${\displaystyle n^{}}$ )${\displaystyle {}^{}}$⟩ ⟩ ⊗ ${\displaystyle F($a\$rangle \otimes b\rangle$ ) = $a$+ b ${\pmod$ {$2^{n}}\rangle \otimes$ a$\rangle }. 그런$ 다음$$출력을 사용하여 입력을 계산할 수 있습니다(즉, 출력 $a{\displaystyle }$+ ${\displaystyle b}$ ${\$$displaystyle a+b}$ 및 {\$displaystyle$ a$}$이 $주어짐$).,$$$입력$을 쉽게 찾을 수 있습니다. ${\displaystyle a}$ 가 주어지고$$(${\displaystyle a}$+ ${\displaystyle b}$) -${\displaystyle }$a $=$ ${\displaystyle b}$ ${\displaystyle (a$+ $b)$ - a = b$$)$$가 주어지며 함수는 객관적으로 됩니다.

예를 들어, Pauli-X, CNOT 및 Toffoli 게이트의 조합을 사용하여 모든 부울 대수식을 유니터리 변환(양자 논리 게이트)으로 인코딩할 수 있습니다.이러한 게이트는 부울 논리 도메인에서 기능적으로 완전합니다.

Q#, QCL, Qiskit 및 기타 양자 프로그래밍 언어의 라이브러리에는 많은 유니터리 변환이 있습니다.그것은 문헌에도 등장합니다.^[42][43]

예를 들어 ${\displaystyle \mathrm{in}}$ c (${\displaystyle x}$ ⟩${\displaystyle }$) = ${\displaystyle x}$+ ${\displaystyle 1}$(${\displaystyle \mathrm{mod}}$ 2 ${\displaystyle x^{}}$ ${\displaystyle {{\text{length}}_{}}^{}}$ )${\displaystyle {{}_{}}^{}}$⟩ ${\displaystyle \mathrm {inc}$( $x\rangle$ ) = x$+1{\pmod {2^{x_{\text{length}}}\rangle$여기서 x ${\displaystyle {\text{길이}}_{}}$ ${\$$displaystyle x_$${\text{length$$}}$는 레지스터$x$를 구성하는 큐비트 수이며$$QCL에서 다음과 같이 구현됩니다.

QCL에서 감소는 "하지 않음" 증가에 의해 이루어집니다.접두사를!대신 함수의 유니터리 인버스를 실행하는 데 사용됩니다.!inc(x)는 의 역입니다.inc(x)${\displaystyle {\mathrm{대신}}^{}}$ ${\displaystyle {\mathrm{c}}^{}}$ † ${\displaystyle x}$ ⟩ = ${\displaystyle {\mathrm{in}}^{}}$ c${\displaystyle {}^{}}$- 1${\displaystyle {}^{}}$( ${\displaystyle x}$ ⟩${\displaystyle }$) = ${\displaystyle \mathrm{x}}$ -${\displaystyle }$1${\displaystyle }$(${\displaystyle \mathrm{mod}}$ 2 ${\displaystyle x}$ ${\displaystyle {{\text{길이}}_{}}^{}}$ )${\displaystyle {{}_{}}^{}}$⟩ ${\displaystyle \mathrm {inc} ^{\$dagger } $x\rangle$ =\$mathrm {inc} ^{-1}( x\rangle$ ) = $x-1{\pmod {2^{x_{\text{length}}\rangle }$ . . . . . .$$.cond키워드는 함수가 조건부일 수 있음을 의미합니다.^[11]

본 논문에서 사용된 계산 모델(양자 회로 모델)에서, 고전적인 컴퓨터는 양자 컴퓨터를 위한 게이트 구성을 생성하고, 양자 컴퓨터는 고전적인 컴퓨터로부터 어떤 원시 게이트를 어떤 큐비트에 적용할지에 대한 명령을 수신하는 코프로세서로서 동작합니다.^{[13]: 36–43 [14]}양자 레지스터의 측정은 고전적인 컴퓨터가 계산에 사용할 수 있는 이진값을 산출합니다.양자 알고리즘은 종종 고전적인 부분과 양자적인 부분을 모두 포함합니다.측정되지 않은 I/O(양자 상태를 붕괴시키지 않고 큐비트를 원격 컴퓨터로 전송)는 양자 컴퓨터의 네트워크를 만드는 데 사용될 수 있습니다.얽힘 스와핑은 직접 연결되지 않은 양자 컴퓨터로 분산 알고리즘을 구현하는 데 사용될 수 있습니다.소수의 양자 논리 게이트만을 사용해야 하는 분산 알고리즘의 예로는 초밀도 부호화, 양자 비잔틴 협정, BB84 암호키 교환 프로토콜 등이 있습니다.

참고 항목

메모들

참고문헌

원천

• Nielsen, Michael A.; Chuang, Isaac (2000). Quantum Computation and Quantum Information. Cambridge: Cambridge University Press. ISBN 0521632358. OCLC 43641333.
• Colin P. Williams (2011). Explorations in Quantum Computing. Springer. ISBN 978-1-84628-887-6.
• Yanofsky, Noson S.; Mannucci, Mirco (2013). Quantum computing for computer scientists. Cambridge University Press. ISBN 978-0-521-87996-5.