프랭크-헤르츠 실험

Franck–
Photograph of a sealed glass cylinder. Wires penetrate the cylinder at its top, bottom, and side. Three wires lead to a cathode assembly; the top and side wires lead to a disk and a mesh that are close and parallel to each other. The wires are attached to feedthroughs on an aluminum panel in the background.
Frank호에 사용된 진공관 사진-교육 실험실에서의 헤르츠 실험. 사진에는 보이지 않지만 튜브 안에는 수은 방울이 있습니다. C - 음극 조립체; 음극 자체가 뜨겁고 주황색으로 빛납니다. 금속 메쉬 그리드(G)를 통과하는 전자를 방출하고 양극(A)에 의해 전류로 수집됩니다.
에 대한 일련의 기사의 일부
양자역학
슈뢰딩거 방정식
배경
펀더멘털
실험
제형
방정식
해석
고급주제
사이언티스트

프랑크-헤르츠 실험은 원자의 양자적 성질을 명확하게 보여준 최초의 전기 측정이었고, 따라서 "세계에 대한 우리의 이해를 변화시켰습니다.[1] 그것은 1914년 4월 24일에 James Frank와 Gustav Hertz의 논문으로 독일 물리학회에 발표되었습니다.[2][3] Frank와 Hertz는 수은 원자의 얇은 증기를 통해 날아오는 에너지 넘치는 전자를 연구하기 위한 진공관을 설계했습니다. 그들은 전자가 수은 원자와 충돌했을 때, 전자는 날아가기 전에 특정 양의 운동 에너지만 잃을 수 있다는 것을 발견했습니다.[4] 이 에너지 손실은 전자를 초당 약 130만 미터의 속도에서 0으로 감속시키는 것에 해당합니다.[5] 더 빠른 전자는 충돌 후에 완전히 감속하지 않고 정확히 같은 양의 운동 에너지를 잃습니다. 속도가 느린 전자는 큰 속도나 운동 에너지를 잃지 않고 수은 원자에서 튕겨나갈 뿐입니다.

이러한 실험 결과는 닐스 보어가 전년도에 제안했던 원자에 대한 보어 모델과 일치하는 것으로 증명되었습니다. 보어 모형은 양자역학과 원자의 전자껍질 모형의 전조였습니다. 그것의 핵심적인 특징은 원자 내부의 전자가 원자의 "양자 에너지 수준" 중 하나를 차지한다는 것이었습니다. 충돌 전에 수은 원자 내부의 전자는 가장 낮은 가용 에너지 수준을 차지합니다. 충돌 후 내부의 전자는 4.9 전자 볼트(eV) 더 많은 에너지로 더 높은 에너지 수준을 차지합니다. 이것은 전자가 수은 원자에 더 느슨하게 결합되어 있다는 것을 의미합니다. 보어의 양자 모델에는 중간 수준이나 가능성이 없었습니다. 이 특징은 전자가 어떤 에너지에 의해서도 원자핵에 속박될 수 있다는 기대와 일치하지 않기 때문에 "혁명적"이었습니다.[4][6]

1914년 5월에 발표된 두 번째 논문에서 Frank와 Hertz는 충돌에서 에너지를 흡수한 수은 원자에 의한 발광에 대해 보고했습니다.[7] 그들은 이 자외선의 파장이 비행하는 전자가 잃어버린 4.9 eV의 에너지와 정확히 일치한다는 것을 보여주었습니다. 에너지와 파장의 관계 역시 1911년 솔베이 대회에서 헨드릭 로렌츠가 제시한 구조를 따랐기 때문에 보어에 의해 예측되었습니다. 솔베이에서 헨드릭 로렌츠는 아인슈타인의 양자 구조에 대한 강연 후 회전자의 에너지를 nhv와 같게 설정할 것을 제안했습니다.[8][9] 그래서 보어는 1911년에 내린 지시를 따랐고 로렌츠 등이 제안한 공식을 1913년의 원자 모형에 복사했습니다.[10] 로런츠는 옳았습니다. 원자의 양자화는 보어 모델에 포함된 그의 공식과 일치했습니다.[4] 몇 년 후 프랑크가 이러한 결과를 발표한 후 알버트 아인슈타인은 "너무 사랑스러워서 눈물이 난다"고 말했다고 합니다.[1]

1926년 12월 10일, 프랭크와 헤르츠는 원자에 대한 전자의 영향을 지배하는 법칙을 발견한 공로로 1925년 노벨 물리학상을 수상했습니다.[11]

실험.

Graph. The vertical axis is labeled "current", and ranges from 0 to 300 in arbitrary units. The horizontal axis is labeled "voltage", and ranges from 0 to 15 volts. The curve is described in the article's text.
양극 전류(임의 단위) 대 그리드 전압(음극 대비). 이 그래프는 Frank and Hertz의 1914년 논문 원본에 기반을 두고 있습니다.[2]

Frank와 Hertz의 원래 실험은 수은 한 방울이 들어있는 가열된 진공관을 사용했습니다. 그들은 115°C의 튜브 온도를 보고했고, 수은의 증기압은 약 100파스칼 (그리고 대기압보다 훨씬 낮습니다.[2][12] 동시대의 프랑크-사진에는 헤르츠 튜브가 나와 있습니다. 전자 방출, 고온 음극, 금속 메쉬 그리드, 양극의 세 가지 전극이 장착되어 있습니다. 그리드의 전압은 음극에 대해 양의 값을 가지므로 뜨거운 음극에서 방출되는 전자가 음극으로 끌어당깁니다. 실험에서 측정된 전류는 그리드를 통과하여 양극에 도달하는 전자에 의한 것입니다. 양극의 전위는 그리드에 비해 약간 음이므로 양극에 도달한 전자는 그리드를 통과한 후 적어도 상응하는 양의 운동 에너지를 갖게 됩니다.[13]

수은 증기 방전과 프랭크에 의해 방출되는 빛의 파장-헤르츠 튜브는 10V에서 작동합니다. 프랑크-헤르츠 튜브는 주로 254 나노미터에 가까운 파장의 빛을 방출하며, 방전은 많은 파장의 빛을 방출합니다. 원래 1914년 그림을 기준으로.[7]

Frank와 Hertz가 발표한 그래프(그림 참조)는 양극에서 흘러나오는 전류가 그리드와 음극 사이의 전위에 미치는 의존성을 보여줍니다.

  • 전위차가 낮은 경우(최대 4.9V) 튜브를 통과하는 전류는 전위차가 증가함에 따라 꾸준히 증가합니다. 이러한 동작은 수은 증기를 포함하지 않는 진정한 진공관의 전형적인 것입니다. 전압이 클수록 "공간 전하 제한 전류"가 커집니다.
  • 4.9V에서는 전류가 급격히 감소하여 거의 0으로 돌아갑니다.
  • 그런 다음 전압이 더 증가하면 전류가 다시 한 번 꾸준히 증가하여 9.8V(정확히는 4.9+4.9V)에 도달합니다.
  • 9.8V에서도 유사한 급격한 하락이 관찰됩니다.
  • 그림의 원래 측정값에서는 분명하지 않지만, 이러한 약 4.9V 단위의 전류 감소는 최소 70V의 전위까지 계속됩니다.[14]

Frank와 Hertz는 그들의 첫 번째 논문에서 그들의 실험의 4.9 eV 특성 에너지가 가스 방전에서 수은 원자가 방출하는 빛의 파장 중 하나와 잘 일치한다고 언급했습니다. 그들은 들뜬 에너지와 그에 상응하는 빛의 파장 사이의 양자 관계를 사용하고 있었습니다. 그들은 일반적으로 요하네스 스타크와 아놀드 소머펠트에게 기인합니다. 그것은 4.9 eV가 254 nm 파장의 빛에 해당한다고 예측합니다.[2] 아인슈타인의 1905년 광전효과 광자 이론에도 같은 관계가 포함되어 있었습니다.[15] 두 번째 논문에서 Frank와 Hertz는 튜브에서 방출되는 광학 방출을 보고했고, 이는 단일 두드러진 파장 254 nm의 빛을 방출했습니다.[7] 오른쪽 그림은 프랑크의 스펙트럼을 보여줍니다.헤르츠 튜브; 방출되는 거의 모든 빛은 단일 파장을 가지고 있습니다. 참고로, 그림은 254 nm 이외의 여러 파장에서 빛을 방출하는 수은 가스 방출광에 대한 스펙트럼도 보여줍니다. 이 수치는 1914년 Frank와 Hertz가 발표한 원래의 스펙트럼을 기반으로 합니다. 프랭크 가족이..그들이 측정한 전압 주기와 거의 정확히 일치하는 단일 파장만을 방출하는 헤르츠 튜브는 매우 중요했습니다.[13]

원자와의 전자충돌 모델링

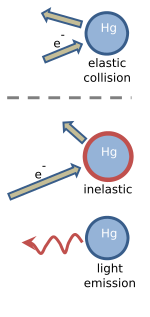
Drawing showing three circles, each with a label "Hg" inside. The top circle is labeled "elastic collision". It is next to two arrows of equal length, one pointing towards the circle, and one pointing away. The middle circle is labeled "inelastic collision", and has a longer arrow pointing towards it, and a shorter arrow leading away. The lowest circle is labeled "light emission", and is next to a squiggly arrow that points away.
전자와 수은 원자의 탄성 및 비탄성 충돌. 이동하는 전자는 탄성 충돌 후 천천히 방향을 바꾸지만 속도는 변하지 않습니다. 더 빠른 전자는 비탄성 충돌에서 속도의 대부분을 잃습니다. 잃어버린 운동 에너지는 수은 원자에 축적됩니다. 원자는 그 후에 빛을 내고, 원래의 상태로 돌아옵니다.

Frank와 Hertz는 그들의 실험을 전자와 수은 원자 사이의 탄성 충돌과 비탄성 충돌의 관점에서 설명했습니다.[2][3] 천천히 움직이는 전자는 수은 원자와 탄성적으로 충돌합니다. 이것은 전자가 움직이는 방향은 충돌에 의해 변경되지만 속도는 변하지 않는다는 것을 의미합니다. 그림에는 탄성 충돌이 나타나 있는데, 화살표의 길이는 전자의 속도를 나타냅니다. 수은 원자는 전자보다 약 40만 배나 더 무겁기 때문에 충돌의 영향을 받지 않습니다.[16][17]

전자의 속도가 초당 약 130만 미터를 넘으면 [5]수은 원자와의 충돌은 비탄성이 됩니다. 이 속도는 수은 원자에 축적되는 4.9eV의 운동 에너지에 해당합니다. 그림과 같이 전자의 속도가 감소하고 수은 원자는 "흥분" 상태가 됩니다. 잠시 후 수은 원자에 침착된 4.9eV의 에너지가 정확히 254nm 파장의 자외선으로 방출됩니다. 발광 후 수은 원자는 들뜬 상태가 아닌 원래의 상태로 돌아갑니다.[16][17]

음극에서 방출된 전자가 그리드에 도착할 때까지 자유롭게 날아간다면 그리드에 인가된 전압에 비례하는 운동 에너지를 얻게 될 것입니다. 1eV의 운동 에너지는 그리드와 음극 사이의 전위차 1V에 해당합니다.[18] 수은 원자와의 탄성 충돌은 전자가 격자에 도달하는 데 걸리는 시간을 증가시키지만, 전자가 격자에 도달하는 평균 운동 에너지는 그다지 영향을 받지 않습니다.[17]

그리드 전압이 4.9V에 도달하면 그리드 근처의 전자 충돌은 비탄성이 되어 전자가 크게 느려집니다. 전형적인 전자가 그리드에 도착하면 전자를 약간 밀어내는 전압을 가진 양극에 도달하기 위해 더 이상 이동할 수 없을 정도로 운동 에너지가 감소합니다. 그래프에서 볼 수 있듯이 양극에 도달하는 전자의 전류가 떨어집니다. 그리드 전압이 더 증가하면 비탄성 충돌을 겪은 전자가 다시 양극에 도달할 수 있는 충분한 에너지가 복원됩니다. 그리드 전위가 4.9V 이상으로 상승함에 따라 전류가 다시 상승합니다. 9.8V가 되면 상황이 또 바뀝니다. 음극에서 그리드까지 대략 절반 정도 이동한 전자는 이미 첫 번째 비탄성 충돌을 겪을 만큼 충분한 에너지를 얻었습니다. 중간 지점에서 격자 쪽으로 천천히 진행하면서 운동 에너지가 다시 쌓이지만, 격자에 도달하면 두 번째 비탄력적인 충돌을 겪을 수 있습니다. 다시 한 번 양극에 대한 전류가 떨어집니다. 이 과정은 4.9V 간격으로 반복되며, 전자는 매번 추가적인 비탄성 충돌을 겪습니다.[16][17]

초기 양자론

The drawing has a wide rectangle at the top labeled "vacuum levels". Underneath the rectangle and to the left is a vertical arrow that ends at the rectangle; the arrow is labeled "electron binding energy". In the middle is a long series of finely separated lines that are parallel to the bottom of the rectangle; these are labeled "classical energy levels". To the right is a series of four well-separated parallel lines; these are labeled "quantum energy levels".
원자의 보어 모형은 전자가 양자 에너지 준위에 해당하는 일련의 특정 에너지 중 하나만으로 원자핵에 결합될 수 있다고 가정했습니다. 이전에는 입자의 결합에 대한 고전적인 모델이 모든 결합 에너지를 허용했습니다.

1914년 Frank와 Hertz가 그들의 실험을 발표했을 때는 그것을 알지 못했지만,[19] 1913년 Niels Bohr는 원자 수소의 광학적 특성을 설명하는 데 매우 성공적인 원자 모델을 발표했습니다. 이것들은 일반적으로 일련의 파장에서 빛을 방출하는 가스 방전에서 관찰되었습니다. 백열전구와 같은 일반 광원은 모든 파장에서 빛을 방출합니다. 보어는 수소가 방출하는 파장을 매우 정확하게 계산했습니다.[20]

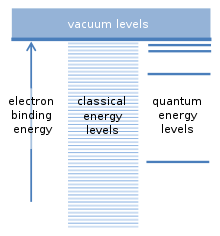
보어 모델의 기본 가정은 원자핵에 대한 전자의 가능한 결합 에너지에 관한 것입니다. 다른 입자와의 충돌이 적어도 이 결합 에너지를 공급한다면 원자는 이온화될 수 있습니다. 이것은 전자를 원자로부터 자유롭게 하고 양전하를 띤 이온을 남깁니다. 지구 주위를 도는 위성과 비유가 있습니다. 모든 위성은 고유의 궤도를 가지고 있으며, 실질적으로 어떤 궤도 거리와 어떤 위성 결합 에너지도 가능합니다. 전자는 비슷한 힘에 의해 원자핵의 양전하에 끌리기 때문에 이른바 "고전적" 계산은 전자에 대해서도 어떤 결합 에너지도 가능해야 함을 시사합니다. 그러나 보어는 전자에 대한 "양자 에너지 수준"에 해당하는 특정한 일련의 결합 에너지만 발생한다고 가정했습니다. 전자는 일반적으로 가장 낮은 에너지 준위에서 발견되며 가장 큰 결합 에너지를 가지고 있습니다. 추가 레벨은 더 높고 결합 에너지는 더 작습니다. 이러한 레벨 사이에 있는 중간 결합 에너지는 허용되지 않습니다. 이것은 혁명적인 가정이었습니다.[6]

Frank와 Hertz는 그들의 실험의 4.9 V 특성이 음극에서 방출되는 날아다니는 전자와의 충돌에 의한 수은 원자의 이온화 때문이라고 제안했습니다. 1915년 보어는 프랑크와 헤르츠의 측정이 원자에 대한 자신의 모델에서 양자 수준의 가정과 더 일치한다고 언급한 논문을 발표했습니다.[21] 보어 모형에서 충돌은 원자 내부의 내부 전자를 가장 낮은 단계에서 그 위의 첫 번째 양자 단계로 들뜨게 했습니다. 또한 보어 모형은 내부 전자가 들뜬 양자 수준에서 가장 낮은 수준으로 되돌아오면서 빛이 방출될 것이라고 예측했는데, 그 파장은 원자 내부 수준의 에너지 차이에 해당하며, 이를 보어 관계라고 부릅니다.[4] 254 nm에서 Frank와 Hertz의 관에서 방출되는 것을 관찰한 것도 Bohr의 관점과 일치했습니다. 1918년 제1차 세계 대전이 끝난 후, Frank와 Hertz는 양자역학의 실험적인 기둥들 중 하나가 된 그들의 실험을 해석하기 위해 대체로 Bohr 관점을 채택했습니다.[1][3] 에이브러햄 파이스가 묘사한 바와 같이, "이제 프랑크와 헤르츠의 업적의 아름다움은 충돌하는 전자의 에너지 손실 E-E의 측정에 있을 뿐만 아니라, 그 전자의 에너지가 4.9eV를 초과하면 수은이 위의 공식에서 정의된 일정한 주파수 ν의 자외선을 방출하기 시작한다는 것도 관찰했습니다. 이로써 그들은 (처음에는 저도 모르게) 보어 관계에 대한 최초의 직접적인 실험적 증거를 내놓았습니다!"[4] Frank 자신은 Frank에 관한 1960년 물리과학연구위원회(PSSC) 영화 에필로그에서 자외선 방출 실험의 중요성을 강조했습니다.헤르츠 실험.[19]

네온을 이용한 실험

네온 가스를 이용한 Frank-Herz 실험: 3개의 빛나는 영역

교육 실험실에서, Frank-헤르츠 실험은 종종 네온 가스를 사용하여 수행되는데, 네온 가스는 진공관에서 눈에 보이는 주황색 빛과 비탄성 충돌의 시작을 보여주며, 튜브가 깨질 경우 무독성입니다. 수은관의 경우 탄성 및 비탄성 충돌 모델은 수은이 빛을 내는 양극과 격자 사이에 좁은 띠가 있어야 하지만 빛은 자외선으로 보이지 않는다고 예측합니다. 네온과 함께, 프랑크-헤르츠 전압 간격은 18.7V이며, 18.7V가 인가되면 그리드 근처에 주황색 광채가 나타납니다. 이 광채는 가속 전위가 증가함에 따라 음극에 가까워지며, 네온 원자를 여기시키는 데 필요한 18.7 eV를 전자가 획득한 위치를 나타냅니다. 37.4V에서는 음극과 그리드 사이의 중간에 하나, 가속 그리드의 오른쪽에 하나, 두 개의 뚜렷한 빛이 보입니다. 전위가 높을수록 18.7V 간격으로 이격되어 튜브 내에 추가적인 발광 영역이 발생합니다.

교육 실험실용 네온의 또 다른 장점은 튜브를 실온에서 사용할 수 있다는 것입니다. 그러나 가시광선 방출의 파장은 보어 관계와 18.7 V 간격에 의해 예측된 것보다 훨씬 더 깁니다. 오렌지 빛에 대한 부분적인 설명은 최저 수준보다 16.6 eV와 18.7 eV가 높은 두 원자 수준을 포함합니다. 18.7 eV 수준까지 들뜬 전자는 오렌지 빛을 동반하면서 16.6 eV 수준까지 떨어집니다.[22]

참고문헌

  1. ^ a b c Rice, Stuart A.; Jortner, Joshua (2010). "James Franck 1882-1964: A Biographical Memoir" (PDF). National Academy of Sciences (US). p. 6. Our understanding of the world was transformed by the results of this experiment; it is arguably one of the most important foundations of the experimental verification of the quantum nature of matter.
  2. ^ a b c d e Franck, J.; Hertz, G. (1914). "Über Zusammenstöße zwischen Elektronen und Molekülen des Quecksilberdampfes und die Ionisierungsspannung desselben" [On the collisions between electrons and molecules of mercury vapor and the ionization potential of the same] (PDF). Verhandlungen der Deutschen Physikalischen Gesellschaft (in German). 16: 457–467. 이 논문의 번역은 초기 논문에서 Frank와 Hertz는 비탄성 전자-수은 충돌과 관련된 4.9 V 전위를 수은의 이온화 전위를 나타내는 것으로 해석했습니다. 원자의 보어 모델과의 관계는 다소 나중에 나타났습니다.
  3. ^ a b c Lemmerich, Jost (2011). Science and Conscience: The Life of James Franck. Translated by Ann Hentschel. Stanford University Press. pp. 45–50. ISBN 9780804779098. Then two papers by Franck and Hertz about measurements on vaporized mercury that were to enter their names on the rolls of the history of physics appeared in quick succession. The first paper was presented by Gustav Hertz at the German Physical Society's meeting on 24 April 1914, the second by James Franck on May 22. (p. 45) 의 번역
  4. ^ a b c d e 주파수 ν는 공식 ν = c/λ에 의한 빛의 파장 λ와 관련이 있으며, 여기서 초당 c=2.99×10미터는 진공에서의 빛의 속도입니다.
  5. ^ a b 전자 볼트를 전자 속도로 변환하는 방법은
  6. ^ a b Cohen, I. Bernard (1985). Revolution in Science. Belknap Press. pp. 427–428. ISBN 9780674767775. In 1912 a young Dane working in Rutherford's laboratory in Manchester proposed a revolutionary new model of the atom. ... What made Bohr's theory difficult to believe in was the idea of discrete and fixed states or orbits, with no intermediate states being possible.
  7. ^ a b c Franck, J.; Hertz, G. (1914). "Über die Erregung der Quecksilberresonanzlinie 253,6 μμ durch Elektronenstöße" [On the excitation of mercury resonance lines at 253.6 nm by electron collisions]. Verhandlungen der Deutschen Physikalischen Gesellschaft (in German). 16: 512–517. μμ라는 기호는 나노미터에 대한 구식의 희귀한 사용법입니다. 이 기사는 다음에서 재인쇄되었습니다.
  8. ^ 1912년 출판된 1911년 솔베이 회의의 원본 절차. 테오리에 뒤 라요네먼트 에틀 레 콴타. 라포츠 등의 토론들 Dela Réunion tenue à Bruxelles, du 30 octobreau 3 november, Sousles Austhost dk M. E. Solvay. Publiés par MM. P. LANGEVIN et M. de Broglie. 프랑스어 번역, p.447.
  9. ^ 헤이브론, 존 L., 토마스 S. 쿤. '보어 원자의 창세기' 물리학의 역사 연구, vol. 1, 캘리포니아 대학 출판부, 1969, pp. vi-290, pp. 244 https://doi.org/10.2307/27757291
  10. ^ 보어 모형 참조
  11. ^ Oseen, C. W. (December 10, 1926). "Nobel Prize in Physics 1925 - Presentation Speech". The Nobel Foundation.
  12. ^ Huber, Marcia L.; Laesecke, Arno; Friend, Daniel G. (April 2006). "The vapor pressure of mercury" (PDF). National Institute of Standards. p. 5. NISTIR 6643.
  13. ^ a b Brandt, Siegmund (2008). "25. The Franck Hertz experiment (1914)". The harvest of a century : discoveries of modern physics in 100 episodes. Oxford University Press. p. 272. ISBN 9780191580123.
  14. ^ Thornton, Stephen; Rex, Andrew (2012). Modern Physics for Scientists and Engineers (4 ed.). Cengage Learning. pp. 154–156. ISBN 9781133103721.
  15. ^ 광자의 에너지 E는 플랑크 상수 h와 빛의 속도 c와 파장 λ의 비 c/λ의 곱입니다.
  16. ^ a b c Melissinos, Adrian Constantin; Napolitano, Jim (2003). "1.3 The Franck–Hertz Experiment". Experiments in Modern Physics. Gulf Professional Publishing. pp. 10–19. ISBN 9780124898516. 이 언급은 Frank와 Hertz가 그들의 실험을 발표했을 때 Bohr 모델을 알고 있었다는 것을 잘못 암시합니다. Frank 자신은 그의 인생 후반에 인터뷰에서 이것에 대해 말했습니다.
  17. ^ a b c d Demtröder, Wolfgang (2010). "3.4.4 Franck–Hertz experiment". Atoms, Molecules and Photons: An Introduction to Atomic-, Molecular- and Quantum Physics. Springer. pp. 118–120. ISBN 9783642102981.
  18. ^ 그들의 원래 실험에서 Frank와 Hertz는 음극과 격자 모두에 백금을 사용했습니다. 다른 물질이 전극에 사용될 때, 외부에서 인가된 전압 이상의 운동 에너지에 추가적인 기여가 있습니다. 참조
  19. ^ a b 1960년, Frank는 그들의 두 1914년 논문이 발표되었을 때, 그와 Hertz는 Bohr의 생각을 알지 못했다고 설명했습니다. Frank는 Frank에 대한 영화의 에필로그로서 자신의 발언을 했습니다.물리학 연구 위원회(1960)의 헤르츠 실험. 영화는 온라인에서 볼 수 있습니다. 참고하세요. 영화가 만들어진 직후 에필로그의 녹취록이 출판되었습니다. 참고하세요.
  20. ^ Heilbron, John L. (1985). "Bohr's First Theories of the Atom". In French, A. P.; Kennedy, P. J. (eds.). Niels Bohr: A Centenary Volume. Cambridge, Massachusetts: Harvard University Press. pp. 33–49. ISBN 9780674624160. OCLC 12051112.
  21. ^ Kragh, Helge (2012). Niels Bohr and the Quantum Atom: The Bohr Model of Atomic Structure 1913-1925. Oxford University Press. p. 144. ISBN 9780191630460. 크라그는 1914년 프랑크와 헤르츠의 논문에 대해 논의한 보어의 1915년 논문 중 한 문장을 인용합니다. "그들의 실험은 이 전압(4.9 V)이 정상 상태에서 중성 원자의 어떤 다른 정지 상태로의 전이에만 해당한다는 가정과 일치할 수 있습니다."
  22. ^ Csele, Mark (2011). "2.6 The Franck–Hertz Experiment". Fundamentals of Light Sources and Lasers. John Wiley & Sons. pp. 31–36. ISBN 9780471675228.

더보기

외부 링크