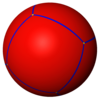
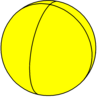
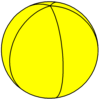
정다면체
Regular polyhedron일반 다면체(多面體)는 다면체로서, 대칭 집단이 깃발에서 전이적으로 작용한다. 일반 다면체는 매우 대칭적이며, 모두 가장자리-변환, 정점-변환, 얼굴-변환이다. 고전적인 맥락에서, 많은 다른 동등한 정의들이 사용된다; 공통적인 것은 얼굴들이 각 꼭지점을 중심으로 같은 방식으로 조립된 합치된 규칙적인 다각형이라는 것이다.
정규 다면체는 형태 {n, m}의 Schléfli 기호로 식별된다. 여기서 n은 각 면의 측면 수이고 m은 각 정점에서 만나는 면의 수입니다. 5개의 유한 볼록 정규 다면체(Platonic solidra)와 4개의 일반 별 다면체(Kepler-Poinsot polyedra)가 있어 모두 9개의 일반 다면체를 만든다. 또 일반 다면체에는 5개의 정규 화합물이 있다.
정다면체
플라토닉 고체로 알려진 5개의 볼록 정규 다면체, 4개의 일반 별 다면체, 케플러-푸인소트 다면체, 5개의 일반 다면체 화합물이 있다.
플라톤 고형
케플러-푸인소트 다면체
 |  |  |  |
| 소절개도면체 {5/2, 5} | 대두면체 {5, 5/2} | 그레이트 스틸 도데카헤드론 {5/2, 3} | 대이코사면체 {3, 5/2} |
| χ = −6 | χ = −6 | χ = 2 | χ = 2 |
정규 화합물
특성.
등가 속성
각 꼭지점 주위에 유사한 면배열을 갖는 특성은 정의에서 다음과 같은 동등한 조건으로 대체될 수 있다.
- 볼록한 일반 다면체의 정점은 모두 구 위에 놓여 있다.
- 다면체의 모든 이면각은 동일하다.
- 다면체의 모든 꼭지점 형상은 규칙적인 다각형이다.
- 다면체의 모든 고체 각도는 응집력이 있다.[1]
동심구
볼록한 일반 다면체는 그 중심을 공유하는 세 개의 관련 구체(다른 다면체는 적어도 한 가지 종류가 없음)를 모두 가지고 있다.
대칭
일반 다면체(多面體)는 모든 다면체(多面體) 중에서 가장 대칭적이다. 그들은 플라토닉 고형물의 이름을 따서 명명된 단 세 개의 대칭 그룹에 있다.
- 사면체
- 팔면체(또는 입방체)
- 이코사헤드랄(또는 도데카헤드랄)
이두면체 또는 팔면체 대칭이 있는 모든 모양은 사면체 대칭도 포함할 것이다.
오일러 특성
5개의 플라토닉 고형물은 오일러 특성이 2이다. 이는 단순히 표면이 위상학적 2-sphere라는 것을 반영하고 있으며, 예를 들어, 일부 내부 지점과 관련하여 별 모양인 모든 다면체의 경우도 마찬가지다.
인테리어 포인트
일반 다면체 내부의 어느 지점에서 옆면까지의 거리의 합은 점의 위치와 무관하다(이것은 비비아니 정리의 연장이다). 그러나, 4면체도 아닌, 그 반전은 유지되지 않는다.[2]
일반 다면체의 이중성
이중 쌍의 다면체에서 한 다면체의 정점은 다른 다면체의 얼굴에 대응하며, 그 반대의 경우도 마찬가지다.
일반 다면체는 이러한 이중성을 다음과 같이 보여준다.
- 사면체는 자기 이중이다. 즉, 자기와 짝을 이룬다.
- 정육면체와 팔면체는 서로 이중이다.
- 이코사면체와 도데카면체는 서로 이중이다.
- 이 작은 도마뱀과 큰 도마뱀은 서로 이중적이다.
- 큰 도마뱀붙이와 큰 고드름은 서로 이중이다.
이중의 Schléfli 기호는 거꾸로 쓰여진 원본일 뿐이다. 예를 들어, {5, 3}의 이중은 {3, 5}이다.
역사
선사시대
구 또는 손잡이의 군집을 닮은 모양으로 조각된 돌들은 스코틀랜드에서 발견되었으며, 4,000년 정도 되었을지도 모른다. 이 돌들 중 일부는 5개의 플라토닉 고형물의 대칭뿐만 아니라 그들 사이의 이중성의 관계도 일부 보여준다(즉, 입방체 면의 중심이 8면체의 정점을 준다는 것이다). 이 돌들의 예는 옥스퍼드 대학교의 애쉬몰린 박물관의 존 에반스 방에 전시되어 있다. 왜 이런 물건들이 만들어졌는지, 혹은 그들의 창조자들이 어떻게 그들에게 영감을 얻었는지는 미스터리다. 이들 물체의 수학적 해석에 대해서는 의심의 여지가 있는데, 이는 많은 이들이 비원형 형태를 가지고 있고, 아마도 오직 한 가지만이 이도사면체인 이도사면체의 재해석과는 반대로 진정한 이도사면체라고 밝혀졌기 때문일 것이다.[3]
또한 19세기 후반에 파두아(북이탈리아) 근처에서 비석으로 만들어진 도데카테론이 발견되었고, 2500년 이상을 거슬러 올라가는 것에서 증명되었듯이, 에트루리아인들이 적어도 일반 다면체의 일부에 대한 인식에서 그리스인들보다 앞서갔을 가능성도 있다(린데만, 1987).
그리스인
일반 볼록 고형물에 대한 가장 일찍 알려진 서면 기록은 고대 그리스에서 유래되었다. 이러한 고형물이 모두 발견되어 누구에 의해서도 알려지지 않았지만, 테아에테투스(아테니아인)가 가장 먼저 다섯 가지 모두에 대한 수학적 묘사를 했다(Van der Waerden, 1954년), (유클리드, 책 XII). H.S.M. Coxeter (Coxeter, 1948, Section 1.9) credits Plato (400 BC) with having made models of them, and mentions that one of the earlier Pythagoreans, Timaeus of Locri, used all five in a correspondence between the polyhedra and the nature of the universe as it was then perceived – this correspondence is recorded in Plato's dialogue Timaeus. 유클리드가 플라톤에 대해 언급한 것은 플라토닉 고형물이라는 그들의 공통적인 서술로 이어졌다.
그리스어의 정의를 다음과 같이 특징지을 수 있다.
- 일반 다각형은 모든 모서리가 같고 모든 모서리가 동일한 (콘벡스) 평면도형이다.
- 일반 다면체는 단단한 (콘벡스) 형상으로, 모든 얼굴이 합치된 일반 다면이며, 동일한 숫자가 각 꼭지점 주위에 모두 똑같이 배열되어 있다.
예를 들어, 이 정의는 정사각형 피라미드(모든 얼굴이 규칙적이긴 하지만, 정사각형 밑부분이 삼각형에 합치되지 않기 때문에), 또는 두 개의 정사각형을 함께 결합하여 형성된 형태를 배제한다(그 삼각형 비피라미드의 모든 면은 정삼각형, 즉 정삼각형, 즉 정삼각형, 정삼각형, 어떤 정점 h.ave 3 삼각형 그리고 다른 것들은 4를 가지고 있다.
일반 다면체의 이 개념은 거의 2000년 동안 문제없이 남아 있을 것이다.
항성 다면체
펜타그램(별의 오각형)과 같은 일반 별 폴리곤은 고대 그리스인들에게도 알려져 있었다. 이 펜타그램은 피타고라스에 의해 비밀 부호로 사용되었지만, 그들은 그것들을 폴리헤드라를 건설하는데 사용하지 않았다. 요하네스 케플러는 17세기 초가 되어서야 펜타그램이 일반 별 다면체의 얼굴로 사용될 수 있다는 것을 깨달았다. 이러한 항성 다면체 중 일부는 케플러 시대 이전의 다른 사람들에 의해 발견되었을지 모르지만, 케플러는 정규 다면체를 볼록하게 한다는 제한을 없앤다면 '정규'로 간주될 수 있다는 것을 가장 먼저 인식했다. 200년 후 루이 푸인소트는 또한 별 정점(각 모서리의 원형)을 허용하여 케플러의 별을 재발견하는 것과 함께 두 개의 새로운 일반 별 다면체를 발견할 수 있었다. 이 네 개는 유일한 일반 항성 다면체로서 케플러-푸인소 다면체로 알려지게 되었다. 포인소트가 출판된 지 수십 년이 지난 19세기 중반이 되어서야 케일리는 그들에게 (케플러의) 작은 도데카헤드론과 큰 도데카헤드론, 그리고 (푸인소트의) 큰 이도면체와 위대한 도데카헤드론이라는 현대식 영어 이름을 지어주었다.
케플러-푸인소트 다면체는 스텔레이션이라고 불리는 공정에 의해 플라토닉 고형물로 구성될 수 있다. 스텔링에 대한 역수 과정을 팩션(또는 팩팅)이라고 한다. 한 다면체의 모든 장식은 이중 다면체의 어떤 면에 대해 이중 또는 상호적이다. 일반 항성 다면체도 플라토닉 고형물을 페이싱하여 얻을 수 있다. 이것은 케일리가 그들에게 이름을 지어준 것과 비슷한 시기에 베르트랑에 의해 처음 행해졌다.
따라서 19세기 말까지 9개의 다면체 – 5개의 볼록과 4개의 별 – 이 있었다.
자연에서 규칙적인 다면체
플라토닉 고형물은 각각 어떤 형태로든 자연적으로 발생한다.
사면체, 정육면체, 팔면체는 모두 결정체로 일어난다. 이것들은 결코 가능한 형태의 결정의 수를 다 써버리지 않으며(Smith, 1982, p212), 그 중 48개가 있다. 일반 이두면체도 일반 도두면체도 그 가운데 있지 않지만, 결정체는 피리토면체의 형태를 가질 수 있는데, 이것은 일반 도두면체와 거의 구별할 수 없다. 진정한 이코사이드 결정체는 자연에서 매우 희귀하지만 실험실에서 생산될 수 있는 퀘이시크리스탈린 물질에 의해 형성될 수 있다.
보다 최근의 발견은 풀렌으로 알려진 일련의 새로운 형태의 탄소 분자에 대한 것이다. (Curl, 1991년 참조) 가장 쉽게 생산되는 풀러렌인 C는60 다소 구형으로 보이지만, 더 큰 품종들(C240480, C, C960 등)의 일부는 가로 몇 나노미터인 약간 둥근 이코사헤드라의 형태를 취하도록 가정되어 있다.

다면체도 생물학에서 나타난다. 20세기 초 에른스트 해켈은 여러 종의 라디올라리아 종을 묘사했는데, 그 중 몇몇 종은 다양한 일반 다면체(多面體) 모양을 하고 있다(Haeckel, 1904년). 예를 들어, Circoporus 옥타헤드루스, Cirogonia icosaheadra, Ritocubus 기하학, Circorrhegma dodecheedra가 있다; 이 생물들의 모양은 그들의 이름으로 표시된다. 많은 바이러스의 외부 단백질 껍질은 규칙적인 다면체를 형성한다. 예를 들어, HIV는 정기적인 동면체로 둘러싸여 있다.
고대 피타고라스는 일반적인 다면체와 행성의 궤도 사이에 조화가 있다고 믿었다. 17세기에 요하네스 케플러는 타이코 브라헤가 편찬한 행성 운동에 관한 데이터를 연구했고 10년 동안 다면체의 크기와 행성의 궤도의 크기 사이의 일치점을 찾아 피타고라스적 이상을 확립하려고 노력했다. 그의 검색은 원래 목적에서 실패했지만, 이 연구로부터 케플러의 케플러 고형물을 일반 폴리토페스로서 발견한 것, 행성의 궤도가 원이 아니라는 사실, 그리고 현재 그가 유명한 행성운동의 법칙이 나왔다. 케플러 시대에는 플라토닉 고형물의 수와 잘 어울리는 5개의 행성(지구 제외)만이 알려져 있었다. 케플러의 연구, 그리고 천왕성과 해왕성의 그 시기 이후 발견된 발견은 피타고라스 사상을 무효로 만들었다.
피타고라스와 비슷한 시기에 플라톤은 다섯 가지 원소(지구, 공기, 불, 물, 정신)가 각각 다섯 가지 일반 고형물 중 한 가지를 아주 작게 복사한 물질 이론을 묘사했다. 물질은 이러한 다면체의 혼합물로부터 만들어졌으며, 각 물질은 혼합물에서 서로 다른 비율을 가지고 있다. 2천년이 지난 뒤 달튼의 원자론은 비록 일반 고형물과 직접 관련이 없기는 하지만 이 사상이 올바른 선상에 있다는 것을 보여줄 것이다.
추가 일반화
20세기에는 일반 다면체 사상의 일반화가 잇따르면서 몇 가지 새로운 계급이 생겨났다.
일반꼬치아페이로헤드라
처음 수십 년 동안, 콕시터와 페트리는 능선과 계곡이 교차하는 정점을 "새들"로 허용하여, 그들이 일반 스큐 폴리헤드라라고 부르는 세 개의 무한 접힌 표면을 만들 수 있었다.[4] Coxeter는 이러한 수치들에 대해 수정된 Schléfli 기호 {l,m n}을(를) 제공했으며, 정점 수치를 의미하는 {l,m}이(가) 정점 주위에 m 일반 l-곤을 표시했다. n은 n-곤 구멍을 정의한다. 그들의 꼭지점 수치는 두 평면 사이에서 지그재그로 지그재그하는 정점인 일반적인 꼬치 다각형이다.
일반 꼬치 다면체
4공간에 유한한 일반 스큐 다면체가 존재한다. 4공간의 유한한 일반적 스큐 폴리헤드라는 균일한 4폴리토프의 얼굴 부분집합으로 볼 수 있다. 그들은 평면적인 일반 다각형 면들을 가지고 있지만, 규칙적인 스큐 다각형 꼭지점을 가지고 있다.
2개의 이중 솔루션이 5-셀과 관련되며, 2개의 이중 솔루션이 24-셀과 관련되며, 무한의 자가 이중 듀오프라임은 {4, 4n}로서 정규 스큐 폴리헤드라를 생성한다. 무한한 한계에서 이것들은 두실린더에 접근하여 3-공간으로의 입체 투영에서 토러스처럼 보인다.
비유클리드 및 기타 공간에 있는 정규 다면체
비유클리드(hyperbolic, 타원형)와 전세기에 걸쳐 발견된 복합 공간과 같은 다른 공간들에 대한 연구는 그 공간들에서 규칙적인 기하학적 형태만 취할 수 있는 복잡한 다면체와 같은 보다 새로운 다면체를 발견하게 했다.
쌍곡선 공간의 정규 다면체
H3 쌍곡선 공간에서 파라콤팩트 일반 꿀콤은 유한 다면체처럼 작용하는 유클리드 타일링 면과 꼭지점 형상을 가지고 있다. 이러한 틸팅은 어느 쪽으로든 굽혀도 닫힐 수 있는 각도 결함을 가지고 있다. 타일링이 적절하게 조정되면 단일 이상 지점에서 점근 한계로 닫힌다. 이러한 유클리드 기울기는 다면체(polyhedra)가 구체(이상점 0점 포함)에 새겨진 것과 마찬가지로 호르스피어에 새겨져 있다. 헵탄 타일링 벌집 {7,3,3}에서처럼 쌍곡선 기울기가 비컴팩트 쌍곡 테셀레이션의 면으로 사용될 때 시퀀스가 확장되며, 이는 두 개의 이상적인 점을 갖는 등거리 표면(2-하이퍼사이클)에 새겨져 있다.
실제 투영 평면의 정기 기울기
일반 다면체의 또 다른 그룹은 실제 투영면의 기울기를 구성한다. 여기에는 헤미-큐브, 헤미-옥타헤드론, 헤미-도-케드론, 헤미-icosahedron이 포함된다. 그것들은 (광택적으로) 투사성 다면체이며 플라토닉 고형물의 투사성 상대물이다. 4면체에는 다른 4개의 플라토닉 고형물처럼 식별할 수 있는 평행면 쌍이 없기 때문에 투영 상대성이 없다.
이것들은 원래의 플라토닉 고형물이 하는 것과 같은 방식으로 이중 쌍으로 발생한다. 그들의 오일러 특성은 모두 1이다.
추상정규다면체
지금쯤, 폴리헤드라는 어떤 차원에서도 보다 일반적인 폴리토페스의 3차원적인 예로 확실히 이해되었다. 세기의 후반부는 폴리헤드랄 콤비네이터(Polyhedral combinatorics)와 같은 추상 대수적 사상의 발달이 부분적으로 순서화된 원소 집합체(poset)로서 추상적 폴리토프 사상의 정점을 찍었다. 추상적인 다면체의 원소는 그 몸체(최대 원소), 그 얼굴, 가장자리, 정점, 그리고 null polytope 또는 빈 집합이다. 이 추상적인 요소들은 평범한 공간에 매핑되거나 기하학적 숫자로 실현될 수 있다. 어떤 추상적인 다면체들은 잘 형성되어 있거나 충실한 깨달음을 가지고 있지만, 다른 것들은 그렇지 않다. 국기는 신체, 얼굴, 얼굴의 가장자리, 가장자리의 꼭지점, 그리고 무효 폴리토프인 다면체에 대해 각 차원의 연결된 원소의 집합이다. 추상적인 폴리토프는 그것의 결합 대칭이 깃발에 전이되는 경우 즉, 모든 깃발은 다면체의 대칭 아래에 다른 깃발에 매핑될 수 있는 경우 규칙적이라고 한다. 추상적인 일반 폴리토페스는 여전히 연구 활동 영역으로 남아 있다.
충실하게 실현될 수 없는 그런 규칙적인 추상적인 다면체 5개는 그의 저서 <레귤러 폴리토페스>(1977년)에서 H. S. M. Coxeter에 의해, 그리고 J. M. Wills는 <인덱스 2의 결합적으로 정규 다면체라>(1987년)에서 다시 확인되었다. 5개의 대칭은2 모두 C×S5 대칭이지만 대칭의 절반인 C2×A5 또는 이두 대칭만으로 실현될 수 있다.[5][6][7] 그것들은 모두 토로이드와 토폴로이드와 동등하다. 각각의 꼭지점 주위에 n개의 면들을 배열함으로써 그들의 구조는 쌍곡면의 기울기로 무한정 반복될 수 있다. 아래 다이어그램에서 쌍곡선 타일링 이미지는 다면체의 이미지와 일치하는 색상을 가진다.
다면체 
중합성삼정면체
도데카데카헤드론
중삼면체
직교 도데코데카헤드론
발굴된 도데면체유형 이중 {5,4}6 {5,4}6 {5,6}4의 이중 {5,6}4 {6,6}6 (v,e,f) (24,60,30) (30,60,24) (24,60,20) (20,60,24) (20,60,20) 정점수 {5}, {5/2} 

(5.5/2)2 
{5}, {5/2} 

(5.5/3)3 

얼굴 30롬비 
펜타곤 12개
5행 12문자

육각형 20개 
펜타곤 12개
5행 12문자

육각 20자 
타일링 
{4, 5}
{5, 4}
{6, 5}
{5, 6}
{6, 6}χ −6 −6 −16 −16 −20
페트리 듀얼
일반 다면체의 페트리 듀얼은 정점과 가장자리가 원래의 다면체의 정점과 가장자리에 해당하며, 얼굴은 꼬치 페트리 폴리곤의 세트인 일반 지도다.[8]
| 이름 | 페트리얼 사면체 | 페트리얼 큐브 | 페트리얼 옥타헤드론 | 페트리얼 도데카헤드론 | 페트리아 이코사면체 |
|---|---|---|---|---|---|
| 기호 | {3,3}π | {4,3}π | {3,4}π | {5,3}π | {3,5}π |
| (v,e,f), χ | (4,6,3), χ = 1 | (8,12,4), χ = 0 | (6,12,4), χ = −2 | (20,30,6), χ = −4 | (12,30,6), χ = −12 |
| 얼굴 | 꼬치 사각형 3개 | 꼬치 6각형 4개 | 꼬치 데카곤 6개 | ||
 |  |  |  | ||
| 이미지 |  |  |  |  |  |
| 애니메이션 |  |  |  |  |  |
| 관련 수치 |  {4,3}3 = {4,3}/2 = {4,3}(2,0) |  {6,3}3 = {6,3}(2,0) | 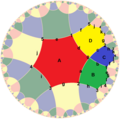 {6,4}3 = {6,4}(4,0) | {10,3}5 | {10,5}3 |
구면 다면체
일반적인 9개의 다면체는 구면 기울기(구체의 기울기)로도 나타낼 수도 있다.
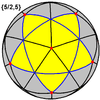 소절개도면체 {5/2,5} | 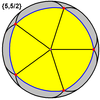 대두면체 {5,5/2} |  그레이트 스틸 도데카헤드론 {5/2,3} | 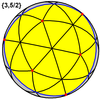 대이코사면체 {3,5/2} |
구면 다면체로만 존재할 수 있는 일반 다면체
Schléfli 기호가 {m, n}인 일반 다면체의 경우 폴리곤 면의 수는 다음을 통해 확인할 수 있다.
고대에 알려진 플라토닉 고형물은 m ≥ 3과 n 3 3의 유일한 정수용액이다. 제한 m ≥ 3은 다각형 면에 최소한 세 개의 면이 있어야 한다고 규정하고 있다.
다면체를 구면 타일링으로 고려할 때, 디곤(2-gon)은 0이 아닌 면적을 가진 구면 LUN으로 나타낼 수 있기 때문에 이 제한이 완화될 수 있다. 허용 m = 2는 새로운 무한 등급의 일반 다면체(hosohedra)를 허용한다. 구면 표면에서 정규 다면체 {2,n}은(는) 내부 각도가 2㎛/n인 n 아부팅 LUN으로 표현된다. 이 모든 LUN은 두 개의 공통 정점을 공유한다.[9]
3차원 유클리드 공간의 일반 다이드론 {n, 2([9]2-헤드론)은 "뒤로" 연결된 두 개의 (평면) n측 다각형으로 구성된 퇴행 프리즘으로 간주할 수 있으므로, 결과 물체는 깊이가 없으며, 두 개의 선 세그먼트로 디곤을 구성할 수 있는 방법과 유사하다. 그러나 구면 타일링으로서 다이헤드론은 비탈면 형태로 존재할 수 있는데, 구를 덮고 있는 두 개의 n면면이 있고, 각 면은 반구가 되며, 큰 원 주위에 정점이 있다. 꼭지점들이 같은 간격으로 있는 것은 규칙적이다.
호소헤드론 {2,n}은(는) 다이헤드론 {n,2}에 이중이다. n = 2일 때, 우리는 다면체 {2,2}을(를) 얻는데, 이는 호소면체(hosoheadron)와 다이면체(diheadron)이다. 이 모든 것들은 오일러 특성 2를 가지고 있다.
참고 항목
참조
- ^ Cromwell, Peter R. (1997). Polyhedra. Cambridge University Press. p. 77. ISBN 0-521-66405-5.
- ^ 첸, 지보, 량, 톈. "비비아니의 정리의 역", 칼리지 수학 저널 37(5), 2006, 페이지 390–391.
- ^ 스코틀랜드 고형물 날조.
- ^ 콕시터, 기하학의 아름다움: 12편의 에세이, 도버 출판물, 1999년 ISBN 0-486-40919-8(3장 4차원의 정규 스큐 폴리헤드라와 그 위상학적 유사점, 런던수학협회의 진행, 제2, 제43호, 1937호)
- ^ 일반 폴리헤드라 (지수 2의), 데이비드 A. 리히터
- ^ 지수 2의 정규 폴리헤드라 I Anthony M. 커틀러, 에곤 슐트, 2010
- ^ 지수 2의 정규 폴리헤드라, II Beitrage jur 대수 und Geometrie 52(2):357–387 · 2010년 11월, 표 3, 페이지 27
- ^ McMullen, Peter; Schulte, Egon (2002), Abstract Regular Polytopes, Encyclopedia of Mathematics and its Applications, 92, Cambridge University Press, p. 192, ISBN 9780521814966
- ^ Jump up to: a b Coxeter, 일반 폴리토페스, 페이지 12
- 버트랜드, J. (1858) 참고 sur la theri des polyédres régulier, Comptes rendus des séance de l'Academie des Science, 46, 페이지 79–82.
- 해켈, E. (1904). 쿤스트포르멘 데르 나투르. 해켈, E. Art formats in the natural, Prestel USA(미국), ISBN 3-7913-1990-6 또는 http://caliban.mpiz-koeln.mpg.de/~stueber/haeckel/kunstformen/natur.http://caliban.mpiz-koeln.mpg.de/에서 이용 가능
- 스미스, J. V. (1982) 기하학적 및 구조 결정학. 존 와일리 앤 선즈
- 소머빌, D. M. Y. (1930) n차원의 기하학개론. 뉴욕주 E. P. 더튼. (Dover Publishments Edition, 1958년) X장: 일반 폴리토페즈.
- Coxeter, H.S.M.; 일반 폴리토페스 (제3판) 도버 출판사 ISBN 0-486-61480-8