길쭉한 삼각 타일링

프리즘 오각형 타일링
프리즘 오각형 타일링
유형	듀얼 유니폼 타일링
얼굴	불규칙한 펜타곤 V3.3.3.4.4
콕시터 다이어그램	;
대칭군	cmm, [message,2+,mess], (2*22)
이중 다면체	길쭉한 삼각 타일링
특성.	면직의

길쭉한 삼각 타일링

유형	반정형 타일링
꼭지점 구성	3.3.3.4.4
슐레플리 기호	{3,6:e s{{∞}h₁{{}}}
와이토프 기호	2 2 (2 2)
콕시터 다이어그램
대칭	cmm, [message,2⁺,mess], (2*22)
회전 대칭	p2, [snf,2,snf],⁺ (2222
보우어 약자	에트랏
이중	프리즘 오각형 타일링
특성.	정점 변환

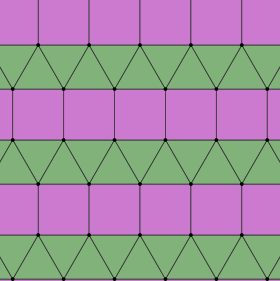
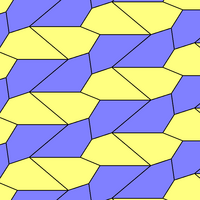
기하학에서 긴 삼각 타일링은 유클리드 평면의 반정형 타일링이다. 각 꼭지점에는 세 개의 삼각형과 두 개의 정사각형이 있다. 사각형 행에 의해 길쭉한 삼각형 타일링(tiling)으로 명명되며, 슐래플리(Schléfli) 기호 {3,6:e)가 주어진다.

콘웨이는 그것을 이소스너브 쿼드릴이라고 부른다.^[1]

평면에 3개의 규칙적인 기울기와 8개의 반정형 기울기가 있다. 이 타일링은 정점에 3개의 삼각형과 2개의 정사각형이 있는 스너브 사각형 타일링과 유사하지만 순서는 다르다.

건설

와이토프 건설로는 유일하게 만들 수 없는 볼록한 유니폼 타일링이기도 하다. 그것은 페이로겐 프리즘과 페이로겐 반격의 대체 층으로 건설될 수 있다.

균일 배색

긴 삼각 타일링의 균일한 색상이 하나 있다. 두 개의 2-제복 색상은 두 가지 색상의 사각형을 가진 하나의 꼭지점인 11123을 가지지만 1-제복이 아니며 반사 또는 활공반사에 의해 반복되거나 일반적으로 각 사각형 행을 독립적으로 이동할 수 있다. 2-제복 기울기는 아르키메데스 색채라고도 불린다. 이러한 아르키메데스의 색채는 정사각형 행 색상의 임의적인 변화에 의해 무한히 변형된다.

11122 (1-115)	11123 (2-통일 또는 1-아키메데스)

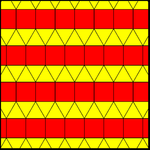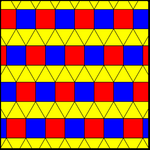cmm(2*22)	pmg(22*)	pgg(22×)

서클패킹

길쭉한 삼각 타일링은 원 패킹으로 사용할 수 있으며, 모든 점의 중심에 동일한 직경의 원을 배치할 수 있다. 모든 원은 패킹의 다른 원 5개와 접촉한다(키스 번호).^[2]

관련 틸팅

쌓인 삼각형과 사각형의 구간은 방사형 형태로 결합할 수 있다. 이것은 전환 시 3.3.3.4.4와 3.3.4.3.4의 두 꼭지점 구성을 혼합한다. 비행기를 다른 중앙 배치로 채우려면 12부가 필요하다. 듀얼은 카이로 오각형 타일링 펜타곤에 혼합될 것이다.^[3]

방사형 형태 예
중심	삼각형		사각형		육각형
대칭	[3]	[3]⁺	[2]	[4]⁺	[6]	[6]⁺
탑
이중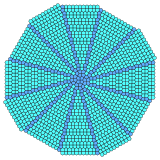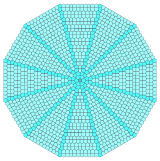

대칭 돌연변이

그것은 2*n2 오비폴드 표기법 대칭, 꼭지점 그림 4.n.4.3.3 및 Coxeter 도표와 같은 쌍곡선 기울기를 가진 일련의 대칭 변이에서^[4] 처음 나타난다. 이중은 쌍곡면에 육각형 면으로 되어 있으며, 면 구성은 V4.n.4.3.3이다.

균일한 기울기의 대칭 돌연변이 2*n2: 4.n.4.3.3

4.2.4.3.3.3	4.3.4.3.3.3	4.4.4.3.3.3
2*22	2*32	2*42

	또는	또는

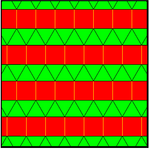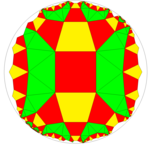2행 또는 3행의 삼각형 또는 정사각형을 혼합하여 4개의 관련 2-통일형 기울기가 있다.^[5]^[6]

이중 신장	삼중연장	반쯤 길어진	1/3이 길어졌다.

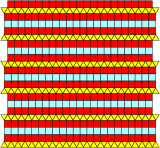프리즘 오각형 타일링

프리즘 오각형 타일링은 유클리드 평면의 이중 제복 타일링이다. 그것은 15개의 알려진 등면체 오각형 기울기 중 하나이다. 그것은 육각형 타일링에 평행 이등분선 세트가 달린 육각형 타일링으로 볼 수 있다.

콘웨이는 그것을 이소(4-)펜티유라고 부른다.^[1] 각각의 오각형 면은 3개의 120°, 2개의 90° 각도를 가지고 있다.

얼굴 구성 V3.3.4.3.4가 있는 카이로 오각형 타일링과 관련이 있다.

기하학적 변이

모노헤드형 오각형 타일링 타입 6은 위상은 동일하지만, 두 개의 가장자리 길이와 낮은 p2(222) 벽지 그룹 대칭:

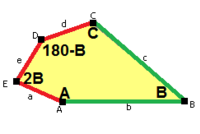	a = d = e, b = c B + D = 180°, 2B = E

참고 항목

메모들

^ ^a ^b 2008년 콘웨이, 페이지 288 표
^ 오더 인 스페이스: 디자인 소스 북, Keith Critchlow, 페이지 74-75, 원 패턴 F
^ 앤드류 오스본 2018 타워에 의한 주기적 기울기
^ 대니얼 허슨의 2차원 대칭 돌연변이
^ Chavey, D. (1989). "Tilings by Regular Polygons—II: A Catalog of Tilings". Computers & Mathematics with Applications. 17: 147–165. doi:10.1016/0898-1221(89)90156-9.
^ "Archived copy". Archived from the original on 2006-09-09. Retrieved 2015-06-03.{{cite web}}: CS1 maint: 타이틀로 보관된 사본(링크)

참조

Grünbaum, Branko; Shephard, G. C. (1987). Tilings and Patterns. New York: W. H. Freeman. ISBN 0-7167-1193-1. (제2.1장: 규칙적이고 균일한 틸팅, 페이지 58-65)
Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. p37
존 H. 콘웨이, 하이디 버기엘, 차임 굿맨-스트라스, 2008년 사물의 대칭, ISBN 978-1-56881-220-5 [1]
Keith Critchlow, Order in Space: 디자인 소스 북, 1970, 페이지 69-61, 패턴 Q₂, 듀얼 페이지 77-76, 패턴 6
데일 시모어와 질 브리튼 테셀레이션 소개, 1989년 ISBN 978-0866514613, 페이지 50-56

외부 링크

Weisstein, Eric W. "Uniform tessellation". MathWorld.
Weisstein, Eric W. "Semiregular tessellation". MathWorld.
Klitzing, Richard. "2D Euclidean tilings elong( x3o6o ) - etrat - O4".

[Conway,_2008,_p.288_table-1] 2008년 콘웨이, 페이지 288 표

[Critchlow-2] 오더 인 스페이스: 디자인 소스 북, Keith Critchlow, 페이지 74-75, 원 패턴 F

[3] 앤드류 오스본 2018 타워에 의한 주기적 기울기

[4] 대니얼 허슨의 2차원 대칭 돌연변이

[5] Chavey, D. (1989). "Tilings by Regular Polygons—II: A Catalog of Tilings". Computers & Mathematics with Applications. 17: 147–165. doi:10.1016/0898-1221(89)90156-9.

[6] "Archived copy". Archived from the original on 2006-09-09. Retrieved 2015-06-03.{{cite web}}: CS1 maint: 타이틀로 보관된 사본(링크)

[1]

[2]

[3]

[4]

[5]

[6]

듀얼: 이중 연장	듀얼: 트리플 롱티드	듀얼: 절반 길어진 상태	이중: 1/3 길림

듀얼: [4⁴; 3³².4]₁ (t=2,e=4)	듀얼: [4⁴; 3³².4]₂ (t=3,e=5)	듀얼: [3⁶; 3³².4]₁ (t=3,e=4)	듀얼: [3⁶; 3³².4]₂ (t=4,e=5)

Search