사각 격자

Square lattice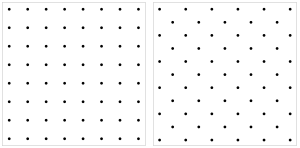
정사각형 격자
Square Lattice.svg
직립사각형
심플		 대각선 사각형
중심적
직립 사각 타일링.모든 정사각형의 꼭지점과 그 중심은 직립 정사각형 격자를 형성한다.각 색상에 대해 해당 색상의 정사각형 중심은 직립 정사각형 격자보다 2배 큰 선형 척도인 대각선 사각 격자를 형성한다.

수학에서 사각 격자는 2차원 유클리드 공간에 있는 격자의 일종이다.이것은2 Z로 표기된 정수 격자의 2차원 버전이다.[1]그것은 대칭 그룹에 의해 분류되는 5가지 형태의 2차원 격자 중 하나이다.[2][3] IUC 표기법에서 그것의 대칭 그룹은 p4m, Coxeter 표기법은 [4,[4]4], 그리고 *442로 오비폴드 표기법이다.[5]

격자 이미지의 두 방향은 단연코 가장 흔하다.직립형 사각 격자 및 대각선 사각 격자라고도 하며, 중앙 사각 격자라고도 한다.[6]그들은 45°의 각도로 다르다.이는 체커보드 착색에서 분명히 알 수 있듯이 정사각형 격자를 두 개의 정사각형 하위 표로 분할할 수 있다는 사실과 관련이 있다.

대칭

사각 격자의 대칭 범주는 벽지 그룹 p4m이다.이 변환 대칭의 격자를 가진 패턴은 더 많이 가질 수 없지만 격자 자체보다 더 적은 대칭을 가질 수 있다.직립형 사각 격자는 망사 크기가 2배인 대각선 사각 격자로 볼 수 있으며, 사각형의 중심이 추가된다.이에 따라 직립형 정사각형 격자의 정사각형 중심을 추가한 후 원래 격자보다 2배 작은 망사 크기의 대각선 사각 격자를 갖게 된다.4배 회전 대칭의 패턴은 4배 회전 대칭의 격자에 비례하여 대각선 방향의 √2 인자인 4배 회전촉진기의 정사각형 격자를 가지고 있다.

반사 축과 관련하여 세 가지 가능성이 있다.

  • 없어, 벽지 그룹 p4야
  • 네 방향으로.벽지 그룹 p4m 입니다.
  • 두 개의 수직 방향으로.벽지 그룹 p4g 입니다.반사 축의 교차점은 4배 회전축의 정사각형 격자처럼 미세하고 방향이 같은 사각 격자를 형성하며, 이 회전 격자는 반사 축에 의해 형성된 정사각형 중심에 있다.
p4, [4,4]+, (442) p4g, [4,4+], (4*2) p4m, [4,4], (*442)
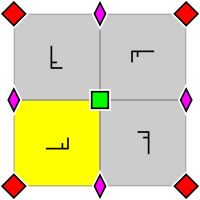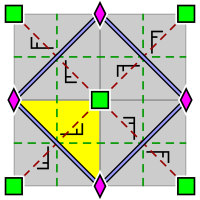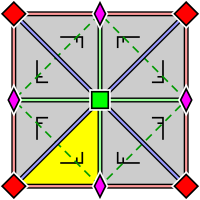Wallpaper group diagram p4 square.svg Wallpaper group diagram p4g square.svg Wallpaper group diagram p4m square.svg
벽지 그룹 p4. 2배 및 4배 회전식 로토센트의 원시 세포 내 배열(p4g 및 p4m에도 적용 가능)기본 도메인은 노란색으로 표시된다. 벽지 그룹 p4g.4배 회전축이 아닌 두 방향으로 반사축이 있다. 벽지 그룹 p4m.4배 회전축(Rotocent)을 통해 4방향으로 반사축이 있다.두 방향에서 반사 축은 p4g의 축과 동일하고 밀도가 높지만 이동한다.다른 두 방향에서 그것들은 선형적으로 √2 밀도 인자이다.

참고 항목

참조

  1. ^ Conway, John; Sloane, Neil J. A. (1999), Sphere Packings, Lattices and Groups, Springer, p. 106, ISBN 9780387985855.
  2. ^ Golubitsky, Martin; Stewart, Ian (2003), The Symmetry Perspective: From Equilibrium to Chaos in Phase Space and Physical Space, Progress in Mathematics, vol. 200, Springer, p. 129, ISBN 9783764321710.
  3. ^ Field, Michael; Golubitsky, Martin (2009), Symmetry in Chaos: A Search for Pattern in Mathematics, Art, and Nature (2nd ed.), SIAM, p. 47, ISBN 9780898717709.
  4. ^ 특히Johnson, Norman W.; Weiss, Asia Ivić (1999), "Quadratic integers and Coxeter groups", Canadian Journal of Mathematics, 51 (6): 1307–1336, doi:10.4153/CJM-1999-060-6 1320페이지의 상단을 보라.
  5. ^ Schattschneider, Doris; Senechal, Marjorie (2004), "Tilings", in Goodman, Jacob E.; O'Rourke, Joseph (eds.), Handbook of Discrete and Computational Geometry, Discrete Mathematics and Its Applications (2nd ed.), CRC Press, pp. 53–72, ISBN 9781420035315. 특히 IUC 표기법과 궤변형 표기법 관련 62페이지의 표를 참조하십시오.
  6. ^ Johnston, Bernard L.; Richman, Fred (1997), Numbers and Symmetry: An Introduction to Algebra, CRC Press, p. 159, ISBN 9780849303012.