격자 그래프

격자 그래프, 메쉬 그래프 또는 격자 그래프는 일부 유클리드 공간 R에ⁿ 내장된 도면이 정규 타일을 형성하는 그래프다. 이는 그래프를 자신에게 보내는 생체적 변환의 집단이 집단 이데올로기적 의미에서의 격자임을 암시한다.

일반적으로 그래프 이론의 보다 추상적인 의미에서는 그러한 그래프와 공간에서의 그림(종종 평면이나 3D 공간) 사이에 명확한 구별이 이루어지지 않는다. 이러한 유형의 그래프는 격자, 망사 또는 격자라고 더 빨리 불릴 수 있다. 더욱이, 이러한 용어들은 "8×8 제곱 격자"에서와 같이 무한 그래프의 유한한 섹션에도 일반적으로 사용된다.

격자 그래프라는 용어는 문헌에서 다수의 완전한 그래프의 데카르트 제품과 같이 일정한 구조를 가진 다양한 종류의 그래프에도 주어졌다.^[1]

사각 격자 그래프

격자형 그래프의 일반적인 유형(제곱 격자 그래프와 같이 다른 이름으로 알려져 있음)은 정점이 정수 $좌표$가 있는 평면의 점에 해당하는 그래프로, x 좌표가 1,${\displaystyle ,,}$ ${\displaystyle n}$ ${\displaystyle 1,\cdots ,n}$ 범위에$$있고, y ${\displaystyle \mathrm{좌표}}$가 1,$⋯,$ {\$displaystystyle$1,\$cdots ,$m}, m$\}$ 및 2 범위에 있다. 정점은 해당 지점이 거리 1에 있을 때마다 가장자리에 의해 연결된다. 즉, 기술된 점 집합에 대한 단위 거리 그래프인 것이다.^[2]

특성.

사각 격자 그래프는 $가장자리$가${\displaystyle }$n - ${\displaystyle 1}$ ${\displaystyle n-1}$과${\displaystyle }$m - ${\displaystyle 1}${\$displaystyle m-1}$인 두 개의 경로 그래프의 데카르트 산물이다.^[2] 경로 그래프는 중위수 그래프이므로, 후자의 사실은 사각 격자 그래프도 중위수 그래프임을 의미한다. 모든 그리드 그래프는 초당적인 것으로, 체크보드 방식으로 정점을 색칠할 수 있다는 사실만으로 쉽게 검증할 수 있다.

경로 그래프는 그리드의 격자 그래프 n 곱하기 1로도 간주될 수 있다. 2×2 격자 그래프는 4 사이클이다.^[2]

모든 평면 그래프 H는 h×${\displaystyle \mathrm{h-그리드}}$의 부차적인 것으로 $여기$서 h${\displaystyle }$= ${\displaystyle 2}$ ${\displaystyle V}$( H${\displaystyle }$)${\displaystyle }$+ ${\displaystyle 4}$ ${\displaystyle \mathrm{E}}$( ${\displaystyle H}$) $displaystyle h=2 V(H) +$4$E(H)$^[3]$}.$

기타종류

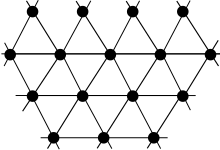
삼각 격자 그래프는 삼각 격자에 해당하는 그래프다.

평면의 유한한 점 집합에 대한 한안 격자 그래프는 집합의 각 점을 통해 모든 수직선과 수평선의 교차점에 의해 얻은 격자에 의해 생성된다.

루크의 그래프(체스판 위에서 루크 체스 조각의 모든 합법적인 움직임을 나타내는 그래프)를 격자 그래프라고도 부르기도 하는데, 이 그래프는 이 글에서 설명한 격자 그래프와는 엄격히 다르다. 요정 체스 조각 와지르의 유효한 움직임은 사각 격자 그래프를 형성한다.

참고 항목

• 격자 경로
• 픽의 정리
• 2D 격자의 정수 삼각형
• 격자(주문)

참조