테트레이션
Tetration

수학에서 테트레이션(tetration)은 반복 또는 반복된 지수 함수를 기반으로 하는 연산입니다.테트레이션에 대한 표준 표기법은 없지만,와 왼쪽 독립 b는 일반적입니다.
반복적인 지수화로 된 a는 를 하며, 여기서 a의 복사본은 오른쪽에서 왼쪽으로 지수화를 통해 반복됩니다. 즉 - 번 적용합니다.n은 함수의 "높이"라고 불리는 반면, a는 지수화와 유사한 "기준"이라고 불립니다.이는 "a의 n번째 테트레이션"으로 읽힙니다.
이것은 지수화 후, 그러나 참회 전의 다음 하이퍼 연산입니다.이 단어는 루벤 루이 굿스타인이 테트라(4)와 반복에서 만들어냈습니다.
테트레이션은 다음과 같이 재귀적으로 정의됩니다.
실수나 복소수와 같은 비자연적인 숫자로 테트레이션을 확장하려는 시도를 허용합니다.
테트레이션의 두 역은 n번째 루트 및 로그 함수와 유사한 슈퍼 루트 및 슈퍼 로그라고 합니다.세 가지 기능 중 기본 기능은 없습니다.
소개
처음 4개의 하이퍼 연산은 여기에 표시되며, 테트레이션은 시리즈의 4번째 연산으로 간주됩니다.'+ a'=로 정의되는 단항 연산 연속은 0번째 연산으로 간주됩니다.
- 추가 n개의 복사본이 연속적으로 결합에 추가되었습니다.
- 곱셈 합본 n부
- 지수화 곱셈에 의해 결합된 n개의 사본.
- 테트레이션오른쪽에서 왼쪽으로, 지수화에 의해 결합된 n개의 복사본.
중첩 지수는 위에서 아래로 해석되는 것이 입니다 {\ 3은 (7이아니라 ( ()\
계승(an = a + 1)은n+1 가장 기본적인 연산이며, 덧셈(a + n)은 일차 연산이며, 자연수의 추가는 a의 n개의 후속자의 연쇄 연속으로 생각할 수 있습니다. 곱셈(a x n) 또한 일차 연산입니다.자연수의 경우, a의 n개의 숫자를 포함하는 연쇄 덧셈으로 유사하게 생각할 수 있습니다.지수화는 a의 n개의 숫자와 n개의 숫자 a를 포함하는 연결된 곱셈과 n개의 숫자 를 포함하는 연결된 으로 생각할 수 있습니다.위의 각 연산은 이전 [1]연산을 반복하여 정의되지만, 이전 연산과 달리 테트레이션은 기본 함수가 아닙니다.
매개변수 a를 기준값이라고 하며, 매개변수 n을 높이라고 할 수 있습니다.테트레이션의 원래 정의에서 높이 매개변수는 자연수여야 합니다. 예를 들어, "3은 마이너스 5배로 상승했다" 또는 "4는 1/2의 시간에 스스로 상승했다"라고 말하는 것은 비논리적입니다.그러나 덧셈, 곱셈 및 지수화를 실수 및 복소수로 확장할 수 있는 방식으로 정의할 수 있듯이, 음의 숫자, 실수 및 복소수로 테트레이션을 일반화하려는 시도가 여러 번 있었습니다.이를 위한 한 가지 방법은 테트레이션에 대한 재귀적 정의를 사용하는 것입니다. 모든 양의 a> {\ a 및 음이 아닌 n n 0에 대해 는 \ 재귀적으로 다음과 같습니다.[1]
재귀적 정의는 자연 높이에 대한 반복적인 지수화와 동일하지만, 이 정의는 0a({\displaystyle ^{0}a), -1a({\displaystyle ^{-1}a), ia({\displaystyle ^{i}a)와 같은 다른 높이로의 확장을 허용한다. 이러한 확장 중 많은 부분은 활발한 연구 영역이다.
용어.
구속에 대한 많은 용어들이 있는데, 각각의 용어들은 그 이면에 약간의 논리를 가지고 있지만, 어떤 것들은 이런저런 이유로 일반적으로 사용되지 않았습니다.다음은 각 항과 그 근거 및 반합리성을 비교한 것입니다.
- Goodstein이 1947년 논문 재귀수 이론의 초미세 서수(Transinite Ordinals in Recursive Number[2] Theory)에서 도입한 테트레이션이라는 용어는 지배적인 지위를 사용하기 위해 Goodstein의 정리에 사용된 재귀 기저 표현을 일반화합니다.그것은 또한 루디 러커의 인피니티 앤 더 마인드에서 대중화되었습니다.
- 초강수라는 [3]용어는 1987년 브로머가 그의 논문 초강수에서 발표했습니다.이것은 1986년 Princeton University Press에서 Ed Nelson이 그의 책 Predictive Armetic에서 일찍이 사용했습니다.
- 초강력이라는[4] 용어는 초강력과 힘의 자연스러운 조합으로, 테트레이션을 적절하게 설명합니다.문제는 하이퍼 연산 시퀀스에 대한 하이퍼의 의미에 있습니다.하이퍼 연산을 고려할 때 하이퍼라는 용어는 모든 등급을 가리키며, 슈퍼라는 용어는 4등급, 즉 테트레이션을 가리킵니다.그래서 이러한 고려 하에서 초강력은 단지 테트레이션을 언급하는 것이기 때문에 오해를 불러일으킵니다.
- 파워 타워[5]라는 용어는 a ⋅a의 디스플레이 스타일에 대해 "순서의 파워 타워"의 형태로 가끔 사용된다.테트레이션은 인스턴스 a^a(이 값 c)가 있는 식의 오른쪽 상단에서 시작하여 반복적인 지수화(이 오른쪽 연관 연산 ^라고 함)입니다.다음 왼쪽 방향 a(이를 '다음 베이스' b라고 함)를 지수화하는 것은 새 값 b^c를 얻은 후 왼쪽 방향으로 작업하는 것입니다.왼쪽으로 작업하면서 왼쪽의 다음 a를 기준 b로 사용하고 새로운 b^c. '타워 아래로 내려감'을 차례로 평가하고 다음 아래로 내려가는 단계에서 c에 대한 새로운 큰 값을 사용합니다.
일부 공통 용어와 유사한 표기 상징성 때문에 테트레이션은 종종 밀접하게 관련된 함수와 표현식과 혼동됩니다.다음은 몇 가지 관련 용어입니다.
| 용어. | 형태 |
|---|---|
| 테트레이션 | |
| 반복된 지수 | |
| 내포된 지수(타워) | |
| 무한 확장 지수(타워) |
처음 두 식에서 a는 기저값이고, a가 나타나는 횟수는 높이입니다(x에는 하나 추가).세 번째 식에서, n은 높이이지만, 각각의 기저는 다릅니다.
반복된 지수를 참조할 때는 이 형식의 반복된 지수 표현식을 호출하는 것이 일반적이며, 이는 반복된 검정력 또는 반복된 지수를 의미할 수 있기 때문에 모호하기 때문에 주의해야 합니다.
표기법
테트레이션을 표현하는 데 사용할 수 있는 다양한 표기법 스타일이 있습니다.일부 표기법은 다른 하이퍼 연산을 설명하는 데도 사용할 수 있는 반면, 일부 표기법은 테트레이션으로 제한되며 즉각적인 확장이 없습니다.
| 이름. | 형태 | 묘사 |
|---|---|---|
| 루디 러커 표기법 | Maurer [1901] 및 Goodstein [1947]에 의해 사용됨;루디 러커의 책 인피니티 앤 더 마인드는 [nb 1]이 표기법을 대중화했습니다. | |
| 크누스의 위쪽 화살표 표기법 | 더 많은 화살표 또는 더 강력하게 색인된 화살표를 추가하여 확장할 수 있습니다. | |
| 콘웨이 체인 화살표 표기법 | 숫자 2(위의 확장자와 동일)를 증가시켜 확장을 허용하지만, 체인을 확장함으로써 더욱 강력하게 확장할 수 있습니다. | |
| 아커만 함수 | 특수 a {{ a = 를 Ackermann 함수의 관점에서 쓸 수 있습니다. | |
| 반복 지수 표기법 | 1 이외의 초기 값에서 반복된 지수로 단순 확장할 수 있습니다. | |
| 후쉬만드[6] 표기법 | M. H. Hooshmand [2006]에 의해 사용되었습니다. | |
| 하이퍼 연산 표기법 | 숫자 4를 늘려서 확장할 수 있습니다. 이는 하이퍼 연산 계열을 제공합니다. | |
| 더블캐럿 표기법 | a^^n | 위쪽 화살표는 캐럿과 동일하게 사용되므로 (^), 테트레이션은 다음과 같이 쓸 수 있습니다.^^ASCII에 편리합니다. |
위의 한 표기법은 반복된 지수 표기법을 사용합니다. 이는 일반적으로 다음과 같이 정의됩니다.
- nas를 사용하여 ( ) ⋅ \ _)=^{을(를) 합니다.
반복되는 지수에 대한 표기법은 많지 않지만 다음은 몇 가지입니다.
| 이름. | 형태 | 묘사 |
|---|---|---|
| 표준 표기법 | 오일러는 ( ) x {\ _)= 라는 표기법을 만들었고, 반복 f (x) {\ f는 대략 그 정도의 기간 동안 사용되었습니다. | |
| 크누스의 위쪽 화살표 표기법 | 화살표 수를 늘려 초강력 및 초지수 기능을 제공합니다. 이는 큰 숫자에 대한 기사에 사용됩니다. | |
| 텍스트 표기법 | exp_a^n(x) | 표준 표기법을 기반으로 하며, ASCII에 편리합니다. |
| J 표기법 | x^^:(n-1)x | 지수화를 반복합니다.J(프로그래밍 언어)[7] 참조 |
| 무한 장벽 표기법 | 조나단 바우어스가 만든 것으로 [8]더 높은 하이퍼 운영으로 확장할 수 있습니다. |
예
테트레이션의 매우 빠른 성장 때문에 다음 표의 대부분의 값은 과학적 표기법으로 쓰기에는 너무 큽니다.이러한 경우 반복된 지수 표기법을 사용하여 기본 10으로 표현합니다.소수점을 포함하는 값은 근사적입니다.
| 1 | 1 | 1 | 1 | 1 | 1 |
|---|---|---|---|---|---|
| 2 | 4 (22) | 16 (24) | 65,536 (216) | 2.00353 x 1019,728 | (29508 \6.03123 x 10자리19,727) |
| 3 | 27 (33) | 7,625,597,484,987 (327) | ( \103,638,334,165,025자리) | ||
| 4 | 256 (44) | 1.34078 x 10154(4256) | ( \187268.0723 x 10자리153) | ||
| 5 | 3,125 (55) | 1.91101 x 102,184 (53,125) | ( \1.33574 x 10자리2,184) | ||
| 6 | 46,656 (66) | 2.65912 x 1036,305(646,656) | ( \2.0692 x 10자리36,305) | ||
| 7 | 823,543 (77) | 3.75982 x 10695,974 | ( 10}^{.842593.16542 x 10자리695,974) | ||
| 8 | 16,777,216 (88) | 6.01452 x 1015,151,335 | ( \5.43165 x 10자리15,151,335) | ||
| 9 | 387,420,489 (99) | 4.28125 x 10369,693,099 | ( \10}^{.567844.08535 x369,693,099 10자리) | ||
| 10 | 10,000,000,000 (1010) | 1010,000,000,000 | () {\1010,000,000,000 + 1자리) |
비고: x가 크기 순서에 따라 10과 다르지 않은 경우, z' {\displaystyle k\geq 3,~^{m}x=\exp_{10}^{z} 예를 들어 z\text}의 경우, 모든 k ⇒ 3, m x = exp 10 k + 1 = exp _10 k + 1 z에 대해 z > z>1~\rightarrow ~m+1 = z' 텍스트 {\text}의 경우,m = 4({displaystyle z-z' 표시) 표에서 약 2 10이며, 다음 행의 경우 차이가 더 작습니다.
특성.
테트레이션에는 지수화와 유사한 여러 속성과 연산에 고유한 속성이 있으며 지수화로 인해 손실되거나 얻을 수 있습니다.지수화가 통근하지 않기 때문에 제품 및 검정력 규칙에는 테트레이션을 갖는 유사체가 없습니다. (x ) (x ) \ ( )= {}^{a는 대부분의 경우에 해당되지 않습니다.[9]
그러나 테트레이션은 x (- ) ({}^{인 다른 특성을 따릅니다.이 사실은 재귀적 정의를 사용하여 가장 명확하게 표시됩니다.이 특성으로부터, ( ( ( + ) (- a) {\left({}^{\left({}^{이 뒤따르며, 특정 방정식에서 b와 c를 전환할 수 있습니다.증명은 다음과 같습니다.
숫자 x와 10이 동일한 경우, 오일러의 정리를 사용하여 임의의 정수 m에 대해 x의 m 소수 자릿수를 계산할 수 있습니다.이것은 다른 기저에서도 마찬가지입니다. 예를 들어, x와 이 동일한 경우의 팔자수를 계산할 수
평가방향
테트레이션을 "표현 타워"로 표현할 때, 직렬 지수화는 가장 깊은 수준(표기법에서 정점)에서 먼저 수행됩니다.예:
지수화는 연관성이 없기 때문에 이 순서가 중요하며, 반대 순서로 식을 평가하면 다음과 같은 다른 대답이 나옵니다.
왼쪽에서 오른쪽으로 표현식을 평가하는 것은 덜 흥미로운 것으로 간주된다. 왼쪽에서 오른쪽으로 평가하는 것은 모든 표현식을 (an - 1) \{\left(a^{n-1}\right)}\!\!}.[10] 이 때문에 타워는 오른쪽에서 왼쪽으로(또는 위에서 아래로) 평가해야 한다.컴퓨터 프로그래머들은 이 선택을 오른쪽 연상이라고 부릅니다.
확장 기능
테트레이션은 두 가지 다른 방식으로 확장될 수 있습니다. ^{에서 기저 a와 높이 n 모두 테트레이션의 정의와 특성을 사용하여 일반화할 수 있습니다.기저와 높이는 음이 아닌 정수를 넘어 i 무한 n의 높이와 같은 함수를 하여 다른 도메인으로 확장될 수 있지만, 테트레이션의 제한된 특성은 테트레이션을 확장하는 능력을 감소시킵니다.
기지에 대한 도메인 확장
기준 0
0 {{ 0이(가) 일관되게 정의되지 않았습니다.따라서, 0 {{은 앞에서 주어진 공식에 의해 명확하게 정의되지 않습니다. 림 x n _ 0는 잘 정의되어 있으며 다음과 같이 [11]존재합니다.
따라서 n x → n = 0x}를 일관되게 할 수 있습니다.이는 ({0^{0}=을(를) 하는 것과 유사합니다.
이 확장에서는 {{{}^{1이므로 정의의 규칙 a {{}=이 여전히 유지됩니다.
복소 기저


복소수를 거듭제곱할 수 있기 때문에 z = a + bi(a와 b가 실수인 경우) 형식의 기저에 테트레이션을 적용할 수 있습니다.예를 들어 z = i인 z에서는 자연 로그의 주 분기를 사용하여 테트레이션을 수행합니다. 오일러의 공식을 사용하면 다음과 같은 관계를 얻을 수 있습니다.
이는 임의의 i = a + bi가 주어졌을 때 i = a' + b'i에 대한 재귀적 정의를 제안합니다.
다음과 같은 대략적인 값을 도출할 수 있습니다.
| 근사값 | |
|---|---|
| i | |
| 0.2079 | |
| 0.9472 + 0.3208i | |
| 0.0501 + 0.6021i | |
| 0.3872 + 0.0305i | |
| 0.7823 + 0.5446i | |
| 0.1426 + 0.4005i | |
| 0.5198 + 0.1184i | |
| 0.5686 + 0.6051i |
이전 섹션에서와 같이 역관계를 해결하면 예상 i = 1 및 i = 0이 산출되며, n의 음수 값은 가상 축에서 무한한 결과를 제공합니다.복잡한 평면에 표시되면 n이 무한한 값으로 해석될 수 있는 한계 0.4383 + 0.3606i까지 전체 시퀀스가 나선형으로 회전합니다.
이러한 테트레이션 시퀀스는 오일러 시대부터 연구되었지만 혼란스러운 행동으로 인해 잘 이해되지 않습니다.역사적으로 발표된 대부분의 연구는 무한 반복 지수 함수의 수렴에 초점을 맞추었습니다.현재의 연구는 프랙탈과 상징적인 수학 소프트웨어를 가진 강력한 컴퓨터의 출현으로 큰 이익을 얻었습니다.테트레이션에 대해 알려진 많은 것은 복잡한 역학에 대한 일반적인 지식과 지수 지도의 [citation needed]특정 연구에서 비롯됩니다.
다른 높이에 대한 도메인 확장
무한 높이

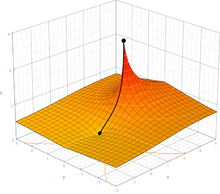
테트레이션은 무한한 높이로 확장될 수 있습니다. 즉, 의 특정 a 및 n 값에 대해 무한 n에 대해 잘 정의된 결과가 있습니다.이는 특정 구간 내의 기저의 경우 높이가 무한대로 증가함에 따라 테트레이션이 유한한 값으로 수렴되기 때문입니다.예를 들어, \ {{2}}^{\cdot ^{\}}}}}은 2로 수렴하므로 2와 같다고 할 수 있습니다.2를 향한 추세는 작은 유한 타워를 평가하여 확인할 수 있습니다.
일반적으로 무한 반복된 x \ x^{\ ^{\cdot n이 무한대로 가면서 x {{의 한계로 정의되는, 대략 0.066에서 1.44 사이의 간격으로 e≤x1/e≤e에 대해 수렴하며−e, 이는 레온하르트 [12]오일러가 보여주는 결과입니다한계가 존재하는 경우 y = xy 방정식의 양의 실제 해입니다.따라서 x = y입니다1/y.x의 무한 지수를 정의하는 한계는 x > e일1/e 때 y의1/y 최대값이 y이기1/e 때문에 존재하지 않습니다.0 < x < e일−e 때도 한계가 존재하지 않습니다.
이는 다음과 같은 정의로 복소수 z로 확장될 수 있습니다.
한계 y = x (양의 실선에 존재하는 경우, 즉 e ≤ x ≤ e에1/e 대해−e)는 x = y를 만족해야y 하므로 x ≤ y = x는1/y y ≤ x = y의 역함수임을 알 수 있습니다.
음의 높이
우리는 테트레이션을 위해 재귀적인 규칙을 사용할 수 있습니다.
하기 - 1
k개의 주어진 값으로 -1로 대체
- a a ( a ) a {{{ =\}\leftsyle}^{)=\ _[10]
더 작은 음수 값은 이러한 방식으로 잘 정의될 수 없습니다.같은 방정식에서 k에 -2를 대입하면 다음과 같은 결과가 나옵니다.
잘 정의되어 있지 않습니다.그러나,[10] 그것들은 때때로 집합으로 간주될 수 있습니다.
n {{ n=에 의 정의는 다음과 같이 규칙과 일치합니다.
- 의 n - {{n={^{-에 0 {{ = - displaystyle \,\!n = {^{-
실제 높이
현재 n의 실수 또는 복소수 값으로 테트레이션을 확장하는 일반적인 문제에 대해 일반적으로 받아들여지는 해결책은 없습니다.그러나 이 문제에 대한 여러 가지 접근 방식이 있으며 아래에는 다양한 접근 방식이 설명되어 있습니다.
일반적으로, 문제는 (어떤 실수 a > 0에 대하여) 실수 x > -2에 대하여 (x a{{\,)={}^{를 만족시키는 초영속 를 찾는 것입니다.
- a ( a) \ 모든 x> - {{ x
보다 자연스러운 확장을 찾으려면 일반적으로 하나 이상의 추가 요구 사항이 필요합니다.이는 일반적으로 다음과 같은 모음입니다.
- 연속성 요구 사항(일반적으로 는x >({{x>에 두 변수 모두에서 연속적입니다.
- 미분 가능성 요구 사항(x 단위로 한 번, 두 번, k번 또는 무한 미분 가능).
- 다음과 같은 규칙성 요구사항(x에서 두 번 미분 가능함을 의미):
- 2 2 (x) >) x >에 대해 {{
네 번째 요구 사항은 저자마다, 그리고 접근법마다 다릅니다.테트레이션을 실제 높이로 확장하는 방법에는 두 가지 주요 접근 방식이 있습니다. 하나는 규칙성 요구 사항을 기반으로 하고 다른 하나는 미분 가능성 요구 사항을 기반으로 합니다.이 두 가지 접근 방식은 너무 달라서 서로 일관성 없는 결과를 낳기 때문에 조정되지 않을 수도 있습니다.
길이 1의 구간에 대해 {\가 되면 모든 x > -2에 대해 전체 함수가 쉽게 따릅니다.
실제 높이에 대한 선형 근사

선형 근사(연속성 요구사항에 대한 솔루션, 미분 가능성 요구사항에 대한 근사치)는 다음과 같이 제공됩니다.
따라서:
| 근사 | 도메인 |
|---|---|
| -1 < x < 0에 대하여 | |
| 0 < x < 1에 대하여 | |
| 1 < x < 2에 대하여 |
등등.그러나 이것은 조각적으로 구별될 수 있을 뿐입니다. x의 정수 값에서 는 \displaystyle {x > -\ x에 연속적으로 미분됩니다. 예를 들어 = e{ a=인 경우에만. 예를 들어, 이러한 방법 ≈ 4 0≈
후스만드의 논문의[6] 주요 정리는 다음과 같습니다.< \ 0 < \ 1}. :( - +∞ ) f이 연속적이고 다음 조건을 만족시킵니다.
- f는 (-1, 0)에서 미분 가능합니다.
- {\ f}}는 (-1, 0)에서 감소하지 않거나 증가하지 않는 함수입니다.
f f는 방정식을 통해 고유하게 결정됩니다.
여기서( - [] {\) = 는 x 및 [의 분수 부분을 나타냅니다. {\displaystyle \ _는 \ _의[ 반복 함수입니다.
그 증거는 두 번째부터 네 번째 조건까지 f가 [-1, 0]에 대한 선형 함수라는 것을 사소한 것으로 암시한다는 것입니다.
자연적인 xe {{에 대한 선형 근사치는 연속적으로 미분할 수 있지만, 두 번째 도함수는 인수의 정수 값에 존재하지 않습니다.후쉬만드는 다음과 같은 또 다른 고유성 정리를 도출했습니다.
: (- +∞ ) { f이가) 다음을 만족하는 연속 함수라면,
- {\ f가 (-1, 0)에 볼록합니다.
f {\ f= [서 f = f=는 자연 사분 함수에 대한 선형 근사에 대한 Hooshmand의 이름입니다.]
증명은 이전과 거의 같습니다. 재귀 방정식은 f (-+ ) (0+ ),\ f} (-1^{+}) = } (를 하고 볼록 은 f f가 (-1, 0)에 선형임을 의미합니다.
따라서 자연 사분면에 대한 선형 근사는 ( (- ( - \\(x)=와 ( f f)=의 유일한 해이며, 이는 (-1, +1)에 볼록합니다.충분히 미분 가능한 다른 모든 솔루션에는 구간(-1, 0)에 변곡점이 있어야 합니다.
실제 높이에 대한 고차 근사
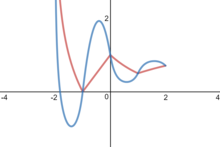
선형 근사치 외에 2차 근사치(미분성 요구사항에 대한)는 다음과 같이 제공됩니다.
는 모든x > { x > 에 대해 미분 가능하지만 두 번 미분 가능하지는 않습니다.예를 들어, ...= a=인 경우 근사치와 동일합니다.[1]
계산 방법 때문에, 이 함수는 지수와 반대로 "계산"되지 않습니다 여기서 ( n) right) 즉,
2차 근사가 있는 것처럼, 입방 근사치와 정도의 근사치로 일반화하는 방법도 존재하지만 훨씬 [1][14]다루기 어렵습니다.
복합 높이

이제 방정식 F(z + 1) = exp(F(z))의 해이며 z가 ±iθ에 접근함에 따라 F(0) = 1 및 F(z)가 로그의 고정점에 접근하는 추가 조건(θ 0.318 ± 1.337i)을 만족하는 고유 함수 F가 존재하고 F가 복소 z 평면 전체에서 정형이라는 것이 증명되었습니다[15].z ≤ -2에서 실제 축의 부분을 제외합니다.이 증거는 이전의 [16]추측을 확인시켜줍니다.그러한 기능의 구성은 1950년에 [17]Kneser에 의해 처음으로 입증되었습니다.이 함수의 복잡한 맵은 오른쪽 그림에 나와 있습니다.이 증명은 또한 가 1 1보다 큰 한, 다른 기저에도 효과가 있습니다. ({ e 1 이후의 작업은 모든 복잡한 [18]기저로 구성을 확장했습니다.
테트레이션이 완전 동형이어야 한다는 요구 사항은 고유성에 중요합니다.많은 함수 S는 다음과 같이 구성될 수 있습니다.
여기서 α와 β는 적어도 Imz의 중간 값에서 직렬의 수렴을 제공할 수 있을 정도로 빠르게 붕괴하는 실제 시퀀스입니다.
함수 S는 테트레이션 방정식 S(z + 1) = exp(S(z)), S(0) = 1을 만족하며, α와n β가 충분히 빠르게 0에 접근하면n 양의 실제 축 근처에서 분석됩니다.그러나, 만약 {α} 또는 {β}의 일부 요소가 0이 아니라면, 함수 S는 가상 축을 따라 죄와 코스의 기하급수적인 성장으로 인해 복소 평면에서 다수의 추가 특이점과 커트라인을 갖습니다. 계수 {α}와 {β}가 작을수록 이러한 특이점은 실제 축에서 더 멀리 떨어져 있습니다.
따라서 복잡한 평면으로 테트레이션을 확장하는 것은 고유성에 필수적입니다. 실제 분석 테트레이션은 고유하지 않습니다.
비원론적 재귀성
테트레이션(로 됨)은 기본 재귀 함수가 아닙니다.모든 기본 재귀 함수 f에 대해 다음과 같은 상수 c가 있다는 것을 유도로 증명할 수 있습니다.
오른쪽을 g로 . 반대로 사분법이 기본 재귀적이라고 가정합니다. x)+ g도 기본 재귀적입니다.위의 부등식에 의해, gx) + ≤() {\g( + g(라는 c가 존재합니다. x { x=를 허용함으로써 + { g(가 모순됩니다
역연산
지수화에는 두 개의 역 연산(루트 연산과 로그 연산)이 있습니다.유사하게, 테트레이션의 역수는 종종 초근(super-root)이라고 불리며, 초 알고리즘(실제로 3보다 크거나 같은 모든 하이퍼 연산은 유사한 역수를 갖습니다.); 예를 , x {{ 함수에서, 두 역수는 y의 초근이고 x의 초 로그 기저입니다.
슈퍼루트
은 기저에 대한 사분원의 역연산입니다. n {{x이면, y는 x( { 또는 {의 n번째 초근입니다.
예를들면,
그래서 2는 65,536의 4번째 초근입니다.
제곱초근

2차 초근, 제곱 초근 또는 초제곱 초근은 와 s의 두 가지 동등한 표기법을 가지고 있습니다. 이는 2 {{}x}}}의 이며 LambertW [19]함수로 나타낼 수 있습니다.
함수는 y () \ y =\
제곱근과 마찬가지로 x의 제곱 초근은 단일 해를 가질 수 없습니다.제곱근과 달리 x의 제곱 초근 수를 결정하는 것은 어려울 수 있습니다.일반적으로 - / <x< \ e} < < 1 이면 x는 0과 1 사이에 두 개의 양의 제곱 초근을 가지며 x > { \ x >이면 x는 1보다 큰 양의 제곱 초근을 갖습니다.x가 양수이고 e- / {{ e보다 실제 제곱 초근이 없지만, 위에 주어진 공식은 [19]1이 아닌 유한 x에 대해 셀 수 없이 많은 복소수 초근을 산출합니다.이 함수는 데이터 [20]클러스터의 크기를 결정하는 데 사용되었습니다.
x ({ x=에서:
기타 슈퍼루트

각각의 정수 n > 2에 대해 x가 정의되고 1 = 1에 대해 증가하므로 x의 n번째 초근 x, xn{가 x ≥ 1에 대해 존재합니다.
3차 초근에 대한 더 간단하고 빠른 공식 중 하나는 재귀 공식입니다. xxx = a, 그리고 다음 x (n + 1) = exp (W (x (n) ln (a)), 예를 들어 x (0) = 1입니다.
그러나 위의 선형 근사치를 사용할 -1 < y ≤ 0이면 + {\ ^{ +s \ ^{는 존재할 수 없습니다.
"큐브 슈퍼루트"는 x3 s로 표현될 수 있고, "4번째 슈퍼루트"는 x4 s로 표현될 수 있으며, "n번째 슈퍼루트"는 xn sdisplaystyle이다.n개 이상의th 루트가 있을 수 있으므로 {}}{x}은(는) 고유하게 정의되지 않을 수 .예를 들어, x는 n이 홀수이면 단일(실제) 초근을 가지며, n이 [citation needed]짝수이면 최대 2개를 갖습니다.
무한한 높이로 테트레이션을 확장하는 것과 마찬가지로, 1/e ≤ x ≤ e인 경우 잘 정의된 n = ∞까지 초근을 확장할 수 있습니다.x = ∞ y = y [ ∞ y ] = y x , {\infty } y = y^{\left[^{\infty } y\right]} = y^{x}}, 따라서 y = x 1 / x ^{1/x}. 따라서 잘 정의될 때 x = x / x sqrt{x}는 정상적인 함수와 달리 {x}이다.예를 들어, 2 = }=}={입니다
겔폰드-슈나이더 정리에 따르면, 임의의 양의 정수 n에 대한은 정수이거나 이며, 는 정수이거나 [21]비합리적입니다.후자의 경우 비이성적인 초근본이 초월적인지 여부는 여전히 미해결 문제입니다.
초논리학
테트레이션의 지속적인 증가(x) 정의 a를 선택하면 모든 실수 x에 대해 해당하는 슈퍼 } log a 4 x \ _4}xx가 정의되고 > 1이 됩니다.
함수a 기호는 다음을 충족합니다.
미해결 질문
테트레이션 확장 문제 외에도 테트레이션과 관련된 몇 가지 미해결 문제가 있으며, 특히 정수와 비합리적 숫자와 같은 수 체계 간의 관계에 관한 문제는 다음과 같습니다.
- π 또는 e가 정수인 양의 정수 n이 있는지 여부는 알려져 있지 않습니다.특히, π 또는 e 중 [citation needed]어느 하나가 정수인지는 알려져 있지 않습니다.
- 양의 정수 n과 양의 비정수 rational [21]q에 대해 q가 합리적인지 여부는 알려져 있지 않습니다.예를 들어, 방정식 x = 2의 양의 근이 합리적인 [citation needed]숫자인지 여부는 알 수 없습니다.
- π 또는 e가 합리적인지 아닌지는 알 수 없으며, 정확한 값도 알 수 없습니다.
참고 항목
메모들
레퍼런스
- ^ a b c d 니링크, 마크산술 연산의 조사.2019년 1월 9일 검색됨.
- ^ R. L. Goodstein (1947). "Transfinite ordinals in recursive number theory". Journal of Symbolic Logic. 12 (4): 123–129. doi:10.2307/2266486. JSTOR 2266486. S2CID 1318943.
- ^ N. Bromer (1987). "Superexponentiation". Mathematics Magazine. 60 (3): 169–174. doi:10.1080/0025570X.1987.11977296. JSTOR 2689566.
- ^ J. F. MacDonnell (1989). "Somecritical points of the hyperpower function ". International Journal of Mathematical Education. 20 (2): 297–305. doi:10.1080/0020739890200210. MR 0994348.
- ^ Weisstein, Eric W. "Power Tower". MathWorld.
- ^ a b Hooshmand, M. H. (2006). "Ultra power and ultra exponential functions". Integral Transforms and Special Functions. 17 (8): 549–558. doi:10.1080/10652460500422247. S2CID 120431576.
- ^ "Power Verb". J Vocabulary. J Software. Retrieved 2011-10-28.
- ^ "Spaces". Retrieved 2022-02-17.
- ^ Meiburg, Alexander (2014). "Analytic Extension of Tetration Through the Product Power-Tower" (PDF). Retrieved 2018-11-29.
- ^ a b c Müller, M. "Reihenalgebra: What comes beyond exponentiation?" (PDF). Retrieved 2018-12-12.
- ^ "Climbing the ladder of hyper operators: tetration". math.blogoverflow.com. Stack Exchange Mathematics Blog. Retrieved 2019-07-25.
- ^ 오일러, L. "디 세리에 람베르티나 플루리미스케이우스 휘니버스 사유 버스."액타 아카드. 과학자. 페트로폴 2호, 29-51, 1783년오일러, L. 오페라 옴니아, 시리즈 프리마, 제6권: 주석 대수학.독일 라이프치히:튜브너, 페이지 350–369, 1921. (팩시밀리)
- ^ Trappmann, Henryk; Kouznetsov, Dmitrii (2010-06-28). "5+ methods for real analytic tetration". Retrieved 2018-12-05.
- ^ 앤드류 로빈스.테트레이션의 분석적인 조각별 확장과 초로그 알고리즘을 위한 해결.확장은 논문의 2부 "결과의 시작"에서 확인할 수 있습니다.
- ^ Paulsen, W.; Cowgill, S. (March 2017). "Solving in the complex plane" (PDF). Advances in Computational Mathematics. 43: 1–22. doi:10.1007/s10444-017-9524-1. S2CID 9402035.
- ^ Kouznetsov, D. (July 2009). "Solution of in complex -plane" (PDF). Mathematics of Computation. 78 (267): 1647–1670. doi:10.1090/S0025-5718-09-02188-7.
- ^ Kneser, H. (1950). "Reelle analytische Lösungen der Gleichung und verwandter Funktionalgleichungen". Journal für die reine und angewandte Mathematik (in German). 187: 56–67.
- ^ Paulsen, W. (June 2018). "Tetration for complex bases". Advances in Computational Mathematics. 45: 243–267. doi:10.1007/s10444-018-9615-7. S2CID 67866004.
- ^ a b Corless, R. M.; Gonnet, G. H.; Hare, D. E. G.; Jeffrey, D. J.; Knuth, D. E. (1996). "On the Lambert W function" (PostScript). Advances in Computational Mathematics. 5: 333. arXiv:1809.07369. doi:10.1007/BF02124750. S2CID 29028411.
- ^ Krishnam, R. (2004), "대규모 무선 센서 네트워크의 효율적인 자체 구성" – 논문, 보스턴 대학교, 공과대학, 37–40페이지
- ^ a b Marshall, Ash J., Tan, Iren, "비합리적인 형식의a 합리적인 수", Mathematical Gazette 96, 2012년 3월, 106-109페이지
- 다니엘 가이스러, 테트레이션
- Ioannis Galidakis, 정수가 아닌 항목으로 하이퍼4 확장(2006년 이전 버전)(다음 참조의 리뷰를 더 간단하고 읽기 쉬움)
- Ioannis Galidakis, On Extending hyper4 및 Knuth의 위쪽 화살표 표기법을 실제로 (날짜 없음, 2006 또는 이전).
- Robert Munafo, hyper4 함수를 실제로 확장(실제 숫자로 테트레이션을 확장하는 것에 대한 비공식 논의).
- 로드 반데벤느, 2의 제곱근의 테트레이션.(2004).(타테레이션을 실수로 확장합니다.)
- Ioannis Galidakis, Mathematics, (타테레이션 연구에 대한 최종 참고 문헌 목록) Lambert W 함수, 리만 표면 및 분석 연속성에 대한 많은 정보.)
- 조셉 맥도넬, 초강력 기능의 몇 가지 중요한 점.
- Dave L. Renfro, 무한 반복 지수 웹 페이지
- Knobel, R. (1981). "Exponentials Reiterated". American Mathematical Monthly. 88 (4): 235–252. doi:10.1080/00029890.1981.11995239.
- Hans Maurer, "Uber die y [ [x ( )] y=)]}} fürganzahliges Arguments (Abundanzen)"Mittheilungender Mathematische Gesellschaft in Hamburg 4, (1901), 페이지 33–50. (노벨의 논문에서 a})의 사용에 대한 참조)
- 제4차 작전
- 루카 모로니, 무한한 파워타워의 기묘한 특성 (https://arxiv.org/abs/1908.05559)
진일보한 내용
- Galidakis, Ioannis; Weisstein, Eric Wolfgang. "Power Tower". MathWorld. Retrieved 2019-07-05.


 왼쪽 독립 b는 일반적입니다.
왼쪽 독립 b는 일반적입니다.









 (
(

 대해
대해









 Ackermann 함수의 관점에서 쓸 수 있습니다.
Ackermann 함수의 관점에서 쓸 수 있습니다.
![{\displaystyle {\begin{aligned}&\operatorname {uxp} _{a}n\\[2pt]&a^{\frac {n}{}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d44510324a0e36390e6a2a190dc9cc5597244759)
![{\displaystyle {\begin{aligned}&a[4]n\\[2pt]&H_{4}(a,n)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/748ac1b86caad44f63e3dd7b50768a79d4b534f6)
 (를)
(를) 

 대략 그 정도의 기간 동안 사용되었습니다.
대략 그 정도의 기간 동안 사용되었습니다.
































 , 다음 행의 경우 차이가 더 작습니다.
, 다음 행의 경우 차이가 더 작습니다. 
 대부분의 경우에 해당되지 않습니다.
대부분의 경우에 해당되지 않습니다.







 (가) 일관되게 정의되지 않았습니다.따라서,
(가) 일관되게 정의되지 않았습니다.따라서,  앞에서 주어진 공식에 의해 명확하게 정의되지 않습니다.
앞에서 주어진 공식에 의해 명확하게 정의되지 않습니다. 잘 정의되어 있으며 다음과 같이
잘 정의되어 있으며 다음과 같이 



 여전히 유지됩니다.
여전히 유지됩니다.
![{\displaystyle {\begin{aligned}a'&=e^{-{\frac {1}{2}}{\pi b}}\cos {\frac {\pi a}{2}}\\[2pt]b'&=e^{-{\frac {1}{2}}{\pi b}}\sin {\frac {\pi a}{2}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/42ede7788090fc4d176fe752d23871f2f7830733)










 대한 무한 반복 지수 수렴 (
대한 무한 반복 지수 수렴 (

 2로 수렴하므로 2와 같다고 할 수 있습니다.2를 향한 추세는 작은 유한 타워를 평가하여 확인할 수 있습니다.
2로 수렴하므로 2와 같다고 할 수 있습니다.2를 향한 추세는 작은 유한 타워를 평가하여 확인할 수 있습니다.








 정의는 다음과 같이 규칙과 일치합니다.
정의는 다음과 같이 규칙과 일치합니다.

 만족시키는 초영속
만족시키는 초영속 
















 연속적이고 다음 조건을 만족시킵니다.
연속적이고 다음 조건을 만족시킵니다.



![{\displaystyle f(x)=\exp _{a}^{[x]}\left(a^{(x)}\right)=\exp _{a}^{[x+1]}((x))\quad {\text{for all}}\;\;x>-2,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f544121fa31a3f82320644bf82487a3182788cb8)
![{\displaystyle (x)=x-[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2d3c5b2b6494c985ffe63ec9548834cfae900bc0) x 및
x 및 ![{\displaystyle \exp _{a}^{[x]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a81a37f010ff0850c71f204426bb68d1964b34bc)

![[x]](https://wikimedia.org/api/rest_v1/media/math/render/svg/07548563c21e128890501e14eb7c80ee2d6fda4d)
 대한 선형 근사치는 연속적으로 미분할 수 있지만, 두 번째 도함수는 인수의 정수 값에 존재하지 않습니다.후쉬만드는 다음과 같은 또 다른 고유성 정리를 도출했습니다.
대한 선형 근사치는 연속적으로 미분할 수 있지만, 두 번째 도함수는 인수의 정수 값에 존재하지 않습니다.후쉬만드는 다음과 같은 또 다른 고유성 정리를 도출했습니다.



 (
( 유일한 해이며,
유일한 해이며, 






 굵은 곡선으로 표시됩니다.
굵은 곡선으로 표시됩니다.










![{\sqrt[{n}]{x}}_{s}](https://wikimedia.org/api/rest_v1/media/math/render/svg/91ceac95b8e3013df90c5fe936f35321b51c80bb)
![{\displaystyle {\sqrt[{n}]{x}}_{4}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2348e19c30eb97e038780ba512de2506d12a186c)


 두 가지 동등한 표기법을 가지고 있습니다. 이는 2
두 가지 동등한 표기법을 가지고 있습니다. 이는 2 


![{\displaystyle {\sqrt[{y}]{x}}=\log _{y}x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1d71585c84cda67f69928d975bd8d1f012355543)







![{\sqrt[{\infty }]{2}}_{s}=2^{1/2}={\sqrt {2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/898b11064bfad6045a6409a07d8dea136187e403)
 {s
{s![{\sqrt[{3}]{n}}_{s}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a97577f561f9772efcb44d1dc7f43beb9099ac47) 정수이거나
정수이거나 







![y=x^{[x^{[x(\cdots )]}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab69cf15b7afca0a5f9cc89da314bbb89b61a749)



