시간 척도 미적분학

수학에서 시간 척도 미적분은 미분방정식과의 차이 방정식 이론의 통일로, 적분 및 미분학을 유한 차이의 미적분과 통일하여 혼합 이산-연속 동력학 시스템을 연구하기 위한 형식주의를 제공한다. 그것은 이산형 데이터와 연속형 데이터를 동시에 모델링해야 하는 모든 분야에서 응용 프로그램을 가지고 있다. 그것은 실제 숫자에 정의된 함수를 구별하는 경우 그 정의는 표준 분화와 동일하지만, 정수에 정의된 함수를 사용하는 경우 선도 차이 연산자와 동일하다는 새로운 파생상품의 정의를 제공한다.

역사

시간 척도 미적분은 1988년 독일의 수학자 스테판 힐거에 의해 소개되었다.^[1] 그러나 이전에도 비슷한 생각이 사용되어 왔으며 적어도 총액과 통합을 통일하는 리만-스티엘트제스의 도입으로 거슬러 올라간다.

동적 방정식

미분방정식에 관한 많은 결과는 차이방정식에 대한 해당 결과에 쉽게 전달되는 반면, 다른 결과는 연속방정식과 완전히 다른 것으로 보인다.^[2] 시간 척도에 대한 동적 방정식의 연구는 그러한 불일치를 밝혀내고 결과를 두 번 증명하는 것을 피하는데 도움이 된다. 미분 방정식은 한 번, 차이 방정식은 한 번이다. 일반적인 생각은 알 수 없는 함수의 영역이 소위 시간 척도(시간 집합이라고도 함)인 동적 방정식에 대한 결과를 증명하는 것인데, 이는 실재의 임의로 닫힌 부분집합일 수도 있다. 이런 식으로 결과는 실수의 집합이나 정수 집합뿐만 아니라 칸토어 집합과 같은 보다 일반적인 시간 척도에도 적용된다.

시간 척도에서 미적분학의 가장 인기 있는 세 가지 예는 미분학, 차이 미적분학, 양자 미적분학이다. 시간 척도의 동적 방정식은 모집단 역학에서와 같은 응용에 대한 잠재력을 가지고 있다. 예를 들어, 그들은 계절에 따라 지속적으로 진화하고, 그들의 알이 배양되거나 휴면 중일 때 겨울에 멸종하고, 그리고 새로운 계절에 부화하여 과대포화하지 않는 개체군을 발생시킬 수 있다.

형식 정의

시간 척도(또는 측정 체인)는 실제 $\mathbb {R}$ R ${\$ 의 닫힌 부분 집합이다 $\mathbb {R}$ 일반적인 시간 척도의 $\mathbb {T}$ 인 표기법은 T ${\$ 이다 $\mathbb {T}$

가장 흔히 접하는 시간 척도의 두 가지 예는 실제 숫자 $\mathbb {R}$ ${\$ 과 $\mathbb {R}$ (와) 이산 시간 척도 $h\mathbb {Z}$ $h\mathbb {Z}$ ${\$ 이다 $h\mathbb {Z}$

시간 척도의 단일 점은 다음과 같이 정의된다.

\mathb {T}에서 \displaystyle t:t\in \mathb {T}

시간 단위 작업

개별 시간 척도의 전방 점프, 후진 점프 및 곡물 처리 연산자

전진 점프와 후진 점프 연산자는 각각 주어진 $점$ t $t$ 의 오른쪽과 왼쪽에 있는 시간 척도에서 가장 가까운 점을 나타낸다 $t$ 공식:

\sigma (t)=\inf\{s\in \mathbb {T} :s>t\}

( t

\sigma (t)=\inf\{s\in \mathbb {T} :s>t\}

)

\sigma (t)=\inf\{s\in \mathbb {T} :s>t\}

=

\sigma (t)=\inf\{s\in \mathbb {T} :s>t\}

\sigma (t)=\inf\{s\in \mathbb {T} :s>t\}

\sigma (t)=\inf\{s\in \mathbb {T} :s>t\}

\sigma (t)=\inf\{s\in \mathbb {T} :s>t\}

: s

\sigma (t)=\inf\{s\in \mathbb {T} :s>t\}

>

\sigma (t)=\inf\{s\in \mathbb {T} :s>t\}

\sigma (t)=\inf\{s\in \mathbb {T} :s>t\}

\sigma(t)=\inf\{s\in \mathb {T

:

s>t\}}(

전방 시프트/점프 연산자)

\rho (t)=\sup\{s\in \mathbb {T} :s<t\}

(

\rho (t)=\sup\{s\in \mathbb {T} :s<t\}

)

\rho (t)=\sup\{s\in \mathbb {T} :s<t\}

=

\rho (t)=\sup\{s\in \mathbb {T} :s<t\}

{

\rho (t)=\sup\{s\in \mathbb {T} :s<t\}

\rho (t)=\sup\{s\in \mathbb {T} :s<t\}

T

\rho (t)=\sup\{s\in \mathbb {T} :s<t\}

: s <

\rho (t)=\sup\{s\in \mathbb {T} :s<t\}

{\displaystyle \rho(t)=\supp\{s\in \mathb {T} :s<t\}}(

뒤로 이동/점프 연산자)

곡물성 $[\displaystyle \mu }$ 은 오른쪽의 한 지점에서 가장 가까운 지점까지의 거리로서 $\mu$ 다음과 같이 주어진다.

\displaystyle \mu(t)=\disma(t)-t.}

오른쪽-dense $t$ {\ $displaystyle t},$ $\sigma (t)=t$ $\sigma (t)=t$ = $\sigma (t)=t$ $\sigma(t)=t$ 및 $\sigma (t)=t$ $\mu (t)=0$ ) $\mu (t)=0$ = $\mu (t)=0$ ${\displaystyle \mu(t)=0$
왼쪽-dense $t$ $t$ 의 경우, $t$ $\rho (t)=t.$ ) $\rho (t)=t.$ = t $\rho (t)=t.$ . ${\displaystyle \rho(t)=t.$ $}$

점분류

서로 다른 분류로 시간 척도의 여러 점

t $t\in \mathbb {T}$ $t\in \mathbb {T}$ ${\$ $t$ $t$ 의 $t$ 경우:

$\rho (t)=t$ ) $\rho (t)=t$ = $\rho (t)=t$ $\rho(t)=t$ 인 경우 왼쪽 조밀도
$\sigma (t)=t$ ) $\sigma (t)=t$ = $\sigma (t)=t$ $\sigma(t)=t$ 인 경우 오른쪽 밀도
$\rho (t)<t$ ( $\rho (t)<t$ ) $\rho (t)<t$ < $\rho(t)$ 이(가) 있는 경우 왼쪽 흩어져 있음
$\sigma (t)>t$ ( $\sigma (t)>t$ ) $\sigma (t)>t$ > t $\sigma (t)>t$ 일 경우 우측 산란
좌측 및 우측 밀도가 모두 밀도가 높은 경우 밀도가 높은 경우
왼쪽과 오른쪽이 모두 흩어진다면 고립된

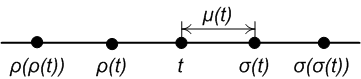
오른쪽 그림에서 설명한 대로:

점 $t_{1}$ $t_{1}$ ${\$ }는 $t_{1}$ 밀도가 높다.
점 $t_{2}$ $t_{2}$ $t_{2}$ ${\$ 좌측 밀도 및 우측 산란
점 $t_{3}$ $t_{3}$ ${\$ 이(가) 분리됨 $t_{3}$
점 $t_{4}$ $t_{4}$ ${\$ 은(는) 흩어져 있고 우측 밀도가 높음 $t_{4}$

연속성

시간 척도의 연속성은 밀도와 동등한 것으로 재정의된다. 시간 척도는 점 $t$ $t$ 에서 우측 밀도가 높은 경우 $t$ 점 $t$ $t$ 에서 우측 연속이라고 하며 $t$ 마찬가지로 점 $t$ ${\displaystyt t}$ 에서 좌측 밀도가 높은 경우 $t$ $점$ t ${\displaystyt}$ 에서 좌측 연속이라고 한다 $t$

파생상품

기능 사용:

f:\mathb {T} \to \mathb {R},

(R은 Banach 공간이 될 수 있지만 단순성을 위해 실제 라인으로 설정됨)

정의: 다음과 같은 경우에만 델타 파생상품(Hilger $)$ f $f^{\Delta }(t)$ Δ $f^{\Delta }(t)$ ) {\ $displaystyle$ f^{\ $Delta$ }(t)}}이 $($ 가) 존재한다 $f^{\Delta }(t)$ .

$\varepsilon >0$ > $\varepsilon >0$ $\varepsilon >0$ 마다 $t$ $t$ 의 $U$ $근린$ U{\ $displaystyle U}$ 이 $\varepsilon >0$ (가) 존재하며, 다음과 $t$ 같다.

\sigma (t)-f^{\Delta }(t)(\sigma (t)-s)\오른쪽 \leq \varepsilon \left \sigma (t)-s\오른쪽

$U$ $U$ 의 $s$ 모든 $s$ {\ $displaystyle s$ $U$ 에 대해

Take $\mathbb {T} =\mathbb {R} .$ Then $\sigma (t)=t$ , $\mu (t)=0$ , $f^{\Delta }=f'$ ; is the derivative used in standard calculus. If $\mathbb {T} =\mathbb {Z}$ (the integers), $\sigma (t)=t+1$ , $\mu (t)=1$ , $f^{\Delta }=\Delta f$ is the forward difference operator used in difference equations.

통합

델타 적분은 델타 파생상품에 대한 반물질로 정의된다. $F(t)$ ( t $F(t)$ ) $F(t)$ 이(가) 연속적인 $f(t)=F^{\Delta }(t)$ $f(t)=F^{\Delta }(t)$ ( $f(t)=F^{\Delta }(t)$ t $f(t)=F^{\Delta }(t)$ ) = $f(t)=F^{\Delta }(t)$ $f(t)=F^{\Delta }(t)$ ( $f(t)=F^{\Delta }(t)$ ) ${\displaystyle f(t)=$ 인 $F(t)$ 경우 $F^{\Delta }(t)$ 1세트 $f(t)=F^{\Delta }(t)$

\int _{r}^{s}f(t)\델타 (t)=F(s)-F(r)

라플라스 변환 및 z 변환

라플라스 변환은 임의의 시간 척도에 대해 동일한 변환 표를 사용하는 시간 척도의 기능에 대해 정의될 수 있다. 이 변환은 시간 척도에서 동적 방정식을 푸는 데 사용될 수 있다. 시간 척도가 음이 아닌 정수인 경우 변환은 수정된^[2] Z 변환과 동일하다.

{\mathcal {Z}\{x[z]\}={\frac {{\mathcal {{Z}\{x[z+1]\}{z+1}1}}}

부분 분화

부분 미분 방정식과 부분 차이 방정식은 시간 척도에서 부분 동적 방정식으로 통일된다.^[3]^[4]^[5]

다중 통합

시간 척도의 다중 통합은 Bohner(2005)에서 처리된다.^[6]

시간 척도에서의 확률론적 동적 방정식

확률적 미분 방정식과 확률적 차이 방정식은 시간 척도에서 확률적 동적 방정식으로 일반화할 수 있다.^[7]

시간 척도로 이론 측정

모든 시간 척도가 다음을 통해 정의되는 자연 측정값과^[8]^[9] 연관됨

\mu ^{\Delta }(A)=\lambda(\rho ^{-1}(A),

여기서 $\lambda$ {\ $displaystyle \lambda }$ 은 $\lambda$ $($ 는) Lebesgue 측정값을 나타내며, { $\rho$ ${\$ 에 $\mathbb {R}$ 된 후진 변속 연산자 $\rho$ $\mathbb {R}$ 델타 적분은 이 측정과 관련하여 일반적인 Lebesgue-Stieltjes 일체형으로 판명되었다.

\int _{r}^{s}f(t)\델타 t=\int _{[r,s)}f(t)d\mu ^{\Delta }(t)

그리고 델타 파생상품은 본 측정치와^[10] 관련하여 라돈-니코디엠 파생상품으로 판명되었다.

f^{\Delta }(t)={\frac {df}{d\mu ^{\Delta }}}(t).

시간 척도 분포

Dirac 델타와 Kronecker 델타는 힐거 델타로 시간 척도로 통일된다.^[11]^[12]

\delta _{a}^{\mathb {H}={\begin{case}{\frac {1}{\mu(a)}},&t=a\0,&t\neq a\case}}}

시간 척도의 적분 방정식

적분 방정식과 합계 방정식은 시간 척도에서 적분 방정식으로 통일된다.^{[citation needed]}

시간 척도 단위 미적분법

시간 척도의 분수 미적분은 바스토스, 모지르스카, 토레스에서 처리된다.^[13]

참고 항목

참조

^ Hilger, Stefan (1989). Ein Maßkettenkalkül mit Anwendung auf Zentrumsmannigfaltigkeiten (PhD thesis). Universität Würzburg. OCLC 246538565.
^ ^a ^b Martin Bohner & Allan Peterson (2001). Dynamic Equations on Time Scales. Birkhäuser. ISBN 978-0-8176-4225-9.
^ Ahlbrandt, Calvin D.; Morian, Christina (2002). "Partial differential equations on time scales". Journal of Computational and Applied Mathematics. 141 (1–2): 35–55. Bibcode:2002JCoAM.141...35A. doi:10.1016/S0377-0427(01)00434-4.
^ Jackson, B. (2006). "Partial dynamic equations on time scales". Journal of Computational and Applied Mathematics. 186 (2): 391–415. Bibcode:2006JCoAM.186..391J. doi:10.1016/j.cam.2005.02.011.
^ Bohner, M.; Guseinov, G. S. (2004). "Partial differentiation on time scales" (PDF). Dynamic Systems and Applications. 13: 351–379.
^ Bohner, M; Guseinov, GS (2005). "Multiple integration on time scales". Dynamic Systems and Applications. CiteSeerX 10.1.1.79.8824.
^ Sanyal, Suman (2008). Stochastic Dynamic Equations (PhD thesis). Missouri University of Science and Technology. ProQuest 304364901.
^ Guseinov, G. S. (2003). "Integration on time scales". J. Math. Anal. Appl. 285: 107–127. doi:10.1016/S0022-247X(03)00361-5.
^ Deniz, A. (2007). Measure theory on time scales (PDF) (Master's thesis). İzmir Institute of Technology.
^ Eckhardt, J.; Teschl, G. (2012). "On the connection between the Hilger and Radon–Nikodym derivatives". J. Math. Anal. Appl. 385 (2): 1184–1189. arXiv:1102.2511. doi:10.1016/j.jmaa.2011.07.041.
^ Davis, John M.; Gravagne, Ian A.; Jackson, Billy J.; Marks, Robert J. II; Ramos, Alice A. (2007). "The Laplace transform on time scales revisited". J. Math. Anal. Appl. 332 (2): 1291–1307. Bibcode:2007JMAA..332.1291D. doi:10.1016/j.jmaa.2006.10.089.
^ Davis, John M.; Gravagne, Ian A.; Marks, Robert J. II (2010). "Bilateral Laplace Transforms on Time Scales: Convergence, Convolution, and the Characterization of Stationary Stochastic Time Series". Circuits, Systems and Signal Processing. 29 (6): 1141–1165. doi:10.1007/s00034-010-9196-2.
^ Bastos, Nuno R. O.; Mozyrska, Dorota; Torres, Delfim F. M. (2011). "Fractional Derivatives and Integrals on Time Scales via the Inverse Generalized Laplace Transform". International Journal of Mathematics & Computation. 11 (J11): 1–9. arXiv:1012.1555. Bibcode:2010arXiv1012.1555B.

추가 읽기

Agarwal, Ravi; Bohner, Martin; O’Regan, Donal; Peterson, Allan (2002). "Dynamic equations on time scales: a survey". Journal of Computational and Applied Mathematics. 141 (1–2): 1–26. Bibcode:2002JCoAM.141....1A. doi:10.1016/S0377-0427(01)00432-0.
시간 척도에서의 동적 방정식 연산 및 응용 수학 저널 특별호(2002)
동적 방정식과 응용의 차이 방정식 발전 특별호(2006)
시간 척도에서의 동적 방정식: 정성적 분석 및 응용 비선형 역학 및 시스템 이론 특별호(2009)

외부 링크

[hilger-1] Hilger, Stefan (1989). Ein Maßkettenkalkül mit Anwendung auf Zentrumsmannigfaltigkeiten (PhD thesis). Universität Würzburg. OCLC 246538565.

[bp-2] Martin Bohner & Allan Peterson (2001). Dynamic Equations on Time Scales. Birkhäuser. ISBN 978-0-8176-4225-9.

[3] Ahlbrandt, Calvin D.; Morian, Christina (2002). "Partial differential equations on time scales". Journal of Computational and Applied Mathematics. 141 (1–2): 35–55. Bibcode:2002JCoAM.141...35A. doi:10.1016/S0377-0427(01)00434-4.

[4] Jackson, B. (2006). "Partial dynamic equations on time scales". Journal of Computational and Applied Mathematics. 186 (2): 391–415. Bibcode:2006JCoAM.186..391J. doi:10.1016/j.cam.2005.02.011.

[5] Bohner, M.; Guseinov, G. S. (2004). "Partial differentiation on time scales" (PDF). Dynamic Systems and Applications. 13: 351–379.

[6] Bohner, M; Guseinov, GS (2005). "Multiple integration on time scales". Dynamic Systems and Applications. CiteSeerX 10.1.1.79.8824.

[7] Sanyal, Suman (2008). Stochastic Dynamic Equations (PhD thesis). Missouri University of Science and Technology. ProQuest 304364901.

[8] Guseinov, G. S. (2003). "Integration on time scales". J. Math. Anal. Appl. 285: 107–127. doi:10.1016/S0022-247X(03)00361-5.

[9] Deniz, A. (2007). Measure theory on time scales (PDF) (Master's thesis). İzmir Institute of Technology.

[10] Eckhardt, J.; Teschl, G. (2012). "On the connection between the Hilger and Radon–Nikodym derivatives". J. Math. Anal. Appl. 385 (2): 1184–1189. arXiv:1102.2511. doi:10.1016/j.jmaa.2011.07.041.

[11] Davis, John M.; Gravagne, Ian A.; Jackson, Billy J.; Marks, Robert J. II; Ramos, Alice A. (2007). "The Laplace transform on time scales revisited". J. Math. Anal. Appl. 332 (2): 1291–1307. Bibcode:2007JMAA..332.1291D. doi:10.1016/j.jmaa.2006.10.089.

[12] Davis, John M.; Gravagne, Ian A.; Marks, Robert J. II (2010). "Bilateral Laplace Transforms on Time Scales: Convergence, Convolution, and the Characterization of Stationary Stochastic Time Series". Circuits, Systems and Signal Processing. 29 (6): 1141–1165. doi:10.1007/s00034-010-9196-2.

[13] Bastos, Nuno R. O.; Mozyrska, Dorota; Torres, Delfim F. M. (2011). "Fractional Derivatives and Integrals on Time Scales via the Inverse Generalized Laplace Transform". International Journal of Mathematics & Computation. 11 (J11): 1–9. arXiv:1012.1555. Bibcode:2010arXiv1012.1555B.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

Search