빌루나비로툰다

빌루나비로툰다
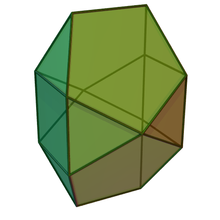유형	존슨 J90 - J91 - J92
얼굴	2x4 삼각형 정사각형 2개 펜타곤 4개
가장자리	26
정점	14
꼭지점 구성	4(3.52) 8(3.4.3.5) 2(3.5.3.5)
대칭군	D2시간
이중 다면체	-
특성.	볼록하게 하다
그물

기하학에서 빌루나비로툰다는 존슨 고형물(J₉₁)의 하나이다.존슨 고체는 일반 폴리곤 면으로 구성되지만 균일한 폴리헤드라(Platonic 고형물, 아르키메데스 고형물, 프리즘 또는 항정신병)가 아닌 92개의 엄격히 볼록한 폴리헤드라 중 하나이다.그것들은 1966년에 처음으로 이 다면체들을 나열한 노먼 존슨이 이름을 지었다.^[1]

기하학

그것은 플라토닉과 아르키메데스 고형물의 "절단과 붙여넣기" 조작에서 발생하지 않는 존슨 고형물 중 하나이다.

그러나, 그것은 아르키메데스 고체인 이코시다데카헤드론과 강한 관계를 가지고 있다.두 개의 펜타곤과 두 개의 삼각형으로 이루어진 두 개의 군집 중 하나는 이코시다데카헤드론 위에 있는 일치된 얼굴 조각과 정렬할 수 있다.만약 두 개의 빌루나비 로툰대가 이코시다데카헤드론의 반대편에 이렇게 정렬되어 있다면, 빌루나비 로튼대의 두 정점이 이코시다데카헤드론의 바로 중심에서 만난다.

빌루나비로툰다의 나머지 두 개의 얼굴 군집, 즉 LUN(한 사각형의 반대편에 인접한 두 개의 삼각형을 나타내는 각 LUN)은 롬비코시도데카헤드론에 있는 서로 합치된 얼굴 조각과 정렬할 수 있다.만약 두 개의 빌루나비 로툰대가 롬비코시도데카헤드론의 반대편에 이렇게 정렬되어 있다면, 롬비코시도데카헤드론의 바로 중심에 있는 빌루나비 로튼대 사이에 큐브를 넣을 수 있다.

인접한 두 쌍의 펜타곤(각 쌍의 가장자리를 공유하는 펜타곤)도 메타비드 제거된 이코사헤드론의 오각형 면과 정렬할 수 있다.

빌루나비로툰다는 큐옥타헤드론과의 관계가 약한데, 큐옥타헤드론의 네모난 면을 펜타곤으로 대체하여 만들 수도 있기 때문이다.

데카르트 좌표, 평행 좌표.

다음은 가장자리 길이 1의 원점을 중심으로 한 빌루나비 로툰다의 정점을 정의한다.

${\displaystyle \left(0,0,\pm {\frac {}{varphi }{2}}\오른쪽)}$

${\displaystyle \left(\pm {\frac {\varphi +1}{2}},\pm {1}{1}{2}},0\right)$

${\displaystyle \left(\pm {\frac {1}{1}:{2}},\pm {\frac {1}{1}:{1}{2}}, 오른쪽)}$

여기서 $\phi {\displaystyle }$= ${\displaystyle 1\frac{\mathrm{}}{}}$+ ${\displaystyle \frac{5\sqrt{\mathrm{}}}{}}$ ${\displaystyle \frac{2}{\mathrm{}}}$ ${\$이 황금비율이다.

관련 다면체 및 허니컴

6개의 빌루나비로툰대는 화농대칭이 있는 정육면체 주위로 증강될 수 있다.B. M. Stewart는 이 6-bilunabirotunda 모델을 6J₉₁(P₄)로 분류했다.^[2]

빌루나비 로툰다는 공간을 채우는 벌집처럼 일반 도데카헤드와 큐브와 함께 사용할 수 있다.

우주충전 벌집

입방체 둘레 6빌루나비로툰대

미디어 재생 정육면체, 도데카헤드라, 빌루나비로툰다 테셀레이션 애니메이션 도데카헤드론 둘레 12빌루나비로툰대

외부 링크

• Eric W. Weisstein, Bilunabirotunda (Johnson solid) at MathWorld.
• 미라클 스페이스필링(도데카헤드론&큐브)&존슨 솔리드 91번)