교대군
Alternating group| 대수구조 → 그룹 이론 집단 이론 |
|---|
 |
수학에서 교번군은 유한 집합의 짝수 순열의 그룹이다.n 원소의 집합에 있는 교번 그룹을 도 n의 교번 그룹이라고 하며, 또는 n 글자에 교번 그룹이라고 하며, An 또는 Alt(n)로 표시한다.null
기본 속성
n > 1의 경우, 그룹 A는n 지수 2를 갖는 대칭 그룹 S의n 정류자 하위 그룹이며, 따라서 n!/2 요소를 가진다.대칭군에서 설명하는 서명군 동형상 sgnn : S → {1, -1}의 커널이다.null
그룹 A는n n ≤ 3인 경우에만 아벨리안이고, n = 3 또는 n ≥ 5인 경우에만 단순하다.A는5 순서가 60인 가장 작은 비아벨리안 단순 집단이며, 해결이 불가능한 가장 작은 집단이다.null
그룹4 A는 클라인 4그룹 V를 적절한3 정상 하위그룹으로 가지고 있는데, 즉 A3 = Z에 대한 A의4 추방의 커널인 ID(), (12)(34), (13)(24), (14)(23)}이다.정확한 순서가 V → A4 → A3 = Z 입니다3.갈루아 이론에서 이 지도, 아니 오히려 해당 지도4 S → S는3 라그랑주 분해능 입방체를 사분위에 연관시키는 것에 해당하며, 로도비코 페라리(Lodovico Perrariar)가 확립한 바와 같이 사분위 다항식을 급진자에 의해 해결할 수 있게 한다.null
커플러시 클래스
대칭 그룹에서와 같이 A의n 요소에 의해 결합되는 A의n 두 요소는 동일한 주기 형태를 가져야 한다.그러나 그 반대가 반드시 사실인 것은 아니다.사이클 모양이 동일한 길이의 사이클이 없는 홀수 길이의 사이클로만 구성되는 경우, 길이 1 사이클이 사이클 유형에 포함되는 경우, 이 사이클 형태에는 정확히 두 개의 결합 등급이 있다(Scott 1987, §11.1, p299).null
예:
- 두 순열(123)과 (132)은 A의3 결합체가 아니므로 S의3 결합형이다.
- 순열 (123)(45678)은 A에서8 역행 (132)(48765)에 결합되지 않지만, 두 순열은 동일한 주기 형태를 가지고 있으므로 S에서8 결합된다.
대칭군과의 관계
- 대칭 그룹을 참조하십시오.
생성자 및 관계
n ≥ 3의 경우, 3 사이클은 전이 쌍을 조합하여 얻을 수 있기 때문에 3 사이클에 의해 A가n 생성된다.이 생성 세트는 종종 A가n n ≥ 5에 대해 단순하다는 것을 증명하기 위해 사용된다.
자동형성군
| n | 자동(An) | 아웃(An) |
|---|---|---|
| n ≥ 4, n ≠ 6 | Sn | Z2 |
| n = 1, 2 | Z1 | Z1 |
| n = 3 | Z2 | Z2 |
| n = 6 | S6 ⋊ Z2 | V = Z2 × Z2 |
n > 3의 경우, n = 6을 제외하고, A의n 자동형 집단은 내부n 자동형 집단이 A이고n 외부 자동형 집단이 Z인2 대칭형 집단이다. 외부 자동형 집단은 홀수 순열에 의한 결합에서 비롯된다.null
n = 1과 2의 경우 자동형성 그룹은 사소한 것이다.n = 3의 경우, 자동형 집단은 Z이며2, 사소한 내적 자동형 집단과 외부 자동형 집단은 Z이다2.null
A의6 외부 오토모르피즘 그룹은 클라인 4그룹 V = Z2 × Z이며2, S의6 외부 오토모르피즘과 관련이 있다.A의6 추가 외부 자동형은 3주기(예: (123)와 형상 3의2 요소(예: (123) (456))를 교환한다.null
예외 이형성
Lie 타입의 작은 교대 그룹과 작은 그룹들, 특히 투사적인 특수 선형 그룹들 사이에는 몇 가지 예외적인 이형성이 있다.다음은 다음과 같다.
- A는4 PSL2(3)[1]에 대해 이형이며, 치랄 4면 대칭의 대칭군이다.
- A는5 PSL2(4), PSL2(5), 그리고 치랄 이코사이드 대칭의 대칭군에 대한 이형이다. (PSL2(F5) → A의5 단순한 순서 60의 분류를 이용한 간접 이형성을 참조하고[1], 여기서 직접 증거를 참조한다.
- A는6 PSL2(9)과 PSP4(2)에 이형이다.'
- A는8 PSL4(2)과 이형이다.
보다 분명한 것은 A는3 주기 그룹 Z에3 이형이며, A0, A1, A는2 사소한 그룹에도 이형이다(또한 SL1(q) = PSL1(q)이다).null
예제44 S 및 A
 A3 = Z3(주문 3) | 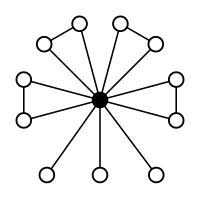 A4 (주문 12) | 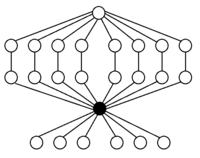 A42 × Z (주문 24) |
 S3 = Dih3 (주문 6) |  S4 (주문 24) |  왼쪽의4 A4 in S |
3-공간5 회전의 부분군으로서의 예제 A
A는5 3공간에 있는 도데카헤드론의 등각류 그룹이기 때문에 표현5 A → SO3(R)가 있다.null
이 그림에서 다면체의 정점들은 집단의 요소들을 나타내며, 구의 중심은 정체성 요소를 나타낸다.각 꼭지점은 중심에서 해당 꼭지점까지의 축에 대한 회전을 라디안 단위로 원점으로부터의 거리와 동일한 각도로 나타낸다.동일한 다면체의 정점은 동일한 결합 등급에 있다.A에5 대한 결합 등급 방정식은 1 + 12 + 12 + 15 + 20 = 60이므로, 우리는 4개의 구별되는 (비경쟁적) 다면체를 얻는다.null
각 다면체의 정점은 그 결합 등급의 요소와 편향적으로 일치하는데, 외부 표면의 ICosidodechedron으로 대표되는 결합 등급(2,2)을 제외하고, 그 반향 정점이 서로 식별된다.이러한 이중화의 이유는 해당 회전이 π 라디안들에 의해 이루어지기 때문에 두 방향 중 어느 방향에서든 길이 π의 벡터로 나타낼 수 있기 때문이다.따라서 (2,2)-주기의 등급은 15개의 요소를 포함하는 반면, 이코시다데카헤드론은 30개의 꼭지점을 가진다.null
A에서5 12개의 5주기 중 2개의 결합 등급은 각각 2개 반경의 2개 반경과 4개 반경의 2개 반경으로 표현된다.Out(A5) ≃ Z의2 비경쟁적 외형 자동형은 이 두 등급과 그에 상응하는 이코사헤드라를 상호 교환한다.null
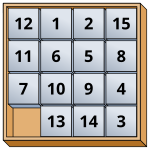
예: 15개 퍼즐
슬라이딩 퍼즐의 유명한 예인 15 퍼즐은 3 사이클로 15 퍼즐의 조합이 생성될 수 있기 때문에 교대 그룹 A로 나타낼15 수 있음을 증명할 수 있다.[2]실제로 같은 크기의 사각 타일을 가진 2k - 1 슬라이딩 퍼즐은 모두 A로2k−1 나타낼 수 있다.null
부분군
A4가장 작은 그룹은 라그랑주 정리의 그 반대는 일반적으로:, 반드시 G의 주문 d와 하위 그룹 존재하지 않습니다. 그 그룹 G=A4,12,6의 서브 그룹이 있는 유한 군 G와 G의 인자 d이 있다는 것을 증명해. 세 요소의 서브 그룹(세개의 물체가 있는 주기 자전에 의해 생성되).w그것은 어떤 뚜렷한 비경쟁적 요소가 그룹 전체를 생성한다.null
모든 n > 4에 대해, A에는n 비교(즉, 적절한) 정규 부분군이 없다.따라서 A는n n > 4 모두를 위한 단순한 그룹이다.A는5 해결 불가능한 가장 작은 그룹이다.null
집단 호몰로지
교대 그룹의 집단 호몰로학은 안정적 호모토피 이론에서와 같이 안정화를 보인다: 충분히 큰 n의 경우, 그것은 일정하다.그러나 저차원적인 예외적인 호몰로지(homology)도 있다.대칭 집단의 호몰로지에는 유사한 안정성이 있지만 저차원 예외(추가 호몰로지 요소)는 없다.null
H1: 아벨리아화
첫 번째 호몰로지 집단은 아벨리아화와 일치하며, (A가n 인용된 예외를 제외하고 완벽하기 때문에) 따라서 다음과 같다.
- H1(An, Z) = n에 대한 Z1 = 0, 1, 2;
- H1(A3, Z) = Aab
3 = A3 = Z3; - H1(A4, Z) = Aab
4 = Z3; - H1(An, Z) = n ≥ 5의 Z1.
이것은 다음과 같이 쉽게 직접 볼 수 있다.A는n 3주기에 의해 생성된다. 따라서 오더-3 원소는 오더-3 원소에 매핑되어야 하기 때문에 유일한 비교 아벨리아화 맵은 An → Z이며3, n ≥ 5의 경우 모든 3주기는 결합이므로 아벨리아화에서 동일한 원소에 매핑되어야 한다. 왜냐하면 아벨리아화 그룹에서는 결합이 사소한 것이기 때문이다.따라서 (123)와 같은 3주기에는 역기(321)와 같은 원소에 매핑해야 하지만, 따라서 2와 3을 나누는 질서를 가져야 하므로 아벨리아화(Abelianization)는 사소한 것이다.null
n < 3에게 A는n 사소한 것이므로 사소한 아벨화(abelianization)를 가지고 있다.A와3 A의4 경우 3주기는 (모든 것이 결합이 아닌) 두 개의 결합 클래스를 형성하고 비독점 지도3 A ↠ Z3(사실상 이형성)와 A4 ↠ Z가3 있다는 점에 주목하여 아벨리아화를 직접 계산할 수 있다.null
H2: 슈르 승수
교대 그룹 A의n 슈르 승수(n이 최소 5인 경우)는 순서 2의 주기적 그룹이다. 단, n이 6 또는 7인 경우, 3중 커버가 있는 경우는 제외한다.이 경우 슈르 승수는 순서 6의 (순환군)이다.[3]이것들은 (Schur 1911)에서 처음 계산되었다.null
- H2(An, Z) = n의 경우 Z1 = 1, 2, 3;
- H2(An, Z) = n의 경우2 Z = 4, 5;
- H2(An, Z) = n의 경우6 Z = 6, 7;
- H2(An, Z) = n ≥ 8의 Z2.
메모들
- ^ a b 로빈슨(1996), 페이지 78
- ^ Beeler, Robert. "The Fifteen Puzzle: A Motivating Example for the Alternating Group" (PDF). faculty.etsu.edu/. East Tennessee State University. Retrieved 2020-12-26.
- ^ Wilson, Robert (October 31, 2006), "Chapter 2: Alternating groups", The finite simple groups, 2006 versions, archived from the original on May 22, 2011, 2.7: Covering groups
{{citation}}: CS1 maint : 포스트스크립트(링크)
참조
- Robinson, Derek John Scott (1996), A course in the theory of groups, Graduate texts in mathematics, vol. 80 (2 ed.), Springer, ISBN 978-0-387-94461-6
- Schur, Issai (1911), "Über die Darstellung der symmetrischen und der alternierenden Gruppe durch gebrochene lineare Substitutionen", Journal für die reine und angewandte Mathematik, 1911 (139): 155–250, doi:10.1515/crll.1911.139.155, S2CID 122809608
- Scott, W.R. (1987), Group Theory, New York: Dover Publications, ISBN 978-0-486-65377-8