실험 설계
Design of experiments실험 설계(DOE, DOX 또는 실험 설계)는 변동을 반영하도록 가정된 조건에서 정보의 변동을 설명하고 설명하는 것을 목적으로 하는 모든 작업의 설계입니다.이 용어는 일반적으로 설계가 변동에 직접적인 영향을 미치는 조건을 도입하는 실험과 관련이 있지만 변동에 영향을 미치는 자연 조건을 관측을 위해 선택하는 준실험의 설계를 나타낼 수도 있습니다.
가장 간단한 형태로, 실험은 "입력 변수" 또는 "예측 변수"라고도 하는 하나 이상의 독립 변수로 표현되는 전제 조건의 변화를 도입함으로써 결과를 예측하는 것을 목표로 한다.하나 이상의 독립 변수의 변경은 일반적으로 "출력 변수" 또는 "반응 변수"라고도 하는 하나 이상의 종속 변수에서 변화를 일으키도록 가정됩니다.실험 설계는 외부 요인이 결과에 영향을 미치지 않도록 하기 위해 일정하게 유지해야 하는 관리 변수를 식별할 수도 있습니다.실험 설계에는 적절한 독립, 종속 및 제어 변수의 선택뿐만 아니라 사용 가능한 자원의 제약 조건을 고려하여 통계적으로 최적의 조건에서 실험 전달을 계획하는 것이 포함됩니다.실험에 사용할 설계점 집합(독립 변수 설정의 고유한 조합)을 결정하는 데는 여러 가지 방법이 있습니다.
실험 설계의 주요 관심사에는 유효성, 신뢰성 및 반복성의 확립이 포함됩니다.예를 들어, 이러한 우려는 독립 변수를 신중하게 선택하고, 측정 오류의 위험을 줄이고, 방법의 문서화가 충분히 상세하게 되도록 함으로써 부분적으로 해결할 수 있다.관련 우려사항에는 적절한 수준의 통계적 힘과 민감도 달성이 포함된다.
올바르게 설계된 실험은 자연 및 사회과학 및 공학 분야의 지식을 향상시킵니다.다른 응용 프로그램에는 마케팅과 정책 수립이 포함됩니다.실험 설계에 대한 연구는 메타과학에서 중요한 주제이다.
역사
찰스 S.에 이은 통계 실험입니다.피어스
통계적 추론 이론은 찰스 S.에 의해 개발되었다. 통계학에서 [3]무작위화 기반 추론의 중요성을 강조한 두 출판물인 "과학 논리의 삽화"(1877–1878)[1]와 "가능성 추론 이론"(1883)[2]의 퍼스.
무작위 실험
찰스 S.Peirce는 지원자를 블라인드 반복 측정 설계에 랜덤으로 할당하여 [4][5][6][7]체중 식별 능력을 평가했습니다.피어스의 실험은 심리학 및 교육 분야의 다른 연구원들에게 영감을 주었고, 이것은 1800년대에 [4][5][6][7]실험실과 전문 교과서에서 무작위 실험의 연구 전통을 발전시켰다.
회귀 모형에 대한 최적 설계
찰스 S. 1876년,[8] 피어스는 회귀 모델을 위한 최적의 디자인에 대한 최초의 영문 출판물을 기고하기도 했다.1815년 거곤은 다항식 회귀를 위한 선구적인 최적 설계를 제안했다.1918년 커스틴 스미스는 6도 [9][10]이하의 다항식을 위한 최적 설계를 발표했다.
실험의 순서
실험을 중단할 수 있는 가능한 결정을 포함하여 각각의 설계가 이전 실험의 결과에 의존할 수 있는 일련의 실험의 사용은 순차 분석의 범위 내에 있으며, 통계 [12]가설의 순차적 테스트의 맥락에서 아브라함 월드에 의해 개척된[11] 분야이다.헤르만 체르노프는 최적의 순차 [13]설계에 대한 개요를 썼으며, 적응형 설계는 S. [14]Zacks에 의해 조사되었습니다.순차 설계의 한 가지 특정한 유형은 "두 팔 밴디트"로, 멀티 팔 밴디트로 일반화되어 있으며,[15] 초기 작업은 1952년에 허버트 로빈스에 의해 수행되었다.
피셔의 원칙
실험 설계를 위한 방법론은 로널드 피셔의 혁신적인 저서에서 제안되었습니다.현장 실험의 배치(1926년)와 실험의 설계(1935년)가 그것이다.그의 선구적 업적의 대부분은 통계적 방법의 농업적 응용에 관한 것이었다.평범한 예로, 그는 어떤 여성이 맛만으로 우유와 차가 처음 컵에 담겨졌는지 구분할 수 있다는 차를 맛보는 여성의 가설을 시험하는 방법을 설명했다.이 방법들은 생물학,[16] 심리학, 농업 연구에 폭넓게 적용되어 왔다.
- 비교
- 일부 연구 분야에서는 추적 가능한 도량형 표준에 대한 독립적인 측정을 수행할 수 없습니다.치료제 간의 비교는 훨씬 더 가치 있고 일반적으로 선호되며, 종종 기준선으로 작용하는 과학적 대조군이나 전통적인 치료제와 비교된다.
- 랜덤화
- 랜덤 할당은 실험의 그룹이나 다른 그룹에 개인을 랜덤하게 할당하는 과정으로, 모집단의 각 개인이 연구의 참여자가 될 수 있는 동일한 기회를 가집니다.집단(또는 집단 내 조건)에 개인을 무작위로 할당하는 것은 엄격한 "참" 실험을 관찰 연구 또는 "준실험"[17]과 구별한다.랜덤 메커니즘(랜덤 번호 표 또는 카드나 주사위 같은 랜덤화 장치의 사용)을 통해 치료에 단위를 할당하는 결과를 탐구하는 광범위한 수학 이론이 있다.무작위로 치료에 단위를 할당하면 교란 요인을 완화하는 경향이 있으며, 이는 치료 이외의 요인에 의한 영향을 치료에서 발생하는 것으로 보인다.
- 무작위 할당과 관련된 위험(예: 치료 그룹과 대조군 사이의 주요 특성에 심각한 불균형이 있는 경우)은 계산 가능하며, 따라서 충분한 실험 단위를 사용하여 허용 가능한 수준으로 관리할 수 있다.그러나 모집단이 다소 다른 여러 개의 하위 모집단으로 나뉘어져 각 하위 모집단의 크기가 동일해야 하는 경우에는 계층화된 표본 추출을 사용할 수 있다.이러한 방식으로 각 하위 모집단의 단위는 랜덤화되지만 전체 표본은 랜덤화되지 않습니다.실험 결과는 실험 단위가 더 큰 모집단에서 무작위로 추출된 표본인 경우에만 실험 단위에서 더 큰 단위의 통계 모집단으로 신뢰성 있게 일반화할 수 있다. 이러한 추정의 가능한 오류는 무엇보다도 표본 크기에 따라 달라진다.
- 통계 리플리케이션
- 측정은 일반적으로 변동과 측정의 불확실성에 노출된다. 따라서 변동의 원천을 식별하고 치료제의 진정한 효과를 더 잘 추정하며 실험의 신뢰성과 타당성을 더욱 강화하고 [18]주제에 대한 기존 지식을 추가하기 위해 반복되고 전체 실험이 복제된다.그러나, 실험의 복제가 시작되기 전에 특정 조건이 충족되어야 한다: 원래 연구 질문은 동료 검토 저널에 게재되거나 널리 인용되었다. 연구자는 원래 실험으로부터 독립적이다. 연구자는 먼저 원본 데이터를 사용하여 원래 발견을 복제하려고 노력해야 한다.e-up은 수행된 연구가 가능한 [19]한 엄격하게 원래의 연구를 따르려고 했던 복제 연구임을 명시해야 한다.
- 막는
- 블럭화는 실험 단위를 서로 유사한 단위로 구성된 그룹(블록)에 랜덤하게 배치하지 않는 것입니다.블럭화는 알려져 있지만 관련이 없는 단위 간 변동원을 줄여주므로 연구 중인 변동원을 추정할 때 더 높은 정밀도를 제공합니다.
- 직교성은 합법적이고 효율적으로 수행될 수 있는 비교(대조)의 형태와 관련이 있습니다.대조도는 벡터로 나타낼 수 있으며, 직교 대비 집합은 상관 관계가 없으며 데이터가 정규 분포인 경우 독립적으로 분포됩니다.이러한 독립성 때문에 각 직교 처리는 서로 다른 정보를 제공합니다.T 처리가 있고 T – 1 직교 대비가 있는 경우, 실험에서 캡처할 수 있는 모든 정보는 대조 집합을 통해 얻을 수 있습니다.
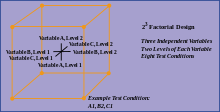
- 요인 실험
- 한 번에 단일 요인 방법 대신 요인 실험 사용.이 값은 여러 요인(독립 변수)의 효과와 가능한 교호작용을 평가하는 데 효과적입니다.실험 설계의 분석은 실험이 추정하거나 검정해야 하는 요인에 따라 관측된 분산을 성분으로 분할하는 모형 집합인 분산 분석을 기반으로 합니다.
예
이 설계 실험의 예는 Frank [20][21][13]Yates의 예를 기반으로 한 Harold Hoteling에 기인합니다.이 예에서 설계된 실험은 조합 [22]설계를 포함합니다.
8개 물체의 무게는 팬 밸런스와 표준 무게 세트를 사용하여 측정됩니다.각각의 무게는 균형이 잡힐 때까지 가벼운 팬에 보정된 무게를 더함으로써 왼쪽 팬에 있는 물체와 오른쪽 팬에 있는 물체의 무게 차이를 측정합니다.각 측정값에는 랜덤 오차가 있습니다.평균 오차는 0이고, 오차의 확률 분포의 표준 편차는 서로 다른 무게에서 동일한 숫자 θ이며, 서로 다른 가중치에서의 오차는 서로 독립적입니다.실제 가중치를 다음과 같이 나타냅니다.
다음 두 가지 실험을 고려합니다.
- 한 팬에 각각의 물체를 넣고 다른 팬은 비우세요.X를 물체의 측정된 무게라고 가정하자i(i = 1, ..., 8).
- 다음 일정에 따라 8개의 무게를 측정하고(측정 매트릭스) Y를 i = 1, ..., 8에 대한 측정된 차이라고 합니다i.
- 그러면 무게 †의1 추정치는
- 다른 항목의 무게에 대해서도 유사한 추정치를 찾을 수 있다.예를들면
실험 설계의 문제는: 어떤 실험이 더 나은가?
첫1 번째 실험을 사용할 경우 추정치1 of의 분산은 if이다2.그러나 두 번째 실험을 사용하면 위에 제시된 추정치의 분산은 δ2/8입니다.따라서 두 번째 실험은 단일 항목의 추정 정밀도를 8배 높이고 모든 항목을 동일한 정밀도로 동시에 추정할 수 있습니다.두 번째 실험에서는 8개의 항목을 개별적으로 측정하면 64개의 무게를 측정해야 합니다.그러나 두 번째 실험에서 얻은 항목의 추정치에는 서로 상관되는 오차가 있습니다.
실험 설계의 많은 문제는 이 예시와 다른 [22]예시와 같이 조합 설계를 포함합니다.
폴스 포지티브 회피
종종 출판 압력이나 저자 자신의 확인 편견에서 비롯되는 잘못된 긍정적인 결론은 많은 분야에서 내재된 위험이다.데이터 수집 단계에서 잠재적으로 잘못된 양성으로 이어지는 편견을 방지하는 좋은 방법은 이중 블라인드 설계를 사용하는 것입니다.이중 블라인드 설계를 사용하면 실험 참가자가 랜덤하게 실험 그룹에 할당되지만 연구자는 어떤 참가자가 어떤 그룹에 속하는지 알지 못합니다.따라서, 연구자는 개입에 대한 참가자의 반응에 영향을 줄 수 없습니다.자유도가 공개되지 않은 실험 설계는 [23]문제가 됩니다.이로 인해 의식적이거나 무의식적인 "p-hacking"이 발생할 수 있습니다. 즉, 원하는 결과를 얻을 때까지 여러 가지 작업을 시도합니다.일반적으로 통계적 [24][25]유의성 p<.05 수준보다 낮은 수치를 반환할 때까지 통계 분석 과정과 자유도를 무의식적으로 조작한다.따라서 실험 설계는 수행할 분석을 제안하는 명확한 문구를 포함해야 한다.P해킹은 연구자가 데이터 수집을 시작하기 전에 논문을 발표하고자 하는 저널에 데이터 분석 계획을 전송해야 하는 사전 등록으로 막을 수 있으므로 데이터 조작은 조작할 수 없습니다(https://osf.io).이를 방지하기 위한 또 다른 방법은 이중 블라인드 설계를 데이터 분석 단계로 가져가는 것입니다. 데이터 분석 단계에서는 데이터가 연구와는 무관한 데이터 분석가가 데이터를 스크램블링하기 때문에 참가자가 이상치로 간주되기 전에 어떤 참가자가 속하는지 알 수 있는 방법이 없습니다.
결과의 [26]복제를 지원하기 위해서는 실험 방법론의 명확하고 완전한 문서화가 중요하다.
실험 설계를 설정할 때 토론 주제
실험 설계 또는 무작위 임상 시험은 실제로 [27]실험을 수행하기 전에 몇 가지 요인을 신중하게 고려해야 합니다.실험 설계는 실험을 수행하기 전에 상세한 실험 계획을 세우는 것입니다.다음 주제 중 일부는 실험 설계 원칙 섹션에서 이미 논의되었다.
- 설계에 포함된 요인의 수와 이러한 요인의 수준이 고정 또는 변량입니까?
- 제어조건이 필요한가?또, 어떤 조건이 필요한가?
- 조작 체크: 조작이 정말 효과가 있었을까?
- 배경 변수는 무엇입니까?
- 샘플 사이즈가 어떻게 되나요?실험이 일반화 가능하고 충분한 힘을 가지려면 몇 개의 단위를 수집해야 합니까?
- 요인 간 상호작용의 관련성은 무엇입니까?
- 실질적인 요인의 지연 효과가 결과에 미치는 영향은 무엇인가?
- 대응 교대제가 자기 보고 척도에 어떤 영향을 미칩니까?
- 다른 상황에서 동일한 측정기기를 동일한 장치에 사후 테스트 및 후속 테스트를 통해 반복적으로 관리하는 것은 얼마나 실현 가능한가?
- 프록시 사전 테스트를 사용하는 것은 어떻습니까?
- 변수가 숨어있나요?
- 고객/환자, 연구자 또는 데이터 분석가가 상황에 대해 잘 알지 못하는 것이 좋습니까?
- 동일한 단위에 다른 조건의 후속 적용 가능성은 무엇인가?
- 각 제어 및 소음 계수의 몇 개를 고려해야 하는가?
연구의 독립 변수는 종종 많은 수준 또는 다른 그룹을 가집니다.진정한 실험에서 연구자들은 개입이 가설을 테스트하는 실험 그룹과 개입 요소가 없는 실험 그룹과 통제 그룹을 가질 수 있습니다.따라서, 하나의 개입을 제외한 다른 모든 것이 일정하게 유지되면, 연구자들은 이 하나의 요소가 관찰된 변화의 원인이라는 것을 어느 정도 확실하게 증명할 수 있다.경우에 따라서는 제어 그룹을 갖는 것은 윤리적이지 않습니다.이것은 때때로 두 가지 다른 실험 그룹을 사용하여 해결됩니다.예를 들어 다른 질병을 가진 두 그룹 간의 차이를 테스트하거나 성별 간의 차이를 테스트하는 경우(참가자를 할당하기 어렵거나 비윤리적인 변수임이 명백함)와 같이 독립 변수를 조작할 수 없다.이 경우 준실험 설계를 사용할 수 있다.
원인 속성
순수 실험 설계에서 독립적(예측 변수) 변수는 연구자에 의해 조작된다. 즉, 연구의 모든 참가자는 모집단에서 랜덤으로 선택되고 선택된 각 참가자는 독립 변수의 조건에 랜덤하게 할당된다.이렇게 해야 결과 변수의 차이가 다른 조건에 의해 발생한다는 것을 높은 확률로 증명할 수 있다.따라서 연구자들은 가능하면 다른 설계 유형보다 실험 설계를 선택해야 합니다.그러나 독립 변수의 특성이 항상 조작을 허용하는 것은 아닙니다.그러한 경우, 연구자들은 그들의 설계가 인과적 귀속에 대해 허용하지 않을 때 인과적 귀속에 대해 증명하지 않는다는 것을 알고 있어야 한다.예를 들어, 관측 설계에서 참가자는 조건에 무작위로 할당되지 않으므로 조건 간의 결과 변수에서 차이가 발견되면 결과 차이를 유발하는 조건 간의 차이, 즉 세 번째 변수가 있을 가능성이 높다.상관 설계를 사용한 연구도 마찬가지입니다.(Adér & Mellenbergh, 2008).
통계 관리
설계된 실험을 수행하기 전에 공정이 합리적인 통계 관리 상태에 있는 것이 가장 좋습니다.이것이 불가능한 경우 적절한 블럭화, 반복실험 및 랜덤화를 통해 설계된 [28]실험을 신중하게 수행할 수 있습니다.방해 변수를 제어하기 위해 연구자들은 추가적인 척도로 제어 검사를 실시합니다.조사자는 통제되지 않은 영향(예: 선원 신뢰도 인식)이 연구 결과를 왜곡시키지 않도록 해야 한다.조작 검사는 제어 검사의 한 예입니다.조작 체크를 통해 주요 변수를 분리하여 이들 변수가 계획대로 작동하고 있다는 지원을 강화할 수 있습니다.
실험 연구 설계의 가장 중요한 요구사항 중 하나는 가짜, 개입 및 선행 변수의 영향을 제거할 필요성이다.가장 기본적인 모형에서는 원인(X)이 효과(Y)로 이어집니다.그러나 (Y)에 영향을 미치는 세 번째 변수(Z)가 있을 수 있으며 X가 전혀 실제 원인이 아닐 수 있습니다.Z는 스플리어스 변수이므로 제어해야 합니다.개입 변수(가정 원인(X)과 효과(Y) 사이에 있는 변수) 및 선행 변수(참 원인인 추정 원인(X)보다 앞의 변수)에 대해서도 마찬가지입니다.세 번째 변수가 관련되어 있고 제어되지 않은 경우 이 관계는 0차 관계라고 합니다.실험 연구 설계의 대부분의 실제 적용에는 여러 가지 원인이 있습니다(X1, X2, X3).대부분의 설계에서는 한 번에 이러한 원인 중 하나만 조작됩니다.
Fisher 이후의 실험 설계
여러 주효과를 추정하기 위한 일부 효율적인 설계는 독립적으로 그리고 거의 연속적으로 Raj Chandra Bose와 K에 의해 발견되었다. 1940년 인도 통계 연구소에서 키센은 발견되었지만 1946년 플랙킷-버먼 디자인이 바이오메트리카에서 발표될 때까지 거의 알려지지 않았다.거의 동시에 C. R. Rao는 직교 배열의 개념을 실험 설계로 도입했습니다.이 개념은 1950년대 초 인도 통계 연구소를 방문한 다구치 겐이치의 다구치 방법 개발에 중심적인 역할을 했다.그의 방법은 일본과 인도 산업에 성공적으로 적용되어 채택되었고, 그 후 약간의 망설임도 있었지만 미국 산업에도 받아들여졌다.
1950년, 거트루드 메리 콕스와 윌리엄 젬멜 코크란은 실험 설계 책을 출판했는데, 이 책은 이후 수년간 통계학자들을 위한 실험 설계에 대한 주요 참고서가 되었다.
선형 모형 이론의 발전은 초기 작가들과 관련된 경우를 포괄하고 능가했다.오늘날, 그 이론은 선형 대수학, 대수학, 조합론의 고급 주제에 기초하고 있다.
통계의 다른 분과와 마찬가지로, 실험 설계는 빈도론과 베이지안 접근법을 모두 사용하여 추구된다.실험설계와 같은 통계절차를 평가할 때 빈도통계학은 표본분포를 연구하는 반면 베이지안 통계는 모수공간의 확률분포를 갱신한다.
실험 설계 분야에 중요한 기여자는 C입니다. S. Peirce, R. A. Fisher, F. 예이츠, R. C. 보스, A. C. 앳킨슨, R. 베일리, D. R. 콕스, G. E. 박스, W. G. 코크란, W. T. 페더러, V. 페도로프, A. S. 헤다얏, O. 켐프, J. 호른. Raghavarao, C. R. Rao, Shrikhande S. S., J. N. Srivastava, William J. Studden, G. Taguchi 및 H. P. Wynn.[29]
D의 교과서.몽고메리, R.마이어스 및 G. 박스/W.헌터 / J.S.헌터는 여러 세대에 걸쳐 학생과 실무가들에게 다가왔다.[30] [31] [32] [33] [34]
시스템 식별(정적 또는 동적 모델을 위한 모델 구축)의 맥락에서 실험 설계에 대한 일부 설명은 및 [36]에 제시되어[35] 있습니다.
인간 참가자의 제약
법률과 윤리적 고려는 인간 실험체에 대한 주의 깊게 설계된 실험을 금지한다.법적 제약은 관할권에 따라 달라집니다.제약사항에는 기관 검토위원회, 임상(의학) 시험과 행동 및 사회과학 [37]실험 모두에 영향을 미치는 정보에 근거한 동의 및 기밀성이 포함될 수 있다.예를 들어 독성학 분야에서는 실험실에서 실험하는 동물을 대상으로 인간을 [38]위한 안전한 피폭 한계를 정의하는 것을 목표로 실험을 수행한다.제약 조건의 균형 조정은 의료 [39]분야의 보기입니다.환자의 무작위화에 관해서는, "...어떤 치료법이 더 나은지 아무도 모른다면, 어떤 치료법을 사용해야 할 윤리적 의무는 없다."(p 380) 실험 설계에 관해서는, "...이 상황을 쉽게 피할 수 있을 때 피험자를 부실하게 설계된 연구에서 데이터를 수집하기 위해 위험에 처하게 하는 것은 분명히 윤리적이지 않다."(p 393)
「 」를 참조해 주세요.
- 적대적 협업
- 베이지안 실험 설계
- 블록 설계
- Box-Behnken 설계
- 중앙 합성 설계
- 임상 시험
- 임상 연구 설계
- 컴퓨터 실험
- 제어 변수
- 변수에 대한 제어
- 경험측정학(경제측정학 관련 실험)
- 인자 분석
- 부분 요인 설계
- 실험 설계 용어집
- 회색 박스 모델
- 산업공학
- 계기 효과
- 대수의 법칙
- 조작 체크
- 실험 소프트웨어의 멀티팩터 설계
- 한 번에 1인자 방식
- 최적의 설계
- Plackett-Burman 설계
- 확률론적 설계
- 프로토콜(자연과학)
- 준실험 설계
- 랜덤화 블럭 설계
- 랜덤화 대조 시험
- 리서치 디자인.
- 견고한 파라미터 설계
- 샘플 크기 결정
- 과포화 설계
- 왕립 동물 자기 위원회
- 조사표본
- 시스템 식별
- 다구치법
레퍼런스
- ^ Peirce, Charles Sanders (1887)."과학논리의 삽화"오픈 코트(2014년 6월 10일). ISBN0812698495.
- ^ 피어스, 찰스 샌더스(1883년)."가능성 추론 이론"C. S. 피어스(Ed.)에서 존스 홉킨스 대학 구성원에 의한 논리학 연구 (p. 126–181).Little, Brown and Co(1883)
- ^ Stigler, Stephen M. (1978). "Mathematical statistics in the early States". Annals of Statistics. 6 (2): 239–65 [248]. doi:10.1214/aos/1176344123. JSTOR 2958876. MR 0483118.
Indeed, Pierce's work contains one of the earliest explicit endorsements of mathematical randomization as a basis for inference of which I am aware (Peirce, 1957, pages 216–219
- ^ a b Peirce, Charles Sanders; Jastrow, Joseph (1885). "On Small Differences in Sensation". Memoirs of the National Academy of Sciences. 3: 73–83.
- ^ a b 의
- ^ a b Stephen M. Stigler (November 1992). "A Historical View of Statistical Concepts in Psychology and Educational Research". American Journal of Education. 101 (1): 60–70. doi:10.1086/444032. JSTOR 1085417. S2CID 143685203.
- ^ a b Trudy Dehue (December 1997). "Deception, Efficiency, and Random Groups: Psychology and the Gradual Origination of the Random Group Design". Isis. 88 (4): 653–673. doi:10.1086/383850. PMID 9519574. S2CID 23526321.
- ^ Peirce, C. S. (1876). "Note on the Theory of the Economy of Research". Coast Survey Report: 197–201., 실제로 1879년 발행된 NOAA PDF Eprint.
논문집 7, 139~157항, 글 4, 페이지 72~78 및 에서 전재 - ^ Guttorp, P.; Lindgren, G. (2009). "Karl Pearson and the Scandinavian school of statistics". International Statistical Review. 77: 64. CiteSeerX 10.1.1.368.8328. doi:10.1111/j.1751-5823.2009.00069.x. S2CID 121294724.
- ^ Smith, Kirstine (1918). "On the standard deviations of adjusted and interpolated values of an observed polynomial function and its constants and the guidance they give towards a proper choice of the distribution of observations". Biometrika. 12 (1–2): 1–85. doi:10.1093/biomet/12.1-2.1.
- ^ 존슨, N.L. (1961년)"순차 분석: 설문 조사"왕립통계학회지 시리즈 A. 제124권 제3호, 372~411. (375~376쪽
- ^ Wald, A.(1945) "통계 가설의 순차적 검정", 수학 통계 연보, 16(2), 117–186.
- ^ a b 헤르만 체르노프, 순차적 분석 및 최적 설계, SIAM Monograph, 순차적 분석 및 최적 설계.
- ^ Jacks, S. (1996) "파라메트릭 모델을 위한 적응형 설계"입력: Ghosh, S. 및 Rao, C. R., (Eds) (1996)"실험의 설계와 분석", 통계 핸드북, 제13권.노스홀랜드.ISBN 0-444-82061-2. (151~180페이지)
- ^ Robbins, H. (1952). "Some Aspects of the Sequential Design of Experiments". Bulletin of the American Mathematical Society. 58 (5): 527–535. doi:10.1090/S0002-9904-1952-09620-8.
- ^ Miller, Geoffrey(2000).짝짓기 정신: 성적 선택이 인간 본성의 진화를 어떻게 형성했는가, 런던:하이네만, ISBN 0-434-00741-2 (Doubleday, ISBN 0-385-49516-1) "생물학자들에게 그는 멘델 유전학과 다윈의 선택 이론을 통합하기 위해 수학적 모델을 사용한 '현대 합성'의 설계자였다.심리학자들에게 피셔는 심리학 저널에서 여전히 사용될 수 있는 다양한 통계 테스트의 발명가였다.농부들에게 피셔는 합리적인 농작물 사육 프로그램을 통해 수백만 명을 기아로부터 구해낸 실험적인 농업 연구의 창시자였습니다." 페이지 54.
- ^ Creswell, J.W.(2008), 교육연구: 양적 및 질적 연구 계획, 실시 및 평가(3판), 어퍼 새들 리버, 뉴저지 주: 프렌티스 홀.2008, 300페이지. ISBN 0-13-613550-1
- ^ Dr. Hani (2009). "Replication study". Archived from the original on 2 June 2012. Retrieved 27 October 2011.
- ^ Burman, Leonard E.; Robert W. Reed; James Alm (2010), "A call for replication studies", Public Finance Review, 38 (6): 787–793, doi:10.1177/1091142110385210, S2CID 27838472, retrieved 27 October 2011
- ^ Hotelling, Harold (1944). "Some Improvements in Weighing and Other Experimental Techniques". Annals of Mathematical Statistics. 15 (3): 297–306. doi:10.1214/aoms/1177731236.
- ^ Giri, Narayan C.; Das, M. N. (1979). Design and Analysis of Experiments. New York, N.Y: Wiley. pp. 350–359. ISBN 9780852269145.
- ^ a b Jack Sifri (8 December 2014). "How to Use Design of Experiments to Create Robust Designs With High Yield". youtube.com. Retrieved 11 February 2015.
- ^ Simmons, Joseph; Leif Nelson; Uri Simonsohn (November 2011). "False-Positive Psychology: Undisclosed Flexibility in Data Collection and Analysis Allows Presenting Anything as Significant". Psychological Science. 22 (11): 1359–1366. doi:10.1177/0956797611417632. ISSN 0956-7976. PMID 22006061.
- ^ "Science, Trust And Psychology in Crisis". KPLU. 2 June 2014. Archived from the original on 14 July 2014. Retrieved 12 June 2014.
- ^ "Why Statistically Significant Studies Can Be Insignificant". Pacific Standard. 4 June 2014. Retrieved 12 June 2014.
- ^ Chris Chambers (10 June 2014). "Physics envy: Do 'hard' sciences hold the solution to the replication crisis in psychology?". theguardian.com. Retrieved 12 June 2014.
- ^ Ader, Mellenberg & Hand(2008) "연구 방법에 대한 조언:컨설턴트의 동반자"
- ^ Bisgaard, S(2008) "설계된 실험을 수행하기 전에 프로세스가 통계적 통제 상태에 있어야 하는가?" , 품질 공학, ASQ, 20(2), 페이지 143–176
- ^ Giri, Narayan C.; Das, M. N. (1979). Design and Analysis of Experiments. New York, N.Y: Wiley. pp. 53, 159, 264. ISBN 9780852269145.
- ^ Montgomery, Douglas (2013). Design and analysis of experiments (8th ed.). Hoboken, NJ: John Wiley & Sons, Inc. ISBN 9781118146927.
- ^ Walpole, Ronald E.; Myers, Raymond H.; Myers, Sharon L.; Ye, Keying (2007). Probability & statistics for engineers & scientists (8 ed.). Upper Saddle River, NJ: Pearson Prentice Hall. ISBN 978-0131877115.
- ^ Myers, Raymond H.; Montgomery, Douglas C.; Vining, G. Geoffrey; Robinson, Timothy J. (2010). Generalized linear models : with applications in engineering and the sciences (2 ed.). Hoboken, N.J.: Wiley. ISBN 978-0470454633.
- ^ Box, George E.P.; Hunter, William G.; Hunter, J. Stuart (1978). Statistics for Experimenters : An Introduction to Design, Data Analysis, and Model Building. New York: Wiley. ISBN 978-0-471-09315-2.
- ^ Box, George E.P.; Hunter, William G.; Hunter, J. Stuart (2005). Statistics for Experimenters : Design, Innovation, and Discovery (2 ed.). Hoboken, N.J.: Wiley. ISBN 978-0471718130.
- ^ Spall, J. C. (2010). "Factorial Design for Efficient Experimentation: Generating Informative Data for System Identification". IEEE Control Systems Magazine. 30 (5): 38–53. doi:10.1109/MCS.2010.937677. S2CID 45813198.
- ^ Pronzato, L (2008). "Optimal experimental design and some related control problems". Automatica. 44 (2): 303–325. arXiv:0802.4381. doi:10.1016/j.automatica.2007.05.016. S2CID 1268930.
- ^ Moore, David S.; Notz, William I. (2006). Statistics : concepts and controversies (6th ed.). New York: W.H. Freeman. pp. Chapter 7: Data ethics. ISBN 9780716786368.
- ^ Ottoboni, M. Alice (1991). The dose makes the poison : a plain-language guide to toxicology (2nd ed.). New York, N.Y: Van Nostrand Reinhold. ISBN 978-0442006600.
- ^ Glantz, Stanton A. (1992). Primer of biostatistics (3rd ed.). ISBN 978-0-07-023511-3.
원천
- Peirce, C. S. (1877–1878), "과학논리의 삽화" (시리즈), Popular Science Monthly, 제12-13권.관련 개별 문서:
- (1878년 3월), "기회론", Popular Science Monthly, v. 12, 3월호, 604–615쪽.인터넷 아카이브의 E프린트랜트.
- (1878년 4월), "유도 확률", Popular Science Monthly, v. 12, 페이지 705–718.인터넷 아카이브의 E프린트랜트.
- (1878년 6월), "자연의 기사단", Popular Science Monthly, v. 13, 페이지 203–217.인터넷 아카이브의 E프린트랜트.
- (1878년 8월), "추론, 귀납, 가설", 대중과학 월간지 v. 13, 페이지 470-482.인터넷 아카이브의 E프린트랜트.
- (1883), "가능성 추론의 이론", 논리학 연구, 126–181, 리틀, 브라운, 회사. (1983년 개정, 존 벤자민 출판사, ISBN 90-272-3271-7)
외부 링크
| 라이브러리 리소스 정보 실험 설계 |
- NIST의 "엔지니어링 통계에 관한 NIST/SEMATECH 핸드북"의 장
- NIST의 "NIST/SEMATECH Handbook on Engineering Statistics"에 수록된 Box-Behnken 설계
- Opera Magicris v3.6 온라인 참조 15장 7.4절 ISBN 978-2-8399-0932-7에서 가장 일반적인 DoE의 상세한 수학적 발전.





![{\displaystyle {\begin{aligned}{\widehat {\theta }}_{2}&={\frac {Y_{1}+Y_{2}-Y_{3}-Y_{4}+Y_{5}+Y_{6}-Y_{7}-Y_{8}}{8}}.\\[5pt]{\widehat {\theta }}_{3}&={\frac {Y_{1}+Y_{2}-Y_{3}-Y_{4}-Y_{5}-Y_{6}+Y_{7}+Y_{8}}{8}}.\\[5pt]{\widehat {\theta }}_{4}&={\frac {Y_{1}-Y_{2}+Y_{3}-Y_{4}+Y_{5}-Y_{6}+Y_{7}-Y_{8}}{8}}.\\[5pt]{\widehat {\theta }}_{5}&={\frac {Y_{1}-Y_{2}+Y_{3}-Y_{4}-Y_{5}+Y_{6}-Y_{7}+Y_{8}}{8}}.\\[5pt]{\widehat {\theta }}_{6}&={\frac {Y_{1}-Y_{2}-Y_{3}+Y_{4}+Y_{5}-Y_{6}-Y_{7}+Y_{8}}{8}}.\\[5pt]{\widehat {\theta }}_{7}&={\frac {Y_{1}-Y_{2}-Y_{3}+Y_{4}-Y_{5}+Y_{6}+Y_{7}-Y_{8}}{8}}.\\[5pt]{\widehat {\theta }}_{8}&={\frac {Y_{1}+Y_{2}+Y_{3}+Y_{4}+Y_{5}+Y_{6}+Y_{7}+Y_{8}}{8}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b6970abd1a6e69f062cddd667a1ea60088e94c8)


