다무장 도적

확률 이론과 기계 학습에서, 다중 무장 밴디트 문제(때로는 K- 또는^[1] N-암 밴디트 문제라고도^[2] 함)는 각 선택의 속성이 단지 부분적으로만 알려져 있을 때, 그들의 예상 이득을 최대화하는 방식으로 경쟁하는 (대체) 선택들 사이에 고정된 제한된 자원 집합을 할당해야 하는 문제입니다.e할당,^[3][4] 시간이 지남에 따라 또는 자원을 선택에 할당함으로써 더 잘 이해될 수 있습니다.이것은 탐색-이용 균형 딜레마를 예시하는 전형적인 강화 학습 문제입니다.이 이름은 슬롯머신의 줄에 있는 도박꾼(때로는 "외팔 도적"이라고도 함)^[5]을 상상하면서 어떤 기계를 플레이할지, 각 기계를 몇 번 플레이할지, 어떤 순서로 플레이할지, 현재의 기계를 계속 플레이할지, 다른 기계를 시도할지를 결정해야 합니다.다중 무장 도적 문제는 확률적 스케줄링의 광범위한 범주에도 속합니다.

문제에서, 각 기계는 a-priori로 알려져 있지 않은, 해당 기계에 특정한 확률 분포로부터 무작위 보상을 제공합니다.도박꾼의 목적은 일련의 지렛대 당기기를 통해 얻는 보상의 합을 극대화하는 것입니다.^[3][4]도박꾼이 각 시도에서 직면하는 중요한 균형은 가장 높은 기대 보수를 받는 기계의 "이용"과 다른 기계의 기대 보수에 대한 더 많은 정보를 얻기 위한 "탐색" 사이입니다.탐험과 착취 사이의 균형은 기계 학습에서도 마주합니다.실제로, 다무장한 도적들은 과학 재단이나 제약 회사와 같은 큰 조직에서 연구 프로젝트를 관리하는 것과 같은 문제를 모델링하는 데 사용되어 왔습니다.^[3][4]문제의 초기 버전에서 도박꾼은 기계에 대한 초기 지식 없이 시작합니다.

1952년 허버트 로빈스(Herbert Robbins)는 문제의 중요성을 깨닫고 "순차적인 실험 설계의 일부 측면"에서 수렴 모집단 선택 전략을 구성했습니다.^[6]존 C에 의해 처음 출판된 정리, 기틴스 지수. Gittins는 예상 할인 보상을 최대화하기 위한 최적의 정책을 제공합니다.^[7]

경험적 동기

다중 무장 도적 문제는 새로운 지식("탐험"이라고 함)을 획득하고 기존 지식("탐험"이라고 함)을 기반으로 결정을 최적화하는 동시에 시도하는 에이전트를 모델링합니다.에이전트는 고려된 기간 동안 경쟁 작업의 총 가치를 최대화하기 위해 이러한 경쟁 작업의 균형을 맞추려고 시도합니다.밴디트 모델에는 다음과 같은 실용적인 응용이 많이 있습니다.

• 환자의 손실을 최소화하면서 다양한 실험적 치료의 효과를 조사하는 ^[3][4][8][9]임상 시험
• 네트워크의 지연을 최소화하기 위한 적응형 라우팅 노력,
• 재무 포트폴리오 설계^[10][11]

이러한 실제 사례에서 문제는 이미 습득한 지식과 지식을 더욱 향상시키기 위한 새로운 행동을 시도하는 것을 기반으로 보상 극대화의 균형을 유지해야 합니다.이것은 기계 학습에서 착취 대 탐사 트레이드오프로 알려져 있습니다.

이 모델은 또한 각 가능성의 난이도와 보상에 대한 불확실성을 고려할 때 어떤 프로젝트를 수행해야 하는지에 대한 질문에 답하면서 다양한 프로젝트에 대한 동적인 자원 할당을 제어하는 데 사용되었습니다.^[12]

원래 제2차 세계 대전에서 연합국 과학자들에 의해 고려되었지만, 그것은 너무 다루기 힘들다는 것이 증명되어서, Peter Whittle에 따르면, 독일 과학자들도 그것에 그들의 시간을 낭비할 수 있도록 그 문제를 독일 상공에 떨어뜨리자고 제안되었습니다.^[13]

현재 일반적으로 분석되는 문제의 버전은 1952년 허버트 로빈스에 의해 공식화되었습니다.

다무장한 도적 모형

다중 무장 밴디트(짧은: 밴디트 또는 MAB)는 실제 분포 $B$ = ${\displaystyle \{{}_{}}$ ${\displaystyle 1_{}}$ ${\displaystyle \dots ,{}_{}}$ ${\displaystyle K_{}}$}$${\$displaystyle$ B =\{$R_{1},\dots,R_{K$ 각 분포는 $K{\displaystyle }$∈${\displaystyle {}^{}}$ +$${\$displaystyle$ K$\in \mathbb {N}^{+}$ 레버 중 하나가 제공하는 보상과 관련되어 있습니다.$\mu {\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$ ${\displaystyle \dots ,}$ ${\displaystyle {\mu K}_{}}$ ${\$를 이러한$$ 보상 분포와 관련된 평균값이라고 합니다.도박꾼은 라운드당 한 레버씩 반복적으로 플레이하며 관련 보상을 관찰합니다.목표는 수집된 보상의 합을 최대화하는 것입니다.지평선 $H{\displaystyle }$ ${\displaystyle H}$은(는) 재생해야 할 라운드 수입니다.밴디트 문제는 공식적으로 1-상태 마르코프 결정 과정과 동등합니다.$T$ ${\displaystyle T}$ 회차 후의 후회 ρ ${\displaystyle \rho}$은(는) 최적 전략과 관련된 보상 합과 수집된 보상의 합 사이의 예상 차이로 정의됩니다.

$1$$T}{\widehat {r}}_{t$

여기서 $\mu$ ∗ ${\displaystyle \mu ^{*}}$는 최대 보상 $평균$이고 μ ∗ = ${\displaystyle \underset{}{max}}$ k ${\displaystyle \underset{}{}{}_{}}$ ${\displaystyle k_{}}${\$displaystyle \mu$ ^{*}=\$max _{k}\{\mu$_{$k$ r${\displaystyle {\stackrel{}{}}_{}}$^ $t${\$displaystyle {\widehat {r}_{t}$는 라운드 t의 보상입니다.

0-후회 전략은 라운드 수가 무한대로 증가할 때 라운드당 $평균{\displaystyle }$ρ / T ${\displaystyle \rho$/ $T}$가 확률 1과 함께 0으로 증가하는 전략입니다.직관적으로 후회 없는 전략은 충분한 라운드를 수행할 경우 (꼭 유일하지는 않은) 최적의 전략으로 수렴될 것이 보장됩니다.

변주곡

일반적인 공식은 이진 다중 무장 도적 또는 베르누이 다중 무장 도적으로 확률 $p{\displaystyle }$ ${\displaystyle p}$인 경우 보상을 발행하고$$그렇지 않은 경우 보상을 0으로 발행합니다.

다중 무장 도적의 또 다른 공식은 각각의 팔이 독립적인 마르코프 기계를 나타냅니다.특정 암이 재생될 때마다, 그 기계의 상태는 마르코프 상태의 진화 확률에 따라 선택된 새로운 암으로 발전합니다.현재 기계 상태에 따라 보상이 있습니다."불안정한 산적 문제"라고 불리는 일반화에서, 놀지 않는 무기의 상태도 시간이 지남에 따라 진화할 수 있습니다.^[15]시간이 지남에 따라 (어떤 팔을 놀지에 대한) 선택의 수가 증가하는 시스템에 대한 논의도 있었습니다.^[16]

컴퓨터 과학 연구원들은 확률적^[1] 및 비^[17] 확률적 팔 보상 모두에 대해 유한한 시간 지평선과 무한한 시간 지평선 모두에서 후회를 최소화하기 위한 알고리듬을 최악의 가정 하에서 연구했습니다.

밴디트 전략

주요 돌파구는 아래에 설명된 연구에서 최적의 인구 선택 전략, 즉 정책(평균이 가장 높은 인구에 대해 균일하게 최대 수렴률을 갖는)을 구축한 것입니다.

최적해

"점근적으로 효율적인 적응적 할당 규칙"이라는 논문에서,Lai and Robbins^[18](1952년 Robbins와 그의 동료들이 Robbins로 돌아가는 논문에 따라)는 인구 보상 분포가 하나의 매개 변수 지수 패밀리인 경우에 대해 가장 빠른 수렴 속도(평균이 가장 높은 모집단에 대한)를 갖는 수렴 인구 선택 정책을 구성했습니다.그런 다음 케이트하키스와 로빈스에서 분산이^[19] 알려진 정상 모집단의 경우 정책을 단순화하고 주요 증거를 제시했습니다.다음으로 주목할 만한 진전은 Burnetas와 Katehakis가 "순차 할당 문제에 대한 최적 적응형 정책"이라는 논문에서 얻었으며,^[20] 여기서 균일하게 최대 수렴률을 갖는 인덱스 기반 정책이 구성되었습니다.각 모집단의 결과 분포가 알려지지 않은 매개변수 벡터에 의존하는 경우를 포함하는 보다 일반적인 조건에서.Burnetas와 Katehakis(1996)는 또한 결과의 분포가 임의의(즉, 모수가 아닌) 이산 일변량 분포를 따르는 중요한 경우에 대한 명시적인 해결책을 제공했습니다.

나중에 "마코프 의사 결정 프로세스를 위한 최적 적응 정책"^[21]에서 Burnetas와 Katehakis는 부분 정보 하에서 훨씬 더 큰 마코프 의사 결정 프로세스 모델을 연구했는데, 여기서 전환 법칙 및/또는 예상되는 한 기간 보상은 알려지지 않은 매개 변수에 의존할 수 있습니다.본 연구에서 저자들은 유한한 상태 작용 공간과 전이 법칙의 축소 불가능성에 대한 충분한 가정 하에서 총 예상 유한 지평선 보상에 대해 균일한 최대 수렴률 특성을 가진 적응형 정책 클래스에 대한 명시적 형태를 구성했습니다.이러한 정책의 주요 특징은 각 상태 및 시간 기간에서 행동을 선택하는 것이 추정된 평균 보상 최적성 방정식의 우측 인플레이션인 지수를 기반으로 한다는 것입니다.이러한 인플레이션은 최근 Tewari와 Bartlett, Ortner^[23] Filippi,^[22] Cappé, Garivier,^[24] Honda와 Takemura의 연구에서 낙관적인 접근법으로 불리고 있습니다.^[25]

Bernouli multi-armed bandits의 경우, Pilarski et al.^[26]은 "Bernouli Bandits: 최적의 정책"이라는 논문에서 동적 프로그래밍을 사용하여 (점근적으로뿐만 아니라) 완전히 최적의 솔루션을 도출하는 계산 방법을 연구했습니다.계산 및 알고리즘 게이지."^[26]인덱싱 체계, 룩업 테이블 및 기타 기술을 통해 이 작업은 시간 지평선과 암 수가 과도하게 커지지 않는 경우 Bernouli 도적에게 실질적으로 적용 가능한 최적의 솔루션을 제공했습니다.필라르스키 ^[27]등은 나중에 이 작업을 "지연된 보상 베르누이 도적들:'최적 정책 및 예측 메타 알고리즘 PARDI'^[27]를 통해 결정 후 보상이 즉시 드러나지 않고 지연될 수 있는 경우 베르누이 도적단에게 최적 정책을 결정하는 방법을 만듭니다.이 방법은 아직 드러나지 않은 보상 결과의 기대 값을 계산하고 보상이 드러났을 때 사후 확률을 업데이트하는 것에 의존합니다.

동물들의 선택의 가치를 도출하기 위해 다중 팔 강도 작업에 대한 최적의 솔루션이 사용될 때 편도체와 복측 선조체의 뉴런의 활동은 이러한 정책에서 도출된 가치를 인코딩하고 동물들이 탐색적 선택과 착취적 선택을 할 때 해독하는 데 사용될 수 있습니다.또한 (아래 설명된) 대안적인 전략보다 최적의 정책이 동물의 선택 행동을 더 잘 예측합니다.이는 다중 암 밴디트 문제에 대한 최적의 솔루션이 계산적으로 까다롭지만 생물학적으로 그럴듯하다는 것을 시사합니다.^[29]

근사 솔루션

밴디트 문제에 대한 근사적인 해결책을 제공하는 많은 전략이 존재하며, 아래에 자세히 설명된 네 가지 범주에 넣을 수 있습니다.

반균일 전략

반균일 전략은 도적 문제를 대략적으로 해결하기 위해 발견된 가장 초기의(그리고 가장 간단한) 전략이었습니다.이러한 모든 전략은 (일률적으로) 무작위한 행동을 취할 때를 제외하고는 항상 최상의 지렛대를 당기는 탐욕스러운 행동을 공통적으로 가지고 있습니다.

• 엡실론 탐욕 전략:^[30]가장 좋은 레버는 시행 중 비율 $1$ -${\displaystyle }$ϵ ${\displaystyle$1 -$\epsilon}$에 선택되고 비율 ϵ ${\displaystyle \epsilon}$에 대해 레버가 임의(균일한 확률로) 선택됩니다$.$ 일반적인 매개 변수 값은 ϵ = ${\displaystyle 0.1}$ ${\displaystyle \epsilon$ = $0.1}$일 수 있지만 이$$값은 상황과 예측에 따라 크게 달라질 수 있습니다.
• 엡실론 최우선 전략^{[citation needed]}:순수탐구 단계는 순수탐구 단계로 이어집니다.총 $N개$의 ${\displaystyle N}$회 시행에 대해 탐색 단계는 ϵ ${\displaystyle \mathrm{N개}}$의$${\$displaystyle$ \$epsilon$N}회 시행 및 탐색 단계$({\displaystyle 1}$ -${\displaystyle }$ϵ${\displaystyle }$) ${\displaystyle \mathrm{N개}}$의$${\$displaystyle$ (1 -$\epsilon ) N}$회 시행을 차지합니다.탐색 단계에서는 레버가 무작위로 선택되고(균일한 확률로), 탐색 단계에서는 항상 최상의 레버가 선택됩니다.
• 엡실론 감소 전략^{[citation needed]}:실험이 진행됨에 따라 ϵ ${\displaystyle \epsilon}$의 값이 감소하여 시작 시 고도의 탐색적 동작과 끝 시 고도의 착취적 동작이 발생한다는 점을 제외하고는 엡실론 탐욕 전략과 유사합니다.
• 가치 차이에 기반한 적응적 엡실론-탐욕적 전략(VDBE): 수동 튜닝 대신 학습 진행률에 기반하여 엡실론을 감소시킨다는 점을 제외하면 엡실론 감소 전략과 유사함(Tokic, 2010).^[31]값 추정치의 높은 변동은 높은 엡실론(높은 탐사, 낮은 탐사)을 초래하고 낮은 엡실론(낮은 탐사, 높은 탐사)으로 낮은 변동을 초래합니다.탐색 행동의 경우 소프트맥스 가중 행동 선택을 통해 추가적인 개선을 달성할 수 있습니다(Tokic & Palm, 2011).^[32]
• 베이지안 앙상블(Epsilon-BMC)을 기반으로 한 적응적 엡실론-그리디 전략: 단조로운 수렴을 보장하는 VBDE와 유사한 강화 학습을 위한 적응적 엡실론 적응 전략.이 프레임워크에서 엡실론 매개 변수는 욕심쟁이 에이전트(학습된 보상을 완전히 신뢰하는)와 균일한 학습 에이전트(학습된 보상을 불신하는)에 가중치를 부여하는 사후 분포의 기대로 간주됩니다.이 후측은 관측된 보상의 정규성 가정 하에 적절한 베타 분포를 사용하여 근사화됩니다.또한, 엡실론을 너무 빨리 감소시킬 수 있는 위험을 해결하기 위해, 학습된 보상의 분산의 불확실성을 모델링하고 정상-감마 모델을 사용하여 업데이트합니다(Gimelfarb et al., 2019).^[33]

확률매칭전략

확률 매칭 전략은 주어진 레버에 대한 당기는 횟수가 최적의 레버일 실제 확률과 일치해야 한다는 생각을 반영합니다.확률 일치 전략은 Thompson 샘플링 또는 베이지안 밴디트라고도 하며,^[34][35] 각 대안의 평균값을 사후에서 샘플링할 수 있으면 구현하기가 매우 쉽습니다.

확률 매칭 전략은 또한 소위 컨텍스트 밴디트 문제에 대한 해결책을 인정합니다.^[34]

가격전략

가격책정 전략은 각 지렛대에 따라 가격을 결정합니다.예를 들어, POKER 알고리즘과 같이,^[14] 가격은 예상 보상과 추가 지식을 통해 얻게 될 추가 미래 보상의 추정치의 합이 될 수 있습니다.최고가의 지렛대는 항상 당겨집니다.

문맥적 도적

다중 무장 도적의 유용한 일반화는 문맥상 다중 무장 도적입니다.각 반복에서 에이전트는 여전히 팔 사이에서 선택해야 하지만, 과거에 플레이한 팔의 보상과 함께 사용할 수 있는 상황 벡터인 d차원 특징 벡터도 볼 수 있습니다.시간이 지남에 따라 학습자의 목표는 컨텍스트 벡터와 보상이 서로 어떻게 관련되는지에 대한 충분한 정보를 수집하여 특징 벡터를 보고 차선책을 예측할 수 있도록 하는 것입니다.^[36]

상황에 맞는 밴디트에 대한 근사 솔루션

문맥적 밴디트 문제에 대한 근사적인 해결책을 제공하는 많은 전략이 존재하며, 아래에 자세히 설명된 두 가지 범주로 나눌 수 있습니다.

온라인 선형 도적

• LinUCB(Upper Confidence Bound) 알고리즘: 저자는 동작의 예상 보상과 그 맥락 사이에 선형 의존성을 가정하고 선형 예측기 세트를 사용하여 표현 공간을 모델링합니다.^[37][38]
• LinRel (Linear Associative Reinforcement Learning) 알고리즘: LinUCB와 유사하지만 Ridge 회귀가 아닌 Singular-value 분해를 사용하여 신뢰도 추정치를 얻습니다.^[39][40]

온라인 비선형 도적단

• UC 프로그램 알고리즘:비선형 보상 함수는 비모수 회귀 분석에서 회귀 프로그램이라는 부분 상수 추정기를 사용하여 추정됩니다.그런 다음 각 상수 조각에 UCB를 사용합니다.컨텍스트 공간의 파티션을 연속적으로 세분화하는 작업이 예약되거나 적응적으로 선택됩니다.^[41][42][43]
• 일반화된 선형 알고리즘:보상 분포는 선형 산적도에 대한 확장인 일반화 선형 모델을 따릅니다.^{[44][45][46][47]}
• 커널 UCB 알고리즘 : 선형의 커널화된 비선형 버전효율적인 구현과 유한한 시간 분석을 제공하는 UCB.^[48]
• Bandit Forest 알고리즘 : 랜덤 포레스트를 구축하고 컨텍스트와 보상의 공동 분포를 알고 구축된 랜덤 포레스트를 분석합니다.^[49]
• Oracle 기반 알고리즘:알고리듬은 맥락적 밴디트 문제를 일련의 지도 학습 문제로 줄이고 보상 함수에 대한 일반적인 실현 가능성 가정에 의존하지 않습니다.^[50]

구속맥락적도적

실제로는 일반적으로 각 작업에서 사용하는 리소스와 관련된 비용이 발생하며 크라우드소싱 및 임상 시험과 같은 많은 애플리케이션에서 총 비용은 예산에 의해 제한됩니다.CCB(Constrainted Contextual Bandit)는 다중 무장 밴디트 설정에서 시간 및 예산 제약을 모두 고려하는 모델입니다.A. Badanidiyuru et al.^[51]은 먼저 리소스풀 컨텍스트 밴디트라고도 불리는 예산 제약이 있는 컨텍스트 밴디트를 연구했으며, $)$ {\$displaystyle$ O$({\sqrt {T})}$개의$$ 후회가 가능함을 보여줍니다.그러나 그들의 작업은 유한한 정책 집합에 초점을 맞추고 있으며 알고리즘은 계산적으로 비효율적입니다.

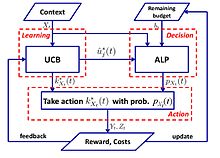
로그 후회를 갖는 간단한 알고리즘은 다음과 같이 제안됩니다.^[52]

• UCB-ALP 알고리즘:UCB-ALP의 프레임워크는 오른쪽 그림에 나와 있습니다.UCB-ALP는 UCB 방법과 ALP(Adaptive Linear Programming) 알고리즘을 결합한 간단한 알고리즘으로, 실제 시스템에 쉽게 배치할 수 있습니다.제약된 맥락적 도적에서 로그 후회를 달성하는 방법을 보여주는 첫 번째 작품입니다.비록 단일 예산 제약과 고정 비용을 가진 특별한 경우에 전념하고 있지만^[52], 그 결과는 보다 일반적인 CCB 문제에 대한 알고리즘의 설계와 분석을 보여줍니다.

적대적 도적

다중 무장 도적 문제의 또 다른 변형은 Auer와 Cesa-Bianchi(1998)에 의해 처음 소개된 적대 도적이라고 불립니다.이 변형에서, 각 반복에서 에이전트는 암을 선택하고, 상대는 각 암에 대한 보상 구조를 동시에 선택합니다.이것은 분포의 모든 가정을 제거하기 때문에 밴디트 문제의^[53] 가장 강력한 일반화 중 하나이며 적대적 밴디트 문제에 대한 해결책은 보다 구체적인 밴디트 문제에 대한 일반화된 해결책입니다.

예:죄수의 딜레마를 반복했습니다.

적대적인 도적들을 위해 종종 고려되는 한 예는 반복되는 죄수의 딜레마입니다.이 예제에서 각 상대는 당기는 팔이 두 개 있습니다.거부 또는 고백을 할 수 있습니다.표준 확률적 도적 알고리즘은 이러한 반복에서는 잘 작동하지 않습니다.예를 들어, 상대방이 처음 100라운드에서 협력하고, 다음 200라운드에서 결함이 발생한 후, 다음 300라운드에서 협력한다면, UCB와 같은 알고리즘은 이러한 변화에 매우 신속하게 대응할 수 없을 것입니다.특정 시점 이후에는 최적의 팔이 거의 당겨지지 않기 때문에 탐험을 제한하고 착취에 집중할 수 있습니다.환경이 변경되면 알고리즘이 조정할 수 없거나 변경을 감지하지 못할 수도 있습니다.

근사 솔루션

Exp3^[54]

EXP3는 Auer et al. 이 설정에서 제안하고 분석한 적대적 다중 무장 도적에 대한 인기 있는 알고리즘입니다.[2002b].최근에는 확률적 환경에서 이 알고리듬의 성능에 대한 관심이 증가했는데, 이는 부가 정보를 가진 확률적 다중 무장 도적에 대한 새로운 적용으로 인해 [Seldin et al., 2011]과 혼합 확률-적대성 환경에서 다중 무장 도적에 대한 새로운 적용 때문입니다 [Bubeck and Slivkins, 2012].본 논문은 확률적 환경에서 "논리적" 후회를 달성할 수 있는 EXP3 알고리즘의 수정 및 확률적 환경에서의 EXP3 알고리즘의 성능에 대한 실증적 평가 및 개선된 분석을 제시하였습니다.

알고리즘.

매개 변수: 실제 γ ∈${\displaystyle }$(${\displaystyle 0,}$ ${\displaystyle 1)}$ ${\displaystyle \$gamma$\in (0,1)}$ 초기화: $i$${\displaystyle {}_{}}$ω (${\displaystyle 1)}$ = i = ${\displaystyle 1}$ ${\displaystyle \{i}(1$)= $1},$ $K}$ 각 t에 $대해$ {\$displaystyle$ i = 1$,$ 2, ...,K} ${\displaystyle {pi}_{}}$( t${\displaystyle )}$ =${\displaystyle }$(${\displaystyle 1}$ -${\displaystyle }$γ${\displaystyle }$) ω ${\displaystyle \frac{\underset{}{\overset{}{i}}}{{}_{}}}$( ${\displaystyle \frac{t)}{}}$ ∑ j = 1 ${\displaystyle \frac{\underset{}{\overset{}{}}}{}}$ ω j${\displaystyle \frac{{}_{}}{}}$( ${\displaystyle \frac{t}{}}$) +${\displaystyle \frac{}{}}$γ$$K {\$displaystyle p_{i}(t)$=$(1-\$gamma) {\frac ${\omega _{i}(t$) ${\sum _{j$=$1}^{K}\omega _{{}$$j}($${\displaystyle t}$$)}}+{\frac {\gamma$}{$K}}$ $i$ $=$ ${\displaystyle 1,}$ ${\displaystyle ...,K}$ ${\displaystyle$ i$=$1, $...,K}$ 2. 확률 p ${\displaystyle 1_{}}$( t ${\displaystyle ),}$ ${\displaystyle ...,}$ ${\displaystyle p_{}}$ K (${\displaystyle {}_{}t}$ )${\displaystyle p_{1}(t$), $...,p_{K}(t)$ 3. 확률에 따라 ${\displaystyle {무작위}_{}}$로 ${\displaystyle i_{t}$를 그립니다.보상 ${\displaystyle {{xit}_{}}_{}}$ (${\displaystyle {{}_{}}_{}t)}$ ∈${\displaystyle }$[${\displaystyle 0,}$ ${\displaystyle 1]}$ ${\displaystyle x_{i_{t}}(t)\in [0,1]}$ 4를 받습니다. = ${\displaystyle 1}$,${\displaystyle }$.${\displaystyle }$.${\displaystyle }$, K ${\displaystyle$j = $1,$ ...,$K}$ 집합: x^ ( ) = {  () / j (  ) $j$ ( t )= 이면 {\$displaystyle {\hat {x}_{j}(t$) = $displaystyle} x_{j}(t)$ / $p_{j}(t)&{\text{if },$$&{\text{otherwise}}\end{case}}$ $ω$ ${\displaystyle j_{}}$( ${\displaystyle \mathrm{t}}$+ 1 )${\displaystyle }$$=$ $ω$ j${\displaystyle {}_{}}$( ${\displaystyle t}$) ${\displaystyle \exp }$ $⁡$ ${\displaystyle (}$$γ$ ${\displaystyle {}_{}}$ ${\displaystyle {\stackrel{}{^}}_{}}$ ${\displaystyle j_{}}$( t${\displaystyle }$)${\displaystyle }$/ K${\displaystyle }$) ${\displaystyle \omega$ _${j}(t$+ 1 )$=$\$omega _{j}(t)\exp(\hat {x}}_{j}(t)/K)}$ $gamma$

설명.

Exp3는 확률$($1 -${\displaystyle }$γ${\displaystyle )}$ ${\displaystyle(1$ -$\gamma)}$인 암을 무작위로 선택합니다. 가중치가 높은 암을 선호하며(익스플로잇) 확률 γ$${\$displaystyle \gamma}$인 암을 선택하여 균일하게 무작위로 탐색합니다.보상을 받은 후 가중치가 업데이트됩니다.기하급수적인 성장은 좋은 무기의 무게를 크게 증가시킵니다.

후회분석

Exp3 알고리즘의 (외부) 유감은 최대 $O{\displaystyle (\sqrt{\mathrm{KT}}}$ ${\displaystyle$ O$({\sqrt {KTlog(K))}}$입니다.

교란 리더(FPL) 알고리즘을 따릅니다.

알고리즘.

매개 변수: Real η$${\$displaystyle \eta}$ 초기화:$$∀ ${\displaystyle i}$: ${\displaystyle {Ri}_{}}$ (${\displaystyle 1{}_{}}$= ${\displaystyle 0}$ ${\displaystyle \for all$ i :$R_{i}(1)=0}$ 각 t $=$ 1,2,...,T 1. 각 암에 대해 지수 분포 $∀$ ${\displaystyle i}$ :${\displaystyle {Zi}_{}}$ (${\displaystyle {}_{}t}$)${\displaystyle }$~ ${\displaystyle \mathrm{Exp}}$ (${\displaystyle }$$η$${\displaystyle }$) ${\displaystyle \forall i:Z_{i}(t)\sim Exp(\eta )}$ 2로부터 랜덤 노이즈를 생성합니다.암 $I{\displaystyle (t)}$ ${\displaystyle I(t)}$: $I{\displaystyle (t)}$ = ${\displaystyle \mathrm{rg}}$ ${\displaystyle \underset{}{maxi}}${ ${\displaystyle {Ri}_{}t)}$+ ${\displaystyle {Zi}_{}t)}$ ${\displaystyle \}}$ ${\displaystyle I(t$) = arg$\max _{i}\{R_{i}(t)$ + $Z_{i}(t)\}$ 각 암에 노이즈를 추가하고 가장 높은 값을 가진 암을 3으로 당깁니다.업데이트 값: ${\displaystyle {RI}_{}}$( t${\displaystyle {}_{}}$)${\displaystyle {}_{}}$( ${\displaystyle t}$+ ${\displaystyle 1}$ )${\displaystyle }$= ${\displaystyle {RI}_{}}$( ${\displaystyle t{}_{}}$)${\displaystyle {}_{}}$( ${\displaystyle t_{}}$)${\displaystyle }$+ ${\displaystyle {}_{}}$ ${\displaystyle I_{}}$( t${\displaystyle {}_{}}$)${\displaystyle {}_{}}$( ${\displaystyle t_{}}$) ${\displaystyle R_{I(t)}(t$+ 1) = $R_{I(t)}(t)$ + $x_{I(t)}(t)}$ 나머지는 동일하게 유지됩니다.

설명.

우리는 지금까지 최고의 성능을 가지고 있다고 생각되는 팔을 따라 그것에 지수적인 소음을 더해 탐사를 제공합니다.^[55]

Exp3 vs FPL

Exp3	FPL
각 암에 대한 가중치를 유지하여 당길 확률 계산	팔당 당기는 확률을 알 필요가 없습니다.
효율적인 이론적 보장이 있음	표준 FPL은 좋은 이론적 보장을 가지고 있지 않습니다.
계산 비용이 많이 들 수 있음(지수 항 계산)	계산적으로 상당히 효율적임

무한 무장 도적

원래 사양과 위의 변형에서 밴디트 문제는 종종 $변수{\displaystyle }$ K ${\displaystyle K}$로 표시되는 이산적이고 유한한 수의 암으로 지정됩니다$.$ Agrawal(1995)에 의해 도입된 무한 무장 사례에서 "암"은 $K{\displaystyle }$ ${\displaystyle K}$ 차원의$$ 연속 변수입니다.^[56]

비정지 산적

이 프레임워크는 고정적이지 않은 환경(즉, 개념 드리프트가 있는 경우)에서 다중 무장 밴디트 문제를 참조합니다.비정지 설정에서 ∈ ${\displaystyle T}$ ${\$$displaystyle k}$ 단계마다 암 k ${\$displaystyle k}의 예상 보상이 변경될 수 있다고 가정합니다. {\$displaystyle t\in {\mathcal {T}}$: ${\displaystyle {\mu t}_{}^{}}$ -${\displaystyle {}_{}^{}}$ ≠ ${\displaystyle {}_{}^{}}$ ${\displaystyle \mu _{t-1}^{k}\neq \mu _{t}^{k$따라서 ${\displaystyle {}_{}^{}}$ ${\displaystyle \mu _{t}^{k}}$는 더 이상 $팔$ k ${\displaystyle k}$에 대한 예상(정지$)$ 보상의 전체 시퀀스를 나타내지 않습니다$.$ 대신 ${\displaystyle {\mu k}^{}}$ ${\displaystyle \mu ^{k}$는 팔 $k$ ${\displaystyle k}$에 대한 예상 보상의 시퀀스를 나타내며$,$ ${\displaystyle {\mu k}^{}}$ =${\displaystyle }${${\displaystyle {}_{}^{}}$ k${\displaystyle {}_{}^{}}$ ${\displaystyle t_{}^{}}$ = 1 ${\displaystyle {}_{}^{}}$ ${\displaystyle \mu ^{k$}=\{\$mu _{t}^{k}\}_{t$=$1}^{T}}.$

동적 오라클은 비정상 설정에서 다른 정책과 비교할 최적의 정책을 나타냅니다.동적 오라클은 ${\displaystyle {항상}_{}^{}}$ μt ∗의 예상 보상과 함께 $최적$의 ${\displaystyle 암}$을$$$선택$하여 각 $단계$ t ∈ T ${\displaystyle$$t\$$in$ {\mathcal {T$}}$에서 예상 보상을 최적화합니다$.$ 따라서,마지막 시간 $단계{\displaystyle }$ T ${\displaystyle T}$에서 동적 오라클에 대한$$ 누적 기대 보상 $D{\displaystyle \mathcal{}(T)}$ ${\mathcal {D}}(T)$는 다음과 같이 정의됩니다.

${\displaystyle {\mathcal {D}}(T)=\sum _{t=1}^{T}{\mu _{t}^{*}}$

따라서 정책 π ${\displaystyle \pi}$에 대한 후회 ρ π${\displaystyle {}^{}T)}$ ${\displaystyle \pi}(T)$은 $정책$$$π {\$displaystyle \pi}$에 대한 $D{\displaystyle (T)}$ ${\displaystyle {\mathcal {D}(T)$와 T $단계$ ${\displaystyle T}$의 누적 기대 보상의 차이로 계산됩니다$.$

${\displaystyle \rho ^{\pi }(T)=\sum _{t=1}^{T}{\mu _{t}^{*}-\mathbb {E} _{\pi}^{\mu}}\left[\sum _{t=1}^{T}{r_{t}}\right]={\mathcal {D}}(T)-\mathbb {E} _{\pi}^{\mu}}\left[\sum_{t=1}^{T}{r_{t}}\right]}$

Garivier와 Moulines는 플레이 중에 기본 모델이 변경될 수 있는 밴디트 문제와 관련하여 몇 가지 첫 번째 결과를 도출합니다.디스카운트드 UCB^[58] 및 슬라이딩 윈도우 UCB를 포함한 많은 알고리즘이 이 경우를 처리하기 위해 제시되었습니다.^[59]톰슨 샘플링 알고리즘을 기반으로 한 유사한 접근 방식은 Cavenaghi et al.에 의해 제안된 f-Discounted-Sliding-Window Thompson 샘플링(f-dsw TS)^[60]입니다.f-dsw TS 알고리즘은 보상 이력에 대한 할인 요소와 암 관련 슬라이딩 윈도우를 활용하여 고정되지 않은 환경에서 개념 드리프트를 대조합니다.Burtini 등의 또 다른 연구는 가중치 최소 제곱 톰슨 샘플링 접근법(WLS-TS)을 소개하고 있으며, 이는 알려진 경우와 알려지지 않은 비 정상적인 경우 모두에서 유익함을 입증합니다.^[61]

기타 변형

최근 몇 년간 이 문제의 많은 변형들이 제안되었습니다.

결투 산적

결투하는 밴디트 변형은 Yue et al. (2012)^[62]에 의해 상대적 피드백을 위한 탐색 대 착취 트레이드오프를 모델링하기 위해 도입되었습니다.이 변형에서 도박꾼은 동시에 두 개의 레버를 당길 수 있지만, 어떤 레버가 최고의 보상을 제공했는지를 알려주는 이진 피드백만 받습니다.이 문제의 어려움은 도박꾼이 자신들의 행동에 대한 보상을 직접 관찰할 방법이 없다는 사실에서 비롯됩니다.이 문제에 대한 가장 초기의 알고리즘은 인터리브 필터링(Interleave Filtering),^[62] Beat-The-Mean입니다.^[63]결투하는 도적들의 상대적인 피드백은 투표 역설을 초래할 수도 있습니다.해결책은 콘도르케트 우승자를 참고인으로 삼는 것입니다.^[64]

보다 최근에는 연구자들이 기존 MAB에서 결투하는 도적떼로 알고리듬을 일반화했습니다. 상대적 상위 신뢰 범위(RUCB),^[65] 상대적 지수 가중치(REX3),^[66] Copeland 신뢰 범위(CCB),^[67] 상대적 최소 경험 발산(RMED)^[68] 및 이중 톰슨 샘플링(DTS).^[69]

협적 도적

성능을 최적화하기 위해 지식을 공유하는 데 협력하는 여러 도적을 사용하는 접근 방식은 2013년 서로 다른 도적 문제 간의 유사성 그래프를 사용하여 지식을 공유하는 알고리즘인 ^[70]"A Gang of Bandits"로 시작되었습니다.유사도 그래프의 필요성은 2014년에 CLUB 알고리즘에 대한 연구에 의해 제거되었습니다.^[71]이 연구 이후, 여러 다른 연구자들은 밴디트 피드백 하에서 여러 모델을 동시에 학습하는 알고리즘을 개발했습니다.예를 들어, COFIBA는 Li and Karatzoglou and Gentile(SIGIR 2016)에 의해 도입되었으며,^[72] 여기서 고전적인 협업 필터링과 콘텐츠 기반 필터링 방법은 훈련 데이터가 주어진 정적 추천 모델을 학습하려고 합니다.

콤비나탈 도적

조합 다중 무장 밴디트(CMAB) 문제는 에이전트가 선택할 단일 이산 변수^[73][74][75] 대신 변수 집합에 대한 값을 선택해야 할 때 발생합니다.각 변수가 이산형이라고 가정하면 반복당 가능한 선택의 수는 변수의 수에 지수적입니다.변수가 이진인^[74] 설정부터 각 변수가 임의의 값 집합을 취할 수 있는 보다 일반적인 설정까지 여러 CMAB 설정이 문헌에서 연구되었습니다.^[75]

참고 항목

• Gittins 지수 – 강도 문제를 분석하는 강력하고 일반적인 전략입니다.
• 그리디 알고리즘
• 최적정지
• 탐색이론
• 확률적 스케쥴링

참고문헌

추가열람

• Guha, S.; Munagala, K.; Shi, P. (2010), "Approximation algorithms for restless bandit problems", Journal of the ACM, 58: 1–50, arXiv:0711.3861, doi:10.1145/1870103.1870106, S2CID 1654066
• Dayanik, S.; Powell, W.; Yamazaki, K. (2008), "Index policies for discounted bandit problems with availability constraints", Advances in Applied Probability, 40 (2): 377–400, doi:10.1239/aap/1214950209.
• Powell, Warren B. (2007), "Chapter 10", Approximate Dynamic Programming: Solving the Curses of Dimensionality, New York: John Wiley and Sons, ISBN 978-0-470-17155-4.
• Robbins, H. (1952), "Some aspects of the sequential design of experiments", Bulletin of the American Mathematical Society, 58 (5): 527–535, doi:10.1090/S0002-9904-1952-09620-8.
• Sutton, Richard; Barto, Andrew (1998), Reinforcement Learning, MIT Press, ISBN 978-0-262-19398-6, archived from the original on 2013-12-11.

• Allesiardo, Robin (2014), "A Neural Networks Committee for the Contextual Bandit Problem", Neural Information Processing – 21st International Conference, ICONIP 2014, Malaisia, November 03-06,2014, Proceedings, Lecture Notes in Computer Science, vol. 8834, Springer, pp. 374–381, arXiv:1409.8191, doi:10.1007/978-3-319-12637-1_47, ISBN 978-3-319-12636-4, S2CID 14155718.

• Weber, Richard (1992), "On the Gittins index for multiarmed bandits", Annals of Applied Probability, 2 (4): 1024–1033, doi:10.1214/aoap/1177005588, JSTOR 2959678.
• Katehakis, M.; C. Derman (1986), "Computing optimal sequential allocation rules in clinical trials", Adaptive statistical procedures and related topics, Institute of Mathematical Statistics Lecture Notes - Monograph Series, vol. 8, pp. 29–39, doi:10.1214/lnms/1215540286, ISBN 978-0-940600-09-6, JSTOR 4355518.
• Katehakis, M.; A. F. Veinott, Jr. (1987), "The multi-armed bandit problem: decomposition and computation", Mathematics of Operations Research, 12 (2): 262–268, doi:10.1287/moor.12.2.262, JSTOR 3689689, S2CID 656323.

외부 링크

• 병렬화 및 시뮬레이션 기능이 내장된 컨텍스트 프리, 파라메트릭 및 비파라메트릭 컨텍스트 정책을 지원하는 밴디트 전략의 오픈 소스 파이썬 구현 MABWiser.
• PyMaBandits, Python 및 Matlab에서 밴디트 전략의 오픈 소스 구현.
• 문맥이 없는 오픈 소스 R 패키지는 문맥이 없는 다중 무장 밴디트 정책의 시뮬레이션과 평가를 용이하게 합니다.
• bandit.sourceforge.net 밴디트 프로젝트, 밴디트 전략 오픈소스 구현
• Banditlib, C++에서 Bandit 전략의 오픈소스 구현.
• 레슬리 팩 케일블링과 마이클 L. 리트먼 (1996). 착취 대 탐사: 단일 국가 사건.
• 자습서:도적 소개:알고리즘과 이론.1부.2부.
• 파인만의 레스토랑 문제, 착취 대 탐사 트레이드오프의 전형적인 예(답변이 알려진).
• 밴디트 알고리즘 vs. A-B 테스트.
• S. 부벡과 N. 세사-비앙키 도적에 대한 조사.
• 맥락적 다무장 도적에 대한 조사, 맥락적 도적에 대한 조사/교습
• 파이썬 코드를 사용한 다중 무장 도적 전략에 대한 블로그 게시물.
• Epsilon-greedy, Thompson 샘플링 및 상위 신뢰 한계 탐색/익스플로팅 밸런싱 전략을 보여주는 애니메이션 대화형 그림입니다.