조정(통계)

통계에서 조정 모델은 중재 변수(중재 변수, 중간 변수 또는 간섭 변수라고도 함)로 알려진 세 번째 가상 변수를 포함시킴으로써 독립 변수와 종속 변수 사이의 관측된 관계를 기초로 하는 메커니즘이나 프로세스를 식별하고 설명하려고 한다.^[1] 독립변수와 종속변수의 직접적인 인과관계보다는 독립변수가 (관찰할 수 없는) 중재변수에 영향을 미치고, 이는 다시 종속변수에 영향을 미친다고 조정모형은 제안한다. 따라서 중재자 변수는 독립변수와 종속변수의 관계의 성격을 명확히 하는 역할을 한다.^[2]

조정 분석은 한 변수가 중재 변수를 통해 다른 변수에 영향을 미치는 기본 메커니즘이나 프로세스를 탐색함으로써 알려진 관계를 이해하기 위해 채택된다.^[3] 특히 조정 분석은 독립변수와 종속변수의 관계가 명확하지 않은 경우 이러한 변수들의 관계를 보다 잘 이해하는 데 기여할 수 있다.

조정 분석을 위한 남작과 케니의 (1986) 단계

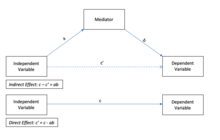
남작과 케니(1986)는 진정한 중재 관계를 형성하기 위해 반드시 충족되어야 할 몇 가지 요건을 제시했다.^[4] 그것들은 실제 사례를 사용하여 아래에 요약되어 있다. 설명될 전체 중재 관계를 시각적으로 표현하려면 위의 다이어그램을 참조하십시오. 참고: 헤이스(2009)는 바론(Barron)과 케니의 조정 단계 접근에 대해 비판했으며,^[5] 2019년 현재 데이비드 A. 케니는 자신의 웹사이트에 '중대한' 총체적 효과가 없을 때 중재가 존재할 수 있으며, 따라서 아래 1단계는 필요하지 않을 수 있다고 말했다. 이런 상황을 '불일치 조정'이라고 부르기도 한다. 이후 헤이스에 의한 출판물들 역시 전체 또는 부분적 조정의 개념에 의문을 제기하고 아래에 요약된 고전적 조정 단계 접근법과 함께 이러한 용어들이 폐기될 것을 주장하였다.

1단계:

독립 변수에 대한 종속 변수를 회귀 분석하여 독립 변수가 종속 변수에 대한 유의한 예측 변수인지 확인하십시오.

독립 변수${\displaystyle }$→ ${\displaystyle \to }$ 종속$$ 변수

${\displaystyle Y=\beta _{10}+\beta _{11}X+\varepsilon _{1}}$

• β는₁₁ 유의하다.

2단계:

독립 변수에 대한 중재자를 회귀시켜 독립 변수가 중재자의 유의미한 예측 변수인지 확인한다. 만약 중재자가 독립변수와 연관되지 않는다면, 그것은 어떤 것도 중재할 수 없을 것이다.

독립 변수${\displaystyle }$→ ${\displaystyle \to }$ 중재자$$

${\displaystyle Me=\beta _{20}+\beta _{21}X+\varepsilon _{2}$

• β는₂₁ 유의하다.

3단계:

중재자와 독립변수 모두에 종속변수를 회귀시켜 a) 중재자가 종속변수의 유의미한 예측자임을 확인하고, b) 이전에 유의미한 독립변수의 계수가 유의하지 않더라도 1단계에서 유의미한 독립변수의 계수의 강도는 현재 크게 감소한다.

${\displaystyle Y=\beta _{30}+\beta _{31}X+\beta _{32}Me+\varepsilon _{3}}}$

• β는₃₂ 유의하다.
• β는₃₁ 독립 변수에 대한 원래 효과보다 절대값에서 작아야 한다(β₁₁ 위)

예

하웰(2009년)에서 도출한 다음의 예는 조정 효과가 어떻게 특징지어지는지를 더 이해하기 위한 바론 및 케니의 요구사항의 각 단계를 설명한다.^[6] 1단계와 2단계는 단순 회귀 분석을 사용하는 반면 3단계는 다중 회귀 분석을 사용한다.

1단계:

당신이 어떻게 양육되었는지(즉, 독립 변수)는 당신이 당신의 자녀들을 양육하는 것에 대해 얼마나 자신감 있는지(즉, 종속 변수)를 예측한다.

어떻게 부모 노릇을 했는지 →${\displaystyle \to }$자신의 양육 능력에 대한 자신감$$.

2단계:

당신이 어떻게 양육되었는가(즉, 독립 변수)는 당신의 능력과 자긍심(즉, 중재자)의 감정을 예측한다.

부모님의 마음${\displaystyle }$→ ${\displaystyle \to$}역량과 자부심의 감정$$.

3단계:

당신의 역량과 자존감(즉, 중재자)에 대한 감정은 자신이 양육된 방식(즉, 종속변수)을 조절하면서, 자신이 자녀 양육에 대해 얼마나 자신감을 갖고 있는지 예측한다.

이러한 발견은 여러분이 어떻게 양육되었는지와 자녀 양육에 대해 얼마나 자신감 있는지 사이의 관계를 여러분의 역량과 자부심에 대한 감정이 중재한다는 결론으로 이어질 것이다.

참고: 1단계에서 유의한 결과가 나오지 않는 경우 2단계로 이동할 수 있는 근거가 있을 수 있다. 때로는 독립변수와 종속변수 사이에 실제로 유의미한 관계가 있지만 표본 크기가 작거나 다른 관련 없는 요인 때문에 실제로 존재하는 효과를 예측하는 데 충분한 검정력이 없을 수 있다.^[7]

직접효과와 간접효과

위에 나타낸 도표에서 간접 효과는 경로 계수 "A"와 "B"의 산물이다. 직접적인 효과는 계수 "C"이다. 직접효과는 독립변수가 1단위씩 증가하고 중재변수가 변하지 않을 때 종속변수의 변화 정도를 측정한다. 이와는 대조적으로, 간접 효과는 독립변수를 고정했을 때 종속변수가 변화하고, 독립변수가 한 단위 증가했을 때 조정변수가 변화했을 정도를 측정한다.^[8][9]

선형 시스템에서 총 효과는 직간접적(위 모형의 C' + AB)의 합과 같다. 비선형 모델에서 총효과는 일반적으로 직간접 효과의 합이 아니라 두 효과의 변형된 조합과 동일하다.^[9]

전체 조정 대 부분 조정

중재자 변수는 두 변수 사이의 관찰된 관계의 전부 또는 일부를 설명할 수 있다.

전면 조정

조정 변수를 포함하면 독립 변수와 종속 변수(위의 다이어그램의 경로 c 참조)의 관계가 0으로 떨어지는 경우 조정의 최대 증거가 전체 조정이라고도 한다.

부분조정

부분 조정은 조정 변수가 독립변수와 종속변수의 관계 중 일부(전부는 아님)를 설명한다고 주장한다. 부분적 조정은 중재자와 종속변수 사이에 유의미한 관계가 있을 뿐만 아니라 독립변수와 종속변수 사이에 어떤 직접적인 관계가 있음을 시사한다.

전체 또는 부분 중 하나가 설정되려면 독립 변수에 의해 설명되는 분산 감소는 소벨 검정과 같은 여러 시험 중 하나에 의해 결정되는 것처럼 유의해야 한다.^[10] 단순히 사소한 분산이 설명된다는 이유(즉, 진정한 중재가 아니라는 이유) 때문에 중재자가 도입될 때 종속변수에 대한 독립변수의 영향은 유의적이지 않을 수 있다. 따라서 완전한 또는 부분적인 조정을 주장하기 전에 독립변수에 의해 설명되는 상당한 분산의 감소를 보여주는 것이 필수적이다. 전체 효과가 없는 경우 통계적으로 유의한 간접 효과를 가질 수 있다.^[5] 이는 서로 취소하는 여러 중재 경로의 존재로 설명될 수 있으며, 취소 중재자 중 한 명이 제어될 때 눈에 띈다. 이는 '부분적'과 '전체적' 조정이라는 용어는 항상 모형에 존재하는 변수 집합과 관련하여 해석되어야 함을 의미한다. 모든 경우에 있어서, 「변수에 대한 제어」의 운용은 문헌에서 부적절하게 사용되어 온 「변수에 대한 제어」의 운용과 구별되어야 한다.^[8][11] 전자는 물리적으로 고정하는 것을 의미하며, 후자는 회귀 모형의 조건화, 조정 또는 추가를 의미한다. 두 개념은 모든 오차항(도표에는 표시되지 않음)이 통계적으로 상관관계가 없을 때에만 일치한다. 오류가 상관된 경우 조정 분석을 시작하기 전에 이러한 상관 관계를 무력화하도록 조정해야 한다(베이지안 네트워크 참조).

소벨 검사

위에서 언급한 바와 같이, 독립변수와 종속변수의 관계가 중재변수를 포함시킨 후 현저하게 감소하였는지를 판단하기 위해 소벨의 시험을^[10] 실시한다. 즉, 이 검사는 조정 효과가 유의적인지 여부를 평가한다. 독립변수와 종속변수의 관계에 비해 조정인자를 포함한 독립변수와 종속변수의 관계를 조사한다.

소벨 테스트는 위에서 설명한 바론 및 케니 단계보다 더 정확하지만, 통계적 힘이 낮다. 이와 같이 유의한 효과를 검출할 수 있는 충분한 검정력을 갖기 위해서는 큰 표본 크기가 필요하다. 소벨 검사의 핵심 가정은 정상성의 가정이기 때문이다. 소벨의 검정은 주어진 표본을 정규 분포에 대해 평가하기 때문에 표본 크기가 작거나 표본 분포의 왜도가 문제가 될 수 있다(자세한 내용은 정규 분포 참조). 따라서 맥키넌 외 연구진, (2002)에서 제시한 경험 법칙은 작은 효과를 검출하려면 표본 크기가 1000이어야 하고, 중간 효과를 검출하려면 표본 크기가 100이면 충분하며, 큰 효과를 검출하려면 표본 크기가 50이면 된다는 것이다.

전도사와 헤이스(2004) 부트스트랩 방법

부트스트래핑 방법은 소벨의 테스트에 몇 가지 이점을 제공하며, 주로 파워가 증가한다. 전도사와 헤이스 부트스트래핑 방법은 비모수 테스트(비모수 테스트 및 그 검정력에 대한 설명은 비모수 통계 참조)이다. 따라서 부트스트랩 방법은 정규성의 가정을 위반하지 않으므로 작은 표본 크기에 권장된다. 부트스트래핑은 각 재샘플에서 원하는 통계를 계산하기 위해 데이터 집합에서 대체하여 관측치를 반복적으로 랜덤하게 샘플링하는 것을 포함한다. 수백 또는 수천 개의 부트스트랩 재샘플을 계산하면 관심 통계량의 표본 분포에 대한 근사치를 제공한다. 헤이스는 통계 분석에 사용되는 컴퓨터 프로그램인 SPSS 내에서 부트스트래핑을 직접 계산하는 매크로 <http://www.afhayes.com/>을 제공한다. 이 방법은 조정 효과의 유의성 또는 비부정성을 평가할 수 있는 점 추정치와 신뢰 구간을 제공한다. 포인트 추정치는 부트스트랩된 샘플의 수에 대한 평균을 나타내며, 부트스트래핑 방법의 결과 신뢰 구간 사이에 0이 들어가지 않으면 보고해야 할 중요한 조정 효과가 있다고 자신 있게 결론을 내릴 수 있다.

조정의 의의

위에서 설명한 것처럼 조정 모델을 평가하기 위해 선택할 수 있는 몇 가지 다른 옵션이 있다.

부트스트래핑은^[13][14] 정규성 가정을 충족시킬 필요가 없고 더 작은 표본 크기(N < 25)로 효과적으로 활용할 수 있기 때문에 조정 테스트의 가장 인기 있는 방법이 되고 있다. 그러나 조정은 남작과 케니의 논리나 소벨 시험을 이용하여 가장 빈번하게 결정되고 있다. 순수하게 배런과 케니법에 근거한 조정 시험이나 소벨 시험과 같은 분배적 가정을 하는 시험들을 발행하는 것이 점점 더 어려워지고 있다. 따라서 어떤 테스트를 수행할지 선택할 때 선택사항을 고려하는 것이 중요하다.^[5]

조정 접근법

심리학 내에서 정의한 조정의 개념은 이론적으로 호소력이 있는 반면, 조정 연구를 위해 경험적으로 사용하는 방법은 통계학자와 역학학자들에^[8][11][16] 의해 도전받아 정식으로 해석되어 왔다.^[9]

(1) 실험-관경-연쇄 설계

제안된 중재자가 실험적으로 조작될 때 실험-관심-사슬 설계가 사용된다. 그러한 설계는 주어진 관계의 근본적인 메커니즘이 될 수 있다고 믿을 수 있는 어떤 통제된 제3의 변수를 조작한다는 것을 의미한다.

(2) 중재의 측정 설계

매개 측정 설계는 통계적 접근방식으로 개념화할 수 있다. 그러한 설계는 제안된 개입 변수를 측정한 다음 통계분석을 사용하여 조정을 설정한다는 것을 의미한다. 이 접근방식은 귀무 가설의 매개 변수의 조작을 수반하지 않고 측정만을 수반한다.^[17]

조정방안 비판

중재에 대한 실험적인 접근은 주의 깊게 수행되어야 한다. 첫째, 잠재적 매개 변수의 탐색적 조사에 대한 강력한 이론적 지지를 갖는 것이 중요하다. 조정 접근법에 대한 비판은 조정 변수를 조작하고 측정할 수 있는 능력에 있다. 따라서, 제안된 중재자를 수용적이고 윤리적 방법으로 조종할 수 있어야 한다. 따라서 결과에 지장을 주지 않고 개입 과정을 측정할 수 있어야 한다. 또한 조정자는 조작의 건설적 타당성을 확립할 수 있어야 한다. 매개 측정 접근법에 대한 가장 일반적인 비판 중 하나는 이것이 궁극적으로 상관 설계라는 것이다. 따라서 제안된 중재자로부터 독립된 일부 다른 제3의 변수가 제안된 효과에 대한 책임이 있을 수 있다. 그러나, 연구원들은 이러한 불균형에 대한 반증권을 제공하기 위해 열심히 노력해왔다. 구체적으로 다음과 같은 반론이 제기되었다.^[3]

(1) 시간적 우선 순위. 예를 들어, 독립 변수가 종속 변수보다 적시에 선행하는 경우, 이는 독립 변수에서 종속 변수로의 연결 방향 및 잠재적으로 인과관계를 암시하는 증거를 제공할 것이다.

(2) 비논리성 및/또는 혼동 없음. 예를 들어, 다른 제3의 변수를 식별하고 독립변수와 종속변수의 관계를 변경하지 않는다는 것을 입증한다면, 그 변수들의 조정 효과에 대해 더 강력한 주장을 할 수 있을 것이다. 아래의 다른 세 번째 변수를 참조하십시오.

조정은 매우 유용하고 강력한 통계적 시험이 될 수 있지만, 적절히 사용되어야 한다. 중재자와 종속변수를 평가하는 데 사용되는 조치가 이론적으로 구별되고 독립변수와 중재자가 상호작용을 할 수 없다는 것이 중요하다. 독립변수와 중재자 사이에 상호작용이 있다면 절제를 조사할 근거가 있을 것이다.

기타 세 번째 변수

(1) 교란:

종종 시험되는 또 다른 모델은 모델에서 경쟁 변수가 대체 잠재적 매개 변수 또는 종속 변수의 측정되지 않은 원인인 모델이다. 인과 모형의 추가 변수는 독립 변수와 종속 변수 사이의 관계를 모호하게 하거나 혼동할 수 있다. 잠재적 교란물은 독립변수와 종속변수 모두에 인과적 영향을 미칠 수 있는 변수다. 여기에는 독립변수와 종속변수 모두가 공유하는 다른 영향뿐만 아니라 (위에서 논의한 바와 같이) 측정오차의 공통적인 원인이 포함된다.

실험 연구에서는 동기부여 이론적 요인보다는 연구 효과를 설명할 수 있는 실험 조작이나 설정의 측면에 대해 특별한 우려가 있다. 이러한 문제들 중 어떤 것이라도 측정된 독립변수와 종속변수 사이에 거짓 관계를 발생시킬 수 있다. 교락 변수를 무시하면 독립 변수의 인과적 효과에 대한 경험적 추정치가 편향될 수 있다.

(2) 억제:

억제 변수는 회귀 방정식에 포함될 때 다른 변수의 예측 유효성을 증가시킨다. 억제는 하나의 인과 변수가 두 개의 분리된 중재 변수를 통해 결과 변수와 연관되어 있을 때 발생할 수 있으며, 그러한 매개 변수 중 하나가 양이고 하나는 음수일 때 발생할 수 있다. 이 경우 각 중재 변수는 다른 중재 변수를 통해 전달되는 효과를 억제하거나 은폐한다. 예를 들어 높은 지능 점수(인과 변수 A)는 오류 감지(중재 변수 B)의 증가를 유발할 수 있으며, 이로 인해 조립 라인(결과 변수 X)에서 작업 중 발생한 오류가 감소할 수 있으며, 동시에 지능은 지루함(C)의 증가와 e의 증가를 야기할 수 있다.오류(X). 따라서 한 인과 경로 지능은 오류를 감소시키고, 다른 인과 경로 지능은 오류를 증가시킨다. 어느 중재자도 분석에 포함되지 않을 경우 지능은 오류에 대한 효과가 없거나 약해 보인다. 그러나 지루함을 통제할 때 지능은 오류를 감소시키는 것처럼 보일 것이고, 오류 감지를 통제할 때 지능은 오류를 증가시키는 것처럼 보일 것이다. 지루함만 일정하게 유지한 상태에서 지능을 높일 수 있다면 오류가 감소하고, 오류 감지만 일정하게 유지한 상태에서 지능을 높일 수 있다면 오류가 증가할 것이다.

일반적으로 억제제나 교란제의 생략은 X에 대한 A의 효과를 과소평가하거나 과대평가하여 두 변수 사이의 관계의 크기를 줄이거나 인위적으로 부풀리게 된다.

(3) 진행자는 다음과 같다.

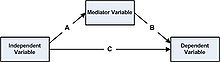
다른 중요한 세 번째 변수는 중재자들이다. 진행자는 두 변수 사이의 관계를 더 강하게 만들거나 약하게 만들 수 있는 변수다. 그러한 변수는 X와 Y의 관계의 방향 및/또는 강도에 영향을 줌으로써 회귀에서 교호작용을 더욱 특성화한다. 온건한 관계는 상호 작용이라고 생각할 수 있다. 변수 A와 B의 관계가 C의 수준에 따라 다를 때 발생한다. 자세한 내용은 절제를 참조하십시오.

조정중재

조정과 절제는 통계적 모델에서 함께 발생할 수 있다. 중용과 온건 조정을 할 수 있다.

조정 조정은 치료 A가 중재자 및/또는 종속 변수에 대한 부분 효과 B가 차례로 다른 변수(조정자)의 수준에 따라 달라지는 경우를 말한다. 본질적으로 조정된 조정에서 조정은 먼저 성립된 다음, 독립변수와 종속변수의 관계를 기술하는 조정효과가 다른 변수(즉, 조정자)의 다른 수준에 의해 조정되는지를 조사한다. 이 정의는 뮬러, 저드, 이저비트(2005)^[18]와 전도사, 러커, 헤이스(2007)에 의해 윤곽이 잡혔다.^[19]

조정의 모델

중재 조정의 가능한 모델은 아래 도표와 같이 다섯 가지가 있다.^[18]

1. 첫 번째 모델에서 독립 변수는 중재자와 종속 변수 사이의 관계도 완화한다.
2. 조정 조정의 두 번째 가능한 모델은 독립 변수와 중재자(A 경로)의 관계를 완화하는 새로운 변수를 포함한다.
3. 조정 조정의 세 번째 모델은 중재자와 종속 변수(B 경로)의 관계를 완화하는 새로운 조정 변수를 포함한다.
4. 조정된 조정은 하나의 조정 변수가 독립변수와 중재자의 관계(A경로)와 중재자와 종속변수의 관계(B경로) 모두에 영향을 미칠 때도 발생할 수 있다.
5. 조정 조정의 다섯 번째 및 마지막 가능한 모델은 두 개의 새로운 조정자 변수를 포함한다. 하나는 A 경로를 조정하고 다른 하나는 B 경로를 조정한다.

첫 번째 옵션: 독립 변수는 B 경로를 완화한다.

두 번째 옵션: 네 번째 변수는 A 경로를 완화한다.

세 번째 옵션: 네 번째 변수는 B 경로를 완화한다.

네 번째 옵션: 네 번째 변수는 A 경로와 B 경로를 모두 완화한다.

다섯 번째 옵션: 네 번째 변수는 A 경로를 낮추고 다섯 번째 변수는 B 경로를 낮춘다.

중재적 절제

중재적 절제는 절제와 조정의 변종이다. 이것은 초기에 전체적인 절제가 있고 결과에 대한 감속 변수의 직접적인 영향이 매개되는 부분이다. 매개된 절제와 감속형 조정의 주요 차이점은 전에는 초기(전반적인) 있어 절제와 이 효과 매체는 후자를 없어 절제지만 중재자(경로 A)에 그 치료의 효과 또는 중재자의(경로 B)를 중재해 준 결과에 미치는 영향은 잠잠해져 있고 있다.[18]

중재적 절제를 확립하기 위해서는 우선 절제를 확립해야 하는데, 이는 독립변수와 종속변수(경로 C)의 관계의 방향 및/또는 강도가 세 번째 변수(감속 변수)의 수준에 따라 다르다는 것을 의미한다. 다음에 연구자들은 독립변수와 감속재(경로 A) 또는 감속재와 종속변수(경로 C) 사이의 관계를 유발하는 메커니즘이나 과정으로 작용하는 네 번째 변수가 있다고 믿을 이론적 이유가 있을 때 중재적 절제의 존재를 찾는다.

예

다음은 심리학 연구의 중재적 절제의 출판된 예다.^[20] 참가자들에게는 도덕을 생각하게 하거나 힘을 생각하게 하는 초기 자극(최고의 자극)이 주어졌다. 이어 이들은 자신과 범죄 파트너가 체포된 것처럼 가장하는 '죄수의 딜레마 게임'(PDG)에 참여했으며, 파트너에 대한 충성심을 유지할 것인지 아니면 파트너와 경쟁하고 당국과 협력할 것인지를 결정해야 한다. 연구원들은 친사회적 개인은 도덕성에 영향을 받고 소수일 수 있지만, 친사회적 개인은 그렇지 않다는 것을 발견했다. 따라서 사회적 가치 지향(proself vs. prosocial)은 프라임(독립 변수: 도덕성 vs. might)과 PDG에서 선택한 행동(의존 변수: 경쟁 대 협동) 사이의 관계를 절제하였다.

그 다음에 연구원들은 중재적 절제 효과가 있는지 찾아보았다. 회귀 분석에서는 프라임(도덕성 대 가능성)의 유형이 PDG 행동에 대한 참여자의 사회적 가치 지향의 절제된 관계를 매개한다는 것을 밝혀냈다. 도덕성 전성기를 경험한 친사회적 참여자들은 파트너가 자신들과 협력하기를 기대했기 때문에 스스로 협력을 선택했다. 전성기를 경험한 친사회적 참여자들은 파트너가 자신들과 경쟁하기를 기대했고, 이로 인해 파트너와 경쟁하고 당국과 협력할 가능성이 높아졌다. 이와는 대조적으로, 친자신적인 사회적 가치 지향성을 가진 참가자들은 항상 경쟁적으로 행동했다.

조정 및 조정 절제에 대한 회귀 방정식

뮬러, 저드, 이저비트(2005)^[18]는 중재와 중재적 중용의 기초가 되는 세 가지 기본 모델을 개략적으로 설명한다. Mo는 감속 변수를 나타내고, Me는 중재 변수를 나타내며, ε은_i 각 회귀 방정식의 측정 오차를 나타낸다.

1단계: 독립 변수(X)와 종속 변수(Y) 사이의 관계를 절제하는 것으로, 전체 처리 효과(도표에서 경로 C)라고도 한다.

${\displaystyle Y=\beta _{40}+\beta _{41}X+\beta _{42}Mo+\beta _{43}XMo+\barepsilon _{4}}}}}}$

• 전체적인 절제를 확립하기 위해서는 β₄₃ 회귀 무게가 유의해야 한다(중간 절제를 확립하기 위한 첫 번째 단계).
• 절제된 조정을 확립하기 위해서는 절충 효과가 없으므로₄₃ β 회귀 무게가 유의하지 않아야 한다.

2단계: 독립 변수와 중재자 사이의 관계(경로 A)의 조정.

${\displaystyle Me=\beta _{50}+\beta _{51}X+\beta _{52}Mo+\beta _{53}XMo+\barepsilon _{5}}}}}}}$

• β₅₃ 회귀중량이 유의미한 경우, 감속재는 독립변수와 중재자 사이의 관계에 영향을 미친다.

3단계: 독립변수와 종속변수의 관계(경로 A) 및 중재자와 종속변수의 관계(경로 B) 모두 절제.

${\displaystyle Y=\beta _{60}+\beta _{61}X+\beta _{62}Mo+\beta _{63}XMo+\beta _{64}MeMo+\beta _{65}MeMo+\barpsilon _{6}}}}}}}}}}}}}}}}}}}}}{6}$

• 2단계의 β와₅₃ 3단계의 β가₆₃ 모두 유의미한 경우, 감속재는 독립변수와 중재자(경로 A) 사이의 관계에 영향을 미친다.
• 2단계의 β와₅₃ 3단계의 β가₆₅ 모두 유의한 경우, 감속재는 중재자와 종속 변수(경로 B)의 관계에 영향을 미친다.
• 위의 조건 중 하나 또는 둘 다 사실일 수 있다.

원인조정분석

고정 대 조건화

조정 분석은 변수가 원인에서 그 효과로의 변화의 투과도에 참여하는 정도를 정량화한다. 그것은 본질적으로 인과적인 개념이기 때문에 통계 용어로 정의할 수 없다. 그러나 전통적으로 조정 분석의 대부분은 관련 관계의 인과적 성격을 가리는 통계 용어로 선형 회귀의 범위 내에서 수행되었다. 이는 인과도와 반사실적 논리에 근거한 현대적인 인과 분석 방법에 의해 완화되어 온 어려움, 편향, 한계로 이어졌다.

이러한 어려움의 근원은 회귀 방정식에 제3의 변수를 추가함으로써 유발되는 변화 측면에서 조정을 정의하는 데 있다. 그러한 통계적 변화는 때때로 중재를 수반하지만 일반적으로 조정 분석이 정량화를 목표로 하는 인과관계를 포착하지 못하는 인식론이다.

인과접근법의 기본 전제는 우리가 X가 Y에 미치는 직접적인 영향을 추정하려고 할 때 중재자 M에 대해 항상 "통제"하는 것이 적절하지 않다는 것이다(위 그림 참조). M에 대한 "제어"에 대한 고전적인 근거는 만약 우리가 M의 변경을 막는 데 성공한다면, 우리가 Y에서 측정한 어떤 변화도 오로지 X의 변화에만 기인하며, 우리는 "Y에 대한 X의 직접적인 영향"으로 관찰된 영향을 선언하는 것이 정당화된다. 불행하게도, "M에 대한 제어"는 M의 변화를 물리적으로 방해하지 않는다. M 값이 동일한 경우에 대한 분석가의 주의를 좁힐 뿐이다. 더구나 확률론 언어는 'M이 변하는 것을 방지한다'거나 '물리학적으로 M 상수를 쥐고 있다'는 생각을 표현하기 위한 표기법을 가지고 있지 않다. 연산자 확률은 우리가 M에 대해 "제어"할 때 또는 Y에 대한 방정식에 M을 리제스터로 추가할 때 우리가 할 수 있는 유일한 "조건"이다. 그 결과 물리적으로 M" 상수(M = m)를 유지하고 X = 1' 이하 단위의 Y를 X = 0 이하 단위의 Y와 비교하는 대신 M = m 값을 달성하는 단위를 제외한 모든 단위는 무시한다. 이 두 연산은 근본적으로 다르며,^[21][22] 생략 변수가 없는 경우를 제외하고는 다른 결과를 산출한다.

예를 들어, M과 Y의 오차항은 상관관계가 있다고 가정한다. 그러한 조건 하에서 구조계수 B와 A(M과 Y 사이, Y와 X 사이)는 더 이상 X와 M에서 Y를 퇴행시켜 추정할 수 없다. 실제로 회귀 기울기는 C가 0인 경우에도 둘 다 0이 아닐 수 있다.^[23] 이것은 두 가지 결과를 낳는다. 첫째, 구조계수 A, B, C를 추정하기 위한 새로운 전략이 고안되어야 한다. 둘째, 직간접 효과의 기본적 정의는 회귀분석을 넘어서야 하며, 'M에 대한 조절'이 아닌 '고정 M'을 모방한 연산을 실행해야 한다.

정의들

이러한 연산자 do(M = m)는 Pearl(1994)^[22]에서 정의되었으며, M의 방정식을 제거하고 상수 m로 대체하여 동작한다. 예를 들어, 기본 조정 모델이 방정식으로 구성되는 경우:

${\displaystyle X=f(\varepsilon _{1}), ~M=g(X,\varepsilon _{2}), ~Y=h(X,M,\varepsilon _{3}),}$

그런 다음 연산자 do(M = m)를 적용한 후 모델은 다음과 같이 된다.

${\displaystyle X=f(\varepsilon _{1}),~~M=m,~~Y=h(X,m,\varepsilon _{3})}$

연산자 do(X = x)를 적용한 후 모델은 다음과 같이 된다.

${\displaystyle X=x, M=g(x,\varepsilon _{2}),Y=h(x,M,\varepsilon _{3}})$

여기서 함수 f와 g는 물론 오차항 ε과₁ ε의₃ 분포도 변경되지 않은 상태로 유지된다. 추가로 do(X = x)에서 비롯된 변수 M과 Y의 이름을 각각 M(x)과 Y(x)로 바꾸면, 우리는 "잠재적 결과"^[24] 또는 "구조적 반사실"이라고 알려진 것을 얻는다.^[25] 이러한 새로운 변수는 직접 및 간접 효과를 정의하기 위한 편리한 표기법을 제공한다. 특히 X = 0에서 X = 1로 전환하기 위해 네 가지 유형의 효과가 정의되었다.

(a) 총 영향:

$[\displaystyle TE=E[Y(1)-Y(0)]}$

(b) 통제된 직접 효과는

${\displaystyle CDE(m)=E[Y(1,m)-Y(0,m)]}$

(c) 자연적 직접적 효과 -

${\displaystyle NDE=E[1,M(0)-Y(0,M(0))]}$

(d) 자연 간접 효과

${\displaystyle NIE=E[0,M(1)-Y(0,M(0))]}$

여기서 E[ ]는 오류 조건을 인수하는 기대치를 나타낸다.

이러한 효과는 다음과 같은 해석을 가지고 있다.

• TE는 X가 X=0에서 X=1로 변화함에 따라 Y 결과의 예상 증가를 측정하고, 중재자는 M = g(X, ε₂) 함수에 의해 지시된 X의 변화를 추적할 수 있다.
• CDE는 X가 X = 0에서 X = 1로 변경됨에 따라 Y 결과의 예상 증가를 측정하고, 중재자는 전체 모집단에 걸쳐 균일하게 사전 지정된 수준 M = m으로 고정된다.
• NDE는 X가 X = 0에서 X = 1로 변경될 때 예상되는 Y의 증가를 측정하는 동시에 X = 0에서 얻었을 값, 즉 변경 전으로 조정 변수를 설정한다.
• NIE는 X가 일정하게 유지될 때 예상되는 Y의 증가를 X = 1로 측정하고, M은 X = 1에 따라 (각 개인에 대해) 얻었을 모든 값으로 변경한다.
• TE-NDE의 차이는 효과를 설명하기 위해 중재가 필요한 정도를 측정하는 반면 NIE는 중재가 지속하기에 충분한 정도를 측정한다.

변수를 상수에 고정하여 직접 효과를 비활성화할 수 있는 방법이 없기 때문에 간접 효과의 제어 버전이 존재하지 않는다.

이러한 정의에 따르면 총효과는 합으로 분해될 수 있다.

${\displaystyle TE=NDE-NIE_{r}}$

여기서 NIE는_r X = 1에서 X = 0으로 역전환을 의미하며, 선형 시스템에서 가법화되어 전환의 역전이 기호 반전을 수반한다.

이러한 정의의 힘은 그 일반성에 있다; 그것들은 임의의 비선형 상호작용, 교란들 사이의 임의의 의존성, 그리고 연속적 및 범주적 변수 모두를 가진 모델에 적용된다.

조정식

선형 분석에서 모든 효과는 구조 계수의 산출물의 합계에 의해 결정되며, 다음과 같은 결과를 제공한다.

${\displaystyle {\reasoned}TE&=C+AB\\CDE(m)&=NDE=C,{\text{{}m\와는 별개NIE&=AB.\end{정렬}}}$

따라서 모델이 식별될 때마다 모든 효과를 추정할 수 있다. 비선형 시스템에서는 직접 및 간접 효과를 추정하기 위해 보다 엄격한 조건이 필요하다.^[27] 예를 들어 교란 요인이 존재하지 않는 경우(예: ε₁, ε₂, ε, ε은₃ 상호 독립적) 다음과 같은 공식을 도출할 수 있다.^[9]

${\displaystyle {\reasoned}TE&=E(Y\mid X=1)-E(Y\mid X=0)\\CDE(m)&=E(Y\mid X=1,M=m)-E(Y\mid X=0,M=m)\\\NDE&=\sum _{m}[E(Y X=1,M=m)-E(Y\mid X=0,M=m)]P(M=m=mid X=0)\\\\NIE&=\sum _{m}[P(M=m\mid X=1)-P(M=mid X=0)]E(Y\mid X=0,M=m]\end{정렬}}}$

마지막 두 방정식은 조정 공식이라고 불리며 조정의 많은 연구에서 추정의 대상이 되었다.^{[26][27][29][30]} 이들은 직접 및 간접 효과에 대해 무분포 식을 제공하고 오차 분포와 함수 f, g 및 h의 임의적 특성에도 불구하고 회귀 분석을 사용한 데이터에서 매개 효과를 추정할 수 있음을 입증한다. 중재 조정 및 중재 중재 중재자의 분석은 인과 중재 분석의 특별한 사례로 분류되며, 조정 공식은 다양한 상호작용 계수가 조정의 필요하고도 충분한 구성요소에 어떻게 기여하는지를 식별한다.^[27][28]

예

모델이 폼을 잡았다고 가정해 보십시오.

${\displaystyle {\begin}X&=\varepsilon _{1}\\M&=b_{0}+b_{1}}X+\varepsilon _{2}\\Y&=c_{0}+c_{1}}X+c_{2}M+c_{3}XM+\varepsilon _{3}\end{aigned}}}$

여기서 $매개변수{\displaystyle {}_{}}$ c ${\$는 M이 Y에 대한 X의 영향을 수정하는 정도를 정량화한다$$. 모든 파라미터가 데이터로부터 추정된다고 해도, 어떤 파라미터의 조합이 X가 Y에 미치는 직간접적인 영향을 측정하는지, 또는 보다 현실적으로 조정으로 설명되는 총 효과 ${\displaystyle T}$ $E{\displaystyle }$ ${\displaystyle TE}$의 부분과 빚지고 있는$$ $T{\displaystyle }$ ${\displaystyle E}$ ${\displaystytle TE}$의 부분을 평가하는 방법을 측정하는지는 여전히 명확하지 않다.중재에 부치다 선형 분석에서 전분수는 제품 ${\displaystyle {b\mathrm{}}_{}}$ 1 ${\displaystyle {c\mathrm{}}_{}}$2 / ${\displaystyle T}$ E ${\displaystyle b_{$1}$c_{2}/TE}$에$$의해,${\displaystyle \mathrm{후자}}$는 ${\displaystyle \mathrm{차이}({}_{}}$ ${\displaystyle {E\mathrm{}}_{}}$-${\displaystyle c}$ ${\displaystyle 1}$ ) /$$T E {\$displaystyle$ ($T-c_{$1}/$TE$에 의해 캡처되고 두 수량은 일치한다. 그러나 교호작용이 있는 경우, 각 분수는 조정식에 따라 다음과 같은 별도의 분석을 요구한다.

${\displaystyle {\reasoned}NDE&=c_{1}+b_{0}c_{3}\\NIE&=b_{1}c_{2}\\TE&=c_{1}+b_{0}c_{0}c_{3}+b_{1}(c_{2}+c_{3})\&=NDE+NE+b_{1}c_{3}.\end{정렬}}}$

따라서 조정으로 충분할 출력 응답의 분율은 다음과 같다.

${\displaystyle {\frac {NIE}{TE}}={\frac {b_{1}c_{2}}:{c_{1}+b_{0}c_{0}c_{3}+b_{1}(c_{2}+c_{3}}),},}$

중재가 필요한 분수는 다음과 같다.

${\displaystyle 1-{\frac {NDE}{TE}}={\frac {b_{1}(c_{2}+c_{3})}{c_{1}+b_{0}c_{0}c_{3}+b_{1}(c_{2}+c_{3}}}}}}}}}}}.}$

이러한 분수는 모델의 매개변수들의 명백한 조합을 포함하며 조정 공식의 도움을 받아 기계적으로 구성될 수 있다. 유의하게 상호작용에 의해 파라미터 c ${\displaystyle {1\mathrm{}}_{}}$ ${\$}가 소멸되어도$$ 직접적 효과를 유지할 수 있고, 더욱이 직접적 효과와 간접적 효과가 모두 소멸되어도 총체적 효과를 유지할 수 있다. 이는 별도로 매개변수를 추정하는 것이 조정의 효과를 거의 알 수 없으며, 보다 일반적으로 조정과 절제가 서로 얽혀 있어 별도로 평가할 수 없음을 보여준다.

참조

2014년 6월 19일 현재, 본 기사는 전체 또는 일부에서 파생되었다. 이론과 실제에서의 인과분석저작권자는 CC BY-SA 3.0 및 GFDL에 따라 재사용을 허용하는 방식으로 콘텐츠에 대한 라이센스를 부여했다. 관련 조항은 모두 준수해야 한다.^{[데드링크]}

메모들

참고 문헌 목록

• Preacher, Kristopher J.; Hayes, Andrew F. (2004). "SPSS and SAS procedures for estimating indirect effects in simple mediation models". Behavior Research Methods, Instruments, and Computers. 36 (4): 717–731. doi:10.3758/BF03206553. PMID 15641418.
• Preacher, Kristopher J.; Hayes, Andrew F. (2008). "Asymptotic and resampling strategies for assessing and comparing indirect effects in multiple mediator models". Behavior Research Methods. 40 (3): 879–891. doi:10.3758/BRM.40.3.879. PMID 18697684.
• Preacher, K. J.; Zyphur, M. J.; Zhang, Z. (2010). "A general multilevel SEM framework for assessing multilevel mediation". Psychological Methods. 15 (3): 209–233. CiteSeerX 10.1.1.570.7747. doi:10.1037/a0020141. PMID 20822249.
• Barron, R. M. and Kenny, D. A.(1986) "사회심리 연구의 사회자-중재자 변수 구분 - 개념적, 전략적, 통계적 고려사항", 제51권(6), 제1173권–1182권.
• 코헨, J. (1988) 행동 과학에 대한 통계적 힘 분석(2차 개정) 뉴욕, 뉴욕: 아카데미 프레스.
• Hayes, A. F. (2009). "Beyond Baron and Kenny: Statistical mediation analysis in the new millennium". Communication Monographs. 76 (4): 408–420. doi:10.1080/03637750903310360.
• 하웰, D. C. (2009) 심리학을 위한 통계적 방법(7차 개정판) C.A: Cengage Learning.
• MacKinnon, D. P.; Lockwood, C. M. (2003). "Advances in statistical methods for substance abuse prevention research". Prevention Science. 4 (3): 155–171. doi:10.1023/A:1024649822872. PMC 2843515. PMID 12940467.
• Preacher, K. J.; Kelley, K. (2011). "Effect sizes measures for mediation models: Quantitative strategies for communicating indirect effects". Psychological Methods. 16 (2): 93–115. doi:10.1037/a0022658. PMID 21500915.
• 러커, D.D., 설교자, K.J., 토르말라, Z.L. & Fetty, R.E.(2011년). "사회 심리학에서의 중재 분석: 현재 관행 및 새로운 권장 사항" 사회 및 성격 심리학 컴퍼스, 5/6, 359–371.
• Sobel, M. E. (1982). "Asymptotic confidence intervals for indirect effects in structural equation models". Sociological Methodology. 13: 290–312. doi:10.2307/270723. JSTOR 270723.
• Spencer, S. J.; Zanna, M. P.; Fong, G. T. (2005). "Establishing a causal chain: why experiments are often more effective than mediational analyses in examining psychological processes". Journal of Personality and Social Psychology. 89 (6): 845–851. doi:10.1037/0022-3514.89.6.845. PMID 16393019.
• Pearl, Judea (2012). "The Mediation Formula: A guide to the assessment of causal pathways in nonlinear models". In Berzuini, C.; Dawid, P.; Bernardinelli, L. (eds.). Causality: Statistical Perspectives and Applications. Chichester, UK: John Wiley and Sons, Ltd. pp. 151–179.
• Shaughnessy J.J., Zechmeister E. & Zechmeister J.(2006). 심리학의 연구 방법 (제7편, 페이지 51-52) 뉴욕: 맥그로우 힐.
• Tolman, E. C. (1938). "The Determiners of Behavior at a Choice Point". Psychological Review. 45: 1–41. doi:10.1037/h0062733.
• Tolman, E. C.; Honzik, C. H. (1930). "Degrees of hunger, reward and nonreward, and maze learning in rats". University of California Publications in Psychology. 4: 241–275.
• Vanderweele, Tyler J. (2015). Explanation in Causal Inference.

외부 링크

• 사이코위키 조정 방법 요약
• 성향 점수를 이용한 인과 조정 사례 펜 주립 대학교 방법론 센터
• SPSS 및 SAS Andrew F에 대한 프로세스 매크로의 소개를 포함하여 절제 및 조정 분석에 대한 책을 읽으십시오. 오하이오 주립 대학교 헤이스
• 온라인 텍스트 "선택 지점에서의 행동 결정자"
• 케네스 맥코쿼데일과 폴 E. Mehl (1948) 심리학의 역사에서 가상의 구성과 개입 변수 고전과의 구별에 관하여, 2011년 8월 22일, 다시 되돌아온다.