와이토프 건설
Wythoff construction기하학에서 수학자 윌렘 아브라함 와이토프의 이름을 딴 와이토프 건축은 획일적인 다면체나 평면 타일링을 건설하는 방법이다. 흔히 와이토프의 케일리디스코픽 건설이라고 한다.
시공공정
이 방법은 구형을 구형 삼각형으로 타일링하는 아이디어에 기초한다 – 슈바르츠 삼각형을 참조한다. 이 구조는 세 개의 거울을 삼각형의 측면에 배열하는데, 마치 케일리도스코프처럼 말이다. 그러나 갈레도스코프와 달리 거울은 평행하지 않고 한 지점에서 교차한다. 따라서 그들은 그 점을 중심으로 하는 어떤 구의 표면에 구면 삼각형을 둘러 싸고 반복된 반사는 그 삼각형의 다수의 복사본을 생성한다. 구면 삼각형의 각도를 적절하게 선택하면 삼각형이 구를 한 번 이상 타일로 장식한다.
거울에 둘러싸인 구형 삼각형 내부의 적절한 지점에 정점을 배치하면 그 점의 반사가 균일한 다면체를 만들 수 있다. 구형 삼각형 ABC의 경우, 우리는 균일한 다면체를 생산할 네 가지 가능성을 가지고 있다.
- 꼭지점은 A 지점에 위치한다. 이것은 Wythoff 기호 a b c를 가진 다면체를 생성하며, 여기서 a는 A에서 삼각형의 각도로 나눈 equals과 같으며, b와 c도 이와 유사하다.
- 꼭지점은 선 AB의 한 지점에 위치하여 C에서 각도를 이등분한다. 이것은 Wythoff 기호가 b c인 다면체를 생산한다.
- 꼭지점은 ABC의 인센티브에 놓이도록 배치된다. 이것은 Wythoff 기호가 b c인 다면체를 생산한다.
- 꼭지점은 삼각형의 모서리를 그 지점에서 각도의 2배만큼 회전할 때 모든 각도에 대해 동일한 거리에 의해 이동될 수 있는 지점에 있다. 원래 꼭지점의 짝수 반사만 사용된다. 다면체에는 와이토프 기호 a b c가 있다.
이 과정은 일반적으로 4차원 균일 4폴리토페를 포함한 고차원 일반 폴리토페에도 적용된다.
  육각 프리즘은 (6 2)와 (3 2) 패밀리로 구성된다. |   잘린 사각 타일링은 (4 4 2) 패밀리의 서로 다른 대칭 위치에 의해 구성된다. | 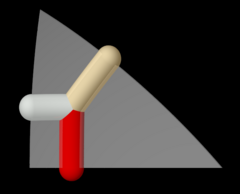 Wythoff 패턴 pq2 = 432. 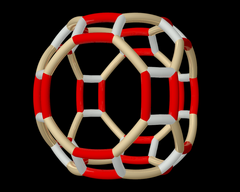 위 와이토프 패턴의 궤도는 전체 팔면 그룹의 작용 하에 있다. |
비Wythoffian 구성
와이토프 미러 구조를 통해 만들 수 없는 균일한 폴리토페스를 비 와이토피안이라고 한다. 그것들은 대체 정점의 삭제 또는 부분 그림의 교대 층의 삽입에 의해 와이토피안 형태에서 도출될 수 있다. 이 두 유형의 수치 모두 회전 대칭을 포함할 것이다. 때때로 스너브 형태는 전지형식의 교대로만 구성될 수 있음에도 불구하고 와이토피안으로 간주된다.
 육각형 항정신병증은 도각형 프리즘의 교대로 형성된다. |  길쭉한 삼각 타일링은 사각 타일링과 삼각 타일링 행을 레이어링하여 구성된다. |  위대한 디롬비코시도데카헤드론은 유일하게 위토피아의 제복 다면체다. |
참고 항목
- Wythoff 기호 - 균일한 다면체 및 균일한 기울기의 Wythoff 구축을 위한 기호.
- Coxeter-Dynkin 다이어그램 - 균일한 폴리토페와 허니콤의 Wythoff 시공에 대한 일반화된 기호.
참조
- CoxeterRegular Polytopes, 제3판, (1973) 도버판, ISBN0-486-61480-8 (V장: 칼리도스코프, 섹션: 5.7 와이토프의 건설)
- 콕시터 기하학의 아름다움: 12편의 에세이, 도버 출판사, 1999년 ISBN 0-486-40919-8 (제3장: 균일한 폴리토페스를 위한 와이토프의 건설)
- 하엘, Z. 균일 폴리헤드라, 기하학적 디디카타 47, 57-110, 1993. [1] (제4장: 케일리도스코프)
- W.A. Wythoff, C600 계열의 폴리토페스, Koninklijke Akademie van Wetenschappen te 암스테르담, 과학 섹션 절차, 20 (1918) 966–970 사이의 관계.
외부 링크
- Jenn, 대칭 그룹에서 (구형) 다면체 및 다면체의 뷰를 생성하는 소프트웨어





