스너브(지오메트리)

아르키메데스 고형물 두 개가 스누브드된 아르키메데스 고형물

스너브 큐브 또는 스너브 큐옥타헤드론	스너브 도데카헤드론 또는 스너브 이코시다데코헤드론

잘린 큐빅 큐브 정점(빨간색 또는 녹색)으로 스너브 큐브에 대한 두 개의 치랄 사본.

스너브 큐브는 6개의 푸른 정사각형 면을 12개의 하얀 정사각형 면이 정삼각형의 쌍이 될 때까지 회전시켜 롬비큐브옥타헤드론으로부터 만들어질 수 있다.

기하학에서 스너브는 다면체에 적용되는 수술이다.이 용어는 스너브 큐브(쿠부스 시무스)와 스너브 도데카헤드론(도데카에드론 시무스)에 대한 케플러의 두 아르키메데스 고형물의 이름에서 유래한다.^[1]일반적으로 스너브는 시계 방향 또는 시계 반대 방향의 두 가지 형태로 키랄 대칭을 가진다.케플러의 이름으로 볼 때 스너브는 일반 다면체의 확장으로 볼 수 있는데, 즉 얼굴을 따로 떼어내고, 얼굴 중심을 중심으로 비틀고, 원래의 정점을 중심으로 한 새로운 다각형을 추가하고, 원래의 가장자리 사이에 맞는 삼각형 쌍을 추가하는 것이다.

이 용어는 콕시터에 의해 약간 다른 정의로 더 넓은 세트의 균일한 폴리토프에 대해 일반화되었다.

콘웨이 스너브

존 콘웨이는 일반화된 다면체 연산자를 탐구하여 현재 다면체 및 기울기에 적용할 수 있는 콘웨이 다면체 표기법이라고 불리는 것을 정의했다.콘웨이는 콕시터의 작전을 반스너브라고 부른다.^[2]

이 표기법에서 스너브는 이중 및 자이로 연산자에 의해 s = dg로 정의되며, 암보 연산자의 잘림 교대로 정의되는 것과 같다.콘웨이의 표기법 자체가 콕세터의 교대(반쪽) 연산을 피하는 것은 짝수 면만 있는 다면체에만 적용되기 때문이다.

스너브드 정규 수치

스너브할 양식	폴리헤드라			유클리드 기울기		쌍곡 틸팅
이름	사면체	큐브 또는 팔면체	이코사헤드론 또는 도데면체	사각 타일링	육각 타일링 또는 삼각 타일링	헵타곤 타일링 또는 순서-7 삼각 타일링
이미지들
스너브드 폼 콘웨이노트	세인트	sC = sO	sI = sD	sQ	sH = Δ	Δ
이미지

콘웨이는 4차원에서는 스너브 24 셀을 세미 스너브 24 셀이라고 불러야 한다고 제안한다. 왜냐하면 3차원 스너브 다면체는 대체적으로 잡면체 24 셀이 아니기 때문이다.대신에 그것은 사실 교대로 잘린 24셀이다.^[3]

Coxeter의 스너브, 정규 및 quasiregular.

입방체 또는 큐보타헤드론에서 파생된 스너브 큐브

이름	큐브	큐폭타헤드론 수정 큐브	잘린 큐옥타헤드론 캔트런드 큐브	스너브 큐옥타헤드론 스너브 정류 큐브
	씨앗	수정됨 r	잘림 t	교대형 h
콘웨이 표기법	C	CO rC	tCO trC 또는 trO	htCO = sCO htrC = srC
슐레플리 기호	{4,3}	${\begin{Bmatrix}4\\3\end{Bmatrix}}$ ${\begin{Bmatrix}4\\3\end{Bmatrix}}$ ${\begin{Bmatrix}4\\3\end{Bmatrix}}$ } ${\$ 또는 ${\begin{Bmatrix}4\\3\end{Bmatrix}}$ r{4,3}	$t{\begin{Bmatrix}4\\3\end{Bmatrix}}$ { $t{\begin{Bmatrix}4\\3\end{Bmatrix}}$ $t{\begin{Bmatrix}4\\3\end{Bmatrix}}$ ${\$ }4 $\\\3\end{Bmatrix}$ 또는 $t{\begin{Bmatrix}4\\3\end{Bmatrix}}$ tr{4,3}	$ht{\begin}4\\3\end{Bmatrix}s{\begin}4\3\end{Bmatrix}}}$ htr{4,3} = sr{4,3}
콕시터 다이어그램		또는	또는	또는
이미지

콕세터의 스너브 용어는 약간 다르며, 스너브 큐브를 스너브 큐빅 큐빅헤드론으로, 스너브 도데케드론을 스너브 아이코시디케이드론으로 도출한다는 뜻이다.이 정의는 존슨 고형물, 즉 스너브 디스페노이드와 스너브 사각형 항정신병, 그리고 확장된 슐래플리 기호 s{3,4,3}와 콕시터 도표와 같은 보다 차원 높은 폴리토페스의 명칭에 사용된다.

A regular polyhedron (or tiling), with Schläfli symbol ${\begin{Bmatrix}p,q\end{Bmatrix}}$ , and Coxeter diagram , has truncation defined as $t{\begin{Bmatrix}p,q\end{Bmatrix}}$ , and , and has snub defined as an alternated truncation $ht{\begin{Bmatrix}p,q\end{Bmatrix}}=s{\begin{Bmatrix}p,q\end{Bmatrix}}$ $ht{\begin{Bmatrix}p,q\end{Bmatrix}}=s{\begin{Bmatrix}p,q\end{Bmatrix}}$ $ht{\begin{Bmatrix}p,q\end{Bmatrix}}=s{\begin{Bmatrix}p,q\end{Bmatrix}}$ $ht{\begin{Bmatrix}p,q\end{Bmatrix}}=s{\begin{Bmatrix}p,q\end{Bmatrix}}$ ${\$ 및 .이 교대 구조는 q가 짝수여야 한다.

A quasiregular polyhedron, with Schläfli symbol ${\begin{Bmatrix}p\\q\end{Bmatrix}}$ or r{p,q}, and Coxeter diagram or , has quasiregular truncation defined as $t{\begin{Bmatrix}p\\q\end{Bmatrix}}$ or tr{p,q}, and or , and has quasiregular snub defined as an교대로 잘린 정류 h $ht{\begin{Bmatrix}p\\q\end{Bmatrix}}=s{\begin{Bmatrix}p\\q\end{Bmatrix}}$ $ht{\begin{Bmatrix}p\\q\end{Bmatrix}}=s{\begin{Bmatrix}p\\q\end{Bmatrix}}$ = $ht{\begin{Bmatrix}p\\q\end{Bmatrix}}=s{\begin{Bmatrix}p\\q\end{Bmatrix}}$ { $ht{\begin{Bmatrix}p\\q\end{Bmatrix}}=s{\begin{Bmatrix}p\\q\end{Bmatrix}}$ $q} {\$ }= $s{\$ begin} $p\p\q$ \end ${Bmatrix}}$ 또는 htr $ht{\begin{Bmatrix}p\\q\end{Bmatrix}}=s{\begin{Bmatrix}p\\q\end{Bmatrix}}$ {p $,$ q} = sr{p,q},q} 및 .

For example, Kepler's snub cube is derived from the quasiregular cuboctahedron, with a vertical Schläfli symbol ${\begin{Bmatrix}4\\3\end{Bmatrix}}$ , and Coxeter diagram , and so is more explicitly called a snub cuboctahedron, expressed by a vertical Schläfli symbol ${\display$ $스타일 s{\begin{Bmatrix}4\\3\end{Bmatrix}}$ 및 Coxeter 다이어그램 .스너브 큐보타헤드론은 잘린 큐보타헤드론, $t{\begin{Bmatrix}4\\3\end{Bmatrix}}$ { $t{\begin{Bmatrix}4\\3\end{Bmatrix}}$ $t{\begin{Bmatrix}4\\3\end{Bmatrix}}$ ${\$ 및 .

Regular polyhedra with even-order vertices can also be snubbed as alternated truncations, like the snub octahedron, as $s{\begin{Bmatrix}3,4\end{Bmatrix}}$ , , is the alternation of the truncated octahedron, $t{\begin{Bmatrix}3,4\end{Bmatrix}}$ , and .스너브 옥타헤드론은 화농대칭이 있는 일반 이코사헤드론인 의사면체를 나타낸다.

The snub tetratetrahedron, as $s{\begin{Bmatrix}3\\3\end{Bmatrix}}$ , and , is the alternation of the truncated tetrahedral symmetry form, $t{\begin{Bmatrix}3\\3\end{Bmatrix}}$ , and .

이름	팔면체	잘린 팔면체	스너브 옥타헤드론
	씨앗	잘림 t	교대형 h
콘웨이 표기법	O	to	htO 또는 sO
슐레플리 기호	{3,4}	t{3,4}	ht{3,4} = s{3,4}
콕시터 다이어그램
이미지

Coxeter's snub operation also allows n-antiprisms to be defined as $s{\begin{Bmatrix}2\\n\end{Bmatrix}}$ or $s{\begin{Bmatrix}2,2n\end{Bmatrix}}$ , based on n-prisms $t{\begin{Bmatrix}2\\n\end{Bmatrix}}$ or $t{\begin{Bmatrix}2,2n\end{Bmatrix}}$ $t{\begin{Bmatrix}2,2n\end{Bmatrix}}$ , while ${\begin{Bmatrix}2,n\end{Bmatrix}}$ is a regular n-hosohedron, a degenerate polyhedron, but a valid tiling on the sphere with digon or lune-shaped faces.

스너브 호소헤드라, {2,2p}

이미지
콕시터 도표							... ...
슐레플리 기호	s{2,4}	s{2,6}	s{2,8}	s{2,10}	s{2,12}	s{2,14}	s{2,16}...	s{2,3}
슐레플리 기호	sr{2,2} $s{\begin{Bmatrix}2\\2\end{Bmatrix}$	sr{2,3} $s{\begin{Bmatrix}2\\3\end{Bmatrix}$	sr{2,4} $s{\begin{Bmatrix}2\\4\end{Bmatrix}$	sr{2,5} $s{\begin{Bmatrix}2\\5\end{Bmatrix}$	sr{2,6} $s{\begin{Bmatrix}2\\6\end{Bmatrix}$	sr{2,7} $s{\begin{Bmatrix}2\\7\end{Bmatrix}$	sr{2,8}... $s{\begin{Bmatrix}2\\8\end{Bmatrix}}$ { 2 $s{\begin{Bmatrix}2\\8\end{Bmatrix}}$ $s{\begin{Bmatrix}2\\8\end{Bmatrix}}$ ${\$	sr{2,610} $s{\begin{Bmatrix}2\\\infit \end{Bmatrix}$
콘웨이 표기법	A2 = T	A3 = O	A4	A5	A6	A7	A8...	A∞

스너브 틸링에도 동일한 프로세스가 적용된다.

삼각 타일링 Δ	잘린 삼각 타일링 Δ	스너브 삼각 타일링 HTΔ = Δ
{3,6}	t{3,6}	ht{3,6} = s{3,6}

예

{p,4} 기반 스너브

공간	구면		유클리드 주	쌍곡선
이미지
콕시터 도표를 만들다								...
슐레플리 심볼	s{2,4}	s{3,4}	s{4,4}	s{5,4}	s{6,4}	s{7,4}	s{8,4}	...s{s},4}

r{p,3} 기반 Quasiregular snubs

콘웨이 표기법	구면				유클리드 주	쌍곡선
이미지
콕시터 도표를 만들다								...
슐레플리 심볼	sr{2,3}	sr{3,3}	sr{4,3}	sr{5,3}	sr{6,3}	sr{7,3}	sr{8,3}	...{{{n3}
슐레플리 심볼	$s{\begin{Bmatrix}2\\3\end{Bmatrix}$	$s{\begin{Bmatrix}3\\3\end{Bmatrix}}$	$s{\begin{Bmatrix}4\\3\end{Bmatrix}}$	$s{\begin{Bmatrix}5\\3\end{Bmatrix}}$	$s{\begin{Bmatrix}6\\3\end{Bmatrix}}$	$s{\begin{Bmatrix}7\\3\end{Bmatrix}}$	$s{\begin{Bmatrix}8\\3\end{Bmatrix}}$	$s{\begin{Bmatrix}\flt \\3\end{Bmatrix}$
콘웨이 표기법	A3	세인트	sC 또는 sO	sD 또는 sI	η 또는 Δ

r{p,4} 기반 Quasiregular 스너브

공간	구면		유클리드 주	쌍곡선
이미지
콕시터 도표를 만들다								...
슐레플리 심볼	sr{2,4}	sr{3,4}	sr{4,4}	sr{5,4}	sr{6,4}	sr{7,4}	sr{8,4}	...{{115,4}
슐레플리 심볼	$s{\begin{Bmatrix}2\\4\end{Bmatrix}$	$s{\begin{Bmatrix}3\\4\end{Bmatrix}}$	$s{\begin{Bmatrix}4\\4\end{Bmatrix}}$	$s{\begin{Bmatrix}5\\4\end{Bmatrix}}$	$s{\begin{Bmatrix}6\\4\end{Bmatrix}}$	$s{\begin{Bmatrix}7\\4\end{Bmatrix}}$	$s{\begin{Bmatrix}8\\4\end{Bmatrix}}$	$s{\begin{Bmatrix}\flt \\4\end{Bmatrix}$
콘웨이 표기법	A4	sC 또는 sO	sQ

통일성 스너브 폴리헤드라

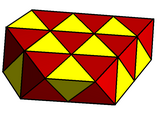
모든 짝수 값 정점이 있는 통일되지 않은 다면체는 일부 무한 세트를 포함하여 스너베딩할 수 있다. 예를 들어,

스너브 비피라미드 sdt{2,p}

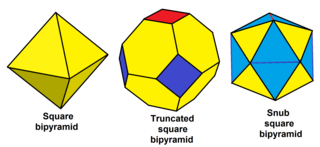스너브 사각형 바이피라미드


육각형 비피라미드 스너브

스너브 정류된 비피라미드 srdt{2,p}

스너브 항정신병 s{2,2p}

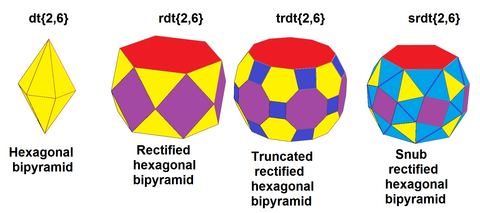이미지				...
슐레플리 기호	ss{2,4}	ss{2,6}	ss{2,8}	ss{2,10}...
슐레플리 기호	ssr{2,2} $ss{\begin{Bmatrix}2\\2\end{Bmatrix}$	ssr{2,3} $ss{\begin{Bmatrix}2\\3\end{Bmatrix}$	ssr{2,4} $ss{\begin{Bmatrix}2\\4\end{Bmatrix}$	ssr{2,5}... $ss{\begin{Bmatrix}2\\5\end{Bmatrix}$

콕시터 유니폼 스너브 별-폴리헤드라

스너브 별-폴리헤드라는 슈바르츠 삼각형(p q r)에 의해 구성되며, 순서가 합리적인 미러-앵글이 있고, 모든 거울이 활성 및 교대로 구성된다.

스너브드 균일 별-폴리헤드라

s{3/2,3/2}	s{{3,5/2)}	sr{5,5/2}	s{{5,5/3)}	sr{5/2,3}
sr{5/3,5}	s{(5/2,5/3,3)}	sr{5/3,3}	s{{(3/2,3/2,5/2)}	s{3/2,5/3}

콕시터의 고차원 스너브드 폴리탑과 허니컴

In general, a regular polychoron with Schläfli symbol ${\begin{Bmatrix}p,q,r\end{Bmatrix}}$ , and Coxeter diagram , has a snub with extended Schläfli symbol $s{\begin{Bmatrix}p,q,r\end{Bmatrix}}$ , and .

A rectified polychoron ${\begin{Bmatrix}p\\q,r\end{Bmatrix}}$ = r{p,q,r}, and has snub symbol $s{\begin{Bmatrix}p\\q,r\end{Bmatrix}}$ = sr{p,q,r}, and .

예

스너브 24-셀 직교 투영

4차원에는 단 하나의 균일한 볼록 스너브, 즉 스너브 24세포가 있다.The regular 24-cell has Schläfli symbol, ${\begin{Bmatrix}3,4,3\end{Bmatrix}}$ , and Coxeter diagram , and the snub 24-cell is represented by $s{\begin{Bmatrix}3,4,3\end{Bmatrix}}$ , Coxeter diagram .It also has an index 6 lower symmetry constructions as $s\left\{{\begin{array}{l}3\\3\\3\end{array}}\right\}$ or s{3^1,1,1} and , and an index 3 subsymmetry as $s{\begin{Bmatrix}3\\3,4\end{Bmatrix}}$ or sr{3,3,4}, and or .

The related snub 24-cell honeycomb can be seen as a $s{\begin{Bmatrix}3,4,3,3\end{Bmatrix}}$ or s{3,4,3,3}, and , and lower symmetry $s{\begin{Bmatrix}3\\3,4,3\end{Bmatrix}}$ or sr{3,3,4,3} and or , and lowest symmetry form as $s\left\{{\begin{array}{l}3\\3\\3\\3\end{array}}\right\}$ $s\left\{{\begin{array}{l}3\\3\\3\\3\end{array}}\right\}$ $s\left\{{\begin{array}{l}3\\3\\3\\3\end{array}}\right\}$ $s\left\{{\begin{array}{l}3\\3\\3\\3\end{array}}\right\}$ $s\left\{{\begin{array}{l}3\\3\\3\\3\end{array}}\right\}$ ${\$ displaystyle s\\{\ $nd{l}}{l$ }3\\ $3\\\3\\\end{array}}\right\}$ 또는 $s\left\{{\begin{array}{l}3\\3\\3\\3\end{array}}\right\}$ s{3^1,1,1,1} 및 .

유클리드 벌집(Eucleidean honeycomb)은 대체된 육각 슬래브 벌집, s{2,6,3} 및 sr{2,3,6}, 또는 sr{2,3^[3]} 및 .

또 다른 유클리드(Scaliform) 벌집형(Honeycomb), s{2,4,4}, sr{2,4^1,1} 및 :

유일한 균일한 스너브 쌍곡선 벌집은 s{3,6,3} 와 같은 스너브 육각형 타일링 벌집이며, 이 벌집 역시 교대로 육각 타일링 벌집, h{6,3,3}로 구성될 수 있다. 또한 s{3^[3,3]}와 .로도 구성된다.

또 다른 쌍곡선(척추형) 벌집은 스너브 순서-4 옥타헤드형 벌집, s{3,4,4} 및 .

참고 항목

스너브 다면체

다면체 연산자
v
t
씨앗	잘림	정류	비트런지화	이중	팽창	잡식성	교대


t₀{p,q} {p,q}	t₀₁{p,q} t{p,q}	t₁{p,q} r{p,q}	t₁₂{p,q} 2t{p,q}	t₂{p,q} 2r{p,q}	t₀₂{p,q} rr{p,q}	t₀₁₂{p,q} tr{p,q}	ht₀{p,q} h{q,p}	ht₁₂{p,q} s{q,p}	ht₀₁₂{p,q} sr{p,q}

참조

^ 케플러, 하모니스 먼디, 1619년
^ 콘웨이, (2008) 페이지 287 콕시터의 반스너브 작전
^ 2008년 콘웨이, 페이지 401 고셋의 반스너브 폴리옥타헤드론

Coxeter, Harold Scott MacDonald; Longuet-Higgins, M. S.; Miller, J. C. P. (1954). "Uniform polyhedra". Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences. The Royal Society. 246 (916): 401–450. Bibcode:1954RSPTA.246..401C. doi:10.1098/rsta.1954.0003. ISSN 0080-4614. JSTOR 91532. MR 0062446. S2CID 202575183.
Coxeter, H.S.M. 일반 폴리토페스 (제3판, 1973년), 도버판, ISBN 0-486-61480-8 (pp. 154–156 8.6 부분 절단 또는 교체)
케일리디스코어: H.S.M. Coxeter의 선별된 글, F가 편집한 글.아서 셔크, 피터 맥멀런, 앤서니 C.Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1], Googlebooks [2]
- (용지 17) Coxeter, The Evolution of Coxeter-Dynkin 도표, [Neyuw Archief voor Wiskunde 9(1991) 233–248]
- (용지 22) H.S.M. Coxeter, 정규 및 반정규 폴리토페스 I, [산술]Zeit. 46 (1940) 380–407, MR 2,10]
- (용지 23) H.S.M. Coxeter, 정규 및 반정규 폴리토페스 II, [수학]Zeit. 188 (1985) 559–591]
- (용지 24) H.S.M. Coxeter, 정규 및 반정규 폴리토페스 III, [산술]Zeit. 200 (1988) 3–45]
콕시터, 기하학의 아름다움: 12편의 에세이, 도버 퍼블리셔스, 1999년 ISBN 978-0-486-40919-1 (제3장: 균일한 폴리토페스를 위한 와이토프의 건설)
Norman JohnsonUniform Polytopes, 원고(1991)
- N.W. 존슨:균일다각체와 허니컴의 이론, 박사학위.1966년 토론토 대학교의 논문
존 H. 콘웨이, 하이디 버기엘, 차임 굿맨-스트라스 2008, ISBN 978-1-56881-220-5
Weisstein, Eric W. "Snubification". MathWorld.
리처드 클라이칭, 스너브스, 대체 면과 스콧-콕시터-딘킨 도표, 대칭: 문화와 과학, Vol. 21, No.4, 329–344, (2010) [3]

[1] 케플러, 하모니스 먼디, 1619년

[2] 콘웨이, (2008) 페이지 287 콕시터의 반스너브 작전

[3] 2008년 콘웨이, 페이지 401 고셋의 반스너브 폴리옥타헤드론

[1]

[2]

[3]

Search