선거제도 비교
Comparison of electoral systems선거제도는 선거를 실시하기 위한 규칙이며, 그 주요 구성요소는 투표에서 승리자(또는 여러 명의 승리자)를 결정하는 알고리즘이다. 이 기사는 '단일 당선자' 선거로부터 독특한 후보를 선출하는 것과 복수 당선자 선거로부터 대표 그룹을 선출하는 것 둘 다, 서로 다른 알고리즘에 대해 제시되어 온 정당성에 대해 논하고 있다. 두 종류의 선거 중 선택은 여기서 논의되지 않은 정치적 질문이다.
2010년 투표 절차에 관한 전문가 22명으로 구성된 패널은 그들이 지지한 18개의 대표 1인 투표 방식 중 어떤 것을 지지했는지에 대해 질문 받았다. 한 멤버는 기권했다. 다양한 시스템의 순위(최대 21명부터 승인자 수 N명)는 다음과 같았다.[1]
실용적 고려사항
투표 이론에 의해 제기되는 지적 문제는 넓은 의미에서 정확한 시스템을 고안하는 것이다. 그러나 주어진 정확성의 한 시스템이 다른 시스템보다 사회적으로 더 허용될 수 있는 많은 실질적인 이유가 있다. 책임 있는 심판은 어떤 형태의 정확성만큼 이러한 요인에 많은 주의를 기울인다. 라즐리어의 워크숍[1] 기록과 리처드 달링턴의 두 논문에서 토론자들의 의견을 확인하십시오.[2][3]
중요한 요인은 다음과 같은 3가지 표제로 분류할 수 있다.
- 티드먼이 '유권자의 신뢰를 얻을 수 있는 룰의 역량'으로 정의하고 있는 '지식성'은 '규칙 논리의 합리성과 이해가능성에 달려 있다'[1]는 것이다.
- 투표 용이성. 투표 용지의 형태가 다르면 유권자들은 자신의 견해를 공정하게 반영하여 투표 용지를 작성하는 것이 다소 어려워진다.
- 셈하기 쉽다. 투표에서 도출된 작은 계수로 결정을 내릴 수 있는 투표 시스템은 전체 투표 세트에 대해 자문할 필요가 있는 투표 시스템보다 물류적으로 덜 부담스럽다. 일부 투표 시스템은 승자를 결정하기 위해 강력한 계산 자원을 필요로 한다. 비록 그 비용이 선거용으로 금지되지 않더라도, 그것은 효과적인 평가를 방해할 수 있다.
입후보효과
별도의 주제는 다른 후보자들이 다른 투표 시스템에 서도록 장려될 수 있다는 사실이다. FPTP에 따른 투표 낭비 우려는 후보를 뽑는 집단의 손에 큰 힘을 실어준다. 다른 투표 시스템은 어떤 추상적인 의미에서 더 공정하지 않아도 더 만족스러운 결정으로 이어질 수 있다. 이 주제는 분석적 연구를 거의 받지 못했다.
선거제도 비교방법
최고의 투표 방법을 결정하기 위해 사용된 3가지 주요 유형의 추리가 있다.
- 예에 의한 논쟁: 이것은 가장 오래된 형태의 논쟁이다.
- 논리적 기준으로부터의 주장: 이것은 예에 의한 논쟁의 체계화라고 볼 수 있다.
- 모의 선거의 경험적 논쟁. 이 방법은 20세기에 디지털 컴퓨터가 개발되기 전까지는 실행 가능하지 않았다.
컴퓨터 시뮬레이션의 사용은 연대기적으로 이것들 중 마지막이지만, 다른 것들과 관련된 개념을 도입하기 때문에 우리는 먼저 그것에 대해 토론할 것이다.
시뮬레이션을 통한 경험적 평가
선거 절차의 모델
투표 방법은 실제 생활에서 선거의 속성에 충실함을 목표로 하는 무작위 모의선거에서 정확도를 측정함으로써 평가할 수 있다. 첫 번째 그러한 평가는 1978년에 챔버린과 코헨에 의해 실시되었는데, 그는 특정 비콘도르셋 시스템이 콘도르셋 수상자를 선출하는 빈도를 측정했다.[4] 선거과정을 대변하는 것으로 제안된 모델은 크게 세 가지 유형이 있으며, 그 중 두 가지가 하이브리드 형태로 결합될 수 있다. 네 번째 유형의 모델인 공리주의 모델은 공간적 모델이 공리주의적으로 나타나기도 하지만 실제로는 사용되지 않음에도 불구하고 개념적으로 의미가 있다.
콘도르케트의 배심원 모델
콘도르셋 후작은 선거는 각 구성원이 후보자의 자질에 대해 독자적인 판단을 하는 배심원 투표와 유사하다고 보았다. 이 때문에 후보자는 객관적 메리트가 다르고, 선거인은 후보자의 상대적 메리트에 대해 독립적인 견해를 표명한다. 유권자들의 판단이 무작위보다 나은 한, 충분히 큰 유권자들은 항상 최고의 후보를 선택할 것이다. 배심원 모델은 때때로 용맹 모델로 알려져 있다.
배심원 모델은 투표 시스템에 대한 자연적인 정확성 개념을 내포하고 있다. 즉, 시스템이 가장 좋은 후보를 선출할 가능성이 높을수록, 시스템은 더 우수하다는 것이다. 이것은 선거 결정에 의미론을 제공하는 것으로 보여질 수 있다.
콘도르셋과 그의 동시대의 라플레이스는 투표 이론이 따라서 확률 이론으로 축소될 수 있다는 것을 깨달았다 – 콘도르셋의 주요 작품은 Essai sur l'[5]application de l'analyse ar l'a probabilité des des desisises ar la domonité des arvoises ab la. 그들의 생각은 20세기에 커메니-영 투표 방식이 유공자별 후보자 순서의 최대 가능성 추정자임을 배심원단 모델에 따라 보여주면서 되살아났다.[6]
블랙의 공간 모델
콘도르셋 모델의 가장 큰 약점은 독립성을 가정한다는 것인데, 이는 B보다 A를 선호하는 유권자들이 D보다 C를 선호하는 경향이 있을 수 없다는 것을 암시한다. 이것은 증거에 비추어 볼 때, 특정 지롱딘보다 특정 몬타냐드를 선호하는 누군가는 아마도 제2의 지롱딘보다 제2의 몬타냐드를 더 선호할 것이다; 그것은 또한 회원들이 흔히 실수를 할 것이기 때문에, 임의로 큰 배심원들 조차도 틀릴 수 있는 이유를 설명해준다.
던컨 블랙은 1948년 선거를 이념적으로 추진한 것으로 보고 투표의 1차원 공간 모델을 제안했다.[7] 그의 생각은 후에 앤서니 다운스에 의해 확장되었다.[8] 유권자의 의견은 하나 이상의 공간에 위치하는 것으로 간주되며, 후보자는 같은 공간에 위치하는 것으로 간주되며, 유권자는 근접성(유클리드 거리 또는 일부 다른 지표에 따라 측정)의 순서로 후보를 선택한다.
공간적 모델은 투표 시스템에 대한 다른 장점 개념을 암시한다. 즉, 당선된 후보가 투표자 분포를 위한 위치 매개변수로 더 잘 수용될 수 있을수록, 시스템은 더 좋다. 정치적 스펙트럼은 1차원 공간 모델이다.
화살의 중성 모델
케네스 애로우는 투표용지가 '메시지'가 되기 보다는 궁극적인 현실인 틀 안에서 일했다(발린스키와 라라키가 표현했듯이[9]). 그 뒤에 있는 어떤 현실에 대한 부분적(그리고 어쩌면 오해의 소지가 있는) 정보를 전달한다. 그는 이러한 불가지론을 투표의 현실적 그림으로 제시하지 않고 오히려 선거를 재산 조사가 가능한 수학적인 대상으로 규정하는 것으로 제시했다. 그의 유명한 불가능성의 정리는 (특정 가정 하에서) 어떤 순위 투표 시스템에도 (중립 모델 하에서 달성 가능한) 일련의 투표용지가 존재하며, 이는 종종 바람직하다고 여겨지는 세 가지 기준 중 적어도 하나를 위반한다는 것을 보여준다.[10]
중립 모델은 투표 시스템에 대한 정확성이나 진실성의 어떤 개념도 가지고 오지 않는다.
공정한 문화 모델은 중립 투표 모델에 따라 투표용지의 분포를 정의하며, 유권자를 무작위 소음원으로 취급한다.
하이브리드 모델
배심원단 모델과 공간 모델을 결합하는 것은 가능하다: 유권자들은 후보자들의 자질에 대한 그들의 견해와 이념적 고려에 의해 부분적으로 영향을 받는다고 가정할 수 있다. 이것은 그들의 선호를 별도의 독립적 요소와 비독립적 요소로 세분화한다. 하이브리드 모델은 달링턴에[2] 의해 간략하게 논의되지만 널리 채택되지는 않았다.
경험적 비교
Tideman과 Plassmann은 2차원 공간 모델이 많은 선거 순위 세트의 3가지 후보 축소에 합리적인 적합성을 보인다는 연구를 수행했다. 배심원 및 중립 모델과 1차원 공간 모델은 부적합한 것으로 나타났으나 하이브리드 모델은 고려되지 않았다.[11]
이들은 유권자 선호도의 콘도르셋 사이클(A가 B보다 선호되고 있는 예, B에서 C로, C에서 A로)을 살펴본 결과, 그 수가 소표본 효과와 일치한다는 것을 밝혀내, "만약 유권자 수가 많은 선거에서는 매우 드물게 투표 주기가 발생할 것"이라고 결론지었다.
표본 크기의 관련성은 고든 툴록이 이전에 연구한 바 있는데, 그는 유한한 선거인단은 항상 순환하기 쉬우나, 유권자의 수가 증가함에 따라 후보들이 순환을 일으킬 수 있는 영역이 점진적으로 작아질 것이라고 그래픽으로 주장했다.[12]
실용주의 모델
공리주의 모델은 유권자들을 효용 순으로 순위를 매기는 후보들로 본다. 이 모델 아래, 정당한 승자는 전반적인 사회적 효용을 극대화하는 후보자다. 공리주의 모델은 다음과 같은 몇 가지 중요한 방법으로 공간 모델과 다르다.
- 그것은 유권자들이 그들의 선호에 이념적 색채가 없는 오직 정보에 입각한 이기심에 의해서만 동기가 부여된다는 추가적인 가정을 요구한다.
- 그것은 공간 모델의 거리 측정 기준을 효용성의 충실한 측정으로 대체하도록 요구한다.
- 결과적으로 그 측정기준은 유권자마다 다를 필요가 있을 것이다. 종종 한 그룹의 유권자들이 두 후보 사이의 선택에 의해 강력한 영향을 받는 반면, 다른 그룹은 거의 위험에 처해 있지 않다; 그러면 그 측정 기준은 매우 비대칭적일 필요가 있을 것이다.
모든 유권자들에게 동등한 영향력을 주는 어떤 투표 시스템도 최대의 사회적 효용을 달성할 수 없다는 것은 마지막 재산에서 비롯된다. 공리주의의 주장과 민주주의의 주장이 대립하는 극단적인 경우를 '다수의 역모'라고 한다. 라즐리어의 기록에서 라즐리어의, 멀린, 누르미의 의견을 참조하십시오.[1]
제임스 밀은 민주주의와 공리주의 사이의 선험적 연관성의 존재를 최초로 주장한 것 같다 – 스탠포드 백과사전 기사와 맥컬레이의 '유명한 공격'[14]을[13] 보라.
배심원 모델에서의 비교
선거에서 i th 후보가 공적이 xi(xi ~ N(0,1972)[15]라고 가정할 수 있고, 유권자 j의 후보 i에 대한 승인 수준은 xi + εij(우리는ij ε이 iid라고 가정할 것이다)이라고 가정해 보자. N (0,1972). 우리는 유권자가 후보자 순위를 감소시키는 것으로 가정한다. 우리는 ε을ij 유권자 j의 후보 i에 대한 평가의 오류로 해석할 수 있으며, 투표 방법은 가장 뛰어난 공로 후보를 찾는 과제를 갖는 것으로 간주할 수 있다.
각 투표자는 결정 확률 p를 사용하여 두 후보 중 덜 좋은 후보보다 높은 순위를 매긴다(여기 요약된 정상 모델 하에서는 + - τ2}}\!}{\ 사분면에[16] 걸친 가우스 적분 표준 공식에서 확인할 수 있음). 콘도르케트의 배심원 정리는 그것을 p > 으로 보여준다. 1⁄2, 배심원 과반수 득표는 어떤 한 사람의 의견보다 두 후보의 상대적 장점을 더 잘 보여주는 길잡이가 될 것이다.
페이튼 영은 임의의 후보수 사이 투표에 3개의 재산이 추가로 적용된다는 것을 보여주면서 콘도르셋이 그 중 1위와 3위를 알고 있었음을 시사했다.[17]
- p가 1⁄2에 가까우면, 보르다 승자는 최고의 후보의 최대우도 추정치가 된다.
- p가 1에 가까우면 Minimax 승자는 가장 적합한 후보의 최대우도 추정치가 된다.
- 어느 p에게나 케메니-영 순위는 진정한 공로 순위의 최대우도 추정자다.
로버트 F. 보들리는 콘도르셋의 배심원 모델을 약간 변형시킨 '유용한' 모델을 만들었다.[18] 그는 투표 방법의 과제를 유권자의 총합이 가장 큰 후보, 즉 개별 유권자의 찬성 수준이 가장 높은 후보를 찾는 것으로 보았다. 이 모델은 σ2 = 0으로도 타당하며, 이 경우 p는 1 + - - 1 여기서 n은 유권자 수입니다. 그는 예상대로 보르다 카운트가 가장 정확하다는 것을 알아내면서 이 모델에 따라 평가를 수행했다.
공간 모델에서 시뮬레이션된 선택
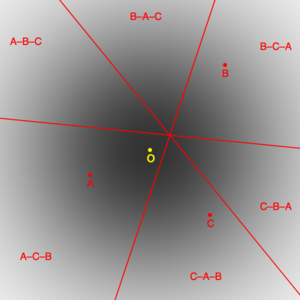
모의 선거는 적절한 공간에 있는 유권자의 분포로부터 구성될 수 있다. 이 삽화는 O를 중심으로 한 이바리테 가우스 분포에 만족하는 유권자들을 보여준다. 무작위로 생성된 후보자는 A, B, C 3명이다. 공간은 6개 부문 3줄로 나뉘어 각 부문별 유권자의 후보 선호도가 같다. 어떤 방식으로든 후보를 주문하는 유권자의 비율은 관련 부문에 대한 유권자 분포의 필수 요소로 주어진다.
후보자의 6가지 가능한 순서에 해당하는 비율은 다른 투표 시스템에서 산출되는 결과를 결정한다. O와 가장 가까운 후보(이 경우 A)를 선출하는 사람은 정확한 결과를 준 것으로 간주되고, 다른 사람을 선출하는 사람은 오류를 나타냈다. 무작위로 생성된 많은 후보들에 대한 결과를 보면 투표 시스템의 경험적 특성을 측정할 수 있다.
여기에 설명된 평가 프로토콜은 Tideman과 Plassmann이 설명한 것으로 모델링된다.[11] 이런 유형의 평가는 1인 선거제도에 가장 흔하다. 순위 투표 시스템은 가장 자연스럽게 프레임워크에 적합하지만, 다른 유형의 투표(예: FPTP 및 승인 투표)는 덜 또는 더 많은 노력으로 수용될 수 있다.
평가 프로토콜은 다음과 같은 여러 가지 방법으로 변경될 수 있다.
- 유권자의 수는 한정되고 크기가 다양할 수 있다. 실제로 이것은 유권자들이 그들의 분포로부터 표본이 추출되고 큰 선거인의 결과가 제한적인 행동을 보여주기 위해 이용되는 다변량 모델에서 거의 항상 행해진다.
- 지원자의 수는 다양할 수 있다.
- 유권자 분포는 다양할 수 있다. 예를 들어, 비대칭 분포의 효과를 조사할 수 있다. 유권자의 수가 유한할 때 무작위 표본 추출 효과에 의해 정규성에서 약간의 이탈이 수반된다. 좀 더 체계적인 출발(이른바 가우스 혼합물 모델 형태)이 2017년 제임슨 퀸에 의해 조사되었다.[19]
정확성 평가
m 방법 | 3 | 6 | 10 | 15 | 25 | 40 |
|---|---|---|---|---|---|---|
| FPTP | 70.6 | 35.5 | 21.1 | 14.5 | 9.3 | 6.4 |
| AV/IRV | 85.2 | 50.1 | 31.5 | 21.6 | 12.9 | 7.9 |
| 보르다 | 87.6 | 82.1 | 74.2 | 67.0 | 58.3 | 50.1 |
| 콘도르케트 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 | 100.0 |
유권자가 성실하게 투표할 때 투표제도의 정확성을 비교하는 것이 평가의 주요 용도 중 하나이다. 무한히 많은 유권자가 가우스 분포를 만족한다면, 선거의 정당한 승자는 평균/중간인과 가장 가까운 후보로 받아들여질 수 있고, 방법의 정확성은 정당한 승자가 선출되는 선거의 비율로 파악할 수 있다. 중위 유권자 정리는 모든 콘도르셋 시스템이 100% 정확성을 부여할 것을 보장한다(Coombs의 방법에도[20] 동일하게 적용된다).
연구논문에 게재된 평가는 다차원 가우스인을 활용하기 때문에 숫자적으로 계산이 어렵다.[4][21][2][3] 유권자의 수는 한정되어 있고 후보자들의 수는 반드시 적다.
계산은 단일 차원으로 훨씬 더 간단해, 무한한 수의 유권자와 임의의 수의 m 후보가 가능하다. 이 간단한 사례에 대한 결과는 첫 번째 표에 나타나 있는데, 체임벌린과 코헨이 인용한 논문의 표 5(1000명의 유권자, 중간 분포)와 직접 비교된다. 후보자들은 유권자 분포에서 무작위로 표본 추출했고, 단일 콘도르셋 방식(미니맥스)이 확인 재판에 포함되었다.
m 방법 | 10 |
|---|---|
| FPTP | 0.166 |
| AV/IRV | 0.058 |
| 보르다 | 0.016 |
| 콘도르케트 | 0.010 |
대안투표(IRV)의 상대적으로 저조한 성과는 도표에서 잘 알려져 있고 공통적인 오류원인에 의해 설명되며, 선거는 일변도의 공간모델을 만족하고 정당한 승자 B는 1차 투표에서 탈락한다. 비슷한 문제가 모든 차원에 존재한다.
정확성을 측정하는 다른 척도는 당선자로부터의 유권자의 평균 거리(소규모는 더 나은 것을 의미한다)이다. 이는 투표 방식의 순위를 바꿀 가능성은 낮지만 거리를 불특정성으로 해석하는 사람들이 선호한다. 두 번째 표는 같은 모델에서 10명의 후보에 대한 평균 거리(표준 편차 단위)에서 2표준 편차 단위)를 뺀 값(*\표준 가우스 분포의 중심에서 변수의 평균 거리)을 나타낸다.
전술적 투표 저항성 평가
James Green-Armytage 등은 유권자들의 조작에 대한 여러 투표 시스템의 취약성을 평가한 연구를 발표했다.[22] 그들은 단순히 '창의적인 프로그래밍이 필요하다'고 언급하면서, 이러한 목적을 위해 그들의 평가를 어떻게 적응시켰는지에 대해서는 거의 말하지 않는다. 첫 번째 작가의 앞선 논문은 조금 더 자세한 내용을 담고 있다.[23]
모의 선거의 후보자 수는 3명으로 제한되었다. 이를 통해 특정 시스템 간의 구분이 제거된다. 예를 들어 블랙의 방법과 다스굽타-마신 방법은 3명의 후보자에게 동등하다.
이 연구의 결론은 요약하기 어렵지만, 보르다 카운트는 좋지 않은 성과를 냈고, 미니맥스는 다소 취약했으며, IRV는 높은 내성을 보였다. 저자들은 어떤 방법이라도 콘도르케 당선자가 없는 선거(콘도르케 당선자가 있을 때 당선자를 선택하는 것)로 제한하면 전술적 투표에 대한 민감도가 결코 높아지지 않는다는 것을 보여주었다. 이들은 콘도르케트 기준으로 해결되지 않은 선거를 위해 IRV를 동점 처리로 사용하는 '콘도르케트-헤어' 제도가 자체 IRV만큼 전술적 투표에 저항성이 있고 정확성이 높다고 보고했다. 콘도르셋-헤어는 3명의 후보가 참여한 선거에서 IRV 타이브레이크를 가진 코프랜드의 수법에 해당한다.
후보 분포 효과에 대한 평가
x m | 0 | 0.25 | 0.5 | 1 | 1.5 |
|---|---|---|---|---|---|
| 3 | 87.6 | 87.9 | 88.9 | 93.0 | 97.4 |
| 6 | 82.1 | 80.2 | 76.2 | 71.9 | 79.9 |
| 10 | 74.1 | 70.1 | 61.2 | 47.6 | 54.1 |
| 15 | 66.9 | 60.6 | 46.4 | 26.6 | 30.8 |
| 25 | 58.3 | 47.0 | 26.3 | 8.1 | 10.1 |
| 40 | 50.2 | 33.3 | 11.3 | 1.5 | 2.1 |
일부 제도, 특히 보르다 카운트는 유권자 분포에 비해 후보 분포가 이탈했을 때 취약하다. 첨부된 표는 유권자의 무한 인구가 일변도의 가우스 분포를 만족하고 m 후보가 x 표준 분포를 통해 유사한 분포 오프셋에서 도출되는 경우 보르다 카운트의 정확성(백분율)을 보여준다. 빨간 색상은 무작위보다 더 나쁜 수치를 나타낸다. 모든 콘도르셋 방법은 이 문제에 대해 100% 정확성을 제공한다는 점을 기억하십시오. (그리고 후보가 3명일 때는 x가 증가함에 따라 정확도가 저하되는 것을 볼 수 없다.)
후보 분포에 대한 민감성은 정확성이나 조작에 대한 저항성의 문제라고 생각할 수 있다. 만약 어떤 사람이 후보자들이 자연스럽게 유권자들과 같은 분배에서 나올 것이라고 예상한다면, 어떤 변위는 전복 시도로 보여질 것이다. 그러나 만약 어떤 사람이 후보자들의 생존 가능성을 결정하는 요소들이 이념적 입장과 상관관계가 있을 수 있다고 생각한다면, 사람들은 그것을 더 자세히 볼 것이다.정확성의 ms
발표된 평가는 후보 분포에 대해 다른 견해를 취한다. 일부에서는 단순히 후보자가 유권자와 같은 분포에서 도출된다고 추측한다.[2][22] 몇 개의 오래된 논문은 동일한 수단을 사용하지만 후보 분포가 유권자 분포보다 다소 긴밀할 수 있도록 허용한다.[24][4] Tideman과 Plassmann의 논문은 경험적 측정에 근거한 후보 분포와 유권자 분포의 관계를 근사하게 다루고 있다.[21] 이는 후보 분포가 투표 시스템의 약점을 이용하기 위해 조정되는 것을 용납하지 않기 때문에 나타날 수 있는 것보다 현실성이 떨어진다. 제임스 그린-아미타주 논문은 후보 분포를 별도의 이슈로 보고 이를 조작의 한 형태로 보고 전략적 입출구의 효과를 측정한다. 당연히 그는 보르다 카운트가 특히 취약하다는 것을 알게 된다.[23]
기타 속성 평가
- 앞서 언급한 바와 같이 챔버린과 코헨은 특정 비콘도르셋 시스템이 콘도르셋 당첨자를 선택하는 빈도를 측정했다. 유권자 및 후보 분포가 동일한 공간 모델에서 주파수는 99%(Coombs), 86%(Borda), 60%(IRV), 33%(FPTP)이다.[4] 이것은 때때로 콘도르셋 효율이라고 알려져 있다.
- 달링턴은 코프랜드의 방식이 콘도르셋 당선자가 없는 선거에서 독특한 당선자를 내는 빈도를 측정했다. 그는 최대 10명의 지원자가 있는 분야의 경우 50% 미만이라는 것을 발견했다.[3]
실험 메트릭스
공간모델에 의한 투표제도의 과제는 유권자의 의견 분포를 가장 정확하게 나타내는 지위를 가진 후보를 파악하는 것이다. 이는 후보자들이 제시한 대안 집합에서 분포에 대한 위치 모수를 선택하는 것과 같다. 위치 매개변수는 평균, 중위수 또는 모드에 기초할 수 있지만, 순위 선호도 표는 순서형 정보만 제공하므로 중위수만이 허용 가능한 통계량이다.
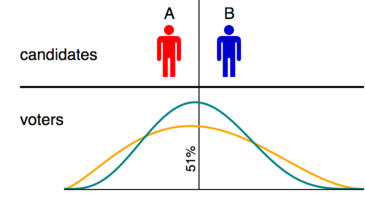
이는 동일한 후보가 있지만 유권자 분포가 다른 두 개의 모의 선거를 보여주는 도표에서 확인할 수 있다. 두 경우 모두 후보 사이의 중간 지점이 유권자 분포의 51번째 백분위수여서 유권자의 51%는 A를 선호하고 49%는 B를 선호한다. 만약 투표인구의 중위수에 가장 가까운 후보를 선출하는 경우 투표방법이 정확하다고 생각한다면, 중위수는 반드시 51% 선에서 약간 왼쪽으로 치우쳐 있기 때문에, 각각의 경우에 A를 선출하는 경우 투표방법이 정확하다고 간주될 것이다.
차알 분포의 평균도 51% 선의 왼쪽에 약간 있지만, 오렌지 분포의 평균은 약간 오른쪽에 있다. 따라서 만약 우리가 투표방법이 유권자의 평균에 가장 가까운 후보를 선출한다면, 어떤 방법은 두 선거에서 같은 투표와 다른 승자를 내지 않는 한 만점을 얻을 수 없을 것이다. 분명히 이것은 투표 방법에 거짓 오류를 범하게 할 것이다. 위치의 어떤 기본적인 측정에 대해서도 동일한 문제가 발생할 것이다. 오직 중앙값만이 일관된 결과를 제공한다.
중위수는 다변량 분포에 대해 정의되지 않지만 일변량 중위수는 쉽게 일반화하는 특성을 가지고 있다. 분포의 중위수는 분포 내의 모든 점으로부터의 평균 거리가 가장 작은 위치를 가리킨다. 이 정의는 기하학적 중위수를 다차원으로 일반화한다. 그 거리는 때로는 후보의 선거로부터 유권자의 '불합치'로 묘사되기도 하지만, 이 식별은 순전히 자의적이다.
만약 우리에게 후보 집합과 유권자 집단이 있다면, 유권자의 기하학적 중위수를 찾는 계산적으로 어려운 문제를 해결할 필요가 없다. 그리고 그것에 가장 가까운 후보를 확인할 필요가 없다. 대신에 우리는 유권자와의 평균 거리가 최소화된 후보를 확인할 수 있다. 이것은 Merrill 이후부터 일반적으로 배치되어온 미터법이다.[24] Green-Armytage와 Darlington도 참조한다.[23][2]
유권자 분포의 기하학적 중위수에 가장 가까운 후보를 '공간적 승리자'라고 부를 수 있다.
지식의 현재 상태
경험적 시험에 투표 시스템을 제출하고자 하는 욕구는 유권자 행동을 합리적인 정확도로 반영하고자 하는 모델에 의존해 왔으며, 그 중에서도 공간적 모델이 앞선다. 선택한 모델은 논리적인 특성을 가지며, 많은 경우 가장 정확한 투표 방법을 선험적으로 식별할 수 있다. 공간 모델에서 대칭 모집단의 경우 정확한 투표 시스템이 콘도르셋 방법(및 Coombs's)으로 판명된다. 논리적인 예측은 실증적으로 확인되었다.
게다가 일부 콘도르셋 방법, 특히 미니맥스 자체와 적절한 타이브레이크를 가진 코프랜드의 방법은 실용적으로 만족스럽다. 이는 전술적 투표에 대한 취약성을 두드러진 쟁점으로 남긴다. 추가 평가에서 조사된 주제로서 (비콘도르셋) IRV의 우수성이 주장되어 왔다. 그러나 이 분야의 평가는 수행하기가 어렵고 방법론적 타협이 필요했다(예: 후보 3명으로 제한). IRV를 어떤 식으로든 투표 시스템에 도입함으로써 어떤 양적 효과가 발생하는지는 명확하지 않다.
예제별 인수
| 유권자 수 | 순위 |
|---|---|
| 30 | A-B-C |
| 1 | A-C-B |
| 29 | B-A-C |
| 10 | B-C-A |
| 10 | C-A-B |
| 1 | C-B-A |
두 방법이 서로 다른 답을 주는 사례를 구성해 한 표방법의 우월성을 입증하려는 오랜 역사가 있는데, 첫 번째 방법은 옳고 두 번째 방법은 틀렸다고 의기양양하게 주장했다. 모든 방법에 불리한 예를 구성할 수 있기 때문에, 이러한 형태의 추론은 결론에 도달할 수 없다. 우리가 1차 투표에서 정당한 승자가 탈락하는 가공의 선거를 통해 IRV의 약점을 보여주는 예가 위에서 발생한다.
최근 도날드 사리에 의해 언급된 사례가 있다.[25] 그는 콘도르셋이 1차 표와 같이 선호도가 높은 81명의 유권자를 가진 3명의 후보 사이의 가상 선거 사례를 재분석했다. 콘도르케트 우승자는 A로, 41:40으로 B보다, 60:21로 C보다 선호되지만, 보르다 우승자는 B이다. 콘도르케트는 보르다 카운트의 잘못이 있다고 결론지었다.[26]: 90 사아리는 2차 표에서 보이는 것처럼 유권자를 3개 그룹으로 나눌 수 있다는 점에 주목하며 이 경우 보르다 카운트가 옳다고 주장한다.
| 유권자 수 | 순위 |
|---|---|
| 10 | A-B-C |
| 10 | B-C-A |
| 10 | C-A-B |
| 1 | A-C-B |
| 1 | C-B-A |
| 1 | B-A-C |
| 20 | A-B-C |
| 28 | B-A-C |
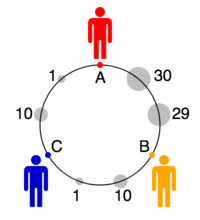
분홍색과 파란색 그룹은 시계방향과 시계반대방향 및 시계반대방향 사이클로 구성되며, 이 사이클은 –Saari에 따라 – 그 결과를 백색 그룹에 의해 결정되도록 남겨둔다; 그리고 (Saari에 따라) 이 그룹에 대한 명확한 선호도는 B에 대한 것이다.
도표는 모든 사람이 단위 원의 둘레에 위치하여 투표와 일치하는 유권자 및 후보자의 가능한 구성을 보여준다. 평균 유권자로부터 A의 거리가 1.15인 반면 B의 거리는 1.09(그리고 C의 거리는 1.70)로 B를 공간적 승자로 만든다는 점에서 Saari의 판단을 확인시켜준다. 그러나 그것은 하나의 예에 불과하다. 우리는 A를 제외한 모든 위치를 고정시킨 채 A를 원의 중심을 향해 방사상으로 움직이는 것을 상상할 수 있다. 비록 백인이 B를 계속 선호하고 있지만, 극히 미미한 단계는 A를 순환집단의 선호로 만들기에 충분하다. 일단 A의 중심으로부터의 거리가 약 0.89 미만이면, 투표용지는 변하지 않지만, 전체적인 선호도는 B에서 A로 넘어간다.
따라서 동등하게 합리적인 공간적 표현은 서로 다른 승자를 암시한다는 점에서 선거는 모호하다. 이것은 우리가 공간 모델에 대한 중앙값 메트릭을 채택함으로써 앞서 피하고자 했던 모호성이다. 그러나 중앙값 메트릭이 단일 차원으로 목표를 달성하고 더 높은 차원으로 유인적으로 일반화하기는 하지만, 모호성을 피하기 위해 필요한 속성은 일반화되지 않는다. 일반적으로, 주기는 외부 사실에 근거하지 않고 공간적 승자를 불확실하게 만들 수 있다. 전방위적 유권자 중위수의 존재는 투표에서 결정되는 결과를 보장하기에 충분한 조건이며, 이 경우 공간적 승자는 콘도르케트 승자가 되며, 유권자 분포의 단일성은 전방위적 중위수를 갖기에 충분하다.[27]
사리의 예는 영향력이 있었다. 달링턴은 "매우 권위 있는 학술지 검토자"가 비슷한 사례를 통해 콘도르셋의 기준이 "연관표를 보여줘도 선거 결과가 달라져서는 안 되기 때문에 우스꽝스럽다"[2]고 말한 것을 상기한다.
1인 선거의 기준
전통적으로 다른 선거제도의 장점은 논리적 기준을 참고하여 주장되어 왔다. 이것들은 선거판단에 대한 추론, 예를 들어, "E와 E가 R (E,E')과 같은 선거라면, 그리고 A가 E의 정당한 승자라면, A가 E의 정당한 승자라면, A가 E의 정당한 승자"라는 추론을 허가하는 일종의 규칙을 가지고 있다.
그 기준은 투표 시스템 자체만큼이나 논란의 여지가 있다. 여기서 우리는 그 타당성에 관하여 진전된 고려사항에 대해 간략히 논의한 후, 어떤 주요 투표 시스템이 그것들을 충족시키는지 표에 보여주면서 가장 중요한 기준을 요약한다.
투표기준의 인식론
예제에서의 인수
투표 시스템의 잘못된 행동의 예를 일반화하여 더 복잡한 경우에도 기준을 충족하는 시스템에서 그러한 결함이 발생할 수 없음을 보장하는 기준을 제공할 수 있다. Saari의 예는 취소 기준(Borda count에서 만족하지만 모든 Condorcet 시스템에 의해 위반됨)을 제시하고, IRV가 정당한 승자를 제거하는 예를 Condorcet 기준(Borda count에서 위반됨)으로 일반화할 수 있다.
보다 흥미로운 일반화는 동일한 도표에서 설명될 수 있는 '노쇼 패러독스'로 알려진 예에서 나온다. B가 정당한 승리자라는 것에 동의하면서, 우리는 모든 유권자가 성실하게 투표하면 B가 정말로 선출될 것이라는 가설을 세울 수 있지만, 이 제도 하에서는 A의 단일 지지자가 기권만 하면 자신이 선호하는 후보에게 결과를 기울일 수 있다. 대부분의 사람들은 이것이 터무니없는 결과가 될 것이라는 데 동의할 것이다. 만약 우리가 그것에 중요성을 부여한다면, 투표자는 투표보다는 기권으로 후보를 도울 수 없다는 참여 기준에 그것을 일반화할 수 있을 것이다.
본보기에서 기준으로의 큰 진전이다. 그 예에서 역설적인 결과는 단순히 잘못된 것이다: A의 지지자가 기권할 때 B는 정당한 승자로 남아 있다. 그러나 우리가 참여 기준을 채택할 때, 우리는 선거 결과를 예측하기 어려운, 정당한 승자를 식별하는 것이 불가능한 복잡한 예들로 제한한다. 이것은 우리가 예상했던 것보다 더 많을 수도 있다.
참여 기준은 놀라울 정도로 강력하다. 보르다 카운트를 수용하면서 모든 콘도르셋 시스템을 거부한다. 그러나 콘도르셋 시스템에서 발생하는 노쇼 역설은 결과가 단순히 틀린 예들이 아니라 결과 쌍이 결정적인 옳고 그름 없이 바람직하지 않은 방식으로 연관되어 있는 경우들이다.
논리적 일관성
널리 수용되는 기준은 여러 그룹에서 상호 모순된다(그 중 첫째는 애로우스의 불가능성 정리로 식별되는 3가지 양립불가능한 기준의 그룹이다). 그들은 또한 모든 투표 시스템에 반대한다. 댄 펠센탈은 16개의 기준과 18개의 투표 시스템을 설명했고 "그의 18개의 모든 시스템이 최소한 6개의 기준을 위반한다"고 보여주었다.[2]
결과기준(절대)
우리는 이제 투표용지 집합이 일정한 방식이라면 특정 후보가 반드시 당선되거나 당선되지 않아야 한다는 절대적 기준에서 출발하여 논리적인 기준 자체에 의존한다.
- 다수결 기준(MC)
- 다수 유권자의 독보적인 지지로 분류되는 후보가 항상 승리할 것인가? 이 기준은 두 가지 버전으로 나온다.
- 순위에 따른 다수결 기준(다수가 다른 사람보다 선호할 뿐인 옵션이 반드시 승리해야 함). (순위에 오른 MC를 합격시키는 것은 아래 표에서 "예"로 표시되는데, 이는 다음 사항도 합격시키는 것을 의미하기 때문이다.)
- 정격다수 기준. 다수가 고유하게 완벽한 등급을 부여한 옵션만 승리해야 한다. 순위와 등급의 MC는 순위의 투표 방식과 동의어지만, 등급이나 등급의 투표 방식은 아니다. 등급 MC는 아니지만 순위에 오른 MC는 아래에 설명된 IIA 기준과 호환되지 않는다.
- 상호 다수결 기준(MMC)
- 유권자의 과반수가 다른 후보들보다 순위가 높은 후보군 중 누가 항상 이길까? 이것은 또한 다수의 유권자들이 특정 후보보다 다른 모든 후보를 선호한다면, 그 후보가 승리하지 못할까? 따라서 열거된 방법 중 상호 다수결에 실패하면서 다수결 패자를 통과시키는 보르다를 제외한 모든 방법이 어느 기준도 통과하지 못하거나 모두 통과하지 못한다.
- 콘도르케트 기준
- 쌍방향 비교에서 다른 모든 후보를 이기는 후보가 항상 이길 것인가? (이것은 위의 다수 기준을 내포하고 있다.)
- 콘도르케트 루저 기준(초) 패배자)
- 쌍방향 비교에서 다른 모든 후보에게 지는 후보는 결코 이길 수 없을까?
결과 기준(상대적)
이는 특정 후보가 한 가지 상황에서 승리할 경우 관련 상황에서 같은 후보가 승리해야 한다(또는 승리해서는 안 된다)고 명시하는 기준이다.
- Independence of Smith-dominated alternatives (ISDA)
- 스미스가 지배하는 후보가 추가되거나 제거될 경우(다른 후보들에 대한 표는 변동이 없다고 가정할 때) 결과가 결코 변하지 않는가? C 후보는 A에게 패하고 B 후보는 A에게 패하지 않는 등 다른 A 후보가 있다면 스미스 후보가 우세하다. 이 기준은 여기서 후보 상대적 요소로 분류되지만, 스미스가 지배하는 후보가 승리하는 것을 배제하는 데 있어 강력한 절대적 요소가 있다는 점에 유의한다. 사실, 그것은 위의 모든 절대적 기준을 내포하고 있다.[specify]
- Independence of irrelevant alternatives (IIA)
- 당선되지 않은 후보가 추가되거나 제거될 경우(다른 후보에 대한 유권자 선호도는 변하지 않는다고 가정할 때) 결과가 결코 변하지 않는가?[28] 예를 들어, 다원성 규칙은 IIA에 실패한다. 후보 X를 추가하면 Y가 이전보다 더 많은 표를 얻지 못하더라도 승자가 W에서 Y로 바뀔 수 있다.
- Local independence of irrelevant alternatives (LIIA)
- 꼴찌를 할 대안이 없어지면 결과가 달라지지 않는가?(그리고 2위로 끝나는 대안이 탈락하면 승자가 되지 못할 수도 있을까?)
- Independence of clone alternatives (cloneproof)
- 기존 후보와 유사한 당선되지 않은 후보가 추가되면 결과가 절대 바뀌지 않는가? 이 기준을 충족하지 못할 수 있는 세 가지 다른 현상이 있다.
- Monotonicity criterion (monotone)
- 만약 W 후보가 한 세트의 투표에서 승리하더라도, 그 투표수가 W 순위를 더 높게 매기도록 바뀌어도 W 후보가 항상 승리할 것인가? (이것은 또한 당신이 패배한 후보를 더 낮게 매겨서 승리하게 할 수 없다는 것을 의미하기도 한다.)
- Consistency criterion (CC)
- 만약 W 후보가 한 세트의 투표에 승리한다면, W 후보가 또한 승리하는 곳에 다른 한 세트의 투표지를 추가함으로써 그 투표지가 바뀌어도 W 후보가 항상 승리할 것인가?
- Participation criterion (PC)
- 정직하게 투표하는 것이 전혀 투표하지 않는 것보다 항상 더 나은가? (이것은 아래 표의 구별되지만 유사한 일관성 기준과 함께 그룹화된다.)[29]
- Reversal symmetry (reversal)
- 유권자 개개인의 선호도가 뒤집힌다면, 원래 우승자는 결코 승리하지 못하는가?
개표기준
이것들은 표를 세고 승자를 결정하는 과정과 관련된 기준이다.
- Polynomial time (polytime)
- 당선자를 후보수에서는 다항식이고 유권자수에서는 선형인 런타임으로 계산할 수 있는가?
- Resolvable
- 동전 던지기 같은 임의의 과정을 사용하지 않고 거의 모든 경우에 승자를 계산할 수 있는가? 즉, 당선자가 두 명 이상의 후보자 중 한 명이 될 수 있는 정확한 유대가 대규모 선거에서 사라지게 되는가?
- Summability (summable)
- 각 투표소에서 투표용지를 따로 집계하고 개별 집계만 하면 당선자를 계산할 수 있을까. 그러한 집계에 필요한 정보의 양은 N 후보 수의 순서 함수로 표현된다. O(N)나 O(N2)와 같은 느리게 성장하는 기능은 셈을 쉽게 하는 반면, O(N!)와 같은 빠르게 성장하는 기능은 선거 관리자들의 사기를 잡는 것을 더 어렵게 할 수 있다.[citation needed]
전략기준
이것들은 특정 형태의 전략을 사용하려는 유권자의 동기와 관련된 기준이다. 그들은 또한 상대적인 결과 기준으로 간주될 수 있다. 그러나, 그 섹션의 기준과 달리, 이 기준은 유권자들과 직접적으로 관련이 있다; 이 기준을 통과한다는 사실은 한 방법이 자신의 최적의 전략 투표를 알아내는 과정을 단순화할 수 있다.
- 사후-위해성 기준 및 후기-도움말 기준
- 유권자들은 투표에 나중의 선호도를 추가하는 것이 이미 등록된 어떤 후보에게도 해를 끼치거나 도움이 되지 않는다고 확신할 수 있는가?[30]
- 즐겨찾는 배신 없음(NFB)
- 유권자들은 그들이 선호하는 결과를 얻기 위해 그들이 좋아하는 어떤 다른 후보보다 순위를 매길 필요가 없다는 것을 확신할 수 있는가?[31]
투표 형식
이것들은 유효투표의 표현성이나 정보내용과 관련된 이슈들이다.
- 투표종류
- 투표자는 어떤 정보를 가지고 있는가?
- 등수
- 유효한 투표용지가 한 명 이상의 후보자에게 동등한 지지를 표현할 수 있는가(둘 이상의 후보에 대한 동등한 반대뿐만 아니라)?
- 2계급 이상
- 투표는 다른 후보들에 대한 두 가지 이상의 지지/반대 수준을 표현할 수 있는가?
약점
용어 참고 사항: 한 기준은 더 많은 투표 방식으로 통과될 때 다른 기준보다 '취약하다'고 한다. 이는 적용 기준이 더 강하다는 것을 의미한다. 예를 들어 다수결 기준(MC)이 다수결 기준(MMC)보다 약한 것은 어떤 규모의 집단이 아니라 단일 후보가 승리해야 하기 때문이다. 즉, MMC를 통과하는 모든 방법은 MC를 통과하지만 그 반대는 아니다. 반면에 MC를 받는 필수 우승자는 MMC에서 승리해야 하지만 그 반대는 아니다.
선택한 단일 승자 방법의 준수
다음 표는 위의 기준 중 몇 가지 단일 승자 방식으로 충족되는 것을 보여준다.
| 정렬: | ||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
기준 방법 | 불가항력 | Maj. 패자 | 상호 maj. | 콘도르셋 | 묵인하다. 패자 | 스미스/ ISDA | 리아 | IIA | 클론프론트 | 모노크톤 | 합의서 | 미립자 | 레베슈탈 심볼메트리 | 폴리시타임/ 분해할 수 있는 | 요약가능 | 나중-노- | 아니요. 마음에 드는 배반하다 | 투표하다 타자를 치다 | 순위 | |||
| 해롭다 | 도움 | = | >2 | |||||||||||||||||||
| 애프러쇼발 | 등급 | 아니요. | 아니요. | 아니요. | 아니요. | 아니오[b] | 네 | 네[d] | 네[e] | 네 | 네 | 네 | 네 | O(N) | 네 | O(N) | 아니요. | 네[f] | 네 | 애프르쇼발스 | 네 | 아니요. |
| 보르다 카운트 | 아니요. | 네 | 아니요. | 아니요. | 네 | 아니요. | 아니요. | 아니요. | 팀 | 네 | 네 | 네 | 네 | O(N) | 네 | O(N) | 아니요. | 네 | 아니요. | 랑슈킹 | 네 | 네 |
| 버클린 | 네 | 네 | 네 | 아니요. | 아니요. | 아니요. | 아니요. | 아니요. | 아니요. | 네 | 아니요. | 아니요. | 아니요. | O(N) | 네 | O(N) | 아니요. | 네 | 동일한 기본 설정인 경우 | 랑슈킹 | 네 | 네 |
| 코퍼랜드 | 네 | 네 | 네 | 네 | 네 | 네 | 아니요. | 아니요. | 팀 인파 | 네 | 아니요. | 아니요. | 네 | O(N2) | 아니요. | O(N2) | 아니요. | 아니요. | 아니오[b] | 랑슈킹 | 네 | 네 |
| IRV(AV) | 네 | 네 | 네 | 아니요. | 네 | 아니오[b] | 아니요. | 아니요. | 네 | 아니요. | 아니요. | 아니요. | 아니요. | O(N2) | 네[g] | O(N!) | 네 | 네 | 아니요. | 랑슈킹 | 아니요. | 네 |
| 케메니-영 | 네 | 네 | 네 | 네 | 네 | 네 | 네 | 아니요. | 스포일러스 | 네 | 아니요. [i] | 아니요. | 네 | O(N!) | 네 | O(N2) | 아니요. | 아니요. | 아니오[b] | 랑슈킹 | 네 | 네 |
| 최고 중위수/주요도[k] 판정 | 등급 | 네[m] | 아니오[n] | 아니요. | 아니요. | 아니오[b] | 네 | 네[d] | 네 | 네 | 아니요. | 아니요. | 디퓨전스 | O(N) | 네 | O(N) | 아니요. | 네 | 네 | 점수[t] | 네 | 네 |
| 미니맥스 | 네 | 아니요. | 아니요. | 네 | 아니요. | 아니요. | 아니요. | 아니요. | 스포일러스 | 네 | 아니요. | 아니요. | 아니요. | O(N2) | 네 | O(N2) | 아니요. | 아니요. | 아니오[b] | 랑슈킹 | 네 | 네 |
| 플라우라블리티/FPTP | 네 | 아니요. | 아니요. | 아니요. | 아니요. | 아니오[b] | 아니요. | 아니요. | 스포일러스 | 네 | 네 | 네 | 아니요. | O(N) | 네 | O(N) | 해당[v] 없음 | 해당[v] 없음 | 아니요. | 싱글 마크 | 해당 없음 | 아니요. |
| 스코어 투표 | 아니요. | 아니요. | 아니요. | 아니요. | 아니요. | 아니오[b] | 네 | 네[d] | 네 | 네 | 네 | 네 | 네 | O(N) | 네 | O(N) | 아니요. | 네 | 네 | 점수 | 네 | 네 |
| 순위 쌍 | 네 | 네 | 네 | 네 | 네 | 네 | 네 | 아니요. | 네 | 네 | 아니요. | 아니요. | 네 | O(N3) | 네 | O(N2) | 아니요. | 아니요. | 아니오[p][b] | 랑슈킹 | 네 | 네 |
| 결선투표 | 네 | 네 | 아니요. | 아니오[b] | 네 | 아니오[b] | 아니요. | 아니요. | 스포일러스 | 아니요. | 아니요. | 아니요. | 아니요. | O(N) | 네 | O(N) | 네 | 네[x] | 아니요. | 싱글 마크 | 해당 없음 | 아니오[y] |
| 슐제 | 네 | 네 | 네 | 네 | 네 | 네 | 아니요. | 아니요. | 네 | 네 | 아니요. | 아니요. | 네 | O(N3) | 네 | O(N2) | 아니요. | 아니요. | 아니오[p][b] | 랑슈킹 | 네 | 네 |
| 스타 투표의 | 아니오[z] | 네 | 아니오[aa] | 아니오[b][c] | 네 | 아니오[b] | 아니요. | 아니요. | 아니요. | 네 | 아니요. | 아니요. | 의존하다[ab] | O(N) | 네 | O(N2) | 아니요. | 아니요. | 아니오[ac] | 점수 | 네 | 네 |
| 정렬, 임의 승자[ad] | 아니요. | 아니요. | 아니요. | 아니오[b] | 아니요. | 아니오[b] | 네 | 네 | 아니요. | 네 | 네 | 네 | 네 | O(1) | 아니요. | O(1) | 네 | 네 | 네 | 없음 | 해당 없음 | 해당 없음 |
| 무작위 투표 | 아니요. | 아니요. | 아니요. | 아니오[b] | 아니요. | 아니오[b] | 네 | 네 | 네 | 네 | 네 | 네 | 네 | O(N) | 아니요. | O(N) | 네 | 네 | 네 | 싱글 마크 | 해당 없음 | 아니요. |
이 표는 포괄적이지 않다. 예를 들어 많은 기준을 만족하는 쿰스의 방법은 포함되지 않는다.
투표 기준의 추가 비교는 슐체 방식(일명 비트 경로)에 관한 기사에서 확인할 수 있다. 일부 데이터는 이 테이블이 진행 중이므로 중복될 수 있다.
| 시스템 | 모노슈토닉 | 콘도르케트 우승자 | 불가항력 | 콘도르케트 루저 | 다수결 패자 | 상호 과반수 | 스미스 | ISDA | 리아 | 클론의 독립성 | 반전대칭 | 참여, 일관성 | 후기 무해 | 나중-노-도움말 | 다항식 시간 | 확인가능성 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 슐제 | 네 | 네 | 네 | 네 | 네 | 네 | 네 | 네 | 아니요. | 네 | 네 | 아니요. | 아니요. | 아니요. | 네 | 네 |
| 순위 쌍 | 네 | 네 | 네 | 네 | 네 | 네 | 네 | 네 | 네 | 네 | 네 | 아니요. | 아니요. | 아니요. | 네 | 네 |
| 분할 주기 | 네 | 네 | 네 | 네 | 네 | 네 | 네 | 네 | 아니요. | 네 | 네 | 아니요. | 아니요. | 아니요. | 네 | 아니요. |
| 티데만의 대안 | 아니요. | 네 | 네 | 네 | 네 | 네 | 네 | 네 | 아니요. | 네 | 아니요. | 아니요. | 아니요. | 아니요. | 네 | 네 |
| 케메니-영 | 네 | 네 | 네 | 네 | 네 | 네 | 네 | 네 | 네 | 아니요. | 네 | 아니요. | 아니요. | 아니요. | 아니요. | 네 |
| 코프랜드 | 네 | 네 | 네 | 네 | 네 | 네 | 네 | 네 | 아니요. | 아니요. | 네 | 아니요. | 아니요. | 아니요. | 네 | 아니요. |
| 난슨 | 아니요. | 네 | 네 | 네 | 네 | 네 | 네 | 아니요. | 아니요. | 아니요. | 네 | 아니요. | 아니요. | 아니요. | 네 | 네 |
| 블랙 | 네 | 네 | 네 | 네 | 네 | 아니요. | 아니요. | 아니요. | 아니요. | 아니요. | 네 | 아니요. | 아니요. | 아니요. | 네 | 네 |
| 즉석 결선투표 | 아니요. | 아니요. | 네 | 네 | 네 | 네 | 아니요. | 아니요. | 아니요. | 네 | 아니요. | 아니요. | 네 | 네 | 네 | 네 |
| 스미스/IRV | 아니요. | 네 | 네 | 네 | 네 | 네 | 네 | 네 | 아니요. | 네 | 아니요. | 아니요. | 아니요. | 아니요. | 네 | 네 |
| 보르다 | 네 | 아니요. | 아니요. | 네 | 네 | 아니요. | 아니요. | 아니요. | 아니요. | 아니요. | 네 | 네 | 아니요. | 네 | 네 | 네 |
| 겔러-IRV | 아니요. | 아니요. | 네 | 네 | 네 | 네 | 아니요. | 아니요. | 아니요. | 아니요. | 아니요. | 아니요. | 아니요. | 아니요. | 네 | 네 |
| 볼드윈 | 아니요. | 네 | 네 | 네 | 네 | 네 | 네 | 아니요. | 아니요. | 아니요. | 아니요. | 아니요. | 아니요. | 아니요. | 네 | 네 |
| 버클린 | 네 | 아니요. | 네 | 아니요. | 네 | 네 | 아니요. | 아니요. | 아니요. | 아니요. | 아니요. | 아니요. | 아니요. | 네 | 네 | 네 |
| 다원성 | 네 | 아니요. | 네 | 아니요. | 아니요. | 아니요. | 아니요. | 아니요. | 아니요. | 아니요. | 아니요. | 네 | 네 | 네 | 네 | 네 |
| 조건부 투표 | 아니요. | 아니요. | 네 | 네 | 네 | 아니요. | 아니요. | 아니요. | 아니요. | 아니요. | 아니요. | 아니요. | 네 | 네 | 네 | 네 |
| 쿰스[32] | 아니요. | 아니요. | 네 | 네 | 네 | 네 | 아니요. | 아니요. | 아니요. | 아니요. | 아니요. | 아니요. | 아니요. | 아니요. | 네 | 네 |
| 미니맥스 | 네 | 네 | 네 | 아니요. | 아니요. | 아니요. | 아니요. | 아니요. | 아니요. | 아니요. | 아니요. | 아니요. | 아니요. | 아니요. | 네 | 네 |
| 반농림성[32] | 네 | 아니요. | 아니요. | 아니요. | 네 | 아니요. | 아니요. | 아니요. | 아니요. | 아니요. | 아니요. | 네 | 아니요. | 아니요. | 네 | 네 |
| 스리랑카 우발투표 | 아니요. | 아니요. | 네 | 아니요. | 아니요. | 아니요. | 아니요. | 아니요. | 아니요. | 아니요. | 아니요. | 아니요. | 네 | 네 | 네 | 네 |
| 보충투표 | 아니요. | 아니요. | 네 | 아니요. | 아니요. | 아니요. | 아니요. | 아니요. | 아니요. | 아니요. | 아니요. | 아니요. | 네 | 네 | 네 | 네 |
| 도그슨[32] | 아니요. | 네 | 네 | 아니요. | 아니요. | 아니요. | 아니요. | 아니요. | 아니요. | 아니요. | 아니요. | 아니요. | 아니요. | 아니요. | 아니요. | 네 |
다중우승제 비교
다승자 선거제도는 1승자 투표에서와 같은 결정을 내리는 것보다 더 넓은 의미에서 대표되는 의회를 만들려고 한다. 뉴질랜드 왕실 선거제도위원회는 뉴질랜드의 가능한 새로운 선거 방법에 대한 평가 기준을 10가지로 열거했다. 여기에는 정당 간의 공정성, 소수[33] 또는 특수 이익 집단의 효과적인 대표성, 정치적 통합, 효과적인 유권자 참여 및 정당성이 포함되었다.
다중 승자 평가를 위한 메트릭스
다승자 투표 방식의 성과를 평가하기 위해서는 1승자 시스템과는 다른 지표가 필요하다. 다음과 같은 제안이 있었다.
- 콘도르셋 위원회 효율성(CCE)은 한 무리의 선출된 우승자들이 쌍방향 경주에서 모든 패자를 이길 가능성을 측정한다.[34]
- 사회-유틸리티 비율(SUP)은 각 투표자가 당첨자 중 적어도 한 명의 높은 효용성을 가진 후보가 있을 가능성을 측정한다.[35]
- 평등-유틸리티비례(UP)는 가장 근접한 당선자를 위한 효용성이 가장 낮은 유권자의 관점에서 비례성을 측정한다.[35]
- 중도 성향(CT)은 정치적 스펙트럼의 중심이나 극한에 가까운 후보를 선출하는 방법의 가능성을 측정한다.[35]
기준표
파티 기반 다중 승자 방법 준수
기준 방법 | 이론상 비례 | 실제 비례 | 반비례 대다수의 유권자가 모든 의석을 차지할 정도로 그 결과를 강요할 수는 없다. | 깨지지 않는 투표 방법은 잠재적인 전략적 투표 피드백 루프가 없다. | 모노톤 | 일관성 | 참여 | 보편적으로 좋아하는 후보 | 멤버 계층이 있나? | 지역 대표성이 필요한가? | 개별 후보의 유권자 선택이 있는가? | 투표하다 유형 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 일반표 | 아니요. | 아니요. | 아니요. | 아니오 – 양당 지배 | 네 | 네 | 네 | 아니요. | 아니요. | 아니요. | 아니오 — 모든 좌석은 미리 정해진 목록 하나로 채워져 있음 | 한 리스트에 대한 단일 표시 |
| 닫힌 당명부 | 네 | 네 | 네 | 예(좌석이 적거나 첫 번째 시트 임계값이 높은 경우는 제외) | 네 | 네 | 네 | 해당 없음 – 보편적으로 선호되는 리스트는 정의상 모든 좌석을 차지해야 한다. | 아니요. | 아니요. | 아니오 - 당명부 내의 후보 순위에 따라 당의 의석을 채우는 순서가 결정된다. | 한 리스트에 대한 단일 표시 |
| 비교적 폐쇄적인 당명부 | 네 | 네 | 네 | 예(좌석이 적거나 첫 번째 시트 임계값이 높은 경우는 제외) | 네 | 네 | 네 | 해당 없음 – 보편적으로 선호되는 리스트는 정의상 모든 좌석을 차지해야 한다. | 아니요. | 아니요. | 예 — 후보자가 하어 쿼터를 획득해야 의석을 보장할 수 있으며, 그렇지 않을 경우 당명부 내의 후보자 순위에 따라 당의 의석을 채우는 순서가 결정된다. | 한 리스트에 포함된 후보 단일 또는 제한 점수 |
| 더 오픈 당명부 | 네 | 네 | 네 | 예(좌석이 적거나 첫 번째 시트 임계값이 높은 경우는 제외) | 네 | 네 | 네 | 해당 없음 – 보편적으로 선호되는 리스트는 정의상 모든 좌석을 차지해야 한다. | 아니요. | 아니요. | 그렇다 — 한 후보가 의석을 보장하기 위해 일정 비율의 표를 얻어야 한다. 그렇지 않을 경우, 정당의 의석을 채우는 순서는 정당명부 내의 후보 순위에 따라 결정된다. | 한 리스트에 포함된 후보 단일 또는 제한 점수 |
| 가장 열려 있음 당명부 | 네 | 네 | 네 | 예(좌석이 적거나 첫 번째 시트 임계값이 높은 경우는 제외) | 네 | 네 | 네 | 해당 없음 – 보편적으로 선호되는 리스트는 정의상 모든 좌석을 차지해야 한다. | 아니요. | 아니요. | 예 — 모든 후보가 받는 표의 수가 당의 의석을 채우는 순서를 결정한다. | 한 리스트 내의 한 후보에 대한 단일 마크 |
| 패너치(panachage) | 네 | 네 | 네 | 예(좌석이 적거나 첫 번째 시트 임계값이 높은 경우는 제외) | 네 | 네 | 네 | 해당 없음 – 보편적으로 선호되는 리스트는 정의상 모든 좌석을 차지해야 한다. | 아니요. | 아니요. | 예 — 모든 후보가 받는 표의 수가 당의 의석을 채우는 순서를 결정한다. | 모든 리스트에 포함된 응시자의 점수가 제한됨 |
| 수정되지 않은 혼합 멤버 비율 | 아니오 – 전략적 유권자가 오버행 좌석 수를 조작할 수 있음 | 예, 초과 좌석에 의한 불균형 제외 — 비례 계층 구성원은 단지 비례 계층 투표에 근거하여 선거구 계층에 의해 야기된 불균형을 보상하기 위해 선택된다. | 네 | No – 오버행 조작 및 단일 승자 의석 간의 양당 지배 | 네 | 아니요. | 네 | 부분적으로 — 보편적으로 좋아하는 리스트는 정의에 따라 비례 계층과 선거구 계층의 모든 의석을 획득해야 할 것이다. 모든 선거구 후보들이 보편적으로 선호한다면, 비례 계층 멤버들의 선택은 전체 멤버쉽의 불균형을 보상하기 위해 이루어질 것이다. | 예 - 선거구 계층 및 비례 계층 | 예 — 단일 구성원 선거구 | 예 — 선거구 후보는 단일 당선자 방식으로 선택되며, 비례대표는 위에서 언급한 정당명부 방식으로 선택될 수 있다. | 선거구 후보 1명에 대한 단일 마크 또는 랭킹, 비례 등급 표시는 선택에 사용되는 정확한 방법에 따라 결정 |
| 베스트-로저 혼합 멤버 비례 | 아니오 – 전략적 유권자가 오버행 좌석 수를 조작할 수 있음 | 그렇다, 의석 과잉으로 인한 불균형 제외 — 비례 계층 구성원은 당의 총합에 근거하여 선거구 계층에 의해 야기된 불균형을 보상하기 위해 선택된다. | 네 | No – 오버행 조작 및 단일 승자 의석 간의 양당 지배 | 네 | 아니요. | 네 | 아니 - 보편적으로 좋아하는 리스트는 정의상 비례 계층과 선거구 계층의 모든 의석을 얻어야 할 것이다. 비례 계층 구성원은 선거구 패배자로부터 뽑히기 때문에 그러한 위업은 불가능하다. 모든 선거구 후보가 보편적으로 선호된다면, 비례 계층 구성원의 선택은 보상하기 위해 만들어질 것이다.뒤이은 전체 회원의 불균형을 위해 먹었다. | 예 - 선거구 계층 및 비례 계층 | 예 — 단일 구성원 선거구 | 예 — 단일 당선자 방식으로 선거구 후보를 선택하고, 비례 계층 구성원은 정당명부 방식으로 선택 | 단일 마크 또는 단일 선거구 후보 순위, 선거구 계층 결과에 따라 결정되는 비례 계층 |
| 평행투표 | 아니요. | 아니오 - 선거구 계층과 비례 계층 구성원은 서로 독립적으로 선택됨 | 네 | No – 단일 승자석 중 양당 우세 | 네 | 아니요. | 네 | 부분적으로 — 보편적으로 좋아하는 리스트는 정의상 비례 계층의 모든 의석을 획득해야 할 것이다; 모든 선거구 후보들이 보편적으로 선호한다면, 비례 계층 멤버의 선택은 영향을 받지 않을 것이다. | 예 - 선거구 계층 및 비례 계층 | 예 — 단일 구성원 선거구 | 예 — 단일 당선자 방식으로 선거구 후보를 선택하고, 비례 계층 구성원은 정당명부 방식으로 선택 | 선거구 후보 1명에 대한 단일 마크 또는 랭킹, 비례 등급 표시는 선택에 사용되는 정확한 방법에 따라 결정 |
| 전갈자리 | 아니오 – 전략적 투표자는 표를 분할하여 보상 감산을 해제하여 선거를 평행 투표로 되돌릴 수 있음 | 부분 — 선거구 계층과 비례 계층 구성원은 서로 독립적으로 선택되지만, 선거구 승자의 투표는 각 정당의 총합에서 제외된다. | 네 | No – decoy 목록 | 아니요. | 아니요. | 아니요. | 그렇다 — 보편적으로 좋아하는 명단은 여전히 선거구 당선자의 표를 총액에서 차감하여 다른 모든 의석 간의 비례적 분배를 보장한다. 만약 모든 선거구 후보들이 보편적으로 선호한다면, 비례 계층의원을 선출하는 것은 정당 총액에서 그들의 표를 뺀 것이다. | 예 - 선거구 계층 및 비례 계층 | 예 — 단일 구성원 선거구 | 예 — 단일 당선자 방식으로 선거구 후보를 선택하고, 비례 계층 구성원은 정당명부 방식으로 선택 | 선거구 후보 1명에 대한 단일 마크 또는 랭킹, 비례 등급 표시는 선택에 사용되는 정확한 방법에 따라 결정 |
| 다수결 상여제 | 부분적으로 – 과반수의 의석은 정당 사이에 비례하여 배분되지만, 나머지는 정당에 가장 많이 투표한 사람에게 보너스로 주어진다. 전략적인 유권자는 이 보너스를 조작할 수 있다. | 부분적으로 – 과반수의 의석은 정당 간에 비례하여 배분되지만, 나머지는 정당에서 가장 많은 표를 얻은 정당에게 보너스로 주어진다. | 네 | 아니오 – 보너스를 위해 경쟁하는 당사자 간의 양당 지배 | 네 | 네 | 네 | 해당 없음 – 보편적으로 선호되는 리스트는 정의상 모든 좌석을 차지해야 한다. | 예 - 비례 계층 및 보너스 계층 | 아니요. | 반드시 그렇지는 않다 — 위에서 언급한 정당명부 방식 중 하나로 비례대표를 선정할 수 있다. | 비례 계층 표시는 선택에 사용되는 정확한 방법에 따라 달라지며, 보너스 계층은 비례 계층 결과에 의해 결정된다. |
| 다수대박제 | 아니 — 대박은 가장 많은 표를 얻은 정당에 할당되고, 비 잭팟 계층 의석은 다른 모든 정당에 비례하여 배분된다; 전략적인 유권자들은 대박을 조작할 수 있다. | 아니 — 대박은 가장 많은 표를 얻은 파티에 할당되며, 잭팟이 아닌 계층의 좌석은 다른 모든 사람들 사이에 비례하여 배분된다. | 네 | No – 대박을 다투는 당사자 간의 양당 지배 | 아니 — 대박을 터뜨린 당이 다른 정당들보다 유리하게 된다; 대박은 대박보다 더 많은 의석을 얻으면 가장 많은 표를 얻은 정당에게 불리하게 된다. | 네 | 네 | 해당 없음 – 보편적으로 선호되는 리스트는 정의상 모든 좌석을 차지해야 한다. | 예 - 비례 계층 및 대박 계층 | 아니요. | 반드시 그렇지는 않다 — 위에서 언급한 정당명부 방식 중 하나로 비례대표를 선정할 수 있다. | 비례 계층 표시는 정확한 선택 방법에 따라 달라지며, 대박 등급은 비례 계층 결과에 의해 결정된다. |
| 이중 멤버 비례 | 아니오 – 전략적 유권자가 이론적으로 2차 의석에서 결과를 조작할 수 있음 | 네 | 네 | 없음 – 2차 시트 조작 및 1차 시트 간 양당 지배 | 아니요. | 네 | 네 | 네 | 아니요. | 예 — 이중 구성원 선거구 | 예 — 가장 많은 표를 얻은 후보는 한 자리를 보장받고, 다른 한 후보는 최고의 패배자 중에서 선택된다. | 단일 후보 또는 후보 쌍에 대한 단일 표시 |
| 농어촌비례대표 | 아니오 – 전략적 유권자가 시골 오버행 좌석 수를 조작할 수 있음 | 부분적으로 - 불균형은 도시 좌석에 STV를 사용하고 시골 좌석을 오버행(overhang)하여 발생할 수 있음 — 시골 지역 선거구 계층에 의해 야기되는 불균형을 보상하기 위해 시골 지역 비례 계층 구성원을 선발하지만, 도시 불균형에 대해서는 그러한 보상이 존재하지 않는다. | 네 | No – 오버행 조작 및 시골 단일 당첨자 의석 간의 양당 지배 | 아니요. | 아니요. | 아니요. | 부분적으로 - 도시 계층에서 그렇다; 보편적으로 좋아하는 시골 지역 리스트는 정의상 농촌 비례 계층의 모든 의석을 차지해야 할 것이다; 모든 농촌 지역 선거구 후보들이 보편적으로 선호한다면, 농촌 비례 계층 멤버를 선발하는 것은 불균형을 보상하기 위해 이루어질 것이다; 어느 경우든, 도시 비례 계층의 선발은 도시 계층의 선택이다.ndidates는 영향을 받지 않을 것이다. | 예 - 도시 계층, 시골 지역 선거구 계층 및 시골 지역 비례 계층 | 예 — 도시 선거구와 시골 1인 선거구 | 예 — 시골지역 선거구 후보는 STV에서, 시골지역 선거구 후보는 단승 방식으로, 농촌지역 비례대표 의원은 정당명부 방식으로, 또는 농촌지역구에서 가장 낙선자 중에서 선택할 수 있다. | 도시지역구 후보 순위, 농촌지역구 후보 1명 1명 1명 1명 1명 1명 1명 1명 1명 1명 1명 1명 1명 1명 1명, 농촌지역비례계층점수 1명 1명 1명 |
비주요 정당 불가지론 다승적 방법 준수
다음 표는 위의 기준 중 어떤 것이 여러 가지 복수 당첨자 방식으로 충족되는지를 보여준다.
기준 방법 | 비례적 | 모노크톤 | 합의서 | 워렌의 다승자 참가 기준 | 아니요. 마음에 드는 배신 | 반정성 | 보편적으로 좋아하는 후보 | 싱글 포함 위너 | 투표하다 유형 |
|---|---|---|---|---|---|---|---|---|---|
| 먼로의 (점수 투표 버전) | 네 | 타이브레이커 사용 여부에 따라 다름 | 네 | 아니요. | 아니요. | 승인 또는 범위 | 승인 또는 점수 | ||
| 체임벌린-쿠랑트 룰 | |||||||||
| 에베르트의 | 네 | 아니요. | 네 | 승인 또는 범위 | 승인 또는 점수 | ||||
| 프시 | 네 | 네 | 네 | 아니요. | 아니요. | 아니요. | 승인 또는 범위 | 승인 또는 점수 | |
| 조화 | 네 | 네 | 네 | 아니요. | 아니요. | 아니요. | 승인 또는 범위 | 승인 또는 점수 | |
| 순차 비례 승인 | 네 | 네 | 아니요. | 아니요. | 아니요. | 아니요. | 승인 | 승인 | |
| 재가중 범위 | 네 | 네 | 아니요. | 아니요. | 아니요. | 아니요. | 범위 | 점수 | |
| 비례적 승인 | 네 | 네 | 네 | 아니요. | 아니요. | 아니요. | 승인 | 승인 | |
| 입찰투표 | 네 | 아니요. | 아니요. | 네 | 승인 또는 범위 | 승인 또는 점수 | |||
| 단일 양도 가능 투표 | 네 | 아니요. | 아니요. | 아니요. | 아니요. | 아니요. | 네 | 순간유출 | 순위 |
| CPO-STV | 네 | 아니요. | 아니요. | 아니요. | 아니요. | 아니요. | 네 | 콘도르셋 방법(어느 것에 따라 다름) | 순위 |
| 슐제 STV | 네 | 네 | 아니요. | 아니요. | 아니요. | 아니요. | 네 | 슐제 | 순위 |
| 승인 규칙 확장 | 승인 | 승인 | |||||||
| 단일 비양도 투표 | 아니요. | 네 | 네 | 네 | 아니요. | 아니요. | 해당 없음(비례적 아님) | 다원성 | 싱글 마크 |
| 제한투표 | 아니요. | 네 | 네 | 네 | 아니오[36] | 아니요. | 해당 없음(비례적 아님) | 다원성 | 제한 마크 |
| 누적투표 | 아니요. | 네 | 네 | 네 | 아니오[36] | 아니요. | 해당 없음(비례적 아님) | 다원성 | 다중 표시 |
| Minmax 승인 | 승인 | 승인 | |||||||
| 정렬, 임의 승자 | 아니요. | 네 | 네 | 네 | 네 | 네 | 해당 없음(비례적 아님) | 정렬, 임의 승자 | 없음 |
| 단일 무작위 투표 | 아니요. | 네 | 네 | 네 | 네 | 네 | 해당 없음(비례적 아님) | 무작위 투표 | 제한 마크 |
| 다중 무작위 투표 | 접근 | 네 | 네 | 네 | 네 | 네 | 해당 없음(비례적 아님) | 무작위 투표 | 제한 순위 |
주요 정당 불가지론 다승적 방법 준수
다음 표는 위의 기준 중 어떤 것이 여러 가지 복수 당첨자 방식으로 충족되는지를 보여준다.
기준 방법 | 모노크톤 | 합의서 | 미립자 | 클론프론트 | 즐겨찾기 없음 | 반정성 | 스미스 세트 우승자들 | 콘도르케트위너 | 콘도르케틀로저 | 싱글위너와 함께 | 투표형 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 복수 당첨자 승인 | 네 | 네 | 네 | 네[e] | 네 | 네 | 아니요. | 아니요. | 아니요. | 승인 | 승인 |
| 멀티 위너 범위 | 네 | 네 | 네 | 네 | 네 | 네 | 아니요. | 아니요. | 아니요. | 범위 | 점수 |
| 멀티 위너 슐제 | 네 | 아니요. | 아니요. | 네 | 아니요. | 아니요. | 네 | 네 | 네 | 슐제 | 순위 |
| 앳 라지 | 네 | 네 | 네 | 아니요. (기울기) | 아니요. | 아니요. | 아니요. | 아니요. | 아니요. | 다원성 | 제한 마크 |
참고 항목
메모들
- ^ 찬성하는 것이 항상 유권자의 절반 이상이 선호하는 후보를 선출하는 것은 아니지만, 항상 가장 많은 유권자가 찬성하는 후보를 선출하기 때문에 대다수의 기준을 충족시키지 못한다.
- ^ Jump up to: a b c d e f g h i j k l m n o p q r s t u v w x y z aa ab ac ad ae af ag ah ai aj ak al am an ao ap aq ar 콘도르케트, 스미스 및 스미스가 지배하는 대안 기준은 관련 없는 대안들의 독립성, 일관성, 참여성, 후기-무해, 후기-도움말 및 즐겨찾기 배신[clarification needed] 기준과 양립할 수 없다.
- ^ Jump up to: a b c d 찬성, 범위 및 다수결에서 모든 유권자가 서로의 진정한 선호에 대한 완벽한 정보를 가지고 있고 합리적인 전략을 사용할 경우 다수결 또는 다수결 승자는 전략적으로 강제된다. 즉, 하나 이상의 강한 내시 평준화에서 승리한다. 특히 모든 유권자가 "A 또는 B가 가장 이길 것 같은 두 가지"라는 것을 알고 둘 사이에 "승인 문턱"을 둔다면, 콘도르셋 승자는, 만일 한 가지가 존재하고 세트 {A,B}에 있다면, 항상 승리할 것이다. 이러한 방법들은 또한 어떤 다수가 그렇게 원한다면 그들의 후보를 이기도록 강요할 수 있다는 약한 의미에서 다수결 기준을 충족시킨다. Laslier, J-F (2006), "Strategic approval voting in a large electorate" (PDF), IDEP Working Papers, Marseille, France (405)
- ^ Jump up to: a b c 유권자가 선거에서 이용할 수 있는 대안을 알고 있는 것과 별개로 후보를 개별적으로 그리고 독립적으로 평가한다고 가정할 경우, 찬성 투표, 범위 투표, 다수결 심판은 IIA를 만족시킨다. 이를 위해 일부 선거에서는 가능한 대안 중 의미 있는 선호도를 갖고 있음에도 불구하고 일부 유권자는 전체 투표권보다 적게 사용하거나 심지어 기권해야 한다. 이러한 가정을 하지 않으면, 이 방법들은 정격 방법보다 순위가 높아지기 때문에 IIA에 실패한다.
- ^ Jump up to: a b 원래 복제의 독립성 기준은 순위 투표 방법에만 적용되었다. (T 니콜라우스 티데만, "투표 규칙의 기준으로 복제의 독립성"), 사회 선택 및 복지 제4권, 제3권(1987년, 페이지 185–206년) 디데만은 "복제의 독립성 정신에서", "그렇게 유사한 후보가 두 명 이상이었다면"고 언급한다.모든 유권자가 순위를 매길 수 있는 기회가 주어진다면 [...], 그러면 존재하는 완벽한 클론의 수는 승인 투표에서 완벽한 클론이 승리하는 후보군에 속하는지 여부에 영향을 미치지 않을 것이다." 그래서, 승인 투표는 정의에 의해 이 수학적 기준을 충족시킨다. 그러나, 그의 표를 작성하는 과정에서 유권자의 고려사항이 (그 사람의 복제본이 도입되었을 때 유권자가 그의 승인 후보를 분산시키는 방식으로) 복제본에 의해 전술적으로 영향을 받을 수 있는지, 그리고 복제의 정의가 이러한 고려사항들에까지 확대되어야 하는지에 대해서는 약간의 의견의 불일치가 있다.실표 처리에만 급급하다
- ^ 나중-불해 및 나중-도움말 - 엄격히 명령된 선호 투표에 나중 선호도를 추가하는 것이 이전의 선호도에 도움이 되거나 해를 끼치지 않아야 한다고 주장한다. 승인 투표용지는 승인을 기록하지만 승인 간의 명시적인 상대적 선호(예: 이후)를 기록하지 않는다(선호는 유권자의 관점에서 존재함). 한편, 선호도가 낮은 후보를 승인하는 유권자는 다른 승인된 후보가 승리할 확률을 해치지만, 도움이 되지 않는다.
- ^ 유권자 수의 제곱근보다 후보 수가 더 빨리 늘어나면, 이 과정에서 어느 시점의 유대가, 심지어 두 명의 비존재 후보 사이의 유대가 최종 결과에 영향을 미칠 수 있기 때문에, 이것은 그렇지 않을 수도 있다. 그러나 그러한 관계를 해결하기 위한 규칙이 무작위성을 포함하지 않는다면, 이 방법은 기준을 통과한다.[citation needed]
- ^ 여러 경내에서 합산할 수 있는 말뚝의 수는 바닥(e-1) N!) - 1이다.
- ^ 케메니영도 당선자 일관성 기준을 통과하지 않고 전체 순위에 대한 일관성 기준, 즉 두 부분으로 나눠서 케메니영도 같은 순위를 선택하면 그 순위를 합산한 유권자가 선택하게 된다.
- ^ 각 예비 Kemeny-Young 오더에는 이에 동의하는 페어 와이즈 항목의 합계와 동일한 점수가 있으므로 페어 와이즈 매트릭스를 사용하여 최상의 오더를 찾을 수 있다.
- ^ 버클린 투표는, 건너뛰고 동등한 순위가 허용되며, 다수결은 다수결 심판과 동일한 기준을 충족한다. 사실 다수결은 버클린 투표의 한 형태로 간주될 수 있다. 동일한 순위를 허용하지 않으면 버클린의 기준 준수는 더욱 악화된다. 특히, 이 변종과 같은 순위 방식은 다수 기준과 호환되지 않는 관련 없는 대안의 독립성을 상실한다.
- ^ 다수결 심판은 항상 유권자의 절반 이상이 다른 모든 사람보다 선호하는 후보를 선출하는 것은 아니지만, 항상 유권자의 절반 이상이 유일하게 최고 등급을 받은 후보를 선출한다.
- ^ 다수결 심판은 유권자의 절반 이상이 선호하지 않는 독특한 후보를 선출할 수 있지만, 유권자의 절반 이상이 선호하지 않는 후보를 선출하지는 않는다.
- ^ 다수결 심판은 상호 다수결 기준에는 해당하지 않지만, 다수결은 상호 선호되는 절대등급 이상과 그 이하의 모든 등급을 매긴다면 기준을 충족한다.
- ^ 다수결의 창안자인 발린스키와 라라키는 그것이 그들이 "등급 일관성"이라고 부르는 더 약한 기준을 충족한다고 지적한다: 두 명의 선거인이 한 후보에 대해 동일한 등급을 준다면, 통합 유권자도 그렇게 될 것이다. 다수결의 원칙은 등급을 "공통어", 즉 각 등급이 절대적인 의미를 갖도록 명시적으로 요구한다. 그들은 이것이 "등급 일관성"을 의미 있게 만드는 것이라고 주장한다. Balinski M, MJ; Laraki, R (2007), "A theory of measuring, electing and ranking", Proceedings of the National Academy of Sciences of the United States of America, USA: National Academy of Sciences, 104 (21): 8720–25, Bibcode:2007PNAS..104.8720B, doi:10.1073/pnas.0702634104, PMC 1885569, PMID 17496140
- ^ Jump up to: a b c d e 다수결, 순위표, 슐체 투표에서는 항상 다른 투표용지를 일정하게 유지한 채 모든 유권자에게 후회가 없는 반정성 투표가 있다. 즉, 다른 사람들이 어떻게 투표할 것인지(예를 들어 다수결의 경우, 당선된 후보 및 당선된 중위점수)에 대해 충분히 알고 있다면, 그들이 더 선호되는 후보보다 덜 선호되는 후보를 채점하지 않고 참여할 수 있는 방법은 항상 하나 이상 있다. 그러나 유권자의 정보가 불충분할 경우 이는 중단될 수 있다.
- ^ 다수결은 유권자 수가 짝수일 때 중위수를 찾는 데 사용되는 라운딩 방식에 따라 실제로 역전 대칭을 통과하거나 실패할 수 있다. 예를 들어, 2차, 2차 레이스에서 등급이 숫자로 전환되고 2개의 중앙 등급이 평균화되면 MJ는 역전 대칭을 충족하지만, 하위 등급이 선택되면, ["공정"]을 가진 후보가 역전의 유무에 상관없이 ["좋은";빈약한"]의 후보를 이길 수 있기 때문에 그렇지 않다. 그러나 반전 대칭을 충족하지 않는 라운딩 방법의 경우, 이를 어길 확률은 회복 불가능한(열린) 결과의 확률과 비교된다. 즉, 다수의 유권자들에게는 소실될 정도로 작다.
- ^ 다수결은 순서 KN에서 합산되며, 여기서 순위 카테고리 수인 K는 사전에 설정된다.
- ^ 다수결은 이 또는 이와 유사한 기준을 통과하지 못하지만, 버클린 투표에 기반한 것과 같은 유사한 중위수 방법이 있는데, 이는 관련되고 약한 기준을 충족할 수 있다: (자신의 학년이 아닌) 추가 후보를 중위수 이하로 서열하면 좋아하는 후보를 해칠 수 없다. 발린스키, M, R. 라라키. 「측정·선별·순위에 관한 이론」. 국립과학원 104호 21호(2007년) 절차: 8720호.
- ^ 실제로 다수결 투표용지는 숫자가 아닌 '공통어'로 표현된 등급을 사용하는데, 즉 각 등급은 절대적인 의미를 갖는다.
- ^ Jump up to: a b 반대가 아닌 쌍방향 반대만을 계산하는 미니맥스의 변종은 콘도르셋 기준을 통과하지 못하고 나중에 해를 입지 않는다.
- ^ Jump up to: a b 복수형은 투표용지에 후기 선호를 표시하는 것을 전혀 허용하지 않기 때문에 후기 선호를 표시해 좋아하는 후보에게 해를 끼치거나 도움을 주는 것은 불가능하며, 따라서 후기-해고-후기-노-도움말 둘 다 경미하게 통과한다. 그러나, 그것은 자르기를 강요하기 때문에, 그것은 단지 나중-No-Harm을 실패함으로써 자르기를 조장하는 방법들과 몇몇 문제를 공유한다. 비슷하게, 비록 덜하지만, 그것은 유권자들이 후보 중 한 명을 제외한 모든 사람들을 구별할 수 있도록 허락하지 않기 때문에, 그것은 유권자들이 부정직하게 그러한 구별을 하도록 장려하는 '나중-노-도움말'을 실패하는 방법들과 약간의 문제를 공유한다.
- ^ Jump up to: a b 한 판에 한 번.
- ^ 즉 2차 투표는 이미 탈락한 후보를 돕거나 해칠 수 없다.
- ^ 이후 선호도는 2라운드에 진출하는 두 후보 사이에서만 가능하다.
- ^ STAR 투표는 X가 결선 투표에 있을 경우 과반수 후보 X를 선출하며, X의 유권자들은 전략적으로 X에 가장 높은 점수를 주고 모든 상대에게 가장 낮은 점수를 줌으로써 결선 투표를 보장할 수 있다. 그러나 X의 유권자들로부터 점수를 얻는 반대자가 둘 이상일 경우 이들 반대자들은 X를 결선투표에서 탈락시킬 수 있다. 따라서, STAR는 다수 기준을 통과하지 못한다.
- ^ 다수결 기준과 마찬가지로, STAR 투표는 상호 다수결 기준을 통과하지 못한다. 다만 상호 과반수 안에 든 후보가 많을수록 최소 1명 이상이 결선투표에 진출할 가능성이 커 승리가 보장된다.
- ^ STAR는 완전한 결과 순서를 정의하지 않고 오직 승자만 정의한다. 3명 외에 후보가 어느 정도 있는 상황에서 표결이 뒤바뀌면 승자가 그대로 있을 수 없다.
- ^ STAR 투표에서, 좋아하는 배신이 전략적으로 유리하기 위해서는 네 가지 분리된 것이 사실이어야 한다: 좋아하는 후보 X는 정직한 투표로 결선투표에 진출해야 하고, 배신 수혜자 Y는 정직한 투표로 결선투표에 진출해서는 안 되며, Y는 전략적으로 결선투표에서 승리해야 한다.투표하다
- ^ 분류, 균일하게 무작위로 뽑은 후보가 당선인이다. 임의의 승자, 유권자가 아닌 일부 외부 실체가 승자를 선정한다. 이 방법들은, 제대로 말하면, 전혀 투표 방법이 아니지만, 투표하지 않는 방법이라도 그 기준의 일부를 여전히 통과할 수 있다는 것을 보여주기 위해 포함되어 있다.
- ^ 무작위 투표, 일률적으로 무작위로 뽑은 투표가 승자를 결정한다. 이 방법들과 밀접하게 연관된 방법들은 수학적 관심사가 된다. 왜냐하면 그것들은 정말로 전략적이지 않은 유일한 방법이기 때문이다. 즉, 여러분의 최선의 투표는 다른 유권자들에 대한 어떤 것에도 의존하지 않을 것이기 때문이다. 그러나, 이 방법은 일반적으로 실용적인 방법에 대한 진지한 제안으로 간주되지 않는다.
참조
- ^ Jump up to: a b c d Jean-François Laslier (2011). And the loser is... Plurality Voting. HAL. ISBN 978-3-642-42955-2. ISSN 2267-828X. Wikidata Q108664719.
- ^ Jump up to: a b c d e f g R. B. 달링턴, '콘도르셋과 미니맥스 투표 시스템이 최고인가?' (v8, 2021).
- ^ Jump up to: a b c R. B. 달링턴, "미니맥스는 결국 최고의 선거 제도다" (2016년)
- ^ Jump up to: a b c d J. R. 챔벌린과 M. D. 코헨, "Toward Applicable Social Choice 이론...", (1978)
- ^ M. J. A. N. 데 카리타트, 데 콘도르셋 후작. 그의 책은 1785년에 출판되었다. 제목은 "다수 투표에 확률론 적용에 대한 설명"으로 번역될 수 있다.
- ^ 콘도르셋과 라플레이스의 경우 G. G. Szpiro, "Numbers Rule"(2010)을 참조한다.
- ^ 던컨 블랙, "그룹 의사결정의 근거에 대하여"(1948)
- ^ 앤서니 다운스, "민주주의의 경제 이론"(1957)
- ^ M. 발린스키와 R. 라라키, "측정, 선택, 서열화 이론"(2007)
- ^ 그 정리는 애로우 박사학위 논문(1951년)에 처음 명시됐다.
- ^ Jump up to: a b T. N. Tideman과 F. Plassmann, "2012년 실제 선거에서 투표-캐스팅의 결과 모델링"
- ^ G. Tullock, "General Impossible Organization of the General Impossibility Organization" (1967년)
- ^ 볼, 테렌스, 앤티스 로지데스, "제임스 밀", 스탠포드 철학 백과사전 (Winter 2020 Edition), 에드워드 N. 잘타 (edd.)
- ^ T. B. 맥컬레이 "Mill on Government" (1829년)는 그의 잡지에 다시 실렸다.
- ^ 표기법은 Normal distribution§Notation 기사에 정의되어 있다. 정규성에 대한 가정은 편리하며, 시뮬레이션에 사용하기에 적합한 생성 모델을 제공하지만, 콘도르셋과 영의 결과는 순수 확률론에서 파생되어 그것에 의존하지 않는다.
- ^ 스테이크체인지에 대해 언급되었다.
- ^ H. P. Young, "콘도르케트의 투표론"(1988)
- ^ R. F. 보들리 "시뮬레이션을 통한 선거제도 평가의 실용적 방법"(1983)
- ^ Quinn, Jameson (2017-02-10). "Voter Satisfaction Efficiency FAQ". GitHub Pages. Retrieved 2019-07-24.
- ^ B. Grofman과 S. L. Feld, "만약 당신이 대안 투표(즉석 결선투표)를 좋아한다면, 당신은 Coombs 룰에 대해 알아야 한다."(2004)
- ^ Jump up to: a b T. N. Tideman과 F. 플라스만 "어떤 투표 규칙이 가장 '최고의' 후보를 선택할 가능성이 높은가(2012년).
- ^ Jump up to: a b J. 그린 아미타주, T. N. 티드먼과 R. 코스만, 「투표규칙 통계적 평가」(2015).
- ^ Jump up to: a b c J. 그린-아미타주, "전략적 투표와 공천"(2011년)
- ^ Jump up to: a b S, Merrill III, "다국간 선거제도의 효율성의 비교" (1984)
- ^ 에릭 파쿠이트, "투표 방법", 스탠포드 철학 백과사전 (Fall 2019 Edition), Edward N. Zalta (ed.
- ^ 조지 G. 스즈피로, "Numbers Rule" (2010)
- ^ 중위 유권자 정리를 참조하십시오.
- ^ Vasiljev, Sergei (April 1, 2008), Cardinal Voting: The Way to Escape the Social Choice Impossibility, SSRN eLibrary, SSRN 1116545.실제로 유권자들은 (특히 추기경 투표 방식에서) 누가 경선에 참여하느냐에 따라 표를 바꿀 수 있다는 점에 유의한다. 그러나 이 가능성을 무시하는 것은, 만약 이 가능성을 설명한다면, 어떤 결정론적 방법도 이 기준을 통과할 수 없기 때문이다.
- ^ 일관성은 참여를 의미하지만, 그 반대는 아니다. 예를 들어, 범위 투표는 참여도와 일관성을 준수하지만, 중간 등급은 참여를 만족시키고 일관성을 상실한다.
- ^ Woodall, Douglas (December 1994), "Properties of Preferential Election Rules", Voting Matters (3)
- ^ Small, Alex (August 22, 2010), Geometric construction of voting methods that protect voters' first choices, arXiv:1008.4331, Bibcode:2010arXiv1008.4331S
- ^ Jump up to: a b c Anti-plurality, 쿰스와 도지슨:동등하게 상장되지 않은 대안의 가능한 순위 apportioning에 의해;예를 들어, 투표 한 을 절단한 선호도를 받는 경우이고, B=C12{\displaystyle{\tfrac{1}{2}로}}한 을 계산된다;B.C와 12{\displaystyle{\tfrac{1}{2}}}<>를 사용하여 가정 된다면 C>b.만약 이러한 방법이 아닌 것으로 가정한다. 잘린 기본 설정을 수신하면 나중에 해를 끼치지 않고 도움말을 사용할 수 없다.
- ^ 투표 제한 지정은 투표권을 나눠 가진 다수당 구성원이 소수자 임명을 개별적으로 결정할 수 없는 경우에만 기술적으로 가능하다.
- ^ Diss, Mostapha; Doghmi, Ahmed (2016). "Multi-winner scoring election methods: Condorcet consistency and paradoxes". Public Choice. 169 (1–2): 97–116. doi:10.1007/s11127-016-0376-x. ISSN 0048-5829. S2CID 73721191.
- ^ Jump up to: a b c Hansen, Jeremy A (2014). "Comparing Approval At-Large to Plurality At-Large in Multi-Member Districts". Conference: Fifth International Workshop on Computational Social Choice.
- ^ Jump up to: a b 에이미, 더글러스 J; 투표함 뒤: 투표 시스템 시민 안내서, 페이지 120 ISBN 0275965864


 유권자 수입니다. 그는 예상대로 보르다 카운트가 가장 정확하다는 것을 알아내면서 이 모델에 따라 평가를 수행했다.
유권자 수입니다. 그는 예상대로 보르다 카운트가 가장 정확하다는 것을 알아내면서 이 모델에 따라 평가를 수행했다.