중위수 유권자 정리

Median voter theorem

중간 투표자 정리는 [1]던컨 블랙이 1948년에 제시한 순위 우선 투표와 관련된 제안이다.유권자와 정책이 1차원 스펙트럼을 따라 분포되고 유권자가 근접한 순서대로 대안을 순위를 매긴다면, 콘도르세트 기준을 충족하는 투표 방법은 중앙 유권자에 가장 가까운 후보를 선출할 것이라고 명시되어 있다.특히 두 가지 옵션 중 과반수 찬성으로 가결된다.

그 정리는 공공 선택 경제학과 통계 정치학과 연관되어 있다.Partha Dasgupta와 Eric Maskin은 그것이 Condorcet [2]기준에 기초한 투표 방법에 대한 강력한 정당성을 제공한다고 주장했다.플로트의 다수 법칙 균형 정리는 이것을 2차원으로 확장한다.

느슨하게 관련된 주장은 [3]해롤드 호텔링에 의해 일찍이 제기되었다.이것은 진정한 정리가 아니며 중앙 투표자 이론 또는 중앙 투표자 모델로 더 잘 알려져 있다.대의제 민주주의에서는 정치인들이 중앙 [4]유권자의 시선으로 수렴할 것이라고 한다.

정리의 진술 및 증명

후보 C는 중위수 유권자 M에 가장 가깝습니다.

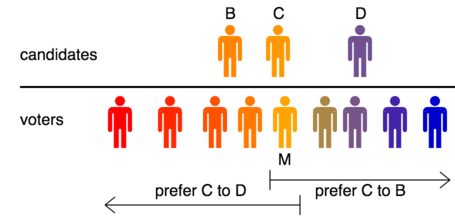
홀수 수의 유권자와 최소 두 명의 후보가 있다고 가정하고 의견이 스펙트럼에 따라 분산된다고 가정합니다.각 유권자는 유권자와 가장 가까운 후보가 첫 번째 선호도를 받고 다음으로 가까운 후보가 두 번째 선호도를 받는 등 근접한 순서대로 후보 순위를 매긴다고 가정합니다.그리고 중간 투표자가 있는데, 우리는 그 혹은 그녀에 가장 가까운 후보가 선거에서 이길 것이라는 것을 보여줄 것이다.

증명 - 중간 투표자를 Marlene으로 합니다.그녀와 가장 가까운 후보에게 첫 번째 선호 투표가 주어질 것이다.이 후보가 찰스이고 그가 그녀의 왼쪽에 거짓말을 한다고 가정해 보자.그러면 마를렌과 그의 왼쪽 유권자(선거인단 과반수 포함)는 그의 오른쪽 모든 후보보다 찰스를, 마를렌과 그녀의 오른쪽 모든 유권자는 그의 왼쪽 모든 후보보다 찰스를 선호할 것이다.∎

Condorcet 기준은 유권자의 과반수에 의해 다른 모든 후보보다 선호되는 후보가 승리하는 것을 보장하는 투표 방법에 의해 충족되는 것으로 정의되며, 이는 Charles의 경우이다. 따라서 Charles는 Condorcet c를 만족시키는 방법을 사용하여 수행된 모든 선거에서 승리할 것이다.리터레이션

따라서 Condorcet 기준을 충족하는 모든 투표 방법에서 승자는 중간 투표자가 선호하는 후보가 될 것이다.이원적 결정의 경우 다수결은 기준을 충족하고, 다원적 투표의 경우 여러 방법이 기준을 충족한다(컨도르세트 방법 참조).

전제 조건

유권자 수가 짝수일 때도 이 정리가 적용되지만, 세부 사항은 어떻게 동점을 해결하느냐에 따라 달라진다.

선호도가 근접한 순서대로 캐스팅된다는 가정은 단순히 단일 [5]피크로만 말할 수 있다.

의견이 실제 노선을 따른다는 가정은 보다 일반적인 [6]토폴로지를 허용하기 위해 완화될 수 있다.

공간/원자가 모델: 각 후보자가 공간에서의 위치 외에도 원자가(매력)를 가지고 있다고 가정하고, 유권자 i가 후보 j를jij v – d의 내림차순으로 순위를 매긴다고 가정합니다. 여기서j v는 j의 원자가이고ij, d는 i에서 j까지의 거리입니다.중간 투표자 정리가 여전히 적용된다.중앙 투표자에 의해 투표된 후보자를 선출할 것이다.

역사

이 정리는 1948년 던컨 블랙에 의해 처음 제시되었다.그는 투표가 정치적 결정을 포함한 결정의 결과를 어떻게 결정하는지에 관한 경제 이론에서 큰 차이를 보았다고 썼다.블랙의 논문은 경제학이 투표 시스템을 어떻게 설명할 수 있는지에 대한 연구를 촉발시켰다.1957년 Anthony Downs는 그의 저서 An Economic Theory of [7]Democracy에서 중간 투표자 정리를 설명했다.

중앙 투표자 속성

1차원 공간 모델에서 중간 유권자에 가장 가까운 후보를 항상 선출한다면 투표 방식은 "1차원의 중간 유권자 속성"을 가지고 있다고 말할 것이다.우리는 중앙 투표자 정리를 모든 Condorcet 방법이 중앙 투표자 속성을 1차원으로 갖는다고 요약할 수 있다.

Condorcet 메서드는 다음과 같은 점에서 고유하지 않은 것으로 나타났습니다.Coombs의 방법은 Condorcet-consistent는 아니지만 그럼에도 불구하고 1차원에서 [8]중앙 투표자 속성을 충족한다.

둘 이상의 차원에 있는 분포로 확장

2차원의 중위수 유권자 정리

중앙 유권자 정리는 제한된 형태로 모든 차원의 유권자 의견 분포에 적용된다.둘 이상의 차원에 분포가 반드시 모든 방향의 중앙값을 갖는 것은 아니다('전방적 중앙값'이라고 할 수 있다). 그러나 가우스를 포함한 광범위한 회전 대칭 분포 클래스는 이러한 [9]종류의 중앙값을 가진다.유권자의 분포가 모든 방향에서 고유한 중앙값을 가지며, 유권자가 후보자를 근접한 순서대로 순위를 매길 때마다 중앙값 유권자 정리가 적용된다: 중앙값과 가장 가까운 후보는 모든 경쟁자보다 다수 선호도를 가지며, 중앙값 유권자 속성을 만족시키는 어떤 투표 방법으로든 선출된다.n.[10] (여기에서의 고유성은 단일 차원에서의 표본 크기의 홀수에 의해 보장되는 속성을 일반화한다.)

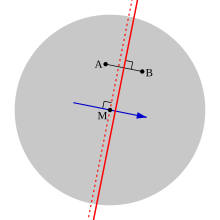
증거입니다. 회색 원반은 유권자 분포를 원 위에서 균일하게 나타내고 M은 모든 방향의 중앙값으로 나타냅니다.A와 B를 두 후보자로 하고, 그 중 A가 중위수에 더 가깝다고 가정합니다.그러면 B 위의 A 순위를 매기는 유권자는 정확히 빨간색 실선의 왼쪽(즉, 'A'쪽)에 해당하며, A가 B에서 M에 가깝기 때문에 중앙값도 이 선의 왼쪽에 있습니다.

모든 방향의 중위수가 없는 분포

M은 모든 방향의 중앙값이기 때문에 파란색 화살표로 표시된 방향의 1차원 중앙값과 일치합니다. 빨간색 실선에 수직입니다.따라서 파란색 화살표와 수직인 M을 통해 끊어진 빨간색 선을 그으면 유권자의 절반이 이 선의 왼쪽에 거짓말을 한다고 할 수 있습니다.그러나 이 선은 빨간색 실선의 왼쪽에 있기 때문에 유권자의 절반 이상이 A를 B보다 위에 랭크하게 됩니다.∎

따라서 모든 Condorcet 방법 및 Coombs는 전방위 중위수를 가진 유권자 분포를 위한 모든 차원의 중앙 유권자 속성을 충족한다.

모든 방향의 중앙값이 없는 유권자 분포를 구축하는 것은 쉽다.가장 간단한 예제는 두 번째 다이어그램의 1, 2, 3과 같이 직선으로 배치되지 않은 3개의 점으로 제한된 분포로 구성됩니다.각 유권자 위치는 특정 1차원 투영 집합의 중앙값과 일치합니다.A, B 및 C가 후보일 경우 '1'은 A-B-C, '2'는 B-C-A, '3'은 C-A-B에 투표하여 Condorcet 사이클을 제공합니다.이것은 맥켈비-스코필드 정리의 주제이다.

모든 방향의 중위수와 기하학적 중위수 사이의 관계

고유한 전방향 중위수가 존재할 때마다 Condorcet 투표 방식의 결과를 결정합니다.동시에 기하학적 중위수는 순위 선호 선거의 이상적인 승자로 식별될 수 있다(선거 시스템 비교 참조).따라서 둘 사이의 관계를 아는 것이 중요합니다.실제로 모든 방향의 중위수가 존재할 때마다(적어도 이산형 분포의 경우), 기하학적 중위수와 일치합니다.

보조 도표

Lema. 이산형 분포에 모든 방향의 중위수 M이 있을 때마다 M에 위치하지 않는 데이터 점은 A-M-A'가 직선인 특성(즉, A-M-A')과 함께 M의 양쪽에 균형 잡힌 쌍(A,A ')이 있어야 합니다.그림 A–M–A와는 2 다릅니다 0 ).

증명. [11]이 결과는 1967년 찰스 플로트에 의해 대수적으로 증명되었다.여기에서는 2차원의 모순에 의한 간단한 기하학적 증거를 제시합니다.

반대로 M을 모든 방향의 중앙값으로 가지지만 M과 일치하지 않는 점들이 균형 쌍으로 오지 않는i 점 A 집합이 있다고 가정합니다.다음으로 M에 있는 모든 점 및 M에 대한 균형 쌍을 제거할 수 있습니다. M은 모든 방향의 중앙값으로 유지되므로 M은 전방향 중앙값으로 유지됩니다.

나머지 점의 수가 홀수일 경우 M을 통해 쉽게 선을 긋고 대부분의 점이 M의 중앙값 속성과 모순되도록 할 수 있습니다.

2n과 같이 짝수이면 점 A, A, ...에1 라벨을 0 붙일 수 있습니다.M에 대해 시계 방향으로 정렬합니다(그림 참조).θ를 M –A에서 0 M –A까지의 n 호에 따른 각도라고 하자.그리고 θ < 180°일 경우, M을 통해 빨간색 선이 끊어진 것과 유사한 선을 그릴 수 있으며, M의 데이터 포인트가 대부분인 경우에는 M의 중앙값 특성에 반한다.그리고 θ = 180°이면 0 A와 n A는 균형쌍을 형성하여 다른 가정과 모순된다.∎

정리.이산형 분포에 모든 방향의 중위수 M이 있을 때마다 해당 기하학적 중위수와 일치합니다.

증명. 균형쌍의 점 P에서 데이터 점 세트까지의 거리 합계(A,A ')는 길이 A–P–A의 합계이다. 이 형태의 각 개별 길이는 선이 직선일 때 P에 대해 최소화되며, P가 M과 일치할 때 최소화된다.P에서 M에 위치한 데이터 지점까지의 거리 합계는 P와 M이 일치할 때 마찬가지로 최소화됩니다.따라서 P가 M과 일치할 경우 데이터 지점에서 P까지의 거리의 합이 최소화됩니다. »

호텔링의 법칙

좀 더 비공식적인 주장, 즉 중간 유권자 모델은 '호텔링의 법칙'이라고도 알려진 해롤드 호텔링의 '최소 차별화 원칙'과 관련이 있다.그것은 정치인들이 중간 유권자들이 차지하고 있는 위치, 또는 더 일반적으로 선거 시스템이 선호하는 위치로 끌린다고 말한다.그것은 [3]1929년 Hoteling에 의해 처음 제시되었다.

호텔링은 경제학자의 눈을 통해 정치인들의 행동을 보았다.그는 특정 상품을 파는 가게들이 종종 마을의 같은 지역에 모인다는 사실에 충격을 받았고, 이것을 정당의 융합으로 보았다.두 경우 모두 시장점유율을 극대화하기 위한 합리적인 정책일 수 있습니다.

인간의 동기 부여의 특징과 마찬가지로, 그것은 쉽게 예측할 수 없는 심리적 요인에 의존하며, 많은 예외의 대상이 된다.그것은 또한 투표 시스템에 달려있다: 정치인들은 선거 과정이 그렇게 하지 않으면 중간 투표자에게 수렴하지 않을 것이다.선거 과정이 도시 유권자보다 농촌에 더 비중을 둔다면, 정당들은 진정한 중앙값보다는 농촌을 선호하는 정책으로 수렴할 가능성이 높다.

중앙 투표자 정리 사용

이 정리는 특정 투표 시스템의 최적성(및 최적성에 대한 한계)을 밝히는 데 중요합니다.

Valerio Dotti는 보다 광범위한 응용 분야를 지적합니다.

중앙 유권자 정리는 정치 경제 문헌에서 매우 인기가 있음이 증명되었다.주요 이유는 투표 인구의 일부 특성과 정책 결과 사이의 관계에 대한 테스트 가능한 암시를 도출하기 위해 채택될 수 있으며, [10]정치적 과정의 다른 특징에서 추상화할 수 있기 때문이다.

그는 덧붙인다...

중간 투표 결과는 믿을 수 없을 정도로 다양한 질문에 적용되어 왔다.재분배 정책에 수입 부등식과 정부의 간섭의 크기 사이의 이민 정책을 과세 소득(Bassetto과 Benhabib, 2006년)[14]의 다른 tyes에 그 범위의(Razin과 Sadka, 1999년)[13]결정 인자의 연구(Meltzer, 리처드, 1981년)[12]은 관계의 예는 분석입니다.더.

「 」를 참조해 주세요.

레퍼런스

  1. ^ 던컨 블랙, "집단 의사결정의 원리에 대하여"(1948).
  2. ^ P. Dasgupta와 E.마스킨, "모든 사람들 중 가장 공정한 투표" (2004); "다수 지배의 견고성에 대하여" (2008)
  3. ^ a b Hotelling, Harold (1929). "Stability in Competition". The Economic Journal. 39 (153): 41–57. doi:10.2307/2224214. JSTOR 2224214.
  4. ^ Holcombe, Randall G. (2006). Public Sector Economics: The Role of Government in the American Economy. p. 155. ISBN 9780131450424.
  5. ^ 블랙의 논문을 참조해 주세요.
  6. ^ 베르노 부첼, "중앙 공간에서 콘도르세트의 우승자들" (2014년)
  7. ^ 앤서니 다운스, '민주주의의 경제이론'(1957)
  8. ^ B. 그로프만과 S. L. 펠드는 "당장 결선투표(즉시 결선투표)를 좋아한다면 쿰스 규칙에 대해 알아야 한다.)
  9. ^ 정확히 말하면, 유권자의 의견의 샘플 분포가 관련성이 있고, 이것은 반드시 별개의 것이다.연속 분포에 대한 결과는 큰 표본의 이상적 또는 근사적 행동을 나타내는 것으로만 관심이 있다.
  10. ^ a b Valerio Dotti의 논문 "다차원 투표 모델"(2016)을 참조하십시오.
  11. ^ C. R. 플로트, "다수 규칙 하에서의 균형과 그 가능성"(1967).
  12. ^ A. H. 멜처와 S. F. 리처드, "정부 규모의 합리적 이론" (1981)
  13. ^ A. 라진과 E.Sadka 「국제 자본 이동에 의한 이민과 연금」(1999년).
  14. ^ M. Bassetto와 J. Benhabib, "재분배, 세금, 그리고 중앙 유권자" (2006)

추가 정보

외부 링크