분자 궤도

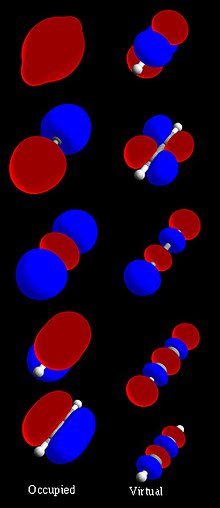
화학에서 분자 궤도란 분자 내 전자의 위치와 파동 같은 행동을 기술하는 수학적 함수다. 이 함수는 특정 지역에서 전자를 찾을 확률과 같은 화학적, 물리적 특성을 계산하는 데 사용할 수 있다. 원자 궤도 및 분자 궤도라는^[a] 용어는 Robert S에 의해 도입되었다. 1932년 멀리켄(Mulliken)은 일렉트로닉 궤도파 함수를 의미한다.^[2] 기초 수준에서 함수가 유의한 진폭을 갖는 공간의 영역을 설명하는 데 사용된다.

고립된 원자에서 궤도 전자의 위치는 원자 궤도라고 불리는 기능에 의해 결정된다. 복수의 원자가 화학적으로 결합하여 분자가 되면 전자의 위치가 전체적으로 분자에 의해 결정되기 때문에 원자 궤도가 결합하여 분자 궤도를 형성한다. 구성 원자의 전자는 분자 궤도를 차지한다. 수학적으로 분자 궤도는 분자의 원자핵 영역에 있는 전자에 대한 슈뢰딩거 방정식의 대략적인 해법이다. 그것들은 보통 분자의 각 원자의 원자 궤도나 혼합 궤도 또는 원자 그룹의 다른 분자 궤도들을 결합하여 만들어진다. 하트리-을 사용하여 정량적으로 계산할 수 있다.Fock 또는 자체 정합성 보장 필드(SCF) 메서드.

분자 궤도는 3가지 유형으로 구성되는 원자 궤도의 에너지보다 낮은 에너지를 가지고 있어 분자를 함께 지탱하는 화학적 결합을 촉진하는 결합 궤도, 구성 원자 궤도의 에너지보다 높은 에너지를 갖는 항균 궤도 궤도, 그래서 어금니의 결합을 반대한다.구성 원자 궤도와 동일한 에너지를 가지므로 분자의 결합에 영향을 미치지 않는 분자 및 비분자 궤도.

개요

분자 궤도(MO)는 그 궤도를 점유하고 있는 전자가 발견될 가능성이 있는 분자의 영역을 나타내기 위해 사용될 수 있다. 분자 궤도는 분자 원자핵의 전기장에 있는 전자에 대한 슈뢰딩거 방정식의 대략적인 해법이다. 그러나 이 방정식에서 직접 궤도를 계산하는 것은 너무 난해한 문제다. 대신에 그것들은 원자 속의 전자의 위치를 예측하는 원자 궤도들의 조합으로부터 얻어진다. 분자 궤도에는 분자의 전자 구성, 즉 한 쌍의 전자의 공간 분포와 에너지가 명시될 수 있다. 가장 일반적으로 MO는 원자 궤도(LCAO-MO 방법)의 선형 조합으로 표현되며, 특히 질적 또는 매우 근사적인 용도에서 그러하다. 그것들은 분자 궤도 이론을 통해 이해되는 분자 내 결합의 단순한 모델을 제공하는 데 있어 매우 중요하다. 계산 화학에서 오늘날 대부분의 방법은 시스템의 MO를 계산하는 것으로 시작한다. 분자 궤도(분자 궤도)는 핵에 의해 생성된 전기장에서 한 전자의 동작과 다른 전자의 일부 평균 분포를 설명한다. 두 전자가 같은 궤도를 차지하는 경우, 파울리 원리는 그들이 반대회전할 것을 요구한다. 필연적으로 이것은 근사치로서 분자 전자파 함수에 대한 매우 정확한 설명은 궤도를 가지고 있지 않다(구성 상호작용 참조).

분자 궤도는 일반적으로 분자 전체에서 소산된다. 더욱이 분자가 대칭 원소를 가지고 있다면, 비분자 분자 궤도는 이러한 대칭 중 어느 하나에 관해서도 대칭이거나 대칭적이지 않다. 즉, 분자 궤도 ψ에 대칭 연산 S(예: 반사, 회전 또는 반전)를 적용하면 분자 궤도 ψ에 변화가 없거나 수학적 기호를 역전시킨다. Sψ = ±ψ. 예를 들어 평면 분자에서 분자 궤도는 분자 평면의 반사와 관련하여 대칭(시그마) 또는 대칭(파이)이다. 만약 퇴보한 궤도 에너지를 가진 분자도 고려한다면, 분자 궤도는 분자의 대칭 그룹의 불가해한 표현을 위한 기초를 형성한다는 보다 일반적인 진술이 있다.^[4] 분자 궤도상의 대칭적 특성은 분자 궤도 이론의 본질적 특징이며, 공명이 공명을 감안하여 국부적인 전자 쌍으로 보는 발란스 결합 이론과 근본적으로 다르다는 것을 의미한다.

이러한 대칭적응 표준분자궤도와는 대조적으로, 국부적 분자궤도는 표준궤도에 특정한 수학적 변환을 적용함으로써 형성될 수 있다. 이 접근법의 장점은 궤도가 루이스 구조로 묘사된 분자의 "본드"와 더 밀접하게 일치한다는 것이다. 단점으로, 이러한 국부적 궤도들의 에너지 수준은 더 이상 물리적 의미를 갖지 않는다.(이 글의 나머지 부분에서의 논의는 표준적인 분자궤도에 초점을 맞출 것이다. 지역화된 분자 궤도에 대한 자세한 내용은 자연 결합 궤도 및 시그마-피와 동등한 오르비탈 모델을 참조하십시오.)

분자 궤도 형성

분자 궤도는 원자 궤도 사이의 허용되는 상호작용에서 발생하는데, 이는 원자 궤도의 대칭(집단 이론으로 결정)이 서로 호환될 경우 허용된다. 원자 궤도 상호작용의 효율성은 두 원자 궤도 사이의 겹침(두 궤도들이 서로 얼마나 잘 건설적으로 상호작용하는지를 측정하는 척도)으로부터 결정되는데, 이는 원자 궤도들이 에너지에서 가까울 경우 중요하다. 마지막으로 형성된 분자 궤도의 수는 분자를 형성하기 위해 결합되는 원자의 원자 궤도의 수와 같아야 한다.

질적 토론

분자 구조에 대한 부정확하지만 질적으로 유용한 논의를 위해 분자 궤도는 "원자 궤도 분자 궤도 방법의 선형 조합" 안사츠에서 얻을 수 있다. 여기서 분자 궤도는 원자 궤도의 선형 결합으로 표현된다.^[5]

원자 궤도(LCAO)의 선형 결합

분자 궤도는 프리드리히 헌트와^[6][7] 로버트 S에 의해 처음 소개되었다. 1927년과 1928년의 멀리켄^[8][9].^[10][11] 분자 궤도에 대한 원자 궤도의 선형 결합 또는 "LCAO" 근사치는 1929년 존 레나드 존스에 의해 도입되었다.^[12] 그의 획기적인 논문은 양자 원리에서 불소와 산소 분자의 전자 구조를 어떻게 도출하는지를 보여주었다. 분자 궤도 이론에 대한 이러한 질적 접근은 현대 양자 화학의 시작의 일부분이다. 원자 궤도(LCAO)의 선형 결합은 분자의 구성 원자들 간에 결합할 때 형성되는 분자 궤도를 추정하는 데 사용될 수 있다. 원자 궤도처럼 전자의 행동을 설명하는 슈뢰딩거 방정식은 분자 궤도에도 사용할 수 있다. 원자 궤도의 선형 결합 또는 원자파 기능의 합과 차이는 Hartree-에 근사적인 해결책을 제공한다.분자 슈뢰딩거 방정식의 독립 입자 근사치에 해당하는 포크 방정식. 단순한 이원자 분자의 경우, 얻은 파장 기능은 방정식으로 수학적으로 표현된다.

${\displaystyle \psi =c_{a}\psi _{a}+c_{b}\psi _{b}}$

${\displaystyle \psi ^{*}=c_{a}\psi _{a}-c_{b}\psi _{b}}}$

$여기$서 ${\$$displaystyle$ $\PSI$ ${\displaystyle {\}}^{}}$과 ${\$ $\$$psi$ $^{*}$은 본딩 및 항균 분자 궤도에 대한 분자파 기능이며$$,$$${\displaystyle {\psi }_{}}$ $a$는 $원자$ 및 b, $b{\displaystyle {}_{}}$$,$ ${\displaystyle c_{}}$에서 각각 원자파 기능이다$$.${\displaystyle c_{a}$ 및 c$$ ${\displaystyle b_{}}$ ${\$은(는) 조정 가능한 계수다$$. 이러한 계수는 개별 원자 궤도의 에너지와 대칭에 따라 양수 또는 음수일 수 있다. 두 원자가 서로 가까워질수록 원자 궤도가 겹치면서 전자 밀도가 높은 영역을 만들어내고, 그 결과 두 원자 사이에 분자 궤도가 형성된다. 원자들은 양극으로 충전된 핵들과 분자 궤도를 결합하는 음극으로 충전된 전자들 사이의 정전기적 인력에 의해 결합된다.^[13]

접합, 항균 및 비결합 MO

원자궤도가 상호작용할 때, 그 결과 분자궤도는 본딩, 항균, 비본딩의 세 가지 유형이 될 수 있다.

본딩 MO:

• 원자 궤도 사이의 결합 상호작용은 건설적인 (상내) 상호작용이다.
• 결합 MO는 그것들을 생산하기 위해 결합하는 원자 궤도보다 에너지가 낮다.

안티콘딩 MO:

• 원자 궤도 사이의 항응력 상호작용은 파괴적인 (위상 밖으로) 상호작용이며, 항응력 궤도 파동 기능이 상호 작용하는 두 원자 사이에 0인 결절면이다.
• MO를 억제하는 것은 그것들을 생산하기 위해 결합하는 원자 궤도보다 에너지가 더 높다.

비결합 MO:

• 비결합 MO는 호환 가능한 대칭이 없기 때문에 원자 궤도 사이의 상호작용이 없는 결과물이다.
• 비결합 MO는 분자 내 원자 중 하나의 원자 궤도와 동일한 에너지를 가질 것이다.

MO에 대한 시그마 및 파이 레이블

원자 궤도 사이의 상호작용 유형은 분자-궤도 대칭 라벨 σ(시그마), π(피), Δ(델타), φ(피), γ(감마) 등으로 더욱 분류할 수 있다. 이것들은 각각 원자 궤도 s, p, d, f, g에 해당하는 그리스 문자들이다. 관련 원자들 사이의 비핵화 축을 포함하는 결절면의 수는 σ MO의 경우 0, π의 경우 1개, Δ의 경우 2개, φ의 경우 3개, γ의 경우 4개이다.

σ 대칭

symmetry 대칭이 있는 MO는 두 개의 원자 s-오르비탈 또는 두 개의 원자 p-오르비탈의_z 상호작용에서 발생한다. MO는 두 개의 핵 중심인 핵융합 축을 결합하는 축과 관련하여 궤도상이 대칭인 경우 σ 대칭성을 갖는다. 이는 국제핵무기축에 대한 MO의 회전은 단계적 변화를 초래하지 않는다는 것을 의미한다. σ* 궤도, 시그마 항응궤도 역시 국제핵 축을 중심으로 회전할 때 동일한 위상을 유지한다. orbital* 궤도에는 핵 사이에 있고 국제핵 축에 수직인 단도면이 있다.^[14]

π 대칭

symmetry 대칭이 있는 MO는 두 원자 p_x 궤도 또는 p 궤도_y 중 하나의 상호작용에서 발생한다. MO는 궤도경사가 핵외 축에 대한 회전과 관련하여 비대칭인 경우 symmetry 대칭을 가질 것이다. 산자부가 국제비핵화 축에 대해 회전하면 단계적 변화가 생긴다는 의미다. 실제 궤도를 고려한다면, 비핵축이 들어 있는 한 개의 결절기가 있다.

π* 궤도, pi 항응궤도도 역시 국제핵 축을 중심으로 회전할 때 위상 변화를 일으킬 것이다. π* 궤도에는 핵 사이에 두 번째 목도면도 있다.^{[14][15][16][17]}

Δ 대칭

대칭이 Δ인 MO는 두 원자 d 또는_xy d 궤도들의_x²-y² 상호작용에서 발생한다. 이러한 분자 궤도는 저 에너지 d 원자 궤도를 포함하기 때문에 전환 금속 복합체에서 볼 수 있다. Δ 본딩 궤도에는 핵 내 축을 포함하는 두 개의 결절면이 있으며, Δ* 항균 궤도 역시 핵 사이에 세 번째 결절면이 있다.

φ 대칭

이론 화학자들은 f 원자 궤도의 중첩에 해당하는 phi 결합과 같은 고차 결합이 가능하다고 추측해 왔다. 피 결합을 함유하고 있다고 알려진 분자의 알려진 예는 없다.

게레이드와 언제레이드 대칭

반전 중심(중심대칭 분자)을 가진 분자의 경우 분자 궤도에 적용할 수 있는 대칭의 추가 라벨이 있다. 중심대칭 분자는 다음을 포함한다.

• 호몬핵 이아토믹스₂,
• 옥타헤드랄, EX₆
• 스퀘어 평면, EX₄.

비대칭 분자는 다음을 포함한다.

• 이성핵 이산화학, XY
• 사면체, EX₄

분자 내 대칭의 중심을 통해 뒤집으면 분자 궤도에서도 같은 위상이 나온다면, MO는 균등하게 독일어 단어에서 게레이드(g) 대칭을 갖는다고 한다. 분자 내 대칭의 중심을 통해 반전하여 분자 궤도 위상 변화를 일으키게 되면, MO는 독일어 단어에서 홀수를 의미하는 언게레이드(u) 대칭을 갖는다고 한다. σ 대칭 MO와 결합하는 MO의 경우 궤도(' + s')는 대칭인_g 반면, σ 대칭인 항균형 MO는_u 대칭인 반면, 궤도(' - s')의 역전은 대칭이기 때문에 대칭이다. πu기 때문에 대칭의 중심을 통해 역전을 위해, 이는 변화(두 p원자 궤도 서로 위상에 있지만 두 로우브 반대 증세가 있다)를 생산하게 된 모건 오닐 π-symmetry과 결합을 위해 궤도 있는 반면 반결합 모건 오닐과 π-symmetry은 πg기 때문에 역전을 통해 센터의 대칭에 없을 것을 배출하는 sig.n 변화(두 p 궤도는 위상별로 대칭이다).^[14]

MO 도표

MO 분석의 정성적 접근법은 분자 궤도도를 사용하여 분자 내 결합 상호작용을 시각화한다. 이러한 유형의 도표에서 분자 궤도는 수평선으로 표현된다. 선이 높을수록 궤도 에너지가 높아지며, 퇴보한 궤도들은 그 사이에 공간이 있는 동일한 레벨에 배치된다. 그런 다음, 분자 궤도에 놓일 전자를 하나씩 배치하여, 파울리 배제 원리와 헌트의 최대 다중성 법칙(반경 회전(반경 회전)을 가진 전자 2개만, 궤도당, 쌍을 만들기 전에 가능한 한 많은 수의 손상된 전자를 한 에너지 레벨에 배치한다. 더 복잡한 분자의 경우, 파동역학 접근법은 결합에 대한 질적 이해에서 효용을 상실한다(정량적 접근법을 위해 여전히 필요하지만). 일부 속성:

• 기본 궤도 집합은 분자 궤도 상호작용에 이용 가능한 원자 궤도를 포함한다. 원궤도는 결합 또는 항균일 수 있다.
• 분자 궤도의 수는 선형 팽창 또는 기본 집합에 포함된 원자 궤도의 수와 같다.
• 분자가 어느 정도 대칭을 이루면 (동일한 원자력을 가진) 퇴행된 원자 궤도를 (대칭적응형 원자궤도(SO)라고 하는) 선형 결합으로 묶어서 대칭적응형 선형 결합(SALC)으로 그룹을 기술하는 파동함수를 알 수 있다.
• 한 그룹 표현에 속하는 분자 궤도의 수는 이 표현에 속하는 대칭 적응 원자 궤도의 수와 같다.
• 특정 표현 내에서 대칭에 적응한 원자 궤도는 원자 에너지 수준이 더 가까우면 더 많이 섞인다.

합리적으로 단순한 분자에 대한 분자 궤도도를 구성하는 일반적인 절차는 다음과 같이 요약할 수 있다.

1. 분자에 포인트 그룹을 할당한다.

2. SALC의 모양을 찾아본다.

3. 각 분자 파편의 SALC를 에너지 증가의 순서로 배열하고, 먼저 s, p, d 궤도(그것들을 s < p < d) 순서에 넣는다)에서 기인하는지, 그 다음 그들의 국제핵 노드 수를 기록한다.

4. 두 조각에서 같은 대칭형의 SALC를 결합하고, N SALC에서 N 분자 궤도를 형성한다.

5. 상위 궤도들의 겹침과 상대 에너지의 고려로부터 분자 궤도들의 상대 에너지를 추정하고, 분자 궤도 에너지 수준 도표(궤도의 기원을 나타냄)에 수준을 그린다.

6. 상용 소프트웨어를 이용하여 분자 궤도 계산을 수행하여 이 질적 순서를 확인하고 수정하고 수정한다.^[18]

분자 궤도에서의 결합

궤도 퇴행성

분자 궤도는 같은 에너지를 가지면 퇴화한다고 한다. 예를 들어, 처음 10개 원소의 호몬핵 이원자 분자에서 p와_x p_y 원자 궤도에서 파생된 분자 궤도는 (저에너지) 2개의 퇴행된 본딩 궤도(저에너지)와 (고에너지) 2개의 퇴행된 항균 궤도(고에너지)를 낳는다.^[13]

이온 결합

두 원자의 원자 궤도 사이의 에너지 차이가 상당히 클 때, 한 원자의 궤도는 거의 전적으로 결합 궤도에 기여하고, 다른 원자의 궤도는 거의 전적으로 항균 궤도에 기여한다. 따라서 한 원자에서 다른 원자로 한 개 이상의 전자가 옮겨진 상황은 사실상 현실적이다. 이것을 (대부분) 이온 결합이라고 한다.

채권순번

분자의 결합 순서, 즉 결합의 수는 결합과 항균 분자 궤도에 있는 전자 수를 결합하여 결정할 수 있다. 본딩 궤도 안에 있는 한 쌍의 전자는 결합을 만드는 반면, 항균 궤도 안에 있는 한 쌍의 전자는 결합을 부정한다. 예를 들어, 궤도를 접합하는 데 8개의 전자가 있고, 항균하는 궤도를 가진 2개의 전자가₂ 있는 N은 결합 순서가 3인데, 이것은 3개의 결합을 구성한다.

본드 강도는 본드 순서에 비례한다. 즉, 더 많은 양의 본드는 더 안정적인 본드를 생산하며, 본드 길이는 그에 반비례한다. 강한 본드 순서는 더 짧다.

분자의 결합 순서가 양의 결합 순서를 갖는 요구 조건에는 드물게 예외가 있다. MO 분석 결과 Be의₂ 본드 순서는 0이지만, Be₂ 분자의 본드 길이 245pm, 본드 에너지는 10kJ/mol이라는 실험적인 증거가 있다.^[14][19]

호모·루모

가장 많이 점유된 분자궤도와 가장 낮은 미점유 분자궤도를 각각 호모(HOMO)와 루모(LUMO)라고 부르는 경우가 많다. HOMO와 LUMO의 에너지의 차이를 HOMO-LUMO 갭이라고 한다. 이 개념은 종종 문학에서 혼란의 문제로서 신중히 고려해야 한다. 그것의 값은 보통 기본 갭(이온화 전위와 전자 친화력의 차이)과 광학 갭 사이에 위치한다. 또, HOMO-LUMO 격차는 벌크 재료 대역 격차나 수송 격차와 관련될 수 있는데, 이는 보통 기본 격차보다 훨씬 작다.

예

호몬핵 디아토믹스

동핵핵 이원자 MO는 기본 집합에서 각 원자 궤도로부터 동일한 기여를 포함한다. 이는₂ H, He, Li에₂₂ 대한 동핵 이원자 MO 도표에 나타나 있으며, 모두 대칭 궤도를 포함하고 있다.^[14]

H₂

간단한 MO 예로서, 수소 분자₂ H(분자 궤도 다이어그램 참조)에 있는 전자를 두 원자가 H'와 H"라고 라벨을 붙인다. 최저 에너지 원자 궤도인 1s와 1s"는 분자의 대칭에 따라 변화하지 않는다. 그러나 다음과 같은 대칭이 각색된 원자 궤도에는 다음과 같은 대칭은 다음과 같다.

1s – 1s"	대칭 조합: 반사에 의해 부정되고 다른 연산에 의해 변경되지 않음
1s' + 1s"	대칭 조합: 모든 대칭 연산에 의해 변경되지 않음

대칭 조합(본딩 궤도라고 함)은 기본 궤도보다 에너지가 낮고, 대칭 조합(항균 궤도라고 함)은 더 높다. H₂ 분자는 두 개의 전자를 가지고 있기 때문에 둘 다 본딩 궤도 안으로 들어갈 수 있기 때문에 두 개의 자유 수소 원자보다 시스템이 더 낮은 에너지(Hence hense more stabilitary)를 갖게 된다. 이것을 공밸런스 결합이라고 한다. 본딩 순서는 본딩 전자 수에서 항균 전자 수를 뺀 값으로 2로 나눈 값이다. 이 예에서 본딩 궤도에는 2개의 전자가 있고 항균 궤도에는 1개의 전자가 없다; 본딩 순서는 1이며, 두 수소 원자 사이에는 단일 결합이 있다.

그₂

반면에 'He'와 'He'라고 표시된 원자를 가진 He의₂ 가상 분자를 생각해 보라. H와₂ 마찬가지로, 가장 낮은 에너지 원자 궤도는 1s와 1s"이며, 대칭 조정된 원자 궤도는 그렇게 하는 반면, 분자의 대칭에 따라 변형되지 않는다. 대칭 조합인 본딩 궤도(bonding arbital)는 기본 궤도보다 에너지가 낮고, 대칭 조합인 항응 궤도(antiboning arbital)는 더 높다. 발란스 전자가 두 개 있는₂ H와는 달리, 그는₂ 그 중립적인 지면 상태에 4개가 있다. 두 전자는 저에너지 본딩 궤도인 σ_g(1s)를 채우고, 나머지 두 전자는 고에너지 항균 궤도인 σ_u*(1s)를 채운다. 그러므로 분자 주위의 결과적인 전자 밀도는 두 원자 사이의 결합 형성을 지원하지 않는다; 원자들을 함께 고정시키는 안정된 결합이 없다면, 분자는 존재할 것으로 예상되지 않을 것이다. 그것을 바라보는 또 다른 방법은 두 개의 본딩 전자와 두 개의 항균 전자가 있다는 것이다. 따라서 본딩 순서는 0이고 본드는 존재하지 않는다(분자는 반데르발스 전위성에 의해 지지되는 하나의 바인딩 상태를 가지고 있다).^{[citation needed]}

리₂

Dilithium Li는₂ 두 Li 원자의 1s와 2s 원자 궤도(기본 설정)의 겹침으로부터 형성된다. 각 Li 원자는 상호작용을 위해 3개의 전자를 기여하며, 6개의 전자는 최저 에너지인 ,(1s), σ_gu*(1s), σ_g(2s)의 3개의 MO를 채운다. 결합순서에 대한 방정식을 이용하여 딜리튬은 결합순서가 1인 단일 결합순서가 있음을 알 수 있다.

노블 가스

He의₂ 가상 분자를 생각해 보면, 원자 궤도의 기본 집합은 H의₂ 경우와 같기 때문에, 우리는 결합 궤도와 항균 궤도가 모두 채워져 있기 때문에, 그 쌍에 에너지 이점이 없다는 것을 알게 된다. HheH는 약간의 에너지 이점이 있을 것이지만₂ H + 2 Hhe만큼 많지는 않기 때문에 분자는 매우 불안정하며 수소와 헬륨으로 분해되기 전에만 잠깐 존재한다. 일반적으로 우리는 He와 같은 완전한 에너지 껍데기를 가진 원자들이 다른 원자들과 거의 결합하지 않는다는 것을 발견한다. 단명 반데르발스 단지를 제외하면 알려진 고귀한 가스 화합물은 거의 없다.

헤테론핵 이산화학

동핵핵 이원자 분자의 MO는 상호 작용하는 각 원자 궤도로부터의 동일한 기여를 포함하고 있는 반면, 이핵 이질 분자의 MO는 서로 다른 원자 궤도 기여를 포함하고 있다. 이핵 디아토믹스에서 결합 또는 항균 궤도를 생성하기 위한 궤도 상호작용은 대칭과 궤도 에너지의 유사성에 의해 결정되는 원자 궤도 사이에 충분한 중복이 있는 경우에 발생한다.

HF

불화수소에서는 H 1s와 F 2s 궤도 사이에 HF가 겹치는 것은 대칭에 의해 허용되지만, 두 원자 궤도 사이의 에너지 차이는 그들이 상호 작용하여 분자 궤도 궤도를 만드는 것을 방해한다. H 1s와 F 2p_z 궤도 사이의 중첩 또한 대칭성이 허용되며, 이 두 개의 원자 궤도에는 작은 에너지 분리가 있다. 따라서, 그들은 상호작용하여 and과 ** MOs의 생성과 결합 순서 1의 분자를 만든다. HF는 비대칭 분자이기 때문에 대칭 레이블 g와 u는 분자 궤도에 적용되지 않는다.^[20]

양적 접근법

분자 에너지 수준에 대한 정량적 값을 얻기 위해서는 구성 상호작용(CI) 팽창이 전체 CI 한계로 빠르게 수렴되도록 분자 궤도를 가져야 한다. 그러한 기능을 얻기 위한 가장 일반적인 방법은 Hartree–이다.분자 궤도를 Fock 연산자의 고유 기능으로 표현하는 Fock 방법. 보통 원자핵을 중심으로 한 가우스 함수의 선형 결합으로 분자 궤도를 확장함으로써 이 문제를 해결한다(원자 궤도와 기본 집합(화학)의 선형 결합 참조). 이러한 선형 결합의 계수에 대한 방정식은 로타 방정식이라고 알려진 일반화된 고유값 방정식이며, 사실상 하트리-하트리의 특정한 표현이다.포크 방정식. 스파르타 등 MO의 양자화학 계산을 수행할 수 있는 프로그램들이 다수 있다.

간단한 설명에 따르면 분자 궤도 에너지는 발란스 궤도를 위한 자외선 광전자 분광법과 핵심 궤도를 위한 X선 광전자 분광법을 통해 얻을 수 있다고 한다. 그러나 이러한 실험들이 하나의 전자를 제거함으로써 발생하는 분자와 이온들 사이의 에너지 차이인 이온화 에너지를 측정하기 때문에 이것은 부정확하다. 이온화 에너지는 대략적으로 구피만의 정리에 의해 궤도 에너지와 연결된다. 이 두 값 사이의 합치는 일부 분자에 대해서는 근접할 수 있지만, 다른 경우에는 매우 빈약할 수 있다.

메모들

참조

Wikiquote는 다음과 관련된 인용구를 가지고 있다: 분자 궤도