다사이클릭군

대수구조 → 그룹 이론 집단 이론
기본 개념 부분군 정규 부분군 지수군 (세미-)직접 생산물 집단동형성 알맹이 이미지 직합 화환제품 소박한 유한한 무한의 연속의 승수의 첨가제의 순환의 아벨의 강하제의 무광의 해결할 수 있는 액션 집단 이론 용어집 그룹 이론 주제 목록
유한군 유한단순군 분류 순환의 교대로 거짓말형 산발적인 코치의 정리 라그랑주의 정리 실로우의 정리 홀의 정리 p그룹 초등 아벨 군 프로베니우스 군 슈르 승수 대칭군n S 클라인 4그룹 V 디헤드랄군n D 쿼터니온 그룹 Q 다사이클릭 그룹 Dicn
이산형 그룹 선반 정수(${\displaystyle \mathbb{}}$ ${\$ $\}$ ) 자유군 모듈 그룹 PSL(2, $Z{\displaystyle \mathbb{}}$ ${\$ $\}$ ) SL(2, $Z{\displaystyle \mathbb{}}$ ${\$ $\}$ ) 산술군 격자 쌍곡군
위상학 및 눕기 그룹 솔레노이드 원 일반 선형 GL(n) 특수 선형 SL(n) 직교 O(n) 유클리드 E(n) 특수직교 SO(n) 유니터리 U(n) 특수 유니터리 SU(n) Simplectic Sp(n) G2 F4 E6 E7 E8 로렌츠 푸앵카레 컨포멀 차이점형성 루프 무한 치수 리 그룹 오(∞) SU(수) Sp(()
대수군 선형대수군 환원군 아벨 품종 타원곡선
v t

이 글은 검증을 위해 인용구가 추가로 필요하다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 기사를 개선할 수 있도록 도와주십시오. 공급되지 않은 재료는 도전하여 제거할 수 있다. 출처 찾기: "Dycyclic group" – 뉴스 · 신문 · 책 · 학자 · JSTOR (2010년 2월) (이 템플릿 메시지를 제거하는 방법과 시기 학습)

집단 이론에서, dicyclic 그룹(통지 Dic 또는_n4n Q,^[1] ,n, 2,22)^[2]은 순서 4n(n > 1)의 특정한 종류의 비아벨리아 그룹이다.순서 2n의 주기적 그룹에 의한 순서 2의 주기적 그룹을 확장한 것으로, 이 주기적 이름을 부여한다.그룹의 정확한 순서에 대한 표기법에서 이 확장은 다음과 같이 표현할 수 있다.

${\displaystyle 1\to C_{2n}\to {\mbox{Dic}_{n}\to 1.,}$

보다 일반적으로 순서-2 원소를 가진 유한 아벨리아 집단을 고려할 때, 다사이클릭 집단을 정의할 수 있다.null

정의

각 정수 n > 1에 대해 dicyclic group Dic은 다음에_n 의해 생성된 단위 쿼터의 하위 그룹으로 정의될 수 있다.

${\displaystyle {\frac{i\pi}a&=e^{\frac {i\pi }{n}}}\coses {\frac {\pi }{n}}\x&=j\end}}}}}}}$

좀 더 추상적으로 말하면, 다사이클릭^[3] 그룹 Dic을_n 다음과 같은 프리젠테이션으로 그룹으로서 정의할 수 있다.

${\displaystyle \operatorname {Dic} _{n}=\x\mid a^{2n}=1,\x^{2}=a^{n},\x^{1}ax=a-1}ax={-1}\-1}\rigle .\,\!}$

이 정의에서 따라야 할 몇 가지 사항:

• ${\displaystyle x^{4}=1}$
• ${\displaystyle x^{2}a^{k}=a^{k+n}=a^{k}x^{2}}$
• $j{\displaystyle }$=${\displaystyle }$± ${\displaystyle 1}$ ${\displaystyle$ j$=\pm 1$인 경우 $x{\displaystyle {}^{}}$ ${\displaystyle j^{}}$ ${\displaystyle a^{}}$= ${\displaystyle {}^{}}$- ${\displaystyle k^{}}$ ${\displaystyle x^{}}$ j ${\$ x$^{j}a^{k}=a^{-k}x^{j}}}}}}}$
• ${\displaystyle a^{k}x^{-1}=a^{k-n}a^{n1}x^{1}=a^{k-n}x^{2}x^{1}=a^{k-n}x}x}x}$

따라서 Dic의_n 모든 요소는 도끼로^kj 고유하게 작성할 수 있으며, 여기서 0 ≤ k < 2n과 j = 0 또는 1이다.곱셈 규칙은 다음에 의해 주어진다.

• ${\displaystyle a^{k}a^{m}=a^{k+m}}$
• ${\displaystyle a^{k}a^{m}x=a^{k+m}x}$
• ${\displaystyle a^{k}xa^{m}=a^{k-m}x}$
• ${\displaystyle a^{k}xa^{m}x=a^{k-m+n}}$

Dic이_n 4n 오더를 가지고 있는 것에 따른다.^[3]null

n = 2일 때, dicyclic 그룹은 쿼터니온 그룹 Q와 이형화된다.보다 일반적으로 n이 2의 검정력일 때, dicyclic 그룹은 일반화된 quaternion 그룹에 이형성이 된다.^[3]null

특성.

각 n > 1에 대해 dicycyclic group은_n 비아벨라니아계 순서 4n의 그룹이다.(dic₁ 그룹은 dicyclic으로 간주되지 않는 c 순환 그룹이다₄.)null

A = ⟨a⟩을 a에 의해 생성되는_n Dic의 부분군으로 한다.그러면 A는 순서 2n의 주기적인 그룹이므로 [Dic_n:A] = 2. 지수 2의 부분군으로서 자동적으로 정상 부분군이 된다.지수 그룹 Dic_n/A는 순서 2의 순환 그룹이다.

Dic은_n 해결할 수 있다; A는 정상이고, 아벨이 되는 것 자체가 해결 가능하다.null

이항 2면체군

다이사이클릭 그룹은 이진 다면체 그룹 - 스핀 그룹 스핀(3)의 하위 그룹인 핀₋(2)의 하위 그룹 중 하나이며, 이러한 맥락에서 바이너리 이면체 그룹으로 알려져 있다.null

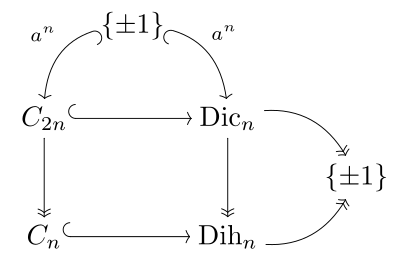
이항 주기_2n 그룹 C, 주기 그룹 C_n, 순서 2n의 이항 주기 그룹 Dih와의_n 연결은 오른쪽 다이어그램에 나타나 있으며, 핀 그룹에 해당하는 도표를 평행하게 한다.Coxeter는 2진법 그룹을 and2,n⟩로 쓰고, 2진법 주기 그룹인 ⟨n⟩로 쓴다.

다발성 순환 그룹과 다이헤드 그룹 사이에는 표면적인 유사성이 있다; 둘 다 기초 순환 그룹의 일종의 "거울링"이다.그러나² dihedral 그룹의 표시는 x = a가ⁿ 아닌² x = 1이 될 것이고, 이것은 다른 구조를 산출한다.특히 Dic은_n A와 ⟨x⟩의 반간접 제품이 아니며, A와 ⟨x⟩은 사소한 것이 아니기 때문이다.null

다사이클릭 그룹은 고유한 비자발성(즉, 순서 2의 요소), 즉² x = a를ⁿ 가진다.이 요소는 Dic의_n 중앙에 위치한다는 점에 유의하십시오.실제로 중심은 신분적 요소와 x만으로² 구성되어 있다. Dic의_n 프레젠테이션에 관계² x = 1을 더하면 dihedral 그룹 dih의_n 프레젠테이션을 얻으므로, 지수 그룹 dic_n/<x²>는 dih에_n 이형성이 있다.null

단위 쿼터니온 그룹부터 쿼터니온과 공간 회전에 설명된 3차원 회전 그룹까지 자연적인 2대 1 동형성이 있다.다사이클릭 그룹이 단위 쿼터 안에 내장될 수 있기 때문에, 이 동형상 아래 그것의 이미지가 무엇인지 물어볼 수 있다.해답은 이음대칭군 디흐일_n 뿐이다.이러한 이유로 다육성 그룹은 바이너리 다이헤드 그룹으로도 알려져 있다.다사이클릭 그룹은 Dih에_n 대한 부분군 이형성을 포함하지 않는다.null

핀₋(2) 대신 핀(2)을₊ 사용한 아날로그 사전 이미지 구조는 다시클릭 그룹이 아닌 또 다른 다이헤드 그룹인 디흐를_2n 산출한다.null

일반화

A를 아벨 그룹으로 하고, A에 특정한 원소 y를 순서 2와 함께 가지도록 하라.그룹 G는 A와 추가 요소 x에 의해 생성되는 경우 Dic(A, y)로 쓰여진 일반화된 다육성 그룹이라고 하며, 그 외에도 우리는 [G:A] = 2, x² = y, 그리고 A에 대한 모든 A에 대해 xax⁻¹ = a를⁻¹ 가진다.

짝수 순서의 순환 그룹에 대해서는 항상 순서 2의 고유한 요소가 있기 때문에, 우리는 순환 그룹이 일반화된 다순환 그룹의 특정한 형태에 불과하다는 것을 알 수 있다.null

참고 항목

• 이항 다면군
• 이항 주기 그룹, nnn, 순서 2n
• 이진 사면군, 2T = =2,3,3⟩,^[2] 순서 24
• 이진 팔면군, 2O = 22,3,4⟩,^[2] 순서 48
• 2진수 이코사헤드 그룹, 2I = 2,3,5⟩,^[2] 주문 120

참조

외부 링크

• GroupNames의 Dicyclic 그룹