확률분포
확률 이론 과 통계 에서 지수 분포 는 포아송 점 공정 에서 사건 사이의 시간의 확률 분포 , 즉 사건이 일정한 평균 속도로 연속적이고 독립적으로 발생하는 과정이다. 그것은 감마 분포 의 특별한 경우다. 기하 분포 의 연속적인 아날로그로, 기억력 이 없다는 핵심 특성을 가지고 있다. 포아송 점 공정의 분석에 사용되는 것 외에도 다양한 다른 맥락에서 찾아볼 수 있다.
지수 분포는 지수 분포 의 등급과 같지 않은데, 지수 분포는 그 구성원의 하나로 지수 분포를 포함 하지만 정규 분포 , 이항 분포 , 감마 분포, 포아송 분포 등을 포함하는 확률 분포의 큰 등급이다.
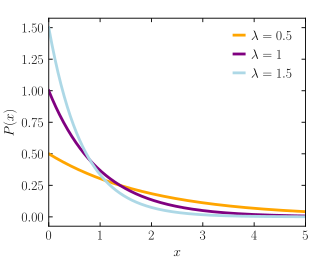
정의들 확률밀도함수 지수 분포의 확률밀도함수 (pdf)는
f ( x ; λ ) = { λ e − λ x x ≥ 0 , 0 x < 0. {\displaystyle f(x;\buffsda )={\preason{case}\buffda e^{-\buffda x}&x\geq 0,\0&x<0. \end{case}}} 여기서 λ > 0은 분포의 모수로, 흔히 속도 모수 라고 한다. 분포는 [0, ∞] 간격에서 지원한다. 랜덤 변수 X 에 이 분포가 있으면 X ~Exp(λ )
지수 분포는 무한의 차이 를 보인다.
누적분포함수 누적 분포 함수 는 다음과 같이 지정된다.
F ( x ; λ ) = { 1 − e − λ x x ≥ 0 , 0 x < 0. {\displaystyle F(x;\lambda )={\begin{base}e^{-\lambda x}&x\geq 0,\0&x<0. \end{case}}} 대체 파라메트리징 지수 분포는 때때로 척도 모수 β =3
f ( x ; β ) = { 1 β e − x / β x ≥ 0 , 0 x < 0. F ( x ; β ) = { 1 − e − x / β x ≥ 0 , 0 x < 0. {\displaystyle f(x;\filency )={\frac {1}{\frac{1}{\filency }e^{-x/\filency }&x\0&x<0. \end{case}\qquad \qquad \qquad F(x;\beta )={\begin}1-e^{-x/\beta }&x\geq 0,\0&x<0. \end{case}}}
특성. 평균, 분산, 모멘트 및 중위수 평균은 확률 질량 중심, 그것 이 첫 번째 순간이다. 지수 분포 랜덤 변수 X 의 평균 또는 기대 값 은 다음과 같다. 비율 매개변수 λ
E [ X ] = 1 λ . {\displaystyle \operatorname {E} [X]={\frac {1}{\lambda }}. }
아래 에 제시된 예에 비추어 볼 때, 이것은 일리가 있다: 만약 당신이 시간당 평균 2의 비율로 전화를 받는다면, 당신은 매 통화마다 30분을 기다릴 것을 기대할 수 있다.
X 의 분산 은 다음과 같다.
VAR [ X ] = 1 λ 2 , {\displaystyle \operatorname {Var} [X]={\frac {1}{\lambda ^{2}}},} 따라서 표준 편차는 평균과 동일하다.
n ∈ N {\ displaystyle n\in \mathb {N} 순간 은 다음과 같다
E [ X n ] = n ! λ n . {\displaystyle \operatorname {E} \left[X^{n}\right]={\frac {n! }}{\lambda ^{n}}. }
n central {\ displaystyle n\in \mathb {N} 모멘트 는 다음과
μ n = ! n λ n = n ! λ n ∑ k = 0 n ( − 1 ) k k ! . {\displaystyle \mu _{n}={\frac {!n}{\boda ^{n}}={\frac {n! }}{\lambda ^{n}}\sum _{k=0}^{n}{\frac {(-1)^{k}}}{k! }}.} 여기서 !n 은 n 의 하위 요인이다.
X 의 중위수 는 다음과 같다.
m [ X ] = ln ( 2 ) λ < E [ X ] , {\displaystyle \operatorname {m} [X]={\frac {\ln(2)}{\lambda }}}<\operatorname {E}[X],} 여기서 ln 은 자연 로그(naturalgative logarithm . 따라서 평균과 중위수의 절대 차이는 E [ X ] − m [ X ] = 1 − ln ( 2 ) λ < 1 λ = σ [ X ] , {\displaystyle \좌측 \operatorname {E} \좌측[X\우측]-\operatorname {m} \좌측[X\우측]\우측 ={\frac {1-\ln(2)}{\lambda }}}{\lambda }}}}}{\operatorname {X,}
중앙값 과 중앙값의 불평등 에 따라
무메모리 기하급수적으로 분포 된 랜덤 변수 T는 관계를 준수한다.
PR ( T > s + t ∣ T > s ) = PR ( T > t ) , ∀ s , t ≥ 0. \displaystyle \Pr \왼쪽(T)s+t\mid T>s\오른쪽)=\Pr(T)\qquad \forall s,t\geq 0.}
이는 보완적 누적분포함수 를 고려함으로써 알 수 있다.
PR ( T > s + t ∣ T > s ) = PR ( T > s + t ∩ T > s ) PR ( T > s ) = PR ( T > s + t ) PR ( T > s ) = e − λ ( s + t ) e − λ s = e − λ t = PR ( T > t ) . {\displaystyle {\begin}\Pr \left(T>s+t\mid T>s\right)&={\pr(T>s+t\cap T>s\right){\Pr \left(T) }}\\\[4pt]&={\frac {\pr \좌(T)+t\우)}{\Pr \좌(T) }}\\[4pt]&={\frac {e^{-\lambda (s+t)}}{e^{-\lambda s}\[4pt]&=e^{-\lambda t}\\\[4pt]&=\Pr(T)} \end{정렬}}}
T 가 어떤 초기 시간에 상대적인 사건이 발생하기 위한 대기 시간으로 해석되는 경우, 이 관계는 T 가 어떤 초기 시간 s 에 걸쳐 사건을 관찰하지 못하여 조건화된다면, 나머지 대기 시간의 분포는 원래의 무조건적인 분포와 동일하다는 것을 의미한다. 예를 들어 사건이 30초 후에도 발생하지 않은 경우, 발생이 최소 10초 이상 더 걸릴 조건부 확률 은 최초 시간 이후 10초 이상 사건을 관측할 수 있는 무조건적인 확률과 동일하다.
지수 분포와 기하 분포 는 기억력 이 없는 유일한 확률 분포 다.
지수 분포는 필연적으로 일정한 고장률 을 갖는 유일한 연속 확률 분포이기도 하다.
퀀텀스 Exp(수치 )에 대한 퀀텀 함수(누적 분포 함수 역)는 다음과 같다.
F − 1 ( p ; λ ) = − ln ( 1 − p ) λ , 0 ≤ p < 1 {\displaystyle F^{-1}(p;\lambda )={\frac {-\ln(1-p)}{\lambda }}{\lambda }},\qquad 0\leq p<1}
따라서 사분위수 는 다음과 같다.
제1 사분위수: ln(4/3)/mits 중위수 : ln(2)/medium 제3 사분위수: ln(4)/mits 그리고 결과적으로 사분위간 범위 는 ln(3)/mit 이다.
쿨백-라이블러 발산 e λ 0 {\ displaystyle e^{\lambda nats 에서의 지시된 Kullback-Leibler 차이 ("다음 {\ displaystystyle lambda 0}})
Δ ( λ 0 ∥ λ ) = E λ 0 ( 통나무를 하다 p λ 0 ( x ) p λ ( x ) ) = E λ 0 ( 통나무를 하다 λ 0 e − λ 0 x λ e − λ x ) = 통나무를 하다 ( λ 0 ) − 통나무를 하다 ( λ ) − ( λ 0 − λ ) E λ 0 ( x ) = 통나무를 하다 ( λ 0 ) − 통나무를 하다 ( λ ) + λ λ 0 − 1. {\displaystyle {\begin{aigned}\delta (\lambda _{0}\병렬 \lambda )&=\mathb {E} _{\lambda _{0}\log {\frac {p_{\lambda }}}}\right) \\&=\mathb {E} _{\lambda_{0}\왼쪽(\log {\frac {\lambda _{0}e^{-\lambda _{0}x}}{\lambda e^{-\lambda x}}\rig}\rig) \\&=\log(\lambda _{0})-\log(\lambda )-(\lambda _{0}-\lambda )E_{\lambda _{0}}(x)\\&=\log(\lambda _{0})-\log(\lambda )+{\frac {\lambda }{\lambda _{0}}}-1. \end{정렬}}}
최대 엔트로피 분포 지지 [0, μ] 와 평균 μ 를 갖는 모든 연속 확률 분포 중에서 μ = 1/μ 를 갖는 지수 분포는 미분 엔트로피 가 가장 크다. 즉, 0보다 크거나 같은 랜덤 변수 X 에 대한 최대 엔트로피 확률 분포 로서 E[X ]가 고정되어 있다.[1]
지수 랜덤 변수의 최소 분포 X 1 , …, X 는n 속도 매개변수 λ 1 , …, λ 과n 함께 기하급수적으로 분포된 랜덤 변수를 갖도록 한다. 그러면
분 { X 1 , … , X n } {\displaystyle \min \{X_{1},\dotsc ,X_{n}\right\}}} 또한 매개변수와 함께 기하급수적으로 분포한다. λ = λ 1 + ⋯ + λ n . {\displaystyle \lambda =\lambda _{1}+\dotsb +\lambda _{n}. }
이는 보완적 누적분포함수 를 고려함으로써 알 수 있다.
PR ( 분 { X 1 , … , X n } > x ) = PR ( X 1 > x , … , X n > x ) = ∏ i = 1 n PR ( X i > x ) = ∏ i = 1 n 생략하다 ( − x λ i ) = 생략하다 ( − x ∑ i = 1 n λ i ) . {\displaystyle {\begin{aigned}&\Pr \left(\min\{X_{1},\dotsc ,X_{n}\}}>x\right) \\={}&\Pr \left(X_{1})x,\dotsc ,X_{n}}x\right) \\={}&\prod _{i=1}^{n}\Pr \left(X_{i}}>x\right) \\={}&\prod _{i=1}^{n}\exp \exp \reftx\lambda _{i}\right)=\exp \reftx\sum _{i=1}^{n}\i}\right). \end{정렬}}}
최소값을 달성하는 변수의 지수는 범주형 분포에 따라 분포한다.
PR ( k ∣ X k = 분 { X 1 , … , X n } ) = λ k λ 1 + ⋯ + λ n . {\displaystyle \Pr \left(k\mid X_{k}=\min\{X_{1},\dotsc ,X_{n}\}\right)={\frac {\lambda _{k}{1}+\lambda +\lambda _{n}}. }
I argmin i { n } X …, X {\displaystyle =\operatorname {argmin} _{i\in 1,\dotsb ,n\}\{X_{1},\dotsc ,X_{n 그러면.
PR ( I = k ) = ∫ 0 ∞ PR ( X k = x ) PR ( X i ≠ k > x ) d x = ∫ 0 ∞ λ k e − λ k x ( ∏ i = 1 , i ≠ k n e − λ i x ) d x = λ k ∫ 0 ∞ e − ( λ 1 + ⋯ + λ n ) x d x = λ k λ 1 + ⋯ + λ n . {\displaystyle{\begin{정렬}(I=k)&,=\int _ᆮ^ᆯ\Pr(X_{k}=x)\Pr(X_{i\neq k}>))\,dx\\&,=\int _{0}^{\infty}\lambda _{k}e^{-\lambda_{k}x}\left(\prod_{i=1,i\neq k}^{n}e^{-\lambda_{나는}x}\right)dx\\&, =\lambda _{k}\int _{0}^{\infty}e^{-\left(\lambda_{1}+\dotsb +\lambda_{n}\right)x}dx\\&, ={\frac{\lambda_{k}}{\lambda_{1}.+\dotsb +\lambda_{ n}.\end{aigned}}
참고:
맥스. { X 1 , … , X n } {\displaystyle \max\{X_{1},\dotsc ,X_{n}\}}} 기하급수적으로 분포되지 않는다.[2]
i.i.d. 지수순 통계량의 합동 모멘트 X 1 X n {\ displaystyle X_{1},\dotsc ,X_{n}} 속도 변수 exponential으로 n {\displaystyle n} 독립적 이고동일하게 분포 된 지수 랜덤 변수가 되도록 X 1 X {\ displaystyle X_{(1)},\dotsc ,X_{(n)}}}}} 주문 통계 를 나타내도록 For i < j {\displaystyle i<j} E [ X ( i ) X ( j ) ] {\displaystyle \operatorname {E} \left[X_{(i)}X_{(j)}\right]} X ( i ) {\displaystyle X_{(i)}} X ( j ) {\displaystyle X_{(j)}}
E [ X ( i ) X ( j ) ] = ∑ k = 0 j − 1 1 ( n − k ) λ E [ X ( i ) ] + E [ X ( i ) 2 ] = ∑ k = 0 j − 1 1 ( n − k ) λ ∑ k = 0 i − 1 1 ( n − k ) λ + ∑ k = 0 i − 1 1 ( ( n − k ) λ ) 2 + ( ∑ k = 0 i − 1 1 ( n − k ) λ ) 2 . {\displaystyle {\begin{aligned}\operatorname {E} \left[X_{(i)}X_{(j)}\right]&=\sum _{k=0}^{j-1}{\frac {1}{(n-k)\lambda }}\operatorname {E} \left[X_{(i)}\right]+\operatorname {E} \left[X_{(i)}^{2}\right]\ \&=\sum _{k=0}^{j-1}{\frac {1}{(n-k)\lambda }}\sum _{k=0}^{i-1}{\frac {1}{(n-k)\lambda }}+\sum _{k=0}^{i-1}{\frac {1}{((n-k)\lambda )^{2}}}+\left(\sum _{k=0}^{i-1}{\frac {1}{(n-k)\lambda }}\right)^{2}. \end{정렬}}}
이는 총체적 기대 와 무기억 재산의 법칙 을 발동함으로써 알 수 있다.
E [ X ( i ) X ( j ) ] = ∫ 0 ∞ E [ X ( i ) X ( j ) ∣ X ( i ) = x ] f X ( i ) ( x ) d x = ∫ x = 0 ∞ x E [ X ( j ) ∣ X ( j ) ≥ x ] f X ( i ) ( x ) d x ( 그 이후 X ( i ) = x ⟹ X ( j ) ≥ x ) = ∫ x = 0 ∞ x [ E [ X ( j ) ] + x ] f X ( i ) ( x ) d x ( 기억없는 재산으로. ) = ∑ k = 0 j − 1 1 ( n − k ) λ E [ X ( i ) ] + E [ X ( i ) 2 ] . {\displaystyle{\begin{정렬}\operatorname{E}\left[X_{(나는)}X_{(j)}\right]&,=\int _{0}^{\infty}\operatorname{E}\left[X_{(나는)}X_{(j)}{(나는)X_ \mid}=x\right]f_{X_{(나는)}}())\,dx\\&,=\int _{x=0}^{\infty}x\operatorname{E}\left[X_{(j)}\mid X_{(j)}\geqx\right]f_{X_{(나는)}}())\,dx&,&\left({\textrm{이후}}~X_{(나는)}X_{(j)}\geq x\ri =x\implies.ght)) \&=\int _{x=0}^{\infit }x\왼쪽[\operatorname {E} \left[X_{(j)\right]+x\f_{X_{x(i)}}}}}{x(x)\,dx&\left({textemoryless 속성}\right)\right)\\\\\\\\\right)\\\\\\\\\\\\\\ \&=\sum _{k=0}^{j-1}{\frac {1}{{(n-k)\lambda }}}}\e} \좌측[X_{(i)}\우측]\operatorname {E} \e} \좌측[X_{(i)^{2}\우측]. \end{정렬}}}
첫 번째 방정식은 전체 기대의 법칙 에서 따온 것이다. 두 번째 방정식은 일단 X i displaystyle X_{( i )}= x } ≥ x {\displaystyle X_{(j)}\geq } . The third equation relies on the memoryless property to replace E [ X ( j ) ∣ X ( j ) ≥ x ] {\displaystyle \operatorname {E} \left[X_{(j)}\mid X_{(j)}\geq x\right]} E [ X ( j ) ] + x {\displaystyle \operatorname {E} \left[X_{(j)}\right]+x}
두 개의 독립 지수 랜덤 변수의 합 두 개의 독립 랜덤 변수 합계의 확률 분포 함수(PDF)는 개별 PDF의 콘볼루션 이다. If X 1 {\displaystyle X_{1}} X 2 {\displaystyle X_{2}} λ 1 {\displaystyle \lambda _{1}} λ 2 , {\displaystyle \lambda _{2},} Z = X 1 + X 2 {\displaystyle Z=X_{1}+X_{2}} 에 의해 주어지다
f Z ( z ) = ∫ − ∞ ∞ f X 1 ( x 1 ) f X 2 ( z − x 1 ) d x 1 = ∫ 0 z λ 1 e − λ 1 x 1 λ 2 e − λ 2 ( z − x 1 ) d x 1 = λ 1 λ 2 e − λ 2 z ∫ 0 z e ( λ 2 − λ 1 ) x 1 d x 1 = { λ 1 λ 2 λ 2 − λ 1 ( e − λ 1 z − e − λ 2 z ) 만일 λ 1 ≠ λ 2 λ 2 z e − λ z 만일 λ 1 = λ 2 = λ . {\displaystyle{\begin{정렬}(z)&, =\int _{-\infty}^{\infty}f_{X_{1}}(x_{1})f_{X_{2}}(z-x_{1})\,dx_{1}\\&,=\int _{0}^{z}\lambda _{1}e^{-\lambda_{1}x_{1}}\lambda _ᆹe^ᆺ(z-x_{1})}\,dx_{1}\\&, =\lambda _{1}\lambda _{2}e^{-\lambda_{2}z}\int _{0}^{z}e^{(\lambda_{2}-\lambda_{1})x_{1}}\,dx_{1}\\&, ={\begin{경우}{\dfrac.{\lambda_{1}\l ambda _{2}}{\lambda _{2}-\lambda _{1}}}\left(e^{-\lambda _{1}z}-e^{-\lambda _{2}z}\right)&{\text{ if }}\lambda _{1}\neq \lambda _{2}\\[4pt]\lambda ^{2}ze^{-\lambda z}&{\text{ if }}\lambda _{1}=\lambda _{2}=\lambda . \end{case}\end{aigned}}} 이 분포의 엔트로피는 닫힌 형태로 이용할 수 있다: λ λ {\ displaystyle \lambda _{1}>\lambda _{2}}( H ( Z ) = 1 + γ + ln ( λ 1 − λ 2 λ 1 λ 2 ) + ψ ( λ 1 λ 1 − λ 2 ) , {\displaystyle {\begin{aligned}H(Z)&=1+\gamma +\ln \left({\frac {\lambda _{1}-\lambda _{2}}{\lambda _{1}\lambda _{2}}}\right)+\psi \left({\frac {\lambda _{1}}{\lambda _{1}-\lambda _{2}}}\right),\end{aligned}}} 여기서 γ {\displaystyle \gamma} 오일러-마스케로니 상수 , and( ) {\displaystyle \psi(\cdot )} 디감마 함수 다.[3]
동일한 비율 모수의 경우, 결과는 형상 2와 파라미터 λ {\displaystyle \lambda ,} Erlang 분포 로, 감마 의 특수한 경우다.
관련 분포 X 라플라스 μ β {\ displaystyle \sim \operatorname {Laplace} \left(\mu ,\beta ^{-1}\right)} X ~ Pareto(1, λ)인 경우 로그(X ) ~ Exp(λ)를 기록한다.X ~ SkewLogistic (skewLogistic)인 경우 log (1 e Exp θ {\displaystyle \log \left(1+e^{-X}\right)\sim \operatorname {Exp}(\ta )}. Xi ~U (0, 임이 있는 n → ∞ n 분 ( X 1 , … , X n ) ∼ 엑스포 ( 1 ) {\displaystyle \lim _{n\put }n\min \left(X_{1},\ldots,X_{n}\right)\sim \operatorname {Exp}(1)} 지수 분포는 척도 베타 분포 의 한계: 임이 있는 n → ∞ n 베타. ( 1 , n ) = 엑스포 ( 1 ) . {\displaystyle \lim _{n\to \infit }n\operatorname {Beta}(1,n)=\operatorname {Exp}(1) } 지수 분포는 타입 3 Pearson 분포 의 특별한 경우다. X ~Ex(Exp) 및 X i i k X ~ Exp λ k {\ displaystyle kX\sim \operatorname {Exp} \left({\frac {\lambda }}{k}\right 1 + X ~ BenktanderWeibull (λ, 1)은 지수 분포가 잘리는 것으로 감소한다. 케X ~파레토 (k , λ)e−X ~ 베타 (λ, 1)1 / k e X PowerLaw (k , λ) X Rayley 1 2 λ {\ displaystyle {\sqrt{X}\sim \operatorname {Rayley} \left({\frac {1}{\sqrt{2\lambda }}}\rieight Rayleigh 분포 X Weibull 1 λ 1 {\ displaystyle X\sim \operatorname {Weibull} \left({\frac }{\lambda }}, 오른쪽 Weibull 분포 X 2 ∼ 바이불 ( 1 λ 2 , 1 2 ) {\displaystyle X^{2}\sim \operatorname {Weibull} \좌측({\frac {1}{\lambda^{2}}},{\frac {1}{2}}\우측)}} μ - β 로그(λX) ~ 쿰벨 (μ, β). ⌊ X ⌋ 기하학적 1 - e {\ displaystyle \lfloor \rfloor \sim \operatorname {Geometh} \좌측(1-e^{-\lambda }\right , 기하학적 분포 ,... ⌈ X ⌉ 기하학 1 e λ {\ displaystyle \lceil rceil \sim \operatorname {Geometer} \좌측(1-e^{-\lambda }\right Y ~ Erlang(n , λ) 또는 Y γ n, 1 λ {\ displaystyle \sim \Gamma \left(n, \frac {1}{\lambda }}}\right) 경우 X 1 Pareto 1 {\frac {x} Y}}+1\sim \operatorname {Pareto}(1,n)} 또한 λ ~ 감마 (k , θ) (모양, 척도 모수))인 경우 X 의 한계 분포는 감마 혼합물 인 로맥스 (k , 1/43)이다. λX1 1 - λY2 2 ~ 라플라스(0, 1) minn {X 1 , ..., X} ~ Exp(exp1 + ... + λn 또한 λi X 1 + ⋯ + X k = ∑ i X i ∼ {\displaystyle X_{1}+\cdots +X_{k}=\sum _{i}X_{i}\sim } Erlang (k , λ) = Gamma (k , λ−1 ) = Gamma(k , λ) (in (k , θ) and (α, β) parametrization, respectively) with an integer shape parameter k.Xi j −1 ).X 도i Xi Xi X j {\ displaystyle {\frac {X_{i}{X_{i}+X_{j}}}}}~ U (0, 1) Z = λ i X i λ j X j {\displaystyle Z={\frac {\lambda _{i}X_{i}}{\lambda _{j}X_{j}}}} f Z ( z ) = 1 ( z + 1 ) 2 {\displaystyle f_{Z}(z)={\frac {1}{(z+1)^{2 λ i λ j {\ displaystyle {\frac {\lambda _{i}}{\lambda {j 신뢰구간 을 구하는 데 사용할 수 있다.또한 λ = 1인 경우: μ β 로그 (e X e X 로지스틱 분포 ( μ β {\displaystyle \mu -\beta \log \left({\frac {e^{-X}}}{1-E^{-X}}\right)\sim \operatorname {로지스틱 분포 . μ − β 통나무를 하다 ( X i X j ) ∼ 로지스틱 ( μ , β ) {\displaystyle \mu -\beta \log \left({X_{i}}{X_{j}}\right)\sim \operatorname {Logistic}(\mu ,\beta )} μ - σ 로그(X ) ~ GEV(μ, σ, 0). Further if Y ∼ Γ ( α , β α ) {\displaystyle Y\sim \Gamma \left(\alpha ,{\frac {\beta }{\alpha }}\right)} X Y ∼ K ( α , β ) {\displaystyle {\sqrt {XY}}\sim \operatorname {K} (\alpha ,\beta )} K-distribution ) 또한 λ = 1/2이면 X χ2 2 ; 즉 X 는 자유도가 2인 카이 제곱 분포 를 가진다. 따라서 다음과 같다. 엑스포 ( λ ) = 1 2 λ 엑스포 ( 1 2 ) ∼ 1 2 λ χ 2 2 ⇒ ∑ i = 1 n 엑스포 ( λ ) ∼ 1 2 λ χ 2 n 2 {\displaystyle \operatorname {Exp} (\lambda )={\frac {1}{2\lambda }}\operatorname {Exp} \left({\frac {1}{2}}\right)\sim {\frac {1}{2\lambda }}\chi _{2}^{2}\Rightarrow \sum _{i=1}^{n}\operatorname {Exp} (\lambda )\sim {\frac {1}{2\lambda }}\chi _{2n}^{2}} If X ∼ Exp ( 1 λ ) {\displaystyle X\sim \operatorname {Exp} \left({\frac {1}{\lambda }}\right)} Y ∣ X {\displaystyle Y\mid X} Poisson(X ) then Y ∼ Geometric ( 1 1 + λ ) {\displaystyle Y\sim \operatorname {Geometric} \left({\frac {1}{1+\lambda }}\right)} geometric distribution ) Hoyt 분포는 지수 분포와 아크사인 분포 로부터 얻을 수 있다.기타 관련 분포:
통계적 추론 아래에서 랜덤 변수 X 가 비율 매개 변수 λ과 함께 기하급수적으로 분포한다고 가정하고, x1 x n {\ displaystyle x_{1},\dotsc ,x_{n}} X 에서 추출한 n개 의 독립 표본이며x ¯'{\ displaystystyle {\x} .
모수 추정 λ에 대한 최대우 도 추정기는 다음과 같이 구성된다.
변수에서 추출한 독립적이고 동일한 분포 의 표본 x = (x 1 , …, x n 우도 함수 는 다음과 같다.
L ( λ ) = ∏ i = 1 n λ 생략하다 ( − λ x i ) = λ n 생략하다 ( − λ ∑ i = 1 n x i ) = λ n 생략하다 ( − λ n x ¯ ) , {\displaystyle L(\lambda )=\prod _{i=1}^{n}\lambda \exp(-\lambda x_{i})=\lambda ^{n}\exp \left(-\lambda \sum _{i=1}^{n}x_{i}\right)=\lambda ^{n}\exp \left(-\lambda n{\overline {x}}\right),}
여기서:
x ¯ = 1 n ∑ i = 1 n x i {\displaystyle {\overline{x}}={\frac {1}{n}\sum _{i=1}^{n}x_{i}}}}} 표본 평균이다.
우도함수의 로그의 파생상품은 다음과 같다.
d d λ ln L ( λ ) = d d λ ( n ln λ − λ n x ¯ ) = n λ − n x ¯ { > 0 , 0 < λ < 1 x ¯ , = 0 , λ = 1 x ¯ , < 0 , λ > 1 x ¯ . {\displaystyle {\frac {d}{d\lambda }}\ln L(\lambda )={\frac {d}{d\lambda }}\left(n\ln \lambda -\lambda n{\overline {x}}\right)={\frac {n}{\lambda }}-n{\overline {x}}\ {\begin{cases}>0,&0<\lambda <{\frac {1}{\overline {x}}},\\[8pt]=0,&\lambda ={\frac {1}{\overline {x}}},\\[8pt]<0,&\lambda >{\frac {1}{\overline {x}}}. \end{case}}}
따라서 속도 모수에 대한 최대우 도 추정치는 다음과 같다.
λ ^ 술래잡기를 하다 = 1 x ¯ = n ∑ i x i {\displaystyle {\widehat{\wideda }}{\text{mle}}={\frac {1}{\frac {1}{x}}={\frac {n}{\sum _{i}x_{i}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}
x {\ displaystyle {\overline{x}} 1 \ displaystyle lambda } [4] [5] 하지만 , 이 ator , {\displaysty lambda } 편향 추정기가 아니다.
λ ^ mle {\ displaystyle {\widehat {\lambda }_{\text{mle}}
b ≡ E [ ( λ ^ 술래잡기를 하다 − λ ) ] = λ n − 1 {\displaystyle b\equiv \operatorname {E} \왼쪽({\widehatt{\lambda }}}{\lambda }}}{\lambda \right)={\frac {\lambda }{n-1}} 편향-편향 최대우도 추정기 를 산출한다. λ ^ 술래잡기를 하다 ∗ = λ ^ 술래잡기를 하다 − b ^ . {\displaystyle {\widehat{\wideda}}{\text{mle}^{*}={\widehat{\wideda}-{\widehat{b}}}. }
예상 오차 제곱의 대략적인 최소값 표본이 세 개 이상 있다고 가정해 보십시오. 기대 평균 제곱 오차 최소화를 추구하는 경우(참조: 최대우도 추정치(즉, 우도 추정치에 대한 승수 보정)와 유사한 치우침-분산 절충 :
λ ^ = ( n − 2 n ) ( 1 x ¯ ) = n − 2 ∑ i x i {\displaystyle {\widehat{\i}}}=\왼쪽-frac {n-2}{n}\오른쪽)\왼쪽-frac {1}{\bar{x}\오른쪽)={\frac {n-2}{\sum _{i}x_{i}}}}}}}}}}}}}}}}}}\prec.
이는 역감마 분포 의 평균과 분산에서 도출된다. Inv-Gamma n λ {\textstyle {\mbox{Inv-Gamma}}(n,\lambda )}. [6]
피셔 정보 속도 매개 변수 λ{\displaystyle \lambda }) I λ ){\displaystyle I}(\lambda Fisher 정보 는 다음과 같이 제공된다
I ( λ ) = E [ ( ∂ ∂ λ 통나무를 하다 f ( x ; λ ) ) 2 λ ] = ∫ ( ∂ ∂ λ 통나무를 하다 f ( x ; λ ) ) 2 f ( x ; λ ) d x {\displaystyle {\mathcal {I}(\lambda )=\operatorname {E}\왼쪽[\왼쪽] \leftda\frac {\recHB{\recHBFFA}}}{\recHBFFF}}}{2}\\\logda \right]=\right \eftda \right}}\reftda \}^{2}f(x;\da )
배포 및 해결을 위한 연결:
I ( λ ) = ∫ 0 ∞ ( ∂ ∂ λ 통나무를 하다 λ e − λ x ) 2 λ e − λ x d x = ∫ 0 ∞ ( 1 λ − x ) 2 λ e − λ x d x = λ − 2 . {\displaystyle {\mathcal {I}}(\lambda )=\int _{0}^{\infty }\left({\frac {\partial }{\partial \lambda }}\log \lambda e^{-\lambda x}\right)^{2}\lambda e^{-\lambda x}\,dx=\int _{0}^{\infty }\left({\frac {1}{\lambda }}-x\right)^{2}\lambda e^{-\lambda x}\,dx=\lambda ^{-2}. }
이것은 지수 분포의 각 독립 표본이 알 수 없는 비율 매개변수 λ {\displaystyle \lambda } .
신뢰구간 지수 분포의 속도 모수에 대한 100(1 - α)% 신뢰 구간은 다음을 통해 주어진다.[7]
2 n λ ^ χ 1 − α 2 , 2 n 2 < 1 λ < 2 n λ ^ χ α 2 , 2 n 2 {\displaystyle {\frac {2n}{{\widehat {\lambda }}\chi _{1-{\frac {\alpha }{2}},2n}^{2}}}<{\frac {1}{\lambda }}<{\frac {2n}{{\widehat {\lambda }}\chi _{{\frac {\alpha }{2}},2n}^{2}}}} 또한 다음과 같다. 2 n x ¯ χ 1 − α 2 , 2 n 2 < 1 λ < 2 n x ¯ χ α 2 , 2 n 2 {\displaystyle {\frac {2n{\overline {x}}}{\chi _{1-{\frac {\alpha }{2}},2n}^{2}}}<{\frac {1}{\lambda }}<{\frac {2n{\overline {x}}}{\chi _{{\frac {\alpha }{2}},2n}^{2}}}} 여기서 χ 은2 p ,v 자유도가 vdegree 인 키 제곱 분포 의 100(p ) ³ 이고, n은 표본 내 간격 시간의 관측치 수이며, x-bar는 표본 평균이다. 정확한 간격 끝점에 대한 간단한 근사치는 χ 2 p ,v 이 근사치는 95% 신뢰 구간에 대해 다음과 같은 값을 제공한다. λ 더 낮게 = λ ^ ( 1 − 1.96 n ) λ 상부의 = λ ^ ( 1 + 1.96 n ) {\displaystyle {\begin{aligned}\lambda _{\text{lower}}&={\widehat {\lambda }}\left(1-{\frac {1.96}{\sqrt {n}}}\right)\\\lambda _{\text{upper}}&={\widehat {\lambda }}\left(1+{\frac {1.96}{\sqrt {n}}}\right)\end{aligned}}}
이 근사치는 최소한 15~20개의 원소를 포함하는 표본에 대해 허용될 수 있다.[8]
베이시안 추론 지수 분포의 이전의 결합 은 감마 분포 (이 중 지수 분포는 특수한 경우)이다. 감마 확률 밀도 함수의 다음과 같은 매개변수가 유용하다.
감마 ( λ ; α , β ) = β α Γ ( α ) λ α − 1 생략하다 ( − λ β ) . {\displaystyle \operatorname {Gamma}(\lambda ;\alpha ,\beta )={\frac {\beta ^{\beta }}{\Bambda (\alpha )}}{\lambda -1}\expa. }
그런 다음 후방 분포 p는 위에서 정의한 우도 함수와 감마 선행으로 표현할 수 있다.
p ( λ ) ∝ L ( λ ) Γ ( λ ; α , β ) = λ n 생략하다 ( − λ n x ¯ ) β α Γ ( α ) λ α − 1 생략하다 ( − λ β ) ∝ λ ( α + n ) − 1 생략하다 ( − λ ( β + n x ¯ ) ) . {\displaystyle {\begin{aligned}p(\lambda )&\propto L(\lambda )\Gamma (\lambda ;\alpha ,\beta )\\&=\lambda ^{n}\exp \left(-\lambda n{\overline {x}}\right){\frac {\beta ^{\alpha }}{\Gamma (\alpha )}}\lambda ^{\alpha -1}\exp(-\lambda \beta )\\&\propto \lambda ^{(\alpha +n)-1}\exp(-\lambda \left(\beta +n{\overline {x}}\right)). \end{정렬}}}
이제 후방 밀도 p 는 누락된 정규화 상수까지 지정되었다. 감마 pdf의 형태를 가지고 있기 때문에 쉽게 채울 수 있으며, 다음과 같은 것을 얻을 수 있다.
p ( λ ) = Γ ( λ ; α + n , β + n x ¯ ) . {\displaystyle p(\lambda )=\Gamma(\lambda ;\alpha +n,\beta +n{\overline{x}). }
여기서 하이퍼 파라미터 α 는 이전 관측치의 수로 해석할 수 있고, β 는 이전 관측치의 합으로 해석할 수 있다. 여기서의 후방 평균은 다음과 같다.
α + n β + n x ¯ . {\displaystyle {\frac {\preason +n}{\n1}{n1}{x}}}. }
발생 및 적용 사건발생 지수 분포는 동종 포아송 공정 에서 도착 간 시간의 길이를 설명할 때 자연적으로 발생한다.
지수 분포는 기하 분포 의 연속적인 상대적 분포로 볼 수 있으며, 이는 이산 공정이 상태를 변화시키는 데 필요한 베르누이 시행 횟수를 설명한다. 이와는 대조적으로 지수 분포는 연속적인 공정이 상태를 변경하기 위한 시간을 설명한다.
실제 상황에서는 일정 비율(또는 단위 시간당 확률)의 가정이 거의 충족되지 않는다. 예를 들어, 수신 전화의 비율은 하루의 시간에 따라 다르다. 그러나 근무일 중 오후 2시부터 4시까지와 같이 비율이 대략 일정한 시간 간격에 초점을 맞추면 지수 분포를 다음 전화가 도착할 때까지의 좋은 대략적인 모델로 사용할 수 있다. 유사한 주의사항이 대략적으로 기하급수적으로 분포된 변수를 산출하는 다음 예에 적용된다.
방사성 입자가 소멸 될 때까지의 시간 또는 가이거 카운터 의 클릭 사이의 시간 다음 전화 통화 전까지 걸리는 시간 감소된 형태의 신용위험 모델링에서 채무불이행(회사채무 보유자에 대한 지급시)까지 소요 시간 지수 변수를 사용하여 특정 사건이 단위 길이당 일정한 확률로 발생하는 상황(예 : DNA Strand의 돌연변이 간 거리 또는 특정 도로의 노면차단 간 거리)을 모델링할 수도 있다.
대기열 이론 에서, 시스템 내 에이전트의 서비스 시간(예: 은행 출납원이 고객에게 서비스를 제공하는 데 걸리는 시간 등)은 기하급수적으로 분산된 변수로 모델링되는 경우가 많다. (예를 들어, 도착이 독립적이고 동일하게 분포되어 있는 경우 고객의 도착도 포아송 분포 에 의해 모델링됨) 여러 독립적인 업무의 연속이라고 생각할 수 있는 프로세스의 길이는 에를랑 분포 (여러 독립적인 지수 분포 변수의 합계의 분포)를 따른다. 신뢰성 이론 과 신뢰성 공학도 지수 분포를 광범위하게 이용한다. 이 분포의 기억력 욕조 곡선 의 일정한 위험률 부분을 모델링하기에 적합하다. 또한 신뢰성 모델에서 고장률 을 추가하는 것이 매우 쉽기 때문에 매우 편리하다. 그러나 지수 분포는 유기체 또는 기술 장치의 전체 수명을 모형화하는 데 적합하지 않다. 여기서 "고장률"은 일정하지 않기 때문이다. 즉, 매우 젊은 시스템 및 매우 오래된 시스템에서 더 많은 고장이 발생한다.
물리학 에서 일정한 온도 에서 기체 를 관찰하고 균일한 중력장 에서 압력 을 관찰하면, 다양한 분자의 높이도 기압 공식 으로 알려진 대략적인 지수 분포를 따른다. 이것은 아래에 언급된 엔트로피 속성의 결과물이다.
수문학 에서 지수 분포는 일일 강우량 및 하천 유량 월별 및 연간 최대값과 같은 변수의 극단값을 분석하는 데 사용된다.[10]
파란색 그림은 지수 분포를 연간 최대 일일 강수량의 순위에 맞추는 예를 보여 주며, 이항 분포 를 바탕으로 한 90% 신뢰 벨트 도 보여준다. 강우 데이터는 누적 빈도 분석 의 일부로 위치를 표시 하여 나타낸다. 수술실 관리에서, 일반적인 업무 콘텐트가 없는 수술 범주의 수술 기간 분포(응급실, 모든 종류의 수술 포함)
예측 알 수 없는 지수 분포에서 데이터 점 의 표본을 관측한 공통 작업은 이러한 표본을 사용하여 동일한 출처의 미래 데이터에 대한 예측을 하는 것이다. 미래 표본에 대한 일반적인 예측 분포는 속도 매개변수 rate에 대한 적절한 추정치를 지수밀도 함수에 연결함으로써 형성된 소위 플러그인 분포다. 추정의 일반적인 선택은 최대우도 원리에 의해 제공되는 것이며, 이를 사용하면 관측된 표본 n +1x = (x 1 , ..., xn )에 대한 예측 밀도가 다음과 같이 산출된다.
p M L ( x n + 1 ∣ x 1 , … , x n ) = ( 1 x ¯ ) 생략하다 ( − x n + 1 x ¯ ) {\displaystyle p_{\rm {ML}(x_{n+1})\mid x_{1},\ldots,x_{n}}=\좌측({\frac {1}{\overline {x}\오른쪽)\exp \좌측(-{\frac_{n+1}{x}}}}\우측)
베이지안 접근방식은 추정된 모수의 불확실성을 고려한 예측 분포를 제공하지만, 이는 이전 모수의 선택에 결정적으로 좌우될 수 있다.
주관적인 베이지안식 접근법에 따라 발생하는 사전 선택 문제에서 자유로운 예측 분포는 다음과 같다.
p C N M L ( x n + 1 ∣ x 1 , … , x n ) = n n + 1 ( x ¯ ) n ( n x ¯ + x n + 1 ) n + 1 , {\displaystyle p_{\rm {CNML}}(x_{n+1})\mid x_{1},\ldots,x_{n}={\frac {n^{n+1}\왼쪽({\overline {x}\right) ^{n}}{{n}}{\refline {x}+x_{n+1}\right)^{n+1},}
라고 볼 수 있는
구심점 수량 x 1 x "{\ displaystyle{x_{n+1}/{\overline{x}} 신뢰 분포 ; [11] profile possibility, parameter likelihood을 x 와n +1λ 의 공동우도로부터 최대로 제거하여 얻은 profile possibility;[12] 비정보적 Jeffreys 이전 1/2 을 사용하여 얻은 베이지안 예측 후방 분포 정보 이론적 고려사항에서 조건부 정규화 최대우도([13] 예측 분포의 정확도는 비율 모수를 가진 실제 지수 0 분포와 표본 x 에 기초한 예측 분포 사이의 거리 또는 차이를 사용하여 측정할 수 있다. Kullback-Leibler 차이점 은 두 분포 간의 차이에 대한 매개변수화 자유 측정값이다. Δ(Δ 0 p )가 속도 매개변수 λ 을0 가진 지수 p 와 예측 분포 p 사이의 Kullback-Leibler 차이를 나타내도록 하는 것은 다음과 같은 것을 보여줄 수 있다.
E λ 0 [ Δ ( λ 0 ∥ p M L ) ] = ψ ( n ) + 1 n − 1 − 통나무를 하다 ( n ) E λ 0 [ Δ ( λ 0 ∥ p C N M L ) ] = ψ ( n ) + 1 n − 통나무를 하다 ( n ) {\displaystyle {\begin{aligned}\operatorname {E} _{\lambda _{0}}\left[\Delta (\lambda _{0}\parallel p_{\rm {ML}})\right]&=\psi (n)+{\frac {1}{n-1}}-\log(n)\\\operatorname {E} _{\lambda _{0}}\left[\Delta (\lambda _{0}\parallel p_{\rm {CNML}})\right]&=\psi (n)+{\frac {1}{n}}-\log(n)\end{aligned}}}
여기서, 속도 매개변수 λ 0 ∈0, ∞), ψ ( · )를 갖는 지수 분포에 대해 기대치를 취하며, digamma 함수가 된다. CNML 예측 분포가 모든 표본 크기 n 0 에 대한 평균 Kullback-Leibler 분산 측면에서 최대우도 플러그인 분포보다 엄격히 우수하다는 것은 분명하다.
계산 방법 지수 변수 생성 지수변수를 생성하는 개념적 으로 매우 간단한 방법은 역변환 표본 추출에 기초한다: 단위 간격(0, 1)의 균일한 분포 에서 추출한 랜덤변수 U 를 고려할 때 변수는 다음과 같다.
T = F − 1 ( U ) {\displaystyle T=F^{-1}(U)}
지수 분포를 가지고 있다. 여기서 F 는−1 계량 함수 로서 정의된다.
F − 1 ( p ) = − ln ( 1 − p ) λ . {\displaystyle F^{-1(p)={\frac {-\ln(1-p)}{\lambda }}. }
또한 U 가 (0, 1)일 경우 1 - U 가 균일하다. 이는 다음과 같이 지수 변동을 발생시킬 수 있다는 것을 의미한다.
T = − ln ( U ) λ . {\displaystyle T={\frac {-\ln(U)}{\lambda }}. }
지수 변동을 생성하는 다른 방법은 Knuth와[14] [15]
정렬 루틴을 사용하지 않고 미리 정렬된 지수 변수의 집합을 생성하는 빠른 방법도 사용할 수 있다.[15]
참고 항목 참조 ^ Park, Sung Y.; Bera, Anil K. (2009). "Maximum entropy autoregressive conditional heteroskedasticity model" (PDF) . Journal of Econometrics . Elsevier: 219–230. Archived from the original (PDF) on 2016-03-07. Retrieved 2011-06-02 . ^ Michael, Lugo. "The expectation of the maximum of exponentials" (PDF) . Archived from the original (PDF) on 20 December 2016. Retrieved 13 December 2016 . ^ Eckford, Andrew W.; Thomas, Peter J. (2016). "Entropy of the sum of two independent, non-identically-distributed exponential random variables". arXiv :1609.02911 ^ Richard Arnold Johnson; Dean W. Wichern (2007). Applied Multivariate Statistical Analysis ISBN 978-0-13-187715-3 . Retrieved 10 August 2012 . ^ NIST/SEMATECH 전자통계편람 ^ Elfessi, Abdulaziz; Reineke, David M. (2001). "A Bayesian Look at Classical Estimation: The Exponential Distribution" . Journal of Statistics Education . 9 (1). doi :10.1080/10691898.2001.11910648 ^ Ross, Sheldon M. (2009). Introduction to probability and statistics for engineers and scientists ISBN 978-0-12-370483-2 ^ Guerriero, V. (2012). "Power Law Distribution: Method of Multi-scale Inferential Statistics" . Journal of Modern Mathematics Frontier . 1 : 21–28. ^ "Cumfreq, a free computer program for cumulative frequency analysis" .^ Ritzema (ed.), H.P. (1994). Frequency and Regression Analysis 175–224 . ISBN 90-70754-33-9 CS1 maint: 추가 텍스트: 작성자 목록(링크 ) ^ Lawless, J. F.; Fredette, M. (2005). "Frequentist predictions intervals and predictive distributions" . Biometrika . 92 (3): 529–542. doi :10.1093/biomet/92.3.529 ^ Bjornstad, J.F. (1990). "Predictive Likelihood: A Review" . Statist. Sci . 5 (2): 242–254. doi :10.1214/ss/1177012175 ^ D. F. 슈미트와 E. Makalic, "지수분포를 위한 범용 모델 ", 정보이론 IEEE 거래 도이 :10.1109/TIT.2018331 ^ 도널드 크누스 (1998년). 컴퓨터 프로그래밍 기술 세미머셜 알고리즘, 제3권 보스턴: 애디슨-웨슬리 ISBN 0-201-89684-2 . 섹션 3.4.1, 페이지 133을 참조한다. ^ Jump up to: a b 뤽 데브로예(1986년). 불균일 랜덤 생성 뉴욕: 스프링거-베를라크. ISBN 0-387-96305-7 IX장 , 섹션 2, 페이지 392–401을 참조한다.
외부 링크
show 이산형 일변도의
연속 일변도의
의 지지를 받고 있는. 경계 간격 의 지지를 받고 있는. 반무한 간격을 두고 지지의 대체로 실선 지지하여 누구의 타입이 다른가.
혼합 일변도의
다변량 (공동) 방향 퇴보하다 그리고 단수 가족들






















![{\displaystyle \operatorname {E} [X]={\frac {1}{\lambda }}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f9efa3ce3c964c59532609b3d6b8f01ce88f6221)
![{\displaystyle \operatorname {Var} [X]={\frac {1}{\lambda ^{2}}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3c450db5013b1cfdaf5ea71106c9d13834e02d61)

![{\displaystyle \operatorname {E} \left[X^{n}\right]={\frac {n!}{\lambda ^{n}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5f5d3a82fbcff5a294e5360fb05b1e5f2166ec09)

![{\displaystyle \operatorname {m} [X]={\frac {\ln(2)}{\lambda }}<\operatorname {E} [X],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7f19becbfbc702d8c33a9698c779384fe3f4dca1)
![{\displaystyle \left|\operatorname {E} \left[X\right]-\operatorname {m} \left[X\right]\right|={\frac {1-\ln(2)}{\lambda }}<{\frac {1}{\lambda }}=\operatorname {\sigma } [X],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e48a50d7c835e2c16f59682fe49712aa41a54d8a)

![{\displaystyle {\begin{aligned}\Pr \left(T>s+t\mid T>s\right)&={\frac {\Pr \left(T>s+t\cap T>s\right)}{\Pr \left(T>s\right)}}\\[4pt]&={\frac {\Pr \left(T>s+t\right)}{\Pr \left(T>s\right)}}\\[4pt]&={\frac {e^{-\lambda (s+t)}}{e^{-\lambda s}}}\\[4pt]&=e^{-\lambda t}\\[4pt]&=\Pr(T>t).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/126da1213459cde98ae372eae857a18183675f5a)















![{\displaystyle \operatorname {E} \left[X_{(i)}X_{(j)}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7d350557a602c2566c092558fff0aefb0049c7c9)


![{\displaystyle {\begin{aligned}\operatorname {E} \left[X_{(i)}X_{(j)}\right]&=\sum _{k=0}^{j-1}{\frac {1}{(n-k)\lambda }}\operatorname {E} \left[X_{(i)}\right]+\operatorname {E} \left[X_{(i)}^{2}\right]\\&=\sum _{k=0}^{j-1}{\frac {1}{(n-k)\lambda }}\sum _{k=0}^{i-1}{\frac {1}{(n-k)\lambda }}+\sum _{k=0}^{i-1}{\frac {1}{((n-k)\lambda )^{2}}}+\left(\sum _{k=0}^{i-1}{\frac {1}{(n-k)\lambda }}\right)^{2}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0135f144a56c4b7565f7faa61cc3abb42afe9c0d)
![{\displaystyle {\begin{aligned}\operatorname {E} \left[X_{(i)}X_{(j)}\right]&=\int _{0}^{\infty }\operatorname {E} \left[X_{(i)}X_{(j)}\mid X_{(i)}=x\right]f_{X_{(i)}}(x)\,dx\\&=\int _{x=0}^{\infty }x\operatorname {E} \left[X_{(j)}\mid X_{(j)}\geq x\right]f_{X_{(i)}}(x)\,dx&&\left({\textrm {since}}~X_{(i)}=x\implies X_{(j)}\geq x\right)\\&=\int _{x=0}^{\infty }x\left[\operatorname {E} \left[X_{(j)}\right]+x\right]f_{X_{(i)}}(x)\,dx&&\left({\text{by the memoryless property}}\right)\\&=\sum _{k=0}^{j-1}{\frac {1}{(n-k)\lambda }}\operatorname {E} \left[X_{(i)}\right]+\operatorname {E} \left[X_{(i)}^{2}\right].\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/be5949313f3639a86ac81484ac8ca7f4f9edb4d4)


![{\displaystyle \operatorname {E} \left[X_{(j)}\mid X_{(j)}\geq x\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/00169b33907d379235fd4561c63c13d4c51a619a)
![{\displaystyle \operatorname {E} \left[X_{(j)}\right]+x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/775aa6cfd6c5d2b1e4b70ce3108a17f93f7b0224)





![{\displaystyle {\begin{aligned}f_{Z}(z)&=\int _{-\infty }^{\infty }f_{X_{1}}(x_{1})f_{X_{2}}(z-x_{1})\,dx_{1}\\&=\int _{0}^{z}\lambda _{1}e^{-\lambda _{1}x_{1}}\lambda _{2}e^{-\lambda _{2}(z-x_{1})}\,dx_{1}\\&=\lambda _{1}\lambda _{2}e^{-\lambda _{2}z}\int _{0}^{z}e^{(\lambda _{2}-\lambda _{1})x_{1}}\,dx_{1}\\&={\begin{cases}{\dfrac {\lambda _{1}\lambda _{2}}{\lambda _{2}-\lambda _{1}}}\left(e^{-\lambda _{1}z}-e^{-\lambda _{2}z}\right)&{\text{ if }}\lambda _{1}\neq \lambda _{2}\\[4pt]\lambda ^{2}ze^{-\lambda z}&{\text{ if }}\lambda _{1}=\lambda _{2}=\lambda .\end{cases}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c2db15dda49fe8482485a68c9d7c9b1c1d46ee95)


 (는)
(는) 
 분포
분포



























![{\displaystyle {\frac {d}{d\lambda }}\ln L(\lambda )={\frac {d}{d\lambda }}\left(n\ln \lambda -\lambda n{\overline {x}}\right)={\frac {n}{\lambda }}-n{\overline {x}}\ {\begin{cases}>0,&0<\lambda <{\frac {1}{\overline {x}}},\\[8pt]=0,&\lambda ={\frac {1}{\overline {x}}},\\[8pt]<0,&\lambda >{\frac {1}{\overline {x}}}.\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/65ec59bc9ccff1952291621e3eccc741ee1341a2)

 (가)
(가)  편향되지
편향되지
![{\displaystyle b\equiv \operatorname {E} \left[\left({\widehat {\lambda }}_{\text{mle}}-\lambda \right)\right]={\frac {\lambda }{n-1}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df60981cd70301a83682e00b553866f627a50bed)





![{\displaystyle {\mathcal {I}}(\lambda )=\operatorname {E} \left[\left.\left({\frac {\partial }{\partial \lambda }}\log f(x;\lambda )\right)^{2}\right|\lambda \right]=\int \left({\frac {\partial }{\partial \lambda }}\log f(x;\lambda )\right)^{2}f(x;\lambda )\,dx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c70bd835b54bb1b7f344dbf1f04d170bd1d4852)












![{\displaystyle {\begin{aligned}\operatorname {E} _{\lambda _{0}}\left[\Delta (\lambda _{0}\parallel p_{\rm {ML}})\right]&=\psi (n)+{\frac {1}{n-1}}-\log(n)\\\operatorname {E} _{\lambda _{0}}\left[\Delta (\lambda _{0}\parallel p_{\rm {CNML}})\right]&=\psi (n)+{\frac {1}{n}}-\log(n)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/02702bfd262096d01f27b67eab961ff7ccb512a9)





