입자 붕괴는 하나의 불안정한 아원자 입자가 여러 개의 다른 입자로 변환되는 자발적인 과정이다.이 프로세스(최종 상태)에서 생성된 입자는 시스템의 총 불변 질량을 보존해야 하지만 각각 원래보다 질량이 작아야 합니다.입자가 붕괴할 수 있는 최소 하나의 최종 상태가 있는 경우 입자는 불안정합니다.불안정한 입자는 종종 붕괴하는 여러 가지 방법을 가지며, 각각은 관련된 확률을 가집니다.붕괴는 하나 또는 여러 기본 힘에 의해 매개된다.최종 상태의 입자 자체가 불안정하여 추가 붕괴가 발생할 수 있습니다.
이 용어는 불안정한 원자핵이 입자 또는 방사선의 방출을 동반하는 가벼운 핵으로 변환되는 방사성 붕괴와 구별된다. 단, 두 원자핵은 개념적으로 유사하며 종종 동일한 용어를 사용하여 설명된다.
생존 확률 및 입자 수명
입자 붕괴는 포아송 과정이며, 따라서 붕괴되기 전 시간 t 동안 입자가 생존할 확률은 시간 상수가 입자의 속도에 따라 달라지는 지수 분포에 의해 주어진다.

- 어디에
- \displaystyle는
 입자의 평균 수명(정지 시)입니다.
입자의 평균 수명(정지 시)입니다. - = 1 - c 2 \displaystyle \displaystyle \displays 은
 입자의 로렌츠 이다.
입자의 로렌츠 이다.
일부 기본 및 복합 입자 수명 표
모든 데이터는 파티클 데이터 그룹의 데이터입니다.
| 유형 | 이름. | 기호. | 질량(MeV) | 평균 수명 |
| 렙톤 | 전자/양전자[1] |  | 0000.511 |  |
| 뮤온/안티무온 |  | 00105.700 |  |
| 타우 렙톤 / 안티토 |  | 01777.000 |  |
| 중간자 | 중성 파이온 |  | 00135.000 |  |
| 충전 파이온 |  | 00139.600 |  |
| 바리온 | 프로톤 / 안티프로톤[2][3] |  | 00938.200 |  |
| 중성자/안티뉴트론 |  | 00939.600 |  |
| 보손 | W보손 |  | 80400.000 |  |
| Z보손 |  | 91000.000 |  |
붕괴율
이 섹션에서는 자연 단위를 합니다. 여기서 .{\ c=\=
입자의 수명은 붕괴율의 역수명인 단위시간당 입자가 붕괴할 인δ(\  질량 M 입자와 4모멘텀 P 입자가 {
질량 M 입자와 4모멘텀 P 입자가 { 인 입자로 붕괴하는 경우, 감쇠율은 일반식(페르미의 황금규칙을 나타냄)으로 구한다.
인 입자로 붕괴하는 경우, 감쇠율은 일반식(페르미의 황금규칙을 나타냄)으로 구한다.

- 어디에
- n은 원래의 붕괴에 의해 생성된 입자의 수입니다.
- S는 구분할 수 없는 최종 상태를 설명하는 조합 요인이다(아래 참조).
- {\은
 (는) 초기 상태와 최종 상태를 연결하는 불변 행렬 요소 또는 진폭입니다(일반적으로 파인만 다이어그램을 사용하여 계산됨).
(는) 초기 상태와 최종 상태를 연결하는 불변 행렬 요소 또는 진폭입니다(일반적으로 파인만 다이어그램을 사용하여 계산됨).  \ d \ _ { } 은 위상공간의 요소입니다.
\ d \ _ { } 은 위상공간의 요소입니다.- p_
 {i}는 입자 i의 4차원입니다.
{i}는 입자 i의 4차원입니다.
계수 S는 다음과 같이 주어진다.

- 어디에
- m은 최종 상태에 있는 구별할 수 없는 입자 집합의 수입니다.
- j(\는
 j타입의 입자수입니다.따라서 j { _ {j=1 }^{j}=n
j타입의 입자수입니다.따라서 j { _ {j=1 }^{j}=n 입니다.
입니다.
위상 공간은 다음에서 확인할 수 있습니다.

- 어디에
- \^{4
 는 4차원 Dirac 델타 함수입니다.
는 4차원 Dirac 델타 함수입니다. - (\는
 입자 i의 (3차원) 값입니다.
입자 i의 (3차원) 값입니다. - 는입자
 i의
i의
지정된 최종 상태의 총 붕괴율을 얻기 위해 위상 공간에 통합될 수 있습니다.
입자가 여러 개의 붕괴 분기 또는 최종 상태가 다른 모드를 가지고 있는 경우, 그 완전한 붕괴 속도는 모든 분기의 붕괴 속도를 합하여 구한다.각 모드의 분기율은 붕괴율을 완전 붕괴율로 나눈 값으로 표시됩니다.
이체 붕괴
이 섹션에서는 자연 단위를 합니다. 여기서 .{\ c=\=
운동량 중심 프레임에서 입자가 두 개의 동일한 질량 입자로 붕괴되면 180°의 각도로 방출됩니다.
...실험 프레임에서는 부모 입자가 빛의 속도에 가까운 속도로 움직이기 때문에 두 개의 방출된 입자가 운동량 프레임의 중심과 다른 각도로 나올 수 있습니다. 붕괴율
질량 M의 부모 입자가 1과 2라는 두 입자로 분해된다고 가정해 봅시다.모입자의 나머지 프레임에서
![{\displaystyle |{\vec {p}}_{1}|=|{\vec {p}}_{2}|={\frac {[(M^{2}-(m_{1}+m_{2})^{2})(M^{2}-(m_{1}-m_{2})^{2})]^{1/2}}{2M}},\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fbc7c73c02bf1575e86be1fea87fbd954fb29e8f)
즉, 부패 시 4분위기를 보존하도록 요구함으로써 얻을 수 있다.

또한 구면 좌표에서는

델타 함수를 사용하여 위상공간에 (\ d 1(\ d 를
1(\ d 를 2체 최종상태에서 실행하면 부모 입자의 나머지 프레임의 붕괴율이
2체 최종상태에서 실행하면 부모 입자의 나머지 프레임의 붕괴율이

2개의 다른 프레임에서
실험실 프레임에서 방출된 입자의 각도는 다음 방정식에 의해 운동량 프레임의 중심에서 방출된 각도와 관련이 있습니다.

복잡한 질량 및 붕괴 속도
이 섹션에서는 자연 단위를 합니다. 여기서 .{\ c=\=
불안정한 입자의 질량은 형식적으로 복소수이며, 실제 부분은 일반적인 의미의 질량이고, 가상 부분은 자연 단위의 붕괴 속도입니다.허구 부분이 실제 부분에 비해 클 때, 일반적으로 입자는 입자보다 공명으로 생각됩니다.이것은 양자장 이론에서 질량 M(실수)의 입자가 종종 불확실성 원리에 따라 다른 두 입자들 사이를 이동하는 시간이 충분히 짧을 때 그것을 만들 에너지가 없을 때, 다른 두 입자들 사이에서 교환되기 때문이다.M + \ \M + \  입자의 경우, 입자는 시간 1/M 동안 이동할 수 있지만 1 / \ \ 1/\
입자의 경우, 입자는 시간 1/M 동안 이동할 수 있지만 1 / \ \ 1/\  의
의 로 시간이 지나면 소멸합니다.I > M \ \ style \ gamma Decript style \ > Decisions > Decript martle > Decript marticle >
로 시간이 지나면 소멸합니다.I > M \ \ style \ gamma Decript style \ > Decisions > Decript martle > Decript marticle >
「 」를 참조해 주세요.
메모들
외부 링크

 입자의 평균 수명(정지 시)입니다.
입자의 평균 수명(정지 시)입니다.




















 (는) 초기 상태와 최종 상태를 연결하는 불변
(는) 초기 상태와 최종 상태를 연결하는 불변 


 j타입의 입자수입니다.따라서
j타입의 입자수입니다.따라서 


 입자 i의 (3차원) 값입니다.
입자 i의 (3차원) 값입니다. i의
i의 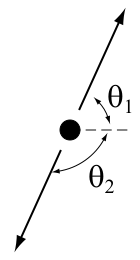

![{\displaystyle |{\vec {p}}_{1}|=|{\vec {p}}_{2}|={\frac {[(M^{2}-(m_{1}+m_{2})^{2})(M^{2}-(m_{1}-m_{2})^{2})]^{1/2}}{2M}},\,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fbc7c73c02bf1575e86be1fea87fbd954fb29e8f)



 2체 최종상태에서 실행하면 부모 입자의 나머지 프레임의 붕괴율이
2체 최종상태에서 실행하면 부모 입자의 나머지 프레임의 붕괴율이






