QR 알고리즘

수치 선형 대수학에서 QR 알고리즘 또는 QR 반복은 고유값 알고리즘이다. 즉, 행렬의 고유값과 고유 벡터를 계산하는 절차이다.QR 알고리즘은 1950년대 후반 John G. F. F. Francis와 ^[1]^[2]^[3]Vera N. Kublanovskaya가 독립적으로 작업하면서 개발되었습니다.QR 분해를 수행하여 행렬을 직교 행렬과 상부 삼각 행렬의 곱으로 쓰고 인자를 역순으로 곱한 후 반복하는 것이 기본 아이디어입니다.

실용적인 QR 알고리즘

공식적으로는 A를 고유값을 계산하려는 실행렬로 하고 A:=A로₀ 하자.k번째 단계(k = 0부터 시작)에서는 QR 분해_k A=QR을_k_k 계산합니다. 여기서_k Q는 직교 행렬(즉^T, Q = Q⁻¹)이고_k R은 상부 삼각 행렬입니다.그런 다음 A = RQ를_k_k 형성합니다_k+1.주의:

{{k+1}=R_{k}Q_{k}=Q_{k}Q_{k}R_{k}Q_{k}=Q_{k}{-1}A_{k}Q_{k}=Q_{k}=Q_{k}=Q_{k}{mathf {K}{K}{K}{K}{K}{K}}{K}{K}}}}{K}A

따라서 모든 A가_k 비슷하고 따라서 동일한 고유값을 가집니다.알고리즘은 직교 유사도 변환을 통해 진행되므로 수치적으로 안정적입니다.

특정 ^[4]조건에서 행렬_k A는 삼각형 행렬, 즉 A의 Schur 형태로 수렴됩니다.삼각형 행렬의 고유값이 대각선에 나열되고 고유값 문제가 해결됩니다.수렴 테스트에서 정확한 ^{[citation needed]}0을 요구하는 것은 비현실적이지만, Gershgorin 원 정리는 오차에 대한 경계를 제공합니다.

이 조잡한 형태에서는 반복이 상대적으로 비싸다.이것은 먼저 행렬 A를 Hessenberg 형태(10 ${\begin{matrix}{\frac {10}{3}}\end{matrix}}n^{3}+{\mathcal {O}}(n^{2})$ 3 + ${\begin{matrix}{\frac {10}{3}}\end{matrix}}n^{3}+{\mathcal {O}}(n^{2})$ ( ${\begin{matrix}{\frac {10}{3}}\end{matrix}}n^{3}+{\mathcal {O}}(n^{2})$ $)(\displaystyle$ {\ $begin{matrix}{\frac {10}{3}}\end{matrix}n^{3}+{\$ mathcal ${O}(n^{2})})$ 로 ${\begin{matrix}{\frac {10}{3}}\end{matrix}}n^{3}+{\mathcal {O}}(n^{2})$ 가져와 완화될 수 있다.ty 변환은 ^[5]^[6]양면 QR 분해와 비슷합니다.(QR 분해의 경우 Hesenberg의 경우 왼쪽과 오른쪽 모두에서 Hesenberg의 경우 Housever reflector를 곱합니다.)상위 Hessenberg 행렬의 QR 분해는 $6n^{2}+{\mathcal {O}}(n)$ + $6n^{2}+{\mathcal {O}}(n)$ ( $6n^{2}+{\mathcal {O}}(n)$ $){displaystyle 6n^{2}+{\mathcal {O}}(n)}$ 의 $6n^{2}+{\mathcal {O}}(n)$ 산술 연산이 $6n^{2}+{\mathcal {O}}(n)$ 됩니다.게다가 헤센버그 형태는 이미 거의 상삼각형(각 대각선 아래에 0이 아닌 엔트리가 1개만 있음)이기 때문에 이를 출발점으로 사용하면 QR 알고리즘의 수렴에 필요한 단계 수를 줄일 수 있다.

만약 원래의 행렬이 대칭이라면, 상부 헤센버그 행렬도 대칭이고, 따라서 3각이고, 모든 A도_k 대칭입니다. ${\begin{matrix}{\frac {4}{3}}\end{matrix}}n^{3}+{\mathcal {O}}(n^{2})$ 절차는 가구원 ^[5]^[6]감축에 기초한 기술을 ${\begin{matrix}{\frac {4}{3}}\end{matrix}}n^{3}+{\mathcal {O}}(n^{2})$ 사용하여 ${\begin{matrix}{\frac {4}{3}}\end{matrix}}n^{3}+{\mathcal {O}}(n^{2})$ 3 + ${\begin{matrix}{\frac {4}{3}}\end{matrix}}n^{3}+{\mathcal {O}}(n^{2})$ ( ${\begin{matrix}{\frac {4}{3}}\end{matrix}}n^{3}+{\mathcal {O}}(n^{2})$ 2 ) ${\begin{matrix}{\frac {4}{3}}\end{matrix}}n^{3}+{\mathcal {O}}(n^{2})$ { $displaystyle$ { \ $frac$ { $4 }$ { \ $frac$ { 4 ${\begin{matrix}{\frac {4}{3}}\end{matrix}}n^{3}+{\mathcal {O}}(n^{2})$ } \ $matrix$ } $n$ ^ {3 $}$ + { \ $mathcal$ { $O$ } ( $n$ ^ {2} ) ${\begin{matrix}{\frac {4}{3}}\end{matrix}}n^{3}+{\mathcal {O}}(n^{2})$ } 。대칭 삼각행렬의 QR 분해는 ${\mathcal {O}}(n)$ O ${\mathcal {O}}(n)$ ( ${\mathcal {O}}(n)$ n ) \ $displaystyle$ \ $mathcal$ { $O}}$ ( $n$ )의 ${\mathcal {O}}(n)$ ^[7]연산이 소요됩니다.

수렴 속도는 고유값 간의 분리에 따라 달라지므로 실제 알고리즘은 분리를 증가시키고 수렴을 가속화하기 위해 명시적 또는 암묵적 이동을 사용합니다.일반적인 대칭 QR 알고리즘은 한 두 번의 반복만으로 각 고유값을 격리(그 후 행렬의 크기를 줄임)하여 효율적이면서도 ^{[clarification needed]}견고합니다.

시각화

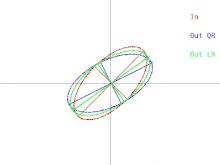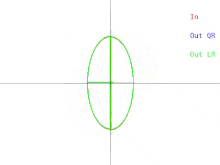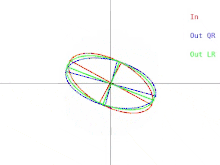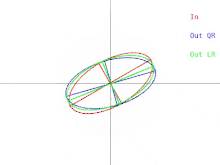
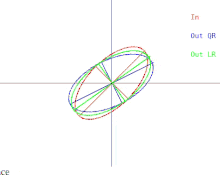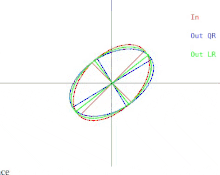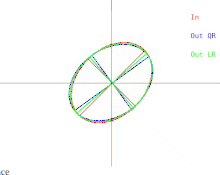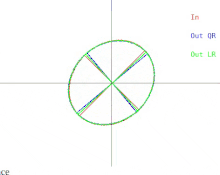
그림 1: QR 알고리즘 또는 LR 알고리즘의 1회 반복 출력과 입력의 차이

기본 QR 알고리즘은 A가 양의-확정 대칭 매트릭스인 경우에 시각화할 수 있다.이 경우 A는 2차원의 타원과 고차원의 타원으로 표현될 수 있다.그런 다음 알고리즘에 대한 입력과 단일 반복 사이의 관계를 그림 1과 같이 나타낼 수 있습니다(클릭하면 애니메이션을 볼 수 있습니다.LR 알고리즘은 QR 알고리즘과 함께 표시됩니다.

한 번 반복하면 타원이 x축 방향으로 기울어지거나 "하강"됩니다.타원의 큰 반축이 x축과 평행한 경우에는 QR을 한 번 반복해도 아무런 효과가 없습니다.알고리즘이 "아무것도 하지 않는" 또 다른 상황은 큰 반축이 x축 대신 y축과 평행한 경우입니다.이 경우 타원은 어느 방향으로도 떨어지지 않고 불안정하게 균형을 잡는다고 생각할 수 있습니다.두 경우 모두 행렬은 대각선입니다.알고리즘의 반복이 「아무것도 하지 않는다」라고 하는 상황을 고정점이라고 부릅니다.알고리즘에 의해 채택된 전략은 고정점을 향한 반복이다.한 고정점은 안정적인 반면 다른 고정점은 불안정한지 관찰합니다.타원이 불안정한 고정점에서 아주 조금만 기울어져 있으면 QR을 한 번 반복하면 타원이 고정점에서 쪽으로 기울지 않고 멀어질 수 있습니다.그러나 결국 알고리즘은 다른 고정점으로 수렴되지만 시간이 오래 걸립니다.

고유값 찾기 대 고유 벡터 찾기

그림 2: 두 고유값이 서로 근접할 때 QR 또는 LR의 단일 반복 출력이 어떤 영향을 받는지

대칭행렬의 단일 고유벡터조차 계산할 수 없다는 것을 지적할 필요가 있다(계산 ^[8]가능한 분석의 정의에 따른 정확한 실제 산술).행렬 고유값의 곱셈을 알 수 없을 때마다 이 어려움이 존재합니다.반면 고유값을 찾는 데 동일한 문제가 없습니다.행렬의 고유값은 항상 계산할 수 있습니다.

이제 기본 QR 알고리즘에서 이러한 어려움이 어떻게 나타나는지 설명하겠습니다.이것은 그림 2에 나타나 있습니다.(섬네일을 클릭하는 것을 잊지 마십시오.타원은 양의-정의 대칭 행렬을 나타냅니다.입력행렬의 두 고유값이 가까워지면 입력타원이 원으로 변한다.원은 항등행렬의 배수에 대응합니다.근원은 고유값이 행렬의 대각선 엔트리와 거의 동일한 동일행렬의 근배수에 대응한다.따라서 이 경우 고유값을 근사적으로 찾는 문제는 쉬운 것으로 나타납니다.하지만 타원의 반축에 무슨 일이 일어나는지 보세요.QR(또는 LR)을 반복하면 입력 타원이 원에 가까워질수록 반축 기울기가 점점 줄어듭니다.고유 벡터는 반축이 x축 및 y축과 평행한 경우에만 알 수 있습니다.입력 타원이 원형이 될수록 경계 없이 거의 평행성을 달성하는 데 필요한 반복 횟수가 증가합니다.

임의의 대칭행렬의 eigendecomposition을 계산하는 것은 불가능할 수 있지만, 항상 임의의 작은 양으로 행렬을 교란하고 결과행렬의 eigendecomposition을 계산하는 것은 가능하다.행렬이 근원으로 묘사될 경우, 행렬은 완전한 원을 묘사하는 행렬로 대체될 수 있다.이 경우 행렬은 항등행렬의 배수이며, 그 eigendecomposition은 즉시 이루어진다.그러나 결과 고유 베이스는 원래 고유 베이스에서 상당히 멀리 떨어져 있을 수 있습니다.

암묵 QR 알고리즘

현대의 컴퓨터 프랙티스에서 QR 알고리즘은 암묵적인 버전으로 수행되며,^[4] 이를 통해 다중 교대제 사용이 도입되기 쉬워집니다.매트릭스는 먼저 상위 Hessenberg $A_{0}=QAQ^{\mathsf {T}}$ 로 $A_{0}=QAQ^{\mathsf {T}}$ 0 $A_{0}=QAQ^{\mathsf {T}}$ $A_{0}=QAQ^{\mathsf {T}}$ $A_{0}=QAQ^{\mathsf {T}}$ $A_{0}=QAQ^{\mathsf {T}}$ T {\ $displaystyle A_{0$ } = $Q$ $AQ^{\mathsf {T}}$ 를 $A_{0}=QAQ^{\mathsf {T}}$ $A_{k}$ 명시 버전과 같이 한 후 각 단계에서 소형 세대주 $유사$ 도 변환을 통해 $A_{k}$ $p(A_{k})$ k $)$ 의 $p(A_{k})$ 번째 열( $p(A_{k})e_{1}$ p ${$ $k})$ $e_style$ 1 $($ )로 변환한다. $p(A_{k})$ ) $p(A_{k})$ ({ $displaystyle p(A_{$ k $p(A_{k})$ ({ $displaystyle$ r $r$ 는 이동전략( $p(x)=(x-\lambda )(x-{\bar {\lambda }})$ p $=$ - $x$ - $λ¯)\displaystyle$ p $(x-{\displaystyle$ r})를 정의하는 다항식입니다 $p(x)=(x-\lambda )(x-{\bar {\lambda }})$ $\lambda$ 서 x-{\displaystyle p(x- ${\$ $da}$ 는 $\lambda$ $\da$ ${\bar {\lambda }}$ 와 r $)$ 를 $표시$ 합니다. $A_{k}$ A $A_{k}$ 의 $2\times 2$ 2 × $(표시$ $스타일$ $2\times 2$ 2 $A_{k}$ $times$ 2) 주요 $2\times 2$ 하위 행렬 값(일명 암묵적 이중 이동).다음으로 작업 $A_{k}$ $A_{k}$ k $(\$ 를 $A_{k}$ 상위 Hessenberg 형식으로 되돌리기 위해 $r+1$ r + $r+1$ (\ $displaystyle$ r $+1)$ 의 $r+1$ 연속적인 세대주 변환이 수행됩니다.이 연산은 알고리즘의 단계를 따라 행렬의 0이 아닌 엔트리의 독특한 모양 때문에 벌지 체이싱이라고 불립니다.첫 번째 버전과 마찬가지로 A $k의$ 서브대각선 $엔트리$ 중 하나가 충분히 작으면 바로 디플레이션을 실시한다.

제안서 이름 변경

현대의 암묵적인 버전의 절차에서는 QR 분해가 명시적으로 수행되지 않기 때문에, ^[9]왓킨스와 같은 일부 저자는 그 이름을 프란시스 알고리즘으로 변경할 것을 제안했다.골럽과 반론은 프란시스 QR 스텝이라는 용어를 사용한다.

해석과 수렴

QR 알고리즘은 기본 "전력" 고유값 알고리즘의 보다 정교한 변형으로 볼 수 있습니다.검정력 알고리즘은 A에 단일 벡터를 반복적으로 곱하여 반복할 때마다 정규화된다는 점을 기억하십시오.벡터는 가장 큰 고유값의 고유 벡터로 수렴됩니다.대신 QR 알고리즘은 벡터의 완전한 기반으로 작동하며 QR 분해를 사용하여 정규화(및 직교화)합니다.대칭행렬 A의 경우 수렴 시 AQ = QΩ입니다. 여기서 δ는 A가 수렴한 고유값의 대각행렬이며 Q는 거기에 도달하는 데 필요한 모든 직교 유사성 변환의 합성입니다.따라서 Q의 열이 고유 벡터입니다.

역사

QR 알고리즘은 QR 분해 대신 LU 분해를 사용하는 LR 알고리즘이 선행되었습니다.QR 알고리즘이 더 안정적이기 때문에 최근에는 LR 알고리즘이 거의 사용되지 않습니다.그러나 이는 QR 알고리즘 개발에 있어 중요한 단계를 나타냅니다.

LR 알고리즘은 1950년대 초에 ETH 취리히에서 Eduard Stiefel의 연구 보조로 일했던 Heinz Rutishauser에 의해 개발되었습니다.스티펠은 루티샤 사용자가 A의₀ 고유값을 찾기 위해 y x^k, k = 0, 1, … (여기서₀ x와₀ y는 임의 벡터)의₀^T 순번을 사용하라고 제안했다.Rutishauser는 이 과제를 위해 Alexander Aitken의 알고리즘을 취하여 그것을 지수 차분 알고리즘 또는 qd 알고리즘으로 개발하였다.연산을 적절한 형태로 배열한 후, 그는 qd 알고리즘이 실제로 LR 알고리즘이 ^[10]이어지는 삼각행렬에 적용되는 반복_k A = LU_k_k(LU 분해)인_k+1_k_k 것을 발견했다.

기타 변종

QR 알고리즘의 변형 중 하나인 Golub-Kahan-Reinsch 알고리즘은 일반 행렬을 쌍대각 ^[11]행렬로 줄이는 것으로 시작합니다.특이값 계산을 위한 QR 알고리즘의 이 변종은 Golub & Kahan(1965) harvhts 오류: no target: CITREFGolubKahan1965(도움말)에 의해 처음 설명되었다.LAPACK 서브루틴 DBDSQR은 이 반복 방법을 구현하고 단수값이 매우 작은 경우(Demmel & Kahan 1990)를 커버하기 위해 몇 가지 수정을 가합니다: no target: CITREFDemmelKahan 1990(도움말).Householder reflections 및 QR 분해(해당하는 경우)를 사용하는 첫 번째 단계와 함께, 이것은 특이값 분해 계산을 위한 DGESVD 루틴을 형성한다.QR 알고리즘은 또한 해당 수렴 ^[12]^[13]결과와 함께 무한 차원에서도 구현될 수 있습니다.

레퍼런스

^ J.G.F. Francis, "QR 트랜스포메이션, I", 컴퓨터 저널, 4(3), 265-271쪽(1961년, 1959년 10월 접수)doi: 10.1093/comjnl/4.3.265
^ Francis, J. G. F. (1962). "The QR Transformation, II". The Computer Journal. 4 (4): 332–345. doi:10.1093/comjnl/4.4.332.
^ Vera N. Kublanovskaya, "완전한 고유값 문제의 해답을 위한 일부 알고리즘에 대하여", 소련 계산 수학 및 수리 물리학, vol. 1, no., 637–657쪽 (1963년, 1961년 2월 수신)또한 Zhille Vichislitel'noi Matematiki i Matematicheskoi Fiziki, vol.1, No.4, 555-570페이지(1961년)에도 게재되었다.doi: 10.1016/0041-5553(63)90168-X
^ ^a ^b Golub, G. H.; Van Loan, C. F. (1996). Matrix Computations (3rd ed.). Baltimore: Johns Hopkins University Press. ISBN 0-8018-5414-8.
^ ^a ^b Demmel, James W. (1997). Applied Numerical Linear Algebra. SIAM.
^ ^a ^b Trefethen, Lloyd N.; Bau, David (1997). Numerical Linear Algebra. SIAM.
^ Ortega, James M.; Kaiser, Henry F. (1963). "The LL^T and QR methods for symmetric tridiagonal matrices". The Computer Journal. 6 (1): 99–101. doi:10.1093/comjnl/6.1.99.
^ "linear algebra - Why is uncomputability of the spectral decomposition not a problem?". MathOverflow. Retrieved 2021-08-09.
^ Watkins, David S. (2007). The Matrix Eigenvalue Problem: GR and Krylov Subspace Methods. Philadelphia, PA: SIAM. ISBN 978-0-89871-641-2.
^ Parlett, Beresford N.; Gutknecht, Martin H. (2011), "From qd to LR, or, how were the qd and LR algorithms discovered?" (PDF), IMA Journal of Numerical Analysis, 31 (3): 741–754, doi:10.1093/imanum/drq003, hdl:20.500.11850/159536, ISSN 0272-4979
^ 보흐카노프 세르게이 아나톨리예비치.ALGLIB 사용자 가이드 - 일반 매트릭스 연산 - 특이값 분해 . ALGLIB 프로젝트.2010-12-11.URL : [ 1 ]접속: 2010-12-11. (WebCite https://www.webcitation.org/5utO4iSnR?url=http 에서 아카이브 완료)
^ Deift, Percy; Li, Luenchau C.; Tomei, Carlos (1985). "Toda flows with infinitely many variables". Journal of Functional Analysis. 64 (3): 358–402. doi:10.1016/0022-1236(85)90065-5.
^ Colbrook, Matthew J.; Hansen, Anders C. (2019). "On the infinite-dimensional QR algorithm". Numerische Mathematik. 143 (1): 17–83. arXiv:2011.08172. doi:10.1007/s00211-019-01047-5.

외부 링크

PlanetMath의 고유값 문제.
직교 베이스 및 Peter J. Olver의 QR 알고리즘 작동에 대한 참고 사항
QR 방법 모듈
C++ 라이브러리

[1] J.G.F. Francis, "QR 트랜스포메이션, I", 컴퓨터 저널, 4(3), 265-271쪽(1961년, 1959년 10월 접수)doi: 10.1093/comjnl/4.3.265

[2] Francis, J. G. F. (1962). "The QR Transformation, II". The Computer Journal. 4 (4): 332–345. doi:10.1093/comjnl/4.4.332.

[3] Vera N. Kublanovskaya, "완전한 고유값 문제의 해답을 위한 일부 알고리즘에 대하여", 소련 계산 수학 및 수리 물리학, vol. 1, no., 637–657쪽 (1963년, 1961년 2월 수신)또한 Zhille Vichislitel'noi Matematiki i Matematicheskoi Fiziki, vol.1, No.4, 555-570페이지(1961년)에도 게재되었다.doi: 10.1016/0041-5553(63)90168-X

[golubvanloan-4] Golub, G. H.; Van Loan, C. F. (1996). Matrix Computations (3rd ed.). Baltimore: Johns Hopkins University Press. ISBN 0-8018-5414-8.

[Demmel-5] Demmel, James W. (1997). Applied Numerical Linear Algebra. SIAM.

[Trefethen-6] Trefethen, Lloyd N.; Bau, David (1997). Numerical Linear Algebra. SIAM.

[7] Ortega, James M.; Kaiser, Henry F. (1963). "The LL^T and QR methods for symmetric tridiagonal matrices". The Computer Journal. 6 (1): 99–101. doi:10.1093/comjnl/6.1.99.

[8] "linear algebra - Why is uncomputability of the spectral decomposition not a problem?". MathOverflow. Retrieved 2021-08-09.

[9] Watkins, David S. (2007). The Matrix Eigenvalue Problem: GR and Krylov Subspace Methods. Philadelphia, PA: SIAM. ISBN 978-0-89871-641-2.

[10] Parlett, Beresford N.; Gutknecht, Martin H. (2011), "From qd to LR, or, how were the qd and LR algorithms discovered?" (PDF), IMA Journal of Numerical Analysis, 31 (3): 741–754, doi:10.1093/imanum/drq003, hdl:20.500.11850/159536, ISSN 0272-4979

[11] 보흐카노프 세르게이 아나톨리예비치.ALGLIB 사용자 가이드 - 일반 매트릭스 연산 - 특이값 분해 . ALGLIB 프로젝트.2010-12-11.URL : [ 1 ]접속: 2010-12-11. (WebCite https://www.webcitation.org/5utO4iSnR?url=http 에서 아카이브 완료)

[12] Deift, Percy; Li, Luenchau C.; Tomei, Carlos (1985). "Toda flows with infinitely many variables". Journal of Functional Analysis. 64 (3): 358–402. doi:10.1016/0022-1236(85)90065-5.

[13] Colbrook, Matthew J.; Hansen, Anders C. (2019). "On the infinite-dimensional QR algorithm". Numerische Mathematik. 143 (1): 17–83. arXiv:2011.08172. doi:10.1007/s00211-019-01047-5.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

v t 수치 선형 대수
주요 개념	부동 소수점 수치 안정성
문제	선형 방정식 체계 행렬 분해 행렬 곱셈(알고리즘) 행렬 분할 희박한 문제
하드웨어	CPU 캐시 TLB 캐시 오비어스 알고리즘 SIMD 멀티프로세서
소프트웨어	매트랩 기본 선형 대수 서브 프로그램(BLAS) 랩 전문 라이브러리 범용 소프트웨어

Search