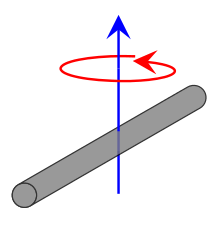
고정 회전 축에 대한 회전 관성의 스칼라 측정
관성 모멘트 플라이휠 은 회전 운동을 부드럽게 하기 위해 관성 모멘트가 큽니다.공통 기호
I SI 단위 킬로미터2 기타 유닛
lbf·ft·s2 파생상품 기타 수량
I = L ω {\displaystyle I=syslogfrac {L}{\obega }} 치수 M L 2
줄타기 를 하는 사람들 은 줄을 걸을 때 긴 막대기의 관성 순간을 균형을 잡습니다.1890년 나이아가라 강 을 건너는 사무엘 딕슨. 기동성을 향상시키기 위해, 전투기는 상업용 비행기에 비해 관성 모멘트가 작도록 설계되었다.
강체 의 관성 모멘트 , 각도 질량 , 두 번째 질량 모멘트 또는 가장 정확하게 는 회전 축에 대한 원하는 각도 가속도 에 필요한 토크를 결정 하는 양으로, 질량이 원하는 가속도에 필요한 힘 을 결정하는 방법 과 유사합니다.이는 차체의 질량 분포와 선택한 축에 따라 달라지며, 모멘트가 클수록 차체의 회전 속도를 변화시키기 위해 더 많은 토크가 필요합니다.
이것 은 광범위 한(가법적) 특성입니다. 점 질량의 경우 관성 모멘트는 단순히 질량에 회전 축에 대한 수직 거리의 제곱을 곱한 값입니다.강체 복합 시스템의 관성 모멘트는 구성 요소 하위 시스템의 관성 모멘트의 합입니다(모두 동일한 축에 대해 취함). 가장 간단한 정의는 축 으로부터의 거리에 대한 두 번째 질량 모멘트입니다.
평면 내에서 회전하도록 구속된 물체의 경우 평면에 수직인 축에 대한 관성 모멘트인 스칼라 값만 문제가 됩니다. 3차원 회전이 자유로운 물체의 경우, 그 모멘트는 대칭 3 × 3 행렬로 설명할 수 있으며, 이 행렬 이 대각선 이고 축 주위의 토크는 서로 독립적으로 작용한다.
서론 Body가 축을 중심으로 자유자재로 회전할 때 Torque를 가하여 각운동량 을 변화시켜야 합니다. 주어진 각가속도 (각속도 의 변화율)를 발생시키는 데 필요한 토크의 양은 물체의 관성 모멘트에 비례합니다.관성 모멘트는 SI 단위 로 킬로그램 미터 제곱(kg·m2 ) 단위, 영국 단위 또는 미국 단위 로 파운드-피트 제곱(lbf·ft·s2 ) 단위로 표시할 수 있다.
관성 모멘트는 질량(관성)이 선형 동력학에서 수행하는 회전 속도학에서 역할을 하며, 둘 다 물체의 운동 변화에 대한 저항의 특성을 나타냅니다. 관성 모멘트는 회전 축을 중심으로 질량이 분포되는 방식에 따라 달라지며 선택한 축에 따라 달라집니다. 점 같은 질량의 경우, 어떤 축 ({displaystyle ^{ }) 여기 r displaystyle } displaystyle } 확장된 강체의 경우, 관성 모멘트는 모든 작은 질량의 조각에 회전하는 축으로부터의 거리의 제곱을 곱한 합입니다. 정규 형태와 균일한 밀도의 확장된 물체의 경우, 이 합계는 물체의 치수, 모양 및 총 질량에 따라 달라지는 단순한 식을 만들어 낼 수 있습니다.
1673년 Christiaan Huygens 는 복합 [1] 관성 모멘트라는 용어 는 레온하르트 오일러에 의해 [1] [2] 그 의 책 Theoryia motus corpusum solidorum seu rigidorum에서 소개되었고, 오일러의 제2법칙에 통합 되었다.
복합진자의 고유진동 주파수는 진자 질량에 중력이 가하는 토크와 관성모멘트에 의해 정의된 가속저항의 비율에서 구한다. 이 고유 주파수와 단일 질량점으로 이루어진 단순한 진자의 주파수를 비교하는 것은 확장된 물체의 [3] [4]
관성 모멘트는 운동량, 운동 에너지, 그리고 강체에 대한 뉴턴의 운동 법칙 에서도 형태와 질량을 결합한 물리적 매개변수로 나타납니다. 평면 운동과 공간 운동에서 관성 모멘트가 나타나는 방식에는 흥미로운 차이가 있다. 평면 이동은 관성 모멘트를 정의하는 단일 스칼라를 가지며, 공간 이동의 경우 관성 매트릭스 또는 관성 [5] [6]
회전 하는 플라이휠의 관성 모멘트는 기계의 회전 출력을 부드럽게 하기 위해 적용된 토크의 변동을 저항하기 위해 사용됩니다.세로, 수평 및 수직 축에 대한 비행기의 관성 모멘트는 날개, 엘리베이터 및 방향타의 제어 표면에 대한 조향력이 롤링, 피치 및 요에서 비행기의 움직임에 어떻게 영향을 미치는지를 결정합니다.
정의. 관성 모멘트 는 단면의 질량과 기준 축과 단면의 중심 사이의 거리 제곱의 곱으로 정의된다.
회전하는 피겨 스케이터는 팔을 끌어당겨 관성 모멘트를 줄일 수 있어 각운동량을 보존 해 회전 속도를 높일 수 있다. 회전 의자 실험 영상으로 관성 모멘트를 보여줍니다. 회전하는 교수가 팔을 당기면 관성 모멘트가 감소하고 각운동량을 보존하기 위해 각속도가 증가한다. 관성 모멘트 I는 또한 주축을 [7] [8] 각속도 θ 에 대한 시스템의 순 각운동량 L의 비율로 정의된다.
시스템의 각운동량이 일정하면 관성모멘트가 작아질수록 각속도는 높아져야 합니다. 이는 회전 하는 피겨 스케이터가 [7] [8] [9] [10] [11] [12] [13] 끌어당기거나 다이빙을 하는 동안 몸을 구부릴 때 발생한다.
물체의 모양이 변하지 않는다면, 뉴턴의 운동 법칙 에서 주축을 중심으로 한 각가속도α 에 대한 물체에 가해진 토크θ 의 비율로 관성 모멘트가 나타난다.
단순 진자의 경우, 이 정의는 진자의 질량 m과 피벗 지점으로부터의 거리 r의 관점에서 관성 모멘트에 대한 공식을 다음과 같이 산출한다.
I = m r 2 . (\displaystyle I=mr^{2}). }
따라서, 진자의 관성 모멘트는 회전축까지의 거리 r에 의해 정의된 물체의 질량 m과 기하학 또는 형태에 따라 달라진다.
이 간단한 공식은 임의의 형태의 물체에 대한 관성 모멘트를 모든 요소 점 질량 각각 축 k에 대한 수직 거리 r의 제곱을 곱한 것으로 정의하기 위해 일반화된다. 따라서 임의의 물체의 관성 모멘트는 질량의 공간적 분포에 따라 달라집니다.
일반적으로 질량 m의 물체가 주어졌을 때 유효 반지름 k는 특정 회전 축에 따라 정의될 수 있으며, 축 주위의 관성 모멘트는 다음과 같다.
I = m k 2 , {\displaystyle I=param^{2}} 여기 서 k는 축을 중심으로 한 회전 반지름 으로 알려져 있습니다.
예 단순 진자 수학적으로 단순 진자의 관성 모멘트는 진자의 축 주위의 중력에 의한 토크와 그 축 점 주위의 각가속도의 비율이다. 단순한 진자의 경우, 이것은 피벗까지의 거리 (\displaystyle ) 입자 displaystyle )
I = m r 2 . (\displaystyle I=mr^{2}). }
이것은 다음과 같이 표시할 수 있습니다. 단순진자 질량에 가해지는 중력은 진자 이동면에 수직인 축을 중심으로 토크 θ = F displaystyle mathbf {r}=\ \mathbf {F}} 여기 displaystyle \mathbf {r}} 벡터 displaystyle \mathbf {F}} 이 토크와 관련된 것은 이 축 주위의 끈과 질량의 각도 가속도α (\ displaystyle\boldsymbol\alpha }) 질량이 원으로 구속되므로 질량의 접선 가속도 =α r displaystyle \ mathbf {a } times mathbf {r} = m 다음 .
τ = r × F = r × ( m α × r ) = m ( ( r ⋅ r ) α − ( r ⋅ α ) r ) = m r 2 α = I α k ^ , {\displaystyle{\begin{정렬}{\boldsymbol{\tau}}&=\mathbf{r}\times(m{\boldsymbol{\alpha}}\mathbf{r}\times)\\&{F}=\mathbf{r}\times \mathbf, =m\left(\left(\mathbf{r}\cdot{r}\right\mathbf){\boldsymbol{\alpha}}-\left(\mathbf{r}\cdot{\boldsymbol{\alpha}}\right)\mathbf{r}\right)\\&, =mr^{2}{\boldsymbol{\alpha}}=I\a.lpha \mathbf {k},\end{aligned}}
여기 ^ {\displaystyle mathbf {k}} (두 번째 단계부터 마지막 단계까지 (\displaystyle\boldsymbol\ (\displaystyle\mathbf }) 벡터 트리플 곱 확장 을 사용합니다.) I = m r displaystyle =mr^{2}}) 관성 모멘트 이다.
I = m r 2 displaystyle mr^{2 각운동량 에도 나타나며, 여기서 피벗 주위의 질량 진자의 속도 = δ r mathbf {v} times \ mathbf r } mathbf { v}) 계산 는 피벗 지점 주변의 질량 의 각 속도입니다. 이 각운동량은 다음과 같이 주어진다.
L = r × p = r × ( m ω × r ) = m ( ( r ⋅ r ) ω − ( r ⋅ ω ) r ) = m r 2 ω = I ω k ^ , \displaystyle \mathbf {L} &=\mathbf {r} \times \mathbf {p} =\mathbf {r} \times \left ( m'bold symbol \ obega }} \times \mathbf {right ) \ \&=m\left(\mathbf {r} \right) {\boldsymbol {mathbf {r}}-\left(\mathbf {r} \cdot \boldsymbol {r} \right) \\mathbf {right} = {\boldsymbol } I\motebf {k},\end {aligned}} 이전 방정식과 유사한 파생물을 사용하여.
마찬가지로, 진자 질량의 운동 에너지는 산출하기 위해 피벗 주위의 진자 속도에 의해 정의된다.
E K = 1 2 m v ⋅ v = 1 2 ( m r 2 ) ω 2 = 1 2 I ω 2 . ({displaystyle E_{\text{K}}=mathbf {v} \cdot \mathbf {v} =mathbf {v} =mathbf {1} {2} =mathfrac {1} {2} =modec frac {1} {2}} 나는 ^{2}. }
이것은 I = m r displaystyle =mr^{2}}) 임의의 형상의 물체의 관성 모멘트는 물체의 모든 질량 요소 값 m ({ 디스플레이 ^{2}})
복합 진자 1897년 과학저널에서 나온 멘덴홀 중력계 장치에 사용된 진자. 휴대용 중력계는 1890년 토마스 C에 의해 개발되었다. 멘덴할은 지구의 국지적 중력장에 대한 가장 정확한 상대적인 측정치를 제공했다. 복합진자 는 피벗을 중심으로 강직하게 회전하는 연속된 형태의 입자의 집합체로 이루어진 물체이다.관성 모멘트는 각 [14] [15] : 395–396 [16] : 51–53 복합진자의 고유 진동수(δ displaystyle \obega {\text{n I (\ displaystyle I_{P
ω n = m g r I P , \displaystyle \mega _{\text{n}}=\displayrt {frac {mgr}{ I_{P}}}},} 여기 displaystyle } displaystyle } displaystyle } 이 진동 주파수를 작은 각도 변위에 걸쳐 측정하는 것은 [17] : 516–517
따라서 신체의 관성모멘트를 결정하려면 원하는 관성모멘트의 방향과 수직인 평면에서 자유롭게 흔들리도록 편리한 피벗점 displaystyle ) t(\displaystyle
I P = m g r ω n 2 = m g r t 2 4 π 2 , ({displaystyle I_{P}=mgr}{\opega_{\text{n}^{2}}=mgrac{mgrt^{2}}{4\pi^{2}}) 여기 displaystyle }
진동의 중심 복합진자와 동일한 고유진자를 갖는 단순진자는 피벗에서 복합진자의 진동중심 이라고 불리는 지점까지의 길이 displaystyle ) 이 점은 타악기의 중심 에도 해당합니다. 길이 displaystyle )
ω n = g L = m g r I P , \displaystyle \mega _{\text{n}}=\displayrt {frac {g}{ L}} = sqrt { frac { mgr } { I_{P}}}},} 또는 L = g ω n 2 = I P m r . {\displaystyle L=black {g}{\otext{n}}^{2}}=black {I_{P}}{mr}}. }
할아버지 시계의 똑딱똑딱 소리를 내는 초진자는 좌우 로 흔들리는 데 1초가 걸린다. 이것은 2초의 주기, 즉 진자의 고유 주파수 θ a displaystyle \ pi mathrm { rad s } 이 경우 진동 중심까지의 거리 displaystyle }
L = g ω n 2 ≈ 9.81 m / s 2 ( 3.14 r a d / s ) 2 ≈ 0.99 m . {{displaystyle L=mathrm {rad/s}^{displaystyle {g}{\offer _{\text{n}^2}}\약 {frac {9.81\\mathrm {m/s^2}}{.14\mathrm {rm {rm {rm}^2}}^{2}\약 0.99\m {m}
초 진자의 진동 중심까지의 거리는 국소 중력 가속에 대한 다른 값을 수용하도록 조정해야 합니다. 케이터의 진자 는 이 성질을 이용해 국부적인 중력가속도를 측정하는 복합진자이며 중력계 라고 불린다.
관성모멘트 측정 수직축을 중심으로 차량이나 비행기와 같은 복잡한 시스템의 관성 모멘트는 시스템을 3개의 지점에서 매달아 3개 의 진자를 형성함으로써 측정할 수 있다. 삼원추는 수직 중심축을 [18] 삼원추의 진동 주기는 시스템의 [19]
면적의 관성 모멘트 면적의 관성 모멘트는 면적 의 두 번째 모멘트 로도 알려져 있습니다. 이러한 계산은 일반적으로 토목 공학에서 보와 기둥의 구조 설계를 위해 사용됩니다. X축 I x x x x x 높이(h )와 폭(b )은 사실상 절반으로 도출된 원을 제외한 선형 측도입니다. r\displaystyle
단면적 모멘트는 다음과 같이 계산됩니다[20] 정사각형: I x = I y = b 12 { displaystyle I_{x = I_{y}=bfrac {b^{4}}{12}} 직사각형: I x = b h 12 { display style xx = flac display I y = h b 12 { display style flac hb 3 12 } 삼각형: I x = b h 3 36 { display style I _ { xx } = fr { frac { snaper^ { 3 } { 36 } 원형: I x = I y = 1 4 r displaystyle I_{x } = I_{y}=blashfrac {1}{4}{\pi }r^{4} 고정 평면에서의 움직임 점질량 같은 질량과 반지름을 가진 4개의 물체가 미끄러지지 않고 구르면서 비행기를 질주합니다.
뒷면부터 앞면까지:
각 물체가 결승선에 도달하는 시간은 관성 모멘트에 따라 달라집니다.(OGV 버전 )물체의 축에 대한 관성 모멘트는 물체의 모든 입자에 대해 m r 2 (\ displaystyle ^{2}) 더하여 여기 \displaystyle 확장된 물체의 이동에 대한 연구에서 관성 모멘트가 어떻게 발생하는지 확인하려면 점 질량의 강성 어셈블리를 고려하는 것이 편리합니다. (이 방정식은 관성 모멘트를 완전히 나타내지 않는 것으로 이해되면 주축이 아닌 축에 사용할 수 있습니다.)[21]
회전축에서 가장 가까운 피벗점 displaystyle ) ri (\ displaystyle r_i}) 거리 (\displaystyle ) 질량 mi (\ displaystyle m_i}) 이것은 개별 [17] : 516–517 [22] : 1084–1085 [22] : 1296–1300
E K = ∑ i = 1 N 1 2 m i v i ⋅ v i = ∑ i = 1 N 1 2 m i ( ω r i ) 2 = 1 2 ω 2 ∑ i = 1 N m i r i 2 . \displaystyle E_{\text{K}=\sum _{i=1}^{N}{\frac {1}{2},m_{i}\mathbf {v}_{i}=\sum _{i=1}^N}{\frac {2},m}{i}_i}{i} }
이는 신체의 관성 모멘트가 각 m r ({ displaystyle ^{2}}) 항의
I P = ∑ i = 1 N m i r i 2 . {\displaystyle I_{P}=\sum _{i=1}^{N}m_{i}r_{i}^2}. }
따라서 관성모멘트는 회전축 주위의 입자의 질량과 분포를 결합한 물리적 특성입니다. 동일한 물체의 서로 다른 축을 중심으로 회전하면 서로 다른 관성 모멘트가 생성됩니다.
지정된 축을 중심으로 회전하는 연속체의 관성 모멘트는 무한히 많은 점 입자를 제외하고 동일한 방법으로 계산됩니다. 따라서 합계의 한계가 제거되고 합계는 다음과 같이 작성됩니다.
I P = ∑ i m i r i 2 {\displaystyle I_{P}=\sum _{i}m_{i}r_{i}^2}
또 다른 식은 합계를 적분 으로 대체한다.
I P = ∭ Q ρ ( x , y , z ) ‖ r ‖ 2 d V \displaystyle I_{P}=\iint_{Q}\rho(x,y,z)\left\mathbf {r}\right\^{2}dV}
여기서 함수 {\{ displaystyle \rho } ( x , y z ) (x,y,z displaystyle \mathbf {r} 회전축상의 (x , , ) 통합은 차체 Q 볼륨 displaystyle }) . 평평한 표면의 관성 모멘트는 면적 밀도로 대체되는 질량 밀도와 면적에 대해 평가된 적분과 유사합니다.
영역 의 두 번째 순간에 대한 주의 :평면 내에서 움직이는 물체의 관성 모멘트와 빔 단면적 의 두 번째 모멘트 는 종종 혼동된다. 단면의 형상을 가진 물체의 관성 모멘트는 밀도로 가중된 단면에 수직인 z(\displaystyle ) 이것은 영역의 극성 모멘트 라고도 불리며 x축 y축 [23] . 빔 의 응력은 부하에 따라 x(\ displaystyle displaystyle )
예 막대의 반대쪽 끝의 피벗을 중심으로 진동하는 얇은 막대의 끝에 장착된 얇은 원반으로 구성 된 복합 진자의 관성 모멘트는 얇은 막대와 얇은 원반의 각각의 [22]
질량 중심을 통과하는 수직축에 대하여 일정한 단면 s displaystyle\rho}, displaystyle\ell} 얇은 막대의 관성 모멘트는 [22] : 1301 x축과 I C , 막대기 = ∭ Q ρ x 2 d V = ∫ − ℓ 2 ℓ 2 ρ x 2 s d x = ρ s x 3 3 − ℓ 2 ℓ 2 = ρ s 3 ( ℓ 3 8 + ℓ 3 8 ) = m ℓ 2 12 , {\displaystyle I_{C,{\text{rod}}=\iint _{Q}\rho \x^{2},dV=\int _{-{\frac {ell}{2}}{\rho },x^{2}s,rho =\left. \rho swarfrac {x^{3}}{-{\frac {ell}{2}}{\frac {2}}=warfrac {rho s}{3}}{left\frac {8}+{\frac {\ell ^3}}{8}}{\fraclac {\frac }{{\fright}{\frec }{frac }{\frac } 여기 = ρ ℓ display rho \ell } 회전대칭축 과 평행한 축을 중심 두께 \displaystyle \, 반지름 displaystyle \ rho θ \displaystyle\ [22] : 1301 [failed verification 적분에 의해 결정된다.z displaystyle } V = s r d † displaystyle dV sr,dr,d\theta } 정의 I C , 디스크 = ∭ Q ρ r 2 d V = ∫ 0 2 π ∫ 0 R ρ r 2 s r d r d θ = 2 π ρ s R 4 4 = 1 2 m R 2 , {\displaystyle I_{C,{\text{disc}}=\iint _{Q}\rho \rho \rho \rho {2}{0}\int _{0}{R}\rho r^{2}sr,dr,dr\theta =2\rho sfrcrcr4}{{0} {0} {0} {0} {rcrcrfrfrcr} {r} 여기 = 2 s displaystyle pi ^{2}\rho } 복합 진자의 관성 모멘트는 다음과 같이 피벗 포인트 displaystyle ) I P = I C , 막대기 + M 막대기 ( L 2 ) 2 + I C , 디스크 + M 디스크 ( L + R ) 2 , {\displaystyle I_{P}=I_{C,{\text{rod}}+M_{\text{rod}}\left({\frac {L}{2}\right)^{2}+I_{C,{\text{disc}}+M_{\text{Disc}}}^{2}, 여기 (\displaystyle ) 평행축 정리는 관성 모멘트를 질량 중심에서 진자의 피벗 점으로 이동시키는 데 사용됩니다. 표준 체형에 대한 관성 모멘트의 목록은 복잡한 체형의 관성 모멘트를 단순한 체형의 집합체로서 얻을 수 있는 방법을 제공한다.평행축 정리는 개별 물체의 기준점을 어셈블리의 기준점으로 이동하는 데 사용됩니다.
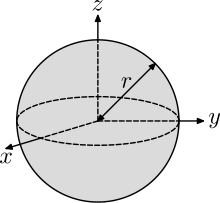
또 하나의 예로, 질량 중심을 통과하는 축 주위의 일정한 밀도의 고체 구체의 관성 모멘트를 생각해 봅시다. 이는 고려 대상으로 선택한 축을 따라 중심이 있는 구를 형성할 수 있는 얇은 디스크의 관성 모멘트를 합산하여 결정됩니다. 볼의 표면이 다음 식에[22] : 1301
x 2 + y 2 + z 2 = R 2 , {\displaystyle x^{2}+y^{2}+z^{2}=R^{2}}
z축 따른 횡단면 디스크 반지름 제곱 같습니다 .
r ( z ) 2 = x 2 + y 2 = R 2 − z 2 . {\displaystyle r(z)^{2}=x^{2}+y^{2}=R^{2}-z^{2}. }
따라서 볼의 관성 모멘트는 z\displaystyle
I C , 공 = ∫ − R R π ρ 2 r ( z ) 4 d z = ∫ − R R π ρ 2 ( R 2 − z 2 ) 2 d z = π ρ 2 [ R 4 z − 2 3 R 2 z 3 + 1 5 z 5 ] − R R = π ρ ( 1 − 2 3 + 1 5 ) R 5 = 2 5 m R 2 , 디스플레이 스타일 I_{C,{\text{ball}}&=int _{-R}^{R}{\frac {pi \rho }{2}{2}{2}{2}{\frac {pi \rho }{-R}^4},dz=\int _{-R}{R}{R}{R}{\frac {\rh}{{{{{\}}}{{{\}}}}{\}}}}{\fright(오른쪽}{{{{\frac {-}}}}}}}}}} R^{5}\\&=sqfrac {2}{5}}mR^{2},\end{aligned}} 여기 = 4 µ 3 µ textstyle specfrac {4}{3}}\pi ^{3}\rho
강체 관성 모멘트가 높은 실린더는 더 많은 잠재적 에너지를 회전 운동 에너지로 변환해야 하기 때문에 더 작은 가속도로 경사면을 굴러 내려갑니다. 기계 시스템 이 고정 평면에 평행하게 움직이도록 구속된 경우 시스템 내 본체의 회전이 이 평면에 수직인축 ^\ displaystyle \mathbf {k} } 이 경우 이 시스템에서 질량의 관성 모멘트는 극성 관성 모멘트 로 알려진 스칼라입니다. 극성 관성 모멘트의 정의는 [14] [17] [24] [25]
n개(\displaystyle ) 입자Pi i = 1 …, n개 displaystyle P_{i i=1,\dots, }) 구성 기준점 displaystyle \mathbf {R 속도 displaystyle i ) \mathbf {v} _{i
Δ r i = r i − R , v i = ω × ) r i − R ) + V = ω × Δ r i + V , {\displaystyle{\begin{정렬}\Delta\mathbf{r}_{나는}&, =\mathbf{r}_{나는}-\mathbf{R},\\\mathbf{v}_{나는}&, ={\boldsymbol{\omega}}\times \left(\mathbf{r}_{나는}-\mathbf{R}\right)+\mathbf{V}={\boldsymbol{\omega}}_{나는}+\mathbf{V},\end{정렬}{r}}};=\mathbf{r\Delta \mathbf{\displaystyle{{정렬되기 시작}\Delta\mathbf{r}_{나는}& \times}_{나는}-\mathb f {r},\\times \left(\mathbf {r}_i}_{i}-\mathbf {r},\mathbf {r},\r},\mathbf {r},\mathbf {r},\mathbf {r},\mathbf {r} 여기 {\({ displaystyle\boldsymbol\mega}}) ({ displaystyle\mathbf {V}) ({ displaystyle\mathbf {R
평면 이동의 경우 각 속도 벡터는 이동 평면에 수직인 단위 벡터 \ displaystyle \mathbf {k} 단위 벡터 e 기준점 (\ displaystyle \mathbf {R}) r (\ displaystyle \mathbf {R , 벡터 t = k e (\ displaystyle \mathbf {t} _mathbf k bf {e}} _{i
e ^ i = Δ r i Δ r i , k ^ = ω ω , t ^ i = k ^ × e ^ i , v i = ω × Δ r i + V = ω k ^ × Δ r i e ^ i + V = ω Δ r i t ^ i + V {\displaystyle{\begin{정렬}\mathbf{\hat{e}}_{나는}&, ={\frac{\Delta \mathbf{r}_{나는}}{\Delta r_{나는}}},\quad\mathbf{\hat{k}}={\frac{\boldsymbol{\omega}}{\omega}},\quad\mathbf{\hat{t}}_{나는}=\mathbf{\hat{k}}}{v}_{나는}& _{나는},\\\mathbf, ={\boldsymbol{\omega}}_{나는}+\mathbf{V}=\ome{r}\Delta \mathbf \times\mathbf{\hat{e}\times.ga \math {displaystyle}\mathbfhat{e}_{display}&, =displayfrac 델타 \mathbf{r}_{delta r_{delta}},\delta r_{delta hat{k}},\delta\mathbf hat{k},\delta\delta\mathbf hat{k}},\mathbfbqsymboldsymbol\mbol{mbol}{mb}{mb}}}{\mb}{\mb}{\mb}{mb}{mb}}}{\mb} ome{r}\Delta \mathbf \times\mathbf hat{ . ga \times
이는 평면 내에서 이동하는 입자의 강체 시스템에 대한 상대 위치 벡터와 속도 벡터를 정의합니다.
크로스 프로덕트에 관한 주의 :본체가 지면과 평행하게 이동하면 본체에 있는 모든 점의 궤적이 이 지면과 평행한 평면에 놓입니다. 이것은 신체가 겪는 모든 회전이 이 평면에 수직인 축 주위에 있어야 한다는 것을 의미합니다. 평면 이동은 종종 회전 축이 점으로 나타나도록 그라운드 평면에 투영된 상태로 나타납니다. 이 경우 물체의 각속도와 각가속도는 스칼라이며 회전축을 따라 벡터라는 사실은 무시된다. 이것은 보통 주제에 대한 소개에 선호됩니다. 그러나 관성 모멘트의 경우, 질량과 기하학의 조합은 교차곱의 기하학적 특성으로부터 이익을 얻는다. 이 때문에 평면운동에 관한 본 절에서는 물체의 각속도 및 가속도는 지면과 수직인 벡터이며, 교차곱 연산은 공간강체운동 연구에 사용되는 것과 같다.
입자의 단단한 시스템의 평면 운동을 위한 각 운동량 벡터는 다음과 같이 주어진다[14] [17]
L = ∑ i = 1 n m i Δ r i × v i = ∑ i = 1 n m i Δ r i e ^ i × ) ω Δ r i t ^ i + V ) = ) ∑ i = 1 n m i Δ r i 2 ) ω k ^ + ) ∑ i = 1 n m i Δ r i e ^ i ) × V . {\displaystyle{\begin{정렬}\mathbf{L}&=\sum _{i=1}^{n}m_{나는}\Delta \mathbf{r}_{나는}\times{v}_{나는}\\& \mathbf,=\sum _{i=1}^{n}m_{나는}\,\Delta r_{나는}\mathbf{\hat{e}};=\sum _{i=1}^{n}m_{나는}\delta \mathbf{r}_{나는}\times)\left(\omega\,\Delta r_{나는}\mathbf{\hat{t}}_{나는}+\mathbf{V}\right){{naligned\displaystyle}\mathbf{L}및 _{나는}\times.mathbf{v}_{ 나는}\&, ={i=1}^n_m_{나는},\delta r_hati}{mathb}{나는}{f}\\&, =\left(\sum_{i=1}^{n}m_{나는}\,\Delta r_{나는}^{2}\right)\omega \mathbf{\hat{k}}}}\\&\mathbf{V}.\end{정렬}+\left(\sum_{i=1}^{n}m_{나는}\,\Delta r_{나는}\mathbf{\hat{e}}_{나는}\right)\times, =\left(\sum_{i=1}^{n{나는},\Delta r_{나는}{2}^\right)\mathbf{k}+\left(\sum _i=1}^{n}m_{나는},\delta r_{e}\ma.thbhat{시간 s}{i})
질량 중심 을 기준점으로 사용합니다(\displaystyle \mathbf {C} 。
Δ r i e ^ i = r i − C , ∑ i = 1 n m i Δ r i e ^ i = 0 , _}^{e},\ {0}) _i})
질량 중심 대한 정의한다.
I C = ∑ i m i Δ r i 2 , _{ ,\2} {\displaystyle I_{\mathbf {C}} =\sum _{i} m_{i} ^2}
그러면 각운동량의 방정식은 으로 단순화된다[22] : 1028
L = I C ω k ^ . \}{C} { {\displaystyle \mathbf {L}=I_{\mathbf {C}}\Omathbf {k}}}
강성계 이동에 수직인 축을 중심으로 질량 중심을 통과하는 관성 C style {\mathbf {C}}} 극성 관성 모멘트 라고 합니다. 구체적으로는 축(또는 극)으로부터의 직교 거리에 대한 두 번째 질량 모멘트 입니다.
주어진 각운동량의 경우 관성모멘트의 감소는 각속도의 증가를 초래한다. 피겨 스케이터는 팔을 끌어당김으로써 관성 순간을 바꿀 수 있다. 따라서 팔을 뻗은 스케이트 선수가 얻는 각속도는 관성 모멘트가 감소하기 때문에 팔을 끌어당길 때 더 큰 각속도를 낳는다. 하지만 피겨 스케이터는 단단한 몸이 아니다.
이 1906년 회전 전단기는 두 개의 플라이휠의 관성 모멘트를 사용하여 운동 에너지를 저장합니다. 국제공대도서관, 1906년) 평면 내에서 움직이는 입자의 단단한 시스템의 운동 에너지는 다음과 같이 주어진다[14] [17]
E K = 1 2 ∑ i = 1 n m i v i ⋅ v i , = 1 2 ∑ i = 1 n m i ) ω Δ r i t ^ i + V ) ⋅ ) ω Δ r i t ^ i + V ) , = 1 2 ω 2 ) ∑ i = 1 n m i Δ r i 2 t ^ i ⋅ t ^ i ) + ω V ⋅ ) ∑ i = 1 n m i Δ r i t ^ i ) + 1 2 ) ∑ i = 1 n m i ) V ⋅ V . {\displaystyle{\begin{정렬}디스플레이 스타일E_{\text{K}}&={\frac{1}{2}}\sum _{i=1}^{n}m_{나는}\mathbf{v}_{나는}\cdot\mathbf{v}_{나는},\\&, ={\frac{1}{2}}\sum _ᆷ^ᆸm_ᆹ\left(\omega\,\Delta r_{나는}\mathbf{\hat{t}}_{나는}+\mathbf{V}\right)\cdot \left(\omega\,\Delta r_{나는}\mathbf{\hat{t}}_{나는}+\mathbf{V}\right),\\&, ={\frac{1}{2}}\omega ^.{2}\left(\su E_{\text{K}}&=sum_{i=1}^{n}m_{sum}\mathbf{v}_{sum}\cdot\mathbf{v}_{sum}\cdot\mathbf{v}_{sum},\&, =smatfrac{1}{2}}{sum}{{sum}{sum}{{sum}{sum}{sum}{sum}{sum}{sum}{sum}{sum}{sum}{sum}{s V}\right)\cdot \left(\omega,\Delta r_{}}\mathbf{\hat{t}}_{나}+\mathbf{ V(\right),\\sum. {cdot}^{ 2mathbf ,\cdot r_{t}_i}\mathbf {i}\cdot {1}{cdot} {cdot}
기준점을 두 번째 항이 0이 되도록 시스템의 질량 (\displaystyle {C}) 관성 I (\ displaystyle I_{\mathbf {C}}}) [22] : 1084
E K = 1 2 I C ω 2 + 1 2 M V ⋅ V . frac displaystyle E_{\text{K}=black {1}{2}} I_{\mathbf {C}}\obega ^{2}+{\frac {1}{2}}M\mathbf {V} \cdot \mathbf {V} .}
관성 I style {\mathbf {C}}} 극성 관성 모멘트 이다.
엔진에 스포크 플라이휠 이 달린 1920년대식 존 디어 트랙터. 플라이휠의 큰 관성 모멘트가 트랙터의 작동을 부드럽게 합니다. n개의 displaystyle } 개 이루어진 대한 Pi , i = 1 …, n i},\ ,n 기준점 displaystyle \mathbf {R [14] [17]
F = ∑ i = 1 n m i A i , τ = ∑ i = 1 n Δ r i × m i A i , & _i}\ _{ {f { {i 여기 \ displaystyle \mathbf {r} _{i}
강체의 운동학 에서는 기준 입자의 위치 (\displaystyle \mathbf { }) 가속도 displaystyle mathbf }) displaystyle \boldsymbo ) 입자 Pi l mega }} 벡터 α( 스타일 boldsymbol {\
A i = α × Δ r i + ω × ω × Δ r i + A . ({displaystyle \mathbf {A}_{i}=\times \delta \mathbf {r}_{i}+{\boldsymbol {i}})\times \delta \mathbf {r}_{i}\times
평면 이동에 구속된 시스템의 경우 각 속도와 각가속도 벡터는 이동 평면에^\displaystyle\mathbf {k}} 이 벡터 i displaystyle \ mathbf e } i mathbf R } i i 、 e \displaystyle \mathbf {t} _{ } = \mathbf k} \times e} _ }
A i = α k ^ × Δ r i e ^ i − ω k ^ × ω k ^ × Δ r i e ^ i + A = α Δ r i t ^ i − ω 2 Δ r i e ^ i + A . {\displaystyle{\begin{정렬}\mathbf{A}_{나는}&, =\alpha \mathbf{\hat{k}}\Delta r_{나는}\mathbf{\hat{e}\times}}}\Delta r_{나는}\mathbf{\hat{e}\times}{A}\\& _{나는}+\mathbf\omega \mathbf{\hat{k}\times,=\alpha \Delta r_{나는}\mathbf{\hat{t}}_{나는}-\omega ^{2}\Delta r_{나는}\mathbf{\hat{e}}{A}.\en _{나는}+\mathbf\mathbf{\hat{k}_{나는}-\omega.d{aligne d}}}
이로 인해 시스템에 다음과 같은 토크가 생성됩니다.
τ = ∑ i = 1 n m i Δ r i e ^ i × ( α Δ r i t ^ i − ω 2 Δ r i e ^ i + A ) = ( ∑ i = 1 n m i Δ r i 2 ) α k ^ + ( ∑ i = 1 n m i Δ r i e ^ i ) × A , {\displaystyle {\boldsymbol {n}{i=1}^{n}m_{i},\Delta r_{i},\times \left(\alpha \Delta r_{i},\mathbf {i},\delta r2},\Delta {i},\delta r}, {i},\ta r}, {i}, {delta}, {i},\ta}, {i},\ta r},\ta}, \\&=\left(\sum _{i=1}^{n_{i},\Delta r_{i}^{2}\right)\alpha \mathbf {k} +\left(\sum _i=1}^{n}m_{i},\delta r_mathbhat {e}\times}{i})
여기 i e i = 0 displaystyle mathbf { e } _ i mathbf 0 mathbf = k ^ displaystyle \ mathbf } _ mathbhat i } i times ticles Pi ( 디스플레이 스타일 {i
질량 C 중심 을 기준점으로 사용하고 질량 I displaystyle I_{\mathbf {C [22] : 1029
τ = I C α k ^ . {\displaystyle\boldsymbol\class}= I_{\mathbf {C}}\alpha \mathbf {k}}.
강체 공간에서의 움직임 및 관성 매트릭스 스칼라 관성 모멘트는 입자 시스템이 3차원 공간에서 움직이는 강체로 조립될 때 매트릭스의 요소로 나타납니다. 이 관성 행렬은 [3] [4] [5] [6] [26]
n개의 displaystyle } , Pi i = …, n displaystyle P_{i},i= dots, 시스템 좌표 r displaystyle \mathbf {r} _{ vi displaystyle \mathbf {v} { (움직일 수 있는 (\displaystyle \mathbf R
Δ r i = r i − R \displaystyle \Delta \mathbf {r} _{i}=\mathbf {r} _{i}-\mathbf {R} } 그리고 (절대) 속도는 v i = ω × Δ r i + V R \displaystyle \mathbf {v} _{i} = bold symbol {i} \times \Delta \mathbf {r} _{i} + \mathbf {R} } 여기서 displaystyle\boldsymbol\mega}}) V R({ displaystyle\mathbf {V_{R}}) ({ displaystyle\mathbf {R}) .
각운동량 첫 번째 피연산자와 연산자를 결합하여 행렬 곱셈으로 동등 하게 쓸 수 있습니다 . b ] display \left[\mathbf b } right b = b x b b display mathbf {b} b} z
b × y ≡ [ b ] y [ b ] ≡ [ 0 − b z b y b z 0 − b x − b y b x 0 ] . \displaystyle \mathbf {b} \times \mathbf {y} &\equiv \left[\mathbf {b} \right] \\equiv {\mathbf {b} \right} &\equiv {\mathbmatrix} 0&\b_{z}&\b} \end { aligned}}
관성행렬은 질량 C displaystyle mathbf }) [3] [6] 선택된 mathbf {R })
L = ∑ i = 1 n m i Δ r i × v i = ∑ i = 1 n m i Δ r i × ( ω × Δ r i + V R ) = ( − ∑ i = 1 n m i Δ r i × ( Δ r i × ω ) ) + ( ∑ i = 1 n m i Δ r i × V R ) , {\displaystyle {displaystyle}\mathbf {L} &=\sum _{i=1}^{n}m_{i} ,\Delta \mathbf {r} _{i} \times \mathbf {v} _{i} \sum {i=1}^{n}m_i},\ta \mathbf {i} {i} \&=\leftsum _{i=1}^{n},\Delta \mathbf {r} _{i} \times \left(\Delta \mathbf {r} _{i} \times \boldsymbol {i} \right) +\left(\sum _i=1}^{n},{i},\delti}) 여기서 V R (\ displaystyle \mathbf V_{R}})( = C displaystyle mathbf C} } 포함 질량 중심의 정의 에 따라 0이 된다.
다음으로 상대위치 벡터 δ r = r i displaystyle \Delta \mathbf {r} _ mathbf {r } mathbf } 스큐-matrix
L = ( − ∑ i = 1 n m i [ Δ r i ] 2 ) ω = I C ω , {\displaystyle \mathbf {L} =\leftsum _{i=1}^{n}\left[\Delta \mathbf {r} _{i}\right]^{2}\right) {\boldsymbol {I} =\mboldbf {C} 여기 (\ displaystyle\mathbf {I_{C . I C = − ∑ i = 1 n m i [ Δ r i ] 2 , \displaystyle \mathbf {I} _{\mathbf {C} =-\sum _{i=1}^{n}m_{i}\left[\Delta \mathbf {r} _{i}\right]^2} 는 질량 C(\ displaystyle \mathbf {C
운동 에너지 입자의 강체계의 운동 에너지는 시스템 의 질량 중심과 관성 모멘트의 매트릭스로 공식화할 수 있다. n개(\displaystyle ) 입자 Pi ,i = 1 ..., n개 displaystyle P_{i i=1,\dots,n}) 시스템 속도 vi (\ displaystyle \mathbf {v}_i {i 좌표 ri (\ displaystyle\ [3] [6]
E K = 1 2 ∑ i = 1 n m i v i ⋅ v i = 1 2 ∑ i = 1 n m i ( ω × Δ r i + V C ) ⋅ ( ω × Δ r i + V C ) , ({displaystyle E_{\text{K}}=sum {1}{n}m_{i}\mathbf {v}_{i}\cdot \mathbf {v}_{i}=sum _{i=1}^{n}m_{boldol}\symboldol {v}) where Δ r i = r i − C {\displaystyle \Delta \mathbf {r} _{i}=\mathbf {r} _{i}-\mathbf {C} }
이 방정식은 3항으로 확장된다.
E K = 1 2 ( ∑ i = 1 n m i ( ω × Δ r i ) ⋅ ( ω × Δ r i ) ) + ( ∑ i = 1 n m i V C ⋅ ( ω × Δ r i ) ) + 1 2 ( ∑ i = 1 n m i V C ⋅ V C ) . ({displaystyle E_{\text{K}}=bladfrac {1}{n_i}\left(\sum _{i=1}^{i}\left\boldsymbol {i}}\times \delta \mathbf {r}_{i}\times)\cdot \lftsymblef {{{{{i}\mbdelf}\ts}\t}\tes}\tembdelf}\temb}\temb}\times rac {1}{2}}\left(\sum _{i=1}^{n_{i}\mathbf {V}_{\mathbf {C}}\cdot \mathbf {V}_{\mathbf {C}\오른쪽) }
C mathbf {C} }) 때문 스큐 대칭 δ r i ] displaystyle [\Delta \mathbf {r} _{i}}}
E K = 1 2 ( ∑ i = 1 n m i ( [ Δ r i ] ω ) ⋅ ( [ Δ r i ] ω ) ) + 1 2 ( ∑ i = 1 n m i ) V C ⋅ V C = 1 2 ( ∑ i = 1 n m i ( ω T [ Δ r i ] T [ Δ r i ] ω ) ) + 1 2 ( ∑ i = 1 n m i ) V C ⋅ V C = 1 2 ω ⋅ ( − ∑ i = 1 n m i [ Δ r i ] 2 ) ω + 1 2 ( ∑ i = 1 n m i ) V C ⋅ V C . 디스플레이 스타일 E_{\text{K}}&={\frac{1}{2}}\left(\sum_{i=1}^{n}m_{나는}\left(\left[\Delta \mathbf{r}_{나는}\right]{\boldsymbol{\omega}}\right)\cdot \left(\left[\Delta \mathbf{r}_{나는}\right]{\boldsymbol{\omega}}\right)\right)+{\frac{1}{2}}}\cdot\mathbf{V}_{\mathbf{C}}\\&, ={\frac{1}{2}}\left{V}_{\mathbf{C}\left(\sum_{i=1}^{n}m_{나는}\right)\mathbf.(\sum_{ I=1}^ᆬm_ᆭ\left({\boldsymbol{\omega}}^{\mathsf{T}}\left[\Delta \mathbf{r}_{나는}\right]^{\mathsf{T}}\left[\Delta \mathbf{r}_{나는}\right]{\boldsymbol{\omega}}\right)\right)+{\frac{1}{2}}}\cdot\mathbf{V}_{\mathbf{C}}\\&, ={\frac{1}{2}}{\boldsymbol{\omega}}\cdot \left(-\sum{V}_{\mathbf{C}\left(\sum_{i=1}^{n}m_{나는}\right)\mathbf. _{i= 1) {{n}m_{i}\left[\Delta \mathbf {r}_{i}\right]^{2}\boldsymbol {\frac {1}{2}}\left(\sum _{i}^{n}m_{i}\right)\mathbf {V}_{F}_F}_F}
따라서, 입자의 강체계의 운동 에너지는 다음과 같이 주어진다.
E K = 1 2 ω ⋅ I C ω + 1 2 M V C 2 . ({displaystyle E_{\text{K}}=boldfrac {1}{2}}{\boldsymbol {\mathbf {I}_{\mathbf {C}_{\boldsymbol {C}}+{\frac {1}{2}}M\mathbf {C} {C}) } where I C {\displaystyle \mathbf {I_{C}} } M {\displaystyle M}
결과 토크 관성행렬은 뉴턴의 제2법칙을 입자의 강체집합에 적용하는 과정에서 나타난다. 이 시스템의 토크는 다음과 같습니다.[3] [6]
τ = ∑ i = 1 n ( r i − R ) × m i a i , {\displaystyle {\boldsymbol {n}={i=1}^{n}\left(\mathbf {r_i} -\mathbf {R} \right)\times m_{i}\mathbf {a}_{i} where a i {\displaystyle \mathbf {a} _{i}} P i {\displaystyle P_{i}} kinematics of a rigid body yields the formula for the acceleration of the particle P i {\displaystyle P_{i}} R {\displaystyle \mathbf {R} } A R {\displaystyle \mathbf {A} _{\mathbf {R} }} ω {\displaystyle {\boldsymbol {\omega }}} α {\displaystyle {\boldsymbol {\alpha }}} a i = α × ( r i − R ) + ω × ( ω × ( r i − R ) ) + A R . {\displaystyle \mathbf {a} _{i} =\times \left(\mathbf {r} ) _{i}-\mathbf {R} \right) + {\times \boldsymbol {a} \times \times \(\mathbf {r} ) _mathbi
질량 C δ ri] = r C displaystyle \left Delta \mathbf {r} _{i} left mathbf {r} _{i} mathbf} { e (\mathbf {r} _{i}-\mathbf {C} times }
τ = ( − ∑ i = 1 n m i [ Δ r i ] 2 ) α + ω × ( − ∑ i = 1 n m i [ Δ r i ] 2 ) ω {\displaystyle {\boldsymbol {\tau }}=\left(-\sum _{i=1}^{n}m_{i}\left[\Delta \mathbf {r} _{i}\right]^{2}\right){\boldsymbol {\alpha }}+{\boldsymbol {\omega }}\times \left(-\sum _{i=1}^{n}m_{i}\left[\Delta \mathbf {r} _{i}\right]^{2}\right){\boldsymbol {\omega }}}
The calculation uses the identity
Δ r i × ( ω × ( ω × Δ r i ) ) + ω × ( ( ω × Δ r i ) × Δ r i ) = 0 , {\displaystyle \Delta \mathbf {r} _{i}\times \left({\boldsymbol {\omega }}\times \left({\boldsymbol {\omega }}\times \Delta \mathbf {r} _{i}\right)\right)+{\boldsymbol {\omega }}\times \left(\left({\boldsymbol {\omega }}\times \Delta \mathbf {r} _{i}\right)\times \Delta \mathbf {r} _{i}\right)=0,} obtained from the Jacobi identity for the triple cross product as shown in the proof below:
Proof
τ = ∑ i = 1 n ( r i − R ) × ( m i a i ) = ∑ i = 1 n Δ r i × ( m i a i ) = ∑ i = 1 n m i [ Δ r i × a i ] … cross-product scalar multiplication = ∑ i = 1 n m i [ Δ r i × ( a tangential , i + a centripetal , i + A R ) ] = ∑ i = 1 n m i [ Δ r i × ( a tangential , i + a centripetal , i + 0 ) ] … R is either at rest or moving at a constant velocity but not accelerated, or the origin of the fixed (world) coordinate reference system is placed at the center of mass C = ∑ i = 1 n m i [ Δ r i × a tangential , i + Δ r i × a centripetal , i ] … cross-product distributivity over addition = ∑ i = 1 n m i [ Δ r i × ( α × Δ r i ) + Δ r i × ( ω × v tangential , i ) ] τ = ∑ i = 1 n m i [ Δ r i × ( α × Δ r i ) + Δ r i × ( ω × ( ω × Δ r i ) ) ] {\displaystyle {\begin{aligned}{\boldsymbol {\tau }}&=\sum _{i=1}^{n}(\mathbf {r_{i}} -\mathbf {R} )\times (m_{i}\mathbf {a} _{i})\\&=\sum _{i=1}^{n}{\boldsymbol {\Delta }}\mathbf {r} _{i}\times (m_{i}\mathbf {a} _{i})\\&=\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times \mathbf {a} _{i}]\;\ldots {\text{ cross-product scalar multiplication}}\\&=\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times (\mathbf {a} _{{\text{tangential}},i}+\mathbf {a} _{{\text{centripetal}},i}+\mathbf {A} _{\mathbf {R} })]\\&=\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times (\mathbf {a} _{{\text{tangential}},i}+\mathbf {a} _{{\text{centripetal}},i}+0)]\\&\;\;\;\;\;\ldots \;\mathbf {R} {\text{ is either at rest or moving at a constant velocity but not accelerated, or }}\\&\;\;\;\;\;\;\;\;\;\;\;{\text{the origin of the fixed (world) coordinate reference system is placed at the center of mass }}\mathbf {C} \\&=\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times \mathbf {a} _{{\text{tangential}},i}+{\boldsymbol {\Delta }}\mathbf {r} _{i}\times \mathbf {a} _{{\text{centripetal}},i}]\;\ldots {\text{ cross-product distributivity over addition}}\\&=\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\alpha }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})+{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\omega }}\times \mathbf {v} _{{\text{tangential}},i})]\\{\boldsymbol {\tau }}&=\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\alpha }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})+{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\omega }}\times ({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i}))]\\\end{aligned}}}
Then, the following Jacobi identity is used on the last term:
0 = Δ r i × ( ω × ( ω × Δ r i ) ) + ω × ( ( ω × Δ r i ) × Δ r i ) + ( ω × Δ r i ) × ( Δ r i × ω ) = Δ r i × ( ω × ( ω × Δ r i ) ) + ω × ( ( ω × Δ r i ) × Δ r i ) + ( ω × Δ r i ) × − ( ω × Δ r i ) … cross-product anticommutativity = Δ r i × ( ω × ( ω × Δ r i ) ) + ω × ( ( ω × Δ r i ) × Δ r i ) + − [ ( ω × Δ r i ) × ( ω × Δ r i ) ] … cross-product scalar multiplication = Δ r i × ( ω × ( ω × Δ r i ) ) + ω × ( ( ω × Δ r i ) × Δ r i ) + − [ 0 ] … self cross-product 0 = Δ r i × ( ω × ( ω × Δ r i ) ) + ω × ( ( ω × Δ r i ) × Δ r i ) {\displaystyle {\begin{aligned}0&={\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\omega }}\times ({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i}))+{\boldsymbol {\omega }}\times (({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})\times {\boldsymbol {\Delta }}\mathbf {r} _{i})+({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})\times ({\boldsymbol {\Delta }}\mathbf {r} _{i}\times {\boldsymbol {\omega }})\\&={\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\omega }}\times ({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i}))+{\boldsymbol {\omega }}\times (({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})\times {\boldsymbol {\Delta }}\mathbf {r} _{i})+({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})\times -({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})\;\ldots {\text{ cross-product anticommutativity}}\\&={\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\omega }}\times ({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i}))+{\boldsymbol {\omega }}\times (({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})\times {\boldsymbol {\Delta }}\mathbf {r} _{i})+-[({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})\times ({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})]\;\ldots {\text{ cross-product scalar multiplication}}\\&={\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\omega }}\times ({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i}))+{\boldsymbol {\omega }}\times (({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})\times {\boldsymbol {\Delta }}\mathbf {r} _{i})+-[0]\;\ldots {\text{ self cross-product}}\\0&={\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\omega }}\times ({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i}))+{\boldsymbol {\omega }}\times (({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})\times {\boldsymbol {\Delta }}\mathbf {r} _{i})\end{aligned}}}
The result of applying Jacobi identity can then be continued as follows:
Δ r i × ( ω × ( ω × Δ r i ) ) = − [ ω × ( ( ω × Δ r i ) × Δ r i ) ] = − [ ( ω × Δ r i ) ( ω ⋅ Δ r i ) − Δ r i ( ω ⋅ ( ω × Δ r i ) ) ] … vector triple product = − [ ( ω × Δ r i ) ( ω ⋅ Δ r i ) − Δ r i ( Δ r i ⋅ ( ω × ω ) ) ] … scalar triple product = − [ ( ω × Δ r i ) ( ω ⋅ Δ r i ) − Δ r i ( Δ r i ⋅ ( 0 ) ) ] … self cross-product = − [ ( ω × Δ r i ) ( ω ⋅ Δ r i ) ] = − [ ω × ( Δ r i ( ω ⋅ Δ r i ) ) ] … cross-product scalar multiplication = ω × − ( Δ r i ( ω ⋅ Δ r i ) ) … cross-product scalar multiplication Δ r i × ( ω × ( ω × Δ r i ) ) = ω × − ( Δ r i ( Δ r i ⋅ ω ) ) … dot-product commutativity {\displaystyle {\begin{aligned}{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\omega }}\times ({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i}))&=-[{\boldsymbol {\omega }}\times (({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})\times {\boldsymbol {\Delta }}\mathbf {r} _{i})]\\&=-[({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})({\boldsymbol {\omega }}\cdot {\boldsymbol {\Delta }}\mathbf {r} _{i})-{\boldsymbol {\Delta }}\mathbf {r} _{i}({\boldsymbol {\omega }}\cdot ({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i}))]\;\ldots {\text{ vector triple product}}\\&=-[({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})({\boldsymbol {\omega }}\cdot {\boldsymbol {\Delta }}\mathbf {r} _{i})-{\boldsymbol {\Delta }}\mathbf {r} _{i}({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot ({\boldsymbol {\omega }}\times {\boldsymbol {\omega }}))]\;\ldots {\text{ scalar triple product}}\\&=-[({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})({\boldsymbol {\omega }}\cdot {\boldsymbol {\Delta }}\mathbf {r} _{i})-{\boldsymbol {\Delta }}\mathbf {r} _{i}({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot (0))]\;\ldots {\text{ self cross-product}}\\&=-[({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})({\boldsymbol {\omega }}\cdot {\boldsymbol {\Delta }}\mathbf {r} _{i})]\\&=-[{\boldsymbol {\omega }}\times ({\boldsymbol {\Delta }}\mathbf {r} _{i}({\boldsymbol {\omega }}\cdot {\boldsymbol {\Delta }}\mathbf {r} _{i}))]\;\ldots {\text{ cross-product scalar multiplication}}\\&={\boldsymbol {\omega }}\times -({\boldsymbol {\Delta }}\mathbf {r} _{i}({\boldsymbol {\omega }}\cdot {\boldsymbol {\Delta }}\mathbf {r} _{i}))\;\ldots {\text{ cross-product scalar multiplication}}\\{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\omega }}\times ({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i}))&={\boldsymbol {\omega }}\times -({\boldsymbol {\Delta }}\mathbf {r} _{i}({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot {\boldsymbol {\omega }}))\;\ldots {\text{ dot-product commutativity}}\\\end{aligned}}}
The final result can then be substituted to the main proof as follows:
τ = ∑ i = 1 n m i [ Δ r i × ( α × Δ r i ) + Δ r i × ( ω × ( ω × Δ r i ) ) ] = ∑ i = 1 n m i [ Δ r i × ( α × Δ r i ) + ω × − ( Δ r i ( Δ r i ⋅ ω ) ) ] = ∑ i = 1 n m i [ Δ r i × ( α × Δ r i ) + ω × { 0 − Δ r i ( Δ r i ⋅ ω ) } ] = ∑ i = 1 n m i [ Δ r i × ( α × Δ r i ) + ω × { [ ω ( Δ r i ⋅ Δ r i ) − ω ( Δ r i ⋅ Δ r i ) ] − Δ r i ( Δ r i ⋅ ω ) } ] … ω ( Δ r i ⋅ Δ r i ) − ω ( Δ r i ⋅ Δ r i ) = 0 = ∑ i = 1 n m i [ Δ r i × ( α × Δ r i ) + ω × { [ ω ( Δ r i ⋅ Δ r i ) − Δ r i ( Δ r i ⋅ ω ) ] − ω ( Δ r i ⋅ Δ r i ) } ] … addition associativity {\displaystyle {\begin{aligned}{\boldsymbol {\tau }}&=\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\alpha }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})+{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\omega }}\times ({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i}))]\\&=\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\alpha }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})+{\boldsymbol {\omega }}\times -({\boldsymbol {\Delta }}\mathbf {r} _{i}({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot {\boldsymbol {\omega }}))]\\&=\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\alpha }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})+{\boldsymbol {\omega }}\times \{0-{\boldsymbol {\Delta }}\mathbf {r} _{i}({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot {\boldsymbol {\omega }})\}]\\&=\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\alpha }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})+{\boldsymbol {\omega }}\times \{[{\boldsymbol {\omega }}({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot {\boldsymbol {\Delta }}\mathbf {r} _{i})-{\boldsymbol {\omega }}({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot {\boldsymbol {\Delta }}\mathbf {r} _{i})]-{\boldsymbol {\Delta }}\mathbf {r} _{i}({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot {\boldsymbol {\omega }})\}]\;\ldots \;{\boldsymbol {\omega }}({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot {\boldsymbol {\Delta }}\mathbf {r} _{i})-{\boldsymbol {\omega }}({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot {\boldsymbol {\Delta }}\mathbf {r} _{i})=0\\&=\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\alpha }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})+{\boldsymbol {\omega }}\times \{[{\boldsymbol {\omega }}({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot {\boldsymbol {\Delta }}\mathbf {r} _{i})-{\boldsymbol {\Delta }}\mathbf {r} _{i}({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot {\boldsymbol {\omega }})]-{\boldsymbol {\omega }}({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot {\boldsymbol {\Delta }}\mathbf {r} _{i})\}]\;\ldots {\text{ addition associativity}}\\\end{aligned}}} = ∑ i = 1 n m i [ Δ r i × ( α × Δ r i ) + ω × { ω ( Δ r i ⋅ Δ r i ) − Δ r i ( Δ r i ⋅ ω ) } − ω × ω ( Δ r i ⋅ Δ r i ) ] … cross-product distributivity over addition = ∑ i = 1 n m i [ Δ r i × ( α × Δ r i ) + ω × { ω ( Δ r i ⋅ Δ r i ) − Δ r i ( Δ r i ⋅ ω ) } − ( Δ r i ⋅ Δ r i ) ( ω × ω ) ] … cross-product scalar multiplication = ∑ i = 1 n m i [ Δ r i × ( α × Δ r i ) + ω × { ω ( Δ r i ⋅ Δ r i ) − Δ r i ( Δ r i ⋅ ω ) } − ( Δ r i ⋅ Δ r i ) ( 0 ) ] … self cross-product = ∑ i = 1 n m i [ Δ r i × ( α × Δ r i ) + ω × { ω ( Δ r i ⋅ Δ r i ) − Δ r i ( Δ r i ⋅ ω ) } ] = ∑ i = 1 n m i [ Δ r i × ( α × Δ r i ) + ω × { Δ r i × ( ω × Δ r i ) } ] … vector triple product = ∑ i = 1 n m i [ Δ r i × − ( Δ r i × α ) + ω × { Δ r i × − ( Δ r i × ω ) } ] … cross-product anticommutativity = − ∑ i = 1 n m i [ Δ r i × ( Δ r i × α ) + ω × { Δ r i × ( Δ r i × ω ) } ] … cross-product scalar multiplication = − ∑ i = 1 n m i [ Δ r i × ( Δ r i × α ) ] + − ∑ i = 1 n m i [ ω × { Δ r i × ( Δ r i × ω ) } ] … summation distributivity τ = − ∑ i = 1 n m i [ Δ r i × ( Δ r i × α ) ] + ω × − ∑ i = 1 n m i [ Δ r i × ( Δ r i × ω ) ] … ω is not characteristic of particle P i {\displaystyle {\begin{aligned}&=\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\alpha }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})+{\boldsymbol {\omega }}\times \{{\boldsymbol {\omega }}({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot {\boldsymbol {\Delta }}\mathbf {r} _{i})-{\boldsymbol {\Delta }}\mathbf {r} _{i}({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot {\boldsymbol {\omega }})\}-{\boldsymbol {\omega }}\times {\boldsymbol {\omega }}({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot {\boldsymbol {\Delta }}\mathbf {r} _{i})]\;\ldots {\text{ cross-product distributivity over addition}}\\&=\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\alpha }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})+{\boldsymbol {\omega }}\times \{{\boldsymbol {\omega }}({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot {\boldsymbol {\Delta }}\mathbf {r} _{i})-{\boldsymbol {\Delta }}\mathbf {r} _{i}({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot {\boldsymbol {\omega }})\}-({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot {\boldsymbol {\Delta }}\mathbf {r} _{i})({\boldsymbol {\omega }}\times {\boldsymbol {\omega }})]\;\ldots {\text{ cross-product scalar multiplication}}\\&=\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\alpha }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})+{\boldsymbol {\omega }}\times \{{\boldsymbol {\omega }}({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot {\boldsymbol {\Delta }}\mathbf {r} _{i})-{\boldsymbol {\Delta }}\mathbf {r} _{i}({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot {\boldsymbol {\omega }})\}-({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot {\boldsymbol {\Delta }}\mathbf {r} _{i})(0)]\;\ldots {\text{ self cross-product}}\\&=\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\alpha }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})+{\boldsymbol {\omega }}\times \{{\boldsymbol {\omega }}({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot {\boldsymbol {\Delta }}\mathbf {r} _{i})-{\boldsymbol {\Delta }}\mathbf {r} _{i}({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot {\boldsymbol {\omega }})\}]\\&=\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\alpha }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})+{\boldsymbol {\omega }}\times \{{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})\}]\;\ldots {\text{ vector triple product}}\\&=\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times -({\boldsymbol {\Delta }}\mathbf {r} _{i}\times {\boldsymbol {\alpha }})+{\boldsymbol {\omega }}\times \{{\boldsymbol {\Delta }}\mathbf {r} _{i}\times -({\boldsymbol {\Delta }}\mathbf {r} _{i}\times {\boldsymbol {\omega }})\}]\;\ldots {\text{ cross-product anticommutativity}}\\&=-\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\Delta }}\mathbf {r} _{i}\times {\boldsymbol {\alpha }})+{\boldsymbol {\omega }}\times \{{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\Delta }}\mathbf {r} _{i}\times {\boldsymbol {\omega }})\}]\;\ldots {\text{ cross-product scalar multiplication}}\\&=-\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\Delta }}\mathbf {r} _{i}\times {\boldsymbol {\alpha }})]+-\sum _{i=1}^{n}m_{i}[{\boldsymbol {\omega }}\times \{{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\Delta }}\mathbf {r} _{i}\times {\boldsymbol {\omega }})\}]\;\ldots {\text{ summation distributivity}}\\{\boldsymbol {\tau }}&=-\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\Delta }}\mathbf {r} _{i}\times {\boldsymbol {\alpha }})]+{\boldsymbol {\omega }}\times -\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\Delta }}\mathbf {r} _{i}\times {\boldsymbol {\omega }})]\;\ldots \;{\boldsymbol {\omega }}{\text{ is not characteristic of particle }}P_{i}\end{aligned}}}
Notice that for any vector u {\displaystyle \mathbf {u} }
− ∑ i = 1 n m i [ Δ r i × ( Δ r i × u ) ] = − ∑ i = 1 n m i ( [ 0 − Δ r 3 , i Δ r 2 , i Δ r 3 , i 0 − Δ r 1 , i − Δ r 2 , i Δ r 1 , i 0 ] ( [ 0 − Δ r 3 , i Δ r 2 , i Δ r 3 , i 0 − Δ r 1 , i − Δ r 2 , i Δ r 1 , i 0 ] [ u 1 u 2 u 3 ] ) ) … cross-product as matrix multiplication = − ∑ i = 1 n m i ( [ 0 − Δ r 3 , i Δ r 2 , i Δ r 3 , i 0 − Δ r 1 , i − Δ r 2 , i Δ r 1 , i 0 ] [ − Δ r 3 , i u 2 + Δ r 2 , i u 3 + Δ r 3 , i u 1 − Δ r 1 , i u 3 − Δ r 2 , i u 1 + Δ r 1 , i u 2 ] ) = − ∑ i = 1 n m i [ − Δ r 3 , i ( + Δ r 3 , i u 1 − Δ r 1 , i u 3 ) + Δ r 2 , i ( − Δ r 2 , i u 1 + Δ r 1 , i u 2 ) + Δ r 3 , i ( − Δ r 3 , i u 2 + Δ r 2 , i u 3 ) − Δ r 1 , i ( − Δ r 2 , i u 1 + Δ r 1 , i u 2 ) − Δ r 2 , i ( − Δ r 3 , i u 2 + Δ r 2 , i u 3 ) + Δ r 1 , i ( + Δ r 3 , i u 1 − Δ r 1 , i u 3 ) ] = − ∑ i = 1 n m i [ − Δ r 3 , i 2 u 1 + Δ r 1 , i Δ r 3 , i u 3 − Δ r 2 , i 2 u 1 + Δ r 1 , i Δ r 2 , i u 2 − Δ r 3 , i 2 u 2 + Δ r 2 , i Δ r 3 , i u 3 + Δ r 2 , i Δ r 1 , i u 1 − Δ r 1 , i 2 u 2 + Δ r 3 , i Δ r 2 , i u 2 − Δ r 2 , i 2 u 3 + Δ r 3 , i Δ r 1 , i u 1 − Δ r 1 , i 2 u 3 ] = − ∑ i = 1 n m i [ − ( Δ r 2 , i 2 + Δ r 3 , i 2 ) u 1 + Δ r 1 , i Δ r 2 , i u 2 + Δ r 1 , i Δ r 3 , i u 3 + Δ r 2 , i Δ r 1 , i u 1 − ( Δ r 1 , i 2 + Δ r 3 , i 2 ) u 2 + Δ r 2 , i Δ r 3 , i u 3 + Δ r 3 , i Δ r 1 , i u 1 + Δ r 3 , i Δ r 2 , i u 2 − ( Δ r 1 , i 2 + Δ r 2 , i 2 ) u 3 ] = − ∑ i = 1 n m i [ − ( Δ r 2 , i 2 + Δ r 3 , i 2 ) Δ r 1 , i Δ r 2 , i Δ r 1 , i Δ r 3 , i Δ r 2 , i Δ r 1 , i − ( Δ r 1 , i 2 + Δ r 3 , i 2 ) Δ r 2 , i Δ r 3 , i Δ r 3 , i Δ r 1 , i Δ r 3 , i Δ r 2 , i − ( Δ r 1 , i 2 + Δ r 2 , i 2 ) ] [ u 1 u 2 u 3 ] = − ∑ i = 1 n m i [ Δ r i ] 2 u − ∑ i = 1 n m i [ Δ r i × ( Δ r i × u ) ] = ( − ∑ i = 1 n m i [ Δ r i ] 2 ) u … u is not characteristic of P i {\displaystyle {\begin{aligned}-\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\Delta }}\mathbf {r} _{i}\times \mathbf {u} )]&=-\sum _{i=1}^{n}m_{i}\left({\begin{bmatrix}0&-\Delta r_{3,i}&\Delta r_{2,i}\\\Delta r_{3,i}&0&-\Delta r_{1,i}\\-\Delta r_{2,i}&\Delta r_{1,i}&0\end{bmatrix}}\left({\begin{bmatrix}0&-\Delta r_{3,i}&\Delta r_{2,i}\\\Delta r_{3,i}&0&-\Delta r_{1,i}\\-\Delta r_{2,i}&\Delta r_{1,i}&0\end{bmatrix}}{\begin{bmatrix}u_{1}\\u_{2}\\u_{3}\end{bmatrix}}\right)\right)\;\ldots {\text{ cross-product as matrix multiplication}}\\[6pt]&=-\sum _{i=1}^{n}m_{i}\left({\begin{bmatrix}0&-\Delta r_{3,i}&\Delta r_{2,i}\\\Delta r_{3,i}&0&-\Delta r_{1,i}\\-\Delta r_{2,i}&\Delta r_{1,i}&0\end{bmatrix}}{\begin{bmatrix}-\Delta r_{3,i}\,u_{2}+\Delta r_{2,i}\,u_{3}\\+\Delta r_{3,i}\,u_{1}-\Delta r_{1,i}\,u_{3}\\-\Delta r_{2,i}\,u_{1}+\Delta r_{1,i}\,u_{2}\end{bmatrix}}\right)\\[6pt]&=-\sum _{i=1}^{n}m_{i}{\begin{bmatrix}-\Delta r_{3,i}(+\Delta r_{3,i}\,u_{1}-\Delta r_{1,i}\,u_{3})+\Delta r_{2,i}(-\Delta r_{2,i}\,u_{1}+\Delta r_{1,i}\,u_{2})\\+\Delta r_{3,i}(-\Delta r_{3,i}\,u_{2}+\Delta r_{2,i}\,u_{3})-\Delta r_{1,i}(-\Delta r_{2,i}\,u_{1}+\Delta r_{1,i}\,u_{2})\\-\Delta r_{2,i}(-\Delta r_{3,i}\,u_{2}+\Delta r_{2,i}\,u_{3})+\Delta r_{1,i}(+\Delta r_{3,i}\,u_{1}-\Delta r_{1,i}\,u_{3})\end{bmatrix}}\\[6pt]&=-\sum _{i=1}^{n}m_{i}{\begin{bmatrix}-\Delta r_{3,i}^{2}\,u_{1}+\Delta r_{1,i}\Delta r_{3,i}\,u_{3}-\Delta r_{2,i}^{2}\,u_{1}+\Delta r_{1,i}\Delta r_{2,i}\,u_{2}\\-\Delta r_{3,i}^{2}\,u_{2}+\Delta r_{2,i}\Delta r_{3,i}\,u_{3}+\Delta r_{2,i}\Delta r_{1,i}\,u_{1}-\Delta r_{1,i}^{2}\,u_{2}\\+\Delta r_{3,i}\Delta r_{2,i}\,u_{2}-\Delta r_{2,i}^{2}\,u_{3}+\Delta r_{3,i}\Delta r_{1,i}\,u_{1}-\Delta r_{1,i}^{2}\,u_{3}\end{bmatrix}}\\[6pt]&=-\sum _{i=1}^{n}m_{i}{\begin{bmatrix}-(\Delta r_{2,i}^{2}+\Delta r_{3,i}^{2})\,u_{1}+\Delta r_{1,i}\Delta r_{2,i}\,u_{2}+\Delta r_{1,i}\Delta r_{3,i}\,u_{3}\\+\Delta r_{2,i}\Delta r_{1,i}\,u_{1}-(\Delta r_{1,i}^{2}+\Delta r_{3,i}^{2})\,u_{2}+\Delta r_{2,i}\Delta r_{3,i}\,u_{3}\\+\Delta r_{3,i}\Delta r_{1,i}\,u_{1}+\Delta r_{3,i}\Delta r_{2,i}\,u_{2}-(\Delta r_{1,i}^{2}+\Delta r_{2,i}^{2})\,u_{3}\end{bmatrix}}\\[6pt]&=-\sum _{i=1}^{n}m_{i}{\begin{bmatrix}-(\Delta r_{2,i}^{2}+\Delta r_{3,i}^{2})&\Delta r_{1,i}\Delta r_{2,i}&\Delta r_{1,i}\Delta r_{3,i}\\\Delta r_{2,i}\Delta r_{1,i}&-(\Delta r_{1,i}^{2}+\Delta r_{3,i}^{2})&\Delta r_{2,i}\Delta r_{3,i}\\\Delta r_{3,i}\Delta r_{1,i}&\Delta r_{3,i}\Delta r_{2,i}&-(\Delta r_{1,i}^{2}+\Delta r_{2,i}^{2})\end{bmatrix}}{\begin{bmatrix}u_{1}\\u_{2}\\u_{3}\end{bmatrix}}\\&=-\sum _{i=1}^{n}m_{i}[\Delta r_{i}]^{2}\mathbf {u} \\[6pt]-\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\Delta }}\mathbf {r} _{i}\times \mathbf {u} )]&=\left(-\sum _{i=1}^{n}m_{i}[\Delta r_{i}]^{2}\right)\mathbf {u} \;\ldots \;\mathbf {u} {\text{ is not characteristic of }}P_{i}\end{aligned}}}
Finally, the result is used to complete the main proof as follows:
τ = − ∑ i = 1 n m i [ Δ r i × ( Δ r i × α ) ] + ω × − ∑ i = 1 n m i Δ r i × ( Δ r i × ω ) ] = ( − ∑ i = 1 n m i [ Δ r i ] 2 ) α + ω × ( − ∑ i = 1 n m i [ Δ r i ] 2 ) ω {\displaystyle {\begin{aligned}{\boldsymbol {\tau }}&=-\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\Delta }}\mathbf {r} _{i}\times {\boldsymbol {\alpha }})]+{\boldsymbol {\omega }}\times -\sum _{i=1}^{n}m_{i}{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\Delta }}\mathbf {r} _{i}\times {\boldsymbol {\omega }})]\\&=\left(-\sum _{i=1}^{n}m_{i}[\Delta r_{i}]^{2}\right){\boldsymbol {\alpha }}+{\boldsymbol {\omega }}\times \left(-\sum _{i=1}^{n}m_{i}[\Delta r_{i}]^{2}\right){\boldsymbol {\omega }}\end{aligned}}}
Thus, the resultant torque on the rigid system of particles is given by
τ = I C α + ω × I C ω , {\displaystyle {\boldsymbol {\tau }}=\mathbf {I} _{\mathbf {C} }{\boldsymbol {\alpha }}+{\boldsymbol {\omega }}\times \mathbf {I} _{\mathbf {C} }{\boldsymbol {\omega }},} where I C {\displaystyle \mathbf {I_{C}} }
Parallel axis theorem The inertia matrix of a body depends on the choice of the reference point. There is a useful relationship between the inertia matrix relative to the center of mass C {\displaystyle \mathbf {C} } R {\displaystyle \mathbf {R} } [3] [6]
Consider the inertia matrix I R {\displaystyle \mathbf {I_{R}} } R {\displaystyle \mathbf {R} }
I R = − ∑ i = 1 n m i [ r i − R ] 2 . {\displaystyle \mathbf {I} _{\mathbf {R} }=-\sum _{i=1}^{n}m_{i}\left[\mathbf {r} _{i}-\mathbf {R} \right]^{2}.}
Let C {\displaystyle \mathbf {C} }
R = ( R − C ) + C = d + C , {\displaystyle \mathbf {R} =(\mathbf {R} -\mathbf {C} )+\mathbf {C} =\mathbf {d} +\mathbf {C} ,} where d {\displaystyle \mathbf {d} } C {\displaystyle \mathbf {C} } R {\displaystyle \mathbf {R} } I R = − ∑ i = 1 n m i [ r i − ( C + d ) ] 2 = − ∑ i = 1 n m i [ ( r i − C ) − d ] 2 . {\displaystyle \mathbf {I} _{\mathbf {R} }=-\sum _{i=1}^{n}m_{i}[\mathbf {r} _{i}-\left(\mathbf {C} +\mathbf {d} \right)]^{2}=-\sum _{i=1}^{n}m_{i}[\left(\mathbf {r} _{i}-\mathbf {C} \right)-\mathbf {d} ]^{2}.}
Distribute over the cross product to obtain
I R = − ( ∑ i = 1 n m i [ r i − C ] 2 ) + ( ∑ i = 1 n m i [ r i − C ] ) [ d ] + [ d ] ( ∑ i = 1 n m i [ r i − C ] ) − ( ∑ i = 1 n m i ) [ d ] 2 . {\displaystyle \mathbf {I} _{\mathbf {R} }=-\left(\sum _{i=1}^{n}m_{i}[\mathbf {r} _{i}-\mathbf {C} ]^{2}\right)+\left(\sum _{i=1}^{n}m_{i}[\mathbf {r} _{i}-\mathbf {C} ]\right)[\mathbf {d} ]+[\mathbf {d} ]\left(\sum _{i=1}^{n}m_{i}[\mathbf {r} _{i}-\mathbf {C} ]\right)-\left(\sum _{i=1}^{n}m_{i}\right)[\mathbf {d} ]^{2}.}
The first term is the inertia matrix I C {\displaystyle \mathbf {I_{C}} } C {\displaystyle \mathbf {C} } [ d ] {\displaystyle [\mathbf {d} ]} d {\displaystyle \mathbf {d} }
The result is the parallel axis theorem,
I R = I C − M [ d ] 2 , {\displaystyle \mathbf {I} _{\mathbf {R} }=\mathbf {I} _{\mathbf {C} }-M[\mathbf {d} ]^{2},} where d {\displaystyle \mathbf {d} } C {\displaystyle \mathbf {C} } R {\displaystyle \mathbf {R} }
Note on the minus sign : By using the skew symmetric matrix of position vectors relative to the reference point, the inertia matrix of each particle has the form − m [ r ] 2 {\displaystyle -m\left[\mathbf {r} \right]^{2}} m r 2 {\displaystyle mr^{2}} m [ r ] T [ r ] {\displaystyle m\left[\mathbf {r} \right]^{\mathsf {T}}\left[\mathbf {r} \right]} [ r ] {\displaystyle [\mathbf {r} ]}
Scalar moment of inertia in a plane The scalar moment of inertia, I L {\displaystyle I_{L}} k ^ {\displaystyle \mathbf {\hat {k}} } R {\displaystyle \mathbf {R} } [6]
I L = k ^ ⋅ ( − ∑ i = 1 N m i [ Δ r i ] 2 ) k ^ = k ^ ⋅ I R k ^ = k ^ T I R k ^ , {\displaystyle I_{L}=\mathbf {\hat {k}} \cdot \left(-\sum _{i=1}^{N}m_{i}\left[\Delta \mathbf {r} _{i}\right]^{2}\right)\mathbf {\hat {k}} =\mathbf {\hat {k}} \cdot \mathbf {I} _{\mathbf {R} }\mathbf {\hat {k}} =\mathbf {\hat {k}} ^{\mathsf {T}}\mathbf {I} _{\mathbf {R} }\mathbf {\hat {k}} ,} where I R {\displaystyle \mathbf {I_{R}} } R {\displaystyle \mathbf {R} } [ Δ r i ] {\displaystyle [\Delta \mathbf {r} _{i}]} Δ r i = r i − R {\displaystyle \Delta \mathbf {r} _{i}=\mathbf {r} _{i}-\mathbf {R} }
This is derived as follows. Let a rigid assembly of n {\displaystyle n} P i , i = 1 , … , n {\displaystyle P_{i},i=1,\dots ,n} r i {\displaystyle \mathbf {r} _{i}} R {\displaystyle \mathbf {R} } k ^ {\displaystyle \mathbf {\hat {k}} } R {\displaystyle \mathbf {R} } L ( t ) = R + t k ^ {\displaystyle \mathbf {L} (t)=\mathbf {R} +t\mathbf {\hat {k}} } P i {\displaystyle P_{i}} Δ r i {\displaystyle \Delta \mathbf {r} _{i}} k ^ {\displaystyle \mathbf {\hat {k}} }
Δ r i ⊥ = Δ r i − ( k ^ ⋅ Δ r i ) k ^ = ( E − k ^ k ^ T ) Δ r i , {\displaystyle \Delta \mathbf {r} _{i}^{\perp }=\Delta \mathbf {r} _{i}-\left(\mathbf {\hat {k}} \cdot \Delta \mathbf {r} _{i}\right)\mathbf {\hat {k}} =\left(\mathbf {E} -\mathbf {\hat {k}} \mathbf {\hat {k}} ^{\mathsf {T}}\right)\Delta \mathbf {r} _{i},} where E {\displaystyle \mathbf {E} } k ^ k ^ T {\displaystyle \mathbf {\hat {k}} \mathbf {\hat {k}} ^{\mathsf {T}}} k ^ {\displaystyle \mathbf {\hat {k}} } L {\displaystyle L}
To relate this scalar moment of inertia to the inertia matrix of the body, introduce the skew-symmetric matrix [ k ^ ] {\displaystyle \left[\mathbf {\hat {k}} \right]} [ k ^ ] y = k ^ × y {\displaystyle \left[\mathbf {\hat {k}} \right]\mathbf {y} =\mathbf {\hat {k}} \times \mathbf {y} }
− [ k ^ ] 2 ≡ k ^ 2 ( E − k ^ k ^ T ) = E − k ^ k ^ T , {\displaystyle -\left[\mathbf {\hat {k}} \right]^{2}\equiv \left \mathbf {\hat {k}} \right ^{2}\left(\mathbf {E} -\mathbf {\hat {k}} \mathbf {\hat {k}} ^{\mathsf {T}}\right)=\mathbf {E} -\mathbf {\hat {k}} \mathbf {\hat {k}} ^{\mathsf {T}},} noting that k ^ {\displaystyle \mathbf {\hat {k}} }
The magnitude squared of the perpendicular vector is
Δ r i ⊥ 2 = ( − [ k ^ ] 2 Δ r i ) ⋅ ( − [ k ^ ] 2 Δ r i ) = ( k ^ × ( k ^ × Δ r i ) ) ⋅ ( k ^ × ( k ^ × Δ r i ) ) {\displaystyle {\begin{aligned}\left \Delta \mathbf {r} _{i}^{\perp }\right ^{2}&=\left(-\left[\mathbf {\hat {k}} \right]^{2}\Delta \mathbf {r} _{i}\right)\cdot \left(-\left[\mathbf {\hat {k}} \right]^{2}\Delta \mathbf {r} _{i}\right)\\&=\left(\mathbf {\hat {k}} \times \left(\mathbf {\hat {k}} \times \Delta \mathbf {r} _{i}\right)\right)\cdot \left(\mathbf {\hat {k}} \times \left(\mathbf {\hat {k}} \times \Delta \mathbf {r} _{i}\right)\right)\end{aligned}}}
The simplification of this equation uses the triple scalar product identity
( k ^ × ( k ^ × Δ r i ) ) ⋅ ( k ^ × ( k ^ × Δ r i ) ) ≡ ( ( k ^ × ( k ^ × Δ r i ) ) × k ^ ) ⋅ ( k ^ × Δ r i ) , {\displaystyle \left(\mathbf {\hat {k}} \times \left(\mathbf {\hat {k}} \times \Delta \mathbf {r} _{i}\right)\right)\cdot \left(\mathbf {\hat {k}} \times \left(\mathbf {\hat {k}} \times \Delta \mathbf {r} _{i}\right)\right)\equiv \left(\left(\mathbf {\hat {k}} \times \left(\mathbf {\hat {k}} \times \Delta \mathbf {r} _{i}\right)\right)\times \mathbf {\hat {k}} \right)\cdot \left(\mathbf {\hat {k}} \times \Delta \mathbf {r} _{i}\right),} where the dot and the cross products have been interchanged. Exchanging products, and simplifying by noting that Δ r i {\displaystyle \Delta \mathbf {r} _{i}} k ^ {\displaystyle \mathbf {\hat {k}} } ( k ^ × ( k ^ × Δ r i ) ) ⋅ ( k ^ × ( k ^ × Δ r i ) ) = ( ( k ^ × ( k ^ × Δ r i ) ) × k ^ ) ⋅ ( k ^ × Δ r i ) = ( k ^ × Δ r i ) ⋅ ( − Δ r i × k ^ ) = − k ^ ⋅ ( Δ r i × Δ r i × k ^ ) = − k ^ ⋅ [ Δ r i ] 2 k ^ . {\displaystyle {\begin{aligned}&\left(\mathbf {\hat {k}} \times \left(\mathbf {\hat {k}} \times \Delta \mathbf {r} _{i}\right)\right)\cdot \left(\mathbf {\hat {k}} \times \left(\mathbf {\hat {k}} \times \Delta \mathbf {r} _{i}\right)\right)\\={}&\left(\left(\mathbf {\hat {k}} \times \left(\mathbf {\hat {k}} \times \Delta \mathbf {r} _{i}\right)\right)\times \mathbf {\hat {k}} \right)\cdot \left(\mathbf {\hat {k}} \times \Delta \mathbf {r} _{i}\right)\\={}&\left(\mathbf {\hat {k}} \times \Delta \mathbf {r} _{i}\right)\cdot \left(-\Delta \mathbf {r} _{i}\times \mathbf {\hat {k}} \right)\\={}&-\mathbf {\hat {k}} \cdot \left(\Delta \mathbf {r} _{i}\times \Delta \mathbf {r} _{i}\times \mathbf {\hat {k}} \right)\\={}&-\mathbf {\hat {k}} \cdot \left[\Delta \mathbf {r} _{i}\right]^{2}\mathbf {\hat {k}} .\end{aligned}}}
Thus, the moment of inertia around the line L {\displaystyle L} R {\displaystyle \mathbf {R} } k ^ {\displaystyle \mathbf {\hat {k}} }
I L = ∑ i = 1 N m i Δ r i ⊥ 2 = − ∑ i = 1 N m i k ^ ⋅ [ Δ r i ] 2 k ^ = k ^ ⋅ ( − ∑ i = 1 N m i [ Δ r i ] 2 ) k ^ = k ^ ⋅ I R k ^ = k ^ T I R k ^ , {\displaystyle {\begin{aligned}I_{L}&=\sum _{i=1}^{N}m_{i}\left \Delta \mathbf {r} _{i}^{\perp }\right ^{2}\\&=-\sum _{i=1}^{N}m_{i}\mathbf {\hat {k}} \cdot \left[\Delta \mathbf {r} _{i}\right]^{2}\mathbf {\hat {k}} =\mathbf {\hat {k}} \cdot \left(-\sum _{i=1}^{N}m_{i}\left[\Delta \mathbf {r} _{i}\right]^{2}\right)\mathbf {\hat {k}} \\&=\mathbf {\hat {k}} \cdot \mathbf {I} _{\mathbf {R} }\mathbf {\hat {k}} =\mathbf {\hat {k}} ^{\mathsf {T}}\mathbf {I} _{\mathbf {R} }\mathbf {\hat {k}} ,\end{aligned}}} where I R {\displaystyle \mathbf {I_{R}} } R {\displaystyle \mathbf {R} }
This shows that the inertia matrix can be used to calculate the moment of inertia of a body around any specified rotation axis in the body.
Inertia tensor For the same object, different axes of rotation will have different moments of inertia about those axes. In general, the moments of inertia are not equal unless the object is symmetric about all axes. The moment of inertia tensor is a convenient way to summarize all moments of inertia of an object with one quantity. It may be calculated with respect to any point in space, although for practical purposes the center of mass is most commonly used.
Definition For a rigid object of N {\displaystyle N} m k {\displaystyle m_{k}} tensor is given by
I = [ I 11 I 12 I 13 I 21 I 22 I 23 I 31 I 32 I 33 ] . {\displaystyle \mathbf {I} ={\begin{bmatrix}I_{11}&I_{12}&I_{13}\\I_{21}&I_{22}&I_{23}\\I_{31}&I_{32}&I_{33}\end{bmatrix}}.}
Its components are defined as
I i j = d e f ∑ k = 1 N m k ( ‖ r k ‖ 2 δ i j − x i ( k ) x j ( k ) ) {\displaystyle I_{ij}\ {\stackrel {\mathrm {def} }{=}}\ \sum _{k=1}^{N}m_{k}\left(\left\ \mathbf {r} _{k}\right\ ^{2}\delta _{ij}-x_{i}^{(k)}x_{j}^{(k)}\right)}
where
i {\displaystyle i} j {\displaystyle j} x {\displaystyle x} y {\displaystyle y} z {\displaystyle z} r k = ( x 1 ( k ) , x 2 ( k ) , x 3 ( k ) ) {\displaystyle \mathbf {r} _{k}=\left(x_{1}^{(k)},x_{2}^{(k)},x_{3}^{(k)}\right)} m k {\displaystyle m_{k}} δ i j {\displaystyle \delta _{ij}} Kronecker delta .Note that, by the definition, I {\displaystyle \mathbf {I} } symmetric tensor .
The diagonal elements are more succinctly written as
I x x = d e f ∑ k = 1 N m k ( y k 2 + z k 2 ) , I y y = d e f ∑ k = 1 N m k ( x k 2 + z k 2 ) , I z z = d e f ∑ k = 1 N m k ( x k 2 + y k 2 ) , {\displaystyle {\begin{aligned}I_{xx}\ &{\stackrel {\mathrm {def} }{=}}\ \sum _{k=1}^{N}m_{k}\left(y_{k}^{2}+z_{k}^{2}\right),\\I_{yy}\ &{\stackrel {\mathrm {def} }{=}}\ \sum _{k=1}^{N}m_{k}\left(x_{k}^{2}+z_{k}^{2}\right),\\I_{zz}\ &{\stackrel {\mathrm {def} }{=}}\ \sum _{k=1}^{N}m_{k}\left(x_{k}^{2}+y_{k}^{2}\right),\end{aligned}}}
while the off-diagonal elements, also called the products of inertia , are
I x y = I y x = d e f − ∑ k = 1 N m k x k y k , I x z = I z x = d e f − ∑ k = 1 N m k x k z k , I y z = I z y = d e f − ∑ k = 1 N m k y k z k . {\displaystyle {\begin{aligned}I_{xy}=I_{yx}\ &{\stackrel {\mathrm {def} }{=}}\ -\sum _{k=1}^{N}m_{k}x_{k}y_{k},\\I_{xz}=I_{zx}\ &{\stackrel {\mathrm {def} }{=}}\ -\sum _{k=1}^{N}m_{k}x_{k}z_{k},\\I_{yz}=I_{zy}\ &{\stackrel {\mathrm {def} }{=}}\ -\sum _{k=1}^{N}m_{k}y_{k}z_{k}.\end{aligned}}}
Here I x x {\displaystyle I_{xx}} x {\displaystyle x} I x y {\displaystyle I_{xy}} y {\displaystyle y} x {\displaystyle x}
These quantities can be generalized to an object with distributed mass, described by a mass density function, in a similar fashion to the scalar moment of inertia. One then has
I = ∭ V ρ ( x , y , z ) ( ‖ r ‖ 2 E 3 − r ⊗ r ) d x d y d z , {\displaystyle \mathbf {I} =\iiint _{V}\rho (x,y,z)\left(\ \mathbf {r} \ ^{2}\mathbf {E} _{3}-\mathbf {r} \otimes \mathbf {r} \right)\,dx\,dy\,dz,}
where r ⊗ r {\displaystyle \mathbf {r} \otimes \mathbf {r} } outer product , E 3 is the 3×3 identity matrix , and V is a region of space completely containing the object.
Alternatively it can also be written in terms of the angular momentum operator [ r ] x = r × x {\displaystyle [\mathbf {r} ]\mathbf {x} =\mathbf {r} \times \mathbf {x} }
I = ∭ V ρ ( r ) [ r ] T [ r ] d V = − ∭ Q ρ ( r ) [ r ] 2 d V {\displaystyle \mathbf {I} =\iiint _{V}\rho (\mathbf {r} )[\mathbf {r} ]^{\textsf {T}}[\mathbf {r} ]\,dV=-\iiint _{Q}\rho (\mathbf {r} )[\mathbf {r} ]^{2}\,dV}
The inertia tensor can be used in the same way as the inertia matrix to compute the scalar moment of inertia about an arbitrary axis in the direction n {\displaystyle \mathbf {n} }
I n = n ⋅ I ⋅ n , {\displaystyle I_{n}=\mathbf {n} \cdot \mathbf {I} \cdot \mathbf {n} ,}
where the dot product is taken with the corresponding elements in the component tensors. A product of inertia term such as I 12 {\displaystyle I_{12}}
I 12 = e 1 ⋅ I ⋅ e 2 , {\displaystyle I_{12}=\mathbf {e} _{1}\cdot \mathbf {I} \cdot \mathbf {e} _{2},} and can be interpreted as the moment of inertia around the x {\displaystyle x} y {\displaystyle y}
The components of tensors of degree two can be assembled into a matrix. For the inertia tensor this matrix is given by,
I = [ I 11 I 12 I 13 I 21 I 22 I 23 I 31 I 32 I 33 ] = [ I x x I x y I x z I y x I y y I y z I z x I z y I z z ] = [ ∑ k = 1 N m k ( y k 2 + z k 2 ) − ∑ k = 1 N m k x k y k − ∑ k = 1 N m k x k z k − ∑ k = 1 N m k x k y k ∑ k = 1 N m k ( x k 2 + z k 2 ) − ∑ k = 1 N m k y k z k − ∑ k = 1 N m k x k z k − ∑ k = 1 N m k y k z k ∑ k = 1 N m k ( x k 2 + y k 2 ) ] . {\displaystyle \mathbf {I} ={\begin{bmatrix}I_{11}&I_{12}&I_{13}\\I_{21}&I_{22}&I_{23}\\I_{31}&I_{32}&I_{33}\end{bmatrix}}={\begin{bmatrix}I_{xx}&I_{xy}&I_{xz}\\I_{yx}&I_{yy}&I_{yz}\\I_{zx}&I_{zy}&I_{zz}\end{bmatrix}}={\begin{bmatrix}\sum _{k=1}^{N}m_{k}\left(y_{k}^{2}+z_{k}^{2}\right)&-\sum _{k=1}^{N}m_{k}x_{k}y_{k}&-\sum _{k=1}^{N}m_{k}x_{k}z_{k}\\-\sum _{k=1}^{N}m_{k}x_{k}y_{k}&\sum _{k=1}^{N}m_{k}\left(x_{k}^{2}+z_{k}^{2}\right)&-\sum _{k=1}^{N}m_{k}y_{k}z_{k}\\-\sum _{k=1}^{N}m_{k}x_{k}z_{k}&-\sum _{k=1}^{N}m_{k}y_{k}z_{k}&\sum _{k=1}^{N}m_{k}\left(x_{k}^{2}+y_{k}^{2}\right)\end{bmatrix}}.}
It is common in rigid body mechanics to use notation that explicitly identifies the x {\displaystyle x} y {\displaystyle y} z {\displaystyle z} I x x {\displaystyle I_{xx}} I x y {\displaystyle I_{xy}}
Alternate inertia convention There are some CAD and CAE applications such as SolidWorks, Unigraphics NX/Siemens NX and MSC Adams that use an alternate convention for the products of inertia. According to this convention, the minus sign is removed from the product of inertia formulas and instead inserted in the inertia matrix:
I x y = I y x = d e f ∑ k = 1 N m k x k y k , I x z = I z x = d e f ∑ k = 1 N m k x k z k , I y z = I z y = d e f ∑ k = 1 N m k y k z k , I = [ I 11 I 12 I 13 I 21 I 22 I 23 I 31 I 32 I 33 ] = [ I x x − I x y − I x z − I y x I y y − I y z − I z x − I z y I z z ] = [ ∑ k = 1 N m k ( y k 2 + z k 2 ) − ∑ k = 1 N m k x k y k − ∑ k = 1 N m k x k z k − ∑ k = 1 N m k x k y k ∑ k = 1 N m k ( x k 2 + z k 2 ) − ∑ k = 1 N m k y k z k − ∑ k = 1 N m k x k z k − ∑ k = 1 N m k y k z k ∑ k = 1 N m k ( x k 2 + y k 2 ) ] . {\displaystyle {\begin{aligned}I_{xy}=I_{yx}\ &{\stackrel {\mathrm {def} }{=}}\ \sum _{k=1}^{N}m_{k}x_{k}y_{k},\\I_{xz}=I_{zx}\ &{\stackrel {\mathrm {def} }{=}}\ \sum _{k=1}^{N}m_{k}x_{k}z_{k},\\I_{yz}=I_{zy}\ &{\stackrel {\mathrm {def} }{=}}\ \sum _{k=1}^{N}m_{k}y_{k}z_{k},\\[3pt]\mathbf {I} ={\begin{bmatrix}I_{11}&I_{12}&I_{13}\\I_{21}&I_{22}&I_{23}\\I_{31}&I_{32}&I_{33}\end{bmatrix}}&={\begin{bmatrix}I_{xx}&-I_{xy}&-I_{xz}\\-I_{yx}&I_{yy}&-I_{yz}\\-I_{zx}&-I_{zy}&I_{zz}\end{bmatrix}}={\begin{bmatrix}\sum _{k=1}^{N}m_{k}\left(y_{k}^{2}+z_{k}^{2}\right)&-\sum _{k=1}^{N}m_{k}x_{k}y_{k}&-\sum _{k=1}^{N}m_{k}x_{k}z_{k}\\-\sum _{k=1}^{N}m_{k}x_{k}y_{k}&\sum _{k=1}^{N}m_{k}\left(x_{k}^{2}+z_{k}^{2}\right)&-\sum _{k=1}^{N}m_{k}y_{k}z_{k}\\-\sum _{k=1}^{N}m_{k}x_{k}z_{k}&-\sum _{k=1}^{N}m_{k}y_{k}z_{k}&\sum _{k=1}^{N}m_{k}\left(x_{k}^{2}+y_{k}^{2}\right)\end{bmatrix}}.\end{aligned}}}
Determine inertia convention (Principal axes method) If one has the inertia data ( I x x , I y y , I z z , I x y , I x z , I y z ) {\displaystyle (I_{xx},I_{yy},I_{zz},I_{xy},I_{xz},I_{yz})} principal axes . With the principal axes method, one makes inertia matrices from the following two assumptions:
The standard inertia convention has been used ( I 12 = I x y , I 13 = I x z , I 23 = I y z ) {\displaystyle (I_{12}=I_{xy},I_{13}=I_{xz},I_{23}=I_{yz})} The alternate inertia convention has been used ( I 12 = − I x y , I 13 = − I x z , I 23 = − I y z ) {\displaystyle (I_{12}=-I_{xy},I_{13}=-I_{xz},I_{23}=-I_{yz})} Next, one calculates the eigenvectors for the two matrices. The matrix whose eigenvectors are parallel to the principal axes corresponds to the inertia convention that has been used.
Derivation of the tensor components The distance r {\displaystyle r} x {\displaystyle \mathbf {x} } n ^ {\displaystyle \mathbf {\hat {n}} } x − ( x ⋅ n ^ ) n ^ {\displaystyle \left \mathbf {x} -\left(\mathbf {x} \cdot \mathbf {\hat {n}} \right)\mathbf {\hat {n}} \right } n ^ {\displaystyle \mathbf {\hat {n}} }
I = m r 2 = m ( x − ( x ⋅ n ^ ) n ^ ) ⋅ ( x − ( x ⋅ n ^ ) n ^ ) = m ( x 2 − 2 x ( x ⋅ n ^ ) n ^ + ( x ⋅ n ^ ) 2 n ^ 2 ) = m ( x 2 − ( x ⋅ n ^ ) 2 ) . {\displaystyle I=mr^{2}=m\left(\mathbf {x} -\left(\mathbf {x} \cdot \mathbf {\hat {n}} \right)\mathbf {\hat {n}} \right)\cdot \left(\mathbf {x} -\left(\mathbf {x} \cdot \mathbf {\hat {n}} \right)\mathbf {\hat {n}} \right)=m\left(\mathbf {x} ^{2}-2\mathbf {x} \left(\mathbf {x} \cdot \mathbf {\hat {n}} \right)\mathbf {\hat {n}} +\left(\mathbf {x} \cdot \mathbf {\hat {n}} \right)^{2}\mathbf {\hat {n}} ^{2}\right)=m\left(\mathbf {x} ^{2}-\left(\mathbf {x} \cdot \mathbf {\hat {n}} \right)^{2}\right).}
Rewrite the equation using matrix transpose :
I = m ( x T x − n ^ T x x T n ^ ) = m ⋅ n ^ T ( x T x ⋅ E 3 − x x T ) n ^ , {\displaystyle I=m\left(\mathbf {x} ^{\textsf {T}}\mathbf {x} -\mathbf {\hat {n}} ^{\textsf {T}}\mathbf {x} \mathbf {x} ^{\textsf {T}}\mathbf {\hat {n}} \right)=m\cdot \mathbf {\hat {n}} ^{\textsf {T}}\left(\mathbf {x} ^{\textsf {T}}\mathbf {x} \cdot \mathbf {E_{3}} -\mathbf {x} \mathbf {x} ^{\textsf {T}}\right)\mathbf {\hat {n}} ,}
where E 3 is the 3×3 identity matrix .
This leads to a tensor formula for the moment of inertia
I = m [ n 1 n 2 n 3 ] [ y 2 + z 2 − x y − x z − y x x 2 + z 2 − y z − z x − z y x 2 + y 2 ] [ n 1 n 2 n 3 ] . {\displaystyle I=m{\begin{bmatrix}n_{1}&n_{2}&n_{3}\end{bmatrix}}{\begin{bmatrix}y^{2}+z^{2}&-xy&-xz\\-yx&x^{2}+z^{2}&-yz\\-zx&-zy&x^{2}+y^{2}\end{bmatrix}}{\begin{bmatrix}n_{1}\\n_{2}\\n_{3}\end{bmatrix}}.}
For multiple particles, we need only recall that the moment of inertia is additive in order to see that this formula is correct.
Inertia tensor of translation Let I 0 {\displaystyle \mathbf {I} _{0}} center of mass , and R {\displaystyle \mathbf {R} }
I = I 0 + m [ ( R ⋅ R ) E 3 − R ⊗ R ] {\displaystyle \mathbf {I} =\mathbf {I} _{0}+m[(\mathbf {R} \cdot \mathbf {R} )\mathbf {E} _{3}-\mathbf {R} \otimes \mathbf {R} ]} where m {\displaystyle m} E 3 is the 3 × 3 identity matrix, and ⊗ {\displaystyle \otimes } outer product .
Inertia tensor of rotation Let R {\displaystyle \mathbf {R} } matrix that represents a body's rotation. The inertial tensor of the rotated body is given by:[27]
I = R I 0 R T {\displaystyle \mathbf {I} =\mathbf {R} \mathbf {I_{0}} \mathbf {R} ^{\textsf {T}}}
Inertia matrix in different reference frames The use of the inertia matrix in Newton's second law assumes its components are computed relative to axes parallel to the inertial frame and not relative to a body-fixed reference frame.[6] [24]
Body frame Let the body frame inertia matrix relative to the center of mass be denoted I C B {\displaystyle \mathbf {I} _{\mathbf {C} }^{B}} A {\displaystyle \mathbf {A} }
x = A y , {\displaystyle \mathbf {x} =\mathbf {A} \mathbf {y} ,} where vectors y {\displaystyle \mathbf {y} } x {\displaystyle \mathbf {x} } I C = A I C B A T . {\displaystyle \mathbf {I} _{\mathbf {C} }=\mathbf {A} \mathbf {I} _{\mathbf {C} }^{B}\mathbf {A} ^{\mathsf {T}}.}
Notice that A {\displaystyle \mathbf {A} } I C B {\displaystyle \mathbf {I} _{\mathbf {C} }^{B}}
Principal axes Measured in the body frame, the inertia matrix is a constant real symmetric matrix. A real symmetric matrix has the eigendecomposition into the product of a rotation matrix Q {\displaystyle \mathbf {Q} } Λ {\displaystyle {\boldsymbol {\Lambda }}}
I C B = Q Λ Q T , {\displaystyle \mathbf {I} _{\mathbf {C} }^{B}=\mathbf {Q} {\boldsymbol {\Lambda }}\mathbf {Q} ^{\mathsf {T}},} where Λ = [ I 1 0 0 0 I 2 0 0 0 I 3 ] . {\displaystyle {\boldsymbol {\Lambda }}={\begin{bmatrix}I_{1}&0&0\\0&I_{2}&0\\0&0&I_{3}\end{bmatrix}}.}
The columns of the rotation matrix Q {\displaystyle \mathbf {Q} } I 1 {\displaystyle I_{1}} I 2 {\displaystyle I_{2}} I 3 {\displaystyle I_{3}} principal moments of inertia . This result was first shown by J. J. Sylvester (1852) , and is a form of Sylvester's law of inertia .[28] [29] figure axis or axis of figure .
A toy top is an example of a rotating rigid body, and the word top is used in names the types of types of rigid bodies. When all principal moments of inertia are distinct, the principal axes through center of mass are uniquely specified and the rigid body is called an asymmetric top . If two principal moments are the same, the rigid body is called a symmetric top and there is no unique choice for the two corresponding principal axes. If all three principal moments are the same, the rigid body is called a spherical top (although it need not be spherical) and any axis can be considered a principal axis, meaning that the moment of inertia is the same about any axis.
The principal axes are often aligned with the object's symmetry axes. If a rigid body has an axis of symmetry of order m {\displaystyle m} 360° /m m > 2 {\displaystyle m>2} Platonic solid .
The motion of vehicles is often described in terms of yaw, pitch, and roll which usually correspond approximately to rotations about the three principal axes. If the vehicle has bilateral symmetry then one of the principal axes will correspond exactly to the transverse (pitch) axis.
A practical example of this mathematical phenomenon is the routine automotive task of balancing a tire , which basically means adjusting the distribution of mass of a car wheel such that its principal axis of inertia is aligned with the axle so the wheel does not wobble.
Rotating molecules are also classified as asymmetric, symmetric, or spherical tops, and the structure of their rotational spectra is different for each type.
Ellipsoid An ellipsoid with the semi-principal diameters labelled a {\displaystyle a} b {\displaystyle b} c {\displaystyle c} The moment of inertia matrix in body-frame coordinates is a quadratic form that defines a surface in the body called Poinsot's ellipsoid .[30] Λ {\displaystyle {\boldsymbol {\Lambda }}}
x T Λ x = 1 , {\displaystyle \mathbf {x} ^{\mathsf {T}}{\boldsymbol {\Lambda }}\mathbf {x} =1,} or I 1 x 2 + I 2 y 2 + I 3 z 2 = 1 , {\displaystyle I_{1}x^{2}+I_{2}y^{2}+I_{3}z^{2}=1,} defines an ellipsoid in the body frame. Write this equation in the form, ( x 1 / I 1 ) 2 + ( y 1 / I 2 ) 2 + ( z 1 / I 3 ) 2 = 1 , {\displaystyle \left({\frac {x}{1/{\sqrt {I_{1}}}}}\right)^{2}+\left({\frac {y}{1/{\sqrt {I_{2}}}}}\right)^{2}+\left({\frac {z}{1/{\sqrt {I_{3}}}}}\right)^{2}=1,} to see that the semi-principal diameters of this ellipsoid are given by a = 1 I 1 , b = 1 I 2 , c = 1 I 3 . {\displaystyle a={\frac {1}{\sqrt {I_{1}}}},\quad b={\frac {1}{\sqrt {I_{2}}}},\quad c={\frac {1}{\sqrt {I_{3}}}}.}
Let a point x {\displaystyle \mathbf {x} } x = ‖ x ‖ n {\displaystyle \mathbf {x} =\ \mathbf {x} \ \mathbf {n} } n {\displaystyle \mathbf {n} } I n {\displaystyle I_{\mathbf {n} }} n {\displaystyle \mathbf {n} }
x T Λ x = ‖ x ‖ 2 n T Λ n = ‖ x ‖ 2 I n = 1. {\displaystyle \mathbf {x} ^{\mathsf {T}}{\boldsymbol {\Lambda }}\mathbf {x} =\ \mathbf {x} \ ^{2}\mathbf {n} ^{\mathsf {T}}{\boldsymbol {\Lambda }}\mathbf {n} =\ \mathbf {x} \ ^{2}I_{\mathbf {n} }=1.}
Thus, the magnitude of a point x {\displaystyle \mathbf {x} } n {\displaystyle \mathbf {n} }
‖ x ‖ = 1 I n . {\displaystyle \ \mathbf {x} \ ={\frac {1}{\sqrt {I_{\mathbf {n} }}}}.}
See also References ^ a b Mach, Ernst (1919). The Science of Mechanics 173 –187. Retrieved November 21, 2014 . ^ Euler, Leonhard (1765). Theoria motus corporum solidorum seu rigidorum: Ex primis nostrae cognitionis principiis stabilita et ad omnes motus, qui in huiusmodi corpora cadere possunt, accommodata [The theory of motion of solid or rigid bodies: established from first principles of our knowledge and appropriate for all motions which can occur in such bodies.] 166 . ISBN 978-1-4297-4281-8 "Definitio 7. 422. Momentum inertiae corporis respectu eujuspiam axis est summa omnium productorum, quae oriuntur, si singula corporis elementa per quadrata distantiarum suarum ab axe multiplicentur." (Definition 7. 422. A body's moment of inertia with respect to any axis is the sum of all of the products, which arise, if the individual elements of the body are multiplied by the square of their distances from the axis.)^ a b c d e f Marion, JB; Thornton, ST (1995). Classical dynamics of particles & systems ISBN 0-03-097302-3 ^ a b Symon, KR (1971). Mechanics (3rd ed.). Addison-Wesley. ISBN 0-201-07392-7 ^ a b Tenenbaum, RA (2004). Fundamentals of Applied Dynamics . Springer. ISBN 0-387-00887-X ^ a b c d e f g h Kane, T. R.; Levinson, D. A. (1985). Dynamics, Theory and Applications . New York: McGraw-Hill. ^ a b Winn, Will (2010). Introduction to Understandable Physics: Volume I - Mechanics ISBN 978-1449063337 ^ a b Fullerton, Dan (2011). Honors Physics Essentials ISBN 978-0983563334 ^ Wolfram, Stephen (2014). "Spinning Ice Skater" . Wolfram Demonstrations Project . Mathematica, Inc. Retrieved September 30, 2014 . ^ Hokin, Samuel (2014). "Figure Skating Spins" . The Physics of Everyday Stuff . Retrieved September 30, 2014 . ^ Breithaupt, Jim (2000). New Understanding Physics for Advanced Level ISBN 0748743146 ^ Crowell, Benjamin (2003). Conservation Laws 107 . ISBN 0970467028 ice skater conservation of angular momentum. ^ Tipler, Paul A. (1999). Physics for Scientists and Engineers, Vol. 1: Mechanics, Oscillations and Waves, Thermodynamics ISBN 1572594918 ^ a b c d e Paul, Burton (June 1979). Kinematics and Dynamics of Planar Machinery . Prentice Hall. ISBN 978-0135160626 ^ Halliday, David; Resnick, Robert; Walker, Jearl (2005). Fundamentals of physics (7th ed.). Hoboken, NJ: Wiley. ISBN 9780471216438 ^ French, A.P. (1971). Vibrations and waves . Boca Raton, FL: CRC Press. ISBN 9780748744473 ^ a b c d e f Uicker, John J.; Pennock, Gordon R.; Shigley, Joseph E. (2010). Theory of Machines and Mechanisms (4th ed.). Oxford University Press. ISBN 978-0195371239 ^ H. Williams, Measuring the inertia tensor , presented at the IMA Mathematics 2007 Conference. ^ Gracey, William, The experimental determination of the moments of inertia of airplanes by a simplified compound-pendulum method, NACA Technical Note No. 1629 , 1948 ^ Morrow, H. W.; Kokernak, Robert (2011). Statics and Strengths of Materials (7 ed.). New Jersey: Prentice Hall. pp. 192–196. ISBN 978-0135034521 ^ In that situation this moment of inertia only describes how a torque applied along that axis causes a rotation about that axis. But, torques not aligned along a principal axis will also cause rotations about other axes. ^ a b c d e f g h i Ferdinand P. Beer; E. Russell Johnston; Jr., Phillip J. Cornwell (2010). Vector mechanics for engineers: Dynamics (9th ed.). Boston: McGraw-Hill. ISBN 978-0077295493 ^ Walter D. Pilkey, Analysis and Design of Elastic Beams: Computational Methods , John Wiley, 2002. ^ a b Goldstein, H. (1980). Classical Mechanics (2nd ed.). Addison-Wesley. ISBN 0-201-02918-9 ^ L. D. Landau and E. M. Lifshitz, Mechanics , Vol 1. 2nd Ed., Pergamon Press, 1969. ^ L. W. Tsai, Robot Analysis: The mechanics of serial and parallel manipulators, John-Wiley, NY, 1999. ^ David, Baraff. "Physically Based Modeling - Rigid Body Simulation" (PDF) . Pixar Graphics Technologies . ^ Sylvester, J J (1852). "A demonstration of the theorem that every homogeneous quadratic polynomial is reducible by real orthogonal substitutions to the form of a sum of positive and negative squares" (PDF) . Philosophical Magazine . 4th Series. 4 (23): 138–142. doi :10.1080/14786445208647087 . Retrieved June 27, 2008 . ^ Norman, C.W. (1986). Undergraduate algebra . Oxford University Press . pp. 360–361. ISBN 0-19-853248-2 ^ Mason, Matthew T. (2001). Mechanics of Robotics Manipulation ISBN 978-0-262-13396-8 . Retrieved November 21, 2014 . External links
Linear/translational quantities Angular/rotational quantities Dimensions 1 L L2 Dimensions 1 θ θ 2 T time : t s absement : A m s T time : t s 1 distance : d position : r s x displacement m area : A m2 1 angle : θ angular displacement : θ rad solid angle : Ω rad2 , sr T−1 frequency : f s−1 , Hz speed : v velocity : v m s−1 kinematic viscosity : ν specific angular momentum : h m2 s−1 T−1 frequency : f s−1 , Hz angular speed : ω angular velocity : ω rad s−1 T−2 acceleration : a m s−2 T−2 angular acceleration : α rad s−2 T−3 jerk : j m s−3 T−3 angular jerk : ζ rad s−3 M mass : m kg weighted position: M ⟨x⟩ = ∑ m x ML2 moment of inertia : I kg m2 MT−1 momentum : p impulse : J kg m s−1 , N s action : 𝒮 , actergy : ℵ kg m2 s−1 , J s ML2 T−1 angular momentum : L angular impulse : ΔL kg m2 s−1 action : 𝒮 , actergy : ℵ kg m2 s−1 , J s MT−2 force : F weight : F g kg m s−2 , N energy : E work : W Lagrangian : L kg m2 s−2 , J ML2 T−2 torque : τ moment : M kg m2 s−2 , N m energy : E work : W Lagrangian : L kg m2 s−2 , J MT−3 yank : Y kg m s−3 , N s−1 power : P kg m2 s−3 , W ML2 T−3 rotatum : P kg m2 s−3 , N m s−1 power : P kg m2 s−3 , W










 축으로부터의 점 거리,
축으로부터의 점 거리, 질량이다.확장된 강체의 경우, 관성 모멘트는 모든 작은 질량의 조각에 회전하는 축으로부터의 거리의 제곱을 곱한 합입니다.정규 형태와 균일한 밀도의 확장된 물체의 경우, 이 합계는 물체의 치수, 모양 및 총 질량에 따라 달라지는 단순한 식을 만들어 낼 수 있습니다.
질량이다.확장된 강체의 경우, 관성 모멘트는 모든 작은 질량의 조각에 회전하는 축으로부터의 거리의 제곱을 곱한 합입니다.정규 형태와 균일한 밀도의 확장된 물체의 경우, 이 합계는 물체의 치수, 모양 및 총 질량에 따라 달라지는 단순한 식을 만들어 낼 수 있습니다. 



 발생시킨다.
발생시킨다. 토크 축에서 질량의 진자 중심까지의 거리
토크 축에서 질량의 진자 중심까지의 거리  질량에 대한 순 힘입니다.이 토크와 관련된 것은 이 축 주위의 끈과 질량의
질량에 대한 순 힘입니다.이 토크와 관련된 것은 이 축 주위의 끈과 질량의 



 진자 평면에 수직인 단위 벡터입니다.(두 번째 단계부터 마지막 단계까지
진자 평면에 수직인 단위 벡터입니다.(두 번째 단계부터 마지막 단계까지 양은 이 단일 질량의 피벗 지점 주위의 관성 모멘트이다.
양은 이 단일 질량의 피벗 지점 주위의 관성 모멘트이다. 





 중력의 국소 가속도,
중력의 국소 가속도,
 매달고 그 고유진동수나 진동주기
매달고 그 고유진동수나 진동주기 
 정의한다.이 점은
정의한다.이 점은 







 있는 N
있는 N





 각 점
각 점

 대해 평가됩니다
대해 평가됩니다


 밀도
밀도 얇은 막대의 관성 모멘트는
얇은 막대의 관성 모멘트는 
 로드의 질량입니다.
로드의 질량입니다.


 질량이다.
질량이다.


![{\displaystyle {\begin{aligned}I_{C,{\text{ball}}}&=\int _{-R}^{R}{\frac {\pi \rho }{2}}r(z)^{4}\,dz=\int _{-R}^{R}{\frac {\pi \rho }{2}}\left(R^{2}-z^{2}\right)^{2}\,dz\\&={\frac {\pi \rho }{2}}\left[R^{4}z-{\frac {2}{3}}R^{2}z^{3}+{\frac {1}{5}}z^{5}\right]_{-R}^{R}\\&=\pi \rho \left(1-{\frac {2}{3}}+{\frac {1}{5}}\right)R^{5}\\&={\frac {2}{5}}mR^{2},\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/42e610139e74980c31f979cff68d8cdd3684dd05)







 시스템의 각속도이고 V
시스템의 각속도이고 V R
R

 })
})












 관점에서
관점에서 







 R
R![{\displaystyle \left[\mathbf {b} \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2ce9643510bd433e0ed612edd5d3a9ed7faecfec)
![{\displaystyle {\begin{aligned}\mathbf {b} \times \mathbf {y} &\equiv \left[\mathbf {b} \right]\mathbf {y} \\\left[\mathbf {b} \right]&\equiv {\begin{bmatrix}0&-b_{z}&b_{y}\\b_{z}&0&-b_{x}\\-b_{y}&b_{x}&0\end{bmatrix}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b4782eb664e98a6d680dd96b77601ff9bc12ab4a)



![{\displaystyle [\Delta \mathbf {r} _{i}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3ee5960e77611f673ab2f2050f356dbf0e403132)
![{\displaystyle \mathbf {L} =\left(-\sum _{i=1}^{n}m_{i}\left[\Delta \mathbf {r} _{i}\right]^{2}\right){\boldsymbol {\omega }}=\mathbf {I} _{\mathbf {C} }{\boldsymbol {\omega }},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/26ff4f4ab9aa3fff11085b8828fc71a4af7de700)

![{\displaystyle \mathbf {I} _{\mathbf {C} }=-\sum _{i=1}^{n}m_{i}\left[\Delta \mathbf {r} _{i}\right]^{2},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6766e8a9ce07ff8f32ec86aaa929f1e5a3ce1a21)


![{\displaystyle {\begin{aligned}E_{\text{K}}&={\frac {1}{2}}\left(\sum _{i=1}^{n}m_{i}\left(\left[\Delta \mathbf {r} _{i}\right]{\boldsymbol {\omega }}\right)\cdot \left(\left[\Delta \mathbf {r} _{i}\right]{\boldsymbol {\omega }}\right)\right)+{\frac {1}{2}}\left(\sum _{i=1}^{n}m_{i}\right)\mathbf {V} _{\mathbf {C} }\cdot \mathbf {V} _{\mathbf {C} }\\&={\frac {1}{2}}\left(\sum _{i=1}^{n}m_{i}\left({\boldsymbol {\omega }}^{\mathsf {T}}\left[\Delta \mathbf {r} _{i}\right]^{\mathsf {T}}\left[\Delta \mathbf {r} _{i}\right]{\boldsymbol {\omega }}\right)\right)+{\frac {1}{2}}\left(\sum _{i=1}^{n}m_{i}\right)\mathbf {V} _{\mathbf {C} }\cdot \mathbf {V} _{\mathbf {C} }\\&={\frac {1}{2}}{\boldsymbol {\omega }}\cdot \left(-\sum _{i=1}^{n}m_{i}\left[\Delta \mathbf {r} _{i}\right]^{2}\right){\boldsymbol {\omega }}+{\frac {1}{2}}\left(\sum _{i=1}^{n}m_{i}\right)\mathbf {V} _{\mathbf {C} }\cdot \mathbf {V} _{\mathbf {C} }.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c246c5646e149b67a600084c164f154ec7dda89)







![{\displaystyle {\boldsymbol {\tau }}=\left(-\sum _{i=1}^{n}m_{i}\left[\Delta \mathbf {r} _{i}\right]^{2}\right){\boldsymbol {\alpha }}+{\boldsymbol {\omega }}\times \left(-\sum _{i=1}^{n}m_{i}\left[\Delta \mathbf {r} _{i}\right]^{2}\right){\boldsymbol {\omega }}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b93d7ec560fb15fbaaba36a2fd0869da807fd92e)

![{\displaystyle {\begin{aligned}{\boldsymbol {\tau }}&=\sum _{i=1}^{n}(\mathbf {r_{i}} -\mathbf {R} )\times (m_{i}\mathbf {a} _{i})\\&=\sum _{i=1}^{n}{\boldsymbol {\Delta }}\mathbf {r} _{i}\times (m_{i}\mathbf {a} _{i})\\&=\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times \mathbf {a} _{i}]\;\ldots {\text{ cross-product scalar multiplication}}\\&=\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times (\mathbf {a} _{{\text{tangential}},i}+\mathbf {a} _{{\text{centripetal}},i}+\mathbf {A} _{\mathbf {R} })]\\&=\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times (\mathbf {a} _{{\text{tangential}},i}+\mathbf {a} _{{\text{centripetal}},i}+0)]\\&\;\;\;\;\;\ldots \;\mathbf {R} {\text{ is either at rest or moving at a constant velocity but not accelerated, or }}\\&\;\;\;\;\;\;\;\;\;\;\;{\text{the origin of the fixed (world) coordinate reference system is placed at the center of mass }}\mathbf {C} \\&=\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times \mathbf {a} _{{\text{tangential}},i}+{\boldsymbol {\Delta }}\mathbf {r} _{i}\times \mathbf {a} _{{\text{centripetal}},i}]\;\ldots {\text{ cross-product distributivity over addition}}\\&=\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\alpha }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})+{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\omega }}\times \mathbf {v} _{{\text{tangential}},i})]\\{\boldsymbol {\tau }}&=\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\alpha }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})+{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\omega }}\times ({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i}))]\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3a1a1b0804a6cf8a550a81732385fca1083051df)
![{\displaystyle {\begin{aligned}0&={\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\omega }}\times ({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i}))+{\boldsymbol {\omega }}\times (({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})\times {\boldsymbol {\Delta }}\mathbf {r} _{i})+({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})\times ({\boldsymbol {\Delta }}\mathbf {r} _{i}\times {\boldsymbol {\omega }})\\&={\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\omega }}\times ({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i}))+{\boldsymbol {\omega }}\times (({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})\times {\boldsymbol {\Delta }}\mathbf {r} _{i})+({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})\times -({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})\;\ldots {\text{ cross-product anticommutativity}}\\&={\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\omega }}\times ({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i}))+{\boldsymbol {\omega }}\times (({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})\times {\boldsymbol {\Delta }}\mathbf {r} _{i})+-[({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})\times ({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})]\;\ldots {\text{ cross-product scalar multiplication}}\\&={\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\omega }}\times ({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i}))+{\boldsymbol {\omega }}\times (({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})\times {\boldsymbol {\Delta }}\mathbf {r} _{i})+-[0]\;\ldots {\text{ self cross-product}}\\0&={\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\omega }}\times ({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i}))+{\boldsymbol {\omega }}\times (({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})\times {\boldsymbol {\Delta }}\mathbf {r} _{i})\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/88ab33d54b34674092a14d55c8ccefb765a2e7ae)
![{\displaystyle {\begin{aligned}{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\omega }}\times ({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i}))&=-[{\boldsymbol {\omega }}\times (({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})\times {\boldsymbol {\Delta }}\mathbf {r} _{i})]\\&=-[({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})({\boldsymbol {\omega }}\cdot {\boldsymbol {\Delta }}\mathbf {r} _{i})-{\boldsymbol {\Delta }}\mathbf {r} _{i}({\boldsymbol {\omega }}\cdot ({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i}))]\;\ldots {\text{ vector triple product}}\\&=-[({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})({\boldsymbol {\omega }}\cdot {\boldsymbol {\Delta }}\mathbf {r} _{i})-{\boldsymbol {\Delta }}\mathbf {r} _{i}({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot ({\boldsymbol {\omega }}\times {\boldsymbol {\omega }}))]\;\ldots {\text{ scalar triple product}}\\&=-[({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})({\boldsymbol {\omega }}\cdot {\boldsymbol {\Delta }}\mathbf {r} _{i})-{\boldsymbol {\Delta }}\mathbf {r} _{i}({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot (0))]\;\ldots {\text{ self cross-product}}\\&=-[({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})({\boldsymbol {\omega }}\cdot {\boldsymbol {\Delta }}\mathbf {r} _{i})]\\&=-[{\boldsymbol {\omega }}\times ({\boldsymbol {\Delta }}\mathbf {r} _{i}({\boldsymbol {\omega }}\cdot {\boldsymbol {\Delta }}\mathbf {r} _{i}))]\;\ldots {\text{ cross-product scalar multiplication}}\\&={\boldsymbol {\omega }}\times -({\boldsymbol {\Delta }}\mathbf {r} _{i}({\boldsymbol {\omega }}\cdot {\boldsymbol {\Delta }}\mathbf {r} _{i}))\;\ldots {\text{ cross-product scalar multiplication}}\\{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\omega }}\times ({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i}))&={\boldsymbol {\omega }}\times -({\boldsymbol {\Delta }}\mathbf {r} _{i}({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot {\boldsymbol {\omega }}))\;\ldots {\text{ dot-product commutativity}}\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bb1ab7d45bf04c0df3101e84282bc6695ddecf68)
![{\displaystyle {\begin{aligned}{\boldsymbol {\tau }}&=\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\alpha }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})+{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\omega }}\times ({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i}))]\\&=\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\alpha }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})+{\boldsymbol {\omega }}\times -({\boldsymbol {\Delta }}\mathbf {r} _{i}({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot {\boldsymbol {\omega }}))]\\&=\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\alpha }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})+{\boldsymbol {\omega }}\times \{0-{\boldsymbol {\Delta }}\mathbf {r} _{i}({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot {\boldsymbol {\omega }})\}]\\&=\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\alpha }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})+{\boldsymbol {\omega }}\times \{[{\boldsymbol {\omega }}({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot {\boldsymbol {\Delta }}\mathbf {r} _{i})-{\boldsymbol {\omega }}({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot {\boldsymbol {\Delta }}\mathbf {r} _{i})]-{\boldsymbol {\Delta }}\mathbf {r} _{i}({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot {\boldsymbol {\omega }})\}]\;\ldots \;{\boldsymbol {\omega }}({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot {\boldsymbol {\Delta }}\mathbf {r} _{i})-{\boldsymbol {\omega }}({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot {\boldsymbol {\Delta }}\mathbf {r} _{i})=0\\&=\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\alpha }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})+{\boldsymbol {\omega }}\times \{[{\boldsymbol {\omega }}({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot {\boldsymbol {\Delta }}\mathbf {r} _{i})-{\boldsymbol {\Delta }}\mathbf {r} _{i}({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot {\boldsymbol {\omega }})]-{\boldsymbol {\omega }}({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot {\boldsymbol {\Delta }}\mathbf {r} _{i})\}]\;\ldots {\text{ addition associativity}}\\\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/66f6f583aacfd008f43218fc24e97547511a6a91)
![{\displaystyle {\begin{aligned}&=\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\alpha }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})+{\boldsymbol {\omega }}\times \{{\boldsymbol {\omega }}({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot {\boldsymbol {\Delta }}\mathbf {r} _{i})-{\boldsymbol {\Delta }}\mathbf {r} _{i}({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot {\boldsymbol {\omega }})\}-{\boldsymbol {\omega }}\times {\boldsymbol {\omega }}({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot {\boldsymbol {\Delta }}\mathbf {r} _{i})]\;\ldots {\text{ cross-product distributivity over addition}}\\&=\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\alpha }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})+{\boldsymbol {\omega }}\times \{{\boldsymbol {\omega }}({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot {\boldsymbol {\Delta }}\mathbf {r} _{i})-{\boldsymbol {\Delta }}\mathbf {r} _{i}({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot {\boldsymbol {\omega }})\}-({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot {\boldsymbol {\Delta }}\mathbf {r} _{i})({\boldsymbol {\omega }}\times {\boldsymbol {\omega }})]\;\ldots {\text{ cross-product scalar multiplication}}\\&=\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\alpha }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})+{\boldsymbol {\omega }}\times \{{\boldsymbol {\omega }}({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot {\boldsymbol {\Delta }}\mathbf {r} _{i})-{\boldsymbol {\Delta }}\mathbf {r} _{i}({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot {\boldsymbol {\omega }})\}-({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot {\boldsymbol {\Delta }}\mathbf {r} _{i})(0)]\;\ldots {\text{ self cross-product}}\\&=\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\alpha }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})+{\boldsymbol {\omega }}\times \{{\boldsymbol {\omega }}({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot {\boldsymbol {\Delta }}\mathbf {r} _{i})-{\boldsymbol {\Delta }}\mathbf {r} _{i}({\boldsymbol {\Delta }}\mathbf {r} _{i}\cdot {\boldsymbol {\omega }})\}]\\&=\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\alpha }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})+{\boldsymbol {\omega }}\times \{{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\omega }}\times {\boldsymbol {\Delta }}\mathbf {r} _{i})\}]\;\ldots {\text{ vector triple product}}\\&=\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times -({\boldsymbol {\Delta }}\mathbf {r} _{i}\times {\boldsymbol {\alpha }})+{\boldsymbol {\omega }}\times \{{\boldsymbol {\Delta }}\mathbf {r} _{i}\times -({\boldsymbol {\Delta }}\mathbf {r} _{i}\times {\boldsymbol {\omega }})\}]\;\ldots {\text{ cross-product anticommutativity}}\\&=-\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\Delta }}\mathbf {r} _{i}\times {\boldsymbol {\alpha }})+{\boldsymbol {\omega }}\times \{{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\Delta }}\mathbf {r} _{i}\times {\boldsymbol {\omega }})\}]\;\ldots {\text{ cross-product scalar multiplication}}\\&=-\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\Delta }}\mathbf {r} _{i}\times {\boldsymbol {\alpha }})]+-\sum _{i=1}^{n}m_{i}[{\boldsymbol {\omega }}\times \{{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\Delta }}\mathbf {r} _{i}\times {\boldsymbol {\omega }})\}]\;\ldots {\text{ summation distributivity}}\\{\boldsymbol {\tau }}&=-\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\Delta }}\mathbf {r} _{i}\times {\boldsymbol {\alpha }})]+{\boldsymbol {\omega }}\times -\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\Delta }}\mathbf {r} _{i}\times {\boldsymbol {\omega }})]\;\ldots \;{\boldsymbol {\omega }}{\text{ is not characteristic of particle }}P_{i}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/adeb5bbad0d607e038f18398c83a2761c4af3102)

![{\displaystyle {\begin{aligned}-\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\Delta }}\mathbf {r} _{i}\times \mathbf {u} )]&=-\sum _{i=1}^{n}m_{i}\left({\begin{bmatrix}0&-\Delta r_{3,i}&\Delta r_{2,i}\\\Delta r_{3,i}&0&-\Delta r_{1,i}\\-\Delta r_{2,i}&\Delta r_{1,i}&0\end{bmatrix}}\left({\begin{bmatrix}0&-\Delta r_{3,i}&\Delta r_{2,i}\\\Delta r_{3,i}&0&-\Delta r_{1,i}\\-\Delta r_{2,i}&\Delta r_{1,i}&0\end{bmatrix}}{\begin{bmatrix}u_{1}\\u_{2}\\u_{3}\end{bmatrix}}\right)\right)\;\ldots {\text{ cross-product as matrix multiplication}}\\[6pt]&=-\sum _{i=1}^{n}m_{i}\left({\begin{bmatrix}0&-\Delta r_{3,i}&\Delta r_{2,i}\\\Delta r_{3,i}&0&-\Delta r_{1,i}\\-\Delta r_{2,i}&\Delta r_{1,i}&0\end{bmatrix}}{\begin{bmatrix}-\Delta r_{3,i}\,u_{2}+\Delta r_{2,i}\,u_{3}\\+\Delta r_{3,i}\,u_{1}-\Delta r_{1,i}\,u_{3}\\-\Delta r_{2,i}\,u_{1}+\Delta r_{1,i}\,u_{2}\end{bmatrix}}\right)\\[6pt]&=-\sum _{i=1}^{n}m_{i}{\begin{bmatrix}-\Delta r_{3,i}(+\Delta r_{3,i}\,u_{1}-\Delta r_{1,i}\,u_{3})+\Delta r_{2,i}(-\Delta r_{2,i}\,u_{1}+\Delta r_{1,i}\,u_{2})\\+\Delta r_{3,i}(-\Delta r_{3,i}\,u_{2}+\Delta r_{2,i}\,u_{3})-\Delta r_{1,i}(-\Delta r_{2,i}\,u_{1}+\Delta r_{1,i}\,u_{2})\\-\Delta r_{2,i}(-\Delta r_{3,i}\,u_{2}+\Delta r_{2,i}\,u_{3})+\Delta r_{1,i}(+\Delta r_{3,i}\,u_{1}-\Delta r_{1,i}\,u_{3})\end{bmatrix}}\\[6pt]&=-\sum _{i=1}^{n}m_{i}{\begin{bmatrix}-\Delta r_{3,i}^{2}\,u_{1}+\Delta r_{1,i}\Delta r_{3,i}\,u_{3}-\Delta r_{2,i}^{2}\,u_{1}+\Delta r_{1,i}\Delta r_{2,i}\,u_{2}\\-\Delta r_{3,i}^{2}\,u_{2}+\Delta r_{2,i}\Delta r_{3,i}\,u_{3}+\Delta r_{2,i}\Delta r_{1,i}\,u_{1}-\Delta r_{1,i}^{2}\,u_{2}\\+\Delta r_{3,i}\Delta r_{2,i}\,u_{2}-\Delta r_{2,i}^{2}\,u_{3}+\Delta r_{3,i}\Delta r_{1,i}\,u_{1}-\Delta r_{1,i}^{2}\,u_{3}\end{bmatrix}}\\[6pt]&=-\sum _{i=1}^{n}m_{i}{\begin{bmatrix}-(\Delta r_{2,i}^{2}+\Delta r_{3,i}^{2})\,u_{1}+\Delta r_{1,i}\Delta r_{2,i}\,u_{2}+\Delta r_{1,i}\Delta r_{3,i}\,u_{3}\\+\Delta r_{2,i}\Delta r_{1,i}\,u_{1}-(\Delta r_{1,i}^{2}+\Delta r_{3,i}^{2})\,u_{2}+\Delta r_{2,i}\Delta r_{3,i}\,u_{3}\\+\Delta r_{3,i}\Delta r_{1,i}\,u_{1}+\Delta r_{3,i}\Delta r_{2,i}\,u_{2}-(\Delta r_{1,i}^{2}+\Delta r_{2,i}^{2})\,u_{3}\end{bmatrix}}\\[6pt]&=-\sum _{i=1}^{n}m_{i}{\begin{bmatrix}-(\Delta r_{2,i}^{2}+\Delta r_{3,i}^{2})&\Delta r_{1,i}\Delta r_{2,i}&\Delta r_{1,i}\Delta r_{3,i}\\\Delta r_{2,i}\Delta r_{1,i}&-(\Delta r_{1,i}^{2}+\Delta r_{3,i}^{2})&\Delta r_{2,i}\Delta r_{3,i}\\\Delta r_{3,i}\Delta r_{1,i}&\Delta r_{3,i}\Delta r_{2,i}&-(\Delta r_{1,i}^{2}+\Delta r_{2,i}^{2})\end{bmatrix}}{\begin{bmatrix}u_{1}\\u_{2}\\u_{3}\end{bmatrix}}\\&=-\sum _{i=1}^{n}m_{i}[\Delta r_{i}]^{2}\mathbf {u} \\[6pt]-\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\Delta }}\mathbf {r} _{i}\times \mathbf {u} )]&=\left(-\sum _{i=1}^{n}m_{i}[\Delta r_{i}]^{2}\right)\mathbf {u} \;\ldots \;\mathbf {u} {\text{ is not characteristic of }}P_{i}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/059812b4501e0672712b5b7adff834e79c3b4bff)
![{\displaystyle {\begin{aligned}{\boldsymbol {\tau }}&=-\sum _{i=1}^{n}m_{i}[{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\Delta }}\mathbf {r} _{i}\times {\boldsymbol {\alpha }})]+{\boldsymbol {\omega }}\times -\sum _{i=1}^{n}m_{i}{\boldsymbol {\Delta }}\mathbf {r} _{i}\times ({\boldsymbol {\Delta }}\mathbf {r} _{i}\times {\boldsymbol {\omega }})]\\&=\left(-\sum _{i=1}^{n}m_{i}[\Delta r_{i}]^{2}\right){\boldsymbol {\alpha }}+{\boldsymbol {\omega }}\times \left(-\sum _{i=1}^{n}m_{i}[\Delta r_{i}]^{2}\right){\boldsymbol {\omega }}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0971bbc71e7ceb3c810afa1043b08aca54608486)


![{\displaystyle \mathbf {I} _{\mathbf {R} }=-\sum _{i=1}^{n}m_{i}\left[\mathbf {r} _{i}-\mathbf {R} \right]^{2}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/93e62233b3acff4fc919fc24e8d6241551543087)


![{\displaystyle \mathbf {I} _{\mathbf {R} }=-\sum _{i=1}^{n}m_{i}[\mathbf {r} _{i}-\left(\mathbf {C} +\mathbf {d} \right)]^{2}=-\sum _{i=1}^{n}m_{i}[\left(\mathbf {r} _{i}-\mathbf {C} \right)-\mathbf {d} ]^{2}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0063409d605348215928372e62f294287f06fb98)
![{\displaystyle \mathbf {I} _{\mathbf {R} }=-\left(\sum _{i=1}^{n}m_{i}[\mathbf {r} _{i}-\mathbf {C} ]^{2}\right)+\left(\sum _{i=1}^{n}m_{i}[\mathbf {r} _{i}-\mathbf {C} ]\right)[\mathbf {d} ]+[\mathbf {d} ]\left(\sum _{i=1}^{n}m_{i}[\mathbf {r} _{i}-\mathbf {C} ]\right)-\left(\sum _{i=1}^{n}m_{i}\right)[\mathbf {d} ]^{2}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/68eee7fefe0e716823fd5d80384303b8aef58b99)
![{\displaystyle [\mathbf {d} ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a5785dcf9605fb6ace7c1a8c8b4d6b365af48366)
![{\displaystyle \mathbf {I} _{\mathbf {R} }=\mathbf {I} _{\mathbf {C} }-M[\mathbf {d} ]^{2},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1c59b0848c4b1d69fff75c4257005225cd42c74d)
![{\displaystyle -m\left[\mathbf {r} \right]^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6b3ed54432828b43d6ae23e9a2e9c009c7336024)
![{\displaystyle m\left[\mathbf {r} \right]^{\mathsf {T}}\left[\mathbf {r} \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/27fed5e06e85cd3d74847c333b7a32cbd6a31fe7)
![{\displaystyle [\mathbf {r} ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ba4c4e0b7a62e35392117d1331b60c9e3276b5c9)

![{\displaystyle I_{L}=\mathbf {\hat {k}} \cdot \left(-\sum _{i=1}^{N}m_{i}\left[\Delta \mathbf {r} _{i}\right]^{2}\right)\mathbf {\hat {k}} =\mathbf {\hat {k}} \cdot \mathbf {I} _{\mathbf {R} }\mathbf {\hat {k}} =\mathbf {\hat {k}} ^{\mathsf {T}}\mathbf {I} _{\mathbf {R} }\mathbf {\hat {k}} ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/78bb7c062959fd615347939341b32bf66de221c6)





![{\displaystyle \left[\mathbf {\hat {k}} \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a515c7495954477be07dee4f29d4c4c4ec50cf98)
![{\displaystyle \left[\mathbf {\hat {k}} \right]\mathbf {y} =\mathbf {\hat {k}} \times \mathbf {y} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/10d1281a399f50084c4d71e516f5d56b1cf5426f)
![{\displaystyle -\left[\mathbf {\hat {k}} \right]^{2}\equiv \left|\mathbf {\hat {k}} \right|^{2}\left(\mathbf {E} -\mathbf {\hat {k}} \mathbf {\hat {k}} ^{\mathsf {T}}\right)=\mathbf {E} -\mathbf {\hat {k}} \mathbf {\hat {k}} ^{\mathsf {T}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d92be0b3adbb50fbe61b31dc0237f0fc102476a0)
![{\displaystyle {\begin{aligned}\left|\Delta \mathbf {r} _{i}^{\perp }\right|^{2}&=\left(-\left[\mathbf {\hat {k}} \right]^{2}\Delta \mathbf {r} _{i}\right)\cdot \left(-\left[\mathbf {\hat {k}} \right]^{2}\Delta \mathbf {r} _{i}\right)\\&=\left(\mathbf {\hat {k}} \times \left(\mathbf {\hat {k}} \times \Delta \mathbf {r} _{i}\right)\right)\cdot \left(\mathbf {\hat {k}} \times \left(\mathbf {\hat {k}} \times \Delta \mathbf {r} _{i}\right)\right)\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9d205a6da935ecfa8f5e13feb1a930f1d032022a)

![{\displaystyle {\begin{aligned}&\left(\mathbf {\hat {k}} \times \left(\mathbf {\hat {k}} \times \Delta \mathbf {r} _{i}\right)\right)\cdot \left(\mathbf {\hat {k}} \times \left(\mathbf {\hat {k}} \times \Delta \mathbf {r} _{i}\right)\right)\\={}&\left(\left(\mathbf {\hat {k}} \times \left(\mathbf {\hat {k}} \times \Delta \mathbf {r} _{i}\right)\right)\times \mathbf {\hat {k}} \right)\cdot \left(\mathbf {\hat {k}} \times \Delta \mathbf {r} _{i}\right)\\={}&\left(\mathbf {\hat {k}} \times \Delta \mathbf {r} _{i}\right)\cdot \left(-\Delta \mathbf {r} _{i}\times \mathbf {\hat {k}} \right)\\={}&-\mathbf {\hat {k}} \cdot \left(\Delta \mathbf {r} _{i}\times \Delta \mathbf {r} _{i}\times \mathbf {\hat {k}} \right)\\={}&-\mathbf {\hat {k}} \cdot \left[\Delta \mathbf {r} _{i}\right]^{2}\mathbf {\hat {k}} .\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/62111ff66a6922e2705a7eb60478088077b7d9bf)
![{\displaystyle {\begin{aligned}I_{L}&=\sum _{i=1}^{N}m_{i}\left|\Delta \mathbf {r} _{i}^{\perp }\right|^{2}\\&=-\sum _{i=1}^{N}m_{i}\mathbf {\hat {k}} \cdot \left[\Delta \mathbf {r} _{i}\right]^{2}\mathbf {\hat {k}} =\mathbf {\hat {k}} \cdot \left(-\sum _{i=1}^{N}m_{i}\left[\Delta \mathbf {r} _{i}\right]^{2}\right)\mathbf {\hat {k}} \\&=\mathbf {\hat {k}} \cdot \mathbf {I} _{\mathbf {R} }\mathbf {\hat {k}} =\mathbf {\hat {k}} ^{\mathsf {T}}\mathbf {I} _{\mathbf {R} }\mathbf {\hat {k}} ,\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1f4a4a61db87467a4b76294e68bba221a2810cdf)













![{\displaystyle [\mathbf {r} ]\mathbf {x} =\mathbf {r} \times \mathbf {x} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f32ba1c18fa5966e4dcd2275a7f7e3bc21f6dc0)
![{\displaystyle \mathbf {I} =\iiint _{V}\rho (\mathbf {r} )[\mathbf {r} ]^{\textsf {T}}[\mathbf {r} ]\,dV=-\iiint _{Q}\rho (\mathbf {r} )[\mathbf {r} ]^{2}\,dV}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f468dc8f2e4246bf78b1916390083f90998be5c)





![{\displaystyle {\begin{aligned}I_{xy}=I_{yx}\ &{\stackrel {\mathrm {def} }{=}}\ \sum _{k=1}^{N}m_{k}x_{k}y_{k},\\I_{xz}=I_{zx}\ &{\stackrel {\mathrm {def} }{=}}\ \sum _{k=1}^{N}m_{k}x_{k}z_{k},\\I_{yz}=I_{zy}\ &{\stackrel {\mathrm {def} }{=}}\ \sum _{k=1}^{N}m_{k}y_{k}z_{k},\\[3pt]\mathbf {I} ={\begin{bmatrix}I_{11}&I_{12}&I_{13}\\I_{21}&I_{22}&I_{23}\\I_{31}&I_{32}&I_{33}\end{bmatrix}}&={\begin{bmatrix}I_{xx}&-I_{xy}&-I_{xz}\\-I_{yx}&I_{yy}&-I_{yz}\\-I_{zx}&-I_{zy}&I_{zz}\end{bmatrix}}={\begin{bmatrix}\sum _{k=1}^{N}m_{k}\left(y_{k}^{2}+z_{k}^{2}\right)&-\sum _{k=1}^{N}m_{k}x_{k}y_{k}&-\sum _{k=1}^{N}m_{k}x_{k}z_{k}\\-\sum _{k=1}^{N}m_{k}x_{k}y_{k}&\sum _{k=1}^{N}m_{k}\left(x_{k}^{2}+z_{k}^{2}\right)&-\sum _{k=1}^{N}m_{k}y_{k}z_{k}\\-\sum _{k=1}^{N}m_{k}x_{k}z_{k}&-\sum _{k=1}^{N}m_{k}y_{k}z_{k}&\sum _{k=1}^{N}m_{k}\left(x_{k}^{2}+y_{k}^{2}\right)\end{bmatrix}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a01acaa1d453d5d3f4c7faf8a74da5b2637bb01)










![{\displaystyle \mathbf {I} =\mathbf {I} _{0}+m[(\mathbf {R} \cdot \mathbf {R} )\mathbf {E} _{3}-\mathbf {R} \otimes \mathbf {R} ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/22568fa28674e243955b8fdddced7496b8e6487d)




























