쿼터니언
Quaternion| ↓ × → | 1 | i | j | k |
|---|---|---|---|---|
| 1 | 1 | i | j | k |
| i | i | −1 | k | −j |
| j | j | −k | −1 | i |
| k | k | j | −i | −1 |
| 참고: 행 또는 열 제목에 역이 나타나지 않으므로 케일리 표가 아닌 곱셈 표입니다.(왼쪽 열에는 전단승수가 표시됩니다.맨 위 행은 사후 승수를 나타냅니다.) | ||||

수학에서 사분위수 체계는 복소수를 확장합니다.쿼터니언은 아일랜드 수학자 윌리엄[1][2] 로완 해밀턴에 의해 1843년에 처음 기술되었고 3차원 공간의 역학에 적용되었습니다.해밀턴은 쿼터니언을 3차원 [3]공간에서 두 방향선의 몫으로 정의하거나, 또는 동등하게 [4]두 벡터의 몫으로 정의했습니다.쿼터니언의 곱셈은 비상호적입니다.
쿼터니언은 일반적으로 다음과 같은 형태로 표시됩니다.
여기서 a, b, c, d는 실수이고, 1, i, j, k는 기저 벡터 또는 기저 [5]요소입니다.
쿼터니언은 순수 수학에서 사용되지만 응용 수학에서도 실용적으로 사용되며, 특히 3차원 컴퓨터 그래픽스, 컴퓨터 비전 및 결정학적 텍스처 [6]분석과 같은 3차원 회전을 수반하는 계산에 사용됩니다.이들은 오일러 각도 및 회전 행렬과 같은 다른 회전 방법과 함께 사용되거나 용도에 따라 이들에 대한 대안으로 사용될 수 있습니다.
현대 수학 언어에서 쿼터니언은 실수 위에 4차원 연관 정규 분할 대수를 형성하며, 따라서 분할 고리이자 정의역이 되는 고리입니다.쿼터니언의 대수는 종종 H(해밀턴의 경우)로 표시되거나,로 굵게 칠판으로 표시됩니다 {H 클리포드 분류 , 2 ( ) ≅ 0 +( R 로 주어질 수도 있습니다 {\ \ _{R \,0{R 사실,그것은 최초로 발견된 비상호적 분할 대수였습니다.
프로베니우스 정리에 따르면, H 는 실수와 동형인 적절한 부분 고리를 포함하는 단 두 개의 유한 차원 분할 고리 중 하나입니다. 다른 하나는 복소수입니다.이 고리들은 또한 유클리드 후르비츠 대수이며, 그 중 쿼터니언은 가장 큰 연관 대수(따라서 가장 큰 고리)입니다.쿼티온을 더 확장하면 비연관적 팔색조가 산출되는데, 이것은 실수에 대한 마지막 정규화된 나눗셈 대수입니다. (팔색조의 확장인 이십진은 0의 나눗셈을 가지므로 정규화된 나눗셈 대수가 될 수 없습니다.)[7]
단위 쿼터니언은 SU(2)와 동형이면서 SO(3)의 보편적 커버에도 해당하는 스핀(3) 그룹을 제공하는 3-sphere3 S 상의 그룹 구조 선택으로 간주될 수 있습니다.

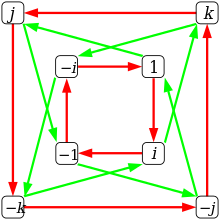
- 파란색:
- 1 ⋅ i = i (1/i 평면)
- i ⋅ j = k (i/k 평면)
- 빨간색:
- 1 ⋅ j = j (1/j 평면)
- j ⋅ i = -k (j/k 평면)
역사

그가 지나가면서 여기.
1843년 10월 16일에
윌리엄 로완 해밀턴 경
눈 깜짝할 사이에 발견된 천재.
의 기본 공식
4차 곱셈
i = j = k = i j k = -1
& 이 다리의 돌에 그것을 베다.
쿼터니언은 [8]1843년 해밀턴에 의해 소개되었습니다.이 연구의 중요한 선구자는 오일러의 4제곱 항등식(1748)과 올린데 로드리게스의 일반적인 회전에 대한 매개변수화(1840)를 포함했지만, 이 두 작가 모두 4개의 매개변수 회전을 [9][10]대수로 취급하지 않았습니다.칼 프리드리히 가우스도 1819년에 쿼터니언을 발견했지만, [11][12]이 작품은 1900년까지 출판되지 않았습니다.
해밀턴은 복소수가 평면상의 점으로 해석될 수 있다는 것을 알고 있었고, 3차원 공간의 점에 대해서도 같은 방법을 찾고 있었습니다.공간에 있는 점들은 숫자의 세 배인 좌표로 표현될 수 있고, 그는 수년 동안 숫자의 세 배를 더하고 뺄 수 있는 방법을 알고 있었습니다.하지만 그는 오랫동안 곱셈과 나눗셈의 문제에 매달렸습니다.그는 공간에 있는 두 점의 좌표의 몫을 계산하는 방법을 알아낼 수 없었습니다.사실, 페르디난트 게오르크 프로베니우스는 나중에 1877년 실수에 대한 나눗셈 대수가 유한 차원이고 연관성이 있는 것은 3차원이 될 수 없으며, 오직 3개의 나눗셈 대수만 존재한다는 것을 증명했습니다: {\}(복소수)와 H 사분수).nsion 1, 2, 4.
쿼터니언의 위대한 돌파구는 마침내 1843년 10월 16일 월요일 더블린에서 Hamilton이 의회 회의를 주재하기 위해 Royal Irish Academy로 가는 길에 나타났습니다.아내와 함께 왕운하의 뱃길을 따라 걸으면서 쿼터니언 뒤의 개념들이 머릿속에서 구체화되고 있었습니다.그 답이 떠올랐을 때에, 해밀턴은 사분면의 공식을 조각하고 싶은 충동을 참을 수 없었습니다.
브로엄 다리의 돌 위에 잠시 멈춰 섰을 때.비록 조각은 그 이후로 희미해졌지만, 해밀턴의 발견을 기념하기 위해 던싱크 천문대에서 로열 캐널 다리까지 걸어가는 과학자들과 수학자들을 위한 해밀턴 워크(Hamilton Walk)라고 불리는 연례 순례가 1989년부터 있어왔습니다.
다음 날, 해밀턴은 그의 친구이자 동료 수학자인 존 T. 그레이브스에게 그의 발견으로 이어진 사고의 과정을 설명하는 편지를 썼습니다.이 편지는 나중에 런던, 에든버러, 더블린 철학 잡지와 과학 [13]저널에 보낸 편지에 실렸습니다. 해밀턴은 다음과 같이 말합니다.
그리고 여기서 나는 우리가 세 배로 계산하기 위해 어떤 의미에서 네 번째 차원의 공간을 인정해야 한다는 생각을 하게 되었습니다.전기 회로가 닫히는 듯했고, 불꽃이 [13]튀었습니다.
해밀턴은 이러한 곱셈의 규칙을 가진 4중주를 4중주라고 불렀고, 그는 그들을 연구하고 가르치는데 그의 남은 인생의 대부분을 바쳤습니다.해밀턴의 처리는 쿼터니언의 대수적 특성을 강조하는 현대적인 접근법보다 더 기하학적입니다.그는 "4중주론자" 학교를 설립했고, 여러 책에서 4중주를 대중화하려고 노력했습니다.그의 책 중 마지막이자 가장 긴 것인 쿼터니언의 [14]요소들은 800페이지 길이였습니다; 그것은 그의 아들에 의해 편집되었고 그가 죽은 직후에 출판되었습니다.
해밀턴의 죽음 이후, 스코틀랜드의 수학 물리학자 피터 테이트는 쿼터니언의 주요 지수가 되었습니다.이 당시 더블린에서는 쿼터니언이 필수 검사 주제였습니다.공간에서의 운동학과 맥스웰 방정식과 같은 벡터를 사용하여 이제 설명될 물리학과 기하학의 주제는 전적으로 4차 이온의 측면에서 설명되었습니다.심지어 쿼터니언과 다른 초복소수 체계 연구에 전념하는 전문 연구 협회인 쿼터니언 협회도 있었습니다.
1880년대 중반부터 쿼터니언들은 조시아 윌러드 깁스, 올리버 헤비사이드, 헤르만 폰 헬름홀츠에 의해 개발된 벡터 분석에 의해 대체되기 시작했습니다.벡터 분석은 쿼터니언과 같은 현상을 묘사했기 때문에 쿼터니언에 대한 문헌에서 자유롭게 몇 가지 아이디어와 용어를 빌려왔습니다.그러나 벡터 분석은 개념적으로 더 간단했고 명목상으로는 더 깨끗했고, 결국 쿼터니언은 수학과 물리학에서 작은 역할로 밀려났습니다.이러한 변화의 부작용은 해밀턴의 작품이 많은 현대 독자들에게 이해하기 어렵다는 것입니다.해밀턴의 독창적인 정의는 생소하고 그의 글쓰기 스타일은 말이 많고 따르기 어려웠습니다.
그러나 쿼터니언은 20세기 후반부터 부활했는데, 주로 공간 회전을 설명하는 데 유용했기 때문입니다.쿼터니언에 의한 회전수의 표현은 행렬에 의한 표현보다 더 압축적이고 계산이 더 빠릅니다.또한 오일러 각도와 달리 "짐발 잠금"에 영향을 받지 않습니다.이러한 이유로 쿼터니언은 컴퓨터 그래픽스,[15][16] 컴퓨터 비전, 로봇 공학,[17] 제어 이론, 신호 처리, 태도 제어, 물리학, 생물 정보학, 분자 역학, 컴퓨터 시뮬레이션, 궤도 역학에 사용됩니다.예를 들어, 우주선의 자세 제어 시스템은 쿼터니언(quation) 단위로 명령을 받는 것이 일반적입니다.4차수는 [18]2차수형과의 관계 때문에 수론으로부터 또 다른 힘을 얻었습니다.
물리학의 사분위수
P.R. Girard의 1984년 에세이 쿼터니언 그룹과 현대[19] 물리학은 물리학에서 쿼터니언의 몇 가지 역할에 대해 논의합니다.에세이는 다양한 물리적 공분산 그룹, 즉 SO(3), 로렌츠 그룹, 일반 상대성 이론 그룹, 클리포드 대수 SU(2) 및 등각 그룹이 현대 대수학에서 쿼터니언 그룹과 쉽게 관련될 수 있는 방법을 보여줍니다.지라드는 그룹 표현에 대해 논의하고 결정학의 일부 공간 그룹을 나타내는 것으로 시작했습니다.그는 강체 운동의 운동학으로 나아갔습니다.다음으로 그는 토마스 세차운동을 포함한 특수 상대성 이론의 로렌츠 그룹을 나타내기 위해 복소수의 쿼터니언(biquaterion)을 사용했습니다.그는 루드윅 실버스타인(Ludwik Silberstein)을 시작으로 맥스웰 방정식을 단일 미분 방정식으로 표현하기 위해 하나의 4차 변수의 퍼텐셜 함수를 사용한 다섯 명의 저자를 인용했습니다.일반 상대성 이론과 관련하여, 그는 룽지-렌츠 벡터를 표현했습니다.그는 클리포드 대수의 한 예로 클리포드 쌍대수(분할 쌍대수)를 언급했습니다.마지막으로, 지라드는 쌍분수의 역수를 불러내어 시공간의 등각 지도를 묘사했습니다.50개의 참고 문헌 중에서, 지라드는 알렉산더 맥팔레인과 그의 쿼터니언 협회 회보를 포함했습니다.1999년에 그는 아인슈타인의 일반 상대성 방정식이 어떻게 [20]사분면과 직접적으로 연결된 클리포드 대수 안에서 공식화될 수 있는지 보여주었습니다.
1924년의 발견은 양자역학에서 전자와 다른 물질 입자(스피너로 알려진)의 스핀을 4차이온(유명한 파울리 스핀 행렬의 형태)을 사용하여 설명할 수 있다는 것입니다. 4차이온은 전자의 360° 회전을 720°로 구별하는 방법을 이해하는 데 도움이 되었습니다.[21][22]2018년 현재[update], 그들의 사용은 회전 [a]그룹을 추월하지 못했습니다.
정의.
쿼터니언은 형태의 표현입니다.
여기서 a, b, c, d는 실수이고 i, j, k는 3개의 공간 축을 따라 가리키는 단위로 해석될 수 있는 기호입니다.실제로 a, b, c, d 중 하나가 0이면 해당 항은 생략되고, a, b, c, d가 모두 0이면 쿼터니언은 0으로 표시되며, b, c, d 중 하나가 1이면 해당 항은 단순히 i, j, k로 표기됩니다.
해밀턴은 =a + + + {\q = a + + + 를 스칼라 부분과 벡터 부분으로 구성하여 설명합니다. + j+ {\ b + +를 q의 벡터부분(때로는 허수부분)이라고 하고, a는 q의 스칼라부분(때로는 실수부분)이라고 합니다. 실수부분과 같은 쿼터니언은 스칼라 또는 실수 쿼터니언이라고 합니다.해당하는 실수로 식별됩니다.즉, 실수는 쿼터니언에 포함됩니다. (더 정확하게는 실수의 필드가 쿼터니언의 부분집합과 동형이라는 것입니다.복소수의 장은 또한 3개의 쿼터니언 부분집합과 동형입니다.)[23]벡터 부분과 같은 쿼터니언을 벡터 쿼터니언이라고 합니다.
쿼터니언들의 집합은 실수들 위의 4차원 벡터 공간이며 단위의 덧셈에 의해 { , k {\ \left{{j{k}\}를 기본으로 합니다.
성분별 스칼라 곱하기
다음과 같은 방법으로 사분면 위에 정의할 수 있는 해밀턴 곱이라 불리는 곱셈 군 구조는 다음과 같은 방법으로 사분면에 정의할 수 있습니다.
- 실제 쿼터니언 1은 아이덴티티 요소입니다.
- 실제 쿼티온은 모든 다른 쿼티온과 통근하는데, 즉 모든 쿼티온 q와 모든 실제 쿼티온 a에 대해 aq = qa입니다.대수학 용어에서 이것은 실제 사분면장이 이 사분면 대수의 중심이라고 말하는 것입니다.
- 생성물은 먼저 기본 요소(다음 하위 절 참조)에 대해 부여된 후, 실제 쿼터니언의 분포 특성과 중심 특성을 사용하여 모든 쿼터니언으로 확장됩니다.해밀턴 곱은 치환이 아니라 연관성이 있으므로, 4차수는 실수 위에 연관 대수를 형성합니다.
- 또한 0이 아닌 모든 쿼터니언은 해밀턴 곱에 대해 역수를 갖습니다.
따라서 쿼터니언들은 나눗셈 대수를 형성합니다.
기저요소의 곱셈
| × | 1 | i | j | k |
|---|---|---|---|---|
| 1 | 1 | i | j | k |
| i | i | −1 | k | −j |
| j | j | −k | −1 | i |
| k | k | j | −i | −1 |
기저 요소 i, j, k 중 1을 갖는 곱셈은 1이 곱셈 항등식이라는 사실, 즉,
다른 기본 요소의 제품은
이 규칙들을 합하면,
중심
비상호환 고리의 중심은 모든 x에 대해 cx = xc인 원소 c의 부분 고리입니다.사분위수 대수의 중심은 실제 사분위수의 하위장입니다.사실, 이것은 실제 쿼터니언이 중심에 속한다는 정의의 한 부분입니다.반대로, 만약 q = a + bi + cj + dk가 중심에 속한다면,
그리고 c = d = 0. i 대신 j와 유사한 계산을 통해 하나도 b = 0을 가짐을 알 수 있습니다.따라서 q = a는 실제 쿼터니언입니다.
쿼터니언들은 나눗셈 대수를 형성합니다.이것은 곱셈의 비가환성이 쿼터니언을 필드와 다르게 만드는 유일한 속성임을 의미합니다.이러한 비가환성은 몇 가지 예상치 못한 결과를 가져오는데, 그 중에서도 쿼터니언 위의 다항식은 다항식의 정도보다 더 뚜렷한 해를 가질 수 있습니다.예를 들어, 방정식 z + 1 = 0은 무한히 많은 4차이온 해를 갖는데, 이것은 b + c + d = 1이 되는 4차이온 z = bi + c j + d k입니다.따라서 이 "-1"의 근은 벡터 쿼터니언의 3차원 공간에서 단위 구를 형성합니다.
해밀턴 제품
두 원소1 a + bi11 + cj + dk1 및 a22 + bi + cj2 + dk의2 경우, 해밀턴 곱(a1 + bi1 + cj1 + dk)(a2 + bi2 + cj2 + dk)이라12 불리는 그들의 곱은 기본 원소와 분배 법칙의 곱에 의해 결정됩니다.유통법은 기초요소의 제품의 총합이 되도록 제품을 확장할 수 있도록 하고 있습니다.이것은 다음과 같은 표현을 갖습니다.
이제 위에 주어진 규칙을 사용하여 기본 요소를 곱하여 다음을 [8]얻을 수 있습니다.
두 회전[24] 쿼터니언의 곱은 회전2 a + bi2 + cj2 + dk2 다음에 회전1 a + bi1 + cj1 + dk와1 같습니다.
스칼라 및 벡터 부분
a가 실수일 때 a + 0 i + 0 j + 0 k 형태의 쿼터니언을 스칼라, 0 + b i + c j + d k 형태의 쿼터니언을 벡터 쿼터니언이라고 합니다. 여기서 b, c, d는 실수이고 b, c d 중 적어도 하나는 0이 아닌 것을 벡터 쿼터니언이라고 합니다.만약 a + bi + cj + dk가 임의의 4차 이온이라면, a는 그것의 스칼라 부분, bi + cj + dk는 그것의 벡터 부분이라고 불립니다.모든 쿼터니언은 4차원 벡터 공간의 벡터로 볼 수 있지만, 벡터 부분은 3차원 공간의 벡터로 언급되는 것이 일반적입니다.이 규칙에서 벡터는 벡터 3의원소와 같습니다 {\
해밀턴은 또한 벡터 쿼터니언을 오른쪽[26][27] 쿼터니언과 실수(벡터 부분이 0인 쿼터니언으로 간주됨) 스칼라 쿼터니언이라고 불렀습니다.
쿼터니언을 스칼라 부분과 벡터 부분으로 나누면,
그렇다면 덧셈, 곱셈, 곱셈의 공식은
여기서 " ⋅ {\ 및 "×{\는 각각 도트 곱과 교차 곱을 나타냅니다.
켤레, 표준, 역수
쿼터니언의 컨쥬게이션은 복소수의 컨쥬게이션과 클리포드 대수의 원소들의 전치(역전이라고도 함)와 유사합니다.정의하기 위해 q = + + + {\q = a + + + 을 쿼터니언이라 합니다.q의 컨쥬게이트는 쿼터니언 ∗=- - - k q^{*} = a - b{j 입니다. 컨쥬게이트는 그 자체의 역수라는 것을 의미하는 진화이므로 원소를 두 번 컨쥬게이트하면 원래의 원소가 반환됩니다.두 개의 4분의 1 이온으로 이루어진 곱의 결합체는 역순으로 결합체의 곱입니다.즉, p와 q가 4차이온이면 pq가 아니라 (pq) = qp입니다.
쿼터니온의 사용은 복잡한 설정과 대조적으로 쿼터니온의 곱셈과 덧셈으로 표현될 수 있습니다.
컨쥬게이션은 쿼터니언의 스칼라와 벡터 부분을 추출하는 데 사용될 수 있습니다.p의 스칼라 부분은 1/2(p + p∗)이고, p의 벡터 부분은 1/2(p∗ - p)입니다.
짝수를 갖는 4분자의 곱의 제곱근을 표준이라 하고 ‖q‖라고 합니다. (해밀턴은 이 양을 q의 텐서라고 불렀지만, 이것은 "텐서"의 현대적 의미와 충돌합니다.)공식에서 이는 다음과 같이 표현됩니다.
이것은 항상 음수가 아닌 실수이며 벡터 {\의 유클리드 노름과 같습니다. 쿼터니언에 실수를 곱하면 그 노름은 그 수의 절대값으로 확장됩니다.즉, α가 실수라면,
이것은 그 규범이 곱셈적이라는 사실의 특별한 경우이다, 즉
임의의 2개의 4분위수 p와 q에 대하여. 곱셈은 곱의 켤레에 대한 공식의 결과입니다.또는 아이덴티티에서 따르게 됩니다.
(여기서 i는 일반적인 허수 단위를 나타냅니다.) 따라서 정방행렬의 행렬식들의 곱셈 성질로부터.
이 표준을 사용하면 p와 q 사이의 거리 d(p, q)를 차이의 표준으로 정의할 수 있습니다.
그러면 H 이(가) 메트릭 공간이 .덧셈과 곱셈은 관련 메트릭 토폴로지와 관련하여 연속적입니다.이는 H 이(가) 정규 대수라는 로부터 실수 {\과(와) 정확히 동일한 증명으로 뒤따릅니다.
단위 사분위수
단위 사분위수는 표준의 사분위수입니다.0이 아닌 쿼터니언 q를 표준으로 나누면 q의 versor라고 하는 단위 쿼터니언 Uq가 생성됩니다.
0이 아닌 모든 쿼터니언은 고유한 극성 q = ‖ ‖ ⋅ ⋅ u U {\ q =\q\ \q}을를) 가지지만, 0 쿼터니언은 모든 단위 쿼터니언에서 형성될 수 있습니다.
공액과 표준을 사용하면 0이 아닌 쿼터니언의 역수를 정의할 수 있습니다.역수를 갖는 쿼터니언의 곱은 1과 같아야 하며, 위의 고려 사항은q {\q}과 ∗ / ‖ ‖2 {\right}}의 곱이 1임을 의미합니다.따라서 q의 역수는 다음과 같이 정의됩니다.
이를 통해 두 개의 쿼터니언 p와 q를 서로 다른 방식으로 나눌 수 있습니다(q가 0이 아닐 때).즉, 그들의 몫은 p q 또는 qp가 될 수 있습니다. 일반적으로, p와 q가 서로의 스칼라 배수인 특별한 경우(p = 0인 경우를 포함)를 제외하고는 곱의 순서에 따라 이 곱들은 다릅니다.따라서 p/q 표기는 q가 왼쪽으로 나눌지 오른쪽으로 나눌지(q가 왼쪽으로 p를 곱할지 오른쪽으로 나눌지−1)를 지정하지 않기 때문에 모호합니다.
대수적 성질
모든 쿼터니언의 H 는 차원 [c]4인 실수 위의 벡터 공간입니다.쿼터니언의 곱셈은 연관성이 있고 벡터 덧셈에 걸쳐 분포하지만 스칼라 부분 집합을 제외하고는 교환이 되지 않습니다.따라서 H{\은 실수에 대한 비상호적 연관 대수입니다.H 이(가) 복소수의 복사본을 하더라도 복소수에 대한 연관 대수가 아닙니다.
쿼터니언을 나누는 것이 가능하기 때문에, 그들은 나눗셈 대수를 형성합니다.이것은 곱셈의 비가환성을 제외하고는 필드와 유사한 구조입니다.실수에 대한 유한 차원 연관 분할 대수는 매우 희귀합니다.프로베니우스 정리는 R 등 세 가지가 있다고 말합니다. 이 표준은 쿼터니언을 정규 대수로 만들고 실수에 대한 정규 나눗셈 대수도 매우 희귀합니다.후르비츠의 정리에 R {RC {H {HO {\{팔각형의 네 가지만 존재합니다.쿼터니언은 또한 구성 대수와 단위 바나흐 대수의 예입니다.
임의의 두 기저 벡터의 곱은 다른 기저 벡터의 덧셈 또는 뺄셈이므로, 집합 {±1, ±i, ±j, ±k}은 곱셈 하에서 그룹을 형성합니다.이 비-아벨 군을 쿼터니언 군이라고 하며 [28]Q로 표시합니다8.Q의 실수8 군환은 [ 8]{\ 이며, 이는 또한R 의 8차원 벡터 공간입니다 {\ \ {R .} 이는 의 각 원소에 대해 하나의 기저 벡터를 갖습니다 {\ _ 쿼터니언은 R[ 8{\}의 몫환과 동형입니다.원소 1 + (-1), i + (-i), j + (-j), k + (-k)에 의해 생성된 이상에 의해 bb {[\ _여기서 각각의 차이에서 첫 번째 항은 기저 요소 1, i, j, k 중 하나이고, 두 번째 항은 기저 요소 -1, -i, -j, -k 중 하나이며, 1, i, j, k의 덧셈 역이 아닙니다.
쿼터니언과 공간기하학
쿼터니언의 벡터 부분은 3의 벡터로 해석될 수 있습니다 {\ ^{ 따라서 쿼터니언의 대수적 연산은 의 기하학을 반영합니다 {\ \3}} 벡터 점과 교차곱과 같은 연산은 쿼터니언으로 정의될 수 있습니다.그리고 이를 통해 공간 벡터가 발생하는 곳에 쿼터니언 기법을 적용할 수 있습니다.쿼터니언의 유용한 응용은 컴퓨터 [15]그래픽에서 키프레임의 방향을 보간하는 것이었습니다.
이 절의 나머지 부분에서, i, j, k는H {\{의[29] 세 가상 기저 벡터와 의 기저를 모두 나타낼 것입니다 {}} i를 -i, j by -j, k by -k로 대체하면 벡터가 그것의 덧셈 역수로 보내지므로 벡터의 덧셈 역수는 4분의 1이온으로서의 그것의 켤레와 같습니다.이러한 이유로, 컨쥬게이션(conjugation)은 때때로 공간 역이라고 불립니다.
두 벡터 쿼터니언 p = bi + cj + dk 및 q = bi + cj + dk의 점 곱에 대해, 벡터에 비유하여 \mathbb 는
성분이 없는 방식으로 다음과 같이 표현할 수도 있습니다.
이는 제품 pq∗, qp∗, pq∗, qp의∗ 스칼라 부분과 같습니다.벡터 부분이 서로 다르다는 것에 유의하십시오.
순서 기준 i, j, k에 의해 결정된 방향에 대한 p와 q의 교차곱은
(표지판을 결정하기 위해 방향이 필요하다는 것을 기억합니다.)이것은 -qp의 벡터∗∗ 부분뿐만 아니라 곱 pq의 벡터 부분(4차 이온)과 같습니다.공식도 있습니다.
정류자의 경우, 두 개의 벡터 쿼터니언의 [p, q] = pq - qp
일반적으로 p와 q를 쿼터니언으로 하고 쓰기
여기서s p와s q는 스칼라 부분이고v, p와v q는 p와 q의 벡터 부분입니다.그럼 우리는 공식을 가지고 있습니다.
이것은 4차 이온 곱셈의 비가환성이 벡터 4차 이온의 곱셈에서 나온다는 것을 보여줍니다.또한 벡터 부분이 공선인 경우에만 두 개의 쿼터니언이 통근한다는 것을 보여줍니다.해밀턴은 이 곱이 주어진 두 꼭짓점으로부터 구면 삼각형의 세 번째 꼭짓점과 그와 관련된 호 길이를 계산한다는 것을 보여주었고, 이는 타원 기하학에서 점의 대수이기도 합니다[30].
단위 쿼터니언은 {\의 회전으로 식별할 수 있으며 [30]해밀턴에 의해 버서라고 불렸습니다.쿼터니언을 사용한 3차원 회전 모델링에 대한 자세한 내용은 쿼터니언 및 공간 회전을 참조하십시오.
쿼터니언의 시각화에 관해서는 핸슨(2005)[31] 참조.
행렬 표현
복잡한 수가 행렬로 표현될 수 있는 것처럼, 쿼터니언도 마찬가지입니다.쿼터니언 덧셈과 곱셈이 행렬 덧셈과 행렬 곱셈에 대응하는 방식으로 쿼터니언을 행렬로 표현하는 방법은 적어도 두 가지가 있습니다.하나는 2×2 복소수 행렬을 사용하는 것이고, 다른 하나는 4×4 실수 행렬을 사용하는 것입니다.각 경우에 주어진 표현은 선형적으로 연관된 표현군 중 하나입니다.추상 대수학 용어에서, 이것들은 H 에서 행렬 고리 M(2,C)과 M(4,R)까지의 주입 동형 사상입니다.
2 × 2 복소수 행렬을 사용하면 4차 이온 a + bi + cj + dk를 다음과 같이 나타낼 수 있습니다.
복소수의 "i"는 쿼터니언의 "i"와 구별됩니다.
이 표현에는 다음과 같은 속성이 있습니다.
- b, c, d 중 어느 두 개를 0으로 제한하면 복소수를 표현할 수 있습니다.예를 들어, c = d = 0을 설정하면 복소수의 대각 복소수 행렬 표현이 생성되고, b = d = 0을 설정하면 실제 행렬 표현이 생성됩니다.
- 쿼터니언의 표준(복소수와 마찬가지로 컨쥬게이트가 있는 제품의 제곱근)은 해당 [32]행렬의 행렬식의 제곱근입니다.
- 쿼터니언의 컨쥬게이트는 매트릭스의 컨쥬게이트 전치에 해당합니다.
- 제한에 의해 이 표현은 단위 쿼터니언의 부분군과 그들의 이미지 SU(2) 사이에 동형을 만듭니다.위상학적으로, 단위 쿼터니언은 3-구이므로 SU(2)의 기저 공간 또한 3-구입니다.그룹 SU(2)는 양자역학에서 스핀을 설명하는 데 중요합니다. 파울리 행렬을 참조하십시오.
- 쿼터니언 단위와 파울리 행렬 사이에는 강한 관계가 있습니다.a, b, c, d를 취하여 8개의 4차 이온 단위 행렬을 구하고, 그 중 3개를 0으로, 4번째를 1 또는 -1로 설정합니다.임의의 두 파울리 행렬을 곱하면 항상 -1을 제외하고 모두 사분위수 단위 행렬이 생성됩니다.i = j = k = i j k = i j k - -1을 통해 -1을 얻습니다. 예를 들어 마지막 등호는
4 × 4 개의 실수 행렬을 사용하면 다음과 같이 같은 4분의 1을 쓸 수 있습니다.
그러나 M(4,R)에서 쿼터니언의 표현은 유일하지 않습니다.예를 들어, 같은 쿼터니언은 다음과 같이 나타낼 수도 있습니다.
이 형태에는 행렬 중 하나가 스칼라 부분을 나타내고 나머지 세 개는 모두 스큐 대칭인 48개의 서로 다른 행렬 표현이 있습니다.더 정확하게 말하면, 1, i, j, k를 4중의 행렬로 보내는 함수가 동형인, 즉 [33]4중의 행렬의 합과 곱을 행렬의 합과 곱으로 보내는 것과 같은 대칭 제약이 있는 48개의 4중의 행렬 집합이 있습니다.이 표현에서, 쿼터니언의 컨쥬게이트는 행렬의 전치에 해당합니다.쿼터니언의 표준의 네 번째 거듭제곱은 해당 행렬의 결정인자입니다.위의 2×2 복소수 표현과 마찬가지로, 복소수는 계수를 적절히 제한함으로써 다시 생성될 수 있습니다. 예를 들어, c = d = 0으로 설정하여 2×2 블록을 갖는 블록 대각 행렬과 같이 말입니다.
쿼터니언의 각 4×4 행렬 표현은 단위 쿼터니언의 곱셈표에 해당합니다.예를 들어, 위에 주어진 마지막 행렬 표현은 곱셈표에 해당합니다.
| × | a | d | −b | −c |
|---|---|---|---|---|
| a | a | d | −b | −c |
| −d | −d | a | c | −b |
| b | b | −c | a | −d |
| c | c | b | d | a |
{a j, {\\{ 1 i jk\}}를통해 동형인 것
| × | 1 | k | −i | −j |
|---|---|---|---|---|
| 1 | 1 | k | −i | −j |
| −k | −k | 1 | j | −i |
| i | i | −j | 1 | −k |
| j | j | i | k | 1 |
그러한 곱셈 테이블이 첫 번째 행과 열에 동일성을 갖도록 제한하고 행 헤더의 부호가 열 헤더의 부호와 반대가 되도록 제한하면, 두 번째 열에 대한 3가지 가능한 선택(무시 기호), 세 번째 열에 대한 2가지 가능한 선택(무시 기호),그리고 네 번째 열에 대해 하나의 가능한 선택(선택 기호), 즉 6개의 가능성을 만듭니다.그러면 두 번째 열은 양 또는 음, 세 번째 열은 양 또는 음, 네 번째 열은 양 또는 음으로 선택할 수 있으므로 기호에 대한 8가지 가능성이 있습니다.글자 위치와 기호에 대한 가능성을 곱하면 48이 됩니다.그런 다음 1을 a, i를 b, j를 c, k로 바꾸고 행과 열 헤더를 제거하면 a + bi + cj + dk의 행렬 표현이 됩니다.
라그랑주의 4제곱 정리
쿼터니언은 라그랑주의 정수론에서 모든 음이 아닌 정수는 4개의 정수 제곱의 합이라는 것을 증명하는 데에도 사용됩니다.라그랑주의 4제곱 정리는 그 자체로 우아한 정리일 뿐만 아니라 조합 설계 이론과 같은 수론 밖의 수학 분야에서 유용한 응용을 가지고 있습니다.쿼터니언 기반 증명은 유클리드 알고리즘의 유사체가 있는 모든 쿼터니언의 고리의 하위 고리인 후르비츠 쿼터니언을 사용합니다.
복소수의 쌍으로서의 쿼터니언
쿼터니언은 복소수의 쌍으로 표현될 수 있습니다.이러한 관점에서, 쿼터니언은 케일리-딕슨 구조를 복소수에 적용한 결과입니다.이것은 실수의 쌍으로 복소수의 구성을 일반화한 것입니다.
2{\를 복소수 위의 2차원 벡터 공간이라고 .1, j 두 요소로 구성된 기저를 선택합니다.{\의 벡터는 기본 요소 1과 j로 나타낼 수 있습니다.
j = -1이고 i j = -ji를 정의하면 분배 법칙을 사용하여 두 벡터를 곱할 수 있습니다.k를 곱 ij의 축약 표기로 사용하면 일반적인 쿼터니언과 같은 곱셈 규칙이 됩니다.따라서 위의 복소수 벡터는 쿼터니언 a + bi + cj + dk에 해당합니다.C {\의 를 순서쌍으로 쓰고 4중항을 쓰면 대응은
제곱근
-1의 제곱근
에서 C 제곱수는 -1인 i와 -i 두 개뿐입니다. {\에는 -1의 제곱근에 대한 제곱근이 무한히 많습니다. -1의 제곱근에 대한 쿼터니언 해는 의 단위 구입니다 {\ 이를 보려면 q = a + b i + c j라고 하자.+ dk는 쿼터니언이고, 제곱은 -1이라고 가정합니다.a, b, c, d의 관점에서, 이것은
마지막 세 개의 방정식을 만족시키기 위해 a = 0 또는 b, c, d는 모두 0입니다.a는 실수이고 첫 번째 방정식은 a = -1을 의미하기 때문에 후자는 불가능합니다.따라서 a = 0이고 b + c + d = 1입니다.즉, 4등분선은 norm 1인 벡터 4등분선일 경우에만 -1로 제곱합니다.정의에 따라 이러한 모든 벡터의 집합은 단위 구를 형성합니다.
음의 실수 4중주만이 무한히 많은 제곱근을 가지고 있습니다.나머지는 모두 2개(또는 [citation needed][d]0인 경우 1개)만 있습니다.
복잡한 평면들의 연합체로서
-1 제곱근의 각 역모형 쌍은 쿼터니언 내부의 복소수에 대한 고유한 복사본을 만듭니다.q = -1이면 복사는 함수에 의해 결정됩니다.
C 에서 H 까지의 주입형 동형이며, C{\에서 이미지로의 필드 동형을 정의합니다.q와 -q에 해당하는 임베딩의 이미지는 동일합니다.
모든 비실수 쿼터니언은 C 와 동형인 쿼터니언의 하위대수를 생성하며 따라서H의 부분공간이다 {\ \ \는 스칼라 부분과 벡터 부분의 합으로 q를 씁니다.
벡터 부분을 그 노름과 그 버서의 곱으로 더 분해합니다.
(는 ‖ ‖ ⋅ ) ⋅ { { +\q}과(와) 같지 않습니다.)q, → 의 벡터 부분의 버전은 -1을 제곱으로 하는 오른쪽 버전입니다.직접적인 검증을 해보면
는 C 에서 정칙 대수의 사분면으로의 주동형을 정의합니다.이 동형 사상 하에서 q는 s+‖ → ‖ i {\{s} +\ {의 이미지입니다.
H 이(가) 이 모든 동형 사상들의 이미지들의 결합이므로, 이것은 쿼터니언들을 실제 선에서 교차하는 복잡한 평면들의 결합으로 볼 수 있게 합니다.각 복소 평면에는 제곱근 구에서 1을 뺀 한 쌍의 반모달 점이 정확히 포함되어 있습니다.
교환 서브링
H 의 복잡한 하위 평면 내에서 서로에 대한 쿼터니언의 관계도 식별할 수 있으며, 이를 교환 서브링으로 표현할 수 있습니다.구체적으로, 두 개의 쿼터니언 p와 q가 H{\의 동일한 복잡한 하위 평면에 놓여있는 경우에만 통근(즉, p q = q p)하기 때문에, 쿼터니언 링의 모든 교환 서브링을 찾으려 할 때 복잡한 평면의 결합으로서 H{\의 프로파일이 발생합니다.
임의의 쿼터니언의 제곱근
의 q = ( → ){\ = (서 스칼라-스칼라 표현으로 표현) displaystyle {\sqrt {\mathbf {q{y}}}}: = {\{\= {y}=\mathbf{ 이 방정식에서 스칼라와 벡터 부분을 따로 보면 두 개의 방정식이 나오는데, 이 방정식이 풀리면 해가 됩니다
서 ‖ v → ‖ → ⋅ = ∗ v→ - → 2 { {v}}}={\ {v는 v→ {\v이고 ‖ = ‖ → +‖ v =‖ {\ \{q} \ ={\{q}=^{2{v}}}:q \{q의 표준입니다.임의의 스칼라 {\에 대하여 v → ‖ {\{\{\가 임의의 단위 벡터로 해석되면 이 방정식은 제곱근을 제공합니다.
따라서, 0이 아닌, 스칼라 쿼터니언 또는 양의 스칼라 쿼터니언은 정확히 두 개의 근을 가지고 있는 반면, 0은 정확히 한 개의 근(0)을 가지고 있고, 음의 스칼라 쿼터니언은 무한히 많은 근을 가지고 있는데, 이는 { × 2( - ){\\{ S{-에 위치한 벡터 쿼터니언입니다. 즉, 스칼라 부분이 0이고 th인 경우e 벡터 부분은 2-sphere에 위치하며 반지름은r {\{-입니다.
쿼터니언 변수의 함수

복잡한 변수의 함수와 마찬가지로 쿼터니언 변수의 함수도 유용한 물리적 모델을 제시합니다.예를 들어 맥스웰이 설명한 원래 전기장과 자기장은 쿼터니언 변수의 함수였습니다.다른 기능의 예로는 만델브로 세트와 줄리아 세트를 4차원 [35]공간으로 확장하는 것이 있습니다.
지수, 로그 및 검정력 함수
쿼터니언이 주어지면,
지수는 다음과 같이 계산됩니다[36].
그리고[36] 로그는
쿼터니언의 극성 분해는 다음과 같이 기록될 수 있습니다.
여기서 각도 {\
단위 n {\{\은(는) 다음과 같이 정의됩니다.
임의의 단위 쿼터니언은 다음과 같이 극성 형태로 표현될 수 있습니다.
임의의 (실제) 지수 x로 상승된 쿼터니언의 거듭제곱은 다음과 같이 주어집니다.
측지선법
단위 사분위수 p와 q 사이의 측지 거리g d(p, q)는 [38]다음과 같이 정의됩니다.
그리고3 구면의 큰 호를 따라 p와 q에 의해 감산된 각도의 절반의 절대값에 해당합니다.이 각도는 다음과 같이 로그를 사용하지 않은 4차 이온 점 곱으로 계산할 수도 있습니다.
3차원 및 4차원 회전 그룹
"결합"이라는 단어는 위에 주어진 의미 이외에도 원소 a를 r로−1 취하는 것을 의미할 수 있는데, 여기서 r은 0이 아닌 쿼터니언입니다.주어진 원소에 결합하는 모든 원소들은 (이 단어의 의미에서) 벡터 부분의 실수부와 노름이 같습니다. (따라서 다른 의미의 결합체는 이 의미의 결합체 중 하나입니다.)
따라서 0이 아닌 쿼터니언의 곱셈군은 실수 부분이 0인 쿼터니언으로 구성된 R {\의 복사본에 공액 작용합니다.실제 부분 cos(θ)와 단위 4차 이온(절대값 1의 4차 이온)에 의한 공액은 각도 2θ만큼의 회전이며, 회전의 축은 벡터 부분의 방향입니다.쿼터니언의 장점은 다음과 같습니다.[40]
- 오일러 각도와 같은 시스템의 문제인 짐벌 잠금을 방지합니다.
- 매트릭스보다 빠르고 콤팩트합니다.
- 비단수 표현(예를 들어 오일러 각도와 비교).
- 단위 쿼터니언 쌍은 4차원 공간에서의 회전을 나타냅니다(4차원 유클리드 공간에서의 회전 참조: 4차원 회전 대수).
모든 단위 쿼터니언(versers)의 집합은 곱셈 하에3 3-sphere S와 그룹(Li 그룹)을 형성하며 SO ( {\{\ 대응 하에서 두 개의 단위 쿼터니언이 모든 회전에 대응하므로, 행렬식 1의 실수 직교 3×3 행렬의 SO접시 트릭 참조.
부분군의 이미지는 점군이고, 반대로 점군의 이전 이미지는 부분군의 부분군입니다.유한한 점군의 전상은 접두사 이진법과 같은 이름으로 불립니다.예를 들어, 이십면체 그룹의 전상은 이진 이십면체 그룹입니다.
변환자 그룹은 행렬식 1의 복소수 유니터리 2×2 행렬의 그룹인 SU(2)와 동형입니다.
A를 a + bi + cj + dk 형태의 쿼터니언 집합이라 하고, 여기서 a, b, c, d는 모두 정수이거나 모두 반수입니다.집합 A는 고리(사실은 정의역)이자 격자이며, 후르비츠 4분면의 고리라고 불립니다.이 고리에는 24개의 단위 쿼티온이 있으며, 슐레플리 기호가 {3,4,3}인 정24 셀의 꼭짓점입니다.그것들은 정사면체의 회전 대칭 그룹의 이중 커버에 해당합니다.마찬가지로, 슐레플리 기호가 {3,3,5}인 정칙 600 셀의 꼭짓점은 정칙 20면체의 회전 대칭군의 이중 커버에 해당하는 단위 이코시안으로 잡을 수 있습니다.정팔면체의 회전 대칭 그룹의 이중 커버는 디스페노이드 288 [41]셀의 꼭짓점을 나타내는 쿼터니언에 해당합니다.
사분위수
쿼터니언은 쿼터니언 대수라고 불리는 더 많은 대수로 일반화될 수 있습니다.F를 2와 다른 특성을 가진 임의의 필드로 하고, a와 b를 F의 요소로 합니다. 4차원 단일 결합 대수는 기저 1, i, j, i j로 F 위에 정의될 수 있으며, 여기서 i = a, j = b, i j = -ji (그래서 (i j) = -a b).
사분위수 대수는 a와 b의 선택에 따라 F보다 2×2 행렬의 대수와 동형입니다.
Cl(R)의3,0 짝수 부분으로서의 쿼터니언
기하 계산에 대한 쿼터니언의 유용성은 쿼터니언을 클리포드 대수 Cl 의 부분 3, 0+ ( )로 으로써 다른 차원으로 일반화할 수 있습니다 _ 이것은 연관 뮤입니다.제품 규칙을 사용하여 기본 기본 요소인 σ, σ, σ로 구성된 ltector 대수
3차원 공간에서 벡터를 표현하기 위해 이러한 기본 기저 요소를 사용하면 단위 벡터 w에 수직인 평면에서 벡터 r의 반사를 쓸 수 있음이 밝혀집니다.
두 반사는 두 반사면 사이의 각도의 두 배만큼 회전합니다.
θ와1 θ를2 포함하는 평면에서 180° 회전에 해당합니다.이는 해당 쿼터니언 공식과 매우 유사합니다.
실제로 두 3 + (R ){\ )}와 H 은(는) 동형입니다.하나의 자연스런 식별은
그리고 이것이 해밀턴 관계를 보존한다는 것을 확인하는 것은 간단합니다.
이 그림에서 소위 "벡터 쿼터니언"(즉, 순수 가상 쿼터니언)은 벡터가 아니라 바이벡터에 해당합니다. 즉, 1차원 방향이 아닌 특정 2차원 평면과 관련된 크기와 방향을 가진 양입니다.복소수와의 관계도 더욱 명확해집니다. 2D에서는 벡터 방향 θ와1 θ2 두 개를 사용하면 쌍벡터 기저 요소 θ가12 하나밖에 없으므로 허수가 하나뿐입니다.그러나 3D에서는 3개의 벡터 방향을 가진 3개의 벡터 기본 요소인12 θ, θ23, θ가31 있으므로 3개의 상상력이 있습니다.
이 추론은 더 확장됩니다.클리포드 에서, 0 (R {\ _{에는 6개의 이벡터 기저 요소가 있는데, 이는 4개의 서로 다른 기본 벡터 방향으로, 6개의 서로 다른 쌍과 6개의 서로 다른 선형 독립 평면을 정의할 수 있기 때문입니다.회전체라고 불리는 이러한 4차 이온의 일반화를 사용하는 이러한 공간에서의 회전은 균질한 좌표를 포함하는 응용에 매우 유용할 수 있습니다.그러나 기저 쌍벡터의 수가 기저 벡터의 수와 동일한 것은 3D에서만 가능하며, 각 쌍벡터는 의사 벡터로 식별될 수 있습니다.
이렇게 넓은 환경에 [42]쿼터니언을 배치하는 데는 다음과 같은 몇 가지 이점이 있습니다.
- 회전자는 기하 대수학의 자연스러운 부분이며 이중 반사의 부호화로 쉽게 이해됩니다.
- 기하 대수학에서 회전자와 회전자가 작용하는 물체는 같은 공간에 삽니다.이를 통해 표현을 변경할 필요가 없고, 기존에 쿼터니언으로 선형 대수를 증강할 때 필요했던 새로운 데이터 구조 및 방법을 인코딩할 필요가 없습니다.
- 회전자는 벡터와 다른 사분면뿐만 아니라 선, 평면, 원, 구, 광선 등 대수학의 어떤 요소에도 보편적으로 적용할 수 있습니다.
- 유클리드 기하학의 등각 모델에서 회전자는 대수의 단일 요소에서 회전, 변환 및 스케일링의 인코딩을 허용하며, 모든 요소에 보편적으로 작용합니다.특히 회전자는 임의의 축을 중심으로 한 회전을 나타낼 수 있는 반면, 쿼터니언은 원점을 통한 축으로 제한됩니다.
- 로터 인코딩 변환은 보간을 특히 단순하게 만듭니다.
- 회전자는 특수 상대성 이론의 민코프스키 공간과 같은 유사 유클리드 공간으로 자연스럽게 전달됩니다.이러한 공간에서 회전자는 로렌츠 부스트를 효율적으로 표현하고 감마 행렬과 관련된 공식을 해석하는 데 사용될 수 있습니다.
클리포드 대수의 기하학적 사용에 대한 자세한 내용은 기하학 대수를 참조하십시오.
브라우어군
쿼터니언은 실수 위의 모든 CSA가 실수 또는 쿼터니언과 동일하다는 점에서 실수 위의 유일한 (사소하지 않은) 중심 단순 대수(CSA)입니다.명시적으로 실수의 브라우어 그룹은 실수와 쿼터니언으로 표현되는 두 개의 클래스로 구성되며, 여기서 브라우어 그룹은 하나의 CSA가 다른 CSA에 대한 행렬 고리가 되는 등가 관계까지의 모든 CSA의 집합입니다.아르틴의 작품웨더번 정리(특히 웨더번의 부분), CSA는 모두 나눗셈 대수 위의 행렬 대수이며, 따라서 쿼터니언은 실수 위의 유일한 자명하지 않은 나눗셈 대수입니다.
CSA – 중심이 정확하게 필드인 단순 대수(필드와 마찬가지로 사소한 양면 이상이 없음)인 필드 위의 유한 차원 링은 확장 필드의 비상호적 유사체이며 일반적인 링 확장보다 더 제한적입니다.쿼터니언이 실수보다 유일한 자명하지 않은 CSA라는 사실(등가성까지)은 실수의 유일한 자명하지 않은 유한장 확장이라는 사실과 비교될 수 있습니다.
인용문
저는 그것이 x, y, z 등에 의지할 필요가 있거나 필요한 것처럼 보일 때마다 그것이 지금까지 펼쳐졌던 상태의 무정함 또는 불완전함으로 간주합니다.
— William Rowan Hamilton (circa 1848)[43]
시간은 단 하나의 차원을 가지고 있고, 공간은 3차원을 가지고 있다고 합니다.수학적 쿼터니언은 이 두 요소를 모두 포함합니다. 기술적인 언어에서 그것은 "시간과 공간" 또는 "공간과 시간"이라고 말할 수 있습니다: 그리고 이런 의미에서 그것은 4차원을 가지고 있거나 적어도 참조를 포함합니다. ...그리고 시간의 하나, 공간의 세 개, 상징의 사슬에 묶여있는 힘이 어떻게 되는지.
— William Rowan Hamilton (circa 1853)[44]
쿼터니언은 해밀턴의 정말 좋은 일이 끝난 후에 생겨났습니다. 그리고 비록 아름답게 기발하기는 하지만, 맥스웰 서기를 포함하여 어떤 식으로든 그들을 건드린 사람들에게는 혼합되지 않은 악이었습니다.
— W. Thompson, Lord Kelvin (1892)[45]
실제로 전자기 이론(그리고 일반적으로 수학 물리학)에서 벡터 분석의 적절성을 인식했음에도 불구하고 데카르트 분석보다 이해하고 작업하는 것이 더 어렵다고 생각한 적이 있습니다.하지만 그것은 제가 이 주제에 대해 접근할 수 있는 유일한 논문인 교수님을 읽을 때 제 어깨에 자신을 묶었던 4인조 바다 노인을 버리기 전의 일이었습니다.Tait은 쿼터니언입니다.그러나 나는 나중에 내가 필요로 하는 벡터 분석에 관한 한, 쿼터니언은 필요하지 않을 뿐만 아니라 상당한 크기가 아닌 긍정적인 악이라는 것을 알게 되었습니다. 그리고 벡터 분석의 성립은 그것의 회피에 의해 꽤 간단해졌으며 작동 또한 단순화되었다는 것을 알게 되었습니다.평범한 데카르트 작업과 편리하게 조화를 이룰 수 있도록 했습니다.제 논문 중에서 특별한 목적이 있는 것을 제외하고는 사분면의 유령은 없습니다.제가 사용하는 벡터 분석은 데카르트 분석의 편리하고 체계적인 축약으로 설명될 수도 있고, 그렇지 않으면 쿼터니언이 없는 쿼터니언으로 설명될 수도 있습니다.쿼터니언은 미국 여학생에 의해 "고대의 종교의식"이라고 정의된 것 같습니다.하지만 이것은 완전한 실수였습니다.고대인들 – 교수님과는 다릅니다.Tait는 몰랐고, Quaternions를 숭배하지 않았습니다.
— Oliver Heaviside (1893)[46]
행렬도, 쿼터니언도, 보통 벡터도 이 열 개의 [추가] 장에서 제거되지 않았습니다.제 생각에, 현대 텐서 미적분학의 강력한 힘에도 불구하고, 그러한 오래된 수학 언어들은 특수 상대성 이론의 제한된 분야에서 눈에 띄는 이점을 제공하기 위해 계속되고 있습니다.게다가, 일상 생활에서 뿐만 아니라 과학에서, 한 언어 이상의 숙달은 또한 소중합니다, 왜냐하면 그것은 우리의 시야를 넓히고, 단어나 수학적 기호로 표현되는 물질에 대한 비판에 도움을 주고, 저위상성[기반이 약한]을 방지하기 때문입니다.
— Ludwik Silberstein (1924)[47]
... 4분의 1은 수학적 사상의 투쟁에서 다소 성공적이지 못한 종으로서 19세기 붕괴의 분위기를 풍기는 것으로 보입니다.인정하건대, 수학자들은 여전히 4차 이온의 놀라운 대수적 특성을 위해 마음속에 따뜻한 자리를 지키고 있지만, 아아, 그러한 열정은 머리가 단단한 물리학자에게 별 의미가 없습니다.
— Simon L. Altmann (1986)[48]
참고 항목
- 쿼터니언과 오일러 각도 사이의 변환 – 수학적 전략
- 이중 쿼터니언 – 실수 위의 8차원 대수 하는 페이지
- 이중복소수 – 실수 위의 4차원 대수 방향 대상에 대한 하는 페이지
- 외대수 – 외대수/웨지 곱
- 후르비츠 사분위수
- 쌍곡 쿼터니언 – 단위 벡터가 +1로 제곱되는 쿼터니언의 돌연변이
- Lenárt sphere – 구면 기하학 교육 모델 을 폴백으로 하는 페이지
- 파울리 행렬 – 양자역학과 스핀 연구에서 중요한 행렬
- 사중이온 다양체
- 쿼터니온 행렬 – 항목이 쿼터니온인 하는 페이지
- 사생이온성 폴리톱
- 사중이온 투영 공간 – 수학의 개념
- 4차원 유클리드 공간에서의 회전 – 특수 직교군
- Slerp – 컴퓨터 그래픽스의 구면 선형 보간
- 분할 쿼터니언 – 실수에 대한 4차원 연상 대수
- 테서랙트 – 입방체의 4차원 유사체
메모들
- ^ 쿼터니언에 대한 좀 더 개인적인 견해는 1995년 요아힘 람벡에 의해 쓰여졌습니다.그는 자신의 에세이에서 해밀턴이 우세했다면 물리학에서의 쿼터니언: "나의 대학원생으로서의 흥미는 실버스타인의 영감을 주는 책에 의해 길러졌습니다."라고 썼습니다.그는 "저는 쿼터니언이 이론 물리학의 특정 측면에 익숙해지길 원하는 순수한 수학자들에게 지름길을 제공할 수 있다고 굳게 믿습니다"라고 말함으로써 결론을 내렸습니다.Lambek, J. (1995). "If Hamilton had prevailed: Quaternions in physics". Math. Intelligencer. Vol. 17, no. 4. pp. 7–15. doi:10.1007/BF03024783.
- ^ 사실, 쿼터니언의 벡터 부분은 Altmann([25]1986)이 공식적으로 증명한 것처럼 보통 또는 "극성" 벡터가 아닌 "축" 벡터 또는 "가동 벡터"라는 것에 주목할 필요가 있습니다.극벡터는 정보의 손실 없이 순수한 가상의 쿼터니언에 의한 계산(예를 들어 "유사성 변환"에 의한 회전)으로 표현될 수 있지만, 둘은 혼동되어서는 안 됩니다."이진"의 축(180°)회전 쿼터니언은 그러한 경우에 표현된 극벡터의 방향과 일치합니다.
- ^ 이에 비해 R 은(는) 차원 1, 복소수 {\은(는) 차원 2, O{\은(는) 차원 8입니다.
- ^ H 에서 -1인 제곱근의 식별은 해밀턴에 의해 제공되었지만[34] 다른 텍스트에서는 종종 생략되었습니다.1971년까지 샘 펄리스(Sam Perlis)는 미국 수학 교사 협의회(National Council of Mathematics of Teachers of Mathematics)에서 발표한 대수학 역사 주제(39페이지)에 포함된 3페이지의 설명문에 이 영역을 포함시켰습니다.최근에는 Ian R. Porteous의 책 Clifford Algebars and the Classical Groups (Cambridge, 1995)에서 -1의 제곱근의 구체가 60페이지의 명제 8.13에 설명되어 있습니다.
- ^ Corke(2017)와 같은 응용수학에 관한 책들은 종종 φ := 1/2π 즉, 또 다른 변수 θ = 2π로 다른 표기법을 사용합니다.
참고문헌
- ^ "On Quaternions; or on a new System of Imaginaries in Algebra". Letter to John T. Graves. 17 October 1843.
- ^ Rozenfelʹd, Boris Abramovich (1988). The history of non-euclidean geometry: Evolution of the concept of a geometric space. Springer. p. 385. ISBN 9780387964584.
- ^ Hamilton. Hodges and Smith. 1853. p. 60.
quaternion quotient lines tridimensional space time
- ^ Hardy 1881. Ginn, Heath, & co. 1881. p. 32. ISBN 9781429701860.
- ^ Curtis, Morton L. (1984), Matrix Groups (2nd ed.), New York: Springer-Verlag, p. 10, ISBN 978-0-387-96074-6
- ^ Kunze, Karsten; Schaeben, Helmut (November 2004). "The Bingham distribution of quaternions and its spherical radon transform in texture analysis". Mathematical Geology. 36 (8): 917–943. doi:10.1023/B:MATG.0000048799.56445.59. S2CID 55009081.
- ^ Smith, Frank (Tony). "Why not sedenion?". Retrieved 8 June 2018.
- ^ a b c Hazewinkel, Gubareni & Kirichenko 2004, 페이지 12 참조
- ^ Conway & Smith 2003, 페이지 9
- ^ Bradley, Robert E.; Sandifer, Charles Edward (2007). Leonhard Euler: life, work and legacy. Elsevier. p. 193. ISBN 978-0-444-52728-8. 그들은 1959년 빌헬름 블라슈케의 주장을 언급합니다. "4개의 이온은 L에 의해 처음 확인되었습니다.오일러는 1748년 5월 4일 골드바흐에게 보낸 편지에서 "이 편지에서 오일러가 쿼터니언을 "식별했다"고 말하는 것은 전혀 말이 되지 않습니다.이 주장은 터무니없는 것입니다.
- ^ 푸졸, J., "해밀턴, 로드리게스, 가우스, 쿼터니언, 그리고 회전: 역사적 재평가" 수학적 분석에서의 커뮤니케이션 (2012), 13(2), 1-14
- ^ Gauss, C.F. (1900). "Mutationen des Raumes [Transformations of space] (c. 1819)". In Martin Brendel (ed.). Carl Friedrich Gauss Werke [The works of Carl Friedrich Gauss]. Vol. 8. article edited by Prof. Stäckel of Kiel, Germany. Göttingen, DE: Königlichen Gesellschaft der Wissenschaften [Royal Society of Sciences]. pp. 357–361.
- ^ a b Hamilton, W.R. (1844). "Letter". London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. Vol. xxv. pp. 489–495.
- ^ Hamilton, Sir W.R. (1866). Hamilton, W.E. (ed.). Elements of Quaternions. London: Longmans, Green, & Co.
- ^ a b Shoemake, Ken (1985). "Animating Rotation with Quaternion Curves" (PDF). Computer Graphics. 19 (3): 245–254. doi:10.1145/325165.325242. SIGGRAPH '85에서 발표.
- ^ Tomb Raider(1996)는 매끄러운 3차원 회전을 달성하기 위해 쿼터니언을 사용한 최초의 대중 시장 컴퓨터 게임으로 자주 인용됩니다.보기, 예를 들어
- ^ McCarthy, J.M. (1990). An Introduction to Theoretical Kinematics. MIT Press. ISBN 978-0-262-13252-7.
- ^ Hurwitz, A. (1919), Vorlesungen über die Zahlentheorie der Quaternionen, Berlin: J. Springer, JFM 47.0106.01후르비츠 쿼터니언과 Hurwitz, A. (1919), Vorlesungen über die Zahlentheorie der Quaternionen, Berlin: J. Springer, JFM 47.0106.01관련하여
- ^ Girard, P.R. (1984). "The quaternion group and modern physics". European Journal of Physics. 5 (1): 25–32. Bibcode:1984EJPh....5...25G. doi:10.1088/0143-0807/5/1/007. S2CID 250775753.
- ^ Girard, Patrick R. (1999). "Einstein's equations and Clifford algebra" (PDF). Advances in Applied Clifford Algebras. 9 (2): 225–230. doi:10.1007/BF03042377. S2CID 122211720. Archived from the original (PDF) on 17 December 2010.
- ^ Huerta, John (27 September 2010). "Introducing The Quaternions" (PDF). Archived (PDF) from the original on 2014-10-21. Retrieved 8 June 2018.
- ^ Wood, Charlie (6 September 2018). "The Strange Numbers That Birthed Modern Algebra". Abstractions blog. Quanta Magazine.
- ^ 이브 (1976, 페이지 391)
- ^ "Maths – Transformations using Quaternions". EuclideanSpace.
A rotation of q1 followed by a rotation of q2 is equivalent to a single rotation of q2 q1. Note the reversal of order, that is, we put the first rotation on the right hand side of the multiplication.
- ^ Altmann, S.L. Rotations, Quaternions, and Double Groups. Ch. 12.
- ^ Hamilton, Sir William Rowan (1866). "Article 285". Elements of Quaternions. Longmans, Green, & Company. p. 310.
- ^ Hardy (1881). "Elements of Quaternions". Science. library.cornell.edu. 2 (75): 65. doi:10.1126/science.os-2.75.564. PMID 17819877.
- ^ "quaternion group". Wolframalpha.com.
- ^ Gibbs, J. Willard; Wilson, Edwin Bidwell (1901). Vector Analysis. Yale University Press. p. 428.
right tensor dyadic
- ^ a b Hamilton, W.R. (1844–1850). "On quaternions or a new system of imaginaries in algebra". David R. Wilkins collection. Philosophical Magazine. Trinity College Dublin.
- ^ "Visualizing Quaternions". Morgan-Kaufmann/Elsevier. 2005.
- ^ "[no title cited; determinant evaluation]". Wolframalpha.com.
- ^ Farebrother, Richard William; Groß, Jürgen; Troschke, Sven-Oliver (2003). "Matrix representation of quaternions". Linear Algebra and Its Applications. 362: 251–255. doi:10.1016/s0024-3795(02)00535-9.
- ^ Hamilton, W.R. (1899). Elements of Quaternions (2nd ed.). Cambridge University Press. p. 244. ISBN 1-108-00171-8.
- ^ "[no title cited]" (PDF). bridgesmathart.org. archive. Retrieved 19 August 2018.
- ^ a b Särkkä, Simo (June 28, 2007). "Notes on Quaternions" (PDF). Lce.hut.fi. Archived from the original (PDF) on 5 July 2017.
- ^ Corke, Peter (2017). Robotics, Vision, and Control – Fundamental Algorithms in MATLAB. Springer. ISBN 978-3-319-54413-7.
- ^ Park, F.C.; Ravani, Bahram (1997). "Smooth invariant interpolation of rotations". ACM Transactions on Graphics. 16 (3): 277–295. doi:10.1145/256157.256160. S2CID 6192031.
- ^ Hanson, Jason (2011). "Rotations in three, four, and five dimensions". arXiv:1103.5263 [math.MG].
- ^ Günaşti, Gökmen (2016). Quaternions Algebra, Their Applications in Rotations and Beyond Quaternions (BS). Linnaeus University.
- ^ "Three-Dimensional Point Groups". www.classe.cornell.edu. Retrieved 2022-12-09.
- ^ "Quaternions and Geometric Algebra". geometricalgebra.net. Retrieved 2008-09-12. 참고 항목:
- ^ Hamilton, William Rowan (1853). Lectures on quaternions. Dublin: Hodges and Smith. p. 522.
- ^ Graves, R.P. Life of Sir William Rowan Hamilton. Dublin Hodges, Figgis. pp. 635–636.
- ^ Thompson, Silvanus Phillips (1910). The life of William Thomson (Vol. 2). London, Macmillan. p. 1138.
- ^ Heaviside, Oliver (1893). Electromagnetic Theory. Vol. I. London, UK: The Electrician Printing and Publishing Company. pp. 134–135.
- ^ 루드윅 실버스타인 (1924).상대성이론 제2판 서문
- ^ Altmann, Simon L. (1986). Rotations, quaternions, and double groups. Clarendon Press. ISBN 0-19-855372-2. LCCN 85013615.
추가열람
도서 및 간행물
- Hamilton, William Rowan (1844). "On quaternions, or on a new system of imaginaries in algebra". Philosophical Magazine. 25 (3): 489–495. doi:10.1080/14786444408645047.
- 해밀턴, 윌리엄 로완 (1853), "쿼터니온 강의"아일랜드 왕립 아카데미.
- 해밀턴 (1866) 더블린 쿼테니언스 대학 출판부의 요소들고인이 된 작가의 아들 윌리엄 에드윈 해밀턴이 편집했습니다.
- 해밀턴 (1899) 쿼터니언의 원소들 제1권, (1901) 제2권.찰스 재스퍼 졸리 편집; 롱만스, 그린 & 코 출판.
- Tait, Peter Guthrie (1873), "4등분선에 관한 기초 논문".2d., Cambridge, [Eng.] : University Press.
- 맥스웰, 제임스 클러커 (1873), "전기와 자기에 관한 논문"클래런던 프레스, 옥스포드
- Tait, Peter Guthrie (1886), ":"Archived copy". Archived from the original on August 8, 2014. Retrieved June 26, 2005.
{{cite web}}CS1 maint: 제목 그대로 보관된 복사본 (링크) CS1 maint: 부적합한 URL (링크)", M.A. Sec. R.S.E. Encyclopyradia Britannica, 9판, Vol. XX, pp. 160–164. (bziped PostScript 파일) - Joly, Charles Jasper (1905). A manual of quaternions. Macmillan. LCCN 05036137.
- Macfarlane, Alexander (1906). Vector analysis and quaternions (4th ed.). Wiley. LCCN 16000048.
- Chisholm, Hugh, ed. (1911). . Encyclopædia Britannica (11th ed.). Cambridge University Press. (쿼니언에 대한 섹션 참조)
- Finkelstein, David; Jauch, Josef M.; Schiminovich, Samuel; Speiser, David (1962). "Foundations of quaternion quantum mechanics". J. Math. Phys. 3 (2): 207–220. Bibcode:1962JMP.....3..207F. doi:10.1063/1.1703794. S2CID 121453456.
- Du Val, Patrick (1964). Homographies, quaternions, and rotations. Oxford mathematical monographs. Clarendon Press. LCCN 64056979.
- 마이클 J. 크로(Michael J. Crowe, 1967), 벡터 분석의 역사:벡터적 체계의 발상의 진화, 노트르담 대학 출판부19세기의 주요 벡터 시스템과 부 벡터 시스템(해밀턴, 뫼비우스, 벨라비티스, 클리포드, 그라스만, 테이트, 피어스, 맥스웰, 맥팔레인, 맥컬리, 깁스, 헤비사이드)을 조사합니다.
- Altmann, Simon L. (1989). "Hamilton, Rodrigues, and the Quaternion Scandal". Mathematics Magazine. 62 (5): 291–308. doi:10.1080/0025570X.1989.11977459.
- Pujol, Jose (2014). "On Hamilton's Nearly-Forgotten Early Work on the Relation between Rotations and Quaternions and on the Composition of Rotations". The American Mathematical Monthly. 121 (6): 515–522. doi:10.4169/amer.math.monthly.121.06.515. S2CID 1543951.
- Adler, Stephen L. (1995). Quaternionic quantum mechanics and quantum fields. International series of monographs on physics. Vol. 88. Oxford University Press. ISBN 0-19-506643-X. LCCN 94006306.
- Ward, J.P. (1997). Quaternions and Cayley Numbers: Algebra and Applications. Kluwer Academic. ISBN 0-7923-4513-4.
- Kantor, I.L.; Solodnikov, A.S. (1989). Hypercomplex numbers, an elementary introduction to algebras. Springer-Verlag. ISBN 0-387-96980-2.
- Gürlebeck, Klaus; Sprössig, Wolfgang (1997). Quaternionic and Clifford calculus for physicists and engineers. Mathematical methods in practice. Vol. 1. Wiley. ISBN 0-471-96200-7. LCCN 98169958.
- Kuipers, Jack (2002). Quaternions and Rotation Sequences: A Primer With Applications to Orbits, Aerospace, and Virtual Reality. Princeton University Press. ISBN 0-691-10298-8.
- Conway, John Horton; Smith, Derek A. (2003). On Quaternions and Octonions: Their Geometry, Arithmetic, and Symmetry. A.K. Peters. ISBN 1-56881-134-9. (검토).
- Jack, P.M. (2003). "Physical space as a quaternion structure, I: Maxwell equations. A brief Note". arXiv:math-ph/0307038.
- Kravchenko, Vladislav (2003). Applied Quaternionic Analysis. Heldermann Verlag. ISBN 3-88538-228-8.
- Hazewinkel, Michiel; Gubareni, Nadiya; Kirichenko, Vladimir V. (2004). Algebras, rings and modules. Vol. 1. Springer. ISBN 1-4020-2690-0.
- Hanson, Andrew J. (2006). Visualizing Quaternions. Elsevier. ISBN 0-12-088400-3.
- Binz, Ernst; Pods, Sonja (2008). "1. The Skew Field of Quaternions". Geometry of Heisenberg Groups. American Mathematical Society. ISBN 978-0-8218-4495-3.
- Doran, Chris J.L.; Lasenby, Anthony N. (2003). Geometric Algebra for Physicists. Cambridge University Press. ISBN 978-0-521-48022-2.
- Vince, John A. (2008). Geometric Algebra for Computer Graphics. Springer. ISBN 978-1-84628-996-5.
- 고전적인 강체로 간주될 수 있는 분자에 대해 분자 역학 컴퓨터 시뮬레이션은 4차 이온을 사용합니다.그들은 이 목적을 위해 처음 도입되었습니다.
- Zhang, Fuzhen (1997). "Quaternions and Matrices of Quaternions". Linear Algebra and Its Applications. 251: 21–57. doi:10.1016/0024-3795(95)00543-9.
- Ron Goldman (2010). Rethinking Quaternions: Theory and Computation. Morgan & Claypool. ISBN 978-1-60845-420-4.
- Eves, Howard (1976), An Introduction to the History of Mathematics (4th ed.), New York: Holt, Rinehart and Winston, ISBN 0-03-089539-1
- Voight, John (2021). Quaternion Algebras. Graduate Texts in Mathematics. Vol. 288. Springer. doi:10.1007/978-3-030-56694-4. ISBN 978-3-030-57467-3.
링크 및 모노그래프
- "Quaternion Notices". 쿼터니언 컨퍼런스 프레젠테이션 관련 공지사항 및 자료
- "Quaternion", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- "Frequently Asked Questions". Matrix and Quaternion. 1.21.
- Sweetser, Doug. "Doing Physics with Quaternions".
- 컴퓨터 그래픽과 역학을 위한 쿼터니언 (Gernot Hoffman)
- Gsponer, Andre; Hurni, Jean-Pierre (2002). "The Physical Heritage of Sir W. R. Hamilton". arXiv:math-ph/0201058.
- Wilkins, D.R. "Hamilton's Research on Quaternions".
- Grossman, David J. "Quaternion Julia Fractals". 3D Raytraceed 쿼터니언 줄리아 프랙탈스
- "Quaternion Math and Conversions". 직선 회전 변환 공식에 대한 링크와 함께 기초 수학을 설명하는 멋진 페이지.
- Mathews, John H. "Bibliography for Quaternions". Archived from the original on 2006-09-02.
- "Quaternion powers". GameDev.net.
- Hanson, Andrew. "Visualizing Quaternions home page". Archived from the original on 2006-11-05.
- Karney, Charles F.F. (January 2007). "Quaternions in molecular modeling". J. Mol. Graph. Mod. 25 (5): 595–604. arXiv:physics/0506177. doi:10.1016/j.jmgm.2006.04.002. PMID 16777449. S2CID 6690718.
- Mebius, Johan E. (2005). "A matrix-based proof of the quaternion representation theorem for four-dimensional rotations". arXiv:math/0501249.
- Mebius, Johan E. (2007). "Derivation of the Euler–Rodrigues formula for three-dimensional rotations from the general formula for four-dimensional rotations". arXiv:math/0701759.
- "Hamilton Walk". Department of Mathematics, NUI Maynooth.
- "Using Quaternions to represent rotation". OpenGL:Tutorials. Archived from the original on 2007-12-15.
- 데이비드 에릭슨, 캐나다 국방 연구 개발(DRDC), DRDC TR 2005-228 논문에서 단일 쿼터니언 표현으로부터 회전 행렬의 완전한 유도.
- Martinez, Alberto. "Negative Math, How Mathematical Rules Can Be Positively Bent". Department of History, University of Texas. Archived from the original on 2011-09-24.
- Stahlke, D. "Quaternions in Classical Mechanics" (PDF).
- Morier-Genoud, Sophie; Ovsienko, Valentin (2008). "Well, Papa, can you multiply triplets?". arXiv:0810.5562 [math.AC]. 는 쿼터니언이 Z/2 × Z/2 × Z/2로 등급화된 스큐-가환 대수로 만들어지는 방법을 설명합니다.
- Joyce, Helen (November 2004). "Curious Quaternions". hosted by John Baez.
- Ibanez, Luis. "Tutorial on Quaternions. Part I" (PDF). Archived from the original (PDF) on 2012-02-04. Retrieved 2011-12-05. Part II (PDF; 현대적 용법과 다른 해밀턴의 용어 사용)
- Ghiloni, R.; Moretti, V.; Perotti, A. (2013). "Continuous slice functional calculus in quaternionic Hilbert spaces". Rev. Math. Phys. 25 (4): 1350006–126. arXiv:1207.0666. Bibcode:2013RvMaP..2550006G. doi:10.1142/S0129055X13500062. S2CID 119651315.
Ghiloni, R.; Moretti, V.; Perotti, A. (2017). "Spectral representations of normal operators via Intertwining Quaternionic Projection Valued Measures". Rev. Math. Phys. 29: 1750034. arXiv:1602.02661. doi:10.1142/S0129055X17500349. S2CID 124709652. 엄밀한 4차 이온 양자역학에 유용한 2차 이온 힐버트 공간에서의 연속 함수 미적분학과 스펙트럼 이론에 관한 두 개의 설명적 논문. - 안드로이드 앱은 기기의 방향에 해당하는 쿼터니언을 보여줍니다.
- 쿼터니언을 이용한 회전 물체 비디오 게임/컴퓨터 그래픽에서 회전을 위한 쿼터니언의 사용에 대해 이야기하는 기사.
외부 링크
 Wikimedia Commons의 쿼터니언 관련 매체
Wikimedia Commons의 쿼터니언 관련 매체- 폴슨, 로렌스 C. 쿼터니언 (Isabelle/HOL의 공식 증명 개발, 공식 증명 아카이브)
- 쿼터니언 – 시각화

 실수와
실수와 




![{\displaystyle {\begin{aligned}&(a_{1}+b_{1}\,\mathbf {i} +c_{1}\,\mathbf {j} +d_{1}\,\mathbf {k} )+(a_{2}+b_{2}\,\mathbf {i} +c_{2}\,\mathbf {j} +d_{2}\,\mathbf {k} )\\[3mu]&\qquad =(a_{1}+a_{2})+(b_{1}+b_{2})\,\mathbf {i} +(c_{1}+c_{2})\,\mathbf {j} +(d_{1}+d_{2})\,\mathbf {k} ,\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b28060ff6bf96faa0a795ecb7a53cf4d9eea13b)



![{\displaystyle {\begin{aligned}\mathbf {i} ^{2}&=\mathbf {j} ^{2}=\mathbf {k} ^{2}=-1,\\[5mu]\mathbf {i\,j} &=-\mathbf {j\,i} =\mathbf {k} ,\qquad \mathbf {j\,k} =-\mathbf {k\,j} =\mathbf {i} ,\qquad \mathbf {k\,i} =-\mathbf {i\,k} =\mathbf {j} .\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/557dac211aa259b3cde6c0aa76d0125562a01c40)





(r_{2},\ {\vec {v}}_{2})&=(r_{1}r_{2}-{\vec {v}}_{1}\cdot {\vec {v}}_{2},\ r_{1}{\vec {v}}_{2}+r_{2}{\vec {v}}_{1}+{\vec {v}}_{1}\times {\vec {v}}_{2})\,,\\[5mu](r,{\vec {v}})^{-1}&=\left({\frac {r}{r^{2}+{\vec {v}}\cdot {\vec {v}}}},{\frac {-{\vec {v}}}{r^{2}+{\vec {v}}\cdot {\vec {v}}}}\right)\,,\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4178f888b4ddf169b4d272583ed331a49ab54739)







 (와) 정확히 동일한 증명으로 뒤따릅니다.
(와) 정확히 동일한 증명으로 뒤따릅니다.



![{\displaystyle \mathbb {R} [\mathrm {Q} _{8}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/95e3ca1ed22f8ae5680236bb417a05d2e38886ae)








![{\displaystyle [p,q]=2p\times q.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c45178772ffab33a9936c42a9df2be320f5d22b8)
![{\displaystyle {\begin{aligned}p&=p_{\text{s}}+p_{\text{v}},\\[5mu]q&=q_{\text{s}}+q_{\text{v}},\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1ab7ef853cfa04d68fc3cd8add199f463e3eb1c8)

 회전으로 식별할 수 있으며
회전으로 식별할 수 있으며 

![{\displaystyle {\begin{aligned}{\begin{bmatrix}a&-b&-c&-d\\b&a&-d&c\\c&d&a&-b\\d&-c&b&a\end{bmatrix}}&=a{\begin{bmatrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{bmatrix}}+b{\begin{bmatrix}0&-1&0&0\\1&0&0&0\\0&0&0&-1\\0&0&1&0\end{bmatrix}}\\[10mu]&\qquad +c{\begin{bmatrix}0&0&-1&0\\0&0&0&1\\1&0&0&0\\0&-1&0&0\end{bmatrix}}+d{\begin{bmatrix}0&0&0&-1\\0&0&-1&0\\0&1&0&0\\1&0&0&0\end{bmatrix}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24dd2e597c2d4e96a82082da462df8e2f73c30e4)
![{\displaystyle {\begin{aligned}{\begin{bmatrix}a&d&-b&-c\\-d&a&c&-b\\b&-c&a&-d\\c&b&d&a\end{bmatrix}}&=a{\begin{bmatrix}1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{bmatrix}}+b{\begin{bmatrix}0&0&-1&0\\0&0&0&-1\\1&0&0&0\\0&1&0&0\end{bmatrix}}\\[10mu]&\qquad +c{\begin{bmatrix}0&0&0&-1\\0&0&1&0\\0&-1&0&0\\1&0&0&0\end{bmatrix}}+d{\begin{bmatrix}0&1&0&0\\-1&0&0&0\\0&0&0&-1\\0&0&1&0\end{bmatrix}}.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/119fe725e8b355a0236e1c710fbf974dd96c2954)

 복소수 위의 2차원 벡터 공간이라고
복소수 위의 2차원 벡터 공간이라고 

![{\displaystyle {\begin{aligned}a^{2}-b^{2}-c^{2}-d^{2}&=-1,{\vphantom {x^{|}}}\\[3mu]2ab&=0,\\[3mu]2ac&=0,\\[3mu]2ad&=0.\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2fff161699a746d453fc9110f35c86a9fbcb4164)


 동형인 쿼터니언의
동형인 쿼터니언의  스칼라 부분과 벡터 부분의 합으로 q를
스칼라 부분과 벡터 부분의 합으로 q를 











 (는) 다음과 같이 정의됩니다.
(는) 다음과 같이 정의됩니다.



















