그룹 링

대수학에서, 그룹 링은 자유 모듈이며 동시에 어떤 주어진 링과 어떤 그룹으로부터도 자연적인 방법으로 구성된다.자유 모듈로서 그 스칼라의 링은 주어진 링이며, 그 기본은 주어진 그룹의 요소 집합이다.링으로서, 그것의 덧셈 법칙은 무료 모듈의 그것이고 그것의 곱셈은 주어진 그룹 법칙을 기초로 "선형으로" 확장한다.덜 형식적으로, 그룹 링은 그룹의 각 요소에 주어진 링에서 "가중 인자"를 부착함으로써 주어진 그룹의 일반화다.null

만약 이 링이 서로 교환된다면, 그룹 링은 또한 그룹 대수라고도 불린다. 왜냐하면 그것은 실제로 주어진 링에 대한 대수이기 때문이다.한 분야에 걸친 그룹 대수학은 홉프 대수학의 추가적인 구조를 가지고 있다. 이 경우, 이를 그룹 홉프 대수라고 부른다.null

집단반지의 기구는 특히 집단표현 이론에 유용하다.null

정의

G를 집단이 되게 하고, 곱셈으로 쓰고, R을 반지가 되게 하라.The group ring of G over R, which we will denote by R[G] (or simply RG), is the set of mappings f : G → R of finite support (f(g) is nonzero for only finitely many elements g), where the module scalar product αf of a scalar α in R and a mapping f is defined as the mapping ${\displaystyle x\mapsto \alpha \cdot f(x)}$, and the두 매핑 f와 g의 모듈 그룹 합은 $매핑{\displaystyle }$ ${\displaystyle x}$↦ f (${\displaystyle x}$)${\displaystyle }$+ ${\displaystyle g}$ ( ${\displaystyle x}$ )${\displaystyle$ x$\mapsto f(x)+g(x)}$로 정의된다$.$ 가법 그룹 R[G]을 링으로 만들기 위해 f와 g의 곱을 매핑으로 정의한다.

$\displaystyle x\mapsto \sum _{uv=x(u)g=\sum _{u\in G}f(u^{-1}x).}$

f와 g는 유한한 지지를 받고 있고, 고리 공리는 쉽게 검증되기 때문에 합계가 정당하다.null

표기법과 용어의 일부 변형이 사용되고 있다.특히 f : G → R과 같은 매핑은 "R로 계수를 갖는 G의 원소들의 공식 선형 결합"이라고 불리는 것으로 기록되기도 한다.^[1]

${\displaystyle \sum _{g\in G}f(g)g,}$

또는 간단히

${\displaystyle \sum _{g\in G}f_{g}g,}$

혼동을 일으키지 않는 곳에 ^[2]말이야null

링 R이 실제로 필드 K인 경우, 그룹 링 RG의 모듈 구조는 사실상 K 위의 벡터 공간이라는 점에 유의한다.

예

1. 제너레이터 $a{\displaystyle }$ ${\displaystyle a}$ 및$$ ID 요소 1을_G 사용하여 순서 3의 순환 그룹인 G = C를₃ 사용하십시오.C[G]의 요소 r은 다음과 같이 쓸 수 있다.

${\displaystyle r=z_{0}1_{G}+z_{1}a+z_{2}a^{2}\,}$

여기서 z₀, z₁, z는₂ C에 있고, 복잡한 숫자들은 C에 있다.${\displaystyle {이것}^{}}$은 3 =${\displaystyle {}^{}{0\mathrm{}}^{}}$ =$$ {\displaystyle a^{$3}=a^{0}=1}$과 같이$$ 변수 $a{\displaystyle }$ ${\$$displaystyle$ $a$$}$의 다항식 링과 같은 것이다.C[G]는 링 C[ ${\displaystyle a}$ ]/$$${\displaystyle }$( ${\displaystyle 3{}^{}}$- ${\displaystyle {1\mathrm{}}^{}}$) ${\displaystyle (a^{3}-1)}$에 대해 이형이다$.$

$다른{\displaystyle }$요소 ${\displaystyle {}_{}}$를 s =${\displaystyle {}_{}{w}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {}_{}}$ G +${\displaystyle }$w ${\displaystyle {a\mathrm{}}_{}}$ + ${\displaystyle {}_{}{}^{}}$ ${\displaystyle {2\mathrm{}}^{}}$a 2 {\$displaystyle s=w_{0}1_{G}+w_{$1}$a+w_{$2}a^{2$}},$합은 다음과 같다.

${\displaystyle r+s=(z_{0}+w_{0})1_{G}+(z_{1}+w_{1}a+(z_{2}+w_{2})a+(z_{2})a^{2}\,},}$

그리고 그들의 제품은

${\displaystyle rs=(z_{0}w_{0}+z_{1}w_{2}+z_{2}w_{1})1_{G}+(z_{0}w_{1}+z_{1}w_{0}+z_{2}w_{2})a+(z_{0}w_{2}+z_{2}w_{0}+z_{1}w_{1})a^{2}.}$

G의 식별 요소 1은 계수 고리_G(이 경우 C)를 C[G]에 표준적으로 내장하도록 유도한다는 점에 유의하십시오. 그러나 엄밀히 말하면 C[G]의 승법적 식별 요소는 1제1제1제1제1제1제1제1제1제1제1항상 C[G]는 1/1이다_G.첨가물 ID 요소는 0이다.null

G가 비협조 그룹일 때, 항을 곱할 때 그룹 요소의 순서를 보존할 수 있도록(그리고 실수로 통근하지 않도록) 주의해야 한다.null

2. 다른 예로는 링 R 위에 있는 Laurent 다항식의 경우: 이것들은 R 위에 있는 무한 순환 그룹 Z의 그룹 링에 지나지 않거나 그 이하도 아니다.

3. Let Q be the quaternion group with elements ${\displaystyle \{e,{\bar {e}},i,{\bar {i}},j,{\bar {j}},k,{\bar {k}}\}}$. Consider the group ring RQ, where R is the set of real numbers.이 그룹 링의 임의 요소는 형식이다.

${\displaystyle x_{1}\cdot e+x_{2}}\cdot {\bar{e}+x_{3}\cdot i+x_{4}}\cdot {\bar{i}+x_{5}\cdot j+x_{6}}\cdot {\bar{j}+x_{7}}\cdot k+x_{8}\cdot {\bar {k}}$

여기서 $x{\displaystyle {}_{}}$ ${\displaystyle i_{}}$ ${\$는 실제$$ 숫자다.null

다른 그룹 링에서와 마찬가지로 곱셈은 그룹 연산을 기반으로 정의된다.예를 들어,

${\displaystyle {\begin{aligned}{\big (}3\cdot e+{\sqrt {2}}\cdot i{\big )}{\big (}{\frac {1}{2}}\cdot {\bar {j}}{\big )}&=(3\cdot e)({\frac {1}{2}}\cdot {\bar {j}})+({\sqrt {2}}\cdot i)({\frac {1}{2}}\cdot {\bar {j}})\\&={\frac {3}{2}}\cdot {\big (}(e)({\bar {j}}){\big )}+{\frac {\sqrt {2}}{2}}\cdot {\big (}(i)({\bar {j}}){\big )}\\&={\frac {3}{2}}\cdot {\bar {j}}+{\frac {\sqrt {2}}{2}}\cdot k\end{aligned}}.}$

RQ는 R에 대한 쿼터니온의 스큐 필드와 같지 않다는 점에 유의하십시오.This is because the skew field of quaternions satisfies additional relations in the ring, such as ${\displaystyle -1\cdot i=-i}$, whereas in the group ring RQ, ${\displaystyle -1\cdot i}$ is not equal to ${\displaystyle 1\cdot {\bar {i}}}$. To be more specific, the group ring RQ has dimension 8쿼터니온의 꼬치장은 실제 벡터 공간으로서 차원 4를 가지고 있는 반면, 실제 벡터 공간으로서.null

4. 비아벨 그룹 링의 또 다른 예는 $Z{\displaystyle \mathbb{}}$ [${\displaystyle {\mathbb{}}_{}}$ ${\displaystyle {\mathrm{}}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle \mathb$ {$Z}[\mathb {S} _{3}]$이며, $여기$서 ${\displaystyle {\mathrm{}}_{}}$ 3 ${\$은 3글자의 대칭 그룹이다$$.This is not an integral domain since we have ${\displaystyle [1-(12)]*[1+(12)]=1-(12)+(12)-(12)(12)=1-1=0}$ where the element ${\displaystyle (12)\in \mathbb {S} _{3}}$ is a transposition-a permutation which only swaps 1 and 2.따라서 그룹 링은 기본 링이 통합 도메인인 경우에도 통합 도메인이 될 필요가 없다.null

일부 기본 속성

1을 사용하여 링 R의 승법적 정체성을 나타내고 그룹 단위를 1로_G 나타냄으로써 링 R[G]은 R에 대한 서브링 이형체를 포함하고, 그 변환 불가능한 원소의 그룹은 G에 대한 서브그룹 이형체를 포함한다.{1_G}의 표시기 기능을 고려하는 경우, 이 기능은 다음에 의해 정의된 벡터 f입니다.

${\displaystyle f(g)=1\cdot 1_{G}+\sum _{g\not =1_{G}}0\cdot g=\mathbf {1} _{\{1_{G}\}}(g)={\begin{cases}1&g=1_{G}\\0&g\neq 1_{G}\end{cases}},}$

f의 모든 스칼라 배수의 집합은 R[G] 이형체의 하위 문자열이다.그리고 G의 각 원소를 {s}의 지표 함수에 매핑하면, 이 함수는 다음에 의해 정의된 벡터 f이다.

${\displaystyle f(g)=1\cdot s+\sum _{g\not=s}0\cdot g=\mathbf {1} _{\s\}(g)={\cdes}g=s\0&g\neq s\case}}}}}$

결과 매핑은 주입군 동형성(R[G]에서 덧셈이 아닌 곱셈에 관한 것)이다.null

R과 G가 모두 역법(즉, R은 역법이고 G는 아벨 그룹)인 경우, R[G]은 역법이다.null

H가 G의 부분군이라면 R[H]은 R[G]의 하위군이다.마찬가지로 S가 R의 서브링이라면 S[G]는 R[G]의 서브링이다.null

G가 1보다 큰 유한한 순서의 그룹이라면, R[G]은 항상 0의 divisor를 가진다.예를 들어, g = m > 1 순서 G의 요소 g를 고려한다.1 - g는 영점 분점:

${\displaystyle(1-g)(1+g+\cdots +g^{m-1}=1-g^{m}=1-1=0.}$

예를 들어 그룹 링 Z[S₃]와 순서 3 g=(123)의 요소를 고려하십시오.이 경우,

${\displaystyle (1-(1123)(1+(1123)+(iii)=1-(1123)^{3}=1-1=0.}$

관련 결과: $그룹{\displaystyle }$ 링 K${\displaystyle }$[ ${\displaystyle G}$ ${\displaystyle ]}$ ${\displaystyle K[G]}$이(가) prime이면 G는 비식별성 유한 정규 부분군이 없다(특히 G는 무한해야 한다).null

Proof: Considering the contrapositive, suppose ${\displaystyle H}$ is a nonidentity finite normal subgroup of ${\displaystyle G}$. Take ${\displaystyle a=\sum _{h\in H}h}$. Since ${\displaystyle hH=H}$ for any ${\displaystyle h\in H}$, we know ${\displaystyle ha=a}$, therefore ${\displaystyle a^{2}=\sum _{h\in H}ha= H a}$. Taking ${\displaystyle b= H \,1-a}$, we have ${\displaystyle ab=0}$. By normality of ${\displaystyle H}$, ${\displaystyle a}$ commutes with a basis of ${\displaystyle K[G]}$, and그러므로

${\displaystyle a}$ ${\displaystyle K}$[ ${\displaystyle G}$ ${\displaystyle ]}$ b${\displaystyle }$= ${\displaystyle K}$[ ${\displaystyle G}$ ${\displaystyle ]}$ ${\displaystyle a}$b = ${\displaystyle 0}$ ${\displaystyle aK[G]b=K[G]ab=0}$.

그리고 $우리$는 ,${\displaystyle b}$ ${\displaystyle a,b}$이(가) 0이 아니라는$$ 것을 알 수 있는데, 이는 $K{\displaystyle }$[ ${\displaystyle G}$ ${\displaystyle ]}$ ${\displaystyle K[G]}$이(가) 프라임이 아님을 보여준다.이것은 원문을 보여준다.null

유한집단에 대한 그룹 대수

집단 알헤브라는 유한집단의 집단표현 이론에서 자연적으로 발생한다.필드 K에 대한 그룹 대수 K[G]는 본질적으로 그룹 링이며, 필드 K가 링을 대신한다.세트 및 벡터 공간으로서 필드 K 위에 있는 G의 자유 벡터 공간이다.즉, K[G]의 x에 대해서는

${\displaystyle x=\sum _{g\in G}a_{g}g.}$

벡터 공간의 대수 구조는 그룹의 곱셈을 사용하여 정의된다.

${\displaystyle g\cdot h=gh,}$

왼쪽에서 g와 h는 그룹 대수학의 요소를 나타내고, 오른쪽의 곱셈은 그룹 연산(대칭으로 표시)이다.null

위의 곱셈은 헷갈릴 수 있기 때문에 K[G]의 기본 벡터를 e_g(g 대신 g)로 쓸 수도 있는데, 이 경우 곱셈은 다음과 같이 쓰여진다.

${\displaystyle e_{g}\cdot e_{h}=e_{gh}.}$

함수로서의 해석

자유 벡터 공간을 G에서 K-값 함수로 생각한다면 대수 곱셈은 함수의 합성이다.null

유한집단의 그룹 대수학은 집단의 함수의 공간으로 식별할 수 있지만, 무한집단의 경우 이들은 다르다.유한 총량으로 구성된 그룹 대수학(group gearge)은 다수의 점을 위해 소멸되는 그룹의 함수에 해당한다. 위상학적으로(분리된 위상 사용), 이것들은 콤팩트한 지지를 받는 함수에 해당한다.null

단, 그룹 대수 K[G]와 함수^G K :=Hom(G, K)의 공간은 이중이다. 그룹 대수학의 요소가 주어진다.

${\displaystyle x=\sum _{g\in G}a_{g}g}$

그룹 f : G → K의 기능을 통해 K의 요소를 부여한다.

${\displaystyle (x,f)=\sum _{g\in G}a_{g}f(g),}$

그것은 한정되어 있기 때문에 잘 정의된 합이다.null

그룹 대수 표현

K[G]를 추상대수학으로 받아들이면 치수 d의 K-벡터 공간 V에 작용하는 대수학 표현을 요구할 수 있다.그런 표현

${\displaystyle {\tilde {\rho }:K[G]\오른쪽 화살표 {\mbox{End}(V)}$

is an algebra homomorphism from the group algebra to the algebra of endomorphisms of V, which is isomorphic to the ring of d × d matrices: ${\displaystyle \mathrm {End} (V)\cong M_{d}(K)}$. Equivalently, this is a left K[G]-module over the abelian group V.

그에 따라, 그룹 표현

${\displaystyle \rho :G\오른쪽 화살표 {\mbox{자동}(V),}$

G에서 V의 선형 자동화 그룹까지의 동형성 그룹이며, 이형성은 일반적인 변위성 행렬의 선형 그룹과 동일하다.${\displaystyle \mathrm{a}}$ ${\displaystyle {\mathrm{}}_{}}$ t${\displaystyle }$(${\displaystyle V}$) ${\displaystyle \cong }$ G L ${\displaystyle {}_{}}$(${\displaystyle K}$ ) ${\displaystyle \mathrmat {Aut}(V)\cong \mathrmat {GL} _{d}(K$ 그러한 표현은 대수표현을 유도한다.

${\displaystyle {\tilde {\rho }:K[G]\오른쪽 화살표 {\mbox{End}(V),}$

단순히 $\rho {\displaystyle \stackrel{}{}}$~${\displaystyle }$( e ${\displaystyle g_{}}$)${\displaystyle }$= ${\displaystyle \rho }$ (${\displaystyle g}$) ${\displaystyle {\tilde {\rho}}}(e_{g})=\rho (g)}$을(를) 그대로 두고 선형적으로$$ 확장하는 것.따라서 집단의 표현은 정확하게 대수학의 표현에 대응하며, 두 이론은 본질적으로 동등하다.null

정규 표현

그룹 대수학은 그 자체로 대수학이다. R과 R[G] 모듈에 대한 표현들의 일치에 따르면, 그것은 그룹의 정규 표현이다.null

표현으로 쓰여, $\rho {\displaystyle }$(${\displaystyle g}$ ) ${\displaystyle \cdot }$ ${\displaystyle e_{}}$ ${\displaystyle {}_{}}$= ${\displaystyle {}_{}}$ ${\displaystyle h_{}}$ ${\$ 또는 or (displaystyle \rh)가 주는 동작으로 표현 g ↦ ρ ρ_g ρ이다.

${\displaystyle \rho (g)\cdot r=\sum _{h}\h\in G}k_{h}\cdot e_{h}=\sum _{h\in G}k_{h}e_{gh}.}$

반이심분해

벡터 공간 K[G]의 치수는 그룹의 원소 수와 동일하다.K 필드는 일반적으로 복잡한 숫자 C 또는 reals R로 간주되어 그룹 알제브라 C[G] 또는 R[G]에 대해 논한다.null

복잡한 숫자에 대한 유한집단의 그룹 대수 C[G]는 반이행 링이다.이 결과, 마슈케의 정리에서는 C[G]를 C에 입력된 매트릭스 링의 유한한 산물로 이해할 수 있게 한다.실제로 우리가 G의 복잡한 해석 불가능한 표현을 k = 1, . . . m에 대해_k V로 나열한다면, 이것들은 집단 동형성 ${\displaystyle {isms}_{}}$ k →${\displaystyle A}$ ${\displaystyle \mathrm{u}}$ t${\displaystyle }$(${\displaystyle {}_{}}$ ${\displaystyle k_{}}$) ${\displaystyle \rho _{k}$에 해당한다.$G\to \mathrm {Aut} (V_{k})}$ and hence to algebra homomorphisms ${\displaystyle {\tilde {\rho }}_{k}:\mathbb {C} [G]\to \mathrm {End} (V_{k})}$. Assembling these mappings gives an algebra isomorphism

${\daystyle {\tilde {\rho }}:\mathb {C}\to \bigoplus _{k=1}{m}\mathrm {End}(V_{k})\cong \bigoplus _{k=1}^{d_{k}}}}},}}}}}}\mathb.$

여기서 d는_k V의_k 치수다.End(V_k)에 해당하는 C[G]의 하위골격은 idempotent에 의해 생성되는 양면 이상이다.

${\displaystyle \epsilon _{k}={\frac {d_{k}}}{g\sum_{g\in G}\chi_{k}(g^{-1})\,g,}$

여기서 ${\displaystyle \chi }$ ${\displaystyle k_{}}$( g${\displaystyle }$)${\displaystyle }$= t ${\displaystyle \mathrm{r}}$ ${\displaystyle \rho }$ k${\displaystyle {}_{}}$( g${\displaystyle }$) ${\displaystyle \chi _{k}(g)=\mathrm {tr} \,\rho _{k}(g)}$는 V의_k 문자다.These form a complete system of orthogonal idempotents, so that ${\displaystyle \epsilon _{k}^{2}=\epsilon _{k}}$, ${\displaystyle \epsilon _{j}\epsilon _{k}=0}$ for j ≠ k, and ${\displaystyle 1=\epsilon _{1}+\cdots +\epsilon _{m}}$.이형성 $~{\$은 유한집단의 푸리에 변환과 밀접한 관련이 있다$$.null

보다 일반적인 필드 K의 경우, K의 특성이 G 그룹의 순서를 나누지 않을 때마다 K[G]를 반실행한다.G가 유한 아벨 그룹일 때 그룹 링 K[G]는 상통적이며, 그 구조는 통일의 뿌리로 표현하기 쉽다.null

K가 G의 순서를 나누는 특성 p의 분야일 때 그룹 링은 반실행이 아니다: 0이 아닌 제이콥슨 급진성을 가지고 있고, 이것은 모듈화 대표 이론의 해당 주제가 그것 자체의, 보다 깊은 성격을 갖게 한다.null

그룹 대수 중심

그룹 대수학의 중심은 그룹 대수학의 모든 요소와 함께 통근하는 요소들의 집합이다.

${\displaystyle \mathrm {Z}(K[G]):=\왼쪽\{z\in K[G]:\all r\in K[G],zr=rz\right\}.}$

중심은 각 결합 등급에 일정한 요소 집합인 클래스 함수 집합과 동일하다.

${\displaystyle \mathrm {Z}(K[G])=\\left\{\sum _{g\in G}a_{g}g:\forall g,h\in G,a_{g}=a_{h^{-1}\right\}.}$

K = C인 경우 G의 수정 불가능한 문자 집합이 내부 제품에 대한 Z(K[G])의 정형화된 기초를 형성한다.

${\displaystyle \left\langle \sum_{g\in G}a_{g}g,\sum_{g\in G}b_{g}g\rigle ={\frac {1}{g\in G}{g}}}\sum {g\in {a}b_{g}.}$

그룹 링을 무한 그룹에 연결

G가 헤아릴 수 없이 무한하거나 헤아릴 수 없는 경우에서 훨씬 덜 알려져 있으며, 이것은 활발한 연구의 영역이다.^[3]R이 복잡한 숫자의 분야인 경우는 아마도 가장 잘 연구된 것일 것이다.이 경우 어빙 카플란스키는 a와 b가 ab = 1을 가진 C[G]의 요소라면 ba = 1을 갖는다는 것을 증명했다.R이 긍정적 특성의 분야라면 이것이 사실인지는 알 수 없다.null

카플란스키(~1940)에 대한 오랜 추측에 따르면 G가 토션 없는 그룹이고 K가 필드라면 그룹 링 K[G]에는 비경쟁적인 제로 디비저가 없다.이 추정치는 K[G]에 대해 동일한 가설 하의 비경쟁 영감(nilpotent)이 없는 것과 같다.

실제로 K가 필드라는 조건은 일체형 영역에 삽입할 수 있는 어떤 링으로도 완화될 수 있다.null

그 추측은 완전히 개방되어 있지만, 일부 특별한 비토션 무집단의 경우는 0분위 추론을 만족시키는 것으로 나타났다.여기에는 다음이 포함된다.

• 고유한 제품 그룹(예: 주문 가능한 그룹, 특히 무료 그룹)
• 초등 어메니블 그룹(예: 사실상 아벨리아 그룹)
• 확산 그룹 - 특히 R-tree에서 자유롭게 등축적으로 작용하는 그룹과 투영 평면의 1, 2 또는 3개의 직접 합계의 기본 그룹을 제외한 표면 그룹의 기본 그룹.

G가 위상학 그룹인 경우는 국소 콤팩트 그룹의 그룹 대수학 논문에서 더 자세히 논의된다.null

범주론

조정

일반적으로 그룹 링 구조는 "단위 그룹"에 맞춰져 있다. 다음 펑커스는 연결 쌍이다.

${\displaystyle R[-]\colon \mathbf {Grp} \to R\mathbf {{\text{-}Alg}}}$

${\displaystyle(-)^{\time }\colon R\mathbf {{\text{-}Alg} \to \mathbf {Grp}}}}$

여기서 $R{\displaystyle }$[${\displaystyle }$- ${\displaystyle ]}$ ${\displaystyle$ R$[-]}$은(는${\displaystyle )}$ R을 통해 그룹 링으로 그룹을 이동하고$,{\displaystyle }$ ( -${\displaystyle {}^{}}$) ${\displaystyle {\times }^{}}$ ${\$은(는) R-알지브라를 해당 유닛 그룹으로 가져간다$$.null

R = Z일 때, 이것은 그룹의 범주와 링의 범주를 연결시켜 주고, 연결 단위는 G × {±1} = {±g}의 사소한 단위를 포함하는 그룹으로 그룹 G를 가져간다.일반적으로 그룹 링은 비경쟁 단위를 포함한다.$G$에 ${\displaystyle n^{}}$= ${\displaystyle 1}$ ${\displaystyle a^{n}=1}$과(와) 같은 요소 a와 b가 포함되어 있고$$ b가 ${\displaystyle ⟨}$ ${\displaystyle \langle a\rangle }$을(를) 정규화하지 않는 경우 다음 제곱을 사용하십시오$$.

${\displaystyle x=(a-1)b\left(1+a+a^{2}+...+a^{n-1}\오른쪽)$

0이므로${\displaystyle }$(${\displaystyle 1}$ +${\displaystyle x}$)${\displaystyle }$( ${\displaystyle 1}$-${\displaystyle \mathrm{x}}$ ) = 1 ${\displaystyle (1+x$)(1-x$)=1$ 원소 1 + x는 무한순서의 단위다.null

유니버설 속성

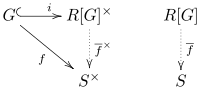
위와 같은 부속물은 집단 고리의 보편적인 속성을 표현한다.^[2][4]내버려두다R한 판 붙게 하다G단체로 하다S…이 되다R-의미.모든 그룹의 동형상 $f{\displaystyle }$: ${\displaystyle G}$→ ${\displaystyle {}^{}}$ ${\displaystyle {\times }^{}}$ ${\$$G\to$ S$^{\times$ 독특한 것이 있다.R-알게브라 동형상주의 $f{\displaystyle \stackrel{}{}\text{'}\text{'}}$ : ${\displaystyle R}$[ ${\displaystyle G}$ ${\displaystyle ]}$→ S ${\displaystyle {\overline{f}:$다음과$같은 R[$G]\$to$ S$$$}$의 $경우{\displaystyle \stackrel{,}{}}$ f${\displaystyle }$= ${\displaystyle {\f}\circle$ i$=f}$i포함 여부

${\displaystyle {\reasoned}i:G&\longrightarrow R[G]\\g&\longmapsto 1_{R}g\ended{aligned}}}$

즉, ${\$는 다음과 같은 다이어그램을 통근하는 고유한 동형상이다.

이 특성을 만족하는 다른 링은 그룹 링과 표준적으로 이형성이다.null

호프 대수

그룹 대수학 K[G]는 홉프 대수학의 자연 구조를 가지고 있다.복합복제는 $\Delta {\displaystyle \mathrm{}}$( ${\displaystyle g}$)${\displaystyle }$= ${\displaystyle g}$ ${\displaystyle \otimes }$ ${\displaystyle g}$ ${\displaystyle \Delta (g)=g\otimes g$ 선형적으로 확장되며, 대척점은 $S{\displaystyle }$( ${\displaystyle g}$)${\displaystyle }$= G${\displaystyle {}^{}}$- ${\displaystyle 1^{}}$ ${\$ 다시 선형적으로 확장된다.null

일반화

그룹 대수학은 모노이드 링까지 일반화한 다음 범주 대수까지 가는데, 그 중 또 다른 예가 발생 대수다.null

여과

이 구간은 확장이 필요하다.덧셈으로 도와줘도 된다. (2008년 12월)

만약 그룹이 길이 함수를 가지고 있다면(예를 들어, Coxeter 그룹과 같이 발전기 선택이 있고 미터법이라는 단어를 받아들인다면) 그룹 링은 필터링된 대수학으로 된다.null

참고 항목

• 로컬 컴팩트 그룹의 그룹 대수
• 모노이드 반지
• 카플란스키의 추측

표현 이론

• 그룹 표현
• 정규 표현

범주론

• 범주형 대수학
• 단위군
• 발생 대수
• 부들부들 대수

메모들

참조

• A. A. Bovdi (2001) [1994], "Group algebra", Encyclopedia of Mathematics, EMS Press
• 밀리스, 세사르 폴치노, 세갈, 수다르산 K.그룹 링에 대한 소개.알헤브라와 응용 프로그램 1권2002년 스프링거ISBN 978-1-4020-0238-0
• 찰스 W. 커티스 어빙 라이너유한군 및 연관성 알헤브라의 표현 이론, 인터사이언스(1962)
• D.S. 패스만, 그룹 링의 대수적 구조, 와일리(1977년)