시계열

Time series
시계열: 랜덤 데이터 + 추세, 최적 맞춤 라인 및 다양한 필터 적용

수학에서 시계열은 시간 순서대로 색인화(또는 나열 또는 그래프화)된 일련의 데이터 지점입니다.가장 일반적으로 시계열은 연속적으로 동일한 간격으로 지정된 시점에서 촬영되는 시퀀스입니다.따라서 이산 시간 데이터의 연속입니다.시계열의 예로는 해조 높이, 흑점 수, 다우존스 산업 평균의 일일 마감 값 등이 있습니다.

시계열은 런 차트(시간 꺽은선형 차트)를 통해 매우 자주 표시됩니다.시계열은 통계, 신호 처리, 패턴 인식, 계량경제학, 수리 금융, 일기 예보, 지진 예측, 뇌파, 제어 공학, 천문학, 통신 공학 및 주로 시간 측정을 포함하는 응용 과학 및 공학 분야에서 사용됩니다.

시계열 분석은 데이터의 의미 있는 통계 및 기타 특성을 추출하기 위해 시계열 데이터를 분석하는 방법을 포함합니다.시계열 예측은 이전에 관측된 값을 기반으로 미래 값을 예측하기 위해 모형을 사용하는 것입니다.회귀 분석은 종종 하나 이상의 다른 시계열 간의 관계를 검정하는 방식으로 사용되지만, 이러한 유형의 분석은 일반적으로 "시계열 분석"이라고 하지 않으며, 이는 특히 단일 시계열 내에서 서로 다른 시점 간의 관계를 말합니다.인터럽트 시계열 분석은 기본 변수에 영향을 미칠 수 있는 일부 개입 전후의 시계열 진화 변화를 감지하는 데 사용됩니다.

시계열 데이터는 자연스러운 시간 순서를 가집니다.따라서 시계열 분석은 관찰의 자연적 순서가 없는 단면적 연구와 구별된다(예: 개인의 데이터가 임의의 순서로 입력될 수 있는 각 교육 수준에 따라 사람들의 임금을 설명한다).시계열 분석은 관측치가 일반적으로 지리적 위치와 관련된 공간 데이터 분석과도 구별된다(예: 위치별 주택 가격 및 주택의 본질적 특성 설명).시계열에 대한 확률적 모형은 일반적으로 시간적으로 서로 가까운 관측치가 더 멀리 떨어진 관측치보다 더 밀접하게 연관되어 있다는 사실을 반영합니다.또한 시계열 모형은 종종 시간의 자연스러운 일방향 순서를 사용하여 특정 기간의 값이 미래 값에서 도출되는 것이 아니라 어떤 방식으로든 과거 값에서 도출되는 것으로 표현됩니다(시간 가역성 참조).

시계열 분석은 실제 값의 연속 데이터, 이산 숫자 데이터 또는 이산 기호 데이터(즉, 영어의[1] 문자 및 단어와 같은 문자의 시퀀스)에 적용할 수 있다.

분석 방법

시계열 분석 방법은 주파수 영역 방식과 시간 영역 방식의 두 가지 클래스로 나눌 수 있습니다.전자는 스펙트럼 분석과 웨이브릿 분석을 포함하며, 후자는 자동 상관 분석과 교차 상관 분석을 포함한다.시간영역에서는 스케일링된 상관관계를 이용해 필터와 같은 방법으로 상관관계와 해석을 할 수 있어 주파수영역에서의 조작 필요성을 경감할 수 있다.

또한 시계열 분석 기술은 파라메트릭 방법과 비파라메트릭 방법으로 나눌 수 있습니다.파라메트릭 접근법은 기초가 되는 정상 확률적 과정이 소수의 파라메타를 사용하여 설명할 수 있는 특정 구조를 가지고 있다고 가정한다(예를 들어, 자기 회귀 또는 이동 평균 모델을 사용).이러한 접근법에서 과제는 확률적 과정을 설명하는 모델의 매개변수를 추정하는 것이다.반면 비모수적 접근법은 공정이 특정 구조를 가지고 있다고 가정하지 않고 공분산 또는 공정의 스펙트럼을 명시적으로 추정한다.

시계열 분석 방법은 선형 및 비선형, 일변량 및 다변량으로 나눌 수도 있습니다.

패널 데이터

시계열은 패널 데이터의 한 유형입니다.패널 데이터는 일반 클래스, 다차원 데이터 세트인 반면 시계열 데이터 세트는 1차원 패널(단면 데이터 세트)입니다.데이터 세트는 패널 데이터와 시계열 데이터 양쪽의 특성을 나타낼 수 있다.한 가지 방법은 어떤 데이터 레코드가 다른 레코드와 다른 레코드에서 고유한지 물어보는 것입니다.정답이 시간 데이터 필드인 경우 시계열 데이터 집합 후보입니다.고유한 기록을 결정하는 데 시간 데이터 필드와 시간과 무관한 추가 식별자(예: 학생 ID, 주식 기호, 국가 코드)가 필요한 경우 패널 데이터 후보입니다.시간 식별자가 아닌 경우 데이터 세트는 단면 데이터 세트 후보가 됩니다.

분석.

시계열에 사용할 수 있는 동기 부여 및 데이터 분석에는 다양한 목적에 적합한 여러 유형이 있습니다.

동기

통계, 계량경제학, 양적 금융, 지진학, 기상학 및 지구물리학에서 시계열 분석의 주요 목표는 예측이다.신호 처리, 제어 엔지니어링 및 통신 엔지니어링에서는 신호 검출에 사용됩니다.다른 애플리케이션은 데이터 마이닝, 패턴 인식 및 머신 러닝에서 시계열 분석을 사용하여 클러스터링,[2][3] 분류,[4] [5]콘텐츠별 쿼리, 이상 검출 및 예측을 [6]수행할 수 있습니다.

탐색적 분석

미국 1953-2009년 결핵 발병률
상세 정보:탐색적 분석

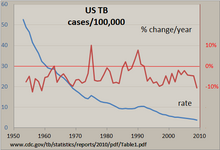
꺽은선형 차트를 사용하여 정기적으로 시계열을 검사하는 간단한 방법은 수동으로 수행하는 것입니다.스프레드시트 프로그램으로 만든 미국의 결핵 발병률에 대한 예제 차트가 오른쪽에 나와 있습니다.건수를 10만 건당 비율로 표준화해 연간 변화율을 산출했다.거의 지속적으로 감소하는 선은 대부분의 해에서 TB 발생률이 감소하고 있음을 나타내지만, 이 비율의 변화율은 +/- 10%만큼 변화했으며, 1975년과 1990년대 초반에는 '급증'이 있었다.두 수직 축을 모두 사용하면 한 그래픽에서 두 개의 시계열을 비교할 수 있습니다.

기업 데이터 분석가들을 대상으로 한 연구에서 시계열 분석의 두 가지 과제, 즉 흥미로운 패턴의 형태를 찾는 것과 이러한 [7]패턴에 대한 설명을 찾는 것이라는 두 가지 과제를 발견했습니다.시계열 데이터를 열 지도 행렬로 나타내는 시각적 도구를 사용하면 이러한 문제를 해결할 수 있습니다.

기타 기술은 다음과 같습니다.

  • 직렬 종속성을 검사하기 위한 자기 상관 분석
  • 계절성과 관련이 없는 주기적 거동을 조사하기 위한 스펙트럼 분석.예를 들어, 흑점 활동은 11년 주기로 [8][9]변화합니다.다른 일반적인 예로는 천체 현상, 날씨 패턴, 신경 활동, 상품 가격, 경제 활동이 있다.
  • 추세, 계절성, 느리고 빠른 변동, 주기적 불규칙성을 나타내는 성분으로 구분: 추세 추정 및 시계열 분해 참조

곡선 피팅

주요 기사:곡선 피팅

곡선[10][11] 적합은 일련의 데이터 [12]점에 가장 적합한 곡선 또는 수학 함수를 구성하는 과정으로,[13][14] 제약 조건이 적용될 수 있습니다.곡선 적합에는 데이터에 대한 정확한 적합이 필요한 [15][16]보간 또는 데이터에 근사적으로 적합한 "평활" 함수가 구성된 [17][18]평활이 포함될 수 있습니다.관련 주제는 회귀 [19][20]분석으로, 랜덤 오차로 관측된 데이터에 적합한 곡선에 얼마나 많은 불확실성이 존재하는지와 같은 통계적 추론의 질문에 더 초점을 맞춘다.적합 곡선은 데이터를 시각화하고,[21][22] 데이터를 사용할 [23]수 없는 함수의 값을 추론하고, 두 개 이상의 [24]변수 간의 관계를 요약하는 데 사용할 수 있습니다.외삽은 관측 [25]데이터의 범위를 벗어난 적합 곡선의 사용을 의미하며, 관측 데이터를 반영하는 만큼 곡선을 구성하는 데 사용되는 방법을 반영할 수 있기 때문에 불확실성의[26] 정도에 노출된다.

경제 시계열의 구축은 일부 날짜에 대한 일부 요소의 추정을 포함하며, 이전 날짜와 이후 날짜에 대한 값("기준점") 사이의 보간을 통해 이루어집니다.보간이란 알려진 두 수량(이력 데이터) 간에 알려지지 않은 양을 추정하거나 사용 가능한 정보("행간 읽기")[27]에서 누락된 정보에 대한 결론을 도출하는 것입니다.보간은 결측 데이터를 둘러싼 데이터를 사용할 수 있고 데이터의 추세, 계절성 및 장기 주기를 알고 있는 경우에 유용합니다.이는 대부분의 경우 모든 관련 [28]날짜에 대해 알려진 관련 시리즈를 사용하여 수행됩니다.또는 다항식 보간 또는 스플라인 보간은 구간별 다항식 함수가 서로 부드럽게 맞도록 시간 간격에 맞는 경우에 사용된다.보간과 밀접하게 관련된 다른 문제는 단순한 함수(회귀라고도 함)에 의한 복잡한 함수의 근사치입니다.회귀 분석과 보간법의 주요 차이점은 다항식 회귀 분석에서 전체 데이터 집합을 모형화하는 단일 다항식을 제공한다는 것입니다.그러나 스플라인 보간은 데이터 세트를 모델링하기 위해 많은 다항식으로 구성된 부분 연속 함수를 산출한다.

외삽은 원래 관측 범위를 벗어나 다른 변수와의 관계를 바탕으로 변수의 값을 추정하는 과정입니다.이는 알려진 관측치 사이의 추정치를 생성하는 보간법과 유사하지만, 외삽법은 불확실성이 커지고 의미 없는 결과를 생성할 위험이 높다.

함수 근사

주요 기사:함수 근사

일반적으로 함수 근사 문제는 작업 고유의 방식으로 목표 함수와 근접하게 일치하는(근사) 함수를 잘 정의된 클래스 중에서 선택하도록 요구한다.함수 근사 문제의 두 가지 주요 클래스를 구별할 수 있습니다.우선, 알려진 목표 함수의 경우, 근사 이론은 특정한 알려진 함수(예: 특수 함수)가 종종 바람직한 특성(비압축 연산, 연속성)을 갖는 특정 함수 클래스(예: 다항식 또는 유리 함수)에 의해 어떻게 근사될 수 있는지를 조사하는 수치 분석의 한 분야이다.적분값 및 한계값 등).

둘째, g라고 불리는 목표함수는 알 수 없을 수 있다.명시적 공식 대신 형식(x, g(x))의 일련의 점(시계열)만 제공된다.g의 도메인 및 코드메인의 구조에 따라 g를 근사하기 위한 몇 가지 기술을 적용할 수 있다.예를 들어 g가 실수에 대한 연산인 경우 보간, 외삽, 회귀 분석 및 곡선 적합 기술을 사용할 수 있습니다.g의 코드메인(범위 또는 타깃 세트)이 유한 집합인 경우 대신 분류 문제를 다루고 있습니다.온라인 시계열 근사치와[29] 관련된 문제는 데이터를 원패스로 요약하고 최악의 경우 오류에 대한 경계를 가진 다양한 시계열 쿼리를 지원할 수 있는 근사 표현을 구성하는 것이다.

어느 정도까지는, 다른 문제들(회귀, 분류, 적합성 근사)은 통계 학습 이론에서 통일된 처리를 받았고, 여기서 그들은 감독 학습 문제로 간주되었다.

예측 및 예측

통계학에서 예측은 통계적 추론의 일부이다.이러한 추론에 대한 한 가지 특정 접근방식은 예측 추론이라고 알려져 있지만, 예측은 통계 추론에 대한 몇 가지 접근방식 중 하나 내에서 수행될 수 있다.실제로, 통계의 한 가지 설명은 전체 모집단과 다른 관련 모집단에 대한 지식을 전달하는 수단을 제공한다는 것인데, 이는 시간에 따른 예측과 반드시 동일하지는 않다.정보가 시간(종종 특정 시점으로)에 걸쳐 전송되는 경우 프로세스를 예측이라고 합니다.

  • 미래 비특정 기간에 걸쳐 일어날 수 있는 일을 나타내는 시계열의 대체 버전을 생성하기 위해 확률적 시뮬레이션을 위해 완전히 구성된 통계 모델
  • 가장 최근의 결과(예측)에 대한 지식이 주어졌을 때, 가까운 미래에 시계열의 가능한 결과를 설명하기 위한 단순하거나 완전히 구성된 통계 모델.
  • 시계열 예측은 일반적으로 Julia, Python, R, SAS, SPSS 등의 자동화된 통계 소프트웨어 패키지와 프로그래밍 언어를 사용하여 수행됩니다.
  • 대규모 데이터에 대한 예측은 타사 패키지인 [30]Spark-TS 라이브러리를 사용하여 Apache Spark를 사용하여 수행할 수 있습니다.

분류

주요 기사:통계구분

특정 카테고리에 시계열 패턴을 할당하는 것. 예를 들어 수화의 일련의 손놀림을 바탕으로 단어를 식별합니다.

신호 추정

참고 항목: 신호 처리 및 추정 이론

이 접근방식은 푸리에 변환을 사용한 주파수 영역의 신호의 조화 분석 및 필터링과 스펙트럼 밀도 추정에 기초하고 있으며, 이는 제2차 세계대전 중 수학자 노르베르트 위너, 전기 엔지니어 루돌프 E. 칼만, 데니스 가보르 등에 의해 신호 필터링을 위해 상당히 가속화되었습니다.om 노이즈 및 특정 시점의 신호 값 예측.Kalman 필터, 추정 이론 및 디지털 신호 처리 참조

세그멘테이션

주요 기사:시계열 세그먼트화

시계열을 일련의 세그먼트로 분할합니다.대개 시계열은 각각 고유한 특성을 가진 개별 세그먼트의 시퀀스로 표현될 수 있습니다.예를 들어, 회의 통화로부터의 음성 신호는, 각자가 통화하고 있던 시간에 대응해 분할할 수 있습니다.시계열 분할의 목적은 시계열에서 세그먼트 경계점을 식별하고 각 세그먼트와 관련된 동적 특성을 특징짓는 것입니다.변화점 검출을 사용하거나 마르코프 점프 선형 시스템과 같은 보다 정교한 시스템으로 시계열을 모델링하여 이 문제에 접근할 수 있습니다.

모델

시계열 데이터에 대한 모형은 다양한 형태를 가질 수 있으며 다양한 확률적 과정을 나타낼 수 있습니다.공정 수준의 변동을 모형화할 때 실질적으로 중요한 세 가지 범주는 자기 회귀(AR) 모형, 통합(I) 모형 및 이동 평균(MA) 모형입니다.이 세 가지 클래스는 이전 데이터 [31]점에 선형으로 종속됩니다.이러한 아이디어의 조합은 자기회귀이동평균(ARMA)과 자기회귀통합이동평균(ARIMA) 모델을 생성합니다.자기 회귀 부분 적분 이동 평균(ARFIMA) 모형은 앞의 세 가지를 일반화합니다.벡터 값 데이터를 처리하기 위한 이러한 클래스의 확장자는 다변량 시계열 모델의 제목으로 사용할 수 있으며, 때로는 벡터 자동 복귀에 대한 VAR에서와 같이 "벡터"에 대한 초기 "V"를 포함시킴으로써 앞의 두문자어가 확장됩니다.이러한 모델의 추가 확장 세트는 관찰된 시계열이 일부 "강제" 시계열에 의해 구동되는 경우(관측된 시계열에 인과적 영향을 미치지 않을 수 있음)에 사용할 수 있다. 다변량 사례와의 차이는 강제 시계열이 결정론적일 수도 있고 실험자의 통제 하에 있을 수도 있다는 것이다.이러한 모델의 경우, 줄임말은 "외생"을 나타내는 최종 "X"로 확장됩니다.

부분적으로는 혼돈된 시계열을 생성할 가능성 때문에 이전 데이터 점에 대한 시계열 수준의 비선형 의존성이 관심 대상입니다.그러나, 더 중요한 것은, 비선형 자기 회귀 외생 모델처럼 비선형 모델에서 파생된 예측보다 경험적 조사가 비선형 모델에서 파생된 예측을 사용하는 이점을 나타낼 수 있다는 것이다.비선형 시계열 해석에 대한 추가 참고 자료: (Kantz 및 Schreiber)[32] 및 (Abarbanel)[33]

다른 유형의 비선형 시계열 모형 중에는 시간에 따른 분산의 변화(헤테로스크탄성)를 나타내는 모형도 있습니다.이러한 모델은 자기회귀 조건부 이질성(ARCH)을 나타내며 컬렉션은 다양한 표현(GARCH, TARCH, EGARCH, FIGARCH, CGARCH 등)으로 구성됩니다.여기서 변동성의 변화는 관측된 영상 시리즈의 최근 과거 값과 관련이 있거나 예측됩니다.이것은 이중 확률적 모델에서와 같이 별도의 시간 변동 프로세스에 의해 변동성이 몰리는 것으로 모델링될 수 있는 국소 변동성의 다른 가능한 표현과는 대조적이다.

모델 프리 분석에 대한 최근 연구에서 웨이브릿 변환 기반 방법(예: 국소 고정 웨이브릿 및 웨이브릿 분해 신경망)이 인기를 끌었다.멀티스케일(종종 멀티레졸루션이라고도 함) 기술은 주어진 시계열을 분해하여 시간 의존성을 여러 척도로 나타내려고 시도합니다.휘발성 진화를 모델링하려면 마르코프 스위칭 멀티프랙탈(MSMF) 기술을 참조하십시오.

숨겨진 마르코프 모델(HMM)은 모델링되는 시스템이 관찰되지 않은(숨겨진) 상태를 가진 마르코프 과정으로 가정되는 통계적 마르코프 모델이다.HMM은 가장 단순한 동적 베이지안 네트워크로 간주할 수 있습니다.HMM 모델은 음성 인식에 널리 사용되며, 일련의 구어를 텍스트로 변환합니다.

표기법

시계열 분석에는 여러 가지 표기가 사용됩니다.자연수로 색인화된 시계열 X를 지정하는 공통 표기법이 작성된다.

X = (X1, X2, ...)

또 다른 일반적인 표기법은

Y = (Yt: t t T),

여기서 T는 [y[index set]입니다.

조건들

이론의 대부분이 구축되는 조건에는 다음 두 가지가 있습니다.

에르고디시티는 정상성을 의미하지만, 그 반대가 반드시 그런 것은 아닙니다.정상성은 보통 엄격한 정상성과 광의 또는 2차 정상성으로 분류됩니다.후자의 경우 모델은 부분적으로만 지정된 것으로 간주될 수 있지만 모델과 애플리케이션 모두 이러한 조건 각각에 따라 개발될 수 있다.

또한 시계열 분석은 시계열이 계절적으로 정지 상태이거나 비정상인 경우에 적용할 수 있습니다.주파수 성분의 진폭이 시간에 따라 변화하는 상황은 시계열 또는 [34]신호의 시간-주파수 표현을 사용하는 시간-주파수 분석에서 다룰 수 있습니다.

도구들

시계열 데이터를 조사하기 위한 도구는 다음과 같습니다.

방안

시계열 분류 또는 회귀 [37]분석에 사용할 수 있는 시계열 메트릭 또는 기능:

시각화

시계열은 두 가지 범주의 차트를 사용하여 시각화할 수 있습니다.겹치는 차트와 구분된 차트가 있습니다.겹치는 차트는 동일한 레이아웃에 모든 시계열을 표시하는 반면 구분된 차트는 서로 다른 레이아웃에 표시합니다(단, 비교를 [41]위해 정렬됨).

겹치는 차트

구분된 차트

  • 수평선 그래프
  • 꺽은선형 차트(작은 배수)
  • 실루엣 그래프
  • 원형 실루엣 그래프

「 」를 참조해 주세요.

레퍼런스

  1. ^ Lin, Jessica; Keogh, Eamonn; Lonardi, Stefano; Chiu, Bill (2003). "A symbolic representation of time series, with implications for streaming algorithms". Proceedings of the 8th ACM SIGMOD workshop on Research issues in data mining and knowledge discovery. New York: ACM Press. pp. 2–11. CiteSeerX 10.1.1.14.5597. doi:10.1145/882082.882086. S2CID 6084733.
  2. ^ Liao, T. Warren (2005). "Clustering of time series data - a survey". Pattern Recognition. Elsevier. 38 (11): 1857–1874. Bibcode:2005PatRe..38.1857W. doi:10.1016/j.patcog.2005.01.025. – Science Direct 경유 (서브스크립션 필요)
  3. ^ Aghabozorgi, Saeed; Shirkhorshidi, Ali S.; Wah, Teh Y. (2015). "Time-series clustering – A decade review". Information Systems. Elsevier. 53: 16–38. doi:10.1016/j.is.2015.04.007. – Science Direct 경유 (서브스크립션 필요)
  4. ^ Keogh, Eamonn J. (2003). "On the need for time series data mining benchmarks". Data Mining and Knowledge Discovery. Kluwer. 7: 349–371. doi:10.1145/775047.775062. ISBN 158113567X. S2CID 41617550. – ACM 디지털 라이브러리 경유(서브스크립션 필요)
  5. ^ Agrawal, Rakesh, Faloutsos,인 크리스토. 스와미 아룬(10월 1993년)."데이터 조직과 알고리즘의 기초".제4회 국제 회의의 자료 기구와 알고리즘의 기초에 논문집.국제 회의 자료 기구와 알고리즘의 기초에.강의 노트 컴퓨터 과학으로.Vol730.를 대신하여 서명함. 69–84. doi:10.1007/3-540-57301-1_5.아이 에스비엔 978-3-540-57301-2.SpringerLink(가입 필요한)을 통해 –
  6. ^ Chen, Cathy W. S.; Chiu, L. M. (September 2021). "Ordinal Time Series Forecasting of the Air Quality Index". Entropy. 23 (9): 1167. Bibcode:2021Entrp..23.1167C. doi:10.3390/e23091167. PMC 8469594. PMID 34573792.
  7. ^ Sarkar, Advait; Spott, Martin; Blackwell, Alan F.; Jamnik, Mateja (2016). "Visual discovery and model-driven explanation of time series patterns". 2016 IEEE Symposium on Visual Languages and Human-Centric Computing (VL/HCC). IEEE: 78–86. doi:10.1109/vlhcc.2016.7739668. ISBN 978-1-5090-0252-8. S2CID 9787931.
  8. ^ Bloomfield, P. (1976). Fourier analysis of time series: An introduction. New York: Wiley. ISBN 978-0471082569.
  9. ^ Shumway, R. H. (1988). Applied statistical time series analysis. Englewood Cliffs, NJ: Prentice Hall. ISBN 978-0130415004.
  10. ^ Sandra Lach Arlinghouse, PHB 커브 피팅 실무 핸드북CRC 프레스, 1994.
  11. ^ 윌리엄 M. 콜브프로그래밍 가능한 계산기를 위한 곡선 피팅.Syntec, Incorporated, 1984.
  12. ^ S.S. 할리, K.V. 라오 1992년고급 인구 분석 기법.ISBN 0306439972 165페이지(cf. ... 기능은 관찰된 데이터에 적합한 경우 충족됩니다.)
  13. ^ 신호와 노이즈: 왜 이렇게 많은 예측이 실패하는가? 하지만 일부는 그렇지 않다.By Nate Silver
  14. ^ 데이터 마이닝을 위한 데이터 준비:문자, 도리안 파일이 썼어
  15. ^ MATLAB®를 사용한 엔지니어링의 수치적 방법.얀 키살라스의 작품.페이지 24.
  16. ^ Python 3을 사용한 엔지니어링의 수치 메서드.얀 키살라스의 작품.페이지 21.
  17. ^ 곡선 피팅의 수치적 방법.P. G. 게스트, 필립 조지 게스트349페이지.
  18. ^ 다음 항목도 참조하십시오.연체자
  19. ^ 선형 및 비선형 회귀 분석을 사용하여 생물학적 데이터에 모형 적합Harvey Motulsky 지음 Arthur Christopulos.
  20. ^ Rudolf J. Freund, William J. Wilson, Ping Sa의 회귀 분석.269쪽.
  21. ^ 비주얼 정보학편집자: 할리마 바디오제 자만, 피터 로빈슨, 마리아 페트로, 패트릭 올리비에, 하이코 슈뢰더.689쪽.
  22. ^ 비선형 엔지니어링 모델을 위한 수치적 방법.존 R.하우저227쪽.
  23. ^ 실험 물리학 방법:분광학, 제13권, 제1부클레어 마틴의 작품.150페이지.
  24. ^ 연구설계 백과사전 제1권.Neil J. Salkind 편집자266쪽.
  25. ^ 커뮤니티 분석 및 계획 기술.리처드 E. 클로스터맨의 작품.1 페이지.
  26. ^ 환경투자의 평가에 있어서의 리스크와 불확실성의 개요.다이앤 출판사69페이지
  27. ^ 해밍, 리처드과학자와 엔지니어를 위한 수치적 방법.Courier Corporation, 2012.
  28. ^ 프리드먼, 밀턴"관련된 급수에 의한 시계열의 보간." 미국 통계협회 저널 57.300(1962): 729~757.
  29. ^ 간디, 소라브, 루카 포시니, 수바쉬 수리."공간 효율적인 시계열 데이터의 온라인 근사: 스트림, 기억상실, 고장." 데이터 엔지니어링(ICDE), 2010년 IEEE 제26회 국제회의 개최.IEEE, 2010.
  30. ^ Sandy Ryza (2020-03-18). "Time Series Analysis with Spark" (slides of a talk at Spark Summit East 2016). Databricks. Retrieved 2021-01-12.
  31. ^ Gershenfeld, N. (1999). The Nature of Mathematical Modeling. New York: Cambridge University Press. pp. 205–208. ISBN 978-0521570954.
  32. ^ Kantz, Holger; Thomas, Schreiber (2004). Nonlinear Time Series Analysis. London: Cambridge University Press. ISBN 978-0521529020.
  33. ^ Abarbanel, Henry (Nov 25, 1997). Analysis of Observed Chaotic Data. New York: Springer. ISBN 978-0387983721.
  34. ^ Boashash, B. (ed.) , (2003) 시간-주파수 신호 분석 및 처리: A Comprehensive Reference, Elsevier Science, Oxford, 2003 ISBN 0-08-044335-4
  35. ^ Nikolić, D.; Muresan, R. C.; Feng, W.; Singer, W. (2012). "Scaled correlation analysis: a better way to compute a cross-correlogram". European Journal of Neuroscience. 35 (5): 742–762. doi:10.1111/j.1460-9568.2011.07987.x. PMID 22324876. S2CID 4694570.
  36. ^ a b Sakoe, Hiroaki; Chiba, Seibi (1978). "Dynamic programming algorithm optimization for spoken word recognition". IEEE Transactions on Acoustics, Speech, and Signal Processing. Vol. 26. pp. 43–49. doi:10.1109/TASSP.1978.1163055. S2CID 17900407. {{cite book}}:누락 또는 비어 있음 title=(도움말)
  37. ^ Mormann, Florian; Andrzejak, Ralph G.; Elger, Christian E.; Lehnertz, Klaus (2007). "Seizure prediction: the long and winding road". Brain. 130 (2): 314–333. doi:10.1093/brain/awl241. PMID 17008335.
  38. ^ Land, Bruce; Elias, Damian. "Measuring the 'Complexity' of a time series".
  39. ^ [1] Chevyrev, I., Kormilitzin, A. (2016) "기계학습에서의 시그니처 방법에 관한 입문서, arXiv:1603.03788v1"
  40. ^ Ropella, G. E. P.; Nag, D. A.; Hunt, C. A. (2003). "Similarity measures for automated comparison of in silico and in vitro experimental results". Engineering in Medicine and Biology Society. 3: 2933–2936. doi:10.1109/IEMBS.2003.1280532. ISBN 978-0-7803-7789-9. S2CID 17798157.
  41. ^ Tominski, Christian; Aigner, Wolfgang. "The TimeViz Browser:A Visual Survey of Visualization Techniques for Time-Oriented Data". Retrieved 1 June 2014.

추가 정보

외부 링크

Wikimedia Commons에는 시계열과 관련된 미디어가 있습니다.