꺽은선형 차트
Line chart |
꺽은선형 차트, 꺽은선형 그래프 또는 원곡선[1] 차트는 정보를 [2]직선 세그먼트로 연결된 '마커'라고 하는 일련의 데이터 점으로 표시하는 차트의 한 유형입니다.이것은 많은 분야에서 공통적인 기본적인 유형의 차트입니다.측정점이 (일반적으로 x축 값으로) 정렬되고 직선 세그먼트와 결합된다는 점을 제외하면 산점도와 유사합니다.꺽은선형 차트는 시간 간격에 따른 데이터 추세(시계열)를 시각화하는 데 자주 사용되며, 따라서 선은 종종 시계열로 그려집니다.이 경우 런 차트라고 합니다.
역사
가장 먼저 알려진 꺽은선형 차트 중 일부는 일반적으로 프랜시스 하우크스비, 니콜라우스 사무엘 크루키우스, 요한 하인리히 램버트, 윌리엄 [3]플레이페어에 의해 인정된다.
예
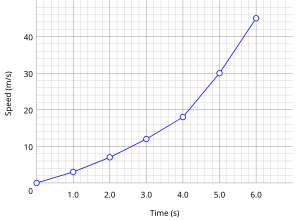
실험 과학에서, 실험에서 수집된 데이터는 종종 그래프로 시각화됩니다.예를 들어 특정 시점의 개체 속도에 대한 데이터를 수집하면 다음과 같은 데이터 테이블에서 데이터를 시각화할 수 있습니다.
| 경과 시간 | 속도(ms−1) |
|---|---|
| 0 | 0 |
| 1 | 3 |
| 2 | 7 |
| 3 | 12 |
| 4 | 18 |
| 5 | 30 |
| 6 | 45.6 |
이러한 데이터 표 표현은 정확한 값을 표시하는 좋은 방법이지만 값 내의 패턴을 발견하고 이해하는 데 방해가 될 수 있습니다.또한 표 표시는 종종 데이터의 객관적이고 중립적인 수집 또는 저장으로 잘못 간주되지만(그런 의미에서 데이터 자체로도 잘못 간주될 수 있음), 실제로는 데이터의 다양한 가능한 시각화 중 하나에 불과합니다.
표의 데이터로 설명된 프로세스를 이해하려면 속도 대 시간의 그래프 또는 꺽은선형 차트를 작성해야 합니다.이러한 시각화는 오른쪽 그림에 나타납니다.이 시각화를 통해 뷰어는 전체 프로세스를 한눈에 빠르게 이해할 수 있습니다.
그러나 이 시각화는 속도 v의존 변수)를 tt의 함수로 표현하는 수학적 v v를 나타내는 것으로 표현될 경우 오해될 수 있습니다.이는 속도가 시간에만 의존하는 변수임을 보여주는 것으로 오해할 수 있다.그러나 이것은 진공에서 작용하는 일정한 힘에 의해서만 물체가 작용하는 경우에만 해당된다.
나타내는 것으로 표현될 경우 오해될 수 있습니다.이는 속도가 시간에만 의존하는 변수임을 보여주는 것으로 오해할 수 있다.그러나 이것은 진공에서 작용하는 일정한 힘에 의해서만 물체가 작용하는 경우에만 해당된다. 그러나 A라고 불리는 어떤 것이 인과관계를 나타내는 것으로서 B라고 불리는 것의 함수라는 수학적인 개념에 대한 그러한 오해는 일반인들 사이에서 흔하며 (그리고 "의존 변수"라는 용어로 강화된다) 꺽은선형 차트의 표현에 의존하지 않는다.
최적
차트에는 종종 산란 데이터의 최적 적합 추세를 나타내는 중첩된 수학 함수가 포함됩니다.이 레이어를 최적 레이어라고 하며, 이 레이어를 포함하는 그래프를 종종 선 그래프라고 합니다.
인접 데이터 점을 연결하는 선분 집합으로 구성된 "최적합" 레이어를 구성하는 것은 간단하지만, 이러한 "최적합"은 다음과 같은 이유로 기본 산란 데이터의 추세를 이상적으로 표현하지 않습니다.
- 최적 적합의 기울기에서의 불연속성이 측정값의 위치와 정확히 일치할 가능성은 매우 낮다.
- 데이터의 실험 오차가 무시할 수 있을 것 같지는 않지만 곡선은 각 데이터 점을 정확히 통과합니다.
두 경우 모두 최적 레이어가 데이터의 추세를 나타낼 수 있습니다.또, 구배나 곡선 아래의 면적등의 측정을 시각적으로 실시할 수 있기 때문에, 데이터 테이블로부터 보다 많은 결론이나 결과를 얻을 수 있다.
진정한 최적 레이어는 데이터 값의 오차에 적절한 가중치를 부여하는 적절한 오차 최소화 방법을 사용하여 매개변수가 결정되는 연속적인 수학 함수를 나타내야 한다.이러한 곡선 맞춤 기능은 그래프 작성 소프트웨어나 스프레드시트에서 자주 볼 수 있습니다.최적 곡선은 단순한 선형 방정식에서 보다 복잡한 2차,[4] 다항식, 지수 및 주기 곡선에 이르기까지 다양할 수 있습니다.
