반복도

기술통계학 및 카오스 이론에서 반복도(RP)는 각 순간 i에 대해 위상공간 궤적이 시간 j와 거의 동일한 영역에 도달하는 시간을 나타내는 그림이다.바꿔 말하면, 그것은 의 그래프이다.

${\displaystyle\vec {x}(i)\약\vec {x}(j),}$

수평 축에 i$(\displaystyle$ i$)$를 $표시$하고 수직 축에$$j(\$displaystyle$ j$)$를 표시합니다. $여기$서 x $→$ {\$displaystyle {x}}$은 위상 공간 궤적입니다.

배경

자연 과정은 주기성(계절 주기 또는 밀란코비치 주기)과 같은 뚜렷한 반복 행동을 가질 수 있지만 불규칙한 주기성(엘니뇨 남부 진동)도 가질 수 있다.또한 상태가 일정 시간 동안 분산된 후 다시 임의로 근접한다는 의미에서의 상태의 반복은 결정론적 동적 시스템의 기본 특성이며 비선형 또는 혼돈 시스템에 대해 전형적이다(cf).푸앵카레 반복 정리).자연 상태의 재발은 오랫동안 알려져 왔고 초기 연구에서도 논의되어 왔다(예: 앙리 푸앵카레 1890).

상세설명

에크만 외 연구진(1987)은 위상 공간을 통해 궤도의 주기적 특성을 시각화하는 방법을 제공하는 반복 그림을 도입했다.고차원 위상 공간은 2차원 또는 3차원 하위 공간에 투영해야만 시각화할 수 있기 때문에 위상 공간은 사진을 찍을 수 있을 만큼 충분히 낮은 차원(2 또는 3)을 가지지 않는 경우가 많습니다.그러나 반복 플롯을 만들면 2차원 표현을 통해 m차원 위상 공간 궤적의 특정 측면을 조사할 수 있다.

반복은 궤적이 이전에 방문한 위치로 되돌아가는 시간입니다.반복 플롯은 (i${\displaystyle ,}$ $)$ $x{\displaystyle \stackrel{}{}}$ ${\displaystyle \to }$ ${\displaystyle x\stackrel{}{}}$ ${\displaystyle \to }$ ( ${\displaystyle j}$ )${\displaystyle }$\$$displaystyle ${$$x}$$$= ( j ) \$displaystyle$ {x} = ( j ) \ displaystyle {$x}$ ( j ) \ displaystyle \ displaystyle \ vec {x}($i)$=$displayvec {$x}(j} ( j$)$ \${\displaystyle }$displayvec {x} ( j ) \ displayvec {x} ( j ) \ displayc {x} ( j ) \ displaysty} ( j )의$$ 집합이$displaystyle${$x$$}(i)}$은$(는)$ $시간$에 궤적의 위치를 나타내며 궤적이 이전에 있었던 지점에 충분히 근접할 때마다($예$를 들어$$\$displaystyle \varepsilon$ $\}$ 내) 반복으로 계산됩니다.

연산적으로 플롯은 다음과 같이 그려집니다.

(a) 시간 $간격$에 따라 연속되는2개의 시간 스텝이 분리되어 있는 경우, w$→$ ${\displaystyle =}$ ${\displaystyle ⟨}$ ${\displaystyle {}_{}}$ 1,$2,$. , $t$⟩ t$⟩$ \ $displaystyle t_{1$}, $t_{T}\right\rangle }$의 $특정{\displaystyle \stackrel{}{}}$ 시간 $윈도우$가 선택됩니다$.$여기서 ${\displaystyle {t\_style}_{}}$은 $다음과 같습니다$$시스템$의 t$)}$이(가) 각 시간 단계마다 기록되므로 궤적 $X{\displaystyle \mathbf{}}$ ${\displaystyle =\delta \stackrel{}{}}$ x ${\displaystyle \to }$ ( ${\displaystyle {t\mathrm{}}_{}}$1${\displaystyle }$) , x${\displaystyle \stackrel{}{\to }}$ ( ${\displaystyle t_{}{}_{}{2\mathrm{}}_{}}$)${\displaystyle }$,${\displaystyle }$. , ${\displaystyle x\stackrel{}{}}$ ${\displaystyle \to }$ (${\displaystyle {}_{}}$ ) ${\$ { \ $displaystyle$\$mathbf { X$ } = \$left$\$vec${ $x$} ( $t$_ { t _ { t$$} ) , { c$_$t } , { t } 。$T)\right\rangle$ 입니다.

(b) x축과 y축이 모두 w$→{$을 $보고$하는 2D 플롯이 생성되어 각각 변이 $측정$되는 작은 정사각형 T$T(\displaystyle$$T$$\times$T$)$ $격자$를 $형성$한다$.$

(c) 데이터$X{\displaystyle \mathbf{}}$(\$displaystyle \mathbf {X})$는 x$→{$의 $반복$/비차이를 기록하는 2진수 요소로 이루어진 $행렬{\displaystyle \mathbf{}}$R(\$displaystyle$ \$mathbf${$R})$을 2진수 함수를 통해 계산하기 위해 사용된다.

${\displaystyle R(i,j)=begin{cases}1&{\text{if}}\quad\{vec {x}(j)\leq \varepsilon \0&{\text{cases},\end{cases}}}}$

$여기$서 i${\displaystyle ,}$ ${\displaystyle j}$ ${\displaystyle \{}$ { ${\displaystyle {}_{}{1\mathrm{}}_{}}$, ${\displaystyle {}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$,${\displaystyle }$.${\displaystyle }$. , ${\displaystyle T_{}}$ $}$ { $displaystyle$i ,$j$ \ $in$\ { $t$_ {1$}$ , $t$_ {2} , $... t$_ { $T$} $。$

(d) 그러면 반복도는${\displaystyle }$R${\displaystyle (i,j}$$)$ $1$이면 R$($$i$, $j)$이고, R${\displaystyle (}$i, j$)$ ${\displaystyle =}$ 0$($i, j$)$이면 R(i, j)의 검은색 작은 정사각형을 ${\displaystyle \mathrm{사용}}$하여 $R{\displaystyle \mathbf{}}$$($${\displaystyle i}$$,$ j${\displaystyle )}$을 ${\displaystyle \mathrm{시각화}}$합니다$.$

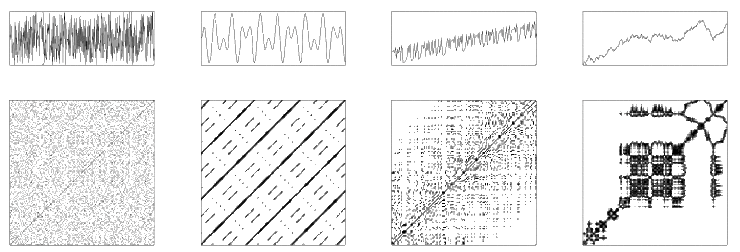
반복도의 시각적 외관은 시스템의 역동성에 대한 힌트를 제공합니다.위상 공간 궤적의 특성 거동에 의해 발생하는 반복 플롯에는 단일 점, 대각선 및 수직/수평선(또는 확장된 군집에 결합된 후자의 혼합)과 같은 전형적인 소규모 구조가 포함된다.텍스처라고도 불리는 대규모 구조는 균질, 주기적, 드리프트 또는 교란으로 시각적으로 특징지을 수 있습니다.예를 들어, 플롯은 궤적이 주기$$T(\$displaystyle$ T$)$로 엄격하게 주기적인지 여부를 나타낼 수 있으며, 이러한 시간 쌍은 모두 T$(\displaystyle$ T$)$의 $배수{\displaystyle }$(배수)로 구분되어 대각선으로 표시됩니다.

RP의 소규모 구조는 재발 정량 분석에 사용된다(Zbilut & Weber 1992; Marwan et al. 2002).이 정량화를 통해 RP를 정량적으로 설명하고 시스템의 천이 또는 비선형 파라미터를 연구할 수 있습니다.매립 파라미터의 선택에 따라 달라지는 반복정량분석의 휴리스틱 접근법과는 대조적으로 매립에 의존하지 않는 상관차원, K2 엔트로피 또는 상호정보로서의 동적 불변량도 반복플롯에서 도출할 수 있다.이러한 동적 불변량의 기초는 반복률과 대각선 길이의 분포입니다.

근접 반환 그림은 반복도와 유사합니다.차이점은 (절대 시간이 아닌$) y축$에 대해 반복 간의 상대 시간이 사용된다는 것입니다.

반복 그림의 주요 장점은 다른 방법이 실패하는 짧은 데이터와 비정상 데이터에도 유용한 정보를 제공한다는 것이다.

내선번호

반복도의 다변량 확장은 교차 반복도와 접합 반복도로 개발되었다.

교차 반복 그림은 동일한 위상 공간에 있는 두 개의 다른 시스템의 위상 공간 궤적을 고려한다(Marwan & Kurth 2002).

$\displaystyle \mathbf {CR} (i,j)=\Theta(\varepsilon -\\vec {x}(i)-{\vec {y}(j)\), \vec {x}(i), \vec {y}(i)\in \mathbb {R}^{m},\vec i=1,\vec {x}, j=1,\vec}, {y}.}$

두 시스템의 치수는 동일해야 하지만 고려된 상태의 수(즉, 데이터 길이)는 다를 수 있다.교차 반복도는 두 시스템의 유사한 상태 발생을 비교합니다.두 개의 다른 시스템 간 동적 진화의 유사성을 분석하거나, 두 시스템에서 유사한 일치 패턴을 찾거나, 시간 척도가 다른 두 개의 유사한 시스템의 시간 관계를 연구하기 위해 사용할 수 있다(Marwan & Kurth 2005).

공동 반복 플롯은 고려된 하위 시스템의 반복 플롯의 아다마르 산물이다(로마노 등).2004년), 예: 두 $시스템$ x ${\displaystyle \stackrel{}{\to }}$ ${\displaystyle${$x$} 및$$y → {\$displaystyle {\vec$ {y$$$}}$에 대한 공동 반복 플롯은 다음과 같습니다.

$\displaystyle \mathbf {JR}(i,j)=\Theta(\varepsilon _{x}-\{vec {x}(i)}-{\vec {x}(j)\)\cdot \Theta(\varepsilon _{y}-\{vec {y}(i)}\,\vec {x}(i)\mathbbbbb)\c {x}\c}\mathbbbbbbbb}\c {x}\c}\c}\c}\c}\Thin {ta}.}$

교차 반복도와 달리 관절 반복도는 두 개 이상의 시스템에서 동시에 발생하는 반복을 비교합니다.또한 고려된 위상 공간의 치수는 다를 수 있지만 고려된 상태의 수는 모든 하위 시스템에 대해 동일해야 한다.위상 동기화를 검출하기 위해 접합 반복도를 사용할 수 있습니다.

예

「 」를 참조해 주세요.

• 푸앵카레 플롯
• 결정론적 및 확률적 동적 시스템 양쪽의 반복 특성을 요약하는 정보이론적인 방법인 반복 주기 밀도 엔트로피.
• 반복 양자화 분석, 반복 플롯을 정량화하기 위한 휴리스틱 접근법.
• 자기유사성행렬
• 도트 그림(생물 정보학)

이 문서에는 일반적인 참조 목록이 포함되어 있지만 대응하는 충분한 인라인 인용이 없습니다. 좀 더 정확한 인용문을 도입하여 이 기사의 개선에 협조해 주십시오.(2009년 12월) (이 템플릿메시지의 삭제 방법 및 삭제 타이밍에 대해 알아보기)

레퍼런스

• J. P. Eckmann, S. O. Kamphorst, D. Ruelle (1987). "Recurrence Plots of Dynamical Systems". Europhysics Letters. 5 (9): 973–977. Bibcode:1987EL......4..973E. doi:10.1209/0295-5075/4/9/004.{{cite journal}}: CS1 maint: 여러 이름: 작성자 목록(링크)
• N. Marwan; M. C. Romano; M. Thiel; J. Kurths (2007). "Recurrence Plots for the Analysis of Complex Systems". Physics Reports. 438 (5–6): 237. Bibcode:2007PhR...438..237M. doi:10.1016/j.physrep.2006.11.001.
• N. Marwan (2008). "A historical review of recurrence plots". European Physical Journal ST. 164 (1): 3–12. arXiv:1709.09971. Bibcode:2008EPJST.164....3M. doi:10.1140/epjst/e2008-00829-1.

외부 링크

• 반복
• Sci 토픽