계절성

이 글에는 여러 가지 문제가 있다. 이 문제를 개선하거나 대화 페이지에서 토의하십시오. (이러한 템플릿 메시지를 제거하는 방법 및 시기 알아보기) 이 글은 일반적인 참고문헌 목록을 포함하고 있지만, 그에 상응하는 인라인 인용구가 충분하지 않기 때문에 대체로 검증되지 않은 상태로 남아 있다. 좀 더 정밀한 인용구를 도입하여 이 기사를 개선할 수 있도록 도와주십시오. (2008년 11월) (이 템플릿 메시지를 제거하는 방법과 시기 알아보기) 이 글은 검증을 위해 인용구가 추가로 필요하다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 기사를 개선할 수 있도록 도와주십시오. 공급되지 않은 재료는 도전하여 제거할 수 있다. 출처 찾기: "계절성" – 뉴스 · 신문 · 책 · 학자 · JSTOR (2010년 11월) (이 템플릿 메시지를 제거하는 방법과 시기 학습) (이 템플릿 메시지를 제거하는 방법 및 시기 알아보기)

시계열 데이터에서 계절성은 주간, 월별 또는 분기별과 같이 1년 미만의 특정 주기적 간격으로 발생하는 변동의 존재다. 계절성은 날씨, 휴가, 공휴일과^[1] 같은 다양한 요인에 의해 야기될 수 있으며, 시계열 수준에서 주기적이고 반복적이며^[2] 일반적으로 규칙적이고 예측 가능한 패턴으로 구성된다.

시계열의 계절적 변동은 주기적인 패턴과 대조될 수 있다. 후자는 일정 기간이 아닌 데이터가 상승하거나 하락할 때 발생한다. 이러한 비 계절적 변동은 대개 경제상황에 기인하며 종종 "경기순환"과 관련이 있다. 그들의 기간은 보통 1년을 초과하며, 그 변동은 보통 2년 이상이다.^[3]

아이스크림 판매업체와 같이 계절적 변동에 직면한 조직들은 종종 일반적인 계절적 변동에 대한 그들의 성과를 아는 데 관심이 있다. 노동시장의 계절적 변화는 학교를 마친 후 노동력에 기여하는 것을 목표로 하기 때문에 고용시장에 학교를 떠나는 사람들의 유입에 기인할 수 있다. 이러한 정기적인 변화는 경제의 근본적인 상태로 인해 발생하는 변화보다 고용 데이터를 연구하는 사람들에게 덜 흥미롭다; 그들의 초점은 정기적인 계절적 변동의 영향에도 불구하고 노동력의 실업이 어떻게 변화했는지에 있다.^[3]

조직이 미래에 대한 계획을 수립할 수 있도록 지원하기 위해 시장 내에서 계절적 변화를 식별하고 측정할 필요가 있다. 이는 특정 기간에 걸쳐 제품 또는 서비스에 대한 수요가 변동함에 따라 노동 요구사항과 재고자산의 일시적인 증가 또는 감소에 대비할 수 있다. 이를 위해서는 미리 정리할 수 있는 훈련, 주기적인 정비 등이 필요할 수 있다. 이러한 고려사항과는 별도로, 조직은 그들이 경험한 변동이 일반적인 계절적 변동이 설명하는 것 이상으로 예상 금액보다 많거나 적었는지 알 필요가 있다.

동기

계절 변동을 연구하는 데는 다음과 같은 몇 가지 주요 이유가 있다.

• 계절적 효과에 대한 설명은 이 성분이 특정 시리즈에 미치는 영향을 더 잘 이해할 수 있게 해준다.
• 계절적 패턴을 확립한 후 시계열에서 제거하는 방법을 구현해 주기적, 불규칙적 변동 등 다른 성분의 효과를 연구할 수 있다. 이러한 계절적 효과의 제거를 데이터의 계절적 변화 또는 계절적 조정이라고 한다.
• 계절적 변동의 과거 패턴을 사용하여 기후 표준과 같은 미래 추세를 예측하고 예측하는 데 기여한다.

탐지

계절성을 탐지하는 데 다음과 같은 그래픽 기법을 사용할 수 있다.

• 런 시퀀스 플롯은 종종 계절성을 보여준다.
  

  미국 전기 사용량의 계절성 그림
• 계절 플롯은 각 계절의 데이터가 겹치는^[4] 것을 보여준다.
• 계절 하위 시리즈 플롯은 계절성을 나타내기 위한 특수 기술이다.
• 계절성을 탐지하기 위해 계절 하위 시계열도의 대안으로 다중 상자 그림을 사용할 수 있음
• 자기 상관 그림(ACF)과 스펙트럼 그림은 계절성을 식별하는 데 도움이 될 수 있다.

정기적인 데이터 시리즈에서 계절성을 포함한 주기성을 찾는 정말 좋은 방법은 먼저 전반적인 추세를 제거한 다음 시간 주기성을 검사하는 것이다.^[5]

런 시퀀스 플롯은 모든 시계열을 분석하는 데 권장되는 첫 번째 단계다. 계절성은 때때로 이 그림으로 나타낼 수 있지만 계절성은 계절 하위 시리즈 그림이나 상자 그림으로 더 명확하게 나타난다. 계절 하위 시리즈 그림은 계절 차이(그룹 패턴 간)와 그룹 내 패턴 모두를 잘 보여준다. 상자 그림은 (그룹 패턴 간의) 계절적 차이를 꽤 잘 보여주지만, 그룹 패턴 내에서 보여주지는 않는다. 그러나 큰 데이터 세트의 경우 일반적으로 상자 그림은 계절 하위 시리즈 그림보다 읽기 쉽다.

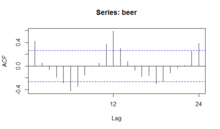
계절 그림, 계절 하위 시리즈 그림 및 상자 그림은 모두 계절 기간을 안다고 가정한다. 대부분의 경우, 분석가는 사실, 이것을 알 것이다. 예를 들어 월별 데이터의 경우 1년에 12개월이 있기 때문에 기간은 12이다. 그러나 기간을 알 수 없는 경우 자기 상관 그림이 도움이 될 수 있다. 유의한 계절성이 있는 경우 자기 상관 그림은 해당 기간과 동일한 시차에서 스파이크를 표시해야 한다. 예를 들어, 월별 데이터의 경우 계절성 효과가 있을 경우 12, 24, 36 등의 지연에서 상당한 정점을 보일 것으로 예상한다(강도는 우리가 더 멀리 나갈수록 감소할 수 있지만).

자기 상관 그림(ACF)은 Y 값과 지연된 Y 값 사이의 차이(잔차 금액)를 계산하기 때문에 계절성을 식별하는 데 사용할 수 있다. 그 결과는 두 값이 서로 가깝고(계절성이 없음) 차이가 큰 다른 점을 제공한다. 이 점들은 데이터의 계절성 수준을 나타낸다.

반주기 순환 변화는 스펙트럼 밀도 추정에 의해 다루어질 수 있다.

계산

계절 변동은 계절 지수라고 불리는 지수의 관점에서 측정된다. 계절 변동이 없을 경우 실제 관측치를 비교하는 데 사용할 수 있는 평균이다. 인덱스 값은 1년 이내에 시계열의 각 기간에 첨부된다. 이는 월별 데이터를 고려할 경우 매월 1개씩 12개의 계절 지수가 별도로 존재함을 의미한다. 다음 방법에서는 시계열 데이터의 계절적 변동을 측정하기 위해 계절 지수를 사용한다.

• 단순 평균 방법
• 비율 대 추세 방법
• 이동 평균 비율법
• 친족연결법

단순 평균 방법

평균 이동 비율 방법을 사용하여 계절 변동을 측정하면 시계열에서 계절 변동의 정도를 측정할 수 있는 지수를 제공한다. 지수는 평균 100을 기준으로 하며, 계절성의 정도는 기준에서 벗어난 변동에 의해 측정된다. 예를 들어, 겨울 휴양지에서 호텔 임대료를 관찰하면 겨울 분기 지수가 124라는 것을 알 수 있다. 124라는 수치는 평균 분기별 임대료의 124%가 겨울에 발생한다는 것을 의미한다. 호텔 경영진이 작년 한 해 동안 1436건의 임대료를 기록한다면, 분기 평균 임대료는 359=(1436/4)가 될 것이다. 겨울/분기 지수가 124이므로 겨울 임대 건수는 다음과 같이 추정한다.

359*(124/100)=445;

여기서 359는 분기별 평균 임대료, 124는 동분기 지수, 445는 계절별 겨울 임대료.

이 방법을 백분율 이동 평균법이라고도 한다. 이 방법에서 시계열의 원래 데이터 값은 이동 평균의 백분율로 표현된다. 단계와 표는 아래에 제시되어 있다.

비율 대 추세 방법

1. 시계열에서 원본 데이터 값의 월별 이동 평균 12개(또는 분기별 4개)를 구하십시오.

2. 각 시계열의 원래 데이터 값을 (1) 단계에서 얻은 해당 중심 이동 평균 값의 백분율로 표시한다. 즉, 곱셈 시계열 모델에서는 (원래 데이터 값) / (추세 값) × 100 = (T × C × S × I) / (T × C) × 100 = (S × I ) × 100을 얻는다.
   이것은 비율 대 이동 평균이 계절 성분과 불규칙 성분을 나타낸다는 것을 의미한다.

3. 이러한 백분율을 주어진 연도의 월 또는 분기별로 정렬하십시오. 해당 연도의 모든 월 또는 분기 동안 평균을 구하십시오.

4. 이러한 지수의 합계가 1200이 아니면(또는 분기별 수치의 경우 400) 보정계수 = 1200 / (월간 지수 합계)를 곱한다. 그렇지 않으면, 12개월 평균은 계절 지수로 간주될 것이다.

이동 평균 비율법

다음 데이터에서 계절 지수를 이동 비율 대 평균 방법으로 계산해 봅시다.

샘플 데이터

연도/4분기	1	2	3	4
1996	75	60	54	59
1997	86	65	63	80
1998	90	72	66	85
1999	100	78	72	93

이제 4분기 이동 평균과 이동 평균 비율에 대한 계산이 아래 표에 나와 있다.

이동 평균

연도	쿼터	원래 값(Y)	총 4개의 그림 이동	4 그림 이동 평균	총 2개의 그림 이동	2 그림 이동 평균(T)	이동 비율-평균(%)/(T)*100
1996	1	75			—	—	—
			—	—
	2	60			—	—	—
			248	62.00
	3	54			126.75	63.375	85.21
			259	64.75
	4	59			130.75	65.375	90.25
			264	66.00
1997	1	86			134.25	67.125	128.12
			273	68.25
	2	65			141.75	70.875	91.71
			294	73.50
	3	63			148.00	74.00	85.13
			298	74.50
	4	80			150.75	75.375	106.14
			305	76.25
1998	1	90			153.25	76.625	117.45
			308	77.00
	2	72			155.25	77.625	92.75
			313	78.25
	3	66			159.00	79.50	83.02
			323	80.75
	4	85			163.00	81.50	104.29
			329	82.25
1999	1	100			166.00	83.00	120.48
			335	83.75
	2	78			169.50	84.75	92.03
			343	85.75
	3	72			—	—	—
			—	—
	4	93			—	—	—

계절지수 계산

연도/4분기	1	2	3	4	합계
1996	—	—	85.21	90.25
1997	128.12	91.71	85.13	106.14
1998	117.45	92.75	83.02	104.29
1999	120.48	92.04	—	—
합계	366.05	276.49	253.36	300.68
계절 평균	122.01	92.16	84.45	100.23	398.85
조정 계절 평균	122.36	92.43	84.69	100.52	400

현재 계절 평균의 총계는 398.85이다. 따라서 해당 보정 계수는 400/398.85 = 1.00288이 될 것이다. 각 계절 평균에 보정계수 1.00288을 곱하여 위의 표와 같이 조정된 계절지수를 구한다.

친족연결법

1. 가법 시계열 모형에서 계절 성분을 다음과 같이 추정한다.

S = Y – (T + C + I )

어디에

S : 계절값

Y : 시계열의 실제 데이터 값

T : 추세 값

C : 주기적 값

I : 불규칙한 값.

2. 승법 시계열 모형에서 계절성 성분은 비율과 백분율의 측면에서 다음과 같이 표현된다.

Seasonal effect ${\displaystyle ={\frac {T\cdot S\cdot C\cdot I}{T\cdot C\cdot I}}\times 100\ ={\frac {Y}{T\cdot C\cdot I}}\times 100}$;

그러나 실제로 시계열의 변위는 ${\displaystyle S}$ ${\displaystyle \cdot }$ ${\displaystyle C}$ ${\displaystyle \cdot }$ I ${\displaystyle S\cdot C\cdot I}$에 도착하기 위해 이루어진다$.$

This is done by dividing both sides of ${\displaystyle Y=T\cdot S\cdot C\cdot I}$ by trend values T so that ${\displaystyle {\frac {Y}{T}}=S\cdot C\cdot I}$.

3. 비합리화된 시계열 데이터는 추세(T ), 주기적(C) 및 불규칙적(I ) 성분만 가지며 다음과 같이 표현된다.

• Multiplicative model : ${\displaystyle {\frac {Y}{S}}\times 100={\frac {T\cdot S\cdot C\cdot I}{S}}\times 100=(T\cdot C\cdot I)\times 100}$

• 가법 모형: Y – S = (T + S + C + I ) – S = T + C + I

모델링.

시계열의 완전한 주기적 변동을 시계열 분석에서 상황에 따라 주기 길이를 알거나 알 수 없는 하나 이상의 사인파 모델을 사용하여 처리할 수 있다. 주기적 변동을 반-명확하게 다루도록 구조화할 수 있는 특수 형태의 ARIMA 모델을 사용하여 덜 완전한 주기적 변동을 처리할 수 있다. 그러한 모델은 사이클로스터리 과정을 나타낸다.

주기적인 계절성을 모델링하는 또 다른 방법은 푸리에 용어 쌍을 사용하는 것이다. 사인파 모델을 사용하는 것과 마찬가지로, 회귀 모형에 추가된 푸리에 항은 계절성을 시뮬레이션하기 위해 사인 항과 코사인 항을 사용한다. 그러나 이러한 회귀 분석의 계절성은 사인 또는 코사인 항이 아니라 사인 또는 코사인 항의 합으로 표현될 수 있다. 모든 주기 함수는 푸리에 항을 포함하면 근사하게 추정할 수 있다.

사인파 모델과 푸리에 항을 사용한 회귀 분석 사이의 차이는 다음과 같이 단순화할 수 있다.

사인파 모델:

${\displaystyle Y_{i}=a+bt+\alpha \sin(2\pi \omega T_{i}+\phi )+E_{i}}}}}}$

푸리에 항을 사용한 회귀 분석:

${\displaystyle Y_{i}=a+bt+(\sum _{k=1}^{K}\alpha _{k}\cdot \sin({\tfrac {2\pi kt}{m}}}})+\beta _{k}\cdot \cos{n})+E_{i}}}$

계절조정

계절 조정 또는 계절 조정은 시계열의 계절 성분을 제거하는 모든 방법이다. 예를 들어 계절에 따라 조정된 데이터는 계절 기간보다 긴 기간에 대한 비 계절적 추세를 분석하거나 보고할 때 사용된다. 계절적 조정을 위한 적절한 방법은 시계열이 "추세", "순환", "계절", "비정규"와 같은 이름으로 지정된 성분으로 분해되는 특정 관점에 기초하여 선택되며, 이러한 요소들이 상호 작용하는 방법을 포함한다. 예를 들어, 그러한 구성요소는 부가적으로 또는 배수로 작용할 수 있다. 따라서 계절적 구성요소가 부가적으로 작용하는 경우 조정방법은 다음의 두 단계를 가진다.

• 시계열 변동의 계절 성분 추정(일반적으로 시계열에서 평균이 0인 형태)
• 원래 시계열에서 추정 계절 성분을 빼서 계절 조정 시리즈: ${\$$T_{t}+E_{t$^[3] .

승수모형이라면 수준에 따라 계절변동 규모가 달라지는데, 이는 경제시리즈와 함께 발생할 가능성이 더 높다.^[3] 계절성을 고려할 때 계절 조정 승법 분해는 $Y{\displaystyle {}_{}}$ ${\displaystyle t_{}}$/ ${\displaystyle S_{}}$ ${\displaystyle t{}_{}}$= T ${\displaystyle {}_{}}$ t${\displaystyle {}_{}{t}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle t_{}}$ ${\$로 기록할 수 있다.$T_{t}*E_{t$ 여기서 원래의 시계열은 추정 계절 성분으로 나눈다.

시계열의 로그를 취함으로써 승법 모델을 가법 모델로 변환할 수 있다.

SA 승법 분해: ${\$$T_{t}*E_{t}}}$

승법 모델의 시계열 로그 가져오기: $l{\displaystyle }$ ${\displaystyle o}$ g ${\displaystyle Y_{}}$ ${\displaystyle {}_{}}$= ${\displaystyle l}$ ${\displaystyle o}$ ${\displaystyle G}$ S ${\displaystyle t_{}}$+ l ${\displaystyle o}$ ${\displaystyle t_{}}$+ ${\displaystyle l}$ o T + ${\displaystyle l}$ ${\displaystyle o}$ ${\displaystyle {}_{}}$ ${\displaystyle t_{}}$ ${\$$T_{t}+logE_{t}}$^[3]

X-12-ARIMA에 의해 계절 조정의 한 가지 특별한 구현이 제공된다.

회귀 분석에서

일반 최소 제곱과 같은 회귀 분석에서 계절에 따라 달라지는 종속 변수가 하나 이상의 독립 변수에 의해 영향을 받는 경우 계절성은 임의로 선택한 기준 계절을 제외하고 각 계절에 하나씩 n-1 더미 변수를 포함함으로써 설명 및 측정할 수 있다. 여기서 n은 계절의 수입니다. (예: 기상 계절의 경우 4개, 월 등의 경우 12개). 데이터 포인트가 더미의 지정된 시즌에서 그려진 경우 각 더미 변수는 1로 설정되고 그렇지 않은 경우 0으로 설정된다. 그런 다음 기준 계절에 대한 종속 변수의 예측 값을 회귀 분석의 나머지 부분으로부터 계산하고, 다른 계절의 경우 회귀 분석의 나머지 부분과 해당 계절에 대한 더미 변수에 대한 값 1을 삽입하여 계산한다.

관련 패턴

계절적 패턴과 관련 패턴을 구분하는 것이 중요하다. 계절적 패턴은 일 년에 한 번, 반기, 분기 등 일 년의 계절이나 시간에 영향을 받을 때 발생한다. 주기적 패턴 또는 단순한 사이클은 데이터 표시 기간이 다른 기간(예: 퇴폐)에서 상승하거나 하락할 때 발생하며, 계절보다 훨씬 더 길거나(예: 주간) 훨씬 짧다. Quasiperiodic은 더 일반적이고 불규칙한 주기성이다.

참고 항목

• 진동
• 주기함수
• 주기성(동음이의)
• 광동기주의

참조

• Barnett, A.G.; Dobson, A.J. (2010). Analysing Seasonal Health Data. Springer. ISBN 978-3-642-10747-4.
• 아미르 D의 전체 비즈니스 통계(12장) 아크젤.
• 비즈니스 통계: 왜 그리고 언제 (15장)의 래리 E. 리차드와 제리 J. 라카바.
• J.K.별 비즈니스 통계(16장) 샤르마
• 비즈니스 통계, David F의 의사결정 접근법(18장) 그로브너와 패트릭 W. 섀넌
• 리차드 1세 경영통계(15장) 레빈과 데이비드 S. 루빈.
• 예측: Rob J. Hyndman과 George Athansopoulos의 실행과 원칙

외부 링크

• Wikimedia Commons의 계절성과 관련된 미디어
• NIST/SEMATECH e-핸드북의 통계적 방법

이 문서에는 국립표준기술원(National Institute of Standards and Technology) 문서의 공용 도메인 자료가 통합되어 있다.