리만 제타 함수
Riemann zeta function

리만 제타 함수 또는 오일러-리만 제타 함수는 그리스 문자 ζ(zeta)로 표시되며 다음과 같이 정의되는 복소 변수의 수학적 함수입니다.
리만 제타 함수는 분석적 정수론에서 중추적인 역할을 하며 물리학, 확률론 및 응용 통계학에 응용됩니다.
레온하르트 오일러는 18세기 전반에 실수에 대한 함수를 처음으로 소개하고 연구했습니다. 베른하르트 리만의 1859년 논문 "주어진 크기보다 작은 소수의 수에 대하여"는 오일러 정의를 복소 변수로 확장하고, 그 동형 연속과 함수 방정식을 증명했으며, 0과 소수의 분포 사이의 관계를 확립했습니다. 이 논문에는 많은 수학자들이 순수수학에서 가장 중요한 미해결 문제로 여기는 리만 제타 함수의 복소수 0의 분포에 대한 추측인 리만 가설도 포함되어 있습니다.[3]
고른 양의 정수에서 리만 제타 함수의 값은 오일러에 의해 계산되었습니다. 그중 첫 번째인 ζ(2)는 바젤 문제의 해결책을 제시하고 있습니다. 1979년 로저 아페리는 ζ의 비합리성을 증명했습니다. 오일러에 의해 발견된 음의 정수점들에서의 값들은 유리수이며 모듈 형태 이론에서 중요한 역할을 합니다. 디리클레 급수, 디리클레 L-함수 및 L-함수와 같은 리만 제타 함수의 많은 일반화가 알려져 있습니다.
정의.

리만 제타 함수 ζ(s)는 복소수 변수 s = σ + it의 함수이며, 여기서 σ와 t는 실수입니다. (제타 함수의 연구에서 전통적으로 사용되는 표기법은 리만 다음과 같습니다.) Re(s) = σ > 1일 때 함수는 수렴 합 또는 적분으로 쓸 수 있습니다.
어디에
감마 함수입니다. 리만 제타 함수는 σ > 1에 대해 정의된 함수의 분석적 연속을 통해 다른 복소값에 대해 정의됩니다.
레온하르트 오일러는 1740년에 s의 양의 정수 값에 대해 위 급수를 고려했고, 이후 체비셰프는 정의를 ( > 로 확장했습니다. \s)> 1.}
위의 급수는 σ > 1이 되도록 s에 대한 분석 함수로 절대 수렴하고 다른 모든 s 값에 대해 발산하는 전형적인 디리클레 급수입니다. Riemann은 수렴의 반평면에서 급수에 의해 정의된 함수가 모든 복소값 ≠ 1로 해석적으로 계속될 수 있음을 보여주었습니다. s = 1인 경우 급수는 + ∞로 발산하는 고조파 급수이고,
오일러 곱 공식
1737년, 제타 함수와 소수 사이의 연관성을 증명한 오일러에 의해 발견되었습니다.
정의에 따라, 좌변은 ζ이고, 우변의 무한곱은 모든 소수 p에 걸쳐 확장됩니다(이러한 표현을 오일러 곱이라고 합니다).
오일러 곱 공식의 양쪽은 Re(s) > 1에 대해 수렴합니다. 오일러 항등식의 증명은 기하급수와 산술의 기본 정리에 대한 공식만을 사용합니다. s = 1일 때 얻어지는 조화급수는 발산하기 때문에 오일러 공식(이 공식은 π p/p - 1이 됨)은 소수가 무한히 많다는 것을 의미합니다. p/p - 1의 로그는 약 1/p이므로, 이 공식을 사용하여 소수의 역수의 합이 무한하다는 더 강력한 결과를 증명할 수도 있습니다. 반면 에라토스테네스의 체와 그것을 결합하면 양의 정수 집합 내의 소수 집합의 밀도가 0임을 알 수 있습니다.
오일러 곱 공식을 사용하여 임의로 선택된 정수가 세트와이즈 코프림일 점근 확률을 계산할 수 있습니다. 직관적으로 임의의 단일수가 소수(또는 임의의 정수) p로 나뉠 확률은 1/p입니다. 따라서 s개의 숫자가 모두 이 소수로 나눌 수 있는 확률은 1/ps 이고, 적어도 하나가 아닐 확률은 1-1/ps 입니다. 이제 서로 다른 소수의 경우, 이러한 분할 이벤트는 후보 분할자가 코프라임이기 때문에 상호 독립적입니다(숫자는 코프라임 분할자 n과 mf로 분할되고 nm로 분할되는 경우에만 1/nm 확률로 발생합니다). 따라서 s개의 수가 코프라임이라는 점근적 확률은 모든 소수에 대한 곱으로 주어집니다.
리만 함수 방정식
증명 1
함수 방정식의 증명은 다음과 같이 진행됩니다. σ> 0displaystyle \sigma >0}인 경우,
결과적으로σ > 1 \sigma > 1}이면
편의상.
세타 기능의 특수한 경우입니다. 그리고나서
하도록
이런 이유로
이는 다음과 같습니다.
그렇게
이는 모든 것에 대해 수렴하므로 분석적 연속에 의해 유지됩니다. 또한 s가 1 - s로 변경되면 RHS는 변경되지 않습니다. 이런 이유로
증명 2
먼저 사용합니다.
함수방정식은 리만이 1859년에 발표한 논문 "주어진 크기보다 작은 소수의 수에 대하여"에서 확립한 것으로 애당초 분석적 연속을 구성하는 데 사용되었습니다. 이와 동등한 관계는 100년 이상 전인 1749년에 오일러에 의해 디리클레 에타 함수( 교대 제타 함수)에 대해 추측되었습니다.
또한 이 관계식은 영역 0 < Re(s) < 1의 ζ을 계산하는 방정식을 제공합니다.
리만은 또한 xi 함수에 적용되는 함수 방정식의 대칭 버전을 발견했습니다.
(리만의 원래 ξ(t)는 조금 달랐습니다.)
π/2 γ (s / 2) {\displaystyle \pi^{-s/2}\Gamma (s/2)} 인자는 리만 당시에는 잘 알려져 있지 않았으며, 이 소위 "Gamma factor"가 사실상 Archimedean place에 해당하는 로컬 L-factor임이 밝혀진 John Tate(1950)의 논문 전까지는, 오일러 곱 확장의 다른 요인은 비아키메데스 지역의 지역 L-요인입니다.
0, 임계선과 리만 가설


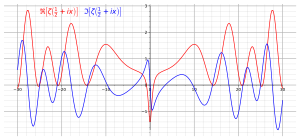
함수 방정식은 리만 제타 함수가 -2, -4,...에서 0을 갖는다는 것을 보여줍니다. 이것들은 사소한 0이라고 불립니다. 이들은 자신의 존재가 상대적으로 증명하기 쉽다는 점에서 사소합니다. 예를 들어 함수 방정식에서 sin π/2가 0일 때부터입니다. 사소하지 않은 0들은 그들의 분포가 훨씬 덜 이해되어 있을 뿐만 아니라, 더 중요한 것은, 그들의 연구가 정수론에서 소수와 관련된 대상에 관한 중요한 결과를 산출하기 때문에 훨씬 더 많은 관심을 끌었습니다. 임의의 사소한 0이 열린 스트립 {∈ : 0 < (s) < 1 } {C} : {Re} (s)<1\}에 놓여 있으며, 이를 임계 스트립이라고 합니다. 집합{ ∈C: Re ( = 1/ } {\ \{s\in \mathbb {C} :\operator name {Re} (s) = 1/2\}을 임계선이라고 합니다. 수학에서 가장 큰 미해결 문제 중 하나로 꼽히는 리만 가설은 사소한 0이 아닌 모든 0이 임계선에 있다고 주장합니다. 1989년 콘레이는 리만 제타 함수의 사소하지 않은 0의 40% 이상이 임계선에 있음을 증명했습니다.[9]
임계선의 리만 제타 함수에 대해서는 Z-함수를 참조하십시오.
| 영 |
|---|
| 1/2 ± 14.134725 i |
| 1/2 ± 21.022040 i |
| 1/2 ± 25.010858 i |
| 1/2 ± 30.424876 i |
| 1/2 ± 32.935062 i |
| 1/2 ± 37.586178 i |
| 1/2 ± 40.918719 i |
임계 스트립의 0 수
을 0< ) < 1 {\{Re}(s)<1}, 허수 부분이 < < T<\operatorname {Im}(s)< 트루지안은 만약 > e T > 이면[12]
하디-리틀우드 추측
1914년, 고드프리 해럴드 하디는 ζ(1/2 + it)가 무한히 많은 실수 0을 가지고 있다는 것을 증명했습니다.
Hardy와 John Edensor Littlewood는 큰 양의 실수 간격에서 ζ의 0(1/2 + it) 사이의 밀도와 거리에 대한 두 가지 추측을 공식화했습니다. 다음에서 N(T)는 실수 0의 총 개수이고 N(T)는 구간 (0, T)에 놓여 있는 함수 ζ(1/2 + it)의 홀수 차수의 총 0의 개수입니다.
- 임의의 ε > 0에 대하여, 다음과 같은 T(ε) > 0이 존재합니다.
- 임의의 ε > 0에 대하여, T(ε) > 0과 c > 0이 존재하여 부등식이 발생합니다.
이 두 추측은 리만 제타 함수의 조사에 새로운 방향을 열었습니다.
제로 프리 영역
리만 제타 함수의 0의 위치는 수론에서 매우 중요합니다. 소수 정리는 Re(s) = 1선 위에 제타 함수의 0이 없다는 사실과 같습니다. Vinogradov의 평균값 정리의 효과적인 형태에서 이어지는 더 나은 결과는σ ≥ -15754( t) 23로그 로그 t) {\displaystyle \sigma \geq 1-{\frac {1}{57.54(\log {t})^{\frac {2}{3}}(\log {\log {t}})^{\frac {1}{3}}} 및 t ≥ 3입니다.
2015년, Mossinghoff와 Trudgian은 제타가 이 지역에 0이 없다는 것을 증명했습니다[16].
포트 ≥ 2. 영역은 3 ⋅ < t< (10151.5) ≈ 5.5 ⋅ 10 4408 {\displaystyle 3.06\cdot 10^{10}< t <\exp(10151.5)\약 5.5\cdot 10^{4408}}의 임계 스트립에서 알려진 가장 큰 제로 프리 영역입니다.
이런 종류의 가장 강력한 결과는 리만 가설의 진리이며, 이 가설은 수론에서 많은 심오한 결과를 가져올 것입니다.
기타결과
임계선에는 무한히 많은 0이 있다고 알려져 있습니다. 리틀우드는 수열(γ)이 상반면에 있는 모든 0의 허수 부분들을 오름차순으로 포함하면,
임계선 정리는 중요하지 않은 0의 양의 비율이 임계선 위에 있다고 주장합니다. (리만 가설은 이 비율이 1임을 의미합니다.)
임계 스트립에서 음이 아닌 허수 부분이 가장 작은 0은 1/2 + 14.13472514...i(OEIS: A058303)입니다. 그 사실을
모든 복소에 대하여 ≠ 1은 리만 제타 함수의 0이 실축에 대하여 대칭임을 의미합니다. 이 대칭성을 함수 방정식과 결합하면 trivial이 아닌 0은 임계선 Re=1/2에 대해 대칭임을 알 수 있습니다.
또한 실수부 1과의 선 위에 0이 놓여 있지 않은 것으로 알려져 있습니다.
특정값
임의의 양의 짝수 정수 2n에 대하여,
양이 아닌 정수의 경우,
분석을 계속하면 다음과 같은 결과를 얻을 수 있습니다.
값이
비록 ~일지라도
특별한 가치의 증명
실수를 통해 →+ ∞ {\ s+\infty }을 취하면 ζ(+ ∞) = 1 {\displaystyle \zeta(+\infty)= 1}을 얻을 수 있습니다. 그러나 리만 구의 복잡한 무한대에서 제타 함수는 본질적인 특이점을 가지고 있습니다.
다양한 속성
정수 및 반 정수 값에서 제타 함수를 포함하는 합계는 유리 제타 급수를 참조하십시오.
역수
제타 함수의 역수는 뫼비우스 함수 μ(n) 위의 디리클레 급수로 표현될 수 있습니다.
실수 부분이 1보다 큰 모든 복소수에 대하여. 잘 알려진 다양한 곱셈 함수를 포함하는 여러 유사한 관계가 있는데, 이들은 디리클레 급수에 관한 기사에 나와 있습니다.
리만 가설은 s의 실수 부분이 1/2보다 클 때 이 표현이 유효하다는 주장과 동등합니다.
보편성
리만 제타 함수의 임계 띠는 보편성이라는 놀라운 성질을 가지고 있습니다. 이 제타 함수의 보편성은 임의의 홀로모픽 함수에 임의로 잘 근접하는 임계 띠 상의 어떤 위치가 존재한다는 것을 말합니다. 복소함수는 매우 일반적이기 때문에 이 성질은 매우 두드러집니다. 보편성에 대한 최초의 증거는 1975년 세르게이 미하일로비치 보로닌에 의해 제공되었습니다.[22] 보다 최근의 연구는 보로닌 정리의[23] 효과적인 버전을 포함하고 있으며, 이를 디리클레 L-함수로 확장했습니다.[24][25]
제타 함수의 최대 계수 추정치
함수 F(T;H)와 G(s; δ)를 등식으로 정의합니다.
여기서 T는 충분히 큰 양수, 0 < H ≪ 로그 로그 T, s = σ + iT, 1/2 ≤ σ ≤ 1, 0 < δ < 1/3 입니다. 아래에서 F와 G 값을 추정하면 임계선의 짧은 간격 또는 임계 스트립 0 ≤ Re(s) ≤ 1에 있는 점의 작은 이웃에서 ζ 값이 얼마나 클 수 있는지 알 수 있습니다.
Case H ≫ 로그 T는 Kanakahali Ramachandra에 의해 연구되었습니다. Case δ > c는 충분히 큰 상수입니다.
특히, Anatolii Karatsuba는 H와 δ 값이 충분히 작은 특정 상수를 초과하는 경우, 추정치는
여기서 c와1 c는2 특정한 절대 상수입니다.
리만 제타 함수의 논거
함수.
는 리만 제타 함수의 인수라고 불립니다. 여기서 arg ζ(1/2 + it)은 점 2, 2 + it 및 1/2 + it을 연결하는 파선을 따라 arg ζ의 임의의 연속 분기의 증분입니다.
함수 S(t)의 성질에 대한 몇 가지 정리가 있습니다. 이러한 결과[28][29] 중에는 S(t)에 대한 평균값 정리와 첫 번째 적분이 있습니다.
실수선의 구간 위에서, 그리고 모든 구간 (T, T + H)에 대하여
적어도 포함하고 있습니다.
함수 S(t)가 부호를 변경하는 점. 이전에도 비슷한 결과가 아틀레 셀버그에 의해 이 사건에 대해 얻어졌습니다.
표현
디리클레 급수
원래 시리즈를 재배열하면 수렴 영역의 확장을 얻을 수 있습니다.[30] 시리즈가.
Re(s) > 0에 대한 수렴, 반면
Re에 대해서도 수렴 > -1. 이러한 방법으로 수렴 영역은 임의의 음의 정수 -k에 대해 Re(s) > -k로 확장될 수 있습니다.
멜린형 적분
함수 f(x)의 멜린 변환은 다음과[31] 같이 정의됩니다.
적분이 정의된 영역에서. 제타 함수는 멜린 변환과 같은 적분으로 다양한 표현이 있습니다. 만약 s의 실수 부분이 1보다 크다면, 우리는
- } 및 (s) 0 x scoh (x ) - 1d x {\displaystyle \ \Gamma(s)\zeta(s){\frac {1}{2s}\int_{0}^{\infty}{\frac {x^{s}}{\cosh(x)-1}}\,\mathrm {d} x},
여기서 γ는 감마 함수를 나타냅니다. 리만은 윤곽선을 수정함으로써
모두에 대하여(여기서 H는 행켈 등고선을 나타냅니다).
우리는 또한 소수와 소수 정리와 관련된 식을 찾을 수 있습니다. π(x)가 소수 계산 함수이면,
Re가 > 1인 값의 경우.
비슷한 멜린 변환은 1/n의 무게로 소수 거듭제곱 p를n 세는 리만 함수 J(x)를 포함하므로,
지금이다
이러한 표현은 멜린 역변환을 통해 소수 정리를 증명하는 데 사용할 수 있습니다. 리만의 소수 계산 함수는 더 쉽게 작업할 수 있으며, 뫼비우스 반전에 의해 π(x)를 복구할 수 있습니다.
세타 함수
리만 제타 함수는 멜린 변환에[32] 의해 주어질 수 있습니다.
야코비의 세타 함수로 볼 때.
그러나 이 적분은 s의 실수 부분이 1보다 큰 경우에만 수렴하지만 정규화할 수 있습니다. 이는 제타 함수에 대해 다음과 같은 식을 제공하며, 0과 1을 제외한 모든 경우에 대해 잘 정의됩니다.
로랑 시리즈
리만 제타 함수는 s = 1에서 순서 1의 단일 극과 동형입니다. 따라서 s = 1에 대한 로랑 시리즈로 확장할 수 있으며, 시리즈 전개는 다음과 같습니다.
여기서 γ인 상수들을 Stieltjes 상수라고 하며, 극한으로 정의할 수 있습니다.
상수항 γ는 오일러-마스케로니 상수입니다.
적분
모든 s ∈ C에 대하여 s ≠ 1, 적분 관계(cf). 아벨-플라나 공식)
hold true이며, 이는 제타 함수의 수치 평가에 사용될 수 있습니다.
상승 요인
전체 복소 평면에 유효한 상승 요인을 사용한 또 다른 급수 전개는 다음과[citation needed] 같습니다.
이를 재귀적으로 사용하여 Dirichlet 시리즈 정의를 모든 복소수로 확장할 수 있습니다.
리만 제타 함수는 또한 가우스-쿠즈민에 대한 적분에서 멜린 변환과 유사한 형태로 나타납니다.x에s − 1 작용하는 위싱 연산자; 이 컨텍스트는 요인이 떨어지는 측면에서 시계열 확장을 발생시킵니다.[34]
하다마드 제품
Weierstrass의 인수분해 정리에 기초하여, Hadamard는 무한 곱 전개를 제공했습니다.
여기서 곱은 ζ의 사소하지 않은 0 ρ 위에 있고 문자 γ은 오일러-마스케로니 상수를 다시 나타냅니다. 보다 단순한 무한한 제품 확장은
이 형식은 s = 1에서 단순 극, 분모의 감마 함수 항으로 인해 -2, -4, ...에서 사소한 0, s = ρ에서 trivial이 아닌 0을 명확하게 표시합니다. (후자 공식에서 수렴을 보장하기 위해 곱은 "matching 쌍", 즉 0을 인수해야 합니다. ρ와 1 - ρ 형태의 0 쌍에 대한 인자를 결합해야 합니다.)
전 세계적으로 수렴하는 급수
일부 정수 n에 대해 = 1 + 2 πi/ln 2n을 제외한 모든 복소수에 대해 유효한 제타 함수에 대한 전역 수렴 급수는 1926년 Konrad Knop에 의해 추측되었고 1930년 Helmut Hasse에 의해 증명되었습니다(cf). 오일러 합):
이 시리즈는 Hasse의 논문의 부록에 실렸고, 1994년 Jonathan Sondow에 의해 두 번째로 출판되었습니다.[37]
Hasse는 또한 글로벌 컨버전스 시리즈를 증명했습니다.
동간에[36] Iaroslav Blagouchine의[38][35] 연구에 따르면 1926년 Joseph Ser에 의해 유사하고 동등한 시리즈가 출판되었습니다.[39]
1997년 K. Ma ś랑카는 리만 제타 함수에 대해 또 다른 전역 수렴 급수(단, = 1)를 제공했습니다.
여기서 실제 계수 는 다음과 같습니다.
여기서 는 Bernoulli 숫자이고( {\는 Pochhammer 기호를 나타냅니다.
제타 함수의 이러한 표현은 본질적으로 노드와의 보간이며, 여기서 는 점 =2 4, 6, … {\display s= 2, 4, 6,\ldots}, 즉 오일러가 보여준 것처럼 제타 값이 정확히 알려진 것입니다. 칼슨의 정리에 기초한 이 제타 함수의 표현에 대한 우아하고 매우 짧은 증거는 2006년에[42] Philippe Flajolet에 의해 제시되었습니다.
계수 의 점근적 동작은 다소 궁금합니다. 값이 증가하면 진폭이 거의 기하급수적으로 감소하고 주파수가 천천히 감소하는 정규 진동을 관찰합니다(약 k- / k 새들 포인트 방법을 사용하여, 우리는 다음을 보여줄 수 있습니다.
여기서κ \kappa}은(는) 다음을 나타냅니다.
(자세한 내용은 참조).
이 표현을 바탕으로 2003년 루이스 바에즈-두아르테는 리만 가설의 새로운 기준을 제시했습니다. 즉, 계수 를 다음과 같이 정의하면 됩니다.
그렇다면 리만 가설은 다음과 같습니다.
급격 수렴 급수
Peter Borwein은 Chebyshev 다항식을 Dirichleteta 함수에 적용하여 높은 정밀도의 수치 계산에 적합한 매우 빠른 수렴 급수를 생성하는 알고리즘을 개발했습니다.[47]
기본값을 통해 양의 정수로 직렬 표현
여기서n p#은 1차 수열이고 J는k Jordan의 토티언트 함수입니다.[48]
불완전한 폴리 베르누이 수에 의한 급수 표현
함수 ζ는 Re(s) > 1의 경우 무한급수로 나타낼 수 있습니다.
여기서 k ∈ {-1, 0}, W는 램버트 W-함수의 k번째 분지이고, B는 불완전한 폴리 베르누이 수이입니다.
엥겔 지도의 멜린 변환
함수 ( = x( ⌊ x - 1 ⌋) - 1 {\displaystyle g(x) = x\left(1+\left\lfloor x^{-1}\right\rfloor \right)-1}을 반복하여 엥겔 전개에 나타나는 계수를 찾습니다.
지도 g의 멜린 변환은 공식에 의해 리만 제타 함수와 관련이 있습니다.
투 모스 수열
계수가 Thue-Morse 시퀀스의 항인 디리클레 급수의 특정 선형 조합은 리만 제타 함수와 관련된 항을 생성합니다(토스, 2022). 예를 들어 다음과 같습니다.
여기서( ≥ 0 })n\geq 0}}은Thue-Morse 시퀀스의 {\rm {th}} 항입니다. 실제로 실수 부분이 보다 큰 1인 에 대해
수치 알고리즘
약 1930년 이전에 사용된 고전적인 알고리즘은 오일러-매클로린 공식을 적용하여 n과 m의 양의 정수를 얻음으로써 진행됩니다.
여기서, {\는 표시된 베르누이 수를 나타냅니다.
그리고 오차는 만족합니다.
σ = Re(s)를 사용합니다.
현대적인 수치 알고리즘은 Odlyzko-Schönhage 알고리즘입니다.
적용들
제타 함수는 응용 통계에서 발생합니다(Zipf의 법칙 및 Zipf–Mandelbrot 법칙 참조).
제타 함수 정규화는 양자장 이론에서 발산 급수와 발산 적분의 정규화의 한 가지 가능한 수단으로 사용됩니다. 한 가지 주목할 만한 예에서, 리만 제타 함수는 카시미르 효과를 계산하는 한 가지 방법에서 명시적으로 나타납니다. 제타 함수는 동적 시스템의 분석에도 유용합니다.[53]
음악적 조율
음악적 동조 이론에서, 제타 함수는 고조파 급수의 간격에 근접한 옥타브(EDO)의 등분수를 찾는 데 사용될 수 있습니다. {R}에서∈ R t\의 값을 증가시키는 경우,
그와 같은 에도에 해당하는 정수 근처의 피크.[54] 예를 들어 12, 19, 53과 같은 인기 있는 선택이 있습니다.[55]
무한급수
등거리 양의 정수에서 평가된 제타 함수는 여러 상수의 무한급수 표현에 나타납니다.[56]
사실 짝수 항과 홀수 항은 두 개의 합을 제공합니다.
그리고.
위 합계의 매개변수화된 버전은 다음과 같습니다.
그리고.
< < 2인 경우 및 서ψ \ 및 γ displaystyle \gamma }는 각각 폴리감마 함수 및 오일러 상수입니다.
이들은 t= 1 {\displaystyle t = 1}에서 연속적입니다. 다른 합은 다음과 같습니다.
여기서 Im은 복소수의 허수 부분을 나타냅니다.
일반화
리만 제타 함수의 일반화라고 볼 수 있는 관련 제타 함수들이 다수 존재합니다. 여기에는 후르비츠 제타 함수가 포함됩니다.
(융합 시리즈 표현은 1930년에 Helmut Hasse에 의해 cf.[36] q = 1일 때 리만 제타 함수와 일치하는 후르비츠 제타 함수)(후르비츠 제타 함수의 합산 하한은 1이 아닌 0), 디리클레 L-함수와 데데킨드 제타 함수. 기타 관련 기능은 zeta 함수 및 L-함수를 참조하십시오.
폴리로그는 다음과 같이 주어집니다.
이는 z = 1일 때 리만 제타 함수와 일치합니다. Clausen 함수 Cl(θ)는 Li(e)의 실수부 또는 허수부로 선택될 수 있습니다.
Lerch 초월은 다음과 같이 주어집니다.
이는 z = 1 및 q = 1일 때 리만 제타 함수와 일치합니다(레흐 초월수에서 합의 하한은 1이 아니라 0).
다중 제타 함수는 다음과 같이 정의됩니다.
이러한 기능을 분석적으로 n차원의 복잡한 공간까지 이어갈 수 있습니다. 양의 정수 인수에서 이 함수들이 취하는 특별한 값은 수론자들에 의해 다중 제타 값으로 불리며 수학과 물리학의 많은 다른 분야와 연결되어 있습니다.
참고 항목
메모들
- ^ "Jupyter Notebook Viewer". Nbviewer.ipython.org. Retrieved 4 January 2017.
- ^ a b Steuding, Jörn; Suriajaya, Ade Irma (1 November 2020). "Value-Distribution of the Riemann Zeta-Function Along Its Julia Lines". Computational Methods and Function Theory. 20 (3): 389–401. doi:10.1007/s40315-020-00316-x. ISSN 2195-3724. S2CID 216323223.
Theorem 2 implies that ζ has an essential singularity at infinity
- ^ Bombieri, Enrico. "The Riemann Hypothesis – official problem description" (PDF). Clay Mathematics Institute. Archived from the original (PDF) on 22 December 2015. Retrieved 8 August 2014.
- ^ Devlin, Keith (2002). The Millennium Problems: The seven greatest unsolved mathematical puzzles of our time. New York: Barnes & Noble. pp. 43–47. ISBN 978-0-7607-8659-8.
- ^ Sandifer, Charles Edward (2007). How Euler Did It. Mathematical Association of America. p. 193. ISBN 978-0-88385-563-8.
- ^ Titchmarsh, E. C. (1986). The Theory of the Riemann Zeta-Function. Oxford Science Publications. p. 14. ISBN 0-19-853369-1.
- ^ Blagouchine, I.V. (1 March 2018). The history of the functional equation of the zeta-function. Seminar on the History of Mathematics. St. Petersburg, RU: Steklov Institute of Mathematics; "online PDF". Archived from the original on 2 May 2018. Retrieved 2 May 2018.
- ^ Blagouchine, I.V. (2014). "Rediscovery of Malmsten's integrals, their evaluation by contour integration methods and some related results". The Ramanujan Journal. 35 (1): 21–110. doi:10.1007/s11139-013-9528-5. S2CID 120943474.
Blagouchine, I.V. (2017). "Addendum". The Ramanujan Journal. 42: 777–781. doi:10.1007/s11139-015-9763-z. S2CID 125198685. Archived from the original on 2 May 2018. Retrieved 2 May 2018. - ^ Conrey, J. B. (1989). "More than two fifths of the zeros of the Riemann zeta function are on the critical line". J. Reine Angew. Math. 1989 (399): 1–26. doi:10.1515/crll.1989.399.1. MR 1004130. S2CID 115910600.
- ^ Eric Weisstein. "Riemann Zeta Function Zeros". Retrieved 24 April 2021.
- ^ The L-functions and Modular Forms Database. "Zeros of ζ(s)".
- ^ Trudgian, Timothy S. (2014). "An improved upper bound for the argument of the Riemann zeta function on the critical line II". J. Number Theory. 134: 280–292. arXiv:1208.5846. doi:10.1016/j.jnt.2013.07.017.
- ^ Hardy, G. H.; Fekete, M.; Littlewood, J. E. (1 September 1921). "The Zeros of Riemann's Zeta-Function on the Critical Line". Journal of the London Mathematical Society. s1-1: 15–19. doi:10.1112/jlms/s1-1.1.15.
- ^ Diamond, Harold G. (1982). "Elementary methods in the study of the distribution of prime numbers". Bulletin of the American Mathematical Society. 7 (3): 553–89. doi:10.1090/S0273-0979-1982-15057-1. MR 0670132.
- ^ Ford, K. (2002). "Vinogradov's integral and bounds for the Riemann zeta function". Proc. London Math. Soc. 85 (3): 565–633. arXiv:1910.08209. doi:10.1112/S0024611502013655. S2CID 121144007.
- ^ Mossinghoff, Michael J.; Trudgian, Timothy S. (2015). "Nonnegative trigonometric polynomials and a zero-free region for the Riemann zeta-function". J. Number Theory. 157: 329–349. arXiv:1410.3926. doi:10.1016/J.JNT.2015.05.010. S2CID 117968965.
- ^ Polchinski, Joseph (1998). An Introduction to the Bosonic String. String Theory. Vol. I. Cambridge University Press. p. 22. ISBN 978-0-521-63303-1.
- ^ Kainz, A. J.; Titulaer, U. M. (1992). "An accurate two-stream moment method for kinetic boundary layer problems of linear kinetic equations". J. Phys. A: Math. Gen. 25 (7): 1855–1874. Bibcode:1992JPhA...25.1855K. doi:10.1088/0305-4470/25/7/026.
- ^ 이 상수에 대한 추가 숫자 및 참조는 OEIS: A059750에서 확인할 수 있습니다.
- ^ Sondow, Jonathan (1998). "An antisymmetric formula for Euler's constant". Mathematics Magazine. 71 (3): 219–220. doi:10.1080/0025570X.1998.11996638. Archived from the original on 4 June 2011. Retrieved 29 May 2006.
- ^ Ogilvy, C. S.; Anderson, J. T. (1988). Excursions in Number Theory. Dover Publications. pp. 29–35. ISBN 0-486-25778-9.
- ^ Voronin, S. M. (1975). "Theorem on the Universality of the Riemann Zeta Function". Izv. Akad. Nauk SSSR, Ser. Matem. 39: 475–486. 수학으로 다시 인쇄됨. USSR Izv. (1975) 9: 443–445.
- ^ Ramūnas Garunkštis; Antanas Laurinčikas; Kohji Matsumoto; Jörn Steuding; Rasa Steuding (2010). "Effective uniform approximation by the Riemann zeta-function". Publicacions Matemàtiques. 54 (1): 209–219. doi:10.5565/PUBLMAT_54110_12. JSTOR 43736941.
- ^ Bhaskar Bagchi (1982). "A Joint Universality Theorem for Dirichlet L-Functions". Mathematische Zeitschrift. 181 (3): 319–334. doi:10.1007/bf01161980. ISSN 0025-5874. S2CID 120930513.
- ^ Steuding, Jörn (2007). Value-Distribution of L-Functions. Lecture Notes in Mathematics. Vol. 1877. Berlin: Springer. p. 19. arXiv:1711.06671. doi:10.1007/978-3-540-44822-8. ISBN 978-3-540-26526-9.
- ^ Karatsuba, A. A. (2001). "Lower bounds for the maximum modulus of ζ(s) in small domains of the critical strip". Mat. Zametki. 70 (5): 796–798.
- ^ Karatsuba, A. A. (2004). "Lower bounds for the maximum modulus of the Riemann zeta function on short segments of the critical line". Izv. Ross. Akad. Nauk, Ser. Mat. 68 (8): 99–104. Bibcode:2004IzMat..68.1157K. doi:10.1070/IM2004v068n06ABEH000513. S2CID 250796539.
- ^ Karatsuba, A. A. (1996). "Density theorem and the behavior of the argument of the Riemann zeta function". Mat. Zametki (60): 448–449.
- ^ Karatsuba, A. A. (1996). "On the function S(t)". Izv. Ross. Akad. Nauk, Ser. Mat. 60 (5): 27–56.
- ^ Knopp, Konrad (1947). Theory of Functions, Part Two. New York, Dover publications. pp. 51–55.
- ^ Riemann, Bernhard (1859). "On the number of primes less than a given magnitude". Monatsberichte der Königlich Preußischen Akademie der Wissenschaften zu Berlin. 번역하여 전재한
- ^ Neukirch, Jürgen (1999). Algebraic number theory. Springer. p. 422. ISBN 3-540-65399-6.
- ^ Hashimoto, Yasufumi; Iijima, Yasuyuki; Kurokawa, Nobushige; Wakayama, Masato (2004). "Euler's constants for the Selberg and the Dedekind zeta functions". Bulletin of the Belgian Mathematical Society, Simon Stevin. 11 (4): 493–516. doi:10.36045/bbms/1102689119. MR 2115723.
- ^ "A series representation for the Riemann Zeta derived from the Gauss-Kuzmin-Wirsing Operator" (PDF). Linas.org. Retrieved 4 January 2017.
- ^ a b Blagouchine, Iaroslav V. (2018). "Three Notes on Ser's and Hasse's Representations for the Zeta-functions". INTEGERS: The Electronic Journal of Combinatorial Number Theory. 18A: 1–45. arXiv:1606.02044. Bibcode:2016arXiv160602044B.
- ^ a b c Hasse, Helmut (1930). "Ein Summierungsverfahren für die Riemannsche ζ-Reihe" [A summation method for the Riemann ζ series]. Mathematische Zeitschrift (in German). 32 (1): 458–464. doi:10.1007/BF01194645. S2CID 120392534.
- ^ Sondow, Jonathan (1994). "Analytic continuation of Riemann's zeta function and values at negative integers via Euler's transformation of series" (PDF). Proceedings of the American Mathematical Society. 120 (2): 421–424. doi:10.1090/S0002-9939-1994-1172954-7.
- ^ Blagouchine, Iaroslav V. (2016). "Expansions of generalized Euler's constants into the series of polynomials in π−2 and into the formal enveloping series with rational coefficients only". Journal of Number Theory. 158: 365–396. arXiv:1501.00740. doi:10.1016/j.jnt.2015.06.012.
- ^ Ser, Joseph (1926). "Sur une expression de la fonction ζ(s) de Riemann" [Upon an expression for Riemann's ζ function]. Comptes rendus hebdomadaires des séances de l'Académie des Sciences (in French). 182: 1075–1077.
- ^ Maślanka, Krzysztof (1997). "The Beauty of Nothingness". Acta Cosmologica. XXIII–I: 13–17.
- ^ Báez-Duarte, Luis (2010). "On Maslanka's Representation for the Riemann Zeta Function". International Journal of Mathematics and Mathematical Sciences: 1–9.
- ^ Flajolet, Philippe; Vepstas, Linas (2006). "On Differences of Zeta Values". Classical Analysis and ODEs. arXiv:math/0611332.
- ^ Maślanka, Krzysztof; Koleżyński, Andrzej (2022). "The High Precision Numerical Calculation of Stieltjes Constants. Simple and Fast Algorithm". Computational Methods in Science and Technology. 28(2): 47–59.
- ^ Báez-Duarte, Luis (2003). "A New Necessary and Sufficient Condition for the Riemann Hypothesis". Number Theory. arXiv:math/0307215.
- ^ Maślanka, Krzysztof (2006). "Báez-Duarte's Criterion for the Riemann Hypothesis and Rice's Integrals". Number Theory. arXiv:math/0603713v2.
- ^ Wolf, Marek (2014). "Some remarks on the Báez-Duarte criterion for the Riemann Hypothesis". Computational Methods in Science and Technology. 20(2): 39–47.
- ^ Borwein, Peter (2000). "An Efficient Algorithm for the Riemann Zeta Function" (PDF). In Théra, Michel A. (ed.). Constructive, Experimental, and Nonlinear Analysis. Conference Proceedings, Canadian Mathematical Society. Vol. 27. Providence, RI: American Mathematical Society, on behalf of the Canadian Mathematical Society. pp. 29–34. ISBN 978-0-8218-2167-1. Archived from the original (PDF) on 26 July 2011. Retrieved 25 November 2017.
- ^ Mező, István (2013). "The primorial and the Riemann zeta function". The American Mathematical Monthly. 120 (4): 321.
- ^ Komatsu, Takao; Mező, István (2016). "Incomplete poly-Bernoulli numbers associated with incomplete Stirling numbers". Publicationes Mathematicae Debrecen. 88 (3–4): 357–368. arXiv:1510.05799. doi:10.5486/pmd.2016.7361. S2CID 55741906.
- ^ "A220335 - OEIS". oeis.org. Retrieved 17 April 2019.
- ^ Tóth, László (2022). "Linear Combinations of Dirichlet Series Associated with the Thue-Morse Sequence". Integers. 22 (article 98). arXiv:2211.13570.
- ^ Odlyzko, A. M.; Schönhage, A. (1988). "Fast algorithms for multiple evaluations of the Riemann zeta function". Trans. Amer. Math. Soc. 309 (2): 797–809. doi:10.2307/2000939. JSTOR 2000939. MR 0961614..
- ^ "Work on spin-chains by A. Knauf, et. al". Empslocal.ex.ac.uk. Retrieved 4 January 2017.
- ^ Gene Ward Smith. "Nearest integer to locations of increasingly large peaks of abs(zeta(0.5 + i*2*Pi/log(2)*t)) for increasing real t". The On-Line Encyclopedia of Integer Sequences. Retrieved 4 March 2022.
- ^ William A. Sethares (2005). Tuning, Timbre, Spectrum, Scale (2nd ed.). Springer-Verlag London. p. 74.
...there are many different ways to evaluate the goodness, reasonableness, fitness, or quality of a scale...Under some measures, 12-tet is the winner, under others 19-tet appears best, 53-tet often appears among the victors...
- ^ 이 섹션의 공식은 대부분 J. M. Borwein 등의 § 4에서 가져온 것입니다. (2000)
참고문헌
- Apostol, T. M. (2010). "Zeta and Related Functions". In Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.). NIST Handbook of Mathematical Functions. Cambridge University Press. ISBN 978-0-521-19225-5. MR 2723248..
- Borwein, Jonathan; Bradley, David M.; Crandall, Richard (2000). "Computational Strategies for the Riemann Zeta Function" (PDF). J. Comput. Appl. Math. 121 (1–2): 247–296. Bibcode:2000JCoAM.121..247B. doi:10.1016/S0377-0427(00)00336-8. Archived from the original (PDF) on 13 December 2013.
- Cvijović, Djurdje; Klinowski, Jacek (2002). "Integral Representations of the Riemann Zeta Function for Odd-Integer Arguments". J. Comput. Appl. Math. 142 (2): 435–439. Bibcode:2002JCoAM.142..435C. doi:10.1016/S0377-0427(02)00358-8. MR 1906742.
- Cvijović, Djurdje; Klinowski, Jacek (1997). "Continued-fraction expansions for the Riemann zeta function and polylogarithms". Proc. Amer. Math. Soc. 125 (9): 2543–2550. doi:10.1090/S0002-9939-97-04102-6.
- Edwards, H. M. (1974). Riemann's Zeta Function. Academic Press. ISBN 0-486-41740-9. 리만의 논문을 영어로 번역했습니다.
- Hadamard, Jacques (1896). "Sur la distribution des zéros de la fonction ζ(s) et ses conséquences arithmétiques". Bulletin de la Société Mathématique de France. 14: 199–220. doi:10.24033/bsmf.545.
- Hardy, G. H. (1949). Divergent Series. Clarendon Press, Oxford.
- Hasse, Helmut (1930). "Ein Summierungsverfahren für die Riemannsche ζ-Reihe". Math. Z. 32: 458–464. doi:10.1007/BF01194645. MR 1545177. S2CID 120392534. (Global convergent series expression)
- Ivic, A. (1985). The Riemann Zeta Function. John Wiley & Sons. ISBN 0-471-80634-X.
- Motohashi, Y. (1997). Spectral Theory of the Riemann Zeta-Function. Cambridge University Press. ISBN 0521445205.
- Karatsuba, A. A.; Voronin, S. M. (1992). The Riemann Zeta-Function. Berlin: W. de Gruyter.
- Mező, István; Dil, Ayhan (2010). "Hyperharmonic series involving Hurwitz zeta function". Journal of Number Theory. 130 (2): 360–369. doi:10.1016/j.jnt.2009.08.005. hdl:2437/90539. MR 2564902. S2CID 122707401.
- Montgomery, Hugh L.; Vaughan, Robert C. (2007). Multiplicative number theory. I. Classical theory. Cambridge tracts in advanced mathematics. Vol. 97. Cambridge University Press. Ch. 10. ISBN 978-0-521-84903-6.
- Newman, Donald J. (1998). Analytic number theory. Graduate Texts in Mathematics. Vol. 177. Springer-Verlag. Ch. 6. ISBN 0-387-98308-2.
- Raoh, Guo (1996). "The Distribution of the Logarithmic Derivative of the Riemann Zeta Function". Proceedings of the London Mathematical Society. s3–72: 1–27. doi:10.1112/plms/s3-72.1.1.
- Riemann, Bernhard (1859). "Über die Anzahl der Primzahlen unter einer gegebenen Grösse". Monatsberichte der Berliner Akademie.라이프치히 테우브너, 게삼멜테 Riemann, Bernhard (1859). "Über die Anzahl der Primzahlen unter einer gegebenen Grösse". Monatsberichte der Berliner Akademie.베르케에서 (1892), 뉴욕 도버에 의해 재인쇄 (1953).
- Sondow, Jonathan (1994). "Analytic continuation of Riemann's zeta function and values at negative integers via Euler's transformation of series" (PDF). Proc. Amer. Math. Soc. 120 (2): 421–424. doi:10.1090/S0002-9939-1994-1172954-7.
- Titchmarsh, E. C. (1986). Heath-Brown (ed.). The Theory of the Riemann Zeta Function (2nd rev. ed.). Oxford University Press.
- Whittaker, E. T.; Watson, G. N. (1927). A Course in Modern Analysis (4th ed.). Cambridge University Press. Ch. 13.
- Zhao, Jianqiang (1999). "Analytic continuation of multiple zeta functions". Proc. Amer. Math. Soc. 128 (5): 1275–1283. doi:10.1090/S0002-9939-99-05398-8. MR 1670846.
외부 링크
 Wikimedia Commons의 Riemann zeta 함수 관련 미디어
Wikimedia Commons의 Riemann zeta 함수 관련 미디어- "Zeta-function". Encyclopedia of Mathematics. EMS Press. 2001 [1994].
- Wolfram Mathworld의 Riemann Zeta Function - 보다 수학적인 접근을 통한 설명
- Wayback Machine에서 2009년 5월 17일 아카이브된 선택된 0의 표
- 소수가 적중하다 소수와 관련하여 제타 함수의 중요성에 대한 일반적이고 비기술적인 설명.
- 제타 기능의 X-레이 제타가 실제 또는 순수하게 가상인 곳에 대한 시각적 방향의 조사.
- 리만 제타 함수에 대한 공식과 항등식.wolfram.com
- Abramowitz와 Stegun의 23.2절, Riemann Zeta Function과 다른 상호 거듭제곱의 합
- Frenkel, Edward. "Million Dollar Math Problem" (video). Brady Haran. Archived from the original on 11 December 2021. Retrieved 11 March 2014.
- 멜린 변환과 리만 제타 함수의 함수방정식 - 리만 제타 함수를 이용한 멜린 변환 방법의 계산 예
- Riemann zeta 함수의 시각화와 3Blue1Brown의 비디오 분석적 연속




















































![{\displaystyle H{\sqrt[{3}]{\ln T}}e^{-c{\sqrt {\ln \ln T}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c2a08b909b3fbdc065cdc21c25e4469fb8136817)




















 다음과 같습니다.
다음과 같습니다. 
 Bernoulli 숫자이고
Bernoulli 숫자이고



![{\displaystyle \kappa :={\sqrt[{3}]{\pi ^{2}k}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0339cf277c68851802c4df552e62d4b84e031820)






![{\displaystyle {\begin{aligned}\int _{0}^{1}g(x)x^{s-1}\,dx&=\sum _{n=1}^{\infty }\int _{\frac {1}{n+1}}^{\frac {1}{n}}(x(n+1)-1)x^{s-1}\,dx\\[6pt]&=\sum _{n=1}^{\infty }{\frac {n^{-s}(s-1)+(n+1)^{-s-1}(n^{2}+2n+1)+n^{-s-1}s-n^{1-s}}{(s+1)s(n+1)}}\\[6pt]&={\frac {\zeta (s+1)}{s+1}}-{\frac {1}{s(s+1)}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0e030b32f7b471b521e7cc74a30548917e1d5443)


























