고조파 진행(수학)

수학에서 조화수열(또는 조화수열)은 산술수열의 왕복선을 취하여 형성된 수열이다.

동등하게, 각 항이 이웃 항들의 조화 평균일 때 시퀀스는 조화진행이다.

제3의 등가특성화로서 양식의 무한 시퀀스다.

${\displaystyle {\frac {1}{a1},\\frac {1}{a+d},\\\frac {1}{a+2d},\pcdots,}$

여기서 a는 0이 아니고 -a/d는 자연수 또는 형식의 유한순서가 아니다.

${\displaystyle {\frac {1}{a1},\\frac {1}{a+d},\\frac {1}{a+2d},\\frac {1}{a+3d},\\frac {1}{a+kd},},}$

여기서 a가 0이 아닌 경우 k는 자연수이고 -a/d는 자연수가 아니거나 k보다 크다.

예

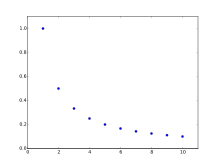
• 1, 1/2, 1/3, 1/4, 1/5, 1/6, 때로는 고조파 시퀀스라고도 함
• ${\displaystyle \frac{12}{}}$, 6, 4, 3, ${\displaystyle \frac{12}{}}$ 5 ${\$ 2, ${\displaystyle \frac{\mathrm{12n}}{}}$ ${\$ …
• 30, -30, -10, -6, ${\displaystyle \frac{-30}{}}$ ${\displaystyle \frac{7}{}}$ ${\$ … ${\displaystyle \frac{10}{}}$ ${\displaystyle \frac{1\mathrm{}}{}}$- ${\displaystyle \frac{\frac{\mathrm{2n}}{}}{}}$ ${\displaystyle \frac{\frac{\mathrm{}}{}}{}}$ ${\displaystyle$ {10$}{1-{\tfrac$ {$2n}{3}}}}}}}}}$
• 10, 30, -30, -10, -6, - $displaystyle$ $\},$ … ${\displaystyle \frac{10}{}}$ ${\displaystyle \frac{1\frac{\mathrm{}}{}}{}}$- 2${\displaystyle \frac{\frac{}{}}{}}$(${\displaystyle \frac{\frac{\mathrm{n}}{}}{}}$- 1${\displaystyle \frac{\frac{}{}}{}}$) ${\displaystyle \frac{\frac{\mathrm{}}{}}{}}$ ${\$

조화진행합계

무한 조화 진보는 합계가 아니다(무한도 합).

구별되는 단위 분수의 고조파 진행(a = 1과 k = 0인 사소한 경우 제외)이 정수에 합치는 것은 불가능하다. 그 이유는, 필연적으로 적어도 진행의 한 분모가 다른 분모를 나누지 않는 소수로서 분할될 것이기 때문이다.^[1]

기하학에서 사용

만약 시준점 A, B, C, D가 A와 B에 관한 C의 조화 결합점이라면, 이들 지점들 중 하나에서 나머지 세 지점까지의 거리는 조화 진행을 형성한다.^[2][3] 구체적으로는 각 시퀀스 AC, AB, AD, BC, BA, BD, CA, CD, CB, DA, DC, DB가 조화진행으로, 여기서 각 거리는 선의 고정된 방향에 따라 서명된다.

삼각형에서, 만약 고도가 산술적 수열이라면, 옆면은 조화 수열이다.

리레의 기울어진 탑

하모니 진행의 훌륭한 예는 리레의 기울어진 탑이다. 그 안에서 균일한 블록을 서로 위로 쌓아 올려 최대 측면 또는 측면 거리를 달성한다. 블록은 원래 블록 아래로 1/2, 1/4, 1/6, 1/8, 1/10, ... 거리를 측면으로 쌓는다. 이것은 무게중심이 붕괴되지 않도록 구조물의 중심에 바로 있도록 한다. 구조물의 무게가 약간 증가하면 불안정해지고 떨어진다.

참고 항목

• 기하급수
• 고조파 계열
• 왕복 총액 목록
• 고조파(음악)

참조

• Stan Gibilisco, Norman H. Crowhurst, (2007) 페이지 221에 의한 기술 수학 마스터링
• 화학고무회사별 표준수학표(1974) 페이지 102
• Webster Wells (1897) 페이지 307에 의한 중등학교 대수학 필수사항