특수수학함수
수학 에서 다변량 (Alfred Jonquiere의 함수 라고도 함)은 순서 s 와 인수 z의 특수 함수 Lis z )이다. s 의 특별한 값에 대해서만 다변량 로그는 자연 로그 나 합리적인 함수 와 같은 기본적인 함수 로 감소한다. 양자 통계 에서 다로그아립트 함수는 페르미-디락 분포와 보스-아인슈타인 분포의 폐쇄된 형태 의 통합으로 나타나며, 페르미-디락 적분 또는 보스-아인슈타인 적분이라고 도 한다. 양자 전자역학 에서는 고차 파인만 다이어그램 으로 대표되는 공정의 계산에서 양 의 정수 순서의 폴리 로가리듬이 발생한다.
폴리로가리템 함수는 허위츠 제타 함수 와 동등하며, 두 함수는 다른 함수 로 표현될 수 있으며, 두 함수는 레르치 초월성 의 특별한 경우다. 다변량 로그는 다변량 함수와 혼동해서는 안 되며, 동일한 표기법을 가지고 있지만 하나의 변수를 갖는 오프셋 로그 적분과 혼동해서는 안 된다.
다변량 함수는 z 단위의 파워 시리즈 에 의해 정의되며, 또한 s 단위의 디리클레 시리즈 :
리 s ( z ) = ∑ k = 1 ∞ z k k s = z + z 2 2 s + z 3 3 s + ⋯ {\displaystyle \operatorname {Li} _{s}(z)=\sum _{k=1}^{{k}{z^{k} \over k^{s}}}=z+{z^{2} \cdots }
이 정의는 임의의 복잡한 순서 s 와 z < 1이 있는 모든 복잡한 인수 z 에 유효하며, 분석적 연속성 과정에 의해 z ≥ 1로 확장될 수 있다. (여기서 분모 n은s exp(s ln(n))로 이해된다.) 특수경우 s = 1은 일반적인 자연 로그인 Li1 (z ) = -ln(1-z)을 포함하며, 특수경우 s = 2와 s = 3은 각각 딜로가림 (스펜스의 함수라고도 함)과 3엽합체라고 한다. 함수의 이름은 함수의 반복적 적분 으로 정의될 수 있다는 사실에서 유래한다.
리 s + 1 ( z ) = ∫ 0 z 리 s ( t ) t d t {\displaystyle \operatorname {Li} _{s+1}(z)=\int_{0}^{z}{\frac {\operatorname {Li} _{s}(t){t}dt}
따라서 dilogarithm은 로그 등을 포함하는 함수의 적분이다. 비양수 정수 순서 s 의 경우 다변량 함수는 합리적인 함수 다.
특성. 다각측량 순서 s {\displaystyle s} n {\displaystyle n}( n {\displaystyle -n}) 그것은 종종 μ을 정의할)ln (z)은 때때로 (z){\displaystyle \operatorname{단풍잎}(z)}은 너무− π<>는 복잡한 로그;나는(μ)≤ π 의 ln(z){\displaystyle \ln(z)}이 주요 지점{\displaystyle \mu =\ln(z)}.{\displaystyle -\pi<>\operatorname{ 난}(\mu)\leq \pi.}또한 알 편리하다.나는 exp onentation은 z s exp ln z {\displaystyle z^{s}=\exp(s\ln( }
순서 displaystyle s Li신규의 주요한 가지 (z){\displaystyle \operatorname{Li}_ᆫ(z)}z<>가 주어질, 위의 시리즈 정의로 1{\displaystyle z<1}, 상처 z1{\displaystyle z=1}∞{\displaystyle \infty로 이루어져는 긍정적인 진정한 축을 제외하고 연속으로 찍힌다.} 이러한는 축은 z{z\displaystyle}의 하단 절반을 비행기에.μ{\displaystyle \mu}의 측면에서 놓고, 그 − π<>arg (− μ)≤ π{\displaystyle -\pi<>\operatorname{아그}(-\mu)\leq \pi}.μ{\displaystyle \mu}에 대한 의존성의 polylogarithm의 불연속성이 때때로con 수 있다.혼합 .
실제 z {\displaystyle z} , z {\displaystyle z<1 \geq 1} 우드 1992 , § 3)인 경우 실제 순서 s displaysty s}
임 ( 리 s ( z ) ) = − π μ s − 1 Γ ( s ) . {\displaystyle \operatorname {Im} \left(\operatorname {Li} _{s}(z)\right)=-{{\pi \mu ^{s-1} \over {\Gamma(s)}}}. }
컷을 통과하여 ε 이 무한히 작은 양의 실수인 경우, 다음과 같이 처리한다.
임 ( 리 s ( z + i ϵ ) ) = π μ s − 1 Γ ( s ) . {\displaystyle \operatorname {Im} \left(\operatorname {Li} _{s}(z+i\epsilon )\오른쪽) ={{\pi \mu ^{s-1} \over {\Gamma(s)}}}. }
두 가지 모두 약 µ 0 의 Lis e µ 아래 참조 ) 에서 결론을 내릴 수 있다.
다변량 분석의 파생상품은 정의 권력 시리즈에서 다음과 같다.
z ∂ 리 s ( z ) ∂ z = 리 s − 1 ( z ) {\displaystyle z{\frac {\partial \operatorname {Li} _{s}(z){\partial z}=\operatorname {Li} _{s-1}(z)} ∂ 리 s ( e μ ) ∂ μ = 리 s − 1 ( e μ ) . {\displaystyle {\frac {\partial \operatorname {Li} _{s}(e^{\mu }}){\partial \mu }{}}{s-1}(e^{\mu }). }
제곱 관계는 시리즈 정의에서 볼 수 있으며, 중복 공식 과 관련이 있다(Clunie(1954년), Schrödinger(1952 ) 참조).
리 s ( − z ) + 리 s ( z ) = 2 1 − s 리 s ( z 2 ) . {\displaystyle \operatorname {Li} _{s}(-z)+\operatorname {Li} _{s}=2^{1-s}\operatorname {Li} _{s}(z^{2}) }
쿠머의 기능 은 매우 유사한 복제 공식을 따른다. 이것은 모든 양의 정수 p :에 대한 곱셈 공식 의 특별한 경우다.
∑ m = 0 p − 1 리 s ( z e 2 π i m / p ) = p 1 − s 리 s ( z p ) , {\displaystyle \sum \sum _{m=0}^{p-1}\operatorname {Li}_{s}{2\pi im/p}=p^{1-s}\operatorname {Li} _{s}(z^{p}),}}
다중 로그의 직렬 정의와 지수 항의 직교성을 사용하여 증명할 수 있다(예: 이산 푸리에 변환 참조).
또 다른 중요한 속성인 반전 공식은 후르비츠 제타 함수 또는 베르누이 다항식 함수를 포함하며, 아래의 다른 함수와의 관계 에서 발견된다.
특정 값 특별한 경우, 다변량(polylogarithm)은 다른 기능(아래 참조 )으로 표현할 수 있다. 따라서 다항목에 대한 특정 값은 이러한 다른 함수의 특정 값으로도 찾을 수 있다.
다로그순서의 정수 값의 경우, Li1 (z )에 z ·limit/limitz 를 반복적으로 적용하여 다음과 같은 명시적 표현을 얻는다. 리 1 ( z ) = − ln ( 1 − z ) {\displaystyle \operatorname {Li} _{1}(z)=-\ln(1-z)} 리 0 ( z ) = z 1 − z {\displaystyle \operatorname {Li} _{0}(z)={z \over 1-z}}} 리 − 1 ( z ) = z ( 1 − z ) 2 {\displaystyle \operatorname {Li} _{-1}(z)={z \over(1-z)^{2}}} 리 − 2 ( z ) = z ( 1 + z ) ( 1 − z ) 3 {\displaystyle \operatorname {Li} _{-2}(z)={z(1+z) \over(1-z)^{3}}} 리 − 3 ( z ) = z ( 1 + 4 z + z 2 ) ( 1 − z ) 4 {\displaystyle \operatorname {Li} _{-3}(z)={z(1+4z+z^{2}) \over(1-z)^{4}}} 리 − 4 ( z ) = z ( 1 + z ) ( 1 + 10 z + z 2 ) ( 1 − z ) 5 . {\displaystyle \operatorname {Li} _{-4}(z)={z(1+z)(1+10z+z^{2} \over(1-z)^{5}. } 따라서 다항식(polylogarithm)은 z 의 다항식(polynomials) 비율로 감소하며, 따라서 모든 비양수 정수 순서 에 대해 z의 합리적인 함수 가 된다. 일반적인 경우는 유한한 합으로 표현할 수 있다. 리 − n ( z ) = ( z ∂ ∂ z ) n z 1 − z = ∑ k = 0 n k ! S ( n + 1 , k + 1 ) ( z 1 − z ) k + 1 ( n = 0 , 1 , 2 , … ) , {\displaystyle \operatorname {Li} _{-n}(z)=\왼쪽(z{\partial \partial z}\오른쪽) ^{n}{z \over{1-z}}=\sum _{k=0}^{n}k! S(n+1,k+1)\왼쪽({z \over {1-z}}\오른쪽) ^{k+1}\qquad (n=0,1,2,\ldots )} 여기서 S (n ,k )는 두 번째 종류의 스털링 번호 다. 음의 정수 순서에 적용되는 등가 공식은 다음과 같다(Wood 1992 , § 6). 리 − n ( z ) = ( − 1 ) n + 1 ∑ k = 0 n k ! S ( n + 1 , k + 1 ) ( − 1 1 − z ) k + 1 ( n = 1 , 2 , 3 , … ) , {\displaystyle \operatorname {Li} _{-n}(z)=(-1)^{n+1}\sum _{k=0}^{n}k! S(n+1,k+1)\왼쪽({{-1} \{1-z}}\오른쪽) ^{k+1}\qquad (n=1,2,3,\ldots )} 및: 리 − n ( z ) = 1 ( 1 − z ) n + 1 ∑ k = 0 n − 1 ⟨ n k ⟩ z n − k ( n = 1 , 2 , 3 , … ) , {\displaystyle \operatorname {Li} _{-n}(z)={1\over (1-z)^{n+1}\sum _{k=0}^{n-1}\left\langle {n atop k}\rigle z^{n-k}\qquad(n=1,2,3,\ldots)}),}) 여기서 ⟨n k ⟩ {\ displaystyle \scriptstyle \left\langle { \atop k}\right\angle } 오일러 숫자다. Li−n (z )의 모든 루트는 구별되고 실제적이며, z = 0을 포함하며, 나머지는 음수이고 로그 척도에서 z = -1을 중심으로 한다. n 이 커짐에 따라 이러한 이성적 표현에 대한 수치적 평가는 점점 취소로 인해 어려움을 겪게 된다(Wood 1992 , § 6). 그러나 Hurwitz zeta 함수와의 일반적인 관계를 통해 Li−n (z )를 계산함으로써 완전한 정확성을 얻을 수 있다(아래 참조 ). 인수 z 의 반정수 값에 대한 일부 특정 표현식은 다음과 같다. 리 1 ( 1 2 ) = ln 2 {\displaystyle \operatorname {Li} _{1}({\tfrac {1}{2}})=\ln 2} 리 2 ( 1 2 ) = 1 12 π 2 − 1 2 ( ln 2 ) 2 {\displaystyle \operatorname {Li} _{2}({\tfrac {1}{1}{2}}:={\tfrac {1}{12}\pi ^{2}-{\tfrac {1}{1}{1}{1}{{1}(\ln 2)^{2}}: 리 3 ( 1 2 ) = 1 6 ( ln 2 ) 3 − 1 12 π 2 ln 2 + 7 8 ζ ( 3 ) , {\displaystyle \operatorname {Li} _{3}({\tfrac {1}{1}{1}{6}(\ln 2)^{3}-{\tfrac {1}{1}}-{12}}\pi ^{2}\tfrac {7}}}}}제타(3),} 여기서 ζ 은 리만 제타 함수 다. 이러한 유형의 공식은 정수 순서가 높은 것으로 알려져 있지 않지만(Lewin 1991 , 페이지 2), 예를 들면 다음과 같다(Borwein, Borwein & Girgenson 1995 ). 리 4 ( 1 2 ) = 1 360 π 4 − 1 24 ( ln 2 ) 4 + 1 24 π 2 ( ln 2 ) 2 − 1 2 ζ ( 3 ¯ , 1 ¯ ) , {\displaystyle \operatorname {Li} _{4}({\tfrac {1}{2}})={\tfrac {1}{360}}\pi ^{4}-{\tfrac {1}{24}}(\ln 2)^{4}+{\tfrac {1}{24}}\pi ^{2}(\ln 2)^{2}-{\tfrac {1}{2}}\zeta ({\bar {3}},{\bar {1}}),} 2분의 1을 교대로 합쳐서 ζ ( 3 ¯ , 1 ¯ ) = ∑ m > n > 0 ( − 1 ) m + n m − 3 n − 1 . {\displaystyle \jeta({\bar{3},{\bar {1})=\sum _{m>n}0(-1)^{m+n^{-3}n^{-1}. } 일반적으로 정수의 순서 는 n 2 2 (Broadhurst 1996 , 페이지 9): 리 n ( 1 2 ) = − ζ ( 1 ¯ , 1 ¯ , { 1 } n − 2 ) , {\displaystyle \operatorname {Li} _{n}({\tfrac {1}{2}})=-\제타({\bar {1}, {\bar {{1},\reft\{1\}^{n-2}),} 여기서 ζ (s 1 , …, s k 다중 제타 함수 (예: 리 5 ( 1 2 ) = − ζ ( 1 ¯ , 1 ¯ , 1 , 1 , 1 ) . {\displaystyle \operatorname {Li} _{5}({\tfrac {1}{2}})=-\zeta({\bar {1},{1}, 1,1,1) } 직렬 정의의 직접적인 결과로서, 통합 의 p번째 복합적 뿌리에서 다변량 값은 푸리에 합 에 의해 다음과 같이 주어진다. 리 s ( e 2 π i m / p ) = p − s ∑ k = 1 p e 2 π i m k / p ζ ( s , k p ) ( m = 1 , 2 , … , p − 1 ) , {\displaystyle \operatorname {Li} _{s}(e^{2\pi im/p}) _{k=1}\sum _{k=1}e^{p^{2\pi imk/p}\제타(s, {\tfrac {k}{p}}}}})\qquad(m=1,2,\dots,p-1}),}} 여기서 ζ 은 후르비츠 제타 함수다. Lis s ) > 1의 경우, 관계도 m = 0 또는 m = p 로 유지된다. 이 공식은 아래의 다른 기능과의 관계 하에 열거된 허위츠 제타 함수와의 보다 일반적인 관계가 함축된 것만큼 단순하지는 않지만, s 의 비음수 정수 값에도 적용할 수 있는 장점이 있다. 평소와 같이 관계를 반전시켜 m = 1, …,p p 를 k = 1, …에 대한 Li 의s k p
다른 기능과의 관계 z = 1의 경우 폴리 로가리듬이 Riemann 제타 함수 로 감소함 리 s ( 1 ) = ζ ( s ) ( 레 ( s ) > 1 ) . {\displaystyle \operatorname {Li} _{s}(1)=\제타(s)\qquad(\operatorname {Re}s)>1. } 폴리로그리듬은 Dirichlet eta 함수 및 Dirichlet 베타 함수 와 관련이 있다. 리 s ( − 1 ) = − η ( s ) , {\displaystyle \operatorname {Li} _{s}(-1)=-\eta,} 여기서 η 은 디리클레 에타 함수다. 순수한 상상의 논쟁에 대해 우리는 다음과 같은 것을 가지고 있다. 리 s ( ± i ) = − 2 − s η ( s ) ± i β ( s ) , {\displaystyle \operatorname {Li} _{s}(\pm i)=-2^{-s}\eta(s)\pm i\beta(s),} 여기서 β (s )는 디리클레 베타 함수다. 폴리로그리듬은 다음 과 같이 완전한 페르미-디락 적분 과 관련이 있다. F s ( μ ) = − 리 s + 1 ( − e μ ) . {\displaystyle F_{s}(\mu )=-\operatorname {Li} _{s+1}(-e^{\mu }). } 다로그는 불완전한 다로그 함수의 특별한 경우다. 리 s ( z ) = 리 s ( 0 , z ) . {\displaystyle \operatorname {Li} _{s}(z)=\operatorname {Li} _{s}(0,z). } 폴리로그리템은 르르흐 초월체 의 특별한 경우다(Erdelyi et al. 1981 , § 1.11-14). 리 s ( z ) = z Φ ( z , s , 1 ) . {\displaystyle \operatorname {Li} _{s}(z)=z\Phi(z,s,1). } 폴리로그리듬은 허위츠 제타 함수 에 다음과 같은 방법으로 관련된다. 리 s ( z ) = Γ ( 1 − s ) ( 2 π ) 1 − s [ i 1 − s ζ ( 1 − s , 1 2 + ln ( − z ) 2 π i ) + i s − 1 ζ ( 1 − s , 1 2 − ln ( − z ) 2 π i ) ] , {\displaystyle \operatorname {Li} _{s}(z)={\Gamma (1-s) \over (2\pi )^{1-s}}\left[i^{1-s}\zeta \left(1-s,{\frac {1}{2}}+{\ln(-z) \over {2\pi i}}\right)+i^{s-1}~\zeta \left(1-s,{\frac {1}{2}}-{\ln(-z) \over {2\pi i}}\right)\right],} 그러나 이 관계는 감마함수 γ(1 - s )의 극 에 의한 양의 정수 s 와 두 제타 함수의 극에 의한 s = 0으로 무효화된다. 이 공식의 도출은 아래의 직렬 표현에 따라 주어진다 . Hurwitz zeta 함수에 대한 함수 방정식의 약간의 도움을 받으면, 다변량도 결과적으로 (Jonquiere 1889 )을 통해 그 함수와 관련이 있다. i − s 리 s ( e 2 π i x ) + i s 리 s ( e − 2 π i x ) = ( 2 π ) s Γ ( s ) ζ ( 1 − s , x ) , {\displaystyle i^{-s}\operatorname {Li} _{s}(e^{2\pi ix}) _{s} _{s}(e^{-2\pi ix}}={(2\pi )^} \over \Gamma(s)\zeta(1-s,x)}),} 이 관계는 임(x )이 0일 경우 0 ≤ Re(x ) < 1을 유지하고, 임(x )이 0일 경우 0 < Re(x ) 1을 유지한다. 모든 복합 s 와 복합 z ] ]0;1에 대해 동등하게, 반전 공식은 다음과 같다. 리 s ( z ) + ( − 1 ) s 리 s ( 1 / z ) = ( 2 π i ) s Γ ( s ) ζ ( 1 − s , 1 2 + ln ( − z ) 2 π i ) , {\displaystyle \operatorname {Li} _{s}(z)+(-1)^{s}\operatorname {Li} _{s}(1/z)={(2\pi i)^{s} \over \Gamma (s)}~\zeta \left(1-s,~{\frac {1}{2}}+{\ln(-z) \over {2\pi i}}\right),} 그리고 모든 복합 s 와 복합 z ] ]1;∞[]에 대하여 리 s ( z ) + ( − 1 ) s 리 s ( 1 / z ) = ( 2 π i ) s Γ ( s ) ζ ( 1 − s , 1 2 − ln ( − 1 / z ) 2 π i ) . {\displaystyle \operatorname {Li} _{s}(z)+(-1)^{s}\operatorname {Li} _{s}(1/z)={(2\pi i)^{s} \over \Gamma (s)}~\zeta \left(1-s,~{\frac {1}{2}}-{\ln(-1/z) \over {2\pi i}}\right). } z ∉ ]0;∞[ 1은 ln(-z ) = -ln(-⁄)1 z 이러한 관계는 정의 권력 시리즈의 수렴 z = 1을 넘어 다변량 연속 분석을 제공한다. (Jonquiere (1889 , eq. 5)와 Erdelyi 외 연구진 (1981 , § 1.11-16)의 해당 방정식은 다로그와 로그의 주요 분기가 동시에 사용된다고 가정할 경우 정확하지 않다.) s 가 정수일 경우 단순화된 공식은 다음 항목을 참조하십시오. 양의 정수 다변량 명령 s 의 경우, Hurwitz zeta 함수 ζ(1-s , x )는 베르누이 다항식 , ζ(1-n, x) = -Bn x ) / n 으로 감소하며, n = 1, 2, 3 …에 대한 Jonquiere의 반전 공식은 다음과 같이 된다. 리 n ( e 2 π i x ) + ( − 1 ) n 리 n ( e − 2 π i x ) = − ( 2 π i ) n n ! B n ( x ) , {\displaystyle \operatorname {Li} _{n}(e^{2\pi ix})+(1)^{n}\operatorname {Li} _{n}(e^{-2\pi ix})=-{(2\pi i)^{n} \overn!} B_{n}(x),} where again 0 ≤ Re(x ) < 1 if Im(x ) ≥ 0, and 0 < Re(x ) ≤ 1 if Im(x ) < 0. Upon restriction of the polylogarithm argument to the unit circle, Im(x ) = 0, the left hand side of this formula simplifies to 2 Re(Lin e 2πix )) if n is even, and to 2i Im(Lin e 2πix )) if n is odd. 반면에 음의 정수 순서의 경우, γ의 차이 는 다음과 같은 모든 z를 암시 한다(Erdelyi et al. 1981 , § 1.11-17). 리 − n ( z ) + ( − 1 ) n 리 − n ( 1 / z ) = 0 ( n = 1 , 2 , 3 , … ) . {\displaystyle \operatorname {Li} _{-n}(z)+(-1)^{n}\operatorname {Li} _{-n}(1/z)=0\qquad(n=1,2,\ldots). } 보다 0, ±1, ±2, ±3 에 대해 다음을 가진다. 리 n ( z ) + ( − 1 ) n 리 n ( 1 / z ) = − ( 2 π i ) n n ! B n ( 1 2 + ln ( − z ) 2 π i ) ( z ∉ ] 0 ; 1 ] ) , {\displaystyle \operatorname {Li} _{n}(z)+(-1)^{n}\operatorname {Li} _{n}(1/z)=-{\frac {(2\pi i)^{n}}{n! }}}{n}\왼쪽({\frac {1}{2}}+{\ln(-z) \over {2\pi i}\}\right)\qquad(z\not \in ]0;1]),} 리 n ( z ) + ( − 1 ) n 리 n ( 1 / z ) = − ( 2 π i ) n n ! B n ( 1 2 − ln ( − 1 / z ) 2 π i ) ( z ∉ ] 1 ; ∞ [ ) , {\displaystyle \operatorname {Li} _{n}(z)+(-1)^{n}\operatorname {Li} _{n}(1/z)=-{\frac {(2\pi i)^{n}}{n! }}}{n}\왼쪽({\frac {1}{1}{2}}-{\ln(-1/z) {2\pi i}\\오른쪽)\qquad(z\not \in ~]1;\inflt []),} 여기서 두 식이 모두 z ] ]0;∞[]에 동의한다. ( Jonquiere(1889 , eq. 1)과 Erdelyi 외 연구진(1981 , § 1.11-18)의 해당 방정식은 다시 정확하지 않다.) 순수한 가상의 μ 를 갖는 폴리로그리듬은 클로스겐 함수Ci s s Lewin 1958 , 7장 1.4, Abramowitz & Stegun 1972, § 27.8). 리 s ( e ± i θ ) = C i s ( θ ) ± i S i s ( θ ) . {\displaystyle \operatorname {Li} _{s}(e^{\pm i\theta })=Ci_{s}(\theta )\pm iSi_{s}(\theta). } 역접선 적분Ti s z ) (Lewin 1958 , Cha. VII § 1.2)는 다항분석의 단위로 표현할 수 있다. 티 s ( z ) = 1 2 i [ 리 s ( i z ) − 리 s ( − i z ) ] . {\displaystyle \operatorname {Ti} _{s}(z)={1 \over 2i}\left[\operatorname {Li} _{s}-\operatorname {Li} _{s}(-iz)\right]. } 특히 그 관계는 다음을 암시한다. 티 0 ( z ) = z 1 + z 2 , 티 1 ( z ) = 아크탄의 z , 티 2 ( z ) = ∫ 0 z 아크탄의 t t d t , … 티 n + 1 ( z ) = ∫ 0 z 티 n ( t ) t d t , {\displaystyle \operatorname {Ti} _{0}(z)={z \over 1+z^{2}},\quad \operatorname {Ti} _{1}(z)=\arctan z,\quad \operatorname {Ti} _{2}(z)=\int _{0}^{z}{\arctan t \over t}dt,\quad \ldots ~\quad \operatorname {Ti} _{n+1}(z)=\int _{0}^{z}{\frac {\operatorname {Ti} _{n}(t)}{t}}dt,} 함수 이름이 설명되는군 Legendre chi 함수 s z ) (Lewin 1958 , Cha. VII § 1.1; Boersma & Dempsey 1992 )는 다변량(polylogarithms) 단위로 표현할 수 있다. χ s ( z ) = 1 2 [ 리 s ( z ) − 리 s ( − z ) ] . {\displaystyle \chi _{s}(z)={\tfrac {1}{1}{1}:{2}}\왼쪽[\operatorname {Li}_{s}-\operatorname {Li} _{s}(-z)\right]. } 정수 순서의 폴리로그는 일반화된 초기하 함수 로 표현될 수 있다. 리 n ( z ) = z n + 1 F n ( 1 , 1 , … , 1 ; 2 , 2 , … , 2 ; z ) ( n = 0 , 1 , 2 , … ) , {\displaystyle \operatorname {Li} _{n}(z)=z_{n+1}F_{n}(1,1,\dots,1,2,\dots,2;z)\qquad(n=0,1,1,2,\ldots )} 리 − n ( z ) = z n F n − 1 ( 2 , 2 , … , 2 ; 1 , 1 , … , 1 ; z ) ( n = 1 , 2 , 3 , … ) . {\displaystyle \operatorname {Li} _{-n}=z_{n-1}F_{n-1}(2,2,\dots,2,1,1,\dots,1;z)\qquad(n=1,2,3,\ldots )~.} 불완전한 제타 함수 또는 "Debye 함수 "(Abramowitz & Stegun 1972 , § 27.1): Z n ( z ) = 1 ( n − 1 ) ! ∫ z ∞ t n − 1 e t − 1 d t ( n = 1 , 2 , 3 , … ) , {\displaystyle Z_{n}(z)={1 \over(n-1)! }\int _{z}^{\infit }{t^{n-1} \over e^{t}-1}dt\qquad (n=1,2,3,\ldots )} 양의 정수 n에 대한 다각측량 Lin z )는 유한 합으로 표현될 수 있다(Wood 1992 , § 16). 리 n ( e μ ) = ∑ k = 0 n − 1 Z n − k ( − μ ) μ k k ! ( n = 1 , 2 , 3 , … ) . {\displaystyle \operatorname {Li} _{n}(e^{\mu }}=\sum _{k=0}^{n-1}Z_{n-k}(-\mu ){\mu ^{k} \over k!}\qquad(n=1,2,3,\ldots). } 상당히 유사한 표현식은 "Debye 함수" Z n z )와 다변량(polylogarithm: Z n ( z ) = ∑ k = 0 n − 1 리 n − k ( e − z ) z k k ! ( n = 1 , 2 , 3 , … ) . {\displaystyle Z_{n}(z)=\sum _{k=0}^{n-1}\operatorname {Li} _{n-k}(e^{-z}){z^{k} \over k!}\qquad(n=1,2,\ldots). } Lambert 시리즈 Js displaystyle J_{s}( 가 라면, ∑ n = 1 ∞ z n J − s ( n ) 1 − z n = 리 s ( z ) . {\displaystyle \sum _{n=1}^{\inflt }{z^{n}J_{-s}(n)}{1-z^{n}}}=\operatorname {Li} _{s}z} } 적분표현 다음 적분 표현 중 하나는 정의 전력 시리즈의 수렴원 z = 1을 넘어 다변량 연속 분석 을 제공한다.
다변량 로그는 보세-아인슈타인 분포 의 적분 단위로 표시할 수 있다. 리 s ( z ) = 1 Γ ( s ) ∫ 0 ∞ t s − 1 e t / z − 1 d t . {\displaystyle \operatorname {Li} _{s}(z)={1 \over \Gamma(s)\int_{0}^{\ft }{t^{s-1} \over e^{t}/z-1}dt. } 이것은 re(s ) > 0과 z real과 ≥ 1을 제외한 모든 z 에 수렴한다. 이 맥락에서 다변량(polylogarithm)은 때때로 보세 적분(Bose integrity)이라고 부르지만, 더 흔히 보세-아인슈타인 적분(Bose-Einstein integrity )이라고 부른다.[1] 이와 유사하게, 다변량 로그는 페르미-디락 분포 의 적분으로 표현될 수 있다. − 리 s ( − z ) = 1 Γ ( s ) ∫ 0 ∞ t s − 1 e t / z + 1 d t . {\displaystyle -\operatorname {Li} _{s}-z={\frac {1}{\frac {1}{0}^{\int _{0}{t^{s-1} \over e^{t}/z+1}dt. } 이것은 re(s ) > 0과 z real과 and -1을 제외한 모든 z 에 수렴한다. 이 맥락에서 다변량(polylogarithm)은 페르미 적분 또는 페르미-디락 적분 [2] GSL 2010 )이라고도 한다. 이러한 표현은 통합의 Taylor 확장 에 의해 z 및 용어 통합과 관련하여 쉽게 검증된다. 딩글의 논문에는 두 종류의 통합에 대한 상세한 조사가 수록되어 있다. 폴리로그는 맥스웰-볼츠만 분포 의 적분과도 관련이 있다. 임이 있는 z → 0 리 s ( z ) z = 1 Γ ( s ) ∫ 0 ∞ t s − 1 e − t d t = 1. {\displaystyle \lim_{z\to 0}{\frac {\operatorname {Li}_{s}{z}}}}}={1 \over \감마(s)\int _{0}^{t^{s-1e^{-t}dt=1. } 이것은 또한 원산지 근처에서 다목적의 점근거동 을 준다. 보완적 적분 표현은 z real과 < 0을 제외한 모든 z 에 적용된다. 리 s ( z ) = ∫ 0 ∞ t − s 죄를 짓다 [ s π / 2 − t ln ( − z ) ] 징징거리다 ( π t ) d t . {\displaystyle \operatorname {Li} _{s}(z)=\int_{0}^{0}{t^{-s}\sin[s\pi /2-t\ln(-z)] \over \sinh(\pi t)}dt. } 이 적분은 Hurwitz zeta 함수( 위 참조) 및 후자의 친숙한 적분 표현과 폴리로그의 일반적인 관계에서 따온 것이다. 다변량 로그는 일반적 으로 보세-아인슈타인 표현을 음의 순서 로 확장하는 행클 등고선 적분(Whittaker & Watson 1927 , § 12.22, § 13.13)으로 나타낼 수 있다. 통합체 의 t = μpole 이 음이 아닌 실제 축에 놓여 있지 않는 한, s ≠ 1, 2, 3, …은 다음과 같다. 리 s ( e μ ) = − Γ ( 1 − s ) 2 π i ∮ H ( − t ) s − 1 e t − μ − 1 d t {\displaystyle \operatorname {Li} _{s}(e^{\mu }}=-{\\\s) \over {2\pi i}\}\point _{H}{-t)^{s-1}{e^{t-\mu }-1}{1}:{s-1dt} 여기서 H 는 행클 윤곽선을 나타낸다. 통합은 0에서 무한대로의 실제 축을 따라 절단되며 축은 t 의 하단 반면에 속한다. 통합은 상부 하프 평면에서 +∞(Im(t ) > 0)에서 시작하여 극 t = µ + 2kπi 중 어느 것도 감싸지 않고 원점을 원을 그리며, 하부 하프 평면에서 +∞(Im(t ) < 0)에서 종료한다. µ 가 실제이고 음이 아닌 경우, 동봉된 t = µpole 의 기여도를 단순히 뺄 수 있다. 리 s ( e μ ) = − Γ ( 1 − s ) 2 π i ∮ H ( − t ) s − 1 e t − μ − 1 d t − 2 π i R {\displaystyle \operatorname {Li} _{s}(e^{\mu })=-{{\Gamma(1-s) \over {2\pi i}\}\point _{H}{-t){s-1}{e^{{t-\mu }}}{1}d-2\pi iR} 여기서 R 은 폴의 잔류물 이다. R = i 2 π Γ ( 1 − s ) ( − μ ) s − 1 . {\displaystyle R={i \over 2\pi }\감마(1-s)(-\mu )^{s-1}. } 아벨-Plana 공식 을 폴리로그의 정의 시리즈에 적용할 때, 모든 복합 z 와 모든 복합 s 에 유효한 헤르미테 형태의 적분 표현 결과: 리 s ( z ) = 1 2 z + Γ ( 1 − s , − ln z ) ( − ln z ) 1 − s + 2 z ∫ 0 ∞ 죄를 짓다 ( s 아크탄의 t − t ln z ) ( 1 + t 2 ) s / 2 ( e 2 π t − 1 ) d t {\displaystyle \operatorname {Li} _{s}(z)={\tfrac {1}{2}}z+{\Gamma (1-s,-\ln z) \over (-\ln z)^{1-s}}+2z\int _{0}^{\infty }{\frac {\sin(s\arctan t-t\ln z)}{(1+t^{2})^{s/2}(e^{2\pi t}-1)}}dt} 여기서 γ은 상부 불완전 감마함수 다. 이 식에서 ln(z )의 모든(부분은 아님)은 -ln(½)1 z 모든 복잡한 s 에도 적용되는 관련 표현, 리 s ( z ) = 1 2 z + z ∫ 0 ∞ 죄를 짓다 [ s 아크탄의 t − t ln ( − z ) ] ( 1 + t 2 ) s / 2 징징거리다 ( π t ) d t , {\displaystyle \operatorname {Li} _{s}(z)={\tfrac {1}{2}}z+z\int_{0}^{0}{0}{0}^{0}\infractan t-t\ln(-z)}{{1+t^{2}{s/}sinh(\pi t)d},d}}},}}}}}}},}}} 만약 Re(s)≤ 0입니다. 이 표현이 Φ는 레르히 대령으로 지금 초월적 존재에− zΦ(다음, s, 1), Φ(다음, s, 1⁄2)고 첫 Φ 시리즈와 1/(e2πt이 포함된 보완적 공식에 Abel–Plana 공식을 적용하는 2초씩 Lis(−z)/(−z))을 써서 발견된 불완전 감마 함수의 z에 대한 긍정적인 실축에서를 사용하지만, 이 적분 실패 Avoids.+1)나는 1 / (e 2πt - 1)의 n 자리와 두 번째 φ 시리즈. 에서 인용한 바와 같이, s ∈ {\ displaystyle s\in \mathb {N} 기하학적 시리즈 를 용어로 통합하여 다변량(polylogarithm)에 대한 적분을 표현할 수 있다.[3] 리 s + 1 ( z ) = z ⋅ ( − 1 ) s s ! ∫ 0 1 통나무를 하다 s ( t ) 1 − t z d t . {\displaystyle \operatorname {Li} _{s+1}(z)={\frac {z\cdot(-1)^{s}}{s! }}}\int _{0}^{1}{\frac {\log ^{s}(t)}{1-tz}dt.}
시리즈 표현 위의 적분 표현 에서 언급한 바와 같이, 다변량 표기는 한클 등고선 통합을 통해 음 의 순서로 확장될 수 있다. 리 s ( e μ ) = − Γ ( 1 − s ) 2 π i ∮ H ( − t ) s − 1 e t − μ − 1 d t , {\displaystyle \operatorname {Li} _{s}(e^{\mu }})=-{\Gamma(1-s) \over 2\pi i}\point _{H}{-t)^{s-1} \over e^{t-\mu }dt,},} 여기서 H 는 한클 등고선, s ≠ 1, 2, 3, …이며, 통합의 t = μ극 은 음이 아닌 실제 축에 놓여 있지 않다. 등고선 은 t - µ = 2kπi 로 통합의 극 을 둘러싸도록 수정할 수 있으며, 적분은 잔여물 의 합으로 평가할 수 있다(우드 1992 , § 12, 13, Gradshteyn & Ryzhik 1980 , § 9.553 harvnb 오류: 대상 없음: SITREFGradshynryhik1980 ). 리 s ( e μ ) = Γ ( 1 − s ) ∑ k = − ∞ ∞ ( 2 k π i − μ ) s − 1 . {\displaystyle \operatorname {Li} _{s}(e^{\mu }}=\감마(1-s)\sum _{k=-\infit }^{\infit }}}(2k\pi i-\mu )^{s-1}. } 이 μ s ) < 0과 e = 1을 제외한 모든 μ 를 지탱한다. 0 < Im(µ ) ≤ 2π의 경우 합을 다음과 같이 나눌 수 있다. 리 s ( e μ ) = Γ ( 1 − s ) [ ( − 2 π i ) s − 1 ∑ k = 0 ∞ ( k + μ 2 π i ) s − 1 + ( 2 π i ) s − 1 ∑ k = 0 ∞ ( k + 1 − μ 2 π i ) s − 1 ] , {\displaystyle \operatorname {Li} _{s}(e^{\mu })=\Gamma (1-s)\left[(-2\pi i)^{s-1}\sum _{k=0}^{\infty }\left(k+{\mu \over {2\pi i}}\right)^{s-1}+(2\pi i)^{s-1}\sum _{k=0}^{\infty }\left(k+1-{\mu \over {2\pi i}}\right)^{s-1}\right],} 현재 두 시리즈를 Hurwitz zeta 기능 으로 식별할 수 있는 위치: 리 s ( e μ ) = Γ ( 1 − s ) ( 2 π ) 1 − s [ i 1 − s ζ ( 1 − s , μ 2 π i ) + i s − 1 ζ ( 1 − s , 1 − μ 2 π i ) ] ( 0 < 임 ( μ ) ≤ 2 π ) . {\displaystyle \operatorname {Li} _{s}(e^{\mu })={\Gamma (1-s) \over (2\pi )^{1-s}}\left[i^{1-s}~\zeta \left(1-s,~{\mu \over {2\pi i}}\right)+i^{s-1}~\zeta \left(1-s,~1-{\mu \over {2\pi i}}\right)\right]\qquad (0<\operatorname {Im} (\mu )\leq 2\pi ). } 위의 다른 기능 과 이미 관계 가 부여된 이 관계는 모든 복합 s ≠ 0, 1, 2, 3을 유지하며 (Jonquiere 1889 , eq. 6)에서 처음 도출되었다. 폴리 로가리듬 을 µ = 0에 대한 파워 시리즈로 표현하기 위해 Hankel 등고선 적분에서 파생된 시리즈를 다음과 같이 기록한다. 리 s ( e μ ) = Γ ( 1 − s ) ( − μ ) s − 1 + Γ ( 1 − s ) ∑ h = 1 ∞ [ ( − 2 h π i − μ ) s − 1 + ( 2 h π i − μ ) s − 1 ] . {\displaystyle \operatorname {Li} _{s}(e^{\mu })=\Gamma (1-s)(-\mu )^{s-1}+\Gamma (1-s)\sum _{h=1}^{\infty }\left[(-2h\pi i-\mu )^{s-1}+(2h\pi i-\mu )^{s-1}\right]. } 합계의 이항력이 µ = 0 정도 확장되고 합계의 순서를 반대로 했을 때 h에 대한 합은 다음과 같이 닫힌 형태로 표현할 수 있다. 리 s ( e μ ) = Γ ( 1 − s ) ( − μ ) s − 1 + ∑ k = 0 ∞ ζ ( s − k ) k ! μ k . {\displaystyle \operatorname {Li} _{s}(e^{\mu })=\감마(1-s)(-\mu )^{s-1}+\sum _{k=0}^{\inft }{\zeta(s-k) \over k! }}\mu ^{k}. } 이 결과는 µ < 2㎛ 그리고, 제타함수 에 의해 제공되는 분석적 연속성 덕분에 모든 s 1 1, 2, 3 … . 순서가 양의 정수 라면 s = n이면 k = n - 1을 가진 항과 감마함수 의 합은 아니지만 모두 무한대가 된다. 1개 획득(Wood 1992 , § 9; Gradshteyn & Ryzhik 1980 , § 9.554 harvnb 오류: 대상 없음: CITREFGradshynRyzhik1980 (도움말 임이 있는 s → k + 1 [ ζ ( s − k ) k ! μ k + Γ ( 1 − s ) ( − μ ) s − 1 ] = μ k k ! [ ∑ h = 1 k 1 h − ln ( − μ ) ] , \displaystyle \lim _{s\to k+1}\왼쪽[{\제타(s-k) \overk! }\mu ^{k}+\감마 (1-s)(-\mu )^{s-1}\right]={\mu ^{k} \over k! }}\왼쪽[\sum _{h=1}^{k}{1 \over h}-\ln(-\mu )\오른쪽,} 여기 서 h 에 대한 합은 k = 0이면 사라진다. 따라서 양의 정수 순서와 μ < 2 μs의 경우 다음과 같은 시리즈가 있다. 리 n ( e μ ) = μ n − 1 ( n − 1 ) ! [ H n − 1 − ln ( − μ ) ] + ∑ k = 0 , k ≠ n − 1 ∞ ζ ( n − k ) k ! μ k , {\displaystyle \operatorname {Li} _{n}(e^{\mu }}={\mu ^{n-1} \over (n-1)! }}\왼쪽[H_{n-1}-\ln(-\mu )\right]+\sum _{k=0,k\neq n-1}^{\nta(n-k) \over k! }}\mu ^{k}} 여기서 H 는n 고조파 수 를 나타낸다. H n = ∑ h = 1 n 1 h , H 0 = 0. {\displaystyle H_{n}=\sum _{h=1}^{n}{1 \over h},\qquad H_{0}=0. } 현재 문제 용어에는 -ln(-μ )이 포함되어 있는데, μ 를n −1n = 1을 제외하고 μ → 0으로 0이 된다. 이는 다음과 같은s Li (z )가 s = 1 과 z = 1에서 참 로그 특이성 을 보인다는 사실을 반영한다. 임이 있는 μ → 0 Γ ( 1 − s ) ( − μ ) s − 1 = 0 ( 레 ( s ) > 1 ) . {\displaystyle \lim _{\mu \to 0}\감마(1-s)(-\mu )^{s-1=0\qquad(\operatorname {Re}s)>1). } s 에 가깝지만 같지는 않은 양의 정수에 대해 µ = 0에 대한 팽창의 상이한 항은 계산상의 어려움을 야기할 것으로 예상할 수 있다(Wood 1992 , § 9). ln(½)1 z z )과 균일하게 같지 않기 때문에 ln(z )의 주요 분기와 logarithm의 주 분기가 동시에 사용된다고 가정할 경우, ln(z)의 힘에서 Erdelyi의 상응하는 팽창(Erdelyi et al. 1981 , § 1.11-15)은 정확하지 않다. s 의 비양수 정수 값의 경우, 약 µ = 0 확장 시 제타 함수 ζ(s - k)는 베르누이 숫자 로 감소한다: :(-n - k ) = -B1+n +k /(1 + n + k ). 이 시리즈에 의한 Li−n (z )에 대한 수치평가는 위의 특정 값에 따라 주어진 유한한 합리적 표현들이 큰 n에 대해 나타내는 취소 효과에 시달리지 않는다. ID를 사용하여 1 = 1 Γ ( s ) ∫ 0 ∞ e − t t s − 1 d t ( 레 ( s ) > 0 ) , {\displaystyle 1={1 \over \Gamma(s)}\int _{0}^{\not^{-t^{-t^{s-1}dt\qquad(\operatorname {Re}s)>0),} 다변량(위 참조 )의 보세-아인슈타인 적분 표현은 다음과 같은 형태로 주조할 수 있다. 리 s ( z ) = 1 2 z + z 2 Γ ( s ) ∫ 0 ∞ e − t t s − 1 나무늘보 t − ln z 2 d t ( 레 ( s ) > 0 ) . {\displaystyle \operatorname {Li} _{s}(z)={\tfrac {1}{2}}z+{z \over 2\Gamma (s)}\int _{0}^{\infty }e^{-t}t^{s-1}\coth {t-\ln z \over 2}dt\qquad (\operatorname {Re} (s)>0). } 쌍곡선 코탄젠트를 쌍곡선 시리즈로 대체하고, 나무늘보 t − ln z 2 = 2 ∑ k = − ∞ ∞ 1 2 k π i + t − ln z , {\displaystyle \coth {t-\ln z \over 2}=2\sum _{k=-\nft }^{\nft }{1 \over 2k\pi i+t-\ln z}} 그런 다음 적분 및 합계의 순서를 반대로 하고 마지막으로 상한 불완전 감마 함수 의 적분 표현을 사용하여 합계를 식별하면 다음과 같은 결과를 얻을 수 있다. 리 s ( z ) = 1 2 z + ∑ k = − ∞ ∞ Γ ( 1 − s , 2 k π i − ln z ) ( 2 k π i − ln z ) 1 − s . {\displaystyle \operatorname {Li} _{s}(z)={\tfrac {1}{2}}z+\sum _{k=-\infit }^{\nft }{\gma(1-s,2k\pi i-\ln z) \over{1-s}. } 이 결과와 쌍곡선 코탄젠트의 경우 모두 -k에서max k 까지의max 대칭 부분 합계가 k max → ∞으로 무조건 수렴된다. 합계가 대칭적으로 수행된다면, Lis z )는 모든 복합 s뿐 만 아니라 모든 복합 z도 보유한다. 두 번째 종류의 스털링 숫자 에 대한 명시적 표현식을 비양수 정수 순서의 다변량(위 참조 )에 대한 유한 합계에 도입하면 다음과 같이 쓸 수 있다. 리 − n ( z ) = ∑ k = 0 n ( − z 1 − z ) k + 1 ∑ j = 0 k ( − 1 ) j + 1 ( k j ) ( j + 1 ) n ( n = 0 , 1 , 2 , … ) . {\displaystyle \operatorname {Li} _{-n}(z)=\sum _{k=0}^{n}\왼쪽({-z \over 1-z}\오른쪽) ^{k+1}\sum _{j=0}^{k}(1)^{j+1}{k \선택 j}(j+1)^{n}\qquad(n=0,1,2,\ldots). } 단순히 외측 합계를 ∞(Guillera & Sondow 2008 , Organization 2.1)으로 확장함으로써 얻은 무한 시리즈: 리 s ( z ) = ∑ k = 0 ∞ ( − z 1 − z ) k + 1 ∑ j = 0 k ( − 1 ) j + 1 ( k j ) ( j + 1 ) − s , {\displaystyle \operatorname {Li} _{s}(z)=\sum _{k=0}^{\infit }\왼쪽({-z \over 1-z}\오른쪽) ^{k+1}~\sum _{j=0}^{k}(1)^{j+1}{k \선택 j}(j+1)^{s}} 모든 복합 s 에 대해, 그리고 복합 z 에 대해, 합계 순서를 거꾸로 하고 다음을 사용하여 −z (1−z ) ½ < 2 ½>에 대해 검증할 수 있듯이, 복합 z에 대해 모든 복합 s에 대해, 그리고 2 복합 z에 대해 수렴하는 것으로 밝혀졌다. ∑ k = j ∞ ( k j ) ( − z 1 − z ) k + 1 = [ ( − z 1 − z ) − 1 − 1 ] − j − 1 = ( − z ) j + 1 . {\displaystyle \sum _{k=j}^{\infit }{k \선택 j}\왼쪽-z \over 1-z}\오른쪽) ^{k+1}=\left[\left-z \over 1-z}\right)^{-1}-1\right]^{-j-1}=(-z)^{j+1}} 이러한 계열의 내부 계수는 일반화된 고조파 수 를 포함하는 스털링 숫자 관련 공식으로 표현할 수 있다. 예를 들어 다음 ID의 증거(증거 참조)를 찾기 위한 함수 변환 생성 을 참조하십시오. 리 2 ( z ) = ∑ j ≥ 1 ( − 1 ) j − 1 2 ( H j 2 + H j ( 2 ) ) z j ( 1 − z ) j + 1 리 3 ( z ) = ∑ j ≥ 1 ( − 1 ) j − 1 6 ( H j 3 + 3 H j H j ( 2 ) + 2 H j ( 3 ) ) z j ( 1 − z ) j + 1 . {\displaystyle {\begin}\operatorname {Li} _{2}(z)&=\sum _{j\geq 1}{\frac {(1)^{j-1}}}{2}}\왼쪽(H_{j}^{2}+) H_{j}^{j}^{(2)}\오른쪽){\frac{z^{j}{j}}{j+1}}{j+1}}\1-z)}\\\\opername {Li}_{3}(z)&=\sum _{j\geq 1}{j-1}}}}{6}}}}}}{{j^}}}}}}}}}}}}}}}}}}}}}}}}}}}}{{{{{{{{{{{{{{j^}}}}} H_{j}H_{j}^{(2)+2 H_{j}^{{j}^{(3)}\오른쪽){\frac {z^{j}}{{(1-z)^{j+1}}}. \end{정렬}}} Re(z ) < 2 ½이 있는 다른 주장의 경우, 분석적 연속성에 의해 결과가 뒤따른다. 이 절차는 오일러의 변환 을 다로그를 정의하는 z 의 시리즈에 적용하는 것과 같다. 점근팽창 z ≫ 1의 경우 ln (-z ):
리 s ( z ) = ± i π Γ ( s ) [ ln ( − z ) ± i π ] s − 1 − ∑ k = 0 ∞ ( − 1 ) k ( 2 π ) 2 k B 2 k ( 2 k ) ! [ ln ( − z ) ± i π ] s − 2 k Γ ( s + 1 − 2 k ) , {\displaystyle \operatorname {Li} _{s}(z)={\pm i\pi \over \Gamma (s)}[\ln(-z)\pm i\pi ]^{s-1}-\sum _{k=0}^{\infty }(-1)^{k}(2\pi )^{2k}{B_{2k} \over (2k)! }{{[\ln(-z)\pm i\pi ]^{s-2k} \over \Gamma(s+1-2k)}}} 리 s ( z ) = ∑ k = 0 ∞ ( − 1 ) k ( 1 − 2 1 − 2 k ) ( 2 π ) 2 k B 2 k ( 2 k ) ! [ ln ( − z ) ] s − 2 k Γ ( s + 1 − 2 k ) , {\displaystyle \operatorname {Li} _{s}(z)=\sum _{k=0}^{\infit }^{k}(1-2^{1-2k})(2\pi )^{2k}{B_{2k} \over(2k)! }{{[\ln(-z)]^{s-2k} \over \Gamma(s+1-2k)}}}
여기서 B 는2k 베르누이 숫자 다. 두 버전 모두 모든 s 및 임의의 arg(z )에 대해 유지된다. 통상적으로, 합계는 용어의 크기가 커지기 시작할 때 종료되어야 한다. 음의 정수 s 의 경우 팽창은 완전히 사라지며, 음이 아닌 정수 s 의 경우 한정된 수의 항 후에 분리된다. Wood(1992 , § 11)는 보스-아인슈타인 적분표현으로부터 이러한 시리즈를 얻기 위한 방법을 설명한다(Lis e µ µ ) ≤ 0을 요구한다).
제한행동 다각측량(Polylogarithm , 1992년 § 22)의 다양한 표현으로부터 다음과 같은 한계 가 나타난다.
임이 있는 z → 0 리 s ( z ) = z {\displaystyle \lim _{z \to 0}\operatorname {Li} _{s}(z)=z} 임이 있는 μ → 0 리 s ( e μ ) = Γ ( 1 − s ) ( − μ ) s − 1 ( 레 ( s ) < 1 ) {\displaystyle \lim _{ \mu }\operatorname {Li}_{s}(e^{\mu }}})=\감마(1-s)(-\mu )^{s-1}\qquad(\operatorname {Re}<1) 임이 있는 레 ( μ ) → ∞ 리 s ( ± e μ ) = − μ s Γ ( s + 1 ) ( s ≠ − 1 , − 2 , − 3 , … ) {\displaystyle \lim \{\operatorname {Re}(\mu )\to \infit }\operatorname {Li} _{s}(\pm e^{\mu }}=-{\mu ^} \over \Gamma(s+1)}\Quad(s\neq -1,-1,-1,-2,\dots)}). 임이 있는 레 ( μ ) → ∞ 리 − n ( e μ ) = − ( − 1 ) n e − μ ( n = 1 , 2 , 3 , … ) {\displaystyle \lim \{\operatorname {Re}(\mu )\to \infit }\operatorname {Li} _{-n}(e^{\mu }=(-1)^{n^{-\mu }\qquad(n=1,2,3,\ldots )})}} 임이 있는 레 ( s ) → ∞ 리 s ( z ) = z {\displaystyle \lim _{\operatorname {Re}(s)\to \infit }\operatorname {Li} _{s}(z)=z} 임이 있는 레 ( s ) → − ∞ 리 s ( e μ ) = Γ ( 1 − s ) ( − μ ) s − 1 ( − π < 임 ( μ ) < π ) {\displaystyle \lim _{\operatorname {Re}\to -\ft }\operatorname {Li} _{s}(e^{\mu }}}}=\Gamma(1-s)(-\mu )^{s-1}\pi <\operatorname {Im}\pi )} 임이 있는 레 ( s ) → − ∞ 리 s ( − e μ ) = Γ ( 1 − s ) [ ( − μ − i π ) s − 1 + ( − μ + i π ) s − 1 ] ( 임 ( μ ) = 0 ) {\displaystyle \lim _{\operatorname {Re} (s)\to -\infty }\operatorname {Li} _{s}(-e^{\mu })=\Gamma (1-s)\left[(-\mu -i\pi )^{s-1}+(-\mu +i\pi )^{s-1}\right]\qquad (\operatorname {Im} (\mu )=0)}
우드의 Re(µ ) → ∞에 대한 첫 번째 한계는 그의 방정식 11.3에 따라 수정되었다. Re(s ) → -properties에 대한 한계는 Hurwitz zeta 함수 (위 참조 )와 폴리 로가리듬의 일반적인 관계에서 나타난다.
딜로가리스름 dilogarithm은 순서 s = 2. 임의 복합 인수 z 에 대한 dilogarithm의 대체 적분 표현은 다음과 같다(Abramowitz & Stegun 1972 , § 27.7).
리 2 ( z ) = − ∫ 0 z ln ( 1 − t ) t d t = − ∫ 0 1 ln ( 1 − z t ) t d t . {\displaystyle \operatorname {Li} _{2}(z)=-\int_{0}^{0}{0}^{0}^{1}{\ln(1-zt) \over t}dt. }
혼동의 근원은 일부 컴퓨터 대수 시스템 이 딜로가리듬을 딜로그(z ) = Li2 (1-z)로 정의한다는 것이다.
real z ≥ 1의 경우 dilogarithm의 첫 번째 적분 식을 다음과 같이 쓸 수 있다.
리 2 ( z ) = π 2 6 − ∫ 1 z ln ( t − 1 ) t d t − i π ln z {\displaystyle \operatorname {Li} _{2}(z)={\frac {\pi ^{6}-{1}-\int _{1}^{z}{\ln(t-1) \over t}dt-i\pi \ln z}
여기서 ln(t-1)을 확장하고 기간별로 용어를 통합한다.
리 2 ( z ) = π 2 3 − 1 2 ( ln z ) 2 − ∑ k = 1 ∞ 1 k 2 z k − i π ln z ( z ≥ 1 ) . {\displaystyle \operatorname {Li} _{2}(z)={\frac {\pi ^{2}}{3}}-{\frac {1}{2}}(\ln z)^{2}-\sum _{k=1}^{\infty }{1 \over k^{2}z^{k}}-i\pi \ln z\qquad (z\geq 1). }
딜로가리듬에 대한 아벨 정체 는 (Abel 1881)에 의해 주어진다.
리 2 ( x 1 − y ) + 리 2 ( y 1 − x ) − 리 2 ( x y ( 1 − x ) ( 1 − y ) ) = 리 2 ( x ) + 리 2 ( y ) + ln ( 1 − x ) ln ( 1 − y ) {\displaystyle \operatorname {Li} _{2}\left({\frac {x}{1-y}}\right)+\operatorname {Li} _{2}\left({\frac {y}{1-x}}\right)-\operatorname {Li} _{2}\left({\frac {xy}{(1-x)(1-y)}}\right)=\operatorname {Li} _{2}(x)+\operatorname {Li} _{2}(y)+\ln(1-x)\ln(1-y)}
( 레 ( x ) ≤ 1 2 ∧ 레 ( y ) ≤ 1 2 ∨ 임 ( x ) > 0 ∧ 임 ( y ) > 0 ∨ 임 ( x ) < 0 ∧ 임 ( y ) < 0 ∨ … ) . {\displaystyle (\operatorname {Re} (x)\leq {\tfrac {1}{2}}\wedge \operatorname {Re} (y)\leq {\tfrac {1}{2}}\vee \operatorname {Im} (x)>0\wedge \operatorname {Im} (y)>0\vee \operatorname {Im} (x)<0\wedge \operatorname {Im} (y)<0\vee \ldots ). }
이 는 즉시 x = 0 또는 y = 0으로 유지되는 것으로 보이며, 일반적인 인수의 경우 분화 differentiation/∂x ∂/∂y 에 의해 쉽게 검증된다. y = 1-x의 경우 ID가 오일러 의 반사 공식 으로 감소함
리 2 ( x ) + 리 2 ( 1 − x ) = 1 6 π 2 − ln ( x ) ln ( 1 − x ) , {\displaystyle \operatorname {Li} _{2}\왼쪽(x\오른쪽)+\operatorname {Li} _{2}\왼쪽(1-x\오른쪽)={\frac {1}{6}\pi ^{2}-\ln(x)\ln(1-x),},} 여기서 Li2 (1) = ζ(2) = 6 ½ = ½π 이2 사용되었고 x 는 어떤 복잡한 값도 취할 수 있다.
새로운 변수 u = x /(1-y), v = y/(1-x
리 2 ( u ) + 리 2 ( v ) − 리 2 ( u v ) = 리 2 ( u − u v 1 − u v ) + 리 2 ( v − u v 1 − u v ) + ln ( 1 − u 1 − u v ) ln ( 1 − v 1 − u v ) , {\displaystyle \operatorname {Li} _{2}(u)+\operatorname {Li} _{2}(v)-\operatorname {Li} _{2}(uv)=\operatorname {Li} _{2}\left({\frac {u-uv}{1-uv}}\right)+\operatorname {Li} _{2}\left({\frac {v-uv}{1-uv}}\right)+\ln \left({\frac {1-u}{1-uv}}\right)\ln \left({\frac {1-v}{1-uv}}\right),} 이는 (Rogers 1907 )에 주어진 오각형 아이덴티티 에 해당한다.
x = y = 1-z에 대한 아벨 정체성과 우리는 랜든 의 정체성을 가지고 있다.
리 2 ( 1 − z ) + 리 2 ( 1 − 1 z ) = − 1 2 ( ln z ) 2 ( z ∉ ] − ∞ ; 0 ] ) , {\displaystyle \operatorname {Li} _{2}(1-z)+\operatorname {Li} _{2}\좌측(1-{\frac {1}{1}{z}\우측)=-{\frac {1}{1}{1}{1}(\ln z)^{2}\qquad(z는 \in ~]]),}). 그리고 각 희석액에 반사 공식을 적용하면 반전 공식을 찾을 수 있다. 리 2 ( z ) + 리 2 ( 1 / z ) = − 1 6 π 2 − 1 2 [ ln ( − z ) ] 2 ( z ∉ [ 0 ; 1 [ ) , {\displaystyle \operatorname {Li} _{2}(z)+\operatorname {Li} _{2}(1/z)=-{\tfrac {1}{1}{6}\pi^{2}-{{{{{1}{{{n(-z)]^{2}\}\in[0;1},},},}),
그리고 real z ≥ 1 또한
리 2 ( z ) + 리 2 ( 1 / z ) = 1 3 π 2 − 1 2 ( ln z ) 2 − i π ln z . {\displaystyle \operatorname {Li} _{2}(z)+\operatorname {Li} _{2}(1/z)={\tfrac {1}{3}\pi ^{2}-{1}{1}{{{1}(\ln z)^{2}-i\ln z.}
특수 논거에서 희석액에 대한 알려진 폐쇄형 평가는 아래 표에 수집된다. 첫 번째 열의 주장은 반영 x 1-x파운드 또는 반전 x ½ x 또는 x = -1에 의해 관련된다. 세 번째 열의 주장은 모두 이러한 연산에 의해 상호 관련된다.
맥시몬(2003 )은 17세기에서 19세기의 참고 문헌을 논한다. 반사 공식은 오일러(Maximon 2003 , § 10)의 1768년 책에 등장하기 전인 1760년 랜든에 의해 이미 출판되었다. 아벨이 1826년(Zagier 1989 , § 2)에 원고를 쓰기 전인 1809년 스펜스 에 의해 아벨의 정체성과 동등한 것이 이미 출판되었다. 빌로가리스미슈 (bilogarithmische)라는 명칭 은 1828년(Maximon 2003 , § 10) 칼 요한 다니엘슨 힐(스웨덴 룬드의 교수)에 의해 도입되었다. 돈 자기 에(1989 )는 희석이리템이 유머감각을 가진 유일한 수학 함수라고 말했다.
딜로가리듬의 특수 값 x {\displaystyle x} 리 2 ( x ) {\displaystyle \operatorname {Li} _{2}(x)} x {\displaystyle x} 리 2 ( x ) {\displaystyle \operatorname {Li} _{2}(x)} − 1 {\displaystyle -1} − 1 12 π 2 {\displaystyle -{\tfrac {1}{12}\pi ^{2}} − ϕ -\phi } − 1 10 π 2 − ln 2 ϕ {\displaystyle -{\tfrac {1}{10}\pi ^{2}-\ln ^{2}\pi } 0 {\displaystyle 0} 0 {\displaystyle 0} − 1 / ϕ -1/\phi } − 1 15 π 2 + 1 2 ln 2 ϕ {\displaystyle -{\tfrac {1}{15}\pi ^{2}+{\tfrac {1}{1}{1}:{2}}\ln ^{2}\pi }} 1 2 {\displaystyle {\tfrac {1}{2}}:} 1 12 π 2 − 1 2 ln 2 2 {\displaystyle {\tfrac {1}{12}\pi ^{2}-{\tfrac {1}{1}{1}{1}\ln ^{2}} 1 / ϕ 2 {\displaystyle 1/\phi ^{2}} 1 15 π 2 − ln 2 ϕ {\displaystyle {\tfrac {1}{15}\pi ^{2}-\ln ^{2}\phi } 1 {\displaystyle 1} 1 6 π 2 {\displaystyle {\tfrac {1}{6}\pi ^{2}} 1 / ϕ "/\displaystaystyle 1/\phi } 1 10 π 2 − ln 2 ϕ {\displaystyle {\tfrac {1}{10}\pi ^{2}-\ln ^{2}\phi } 2 {\displaystyle 2} 1 4 π 2 − π i ln 2 {\displaystyle {\tfrac {1}{4}\pi ^{2}-\pi i\ln 2} ϕ \displaystyle \phi } 11 15 π 2 + 1 2 ln 2 ( − 1 / ϕ ) {\displaystyle {\tfrac {11}{15}\pi ^{2}+{\tfrac {1}{1}:{1}{1}\ln ^{2}(-1/\phi )}} ϕ 2 {\displaystyle \phi ^{2}} − 11 15 π 2 − ln 2 ( − ϕ ) {\displaystyle -{\tfrac {11}{15}\pi ^{2}-\ln ^{2}(-\phi )}
여기서 1 2 5 {\displaystyle \phi ={\tfrac {1}{1 }}({\sqrt{5}+1 황금 비율 을 나타낸다 폴리로가리듬 사다리 레오나드 르윈 은 다원적 가치관 위에서 다수의 고전적 관계를 특별하고 광범위하게 일반화한다는 것을 발견했다. 이것들은 현재 다층 사다리 라고 불린다. ratio 2 5 1 {\displaystyle \rho ={\tfrac {1}{1 }}({\sqrt{5}-1) 황금 비율의 역수로 정의하십시오. 그렇다면 희석 래더의 두 가지 간단한 예는 다음과 같다.
리 2 ( ρ 6 ) = 4 리 2 ( ρ 3 ) + 3 리 2 ( ρ 2 ) − 6 리 2 ( ρ ) + 7 30 π 2 {\displaystyle \operatorname {Li} _{2}(\rho ^{6})=4\operatorname {Li} _{2}(\rho ^{3})+3\operatorname {Li} _{2}(\rho ^{2})-6\operatorname {Li} _{2}(\rho )+{\tfrac {7}{30}}\pi ^{2}} Coxeter (1935년 )가 준 것 리 2 ( ρ ) = 1 10 π 2 − ln 2 ρ {\displaystyle \operatorname {Li} _{2}(\rho )={\tfrac {1}{10}\pi ^{2}-\ln ^{2}\rho } 랜든 이 준 다층 사다리들은 K 이론 과 대수 기하학 에서 자연스럽고 깊게 발생한다. 다각측량 사다리들은 BBP 알고리즘을 통해 다양한 수학 상수의 신속한 계산에 대한 기초를 제공한다(Bailey, Borwein & Plouffe 1997 ).
모노드로미 다변량에는 두 개의 분기점 이 있다. 하나는 z = 1이고 다른 하나는 z = 0이다. 두 번째 분기점(z = 0)은 다각측량 주 시트에서 볼 수 없으며, 기능이 다른 시트까지 분석적 으로 계속되어야만 볼 수 있다. 다목적의 모노드로미 그룹은 두 가지 지점 둘레를 감는 루프의 호모토피 등급으로 구성된다. 이 둘을 m 과0 m 로1 나타내며, 모노드로미 그룹은 그룹 프레젠테이션 을 한다.
⟨ m 0 , m 1 w = m 0 m 1 m 0 − 1 m 1 − 1 , w m 1 = m 1 w ⟩ . {\displaystyle \langle m_{0}m_{1}m_{1}{0}^{-1m_{0}^{1}^{-1},wm_{1}=m_{1}w_{1}w_{1}w\wangle .}
dilogarithm의 특수한 경우에 대해서도 wm 0 = mw 를0 가지고 있으며, 모노드로미 집단은 하이젠베르크 집단 이 된다(x0 , y , z 로 m, m 1 , w 를 식별). (베프스타스 2008 )
참조 ^ R.B. 딩글, 애플. Sci. Res. B6 (1957) 240-244, B4 (1955) 401; R.B. 딩글, D. 아른트와 S.K. 로이, 애플. Sci.Res. B6 (1957년) 144. ^ R.B. 딩글, 애플. Sci.Res. B6 (1957년) 225-239. ^ Borwein, Borwein, Girgenson의 글 Oiler 합계에 대한 명시적 평가 (1994)의 2절에서 방정식 (4)을 참조한다. 아벨, N.H.(1881년)[1826년]."참고)x+x222+x332+⋯+)nn2+⋯{\displaystyle\scriptstyle\psi x=x+{\frac{x^{2}}{2^{2}}}와{\frac{x^{3}}{3^{2}}}+\cdots+{\frac{x^{n}}{{2}}}+\cdots n^}드 라 fonction ψ xsur"(PDF).Sylow, L., 리, S(eds.)에서.제édition, 그들 2세(프랑스어로)− 닐스 헨리크 아벨 드 complètes Œuvres.크리스티아니아[오슬로]:Grøndahl&Søn.를 대신하여 서명함. 189–193.(이인 1826년 원고만 사후에 출판되었다.). Abramowitz, M.; Stegun, I.A. (1972). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables ISBN 978-0-486-61272-0 Apostol, T.M. (2010), "Polylogarithm" , in Olver, Frank W. J. ; Lozier, Daniel M.; Boisvert, Ronald F.; Clark, Charles W. (eds.), NIST Handbook of Mathematical Functions ISBN 978-0-521-19225-5 MR 2723248 Bailey, D.H. ; Borwein, P.B. ; Plouffe, S. (April 1997). "On the Rapid Computation of Various Polylogarithmic Constants" (PDF) . Mathematics of Computation . 66 (218): 903–913. Bibcode :1997MaCom..66..903B . doi :10.1090/S0025-5718-97-00856-9 Bailey, D.H.; Broadhurst, D.J. (June 20, 1999). "A Seventeenth-Order Polylogarithm Ladder". arXiv :math.CA/9906134 Berndt, B.C. (1994). Ramanujan's Notebooks, Part IV . New York: Springer-Verlag. pp. 323–326. ISBN 978-0-387-94109-7 Boersma, J. ; Dempsey, J.P. (1992). "On the evaluation of Legendre's chi-function" . Mathematics of Computation . 59 (199): 157–163. doi :10.2307/2152987 . JSTOR 2152987 .Borwein, D. ; Borwein, J.M. ; Girgensohn, R. (1995). "Explicit evaluation of Euler sums" (PDF) . Proceedings of the Edinburgh Mathematical Society . Series 2. 38 (2): 277–294. doi :10.1017/S0013091500019088 Borwein, J.M.; Bradley, D.M.; Broadhurst, D.J.; Lisonek, P. (2001). "Special Values of Multiple Polylogarithms". Transactions of the American Mathematical Society . 353 (3): 907–941. arXiv :math/9910045 doi :10.1090/S0002-9947-00-02616-7 . S2CID 11373360 . Broadhurst, D.J. (April 21, 1996). "On the enumeration of irreducible k-fold Euler sums and their roles in knot theory and field theory". arXiv :hep-th/9604128 Clunie, J. (1954). "On Bose-Einstein functions". Proceedings of the Physical Society . Series A. 67 (7): 632–636. Bibcode :1954PPSA...67..632C . doi :10.1088/0370-1298/67/7/308 . Cohen, H.; Lewin, L.; Zagier, D. (1992). "A Sixteenth-Order Polylogarithm Ladder" (PS) . Experimental Mathematics . 1 (1): 25–34. Coxeter, H.S.M. (1935). "The functions of Schläfli and Lobatschefsky". Quarterly Journal of Mathematics . 6 (1): 13–29. Bibcode :1935QJMat...6...13C . doi :10.1093/qmath/os-6.1.13 . JFM 61.0395.02 .Cvijovic, D.; Klinowski, J. (1997). "Continued-fraction expansions for the Riemann zeta function and polylogarithms" (PDF) . Proceedings of the American Mathematical Society . 125 (9): 2543–2550. doi :10.1090/S0002-9939-97-04102-6 Cvijovic, D. (2007). "New integral representations of the polylogarithm function". Proceedings of the Royal Society A 463 (2080): 897–905. arXiv :0911.4452 Bibcode :2007RSPSA.463..897C . doi :10.1098/rspa.2006.1794 . S2CID 115156743 . Erdélyi, A. ; Magnus, W.; Oberhettinger, F.; Tricomi, F.G. (1981). Higher Transcendental Functions, Vol. 1 (PDF) . Malabar, FL: R.E. Krieger Publishing. ISBN 978-0-89874-206-0 Fornberg, B.; Kölbig, K.S. (1975). "Complex zeros of the Jonquière or polylogarithm function" . Mathematics of Computation . 29 (130): 582–599. doi :10.2307/2005579 . JSTOR 2005579 . GNU Scientific Library (2010). "Reference Manual" . Retrieved 2010-06-13 . Gradshteyn, Izrail Solomonovich ; Ryzhik, Iosif Moiseevich ; Geronimus, Yuri Veniaminovich ; Tseytlin, Michail Yulyevich ; Jeffrey, Alan (2015) [October 2014]. "9.553.". In Zwillinger, Daniel; Moll, Victor Hugo (eds.). Table of Integrals, Series, and Products Academic Press, Inc. p. 1050. ISBN 978-0-12-384933-5 LCCN 2014010276 .Guillera, J.; Sondow, J. (2008). "Double integrals and infinite products for some classical constants via analytic continuations of Lerch's transcendent". The Ramanujan Journal . 16 (3): 247–270. arXiv :math.NT/0506319 doi :10.1007/s11139-007-9102-0 . S2CID 119131640 . Hain, R.M. (March 25, 1992). "Classical polylogarithms". arXiv :alg-geom/9202022 Jahnke, E.; Emde, F. (1945). Tables of Functions with Formulae and Curves (4th ed.). New York: Dover Publications. Jonquière, A. (1889). "Note sur la série ∑ n = 1 ∞ x n n s {\displaystyle \scriptstyle \sum _{n=1}^{\infty }{\frac {x^{n}}{n^{s}}}} (PDF) . Bulletin de la Société Mathématique de France (in French). 17 : 142–152. doi :10.24033/bsmf.392 JFM 21.0246.02 . Kölbig, K.S.; Mignaco, J.A.; Remiddi, E. (1970). "On Nielsen's generalized polylogarithms and their numerical calculation" . BIT . 10 : 38–74. doi :10.1007/BF01940890 . S2CID 119672619 . Kirillov, A.N. (1995). "Dilogarithm identities". Progress of Theoretical Physics Supplement . 118 : 61–142. arXiv :hep-th/9408113 Bibcode :1995PThPS.118...61K . doi :10.1143/PTPS.118.61 . S2CID 119177149 . Lewin, L. (1958). Dilogarithms and Associated Functions . London: Macdonald. MR 0105524 . Lewin, L. (1981). Polylogarithms and Associated Functions . New York: North-Holland. ISBN 978-0-444-00550-2 Lewin, L., ed. (1991). Structural Properties of Polylogarithms . Mathematical Surveys and Monographs. 37 . Providence, RI: Amer. Math. Soc. ISBN 978-0-8218-1634-9 Markman, B. (1965). "The Riemann Zeta Function". BIT . 5 : 138–141. Maximon, L.C. (2003). "The Dilogarithm Function for Complex Argument". Proceedings of the Royal Society A 459 (2039): 2807–2819. Bibcode :2003RSPSA.459.2807M . doi :10.1098/rspa.2003.1156 . S2CID 122271244 . McDougall, J.; Stoner, E.C. (1938). "The computation of Fermi-Dirac functions" . Philosophical Transactions of the Royal Society A 237 (773): 67–104. Bibcode :1938RSPTA.237...67M . doi :10.1098/rsta.1938.0004 JFM 64.1500.04 . Nielsen, N. (1909). "Der Eulersche Dilogarithmus und seine Verallgemeinerungen. Eine Monographie". Nova Acta Leopoldina (in German). Halle – Leipzig, Germany: Kaiserlich-Leopoldinisch-Carolinische Deutsche Akademie der Naturforscher. XC (3): 121–212. JFM 40.0478.01 .Prudnikov, A.P.; Marichev, O.I.; Brychkov, Yu.A. (1990). Integrals and Series, Vol. 3: More Special Functions . Newark, NJ: Gordon and Breach. ISBN 978-2-88124-682-1 Robinson, J.E. (1951). "Note on the Bose-Einstein integral functions". Physical Review . Series 2. 83 (3): 678–679. Bibcode :1951PhRv...83..678R . doi :10.1103/PhysRev.83.678 . Rogers, L.J. (1907). "On function sum theorems connected with the series ∑ n = 1 ∞ x n n 2 {\displaystyle \scriptstyle \sum _{n=1}^{\infty }{\frac {x^{n}}{n^{2}}}} . Proceedings of the London Mathematical Society (2) . 4 (1): 169–189. doi :10.1112/plms/s2-4.1.169 . JFM 37.0428.03 . Schrödinger, E. (1952). Statistical Thermodynamics (2nd ed.). Cambridge, UK: Cambridge University Press.Truesdell, C. (1945). "On a function which occurs in the theory of the structure of polymers". Annals of Mathematics . Second Series. 46 (1): 144–157. doi :10.2307/1969153 . JSTOR 1969153 . Vepstas, L. (2008). "An efficient algorithm for accelerating the convergence of oscillatory series, useful for computing the polylogarithm and Hurwitz zeta functions". Numerical Algorithms . 47 (3): 211–252. arXiv :math.CA/0702243 Bibcode :2008NuAlg..47..211V . doi :10.1007/s11075-007-9153-8 . S2CID 15131811 . Whittaker, E.T. ; Watson, G.N. (1927). A Course of Modern Analysis ISBN 0-521-09189-6 이 있다.)Wirtinger, W. (1905). "Über eine besondere Dirichletsche Reihe". Journal für die Reine und Angewandte Mathematik (in German). 1905 (129): 214–219. doi :10.1515/crll.1905.129.214 . JFM 37.0434.01 . S2CID 199545536 . Wood, D.C. (June 1992). "The Computation of Polylogarithms. Technical Report 15-92*" (PS) . Canterbury, UK: University of Kent Computing Laboratory. Retrieved 2005-11-01 . Zagier, D(1989년)."기하학과 정수론에서의 그 dilogarithm 기능".번호 이론과 관련 토픽:신문들은 그 전 라마누잔 콜로퀴움, 봄베이, 1988년에 발표된.수학의 연구. 12.봄베이:타타 연구소 기초적 연구와 옥스퍼드 대학 출판부.를 대신하여 서명함. 231–249.아이 에스비엔 0-19-562367-3.(또한"그 유명한 dilogarithm"로 저널 수학 및 물리적의 과학 22(1988년 나타났다),를 대신하여 서명함. 131–145,장 1세(2007년Zagier).). Zagier, D. (2007). "The Dilogarithm Function" (PDF) . In Cartier, P.E.; et al. (eds.). Frontiers in Number Theory, Physics, and Geometry II – On Conformal Field Theories, Discrete Groups and Renormalization . Berlin: Springer-Verlag. pp. 3–65. ISBN 978-3-540-30307-7 외부 링크 
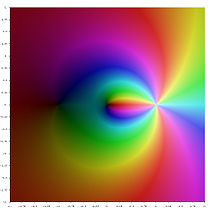

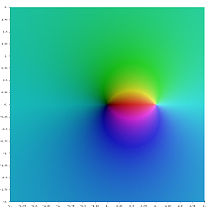
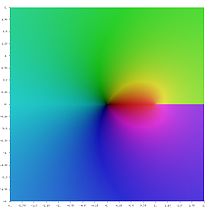
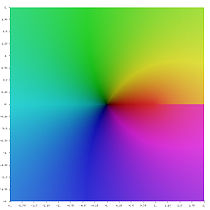









 대한 가상 부분이 (
대한 가상 부분이 (















 (는)
(는) 













![{\displaystyle \operatorname {Li} _{s}(z)={\Gamma (1-s) \over (2\pi )^{1-s}}\left[i^{1-s}\zeta \left(1-s,{\frac {1}{2}}+{\ln(-z) \over {2\pi i}}\right)+i^{s-1}~\zeta \left(1-s,{\frac {1}{2}}-{\ln(-z) \over {2\pi i}}\right)\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/19740cee6db60c818e9a23f29b7daf16940ff3ce)





![{\displaystyle \operatorname {Li} _{n}(z)+(-1)^{n}\operatorname {Li} _{n}(1/z)=-{\frac {(2\pi i)^{n}}{n!}}B_{n}\left({\frac {1}{2}}+{\ln(-z) \over {2\pi i}}\right)\qquad (z\not \in ]0;1]),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e61df2396fffd54addb3533ed5639a2c5e14f22)
![{\displaystyle \operatorname {Li} _{n}(z)+(-1)^{n}\operatorname {Li} _{n}(1/z)=-{\frac {(2\pi i)^{n}}{n!}}B_{n}\left({\frac {1}{2}}-{\ln(-1/z) \over {2\pi i}}\right)\qquad (z\not \in ~]1;\infty [),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d078df0ffd07052e579bbc21d440a63e65236155)

![{\displaystyle \operatorname {Ti} _{s}(z)={1 \over 2i}\left[\operatorname {Li} _{s}(iz)-\operatorname {Li} _{s}(-iz)\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/27ed950b06eb27a6dcef09792f589c699be39f84)

![{\displaystyle \chi _{s}(z)={\tfrac {1}{2}}\left[\operatorname {Li} _{s}(z)-\operatorname {Li} _{s}(-z)\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/93c1910b88b64db413955b6a0834fa3e4ab4dcc5)





 ) Jordan의 토털 함수
) Jordan의 토털 함수



![{\displaystyle \operatorname {Li} _{s}(z)=\int _{0}^{\infty }{t^{-s}\sin[s\pi /2-t\ln(-z)] \over \sinh(\pi t)}dt.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b8e8103742f74c68157500b4acd5aa3de6152540)




![{\displaystyle \operatorname {Li} _{s}(z)={\tfrac {1}{2}}z+z\int _{0}^{\infty }{\frac {\sin[s\arctan t-t\ln(-z)]}{(1+t^{2})^{s/2}\sinh(\pi t)}}dt,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8dacc6c599aba955801085a0f421f8db660a9c65)
 대한 일반적인
대한 일반적인 


![{\displaystyle \operatorname {Li} _{s}(e^{\mu })=\Gamma (1-s)\left[(-2\pi i)^{s-1}\sum _{k=0}^{\infty }\left(k+{\mu \over {2\pi i}}\right)^{s-1}+(2\pi i)^{s-1}\sum _{k=0}^{\infty }\left(k+1-{\mu \over {2\pi i}}\right)^{s-1}\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f5229719b08bd2a5537d09d5d6151a617dcb32d2)
![{\displaystyle \operatorname {Li} _{s}(e^{\mu })={\Gamma (1-s) \over (2\pi )^{1-s}}\left[i^{1-s}~\zeta \left(1-s,~{\mu \over {2\pi i}}\right)+i^{s-1}~\zeta \left(1-s,~1-{\mu \over {2\pi i}}\right)\right]\qquad (0<\operatorname {Im} (\mu )\leq 2\pi ).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c08143d12ea8d0f3a545987167ac9e5533e42923)
![{\displaystyle \operatorname {Li} _{s}(e^{\mu })=\Gamma (1-s)(-\mu )^{s-1}+\Gamma (1-s)\sum _{h=1}^{\infty }\left[(-2h\pi i-\mu )^{s-1}+(2h\pi i-\mu )^{s-1}\right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7d5265340491e5f8ce1fc1e7d8431345723df2d6)

![{\displaystyle \lim _{s\to k+1}\left[{\zeta (s-k) \over k!}\mu ^{k}+\Gamma (1-s)(-\mu )^{s-1}\right]={\mu ^{k} \over k!}\left[\sum _{h=1}^{k}{1 \over h}-\ln(-\mu )\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3c1186dab788a0ce1f58a2b956645cc0e324ba20)
![{\displaystyle \operatorname {Li} _{n}(e^{\mu })={\mu ^{n-1} \over (n-1)!}\left[H_{n-1}-\ln(-\mu )\right]+\sum _{k=0,k\neq n-1}^{\infty }{\zeta (n-k) \over k!}\mu ^{k},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d5feb14aa81c2afb598f8708c7f6eeb54deb410d)








![{\displaystyle \sum _{k=j}^{\infty }{k \choose j}\left({-z \over 1-z}\right)^{k+1}=\left[\left({-z \over 1-z}\right)^{-1}-1\right]^{-j-1}=(-z)^{j+1}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3339c1597e1b844ed6134270dc89e03ee7f75caa)

![{\displaystyle \operatorname {Li} _{s}(z)={\pm i\pi \over \Gamma (s)}[\ln(-z)\pm i\pi ]^{s-1}-\sum _{k=0}^{\infty }(-1)^{k}(2\pi )^{2k}{B_{2k} \over (2k)!}{[\ln(-z)\pm i\pi ]^{s-2k} \over \Gamma (s+1-2k)},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cb9c5a4b37ca161c9058827000feddc2588895da)
![{\displaystyle \operatorname {Li} _{s}(z)=\sum _{k=0}^{\infty }(-1)^{k}(1-2^{1-2k})(2\pi )^{2k}{B_{2k} \over (2k)!}{[\ln(-z)]^{s-2k} \over \Gamma (s+1-2k)},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a8fefbb8be3978b53224e5f58bc63280fd1a0fc9)






![{\displaystyle \lim _{\operatorname {Re} (s)\to -\infty }\operatorname {Li} _{s}(-e^{\mu })=\Gamma (1-s)\left[(-\mu -i\pi )^{s-1}+(-\mu +i\pi )^{s-1}\right]\qquad (\operatorname {Im} (\mu )=0)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9238c4efe1886a563653d74911fe36c61044ba3f)







![{\displaystyle \operatorname {Li} _{2}(1-z)+\operatorname {Li} _{2}\left(1-{\frac {1}{z}}\right)=-{\frac {1}{2}}(\ln z)^{2}\qquad (z\not \in ~]-\infty ;0]),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5382f3386515a5d18bb0cfcc28f675f7de5bd9db)
![{\displaystyle \operatorname {Li} _{2}(z)+\operatorname {Li} _{2}(1/z)=-{\tfrac {1}{6}}\pi ^{2}-{\tfrac {1}{2}}[\ln(-z)]^{2}\qquad (z\not \in [0;1[),}](https://wikimedia.org/api/rest_v1/media/math/render/svg/18de9d7e5f127ec54d75da4519ae05cb2b518930)

































