행클 윤곽선

긍정적인 의미로 가로지른 한클 등고선 경로.

이것은 실제 축을 가로지르는 선형 미러 이미지로만 구성된 한클 윤곽선의 버전이다.

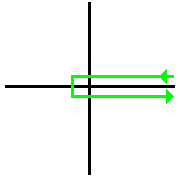
수학에서 한클 등고선은 복잡한 평면에서 시계 반대방향으로 원점 주위를 돌고 다시 (+∞, Δ)까지 확장되는 경로로, 여기서 Δ는 임의로 작은 양의 숫자다.따라서 등고선은 x의 음수 값을 제외하고 실제 축을 교차하지 않고 실제 축에 임의로 가깝게 유지된다.한클 등고선은 또한 실제 축 바로 위와 아래에 미러 영상이 있는 경로로 나타낼 수 있으며, 여기서 ε은 임의로 작은 숫자인 원점을 중심으로 반경 ε의 원에 연결된다.등고선의 두 선형 부분은 실제 축에서 Δ의 거리라고 한다.따라서 등고선의 선형 부분 사이의 총 거리는 2Δ이다.^[1]등고선은 양지향의 의미로 가로지르는데, 이는 원점 주위의 원이 시계 반대 방향으로 가로지른다는 것을 의미한다.

Hankel 등고선의 사용은 등고선 통합 방법 중 하나이다.등고선 통합을 위한 이러한 유형의 경로는 헤르만 행클이 감마 함수에 대한 조사에서 처음 사용되었다.

한클 등고선은 감마함수, 리만 제타함수, 기타 한클함수(제3종 베셀함수)와 같은 통합성을 평가하는 데 사용된다.^[1]^[2]

적용들

한클 윤곽선 및 감마 함수

한클 윤곽선은 복합 t-평면에서 감마 함수를 표현하고 해결하는 데 도움이 된다.감마 함수는 행클 윤곽선을 따라 적분을 평가하면 평면의 모든 복합 값에 대해 정의할 수 있다.Hankel 등고선은 등고선의 끝점이 사라지기 때문에 모든 복잡한 값에 대해 감마 함수를 표현하는 데 특히 유용하며, 따라서 감마 함수의 기본 특성이 충족되도록 허용하는데, $\Gamma (z+1)=z\Gamma (z)$ ( $\Gamma (z+1)=z\Gamma (z)$ + $\Gamma (z+1)=z\Gamma (z)$ ) $\Gamma (z+1)=z\Gamma (z)$ = $\Gamma (z+1)=z\Gamma (z)$ $\Gamma (z+1)=z\Gamma (z)$ ( z ) ${\displaystyle \Gamma (z+1)=z\\$ $감마(z)}$ ^[2].

감마함수의^[2] 등고선 적분 식의 유도

감마 함수의 공식 표현은 $\Gamma (z)=\int _{C}f(t)t^{z-1}dt$ ( $\Gamma (z)=\int _{C}f(t)t^{z-1}dt$ ) $\Gamma (z)=\int _{C}f(t)t^{z-1}dt$ = $\Gamma (z)=\int _{C}f(t)t^{z-1}dt$ $\Gamma (z)=\int _{C}f(t)t^{z-1}dt$ $\Gamma (z)=\int _{C}f(t)t^{z-1}dt$ ( t $\Gamma (z)=\int _{C}f(t)t^{z-1}dt$ ) $\Gamma (z)=\int _{C}f(t)t^{z-1}dt$ - $\Gamma (z)=\int _{C}f(t)t^{z-1}dt$ $\Gamma (z)=\int _{C}f(t)t^{z-1}dt$ $\Gamma (z)=\int _{C}f(t)t^{z-1}dt$ $\Gamma (z)=\int _{C}f(t)^{z-1}dt$ 입니다 $\Gamma (z)=\int _{C}f(t)t^{z-1}dt$

감마 함수의 기본 특성을 만족시키기 위해 다음과 같다.

$\int _{C}f(t)^{z}dt=[t^{z}f(t)]-\int _{C}t^{z}f'(t)dt$

양쪽을 z로 곱한 후

따라서 한클 등고선의 끝점이 사라진다는 점을 감안하여 좌우측면에서는 다음과 같이 줄어든다.

$f(t)+f'(t)=0$ ( $f(t)+f'(t)=0$ ) $f(t)+f'(t)=0$ + $f(t)+f'(t)=0$ $f(t)+f'(t)=0$ ( $f(t)+f'(t)=0$ ) $f(t)+f'(t)=0$ = $f(t)+f'(t)=0$ $f(t)+f'=0$ .

미분 방정식을 사용하여,

$[\displaystyle f(t)=]Ae^{-t}}$

일반적인 해결책이 되다A는 t에 대해서는 일정하지만, 복합수 z에 따라 A가 변동할 수 있다는 것을 유지한다.A(z)는 임의적이기 때문에 z의 복잡한 지수화는 A(z)의 정의에 흡수될 수 있다.f( $\Gamma (z)=A(z)\int _{C}e^{-t}(-t)^{z-1}dt$ )를 원래의 적분으로 대체하면 $\Gamma (z)=A(z)\int _{C}e^{-t}(-t)^{z-1}dt$ ( $\Gamma (z)=A(z)\int _{C}e^{-t}(-t)^{z-1}dt$ z $\Gamma (z)=A(z)\int _{C}e^{-t}(-t)^{z-1}dt$ ) $\Gamma (z)=A(z)\int _{C}e^{-t}(-t)^{z-1}dt$ = $\Gamma (z)=A(z)\int _{C}e^{-t}(-t)^{z-1}dt$ ( ) = $\Gamma (z)=A(z)\int _{C}e^{-t}(-t)^{z-1}dt$ $\Gamma (z)=A(z)\int _{C}e^{-t}(-t)^{z-1}dt$ $\Gamma (z)=A(z)\int _{C}e^{-t}(-t)^{z-1}dt$ - t $\Gamma (z)=A(z)\int _{C}e^{-t}(-t)^{z-1}dt$ ( $\Gamma (z)=A(z)\int _{C}e^{-t}(-t)^{z-1}dt$ - t $\Gamma (z)=A(z)\int _{C}e^{-t}(-t)^{z-1}dt$ ) $\Gamma (z)=A(z)\int _{C}e^{-t}(-t)^{z-1}dt$ - $\Gamma (z)=A(z)\int _{C}e^{-t}(-t)^{z-1}dt$ d $\Gamma (z)=A(z)\int _{C}e^{-t}(-t)^{z-1}dt$ ${\d$ 디스플레이 스타일 $\Gamma (z)=A(z)\int _{C}e^{-t}(-t)^{z-1}dt$

By integrating along the Hankel contour, the contour integral expression of the Gamma function becomes $\Gamma (z)={\frac {i}{2\sin {\pi z}}}\int _{C}e^{-t}(-t)^{z-1}dt$ .^[2]

참조

^ ^a ^b Krantz, Steven G. (Steven George), 1951- (1999). Handbook of complex variables. Boston, Mass.: Birkhäuser. ISBN 0-8176-4011-8. OCLC 40964730.{{cite book}}: CS1 maint : 복수이름 : 작성자 목록(링크)
^ ^a ^b ^c ^d Moretti, Gino (1964). Functions of a Complex Variable. Englewood Cliffs, N.J.: Prentice-Hall, Inc. pp. 179–184. LCCN 64012240.

추가 읽기

슈멜저, 토마스; 트레페헨, 로이드 N. (2007-01)"윤곽 집적 및 합리적인 근사치를 사용한 감마 함수 계산"수치 분석에 관한 SIAM 저널. 45(2): 558–571. 도이:10.1137/050646342.ISSN 0036-1429.
Hugh L. Montgomery; Robert C. 본(2007)승수 이론 I. 고전 이론.케임브리지 대학은 고급수학을 공부한다. 97. 페이지 515.ISBN 0-521-84903-9

외부 링크

[:0-1] Krantz, Steven G. (Steven George), 1951- (1999). Handbook of complex variables. Boston, Mass.: Birkhäuser. ISBN 0-8176-4011-8. OCLC 40964730.{{cite book}}: CS1 maint : 복수이름 : 작성자 목록(링크)

[:1-2] Moretti, Gino (1964). Functions of a Complex Variable. Englewood Cliffs, N.J.: Prentice-Hall, Inc. pp. 179–184. LCCN 64012240.

[1]

[2]

Search

행클 윤곽선

네임스페이스

더

목차

적용들

한클 윤곽선 및 감마 함수

감마함수의^[2] 등고선 적분 식의 유도

참조

추가 읽기

외부 링크

Search

행클 윤곽선

적용들

한클 윤곽선 및 감마 함수

감마함수의[2] 등고선 적분 식의 유도

참조

추가 읽기

외부 링크

감마함수의^[2] 등고선 적분 식의 유도