평등한 기질
Equal temperament평등한 기질이란 음악적 기질이나 튜닝 시스템을 말하는데, 이것은 옥타브(또는 다른 간격)를 평등한 단계로 나누어 단지 간격을 근사하게 한다. 이것은 인접한 음 쌍의 주파수 비율이 동일하다는 것을 의미하며, 이는 음이 대략 주파수의 로그로 인식되는 것과 동일한 단계 크기를 제공한다.[2]
일반적으로 고전음악과 서양음악에서 18세기 이후 가장 보편적인 튜닝 체계는 12음계의 등가 기질(일명 12 ET 또는 12 ET, 약칭 12 ET로 알려져 있음)으로 옥타브를 12부분으로 나눈 것으로, 모두 로그 눈금으로 동일하며, 그 비율은 1과 같다.2의 두 번째 뿌리(√122 ≈ 1.05946). 그 결과 가장 작은 간격, ½ 옥타브의 폭은 반음계 또는 반음계라고 한다. 서구 국가에서 동등한 기질이라는 용어는 자격 없이 일반적으로 12-TET를 의미한다.
현대에 있어서 12-TET는 보통 440Hz의 표준 피치에 상대적으로 튜닝된다. 즉, 한 노트, A는 440헤르츠로 튜닝되고 다른 모든 노트는 주파수가 높거나 낮을 때 그것과 떨어져 있는 몇 개의 세미톤 배수로 정의된다. 표준 피치가 항상 440Hz인 것은 아니다. 그것은 지난 몇백년 동안 다양하고 일반적으로 증가했다.[3]
다른 평등한 성질은 옥타브를 다르게 나눈다. 예를 들어 아랍어 톤 시스템은 24-TET를 사용하는 반면, 일부 음악은 19-TET와 31-TET로 작곡되었다.
평등한 기질은 옥타브를 나누는 대신, 볼렌-피에르체 눈금의 평등한 성질의 버전처럼 다른 간격을 13개의 평등한 부분으로 나눌 수 있는데, 이것은 그 계통에서 "티타브" 또는 "사이비오-옥타브"라고 불리는 옥타브와 5분의 1(비율 3:1)의 정의 간격을 13개의 평등한 부분으로 나눈다.
옥타브를 균등하게 나누되, 단지 간격의 근사치가 아닌 튜닝 시스템의 경우, 옥타브의 등분할 또는 EDO라는 용어를 사용할 수 있다.
개방형 문자열을 제외한 모든 노트의 튜닝을 조절할 수 있는 미개봉 문자열 앙상블과 기계적 튜닝 제한이 없는 보컬 그룹은 음향적 이유로 단지 억양에 훨씬 가까운 튜닝을 사용하기도 한다. 일부 바람, 키보드, 조바심 나는 기구와 같은 다른 기구들은 기술적 한계가 정확한 튜닝을 방해하는 동등한 기질만 근사하게 하는 경우가 많다.[4] 그들의 음색을 쉽고 자연스럽게 구부릴 수 있는 일부 관악기들, 특히 트롬본은 현악 앙상블이나 보컬 그룹과 유사한 튜닝을 사용한다.
일반 속성
동일한 기질에서 척도의 인접한 두 단계 사이의 거리는 동일한 간격이다. 구간의 인식된 정체성은 비율에 따라 다르기 때문에, 짝수 단계의 이 척도는 승수의 기하학적 배열이다. (구간의 산술적 순서는 일정한 간격으로 들리지 않을 것이며, 다른 키로 전이되는 것을 허용하지 않을 것이다.) 특히 성질이 같은 척도에서 가장 작은 간격은 비율이다.
여기서 r 비율은 p(옥타브를 2:1로 나눈 값)를 n개의 동일한 부분으로 나눈다. (아래 12음 동일 기질을 참조하십시오.)
비늘은 종종 센트로 측정되는데, 이것은 옥타브를 1200개의 동일한 간격(각각 센트라고 부른다)으로 나눈다. 이 로그 스케일은 서로 다른 튜닝 시스템을 비교하는 것보다 비교하는 것을 더 쉽게 만들며, Ethnomusicology에서 상당한 활용도를 가지고 있다. 모든 동등한 기질에 대한 센트의 기본 단계는 위 p의 폭을 센트(일반적으로 폭이 1200 센트인 옥타브)로 하여 w 아래로 부르고 n 부분으로 나누면 찾을 수 있다.
음악적 분석에서, 동일한 기질에 속하는 물질은 종종 정수 표기법이 주어지는데, 이는 하나의 정수가 각 음조를 나타내기 위해 사용된다는 것을 의미한다. 이것은 곱셈의 로그를 취하면 덧셈으로 감소하는 것과 같은 방법으로 기질 내의 음치 물질에 대한 논의를 단순화하고 일반화한다. 더욱이, 계수가 옥타브(보통 12)의 눈금수인 모듈식 산수를 적용함으로써, 이러한 정수를 피치 등급으로 줄일 수 있어, 같은 이름의 피치 사이의 구별(또는 유사성)을 제거할 수 있다(예: c는 옥타브 레지스터와 무관하게 0이다). MIDI 인코딩 표준은 정수 노트 지정을 사용한다.
성질이 같은 간격에 대한 일반 수식
12음 동일 기질
옥타브를 12개의 동일한 크기의 간격으로 나누는 12음질 균등 기질은 오늘날 서양 음악에서 특히 많이 사용되는 음악 시스템이다.
역사
평등한 기질을 정확히 계산한 공적이 빈번한 두 인물은 주자이유(추차이유라고도 로마자로 표기됨)이다. 중국어: 1584년 朱載堉), 1585년 사이먼 스테빈. 프리츠 A에 의하면 Kuttner, 그"Chu-Tsaiyu 1584년에 평균율 mono-chords의 산술 계산에 매우 정밀한과 기발한 간단한 방법을 설명했다."며"시몬 스테빈 평균율의 움직임을 수학적 정의와 이에 해당하는 수치 값은 다소 덜 정확한 계산을 제공했다 알려진 것은 theory,[5]의 비평가. 1585세 이상." 그 발전은 독립적으로 일어났다.[6]
케네스 로빈슨은 평등한 기질의 발명을 주자이유[7] 탓으로 돌리며 텍스트 인용문을 증거로 제시한다.[8] 주자이유는 1584년부터 작성된 문자에서 "나는 새로운 시스템을 구축했다. 나는 한 발을 다른 발을 추출할 숫자로 설정하고, 그것을 추출하는 비율을 사용한다. 모두 합쳐서 12개 작전에서 피치파이퍼의 정확한 수치를 찾아내야 한다."[8] 쿠트너는 이에 동의하지 않으며 자신의 주장이 "중대한 자격요건 없이는 옳다고 볼 수 없다"[5]고 말했다. 쿠트너는 주 자이유나 사이먼 스테빈 어느 쪽도 동등한 기질을 달성하지 못했으며 둘 다 발명가로 취급되어서는 안 된다고 제안한다.[9]
중국
앞서 중국이 12-TET에 대한 근사치를 내놓았지만,[10] 주자이유는 1580년 자신의 퓨전 음악 달력 律暦通 and과 1584년 음악·피치 종합편찬(Yuelüuan shu shu全書書)에서 설명한 12음 평등한 기질을 수학적으로 푼 최초의 인물이었다.[11] 조셉 니덤에 의해 연장된 계좌도 제공된다.[12] 주씨는 끈과 파이프의 길이를 연속적으로 dividing2 ≈ 1.059463으로, 파이프 길이에 대해서는 √2로 나누어 수학적으로 결과를 얻었는데,[13] 12 눈금(옥타브) 후에 길이를 2배수로 나누었다.
주자이유는 대나무 파이프를 포함하여 그의 시스템에 맞춘 여러 악기를 만들었다.[14]
유럽
평등한 기질을 옹호한 최초의 유럽인 중에는 루텐주의자인 빈첸초 갈릴레이, 지아코모 고르자니스, 프란체스코 스피나치노 등이 있었는데, 이들은 모두 그 속에 음악을 작곡했다.[15][16][17][18]
사이먼 스테빈은 1884년 거의 3세기 후 사후에 출판된 반 드 슈피겔링 데르 싱콘스(ca. 1605)에서 설명한 2의 12번째 뿌리를 바탕으로 12-TET를 개발한 최초의 사람이었다.[19]
몇 세기 동안 유럽은 12개의 동등한 기질뿐만 아니라 평균적인 기질, 우물 기질 등 다양한 튜닝 시스템을 사용했는데, 각각은 전자의 근사치로 볼 수 있다. 뽑은 악기 연주자(루텐리스트와 기타리스트)는 대체로 평등한 기질을 선호했고,[20] 다른 연주자들은 더욱 의견이 갈렸다.[21] 결국 12음 대등한 기질이 승리했다. 이것은 대칭적인 톤과 다음성의 새로운 스타일을 허용했고, 12음 기법이나 연재주의로 쓰여진 것과 같은 무조 음악, 재즈(적어도 그 피아노 구성 요소)가 발달하고 번창했다.
수학
옥타브를 12등분하는 12음등성 기질에서, 세미톤의 폭, 즉 인접한 두 음의 간격의 빈도비(prequency ratio)는 2의 12번째 근이다.
이는 다음과 같다.
이 간격은 100센트로 나뉜다.
절대 주파수 계산
12-TET에서 노트의 주파수 P를n 찾으려면 다음 정의를 사용할 수 있다.
이 공식에서 P는n 음치, 즉 주파수(보통 헤르츠 단위)를 가리키며, 당신은 찾으려 하고 있다. P는a 기준 피치의 주파수를 가리키며, n은 각각 원하는 피치와 기준 피치에 할당된 숫자를 가리킨다. 이 두 숫자는 연속된 의미에 할당된 연속 정수의 목록에서 나온 것이다. 예를 들어 A4(기준 피치)는 피아노 왼쪽 끝에서 49번째 키(440Hz로 튜닝됨), C(중간 C)와 F#4는4 각각 40번째와 46번째 키다. 이 숫자들은 C와4 F#4의 주파수를 찾는 데 사용될 수 있다.
주파수를 동등한 기질의 상대방으로 변환
주파수(Hz)를 동일한 12-TET 상대 주파수로 변환하려면 다음 공식을 사용할 수 있다.
여기서 E는n 평등한 기질에서 피치의 빈도를 가리키며, a는 기준 피치의 빈도를 가리킨다. 예를 들어 (기준 피치를 440Hz로 하면) E와5 C#5가 각각 다음과 같은 주파수와 같다는 것을 알 수 있다.
억양만으로 비교
12-TET의 간격은 억양만으로 어떤 간격에 근접한 값이다.[22] 5,4차는 거의 구별할 수 없을 정도로 단지 간격에 가깝고, 3분의 3과 6분의 1은 더 멀리 떨어져 있다.
다음 표에서 다양한 정의 간격의 크기를 성질이 같은 상대와 비교하며, 비율은 센트(cent)이다.
| 간격 이름 | 12-TET 단위의 정확한 값 | 12-TET 단위의 십진수 값 | 센트 | 억양 간격 | 억양만으로 센트 | 차이점 |
|---|---|---|---|---|---|---|
| 유니슨 (C) | 20⁄12 = 1 | 1 | 0 | 1⁄1 = 1 | 0 | 0 |
| 증강된 일치/최소 초(CND/DR) | 21⁄12 = 12√2 | 1.059463 | 100 | 16⁄15 = 1.066... | 111.73 | -11.73 |
| 주요초(D) | 22⁄12 = 6√2 | 1.122462 | 200 | 9⁄8 = 1.125 | 203.91 | -3.91 |
| 증강된 2차/최소 3차(DJ/Ee) | 23⁄12 = 4√2 | 1.189207 | 300 | 6⁄5 = 1.2 | 315.64 | -15.64 |
| 제3장(E) | 24⁄12 = 3√2 | 1.259921 | 400 | 5⁄4 = 1.25 | 386.31 | +13.69 |
| 퍼펙트 4위(F) | 25⁄12 = 12√32 | 1.33484 | 500 | 4⁄3 = 1.33333… | 498.04 | +1.96 |
| 트리톤(F♯/G♭) | 26⁄12 = √2 | 1.414214 | 600 | 64⁄45= 1.422... | 609.78 | -9.78 |
| 퍼펙트 5위(G) | 27⁄12 = 12√128 | 1.498307 | 700 | 3⁄2 = 1.5 | 701.96 | -1.96 |
| 증강된 5/6차(GA/AA) | 28⁄12 = 3√4 | 1.587401 | 800 | 8⁄5 = 1.6 | 813.69 | -13.69 |
| 6장조 (A) | 29⁄12 = 4√8 | 1.681793 | 900 | 5⁄3 = 1.66666… | 884.36 | +15.64 |
| 증강된 6/7차(A♯/B♭) | 210⁄12 = 6√32 | 1.781797 | 1000 | 16⁄9 = 1.77777… | 996.09 | +3.91 |
| 7장조 (B) | 211⁄12 = 12√2048 | 1.887749 | 1100 | 15⁄8= 1.875 | 1088.270 | +11.73 |
| 옥타브(C) | 212⁄12 = 2 | 2 | 1200 | 2⁄1 = 2 | 1200.00 | 0 |
제5음 7음등분
비올린, 비올라와 첼로는 완벽한 5분의 1(비올린의 경우 G – D – A – E, 비올라와 첼로의 경우 C – G – D – D – A)로 튜닝되어 있어 기존의 12음 동일 기질보다 반음 비율이 약간 높은 것으로 보인다. 완벽한 5번째는 그 기본 톤과 3:2의 관계에 있고, 이 간격은 7단계로 되어 있기 때문에, 각각의 톤은 3/2 대 다음(100.28 센트)의 비율로, 3:2의 비율로 완벽한 5번째를 제공하지만, 12 piff가 되기 때문에, 보통 2:1의 비율보다는 517:258 또는 2.00388:1의 약간 넓은 옥타브를 제공한다.그들은 7옥타브와 같지 않다.[23] 그러나 실제 연주에서는 바이올리니스트가 귀로 공을 고르고, 현악기의 4개만 이 3:2 비율을 보여줄 수 있다.
기타 평등한 기질
자기 민족학에서 5와 7 톤의 기질
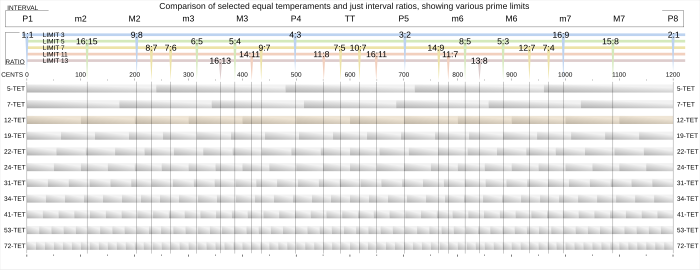
플레이(Help·info)가 240개, 플레이(Help·info)가 171개(Help·info)가 171개(Help·info)인 5개, 7개 톤 동일 기질(5-TET Play·Help·info)이 상당히 일반적이다.
5-TET와 7-TET는 그림 1과 같이, 싱토닉 기질의 유효한 튜닝 범위의 끝점을 표시한다.
- 5-TET에서 강화형 퍼펙트 5위는 720센트 폭(튜닝 연속체의 맨 위)이며, 마이너 초의 폭이 0센트로 축소되는 튜닝 연속체에 엔드포인트를 표시한다.
- 7-TET에서 강화형 퍼펙트 5위는 686센트 폭(튜닝 연속체의 하단)이며, 튜닝 연속체에 엔드포인트를 표시하며, 여기서 마이너 2초는 주요 2초만큼 넓어진다(각 171센트).
5음 동일 기질
인도네시아 게이멜란들은 쿤스트(1949년)에 따라 5-TET에 맞춰 튜닝되지만 후드(1966년)와 맥피(1966)에 따라 튜닝이 매우 다양하며 텐저(2000년)에 따르면 연장된 옥타브를 포함하고 있다. 이제 슬렌드로와 펠로그의 두 가지 일차 튜닝 시스템 중 슬렌드로만이 5음 동일 기질을 다소 닮았을 뿐 펠로그는 매우 불평등한 반면, Surjodiningrat 외 연구진(1972)은 펠로그를 9음 동일 기질의 7음 부분집합(133-cent step Play(도움/info)으로 분석하였다.
7음 동일 기질
모튼(1974)이 측정한 태국식 실로폰은 7-TET에서 "봉급 플러스 마이너스 5센트"라고 한다. 모튼에 따르면, "고정 피치의 타이 악기들은 옥타브 당 7개의 피치의 등거리 시스템에 맞춰져 있다... 그러나 서양의 전통음악처럼 튜닝 시스템의 모든 음을 하나의 모드(흔히 '스케일'이라고 한다)에서 사용하지 않고, 태국 시스템에서는 7개 중 5개가 모드의 주음에서 사용되므로 모드에 대한 불분명한 간격의 패턴을 확립한다."[24] ![]() 재생(도움말/인포)
재생(도움말/인포)
Boiles(1969년)가 측정한 제도 이전의 문화에서 나온 남미계 인도계 척도는 175센트의 7톤 동일 기질을 나타냈는데, 기악기 가멜란 음악처럼 옥타브를 약간 길게 늘어뜨렸다.
중국 음악은 전통적으로 7-TET를 사용해 왔다.[25][26]
다양한 평등한 기질
이 섹션은 검증을 위해 추가 인용구가 필요하다.할 수 2020년 3월(이 메시지 제거 및 ) |

24 EDO, 즉 4분의 1 톤 음계(24-TET)는 20세기에 유행한 마이크로 톤 튜닝으로, 아마도 이 음계가 역시 마이크로 톤에 관심이 있는 서양의 12 EDO 표준 음조와 표기 연습에 조건부 작곡가의 편리한 접근 지점을 나타냈기 때문일 것이다. 24개의 EDO는 12개의 EDO의 모든 투구와 12개의 EDO의 각 인접한 투구들 사이의 중간 지점에 새로운 투구를 포함하고 있기 때문에, 그들은 12 톤의 조화로 가능한 어떤 전술도 잃지 않고 추가 색상을 사용할 수 있었다. 24가 12의 배수라는 사실 또한 피아노 2대와 같이 일부러 쿼터 톤을 구분하여 조율한 두 대의 전통적인 에도 악기를 채용함으로써 24개의 에도를 악기적으로 쉽게 달성하게 하였는데, 이 악기는 각 연주자(또는 각 손으로 다른 피아노를 연주하는 한 연주자)가 친숙한 12음표 표기법을 읽을 수 있게 해주기도 했다. 샤를 이베스를 비롯한 다양한 작곡가들이 쿼터톤 피아노의 음악을 실험했다. 24 EDO는 12 EDO와는 달리 11번째의 하모닉에 매우 근사하다.
19 에도가 유명하고 19 에도에서 일부 악기가 튜닝되어 있다. 5위(695센트)에 약간 아첨하지만 6위는 억양의 6위(884센트)에서 1센트도 채 안 된다. 마이너 3위 역시 억양만으로 1센트가 채 되지 않는다.(19 에도보다 더 나은 마이너 3위, 메이저 6위를 생산하는 최저의 에도는 232 에도) 그것의 완벽한 4번째(505 센트)는 억양보다 5 센트, 12 테트에서 3 센트밖에 안 된다.
23 EDO는 20센트 이내에서 3차, 5차, 7차, 11차 고조파(3:2, 5:4, 7:4, 11:8)의 근사치를 하지 못하는 가장 큰 에도로, 특이한 미세 톤의 고조파 영역을 찾는 마이크로톤리스트들에게 매력적이다.
26 에도는 거의 순수하게 제7대 고조파(7:4)를 조율한 가장 작은 에도다. 또한 4 5분의 1이 지나면 주요 3위가 아닌 중립 3위가 된다는 것을 의미하는 매우 평평한 평균 기질이기도 하다. 26 에도에는 2개의 3분의 1소수, 2개의 6소수가 있다. 중성 3번을 연주하면 아주 평평한 메이저 3번으로 들리기 때문에 얼핏 보면 좀 헷갈릴 수 있다. 26EDO는 바버샵 조화의 대체 기질일 수 있다.
27 에도는 처음 8개의 고조파를 포함하는 모든 간격을 독특하게 나타내는 가장 작은 에도이다. 그것은 9진수 쉼표를 템퍼링하지만 구음 쉼표는 아니다.
29 EDO는 12 EDO보다 더 완벽한 5분의 1을 생산하는 옥타브 중 가장 낮은 수다. 그것의 세 번째 주요 내용은 대략 12-TET만큼 부정확하지만, 그것은 14 센트 급이 아니라 14 센트 급으로 조정된다. 7번째, 11번째, 13번째 고조파도 거의 같은 양으로 평탄하게 조율한다. 이는 7:5, 11:7, 13:11 등과 같은 구간이 29-TET에서 모두 매우 잘 일치한다는 것을 의미한다.
31 EDO는 크리스티아안 후이겐스와 아드리아안 포크커가 주창했다. 31 EDO는 12 EDO보다 정확도가 약간 떨어지지만 3분의 1에 가까운 장조를 제공하며, 최소 13까지 적절한 조화를 제공하며, 그 중 7번째 고조파는 특히 정확하다.
34 EDO는 5-한계에 대한 총합 오차 합계가 약간 적지만 3:2, 5:4, 6:5와 그 반전은 EDO 31보다 약간 적다. 34 EDO는 프라임 7과 관련된 대략적인 비율이 아니다. 짝수 EDO이므로 600센트의 트리톤을 함유하고 있다.
41 EDO는 12 EDO보다 완벽한 5분의 1을 생산하는 등분할의 두 번째로 낮은 수다. 주요 3위는 약 6센트 플랫인 12개의 에도와 29개의 에도보다 더 정확하다. 뜻이 아니어서 31도와는 달리 10:9와 9:8을 구별한다. 31도보다 13한계가 더 정확하다.
46 EDO는 약간 날카로운 3분의 1과 완벽한 5분의 1을 제공하여 트라이애드 특유의 밝은 소리를 낸다. 최대 11개의 고조파들은 정확도 5센트 이내에서 대략적으로 추정되며, 10:9와 9:5는 순수와 5분의 1 떨어져 있다. 평균적인 시스템이 아니기 때문에 10:9와 9:8을 구분한다.
53 EDO는 12, 19, 31 에도보다 전통적인 일치에 근사치하는 데 더 뛰어나지만, 가끔씩만 사용해 왔다. 그것의 극도로 완벽한 5분의 1은 확장된 피타고라스적 튜닝과 호환되도록 만들지만, 또한 분열적인 기질을 수용하기도 하며, 터키 음악 이론에서 종종 사용된다. 그러나 그것은 5분의 1의 주기를 통해 쉽게 도달할 수 있는 범위 내에 3분의 1을 두는 평균적인 성질의 요건에 맞지 않는다. 53 EDO에서는 피타고라스를 사용하여 자음 3분의 1이 대신 도달했는데, 이는 EDO 41과 마찬가지로 분열적 기질의 예로서 4번째(C-Ff)가 줄어들었다.
72 EDO는 7:4, 9:7, 11:5, 11:6, 11:7과 같은 7 한계와 11 한계까지 많은 단순한 억양 간격을 잘 나타낸다. 72 EDO는 Joe Maneri와 그의 제자들에 의해 실제로 가르치고, 쓰고, 수행되었다(대개 직설적인 경향은 단지 억양에 대한 언급을 회피한다). 72는 12의 배수이므로 12 에도의 연장으로 볼 수 있다. 72 에도는 12 에도의 최소 간격인 12 에도의 6배수로 가장 작은 간격인 12 에도보다 6배 작기 때문에 다른 음으로 시작하는 12 에도의 6부를 포함하고 있다. 또한, 24 에도의 3부, 36 에도의 2부, 그 자체가 12 에도의 배수로 되어 있다 72 에도는 단지 억양의 하한(예: 5한)에 대해서는 필요 없음에도 불구하고 12 에도에 수록된 빈약한 근사를 그대로 유지함으로써 중복성을 지적받고 있다.
96 EDO는 모든 구간이 6.25 센트 이내로 거의 구분할 수 없는 수준이다. 12의 8배수로 일반 12 에도처럼 충분히 사용할 수 있다. 1924년부터 1940년대까지 여러 작곡가, 특히 훌리안 카리요에 의해 주창되어 왔다.[28]
그 밖에 간혹 사용되어 온 옥타브의 등분할로는 에도 15개, 에도 17개, 에도 22개가 있다.
log2(3)의 첫번째 convergents의 2,5,12,41,53,306,665년과 15601 있denominators, 그렇게 2,5,12,41,53,306,665년과 15601 twelfths(그리고 다섯번째), 특파원 동등한 기질을 옥타브의 정수된 상태에 있는 동등한 기질보다 2,5,12,41,53,306,665년과 15601의 더 나은 근사 단지 twelfths/fifths w.i더 적은 톤.[29][30]
1, 2, 3, 5, 7, 12, 29, 41, 53, 200... (OEIS에서 시퀀스 A060528)은 완벽한 5번째에 더 좋고 더 나은 근사를 제공하는 옥타브의 분할 순서다. 관련 시퀀스에는 다른 정의 간격에 가까운 구획이 포함되어 있다.[31]
이 적용: [1]은 옥타브 균등분할 시스템의 주파수, 근사치 및 MIDI 피치 벤딩 값을 계산한다. '원형'과 '플로어'는 동일한 MIDI 피치 벤딩 값을 생성한다는 점에 유의하십시오.
비옥타브 간격의 동일한 템퍼링
볼렌-피에르체 척도의 동일한 성질의 버전은 3:1, 1902센트의 비율로 구성되며, 통상적으로 완벽한 5분의 1 플러스 옥타브(즉, 완벽한 12분의 1), 이 이론에서 트리타브(![]() 놀이·도움말·인포)라고 부르고, 13개의 동등한 부분으로 나누어져 있다. 이것은 홀수만으로 구성된 정당하게 조정된 비율과 매우 가까운 일치를 제공한다. 각 단계는 146.3센트(
놀이·도움말·인포)라고 부르고, 13개의 동등한 부분으로 나누어져 있다. 이것은 홀수만으로 구성된 정당하게 조정된 비율과 매우 가까운 일치를 제공한다. 각 단계는 146.3센트(![]() 놀이(도움말·인포) 또는 √3이다.
놀이(도움말·인포) 또는 √3이다.
웬디 카를로스는 스텝 사이즈가 30에서 120 센트 사이인 가능한 템포의 성질을 철저히 연구한 후 세 가지 특이한 균등 템포를 만들었다. 이것들은 알파, 베타, 감마라고 불렸다. 그들은 완벽한 5등분이라고 여겨질 수 있다. 그들 각각은 몇 개의 정의구간에 대한 아주 좋은 근사치를 제공한다.[32] 단계 크기:
Alpha와 Beta는 1986년 앨범 Beauty in the Beast의 타이틀곡에서 들을 수 있다.
세미톤과 전체 톤 사이의 비율
이 섹션은 검증을 위해 추가 인용구가 필요하다. (2017년 8월)(이과 시기 |
이 절에서 세미톤과 전체 톤은 그들이 원하는 관계를 만들기 위해 어떻게 정의 버전과 다른 방식으로 담금질되는지에 대해 논의하기 때문에 일반적인 12-EDO 의미를 갖지 않을 수 있다. 반음절의 단계 수는 s로 하고, 톤의 단계 수는 t로 한다.
음을 올바른 순서(예: C, D, E, F, F)로 유지하면서 음을 전체 음의 어느 적절한 부분에라도 반석을 고정시키는 평등한 기질의 가족이 정확히 한 개 있다. 즉, qt = s 관계에서 q를 적절한 분수에 고정시키는 것은 또한 하나의 동일한 기질과 이 관계를 충족시키는 그것의 배수의 독특한 가족을 정의한다.
예를 들어, 여기서 k는 정수인 경우 12k-EDO는 q = ½을, 19k-EDO는 q = ½을 설정한다. 이러한 계열에서 가장 작은 배수(예: 위 12와 19)는 5의 원 바깥에 음이 없다는 추가적인 속성을 가진다.(일반적으로 이것은 사실이 아니다, 24-EDO에서 반음반과 반음반은 C부터 생성되는 5의 원 안에 있지 않다.) 극단적인 경우는 5k-EDO로 q = 0이 되고 세미톤이 일체가 되는 경우, 7k-EDO로 q = 1과 세미톤과 톤이 같은 간격이다.
일단 이 평등한 기질에서 세미톤과 어조가 몇 걸음인지 알게 되면 옥타브에서 몇 걸음인지 알 수 있다. 위의 성질을 만족시키는 동등한 기질(5초 원 외부에 음이 없는 것 포함)은 옥타브를 7t - 2s 단계로, 완벽한 5번째는 4t - s 단계로 나눈다. 5초 원 외부에 음이 있을 경우, 이 결과를 n으로 곱해야 한다. 이는 모든 음을 생성하는 데 필요한 5초 중 겹치지 않는 원의 수입니다(예: 24-EDO의 2개, 72-EDO의 6개).(19-EDO의 작은 세미톤은 2개의 세미톤을 가져야 한다. 19-EDO는 1/3 톤이고 다른 것은 2/3이다.)
이들 가족 중 가장 작은 가족은 12k-EDO이며, 특히 12-EDO는 위의 성질을 가진 가장 작은 평등한 기질이다. 게다가, 그것은 또한 세미톤을 정확히 반 톤의 전체 톤으로 만들어, 가능한 가장 간단한 관계를 만든다. 12-EDO가 가장 일반적으로 사용되는 동일 기질이 된 이유 중 하나이다.(또 다른 이유는 12-EDO가 거의 5-제한 조화에 가까운 가장 작은 동일 기질이고, 다음으로 가장 작은 기질은 19-EDO라는 점이다.)
관계를 위한 fraction q의 각각의 선택은 정확히 하나의 동일한 기질 계열로 귀결되지만, 그 반대는 사실이 아니다: 47-EDO는 두 개의 다른 세미톤을 가지고 있다. 여기서 하나는 ½톤이고 다른 하나는 ½톤이며, 이는 19-EDO (1/3과 2/3)와 같이 서로 보완되지 않는다. 각각의 세미톤을 복용하면 완벽한 5번째를 선택할 수 있다.
관련 튜닝 시스템
일반 이음 튜닝
12 등가의 이온 튜닝은 모든 T와 모든 S의 크기가 같고 S의 크기가 T보다 작은 일련의 TSTTTS(또는 그것의 회전)로 옥타브를 나누는 일반적인 이온 튜닝으로 일반화할 수 있다. 12등에서 S는 반음이며 정확히 T음조의 절반이다. S가 0으로 줄었을 때 결과는 TTTT 또는 5음 동일 기질일 때, 세미톤이 커짐에 따라 결국 스텝은 모두 같은 크기가 되고, 결과는 7음 동일 기질이다. 이 두 엔드포인트는 일반 이온 튜닝으로 포함되지 않는다.
규칙적인 이음조의 음은 7개의 강화 5분의 1 사이클로 서로 연결된다. 12음계 시스템은 유사하게 12 5분의 1의 주기로 서로 연결된 색채와 이온성 반점의 순서 CDCDDCDCDD(또는 그것의 회전)와 일반화된다. 이 경우 C의 크기가 0이 되는 경향이 있고 5는 D가 0이 되는 경향이 있으므로 한계치에서 7은 동일하며 12는 물론 C = D이다.
톤과 세미톤의 중간 크기의 일부는 동일한 기질 체계에서도 생성될 수 있다. 예를 들어, 이음계 세미톤이 색도계 세미톤의 두 배 크기인 경우, 즉 D = 2*C 결과는 색도계 세미톤에 대한 한 단계, 이음계 세 단계 및 음조에 대한 세 단계와 총 5*T + 2*S = 15 + 4 = 19단계가 된다. 그 결과 12음계는 역사적으로 중요한 1/3 쉼표와 거의 비슷하다.
색도 세미톤이 이음계 세미톤 크기의 3분의 2 즉, C = (2/3)*D인 경우 결과는 31과 같으며, 색도 세미톤은 2단계, 이음계 세미톤은 3단계, 이음계 세미톤은 5*T + 2*S = 25 + 6단계 = 31단계인 톤은 5단계다. 그 결과 12음계는 역사적으로 중요한 1/4 쉼표와 거의 비슷하다.
참고 항목
참조
인용구
- ^ Jump up to: a b 세타레스는 그래프의 몇 개의 동일한 성질을 동일 성질의 첫 번째 비교에서 축으로부터 역행한 축과 두 번째 축의 동일한 축과 비교한다. (그림 4.6, 페이지 58)
- ^ O'Donnell, Michael. "Perceptual Foundations of Sound". Retrieved 2017-03-11.
- ^ 유럽 음악 피치의 역사 p493-511 허먼 헬름홀츠, 알렉산더 J. 엘리스 온 톤의 감각, 도버 출판사, 뉴욕
- ^ 바리치, G, & Gower, C. (2010) 초조해 하는 현악기의 억양과 보상. 미국 물리학 저널 78(47), 47-55. https://doi.org/10.1119/1.3226563
- ^ Jump up to: a b 프리츠 A. 커트너. 페이지 163.
- ^ 프리츠 A. 쿠트너. 『추차이위 왕자의 생애와 작품: 평등한 기질 이론에 대한 기여도 재평가』, p.200, ethomusicology, 19권, 2권(1975년 5월), 163~206권.
- ^ 케네스 로빈슨: 추차위가 중국 음악에서 평등한 기질 이론에 기여한 것에 대한 비판적 연구. (Sinologica Colonliensia, Bd. 9.) x, 136 pp. 비즈바덴: Franz Steiner Verlag GmbH, 1980. DM 36. p.vii "Chu-Tsaiuu는 세계 어느 곳에서나 "평등한 기질"의 수학의 첫 공식화자
- ^ Jump up to: a b 로빈슨, 케네스 G, 조셉 니덤 1962년 "물리학과 물리 기술". 중국의 과학과 문명화에서 제4권: "물리학과 물리 기술", 제1부: 조셉 니덤이 편집한 "물리학"이다. 케임브리지: 대학신문 221쪽
- ^ 프리츠 A. 커트너. 페이지 200.
- ^ 진 J. 조 "문화사적 음악적 평등한 기질 발견의 의의", http://en.cnki.com.cn/Article_en/CJFDTOTAL-XHYY201002002.htm 웨이백머신에 2012-03-15 보관
- ^ "Quantifying Ritual: Political Cosmology, Courtly Music, and Precision Mathematics in Seventeenth-Century China Roger Hart Departments of History and Asian Studies, University of Texas, Austin". Uts.cc.utexas.edu. Archived from the original on 2012-03-05. Retrieved 2012-03-20.
- ^ 중국의 과학과 문명화, Vol IV:1 (물리학), 조셉 니덤, 캠브리지 대학 출판부, 1962–2004, 페이지 220 fff
- ^ 중국의 짧은 과학과 문명화, 조셉 니덤의 콜린 로난의 축약 p385
- ^ 라우한손, 아바쿠스, 실용수학 p389(중국어 劳汉生生《》》》》》》》》》》》》》》》》》》》》》》》》》》》》》》 389页)
- ^ 갈릴레이, V. (1584년). 일 프론리모... Dialogo sopra l'arte del bene intavolare. Dialogo sopra G. 스코토: 베니스, ff. 80-89
- ^ "Resound – Corruption of Music". Philresound.co.uk. Archived from the original on 2012-03-24. Retrieved 2012-03-20.
- ^ 자코모 고르자니스, C. 1525 – C. 1575 인타볼라투라 디 리우토. 1982년 제네바
- ^ "Spinacino 1507a: Thematic Index". Appalachian State University. Archived from the original on 2011-07-25. Retrieved 2012-06-14.
- ^ "Van de Spiegheling der singconst, ed by Rudolf Rasch, The Diapason Press". Diapason.xentonic.org. 2009-06-30. Archived from the original on 2011-07-17. Retrieved 2012-03-20.
- ^ 마크 린들리 ISBN 978-0-521-2883-5
- ^ 안드레아스 베르크메이스터: 뮤지컬리스 패러독스-디스코스, 1707
- ^ Partch, Harry (1979). Genesis of a Music (2nd ed.). Da Capo Press. p. 134. ISBN 0-306-80106-X.
- ^ Cordier, Serge. "Le tempérament égal à quintes justes" (in French). Association pour la Recherche et le Développement de la Musique. Retrieved 2010-06-02.
- ^ 모튼, 데이비드(1980). "태국의 음악" , Music of Multi Cultures, p.70. 메이, 엘리자베스, 에드 ISBN 0-520-04778-8
- ^ 有关"七平均律"新文献著作的发现 [Findings of new literatures concerning the hepta – equal temperament] (in Chinese). Archived from the original on 2007-10-27.
'Hepta-equal temperament' in our folk music has always been a controversial issue.
- ^ 七平均律"琐谈--兼及旧式均孔曲笛制作与转调 [abstract of About "Seven- equal- tuning System"] (in Chinese). Archived from the original on 2007-09-30. Retrieved 2007-06-25.
From the flute for two thousand years of the production process, and the Japanese shakuhachi remaining in the production of Sui and Tang Dynasties and the actual temperament, identification of people using the so-called 'Seven Laws' at least two thousand years of history; and decided that this law system associated with the flute law.
- ^ 마일스 리 스키너(2007) 쿼터톤 구문에 대하여: 블랙우드, 하바, 이브스, 위슈네그라스키의 선별된 작품 분석, 페이지 55. ISBN 9780542998478.
- ^ Monzo, Joe (2005). "Equal-Temperament". Tonalsoft Encyclopedia of Microtonal Music Theory. Joe Monzo. Retrieved 26 February 2019.
- ^ "665edo". xenoharmonic (microtonal wiki). Archived from the original on 2015-11-18. Retrieved 2014-06-18.
- ^ "convergents(log2(3), 10)". WolframAlpha. Retrieved 2014-06-18.
- ^
- 3:2 및 4:3, 5:4 및 8:5, 6:5 및 5:3(OEIS에서 시퀀스 A054540)
- 3:2 및 4:3, 5:4 및 8:5(OEIS에서 시퀀스 A060525)
- 3:2 및 4:3, 5:4 및 8:5, 7:4 및 8:7(OEIS에서 시퀀스 A060526)
- 3:2, 4:3, 5:4 및 8:5, 7:4 및 8:7, 16:11 및 11:8(OEIS의 경우 시퀀스 A060527)
- 4:3, 3:2, 5:4 및 8:5, 6:5, 5:3, 7:4 및 8:7, 16:11 및 11:8, 16:13 및 13:8(OEIS의 경우 시퀀스 A060233)
- 3:2, 4:3, 5:4 및 8:5, 6:5, 5:3, 9:8 및 16:9, 10:9 및 9:5, 16:15 및 15:8, 45:32 및 64:45 (OEIS의 경우 후속 A061920)
- 3:2 and 4:3, 5:4 and 8:5, 6:5 and 5:3, 9:8 and 16:9, 10:9 and 9:5, 16:15 and 15:8, 45:32 and 64:45, 27:20 and 40:27, 32:27 and 27:16, 81:64 and 128:81, 256:243 and 243:128 (sequence A061921 in the OEIS)
- 5:4 및 8:5(OEIS에서 시퀀스 A061918)
- 6:5 및 5:3(OEIS에서 시퀀스 A061919)
- 6:5 및 5:3, 7:5 및 10:7, 7:6 및 12:7(OEIS에서 시퀀스 A060529)
- 11:8 및 16:11(OEIS에서 시퀀스 A061416)
- ^ Carlos, Wendy. "Three Asymmetric Divisions of the Octave". wendycarlos.com. Serendip LLC. Retrieved 2016-09-01.
- ^ Milne, A, Sethares, W.A. 및 Plamondondon, J."이소모픽 컨트롤러 및 동적 튜닝: Tuning Continuum을 가로지르는 불변 손가락" Wayback Machine, Computer Music Journal, Winter 2007, Vol. 31, 4번, 15-32페이지에 2016-01-09 보관.
원천
- 조, 진진시옹. (2003). 16세기 중국과 유럽에서 음악적 평등한 기질의 발견 뉴욕주 르위스톤: 에드윈 멜렌 프레스.
- 더핀, 로스 W. 평등한 기질이 어떻게 조화를 망쳤는가(그리고 왜 신경을 써야 하는가). W.W.Norton & Company, 2007.
- 조겐슨, 오웬 튜닝. 1991년 미시간 주립대학 출판부. ISBN 0-87013-290-3
- Sethares, William A. (2005). Tuning, Timbre, Spectrum, Scale (2nd ed.). London: Springer-Verlag. ISBN 1-85233-797-4.
- Surjodingrat, W, Sudarjana, P.J., Susanto, A. (1972) Jogjakarta와 Surakarta, Gadjah Mada University Press, Jogjakarta 1972. https://web.archive.org/web/20050127000731/http:///web.telia.com/~u57011259/pelog_main.htm에서 인용. 2006년 5월 19일 회수.
- 스튜어트, P. J. (2006) "갤럭시에서 갤럭시까지: 구들의 음악" [2]
- 흐라모프, 미하일로 "5한계의 근사치, 억양만 있으면 된다. 옥타브 등분할 음수계에서의 컴퓨터 MIDI 모델링", 국제회의 SIGMAP-2008[permanent dead link], 2008년 7월 26–29, Porto, 181–184, ISBN 978-989-8111-60-9
추가 읽기
- 톤의 감각은 음향과 헤르만 폰 헬름홀츠에 의한 소리의 인식에 관한 기초적인 저작이다. 특히 부록 XX: 번역자에 의한 추가사항, 페이지 430-556, (pdf 페이지 451-577)]
외부 링크
- EDO의 Xenharmonic wiki vs. 이퀄리티 템즈
- Huygens-Fokker Foundation Center for Microtonal Music
- 올란디니: 음악 음향학
- 체임버스의 사이클로페디아(1753) 부록의 "온도"
- 바르비에리, 파트리치오. Enharmonic 악기와 음악, 1470–1900. (2008) 라티나, 일 레반테 리브리아 편집리스
- 프랙탈 마이크로토널 뮤직, 짐 쿠쿨라.
- 현존하는 모든 18세기의 인용구는 J.S. 바흐와 기질에 관한 것이다.
- 도미니크 에커슬리: "로세타 재방문: 바흐의 아주 평범한 기질"
- Well Meatments, Werckmeister 정의에 기초한 웰 템스
- Peter Buch가 선호하는 척도 기준


![{\displaystyle r={\sqrt[{n}]{p}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b55fb394d767c50fb569ca27fd636072c72fbd7c)



![{\displaystyle {\sqrt[{12}]{2}}=2^{\frac {1}{12}}\approx 1.059463}](https://wikimedia.org/api/rest_v1/media/math/render/svg/232c2beab28b1c46c328080d982595d9ef196e08)

![{\displaystyle P_{n}=P_{a}\left({\sqrt[{12}]{2}}\right)^{(n-a)}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3381e111c79f7e16a073bbe05c6cabeaba2ff79a)
![{\displaystyle P_{40}=440\left({\sqrt[{12}]{2}}\right)^{(40-49)}\approx 261.626\ \mathrm {Hz} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/f16dc9af5bbe778786f73eca304c80c72584cd70)
![{\displaystyle P_{46}=440\left({\sqrt[{12}]{2}}\right)^{(46-49)}\approx 369.994\ \mathrm {Hz} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c7144b8e3148077acb97a47d384a62a1f2a5445)









