지수 함수

지수
지수
	실제 축의 일부를 따르는 자연 지수 함수
일반 정보
일반적인 정의
발명의 동기	분석 증거
적용 분야	순수와 응용 수학
도메인 Codomain과 이미지
도메인
이미지
특정 값
0에서	1
1로 평가하다.	e
구체적인 특징
점 고정된	n∈ Z{\displaystylen\in \mathbb{Z}에 −Wn(−1)}.
연관된 기능
상호
Inverse	복소수 로그;
파생상품
반파생적
시리즈 정의
테일러 급수

기저 2와 1/2를 갖는 지수 함수

지수함수는 f $f(x)=\exp(x)$ $=$ $f(x)=\exp(x)$ $f(x)=\exp(x)$ ( $f(x)=\exp(x)$ ) { $displaystyle$ f $(x)=\exp($ x $f(x)=\exp(x)$ )} $e^{x}$ e $e^{x}$ x { $displaystyle$ e $^{x}($ $인수$ x가 지수로 작성됨)로 표시되는 수학 함수입니다.달리 명시되지 않는 한, 이 용어는 복소수까지 확장되거나 행렬이나 리 대수와 같은 다른 수학적 객체로 일반화될 수 있지만, 일반적으로 실변수의 양의 값 함수를 가리킨다.지수함수는 지수(반복 곱셈)의 개념에서 비롯되었지만, 현대적 정의(몇 가지 동등한 특성화가 있음)는 무리수를 포함한 모든 실제 인수로 엄격하게 확장될 수 있도록 한다.순수하고 응용적인 수학에서의 그것의 흔한 발생은 수학자 월터 루딘이 지수함수가 "수학에서 가장 중요한 함수"^[1]라고 주장하게 만들었다.

지수 함수는 지수 정체성을 만족합니다.

\displaystyle e^{x+y}=e^{x}e^{y}{\text{모든 }}x,y\in \mathbb {R},}

정의

e=\exp(1)

e=\exp(1)

e=\exp(1)

e=\exp(1)

e=\exp(1)

） {

displaystyle

e

e^{n}=\underbrace {e\times \cdots \times e} _{n{\text{ factors}}}

\

exp

(

1)

}과(와)

e^{n}=\underbrace {e\times \cdots \times e} _{n{\text{ factors}}}

e^{n}=\underbrace {e\times \cdots \times e} _{n{\text{ factors}}}

n =

e^{n}=\underbrace {e\times \cdots \times e} _{n{\text{ factors}}}

×

e^{n}=\underbrace {e\times \cdots \times e} _{n{\text{ factors}}}

e^{n}=\underbrace {e\times \cdots \times e} _{n{\text{ factors}}}

e^{n}=\underbrace {e\times \cdots \times e} _{n{\text{ factors}}}

인수 {

displaystyle

e

^{n

}=\

underbrace {e\times

\

cdots \times e}} _{n

}}}}}}}}}}이

e^{n}=\underbrace {e\times \cdots \times e} _{n{\text{ factors}}}

정의와 지수함수가 양의

정수

n에 대해 지수함수와 관련이 있음을

e^{n}=\underbrace {e\times \cdots \times e} _{n{\text{ factors}}}

.지수 함수의

e=\exp(1)

인 e

=

e=\exp(1)

e=\exp(1)

(

e=\exp(1)

) {

displaystyle

e=\

exp(1

)는

e=\exp(1)

오일러 수라고 불리는 유비쿼터스 수학 상수이다.

$f:\mathbb {R} \to \mathbb {R}$ 항등식을 만족시키는 다른 연속 비제로 $f:\mathbb {R} \to \mathbb {R}$ f : R $f:\mathbb {R} \to \mathbb {R}$ {\ $displaystyle$ f $:\mathbb {R}$ \ $to \mathbb {R}}$ 도 $f:\mathbb {R} \to \mathbb {R}$ 지수 함수라고 하지만, 지수 함수 exp는 도함수 자체이고 값이 $0인$ 실수 변수의 고유한 실수 함수이다. 즉 $\exp '(x)=\exp(x)$ 입니다 $\exp '(x)=\exp(x)$ $\exp '(x)=\exp(x)$ $실수$ x에 대해 $\exp '(x)=\exp(x)$ ( x $\exp '(x)=\exp(x)$ ) = $\exp '(x)=\exp(x)$ ( $x$ ) \exp ' ( x )= $\exp$ ( $x$ ) $\exp '(x)=\exp(x)$ $\exp(0)=1.$ ( x ) $\exp(0)=1.$ 1 $.$ \ $displaystyle \exp$ ( 0 ) $=$ 1 .} 따라서 $\exp(0)=1.$ exp를 다른 지수함수와 구별하기 위해 자연 지수함수라고 부르기도 합니다 $.$ exp는 $f(x)=ab^{x},$ x $f(x)=ab^{x},$ = $f(x)=ab^{x},$ x $,$ \ $display f(x)=ab^{$ x $f(x)=ab^{x},$ } $f(x)=ab^{x},$ 의 $f(x)=ab^{x},$ 함수이며, 여기서 $b$ 는 양의 실수입니다. $양수$ b와 실수 $또는$ 복소수 x에 $b^{x}=e^{x\ln b}$ b $b^{x}=e^{x\ln b}$ $b^{x}=e^{x\ln b}$ $b^{x}=e^{x\ln b}$ x ln $b^{x}=e^{x\ln b}$ { $displaystyle$ b $^{$ x } $= e^{x\ln$ b $}}$ 관계는 $b^{x}=e^{x\ln b}$ 함수 사이에 강한 관계를 설정하며, 이는 이 애매한 용어를 설명한다.

실제 지수 함수는 멱급수로도 정의할 수 있습니다.이 멱급수 정의는 복소수 $\exp :\mathbb {C} \to \mathbb {C}$ : C $\exp :\mathbb {C} \to \mathbb {C}$ \ $style \exp$ : \ $mathbb {C}$ \ $to \mathbb {C}$ 를 정의할 $\exp :\mathbb {C} \to \mathbb {C}$ $\exp :\mathbb {C} \to \mathbb {C}$ 수 있도록 복소수 인수로 쉽게 확장됩니다.복소 지수 함수는 0을 제외한 모든 복소 값을 취하며, 오일러의 공식에서 알 수 있듯이 복소 삼각 함수와 밀접하게 관련되어 있습니다.

지수함수의 보다 추상적인 속성과 특성화에 의해 동기 부여되어, 지수는 완전히 다른 종류의 수학적 객체(예: 정사각형 매트릭스 또는 Lie 대수)로 일반화되고 정의될 수 있습니다.

적용된 설정에서 지수 함수는 독립 변수의 지속적인 변화가 종속 변수에 동일한 비례 변화(즉, 백분율 증가 또는 감소)를 제공하는 관계를 모형화합니다.이는 자연과학 및 사회과학에서 광범위하게 발생하는데, 이는 자가생산인구, 복합이자, 제조업 전문지식의 증가 등입니다.따라서, 지수 함수는 물리학, 컴퓨터 과학, 화학, 공학, 수리 생물학, 그리고 경제학의 다양한 맥락에서도 나타난다.

실제 지수함수는 R $\$ 에서 $\mathbb {R}$ ( $))\displaystyle(0;\infty$ ^[2]로의 $(0;\infty )$ 분사입니다.그 역함수는 $\ln ,$ ln $,\displaystyle \ln,}$ $\log ,$ log $,\displaystyle$ \ $log$ $,}$ $\log _{e};$ $\log _{e};$ e $'{displaystyle \log_{e};}$ 로 $\log _{e};$ 표기된 자연 로그입니다.이 때문에 일부 오래된^[3] 텍스트에서는 지수함수를 반대수라고 부릅니다.

그래프

$y=e^{x}$ $y=e^{x}$ $y=e^{x}$ x {\ $style$ y $=e^{x}}$ 그래프는 $y=e^{x}$ 상향 경사이며 x가 ^[4] $증가$ 할수록 더 빠르게 증가합니다.그래프는 항상 x축 위에 있지만 큰 $음수$ x의 경우 그래프에 임의로 가까워집니다. 따라서 x축은 수평 점근선입니다. ${\tfrac {d}{dx}}e^{x}=e^{x}$ d ${\tfrac {d}{dx}}e^{x}=e^{x}$ e ${\tfrac {d}{dx}}e^{x}=e^{x}$ ${\tfrac {d}{dx}}e^{x}=e^{x}$ ${\tfrac {d}{dx}}e^{x}=e^{x}$ x x \ $displaystyle$ \ $tfrac {d}$ { }}} $e^{x$ } = $e^{x}$ means ${\tfrac {d}{dx}}e^{x}=e^{x}$ 、 각 점에서 그래프에 대한 탄젠트의 기울기가 해당 지점의 y좌표와 같다는 것을 의미합니다.

보다 일반적인 지수 함수와의 관계

지수 $f(x)=e^{x}$ f $f(x)=e^{x}$ $=$ $f(x)=e^{x}$ x {\ $displaystyle$ f $(x$ )= $e^{x}$ 는 $f(x)=e^{x}$ 다른 지수 함수와의 구별을 위해 자연 지수 함수라고 불리기도 한다.어떤 지수함수에 대한 연구는 정의상 $양$ 의 b에 대해 자연 지수함수의 연구로 쉽게 축소될 수 있다.

ab^{x}:=ae^{x\ln b}

실수변수의 함수로서 지수함수는 그러한 함수의 도함수가 함수의 값에 정비례한다는 사실에 의해 고유하게 특징지어진다.이 관계의 비례 상수는 기저 $b$ 의 자연 로그입니다.

\displaystyle\frac{d}{x}\stackrel{def}{=}\frac{d}{frac}{x\ln(b)}=e^{x\ln(b)}=b^{x}\ln(b)}.}

b>왜냐하면 ln ⁡ b>1, 그 기능 b){\displaystyle b^{)}}(로 b)e와 b)2에 묘사되어)가 늘고 있어; 들어 0{\displaystyle \ln b>0}이 미분 항상 긍정적인;b<>는 동안, 1, 그 기능(로 b가 묘사되어 .mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion 감소하고 있게 만든다.,.mw-parser-output.sfrac .tion{디스플레이:inline-block, vertical-align:-0.5em, font-size:85%;text-align:센터}.mw-parser-output.sfrac.num,.mw-parser-output.sfrac .den{디스플레이:블록, line-height:1em, 마진:00.1em}.mw-parser-output.sfrac .den{border-top:1px 고체}.mw-parser-output .sr-only{.국경:0;클립:rect(0,0,0,0), 높이:1px, 마진:-1px, 오버 플로: 숨어 있었다. 패딩:0;위치:절대, 너비:1px}1/2컵, 그리고 b)1상수 함수다.

오일러의 수 $e$ = $2.71828...$ 는 비례 상수가 1인 고유한 기저값입니다. 이는 $\ln(e)=1$ ( e ) $=$ $\ln(e)=1$ (\ $displaystyle \ln$ (e $1$ }이므로 함수는 다음과 같이 그 자체의 도함수입니다.

{\displaystyle\frac {d}{x}=e^{x}\ln(e)=e^{x}.}

$exp x$ 라고도 하는 이 함수는 "자연 지수 함수"^[5]^[6] 또는 간단히 "지수 함수"라고 불립니다.어떤 지수함수도 $b^{x}=e^{x\ln b}$ $b^{x}=e^{x\ln b}$ $b^{x}=e^{x\ln b}$ $b^{x}=e^{x\ln b}$ x ln $b^{x}=e^{x\ln b}$ b { $display$ b $^$ {x } = $e^ {x\ln$ b $b^{x}=e^{x\ln b}$ $b^{x}=e^{x\ln b}$ 자연 지수함수로 쓸 수 있으므로, 지수함수에 대한 연구를 이 함수로 줄이는 것이 계산적으로나 개념적으로 편리하다.따라서 자연지수는 다음과 같이 표현된다.

\displaystyle x\mapsto e^{x}

또는

\displaystyle x\mapsto \exp x.}

전자의 표기법은 일반적으로 단순한 지수에 사용되며, 후자는 지수가 복잡한 식일 때 선호됩니다.

$실수$ $c$ 와 d의 경우 $f(x)=ab^{cx+d}$ f $f(x)=ab^{cx+d}$ ) $=$ $f(x)=ab^{cx+d}$ $f(x)=ab^{cx+d}$ x + $f(x)=ab^{cx+d}$ {\ $displaystyle$ f $(x$ )= ab $^{cx+$ d $f(x)=ab^{cx+d}$ } $f(x)=ab^{cx+d}$ 의 함수도 지수 함수이다. 왜냐하면 다음과 같이 다시 쓸 수 있기 때문이다.

ab^{cx+d}=\left(ab^{d}\right)\left(b^{c}\right)^{x}

형식적 정의

지수 함수(파란색)와 해당 멱급수의 첫

번째

n +

1

항의 합계(빨간색)입니다.

실수 지수 $\exp \colon \mathbb {R} \to \mathbb {R}$ exp : $\exp \colon \mathbb {R} \to \mathbb {R}$ $\exp \colon \mathbb {R} \to \mathbb {R}$ {\ $displaystyle \exp$ \display $\mathbb {R}$ \ $to$ \ $mathbb$ {R} $}$ 은 $\exp \colon \mathbb {R} \to \mathbb {R}$ (는) 다양한 방법으로 특성화할 수 있습니다.일반적으로 다음과 같은 전원 ^[1]^[7]시리즈로 정의됩니다.

\exp x:=\sum _{k=0}^{\infty}{\frac {x^{k}}{k!}=1+x+{\frac {x^{2}}{2}}+{\frac {x^{3}}{6}}+{\frac {x^{4}}{24}}+\cdots

이 멱급수의 수렴반경은 무한하기 때문에 이 정의는 사실상 모든 $z\in \mathbb {C}$ z ${\$ $z\in \mathbb {C}$ {\ $displaystyle z\in$ \ $mathbb$ {C $}$ 에 적용할 수 있습니다(복소평면으로 exp $\exp x$ x \ $displaystyle$ \ $exp$ x}를 $\exp x$ 복소평면으로 확장하기 위한 "복소평면" 참조). $상수$ ${\textstyle e=\exp 1=\sum _{k=0}^{\infty }(1/k!).}$ 는 e ${\textstyle e=\exp 1=\sum _{k=0}^{\infty }(1/k!).}$ ${\textstyle e=\exp 1=\sum _{k=0}^{\infty }(1/k!).}$ 1 $=$ k $=$ ${\textstyle e=\exp 1=\sum _{k=0}^{\infty }(1/k!).}$ ${\textstyle e=\exp 1=\sum _{k=0}^{\infty }(1/k!).}$ ( ${\textstyle e=\exp 1=\sum _{k=0}^{\infty }(1/k!).}$ / ${\textstyle e=\exp 1=\sum _{k=0}^{\infty }(1/k!).}$ ! ) ${\textstyle e=\exp 1=\sum _{k=0}^{\infty }(1/k!).}$ . { $textstyle$ e=\ $exp$ 1 =\ $sum$ _{ $k=0}^{\$ infty }(1/k $!)로 정의할$ 수 있습니다. $}$

이 멱급수의 항별 미분에서는 모든 $실수$ x에 ${\textstyle {\frac {d}{dx}}\exp x=\exp x}$ d d ${\textstyle {\frac {d}{dx}}\exp x=\exp x}$ exp ${\textstyle {\frac {d}{dx}}\exp x=\exp x}$ x $=$ exp $x$ x { $frac$ { d $}$ \ $exp$ x ${\textstyle {\frac {d}{dx}}\exp x=\exp x}$ } \ $exp$ x 가 ${\textstyle {\frac {d}{dx}}\exp x=\exp x}$ 나타나므로 exp $\exp x$ {\ $\exp x$ { $display$ style \ $exp$ x $\exp x$ } 가 $\exp x$ 미분방정식의 고유한 해로서 $\exp x$ 인 특성이 됩니다.

y'(x)=y(x)

초기

y(0)=1.

y(

y(0)=1.

=

.

y(0)=1.

\

displaystyle y

(0)=

1

을 만족합니다

.

}

이 특성화에 기초하여, 연쇄 법칙은 역 함수, 자연 로그,가 d진동계 측 로그 e(y)y을을 위해 1/y{\textstyle{\frac{d}{퇴적물의 일종}}\log _{e}y=1/y};0, 또는 통나무{\displaystyle y>0,}e(y)∫ 1ydt.{\textstyle \log_{e}y=\int _{1}^{y}{\frac{dt}{t}y}을 보여 준다.\,.} 이 관계에 따라 방정식의 $해법$ 으로서 실제 $\exp x$ exp $\exp x$ x $(\$ $displaystyle$ $\exp$ x)의 $\exp x$ $y$ 정의가 일반적이지 않다.

x=\int _{1}^{y}{\frac {1}{t}},dt.

이항 정리 및 멱급수 정의를 통해 지수 함수는 다음과 같은 ^[8]^[7]한계로도 정의할 수 있습니다.

\displaystyle \exp x=\lim _{n\to\infty}\left(1+{\frac {x}{n}}\right)^{n}}.

함수 $f(x+y)=f(x)f(y)$ f $f(x+y)=f(x)f(y)$ + $f(x+y)=f(x)f(y)$ $=$ $f(x+y)=f(x)f(y)$ ) f(x ) f $)$ {\ $displaystyle f($ x+y)= $f(x)$ f( $y)}$ 의 $f(x+y)=f(x)f(y)$ 모든 연속 0이 아닌 해는 지수 $f:\mathbb {R} \to \mathbb {R} ,\ x\mapsto e^{kx},$ f $f:\mathbb {R} \to \mathbb {R} ,\ x\mapsto e^{kx},$ $f:\mathbb {R} \to \mathbb {R} ,\ x\mapsto e^{kx},$ $f:\mathbb {R} \to \mathbb {R} ,\ x\mapsto e^{kx},$ $f:\mathbb {R} \to \mathbb {R} ,\ x\mapsto e^{kx},$ $f:\mathbb {R} \to \mathbb {R} ,\ x\mapsto e^{kx},$ $f:\mathbb {R} \to \mathbb {R} ,\ x\mapsto e^{kx},$ x $,$ {\ $displaystyle f:\mathbb$ {\ $to}$ X $,$

개요

빨간색 곡선은 지수 함수입니다.검은색 수평선은 녹색 수직선과 교차하는 위치를 나타냅니다.

지수 함수는 수량이 현재 값에 비례하는 속도로 증가하거나 감소할 때마다 발생합니다.그러한 상황 중 하나는 지속적으로 복합적인 관심사이고, 사실 1683년에^[9] 제이콥 베르누이가 그 숫자를 알게 된 것은 이 관찰이었다.

\displaystyle \lim _{n\to\infty}\left(1+{\frac {1}{n}}\오른쪽)^{n}}

현재는 e로

알려져

있습니다.나중에, 1697년에 요한 베르누이는 지수함수의 ^[9]미적분을 연구했다.

원금 1이 매월 $x배율$ 로 이자를 받는 경우 매월 이자는 현재 가치의 $x$ / $12배$ 이므로 매월 총가치에 ( $1$ + $x /$ 12)를 곱하고 연말의 가치는 (1+ $x / 12) 12$ 이다 $.$ 대신 매일 이자를 더하면 ( $1$ + $x$ / $365) 365$ 가 됩니다 $.$ 연간 시간 간격의 수를 제한 없이 증가시키면 지수 함수의 한계 정의로 이어집니다.

\displaystyle \exp x=\lim _{n\to\infty}\left(1+{\frac {x}{n}}\오른쪽)^{n}}

레온하르트 ^[8]오일러에 의해 처음 주어졌다.이는 지수 함수의 여러 특성 중 하나이며, 다른 특성에는 급수 방정식 또는 미분 방정식이 포함됩니다.

이러한 정의 중 하나에서 지수 함수가 기본 지수 동일성에 준거한다는 것을 알 수 있다.

\displaystyle \exp(x+y)=\exp x\cdot \exp y}

exp

x

표기법e

가^x 됩니다

지수함수의 도함수(변화율)는 지수함수 그 자체입니다.일반적으로 함수 자체에 비례하는 변화율을 갖는 함수는 지수함수로 표현할 수 있습니다.이 함수 특성은 지수 성장 또는 지수 감소를 초래합니다.

지수 함수는 복합 평면의 전체 함수로 확장됩니다.오일러의 공식은 순수하게 상상의 인수에서의 값을 삼각함수와 관련짓는다.지수함수는 또한 인수가 행렬이거나 바나흐 대수나 리 대수의 요소인 유사체도 가지고 있다.

미분 및 미분 방정식

지수 함수의 도함수는 함수의 값과 같습니다.곡선(파란색)의

임의

의 점 P에서

높이

h의 접선(빨간색)과 수직선(녹색)을 그려 X축에 밑면

b

를 둔 직각 삼각형을 형성한다.P에서

빨간색

접선(도함수)의 기울기는 삼각형의 밑면에 대한 삼각형의 높이의 비율(상승 런)과 같으며, 도함수는 함수의 값과

같으므로

h

는 h 대

b

의 비율과 같아야 합니다.따라서

b

는 항상 1이어야 합니다.

수학과 과학에서 지수 함수의 중요성은 주로 도함수와 같으며 x = $0일$ 때 1과 같은 고유한 함수로서의 특성에서 비롯된다.그것은,

\displaystyle\frac{d}{x}=e^{x}\displaystyle\text{and}\display e^{0}=1.}

$상수$ c에 대한 $형식 x$ ce의 함수는 (피카드-린델뢰프 정리에 의해) 그 도함수와 동일한 유일한 함수이다.같은 말을 하는 다른 방법은 다음과 같습니다.

그래프의 기울기는 해당 지점의 함수 높이입니다.
$x$ 에서 함수의 증가율은 $x$ 에서 함수의 값과 같습니다.
이 함수는 미분 $방정식$ yθ = $y$ 를 해결합니다.
$exp$ 는 함수로서 미분의 고정점입니다.

무한 인구 증가(맬서스 재앙 참조), 연속 복합 관심 또는 방사성 붕괴와 같이 변수의 성장률 또는 감소율이 그 크기에 비례하는 경우 변수는 일정 시간 지수 함수로 기록될 수 있다.모든 실수 $상수$ k에 대해, $함수 f$ : $R$ → R은 어떤 $상수$ c에 대해 f $(x)$ = $ce일 kx$ $경우$ 에만fθ = $kf$ 를 $만족$ 한다.상수 k를 붕괴 상수, 분해 상수,^[10] 속도 ^[11]상수 또는 변환 ^[12]상수라고 합니다.

또한, 미분 가능한 $함수$ f에 대해, 사슬 규칙에 의해 다음과 같은 것을 알 수 있다.

{\displaystyle\frac {d}{f(x)}=f'(x)e^{f(x)}}

$e$ 에^x 대한 연속 분수

e에 $대한 x$ 연속 분수는 오일러의 항등식을 통해 구할 수 있다.

e^{x}=1+{\displayac {x}{x+2-{\displayac {2x}{x+3-{\displayac {3x}{x+4-\dots}}}}}}

e에 $대한 z$ 다음과 같은 일반화된 연속 분수는 보다 ^[13]빠르게 수렴됩니다.

\displaystyle e^{z}=1+{\displayac {2z}{2-z+{\displayac {\displayac {z^{2}}{10+{\displayac {z^{2}}}}}}{10+{14+\dots}}}}}}}}}

또는 $치환$ z = $x / y$ 를 적용하여 다음을 수행합니다.

e^{\frac {x}{\frac {2x}=1+{2y-x+{x^{2}}{6y+{\fac {x^{2}}{\frac {x^{2}}}}}}{14y+\dots}}}}

z =

2

에

대한

특수 케이스 포함:

{\displaystyle e^{2}=1+{\displayac {4}{0+{\displayac {2^{2}}{10+{\displayac {2^2}}{14+\dots}}}}}=7+{\displayac {5+{\dots}{1}{ac}{6+}{6}{\displayac {2}}{2}}{\c}{c}{c}}}{c}}{c}}}}{c}}}}}{c}}}}}{c

이 공식은 z > $2$ 에 $대해서도$ 더 느리게 수렴됩니다.예를 들어 다음과 같습니다.

{\displaystyle e^{3}=1+{\displayac {6}{-1+{\displayac {3^{2}}{10+{\displayac {3^{2}}}}}}=13+{\displayac {7+}{\dots}}{\displayac {9}{ac}{6+{\c}{c}}}{c}{c}{c}{c}{c}}{c}}{c}}{c}}{c}}}}}{c}}}{cap}{c

복소 평면

인수

Arg

\operatorname {Arg} \exp z

exp

\operatorname {Arg} \exp z

z

z\mapsto \exp z

\

displaystyle

\

operatorname

{

Arg

\

exp

z 의

z\mapsto \exp z

플롯. 다양한 색상으로 나타납니다

\operatorname {Arg} \exp z

.어두운 색상에서 밝은 색상으로의 이행은 exp

\left|\exp z\right|

\

displaystyle \left \exp

z

\right }

가

\left|\exp z\right|

오른쪽에서만 증가하고 있음을

\left|\exp z\right|

.같은 색상에 대응하는 주기적인 수평 대역은

z

의

허구

부분에서 z

z\mapsto \exp z

exp

z\mapsto \exp z

z

z

displaystyle

z \

mapsto

\

exp

z }가

z\mapsto \exp z

주기적이라는 것을

z\mapsto \exp z

.

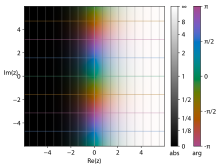
실제의 경우와 마찬가지로 지수함수는 복소평면에서 여러 등가형태로 정의할 수 있다.복소수 지수 함수의 가장 일반적인 정의는 실수 인수에 대한 멱급수 정의와 평행하며, 여기서 실수 변수는 복소수로 대체됩니다.

\exp z:=\sum _{k=0}^{\infty}{\frac {z^{k}}{k!}}

또는, 복잡한 지수 함수는 실제 변수에 대한 한계 정의를 모델링하여 정의할 수 있지만, 실제 변수는 복잡한 변수로 대체된다.

\displaystyle \exp z:=\lim _{n\to\infty}\left(1+{\frac {z}{n}}\오른쪽)^{n}}

멱급수 정의의 경우, Mertens의 정리에 의해 허용된 코시 의미에서 이 멱급수의 두 복사본의 항별 곱셈은 모든 복잡한 인수에 대해 지수 함수의 정의 곱셈 특성이 계속 유지됨을 보여준다.

\exp(w+z)=\exp w\exp z(text{모든}}w,z\in \mathbb {C}}

복잡한 지수함수의 정의는 삼각함수를 복잡한 인수로 확장하는 적절한 정의로 이어집니다.

특히 z = $it$ ( $t$ real)일 때 시리즈 정의는 확장을 생성합니다.

\displaystyle \exp(it)=\left(1-{\frac {t^{2}}}{2!}+{\frac {t^{4}}{4}!}-{\frac {t^{6}}{6}!}}+\cdots\right)+i\left(t-{\frac {t^{3}}}{3!}+{\frac {t^{5}}{5}!}-{\frac {t^{7}}{7}!}}+\cdots\right)}

이 확장에서 항을 실수 부분과 허수 부분으로 재배치하는 것은 급수의 절대 수렴에 의해 정당화된다.위의 표현식의 실수 부분과 허수 부분은 각각 $cos$ $t$ 와 $sin$ $t$ 의 급수 팽창에 대응한다.

이 대응은 exp $\exp(\pm iz)$ ( ± $\exp(\pm iz)$ ) $\exp(\pm iz)$ { $displaystyle \exp(\pm$ iz $)}$ 및 동등한 $\exp(\pm iz)$ 멱급수 ^[14] $\exp(\pm iz)$ 에서 모든 복잡한 인수에 대해 코사인 및 사인(sine)을 정의하려는 동기를 제공합니다.

&quot;디스플레이 스타일&quot;\cos z&:=frac&quot;\exp(iz)+\expairiz}{2}=\sum _{k=0}^{\infty}(-1)^{k}{\frac {z^{2k}{(2k!}}}},\sin z&:\snfrac {expair(iz)}{i}=\sum={xpy}_xpy={k}^0}{xpy}{xpy}{{{xpy}{{{xpy}{{k}{{{{{{{\fty}}}}}}}}{{}}\end{aligned}}{\text{모든 }}z\in \mathbb {C} .}

이렇게 정의된 함수 $exp$ , $cos$ $및$ sin은 비율 테스트에 의해 수렴 반지름이 무한하므로 전체 함수(즉 $,$ C \ $displaystyle \mathbb {C}$ $}$ )입니다.지수함수의 범위는 C $\mathbb {C} \setminus \{0\}$ { $}({displaystyle \mathbb {C}$ \ $setminus$ \{ $0$ 이며 $\mathbb {C}$ , 복소 사인함수와 코사인 함수의 $\mathbb {C}$ 는 모두 $\mathbb {C}$ C $({displaystyle$ \ $mathbb$ {C $})$ 이며, 피카르의 정리에 따라 모든 함수의 범위는 모든 함수의 범위입니다. $\mathbb {C}$ $\mathbb {C}$ \ $displaystyle \mathbb {C$ 또는 C $\mathbb {C}$ \ $displaystyle \mathbb {C} }($ 하나의 $\mathbb {C}$ 소수점 제외).

지수함수와 삼각함수에 대한 이러한 정의는 3차적으로 오일러의 공식으로 이어집니다.

\displaystyle \exp(iz)=\cos z+i\sin z(모든 }}z\in \mathbb {C} .}

이 관계를 바탕으로 복잡한 지수 함수를 정의할 수도 있습니다. $z$ $= x$ + $iy$ 이고, $여기$ 서 $x$ 와 y는 모두 실재한다면, 우리는 그 지수를 다음과 같이 정의할 수 있다.

\displaystyle \exp z=\exp(x+iy):=(\exp x)(\cos y+i\sin y)}

여기

서 정의 부호의 오른쪽에 있는 exp,

cos

및

sin은 이전에 다른 ^[15]방법으로 정의된 실제 변수의 함수로 해석됩니다.

t $t\in \mathbb {R}$ R \ $displaystyle$ t \ $in$ \ $mathbb$ { $R$ ${\overline {\exp(it)}}=\exp(-it)$ 의 ${\overline {\exp(it)}}=\exp(-it)$ 관계 $（$ ${\overline {\exp(it)}}=\exp(-it)$ t ${\overline {\exp(it)}}=\exp(-it)$ exp ${\overline {\exp(it)}}=\exp(-it)$ - ${\overline {\exp(it)}}=\exp(-it)$ ${\overline {\exp(it)}}=\exp(-it)$ ） \ $displaystyle$ \ $exp$ ( $it )$ $}=\expit)}은$ 는 $\left|\exp(it)\right|=1$ $\left|\exp(it)\right|=1$ 되므로 $\left|\exp(it)\right|=1$ t $\$ $displaystyle$ t $t\mapsto \exp(it)$ $t\mapsto \exp(it)$ t $\display$ $t\mapsto \exp(it)$ $1$ { $displaystyle \exp$ $(it$ )} {displaystyle $t\mapsto \exp(it)$ t\ $mapsto \exp$ (it $t\mapsto \exp(it)$ )}에 $대해$ 실제 선 $\left|\exp(it)\right|=1$ $mod$ 2)을 복합 평면 내의 원에 매핑합니다. $\gamma (t)=\exp(it)$ t $t=0$ { $displaystyle$ $t$ $=0}$ 에서 $t=0$ t $t=t_{0}$ $\gamma (t)=\exp(it)$ 0 { $displaystyle t= t_{$ $0$ $t=t_{0}$ 까지 $\gamma (t)=\exp(it)$ ( $t$ ) $\gamma (t)=\exp(it)$ exp $\gamma (t)=\exp(it)$ ( $t )$ 로 $\gamma (t)=\exp(it)$ 정의된 곡선은 길이의 단위 원의 세그먼트를 추적합니다.

\displaystyle \int _{0}^{t_{0} \display '(t) dt=\int _{0} i\exp(it) dt=t_{0}

복합 평면에서 z =

1

에서 시작하여 시계 반대 방향으로 이동합니다.이러한 관찰과 라디안에서의 각도의 측정이 각도에 의해 하위화된 단위 원상의 호 길이라는 사실에 기초하여, 실제 인수로 제한되면, 위에서 정의한 사인 및 코사인 함수는 기하학적 개념을 통해 초등 수학에서 도입된 사인 및 코사인 함수와 일치함을 쉽게 알 수 있다..

복소 지수 함수는 $z\in \mathbb {C} ,k\in \mathbb {Z}$ $z$ $z\in \mathbb {C} ,k\in \mathbb {Z}$ and $z\in \mathbb {C} ,k\in \mathbb {Z}$ , k $\exp(z+2\pi ik)=\exp z$ $Z$ \ $\exp(z+2\pi ik)=\exp z$ $z$ \ $\exp(z+2\pi ik)=\exp z$ ( $z +$ 2 \ $pi$ $ik$ ) = \ $exp$ z } $z\in \mathbb {C} ,k\in \mathbb {Z}$ 홀드에 대해 주기 2 $µi$ 및 $exp$ $\exp(z+2\pi ik)=\exp z$ ( $z$ + 2 $\exp(z+2\pi ik)=\exp z$ $\exp(z+2\pi ik)=\exp z$ $z\in \mathbb {C} ,k\in \mathbb {Z}$ $\exp(z+2\pi ik)=\exp z$ $z\in \mathbb {C} ,k\in \mathbb {Z}$ \ $exp z$ for $\exp(z+2\pi ik)=\exp z$ $。$

도메인이 실제 선에서 복소 평면으로 확장되면 지수 함수는 다음 속성을 유지합니다.

\displaystyle \tfrac {d}e^{z+w}=e^{w},\e^{0}=1,\e^{z}\neq 0\{\tfrac {d}{dz}=e^{z}\left(e^{z}\right)^{n}=e^{nz},n\in \mathbb {Z} \end{aligned}}{\text{모든}}w,z\in \mathbb {C} .}

자연 로그를 복소 인수로 확장하면 $복합$ $로그$ 로그 z가 생성됩니다. 이는 다치 함수입니다.

다음으로 보다 일반적인 지수를 정의할 수 있습니다.

z^{w}=e^{w\log z}

모든

복소수

z

와 w에 대해.이 기능은 z가 실재하는

경우

에도 다중값 함수입니다.이러한 구별은 문제가 됩니다. 왜냐하면

다치

함수

로그

z

와^w z는

z

의 실수를 대체할 때 단일 값 등가 함수와 혼동하기 쉽기 때문입니다.양의 실수의 경우 지수를 곱하는 규칙은 다중값 컨텍스트에서 수정해야 합니다.

(e z) w

≠

e zw

, 그러나

오히려 z

(w e (z + 2 niπ) w)

=

정수

n에 대한 e 다중값

검정력 조합 문제에 대한 자세한 내용은 검정력 및 로그 식별성의 고장을 참조하십시오.

지수 함수는 복소 평면의 모든 선을 원점에 중심이 있는 복소 평면의 로그 완화곡선에 매핑합니다.두 가지 특수한 경우가 있습니다.원래 선이 실제 축에 평행할 경우 결과 나선형은 그 자체로 닫히지 않습니다.원래 선이 가상 축에 평행할 경우 결과 나선형은 반지름의 원이 됩니다.

실수 부분, 가상 부분 및 지수 함수의 계수 3D 그림
$z = Re(e x + iy)$
$z = Im(e x + iy)$
$z = e x + iy$

복잡한 지수 함수를 네 개의 실제 변수를 포함하는 함수로 간주합니다.

v+display=\exp(x+iy)

지수 함수의 그래프는 4차원을 통과하는 2차원 표면이다.

$(\displaystyle$ xy $)$ $xy$ 의 $xy$ 컬러 코딩된 부분을 시작으로 2차원 또는 3차원으로 다양하게 투영된 그래프를 다음에 나타냅니다.

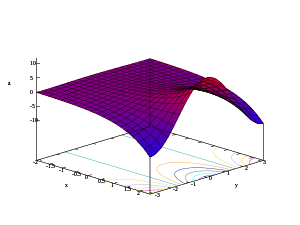
복소 지수 함수 그래프
체커 보드 키:
$\displaystyle x> 0:\;{\text{green}}}$
$x<0:\;{\text{red}$
$0:\;{\text{노란색}}}$
$y<0:\;{\text{blue}}$
레인지 복합 평면에 투영(V/W).다음 원근법 사진과 비교해보세요.
$(\displaystyle$ x $x$ $(\displaystyle$ v $v$ 및 $w$ (\ $displaystyle$ w $)$ 치수로 $w$ 투영하여 플레어 경적 또는 깔때기 모양을 생성합니다(2D 투시 이미지로 표시).
$($ $디스플레이$ $스타일$ y), $y$ v $($ 디스플레이 $스타일$ v) 및 $(디스플레이 스타일$ w $)$ 차원으로 $w$ 투영하여 나선형 모양을 생성합니다.( $y$ \ $displaystyle$ y} 범위는 $y$ ±2º로 확장되며, 다시 2-D 투시 영상으로 표시됩니다).

두 번째 이미지는 도메인 복합 평면이 범위 복합 평면에 매핑되는 방법을 보여 줍니다.

0은 1에 매핑됩니다.
$실제 x축$ 은 $x$ 양의 $v축$ 에 $v$ 매핑됩니다 $.$
$y$ 의 $y$ $y축$ 은 일정한 각도 속도로 단위 원을 감싸고 있습니다.
음의 실제 부품이 있는 값은 단위 원 안에 매핑됩니다.
양의 실제 부분이 있는 값은 단위 원 외부에 매핑됩니다.
실제 부분이 일정한 값은 0을 중심으로 한 원에 매핑됩니다.
일정한 가상 부분을 가진 값은 0에서 연장되는 광선에 매핑된다

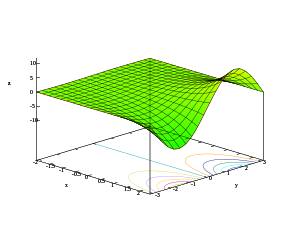
세 번째 및 네 번째 이미지는 두 번째 이미지에서 그래프가 두 번째 이미지에서 표시되지 않는 다른 두 가지 차원 중 하나로 확장되는 방식을 보여 줍니다.

세 번째 이미지는 실제 $(\displaystyle$ x $)$ 축을 $x$ 따라 확장된 그래프를 보여 줍니다.이 그래프는 실제 지수함수 그래프의 $x축$ 에 $x$ 대한 회전면이며 경적 또는 깔때기 모양을 $생성$ 합니다.

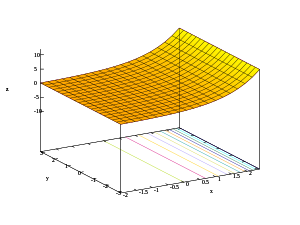
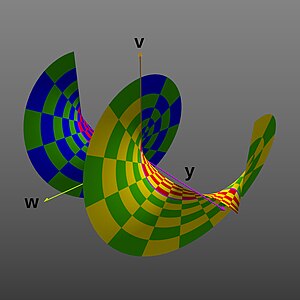
네 번째 이미지는 $y$ 의y축(\ $displaystyle$ y $)$ 을 $y$ 따라 확장된 그래프를 보여줍니다.이 예에서는 양의 $y$ 과 $음의 y값$ 의 $y$ 그래프 표면이 음의 $v축$ 에서 $v$ 실제로 만나는 것이 아니라 $y축$ 주위에 나선형 표면을 형성하고 있음을 보여 줍니다. $y($ 표시 스타일 y) 값이 $y$ $\pm2$ '로 확장되었기 때문에 $이$ 이미지에서는 상상의 y $(표시$ 스타일 $y$ y $)$ 값에서 2' 주기성도 더 잘 표현됩니다.

$a$ 와 b가 모두 $복잡한$ 경우의 a의 $계산 b$

복소수 $지수 b$ a는 a를 극좌표로 $변환$ 하고 등식 $(e ln a) b$ = $a b$ :

\displaystyle a^{b}=\left(re^{\theta i}\right)^{\left(\ln r)+\theta i\right)^{b}=e^{\left(\ln r)+\theta i\right}}

단, b가 정수가 아닌 $경우$ , $θ$ 는 고유하지 않기 때문에 이 함수는 다중값입니다(멱함수 및 로그 ID의 고장 참조).

행렬과 바나흐 대수

지수 함수의 멱급수 정의는 제곱 행렬(함수를 지수 행렬이라고 함)에 의미가 있으며, 일반적으로 단수 바나흐 $대수$ B에서 의미가 있습니다.이 설정에서 e = $1$ , $e$ 는^x $B$ 의⁰ $모든$ $x$ 에 대해 $역e$ 로^−x 반전할 수 있습니다. $xy$ = $yx이면$ $e x + y$ = $ee$ 이지만^x^y, 이 동일성은 $비소통$ x 및 $y$ 에 대해 실패할 수 있습니다.

일부 대체 정의는 동일한 기능으로 이어집니다. $예$ 를^x 들어 e는 다음과 같이 정의할 수 있습니다.

\displaystyle \lim _{n\to \infty}\left(1+{\frac {x}{n}}\right)^{n}}.

$또는 x$ e는 $f($ 1)로 $정의$ 할_x 수 있다. $여기$ 서_xf : R → $B$ 는 초기 $조건 x$ f(0)= $1인$ 미분 $방정식 x$ df $/ dt (t)$ = x $f x (t)$ 에 대한 해이다. 즉, $R$ 의 $모든$ t에 대해 $f(t$ ) = $e$ 가^tx $된다 x$ .

리 대수

Lie $군$ G와 그 관련 Lie ${\mathfrak {g}}$ g {\ $displaystyle$ {\ $mathfrak$ ${g$ ${\mathfrak {g}}$ 일 때, 지수 맵은 유사한 성질을 만족하는 ${\mathfrak {g}}$ g {\ $displaystyle$ {\ $mathfrak$ {g $}}$ $g$ G이다.사실, R은 곱셈 아래의 모든 양의 실수의 Lie 그룹의 Lie 대수이므로, $실수$ 인수에 대한 일반적인 지수 함수는 Lie 대수 상황의 특별한 경우이다.마찬가지로, $가역$ n × $n$ 행렬의 Lie $군$ GL( $n, R)$ 은 $모든$ n × $n$ 행렬의 공간인 Lie $대수$ M $(n, R)$ 을 가지므로, 제곱 행렬에 대한 지수 함수는 Lie 대수 지수 맵의 특수한 경우이다.

이동하지 않는 리 대수 $요소$ $x$ 와 y에 대하여 $항등식$ exp( $x + y$ ) = $exp$ x $exp$ y는 실패할 수 있다. 베이커-캠벨-하우스도르프 공식은 필요한 보정 항을 제공한다.

초월성

$함수 z$ e는 C $(z)$ 에 있지 않습니다(즉, 계수가 복잡한 두 다항식의 몫이 아닙니다).

n개의 고유한 복소수 { $a 1, ...,$ $a n}$ 에 $대해$ 집합 { $e a 1 z, ...,$ $e a n z}$ 은(는) C $(z)$ 에 대해 선형 독립적입니다.

$함수 z$ e는 C $(z)$ 보다 초월적입니다.

계산

$인수$ 0에 가까운 지수함수를 계산(근사)하면 결과는 1에 가깝고, $e^{x}-1$ 산술로 차이 e $e^{x}-1$ x - $(\displaystyle$ e $^{x}-1)$ 의 $e^{x}-1$ 값을 계산하면 유의한 수치가 손실될 수 있으며, 큰 계산 오차(아마도 평균)이 발생할 수 있습니다.gless 결과.

William Kahan의 제안에 따라, 종종 이라고 불리는 전용 루틴을 갖는 것이 유용할 수 있습니다.expm1e - $1$ 을 직접 계산하기 $x$ 위해 $e$ 의^x 계산을 생략합니다.예를 들어, 지수가 해당 Taylor 급수를 사용하여 계산되는 경우

e^{x}=1+x+{\frac {x^{2}}{2}}+{\frac {x^{3}}{6}+\cdots +{\frac {x^{n}}{n}!}}+\cdots,

e^{x}-1

x

e^{x}-1

-

e^{x}-1

의 Taylor 시리즈를 사용할 수 있습니다(\

displaystyle

e

^{x}-1

e^{x}-1=x+{\frac {x^{2}}{2}}+{\frac {x^{3}}{6}+\cdots +{\frac {x^{n}}{n}!}}+\cdots .

이는 1979년 Hewlett-Packard HP-41C 계산기에 처음 구현되었으며 여러 계산기,^[16]^[17] 운영 체제(예: Berkeley UNIX 4.3BSD^[18]), 컴퓨터 대수 시스템 및 프로그래밍 언어(예: C99)^[19]에 의해 제공됩니다.

IEEE 754-2008 표준에서는 $base$ e 외에 base 2 및 10: $2^{x}-1$ x - $2^{x}-1$ ({ $displaystyle$ 2 $^{x}-1$ $10^{x}-1$ 10 $10^{x}-1$ - 1 ({ $displaystyle$ 10 $^{x}-1$ 에 대해 0에 가까운 유사한 지수 함수를 정의하고 있습니다.

로그에도 유사한 접근방식이 사용되었습니다(lnp1 ^{[nb 3]}참조).

쌍곡선 접선의 항등식,

{\displaystyle \operatorname {expm1}(x)=e^{x}-1=snapfrac {2\tanh(x/2)}{1-\tanh(x/2)}},

에

expm1(x)

을 실장하지 않은 시스템의 작은 값

x

에 대한 높은 지연값을 나타냅니다.

또는 다음 식을 ^[20]사용할 수 있습니다.

$e^{x}-1=\lim _{n\to \infty}{\frac {x}}\sum _{k=1}^{n}(1+{\frac {1}{n}})^{kx}}$

「」를 참조해 주세요.

$특성$ p 아날로그인 Carlitz 지수
이중 지수 함수 – 지수 함수의 지수 함수
지수장 – 지수장의 함수 방정식을 만족시키는 연산을 갖춘 수학장
가우스 함수
지수 함수의 구성 제곱근인 반지수 함수
지수 토픽 목록
지수함수의 적분 목록
지수 함수의 일반화인 Mittag-Leffler 함수
p-adic 지수 함수
지수함수에 대한 파데 표 – 다항식 함수의 분수에 의한 지수함수의 파데 근사
테트레이션 – 반복 또는 반복된 지수화

메모들

^ $ln$ x $표기법$ 은 ISO 표준으로 자연과학 및 중등교육(미국)에서 널리 사용되고 있지만 일부 수학자(예: Paul Halmos)는 이 표기법을 비판하고 로그 x를 $x$ 의 자연대수로 $사용$ 하는 것을 선호합니다.
^ 순수 수학에서 $로그$ x $표기법$ 은 일반적으로 x의 $자연$ 로그 또는 밑이 중요하지 않은 경우 일반적으로 로그를 가리킵니다.
^ 삼각함수의 특정 입력값에 대한 계산의 반올림 오류를 줄이기 위한 유사한 접근법은 덜 일반적인 삼각함수 versine, vercosine, covercosine, haversine, habovercosine, execant 및 excant를 사용하는 것이다.

레퍼런스

^ ^a ^b Rudin, Walter (1987). Real and complex analysis (3rd ed.). New York: McGraw-Hill. p. 1. ISBN 978-0-07-054234-1.
^ Meier, John; Smith, Derek (2017-08-07). Exploring Mathematics. Cambridge University Press. p. 167. ISBN 978-1-107-12898-9.
^ Converse, Henry Augustus; Durell, Fletcher (1911). Plane and Spherical Trigonometry. Durell's mathematical series. C. E. Merrill Company. p. 12. Inverse Use of a Table of Logarithms; that is, given a logarithm, to find the number corresponding to it, (called its antilogarithm) ... [1]
^ "Exponential Function Reference". www.mathsisfun.com. Retrieved 2020-08-28.
^ Goldstein, Larry Joel; Lay, David C.; Schneider, David I.; Asmar, Nakhle H. (2006). Brief calculus and its applications (11th ed.). Prentice–Hall. ISBN 978-0-13-191965-5. (467페이지)
^ Courant; Robbins (1996). Stewart (ed.). What is Mathematics? An Elementary Approach to Ideas and Methods (2nd revised ed.). Oxford University Press. p. 448. ISBN 978-0-13-191965-5. This natural exponential function is identical with its derivative. This is really the source of all the properties of the exponential function, and the basic reason for its importance in applications…
^ ^a ^b Weisstein, Eric W. "Exponential Function". mathworld.wolfram.com. Retrieved 2020-08-28.
^ ^a ^b Maor, Eli. e: the Story of a Number. p. 156.
^ ^a ^b O'Connor, John J.; Robertson, Edmund F. (September 2001). "The number e". School of Mathematics and Statistics. University of St Andrews, Scotland. Retrieved 2011-06-13.
^ Serway, Raymond A.; Moses, Clement J.; Moyer, Curt A. (1989). Modern Physics. Fort Worth: Harcourt Brace Jovanovich. p. 384. ISBN 0-03-004844-3.
^ Simmons, George F. (1972). Differential Equations with Applications and Historical Notes. New York: McGraw-Hill. p. 15. LCCN 75173716.
^ McGraw-Hill Encyclopedia of Science & Technology (10th ed.). New York: McGraw-Hill. 2007. ISBN 978-0-07-144143-8.
^ Lorentzen, L.; Waadeland, H. (2008). "A.2.2 The exponential function.". Continued Fractions. Atlantis Studies in Mathematics. Vol. 1. p. 268. doi:10.2991/978-94-91216-37-4. ISBN 978-94-91216-37-4.
^ Rudin, Walter (1976). Principles of Mathematical Analysis. New York: McGraw-Hill. p. 182. ISBN 978-0-07-054235-8.
^ Apostol, Tom M. (1974). Mathematical Analysis (2nd ed.). Reading, Mass.: Addison Wesley. pp. 19. ISBN 978-0-201-00288-1.
^ HP 48G Series – Advanced User's Reference Manual (AUR) (4 ed.). Hewlett-Packard. December 1994 [1993]. HP 00048-90136, 0-88698-01574-2. Retrieved 2015-09-06.
^ HP 50g / 49g+ / 48gII graphing calculator advanced user's reference manual (AUR) (2 ed.). Hewlett-Packard. 2009-07-14 [2005]. HP F2228-90010. Retrieved 2015-10-10. [2]
^ Beebe, Nelson H. F. (2017-08-22). "Chapter 10.2. Exponential near zero". The Mathematical-Function Computation Handbook - Programming Using the MathCW Portable Software Library (1 ed.). Salt Lake City, UT, USA: Springer International Publishing AG. pp. 273–282. doi:10.1007/978-3-319-64110-2. ISBN 978-3-319-64109-6. LCCN 2017947446. S2CID 30244721. Berkeley UNIX 4.3BSD introduced the expm1() function in 1987.
^ Beebe, Nelson H. F. (2002-07-09). "Computation of expm1 = exp(x)−1" (PDF). 1.00. Salt Lake City, Utah, USA: Department of Mathematics, Center for Scientific Computing, University of Utah. Retrieved 2015-11-02.
^ "Calculus - A limit calculation using Riemann integral".

외부 링크

"Exponential function", Encyclopedia of Mathematics, EMS Press, 2001 [1994]

[lnx-3] $ln$ x $표기법$ 은 ISO 표준으로 자연과학 및 중등교육(미국)에서 널리 사용되고 있지만 일부 수학자(예: Paul Halmos)는 이 표기법을 비판하고 로그 x를 $x$ 의 자연대수로 $사용$ 하는 것을 선호합니다.

[Logx-4] 순수 수학에서 $로그$ x $표기법$ 은 일반적으로 x의 $자연$ 로그 또는 밑이 중요하지 않은 경우 일반적으로 로그를 가리킵니다.

[Alternative_funcs-22] 삼각함수의 특정 입력값에 대한 계산의 반올림 오류를 줄이기 위한 유사한 접근법은 덜 일반적인 삼각함수 versine, vercosine, covercosine, haversine, habovercosine, execant 및 excant를 사용하는 것이다.

[Rudin_1987-1] Rudin, Walter (1987). Real and complex analysis (3rd ed.). New York: McGraw-Hill. p. 1. ISBN 978-0-07-054234-1.

[2] Meier, John; Smith, Derek (2017-08-07). Exploring Mathematics. Cambridge University Press. p. 167. ISBN 978-1-107-12898-9.

[Durell_1911-5] Converse, Henry Augustus; Durell, Fletcher (1911). Plane and Spherical Trigonometry. Durell's mathematical series. C. E. Merrill Company. p. 12. Inverse Use of a Table of Logarithms; that is, given a logarithm, to find the number corresponding to it, (called its antilogarithm) ... [1]

[6] "Exponential Function Reference". www.mathsisfun.com. Retrieved 2020-08-28.

[Goldstein_2006-7] Goldstein, Larry Joel; Lay, David C.; Schneider, David I.; Asmar, Nakhle H. (2006). Brief calculus and its applications (11th ed.). Prentice–Hall. ISBN 978-0-13-191965-5. (467페이지)

[Courant_1996-8] Courant; Robbins (1996). Stewart (ed.). What is Mathematics? An Elementary Approach to Ideas and Methods (2nd revised ed.). Oxford University Press. p. 448. ISBN 978-0-13-191965-5. This natural exponential function is identical with its derivative. This is really the source of all the properties of the exponential function, and the basic reason for its importance in applications…

[:0-9] Weisstein, Eric W. "Exponential Function". mathworld.wolfram.com. Retrieved 2020-08-28.

[Maor-10] Maor, Eli. e: the Story of a Number. p. 156.

[O'Connor_2001-11] O'Connor, John J.; Robertson, Edmund F. (September 2001). "The number e". School of Mathematics and Statistics. University of St Andrews, Scotland. Retrieved 2011-06-13.

[Serway-Moses-Moyer_1989-12] Serway, Raymond A.; Moses, Clement J.; Moyer, Curt A. (1989). Modern Physics. Fort Worth: Harcourt Brace Jovanovich. p. 384. ISBN 0-03-004844-3.

[Simmons_1972-13] Simmons, George F. (1972). Differential Equations with Applications and Historical Notes. New York: McGraw-Hill. p. 15. LCCN 75173716.

[McGrawHill_2007-14] McGraw-Hill Encyclopedia of Science & Technology (10th ed.). New York: McGraw-Hill. 2007. ISBN 978-0-07-144143-8.

[Lorentzen_2008-15] Lorentzen, L.; Waadeland, H. (2008). "A.2.2 The exponential function.". Continued Fractions. Atlantis Studies in Mathematics. Vol. 1. p. 268. doi:10.2991/978-94-91216-37-4. ISBN 978-94-91216-37-4.

[Rudin_1976-16] Rudin, Walter (1976). Principles of Mathematical Analysis. New York: McGraw-Hill. p. 182. ISBN 978-0-07-054235-8.

[Apostol_1974-17] Apostol, Tom M. (1974). Mathematical Analysis (2nd ed.). Reading, Mass.: Addison Wesley. pp. 19. ISBN 978-0-201-00288-1.

[HP48_AUR-18] HP 48G Series – Advanced User's Reference Manual (AUR) (4 ed.). Hewlett-Packard. December 1994 [1993]. HP 00048-90136, 0-88698-01574-2. Retrieved 2015-09-06.

[HP50_AUR-19] HP 50g / 49g+ / 48gII graphing calculator advanced user's reference manual (AUR) (2 ed.). Hewlett-Packard. 2009-07-14 [2005]. HP F2228-90010. Retrieved 2015-10-10. [2]

[Beebe_2017-20] Beebe, Nelson H. F. (2017-08-22). "Chapter 10.2. Exponential near zero". The Mathematical-Function Computation Handbook - Programming Using the MathCW Portable Software Library (1 ed.). Salt Lake City, UT, USA: Springer International Publishing AG. pp. 273–282. doi:10.1007/978-3-319-64110-2. ISBN 978-3-319-64109-6. LCCN 2017947446. S2CID 30244721. Berkeley UNIX 4.3BSD introduced the expm1() function in 1987.

[Beebe_2002-21] Beebe, Nelson H. F. (2002-07-09). "Computation of expm1 = exp(x)−1" (PDF). 1.00. Salt Lake City, Utah, USA: Department of Mathematics, Center for Scientific Computing, University of Utah. Retrieved 2015-11-02.

[23] "Calculus - A limit calculation using Riemann integral".

[1]

[2]

[nb 1]

[nb 2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[nb 3]

[20]

v t 미적분학.
계산 전	이항 정리 오목함수 연속 함수 요인 유한차이 자유 변수 및 한계 변수 함수의 그래프 선형 함수 라디안 롤의 정리 섹트 경사 접선
한계	부정 형식 함수의 한계 단측 한계 시퀀스의 제한 근사순서 제한의 정의(약어, ))-한도의 정의
미적분	파생상품 이차 도함수 편도함수 차동 미분 연산자 평균값 정리 표기법 라이프니츠 표기법 뉴턴 표기법 차별화 규칙 직선성 힘 합 체인 로피탈스 제품. 라이프니츠 장군의 법칙 몫 기타 기술 암묵적 미분 역함수와 미분 로그 도함수 관련 요금 정지점 제1도함수 검정 2차 도함수 극단값 정리 맥시멈과 미니마 기타 응용 프로그램 뉴턴의 방법 테일러의 정리 미분 방정식 상미분 방정식 편미분 방정식 확률 미분 방정식
적분학	반파생적 호 길이 리만 적분 기본 속성 통합 상수 미적분의 기본 정리 적분 기호로 구분 부품별 통합 대체에 의한 통합 삼각형의 오일러 접선 반각 치환 적분에서의 부분 분수 이차 적분 사다리꼴 규칙 볼륨 워셔 방법 셸 방식 적분 방정식 Integro-differential 방정식
벡터 미적분학	파생상품 꼬아 파생적 지향성 격차 그라데이션 Laplacian 기본 정리 선 적분. 그린의 스토크스 가우스의
Multivariable 미적분	발산 정리 기하학 헤시 안 행렬 야코비 행렬과 행렬식 라그랑주 승수 라인 적분 매트릭스 다중 적분 편도함수 표면적분 볼륨 적분 상세 토픽 미분 형식 외부파생상품 일반화 스톡스의 정리 텐서 미적분
시퀀스 및 시리즈	산술-기하수열 시리즈의 종류 교대로 이항 푸리에 기하학 고조파 인피니트 힘 마크로린 테일러 텔레스코핑 수렴 테스트 아벨스 교대 급수 코시 응축 직접 비교 디리클레즈 일체형 한계 비교 비율 뿌리 용어
특수 기능 및 숫자	베르누이 수 e(역학적 상수) 지수 함수 자연 로그 스털링 근사
미적분의 역사	적절성 브룩 테일러 콜린 매클로린 대수의 일반성 고트프리트 빌헬름 라이프니츠 무한소수 미적분학 아이작 뉴턴 플럭션 연속성의 법칙 레온하르트 오일러 플럭션법 역학적 이론의 방법
리스트	차별화 규칙 지수함수의 적분 목록 쌍곡선 함수의 적분 목록 역쌍곡선 함수의 적분 목록 역삼각함수의 적분 목록 비합리함수 적분 목록 로그 함수 적분 목록 합리적인 함수의 적분 목록 삼각함수의 적분 목록 섹트 세컨트 큐브 제한 목록 적분 목록
기타 토픽	복소 미적분 등고선 적분 미분 지오메트리 다지관 곡률 곡선의 표면의 텐서 오일러-마클로린 공식 가브리엘의 뿔 인테그레이션 22/7이 †를 초과하는 증거 레지오몬타누스의 각도 최대화 문제 슈타인메츠 고체

Search

지수 함수

네임스페이스

더

목차

그래프

보다 일반적인 지수 함수와의 관계

형식적 정의

개요

미분 및 미분 방정식

$e$ 에^x 대한 연속 분수

복소 평면

$a$ 와 b가 모두 $복잡한$ 경우의 a의 $계산 b$

행렬과 바나흐 대수

리 대수

초월성

계산

「」를 참조해 주세요.

메모들

레퍼런스

외부 링크

Search

지수 함수

그래프

보다 일반적인 지수 함수와의 관계

형식적 정의

개요

미분 및 미분 방정식

e에x 대한 연속 분수

복소 평면

a와 b가 모두 복잡한 경우의 a의 계산b

행렬과 바나흐 대수

리 대수

초월성

계산

「 」를 참조해 주세요.

메모들

레퍼런스

외부 링크

$e$ 에^x 대한 연속 분수

$a$ 와 b가 모두 $복잡한$ 경우의 a의 $계산 b$

「」를 참조해 주세요.