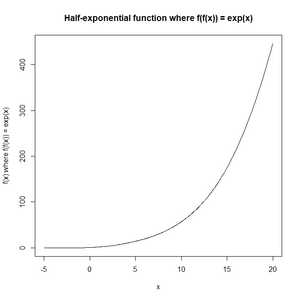
반감수함수

수학에서 반감수 함수는 지수함수의 함수 제곱근, 즉 함수 ƒ 자체로 구성되면 지수함수가 되는 함수 ^[1][2]ƒ:

${\displaystyle f(f(x)=ab^{x}.}$

또 다른 정의는 ƒ이 비감소(non-dreaming)이고 ƒ⁻¹(x^C) ≤ o(log x)일 경우 반감한다는 것이다.C >^[3] 0마다

만약 함수 operations이 표준 산술 연산, 지수, 로그, 실제 값 상수를 사용하여 정의된다면, ƒ(()은 부존재 또는 초존재라는 것이 증명되었다.^[4][5]따라서 Hardy L 기능은 절반 이상일 수 없다.

자기 구성이 서로 같은 지수함수인 함수는 무한히 많다.특히 개방간격$({\displaystyle }$0${\displaystyle }$, ${\displaystyle 1}$ )${\displaystyle ($0,1$)}$의 $모든{\displaystyle }$$$$A${\$displaystyle$ (0,1$)$과${\displaystyle }$[${\displaystyle 0}$${\displaystyle ,}$A$]$에서${\displaystyle }$[${\displaystyle 0}$${\displaystyle }$, ${\displaystyle A}$ ${\displaystyle ]}$ ${\displaystyle[0$$,A$$]}$까지의 모든 연속적인 증가함수에 대해 이 함수의 확장이 있다$.$$f{\displaystyle (f}$( ${\displaystyle x}$)${\displaystyle }$= ${\displaystyle \exp }$ ${\displaystyle }$ ${\displaystyle x}$ ${\displaystyle f(x))$와 같은 실수의$$ f ${\displaystyle f}$$=\exp x}$^[6].함수 $f{\displaystyle }$ ${\displaystyle f}$는 함수 방정식의 고유한 솔루션임

${\displaystyle f(x)={\begin}g(x)&{\mbox{{}in [0,A],\exp(g^{-1})(x))&{\mbox{{{\x\in (A,1]),\\exp(\ln(x))]&#{\mbox{}}{}x\in (1,\inflt)],\\ln(f(\ex)(x))&#mbox{}x\in(-\\\inft,0)&.\\end{case}}$

절반만 만족하는 함수의 예

ƒ이 도처에 연속적인 첫 번째 파생상품을 갖게 되는 간단한 예는 A${\displaystyle }$= 1 ${\displaystyle \frac{2}{}}$ ${\$및 $g$ (${\displaystyle x}$ )${\displaystyle }$= ${\displaystyle 1}$ +${\displaystyle 1\frac{\mathrm{}}{}}$ ${\displaystyle \frac{2}{}}$ ${\$1}:{1}:{1$}}}}}}}}}}}$을 취하는 것이다$.$

${\displaystyle f())={\begin{경우}\log _ᆫ\left(e^{x}와{\tfrac{1}{2}}\right)&,{\mbox{만약}}x\leq -\log _{e}2,\\e^{)}-{\tfrac{1}{2}}&{\mbox{만약}}_{e}2\leq x\leq 0,\\x+{\tfrac{1}{2}}및 -\log,{\mbox{만약}}0\leqx\leq{\tfrac{1}{2}},\\e^{x-1/2}&,{\mbox{만약}}{\tfrac{1}{2}}\leq x\leq 1,\\x{\sqrt{e}}&{\mbox{만약}}1\leqx\leq{\sqrt{e}}.,\\e^{x/{\sqrt{e}}}&{\mbox{if }}{\sqrt {e}}\leq x\leq e,\\x^{\sqrt {e}}&{\mbox{if }}e\leq x\leq e^{\sqrt {e}},\\e^{x^{1/{\sqrt {e}}}}&{\mbox{if }}e^{\sqrt {e}}\leq x\leq e^{e},\ldots \\\end{cases}}}$

다항식과 지수 사이의 "중간" 성장률을 위한 계산 복잡성 이론에 절반의 우수함수가 사용된다.^[2]

참조

외부 링크

• 지수함수는 제곱근을 가지고 있는가?
• 절반 이상의 성장률을 보이는 "폐쇄형" 기능